绝热过程、多方过程
热力学2
共同特点 对外作功 工质吸热增加内能 热量散发
热机的工作原理
上页
下页
AaB为膨胀过程：Aa 为膨胀过程： 为膨胀过程 BbA为压缩过程：-Ab 为压缩过程： 为压缩过程
PA
P A a
净功： 净功：
PB
b
B V
A = Aa Ab
VA
VB
结论：在任何一个循环过程中，系统所作的净功 结论：在任何一个循环过程中， 在数值上等于P-V图上循环曲线所包围的面积。 图上循环曲线所包围的面积。
两边微分得： 两边微分得：
M PdV +VdP = RdT Mmol
(2)
）、（2）式可得： 由（1）、（ ）式可得： ）、（
(Cp CV )PdV RPdV = PdV +VdP = CV CV
CVVdP + Cp PdV = 0
γ=
Cp CV
dP dV +γ =0 P V
两边积分： 两边积分：
M RdT 由理想气体方程： 由理想气体方程： PdV +VdP = Mmol
微分： 微分： PV
n
= 恒量
dP dV +n =0 P V
解方程组： 解方程组：
n γ C= CV n 1
多方过程功的推导： 多方过程功的推导：
PV = PV
n 1 1
V2
n
A = ∫ PdV = ∫
V 1
n 1 1
V2
QAB
V2 M = AAB = RT1 ln Mmol V1
吸热
A
T1=300K B D T2=200K C
QBC = EBC
M 5 = R(T2 T1 ) Mmol 2
理想气体的绝热过程和多方过程
由pγ-1Vγ(γ-1) = C1γ-1，V (γ-1)γTγ = C2γ，得pγ-1T-γ = C1γ-1/C2γ= C3，
这些都是理想气体准静态绝热过程的状态方程。
(容易记忆)
{范例8.7} 理想程？绝热方程是什么？理想气体在多方过程中的p-V有什么特点？
理想气体在准静态绝热过程中有关系dQ = dE+pdV = 0，
因此得
利用理想气体状态方程
两边同时微分得
其中利用了迈耶公式Cp – CV = R。
两式相除可得
根据比热容比的定义
可得
积分得lnp + γlnV = C，
即 pVγ = eC = C1，
除以理想气体方程可得Vγ-1T = C1μ/MR = C2，
下列方程组中的任何一个都能表示理想气体的多方过程
pVn = C1，Vn-1T = C2，pn-1T -n = C3，
C1、C2和C3是不同的常数。
方程组可化为
①当n = 1时，方程组表示等温过程：pV = p0V0，T = T0 。
②当n = 0时，方程组表示等压过程：p = p0，V/T = V0/T0 。
在同一点，绝热过程的斜率大于等温过程的斜率，这是因为在等温过程中，外力做功时压缩体积而不使气体温度升高，从而使压强增加；在绝热过程中，外力做同样多的功还使气体温度升高，因而使压强增加得更快。
分子的自由度越小，比热容比就越大，绝热过程的斜率就越大。
当温度一定时，对理想气体状态方程求微分得pdV + Vdp = 0，因此
对第一个绝热方程求微分得pγVγ-1dV + Vγdp = 0，因此
由于γ > 1，所以有
说明：在p-V图中的同一点，绝热线比等温线陡峭。
§13.3 绝热过程 多方过程
对始、末两平衡态可用气体状态方程。
Chapter 13作. 热者力：学杨基茂础田
§13. 3 绝热过程 多方过程
自由膨胀过程： Q E W E 0
T1 T2
初态： p1V0 RT1
Q0 , W 0
p2 , 2V0 ,T2
☻自由膨胀过程为非准静态过程，绝热方程不适应！ ☻虽为非准静态过程，但仍可应用热力学第一定律；
m k
2
mV
pS2
振动频率：
f
1 T
1
2
pS2
mV
m
dx 平衡位置
(
p
p0
mg S
)
(解毕)
S
(2 f )2
pS2
mV
测量比热比的一种方法。
V
Chapter 13作. 热者力：学杨基茂础田
§13. 3 绝热过程 多方过程
课堂练习 如图，判断acb过程Q、△E、W的正负号。
TV n1 C pn1T n C
p
n
n1 绝
等热 温
n0
定压
o
n
定 体
V
Chapter 13作. 热者力：学杨基茂础田
§13. 3 绝热过程 多方过程
1. 绝热方程：
pV C1 TV 1 C2
p 1T C3
2. 绝热过程的功：
Chapter 13作. 热者力：学杨基茂础田
§13. 3 绝热过程 多方过程
1. 绝热过程的功 WQ：
p
pV C1 p V
p1
pV p1V1 p2V2 C1
WQ
热力学第一定律应用
3 2 V1(
pa
pc )
450R
300
c
b
循环过程中系统吸热
O
1
2 V（10-3m3）
Q1 Qab Qca 600R ln 2 450R 866R
循环过程中系统放热
此循环效率
Q2 Qbc 750R
1
Q2 Q1
1
750R 866R
13.4 00
29
例 逆向斯特林致冷循环的热力学循环原理如图所示
当高温热源的温度T1一定时，理想气体卡诺循环的致 冷系数只取决于T2 。 T2 越低，则致冷系数越小。
26
三、 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机，其效率 相同，都等于理想气体可逆卡诺热机的
效率，即
1 Q2 1 T2
Q1
T1
2. 在相同的高、低温热源之间工作的一切不可逆热机，其
曲线起始于同一点. n可取任意值，不同n对应不同的过程曲线。
16
3种多方过程方程：
理想气体多方过程的定义 ：
pV n C
再根据理想气体的状态方程：
PV RT
以T、V或T、p为独立变量，还可有如下多方过程方程 ：
TV n1 C
p n1 Tn
C
17
二、多方过程摩尔热容
设多方过程的摩尔热容为Cn.m ，则：
dQ Cn,mdT
根据理想气体的热一律，可得：
Cn,m dT CV ,m dT pdV
在两边分别除以 dT
Cn,m
CV ,m
p( dVm dT
)n
CV ,m
p( Vm T
)n
式中的下标n 表示是沿多方指数为n 的路径变化。
物理化学知识点总结
热力学第一定律一、基本概念1、体系和环境（1）、体系和环境体系：作为研究对象的物质及其所在的空间称为体系；环境：体系以外且与体系密切相关的物质及其所在空间称为环境；界面：体系和环境之间存在有界面，界面可以是容器的器壁，也可以是假想的界面，本质上，界面是认为设想的几何面，其中不包含物质，不具备物理和化学性质。
（2）、体系的分类体系和环境之间可以有物质和能量的交换，依据此，可将体系分为敞开体系、封闭体系、隔离体系。
①、敞开体系：体系与环境之间既有能量交换又有物质交换；②、封闭体系：体系与环境之间只有能量交换而无物质交换；③、隔离体系：体系与环境之间既无能量交换也无物质交换。
2、状态和状态函数（1）、状态和状态函数的定义状态：状态是指体系所有性质的总体表现；状态函数：体系的热力学性质称为状态函数。
（2）、状态函数的性质：①、体系的状态一定，状态函数就有定值。
②、状态函数的变化值只取决于始、末状态，与变化的经历无关。
③、状态函数的微分为全微分。
（3）、状态函数的分类。
①、广度性质：体系的广度量与物质的数量成正比，如V，U等，它具有加和性②、强度性质：体系的强度量与物质的数量无关，如T，p等，它不具有加和性。
（4）、热力学平衡态一定条件下，体系中各个相的宏观性质不随时间变化，将体系与环境隔离体系的性质仍不改变的状态。
热力学平衡态应满足如下条件：①、热平衡：体系中的各个部分温度相等，即体系内部处于热平衡，有单一的温度；②、力学平衡：体系内部处于力平衡，有单一的压力；③、相平衡：体系内部各相之间的分布达到平衡，宏观上没有任何一种物质从一个相转移到另一个相；④、化学平衡：体系内部处于化学平衡，宏观上表现为体系的组成不随时间变化。
（5）、状态函数的数学性质若状态函数①、单值性：环形积分等于零，，或可写作全微分性质：③、归一化关系④、复合函数的偏微分，则⑤、偏微商的分离⑥、完全微分3、过程与途径在一定环境条件下，体系发生由始态到终态的变化，则称体系发生了一个热力学过程，（1）、变化过程①、等温过程：体系始态与终态温度相同，且变化过程中温度始终等于环境温度、等于；②、等压过程：体系始态与终态压力相同，且变化过程中压力始终等于环境压力、等于；④、体系由变化到，程，计算其热力学函数，如热力学能、熵变等要设计过程。
大学物理第二十五讲 绝热过程、多方过程、循环过程、卡诺循环
C p ,m
c a，绝热过程。
Qca 0
循环效率
p p2
a
Q2 1 Q1 1 | Qp | QT 8ln 4 1 1/ 7(4 4 )
p1
c
Va Vc
b
Vb V
o
21
例：效率为20%的热机的机械功率为1GW。求: 1.热机 工作时吸热和放热的速率；2.若热机吸热和放热是分 别在5ºC和25ºC的表层和深层的海水间完成的，则吸 热时每秒需要多少海水?（设海水比热 c = 4.18kJ/kgK）
热机
Q2
A
U 0, A Q1 Q2
p
低温热源T2
Q1
p
a
b
Q2
A
V
o
o
d
V1
c
V2
V
10
热机效率
●在循环过程中，热机对外做的静功与吸收的热 量之比。
A Q1 Q2 Q2 1 Q1 Q1 Q1
p
♠效率反映一个循环中吸收的 热量有多少转化为有用的功。 ♠一般情况，不同的工作物质 具有不同的效率。
5. n : V c, Cn CV ,m —等容过程 pV n c p1/ nV c
证明
n V c 等容
8
§12-7 循环过程、卡诺循环
♠热力学理论的发展与热机的研制和使用密切相关。
♠热机就是不断把热量转换为机械功的装置。
♠热机中用于吸热做功的物质叫工作物质。
2.理想气体的绝热过程方程 绝热过程
AQ dU pdV CV ,m dT
pV RT pdV Vdp RdT
状态方程
两式消去 dT 得
22.多方过程+循环过程
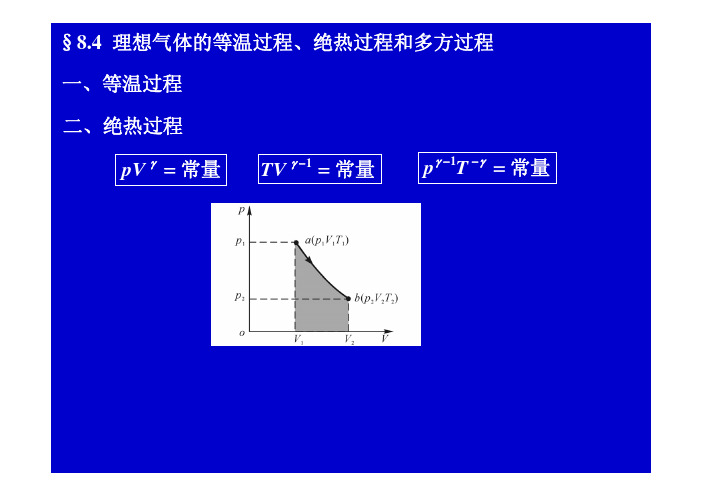
V4 Q2 RT2 ln V3
V3 V2 RT1 ln - RT1 ln Q1 Q2 V1 V4 c V Q1 RT1 ln 2 V1
b c : T1V2 1 T2V3 1 V3 V2 1 1 d a : T2V4 T1V1 V4 V1 Q1 Q2 ＋ 0 从以上诸式还可得到： T1 T2
p1V1 RT1 p1 1.52 10 7 Pa V1 p1V1 p2V2 p2 ( ) p1 0.11.4 p1 6.05 10 5 Pa V2
( pV ) p2V2 p1V1 ... 3751 .5 3751 .5 A 9.38 10 3 J 1 .4 1
显然，系统经历一个循 环内能变化 E 0。
( a ) 正循环 系统对外界作功
( b ) 负循环 外界对系统作功
二、热机效率 利用正循环将吸收的热 量转变为对外作功的机 器叫热机。
设系统在一个循环中吸 热 Q1，放热 Q2 ，对外作净功 A，
A Q1 Q 2 Q1 Q1
叫热机效率。
§8.6 卡诺循环
由两个等温准静态过程 和两个绝热准静态过程 组成的循环 叫卡诺循环。
这是因 如果在一个循环中只有 两个热源，则必为卡诺 循环。 为，除等温和绝热过程 外，其它准静态过程都 需要无限多个温差 无限小的热源。
一、卡诺热机的效率 V2 Q1 Rபைடு நூலகம்1 ln V1
(a b) （ c d）
绝热线较陡。
Q绝热 0 C 绝热 0
A E CV T CV
( pV ) R CV CV ( pV ) ( pV ) ( pV ) 1 R C p CV E CV T 或由热力学第一定律求 解。
13-4 等温、绝热过程,多方过程
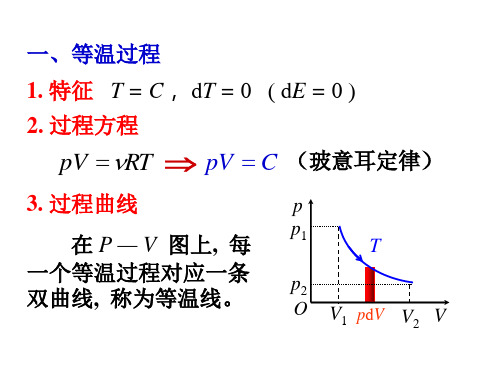
CV dT pdV 0 （ 1 ）
由 pV RT 两边取微分,得
pdV Vdp RdT （2）
由 (1)，(2) 两式，得
CV pdV CVVdp RpdV
(CV R) pdV CVVdp
由 得到
R Cp CV ; Cp / CV
3. 过程曲线 在P - V 图上，每一个绝热过程对应一条 双曲线，称为绝热线。 4. 热量 dQ = 0
5. 内能变化 dE CV dT 6. 绝热功 p2
P p1
Q
（1） 由温度变化引起的
O
V1
pdV V2
V
dA dE CV dT
A CV T
（2） 用功的定义计算
V1 1.41 992K T2 T1 V 320 (16.9) 2
1
终了时的压强为
V1 P2 P 1 V 2
1.013 10 (16.9)
5
1.4
45.110 pa
5
例2 一热机用5.8×10-3Kg的空气作为工质，从 初态1（p1=1.013×105pa , T1=300K）等体加热 到状态2（T2=900K），再经绝热膨胀到状态3 （p3=p1），最后经等压过程又回到1，如图。 假定空气可视为理想气体，且γ=1.4， CV=20.8J/(mol· K)， p 2 Cp=29.09J/(mol· K)摩尔质量 p2 M=29×10-3Kg· mol。试求各 3 过程中气体所做的功及从外 p1 1 O 界吸收的热量。 V1 V3 V
V1
V2
V2
V1
dV V
T V1 pdV V2 V
课件：理想气体的等温过程和绝热过程 多方过程
p
p2
2 T2
Q0
p2' T2' T1
p1
2'
T1
T 常量 1
o V2 V2' V1 10 V1 V
3）对等温过程
T2 753K
W12 CV ,m (T2 T1)
CV ,m 20.44J mol1 K1
W12 4.70104 J
p'2
p1
(V1 V2
)
1.013106 Pa
对绝热过程, 有 p2 p1(VV12 ) 2.55106 Pa
绝热膨胀
p
p1
1( p1,V1,T1)
p2
( p2,V2,T2)
W2
o V1
V2 V
绝热压缩
p
p2
2( p2,V2,T2)
p1
o V2
( p1,V1,T1)
W1
V1 V
§13-4 理想气体的等温过程和绝热过程 多方过程
三 绝热线和等温C
B
o V A V V B V
§13-4 理想气体的等温过程和绝热过程 多方过程
四 多方过程
pVn=C
（1）当n= ( =Cp,m/C V,m)时，为理想气体的绝热方程
pV=C1
（2）当n=1时，为理想气体的等温方程 pV=C2
（3）当n=0时， p=C3为理想气体的等压方程 （4）当n=时， V=C4为理想气体的等体方程
理想气体在多方过程中的W、E、Q
特征 dQ O
p
p1
1( p1,V1,T1)
热一律 dW dE 0
dW dE
p2
( p2,V2,T2)
2
dE CV ,mdT
理想气体多方过程的概念
理想气体多方过程的概念理想气体多方过程是热力学中用来描述理想气体状态变化的一种过程。
在理想气体多方过程中，气体的体积、压强和温度会同时发生变化，且遵循一定的数学关系。
其特点是气体分子之间没有相互作用、无摩擦且无内能损失。
在理想气体多方过程中，可以通过改变气体的体积、压强或温度来实现不同的多方过程，包括等体过程、等压过程、等温过程、绝热过程和绝热指数过程等。
下面将对这些多方过程进行详细介绍。
1. 等体过程（Isochoric Process）：在等体过程中，气体的体积保持不变，即气体分子在容器中自由运动，但体积不发生改变。
在等体过程中，由于体积不变，所以系统对外不做功。
根据理想气体状态方程PV=nRT可知，当体积不变时，温度和压强呈正比关系。
2. 等压过程（Isobaric Process）：在等压过程中，气体的压强保持不变，即气体在容器中扩张或收缩，但压强不发生改变。
在等压过程中，气体对外做功的大小等于压强乘以体积的变化量。
根据理想气体状态方程PV=nRT可知，在等压过程中温度和体积呈正比关系。
3. 等温过程（Isothermal Process）：在等温过程中，气体的温度保持不变，即气体在容器中的温度始终为常数。
在等温过程中，根据理想气体状态方程PV=nRT可知，温度不变意味着压强和体积的乘积也保持不变。
在等温过程中，气体对外做功与体积的改变量和压强的大小有关。
4. 绝热过程（Adiabatic Process）：在绝热过程中，气体与外界没有热量交换，即没有热量进入或离开气体系统。
由于没有热量交换，绝热过程中的气体内能保持不变。
在绝热过程中，气体分子之间发生弹性碰撞，从而使得气体的温度、体积和压强发生变化。
5. 绝热指数过程（Adiabatic Index Process）：绝热指数过程是绝热过程的一种特例，指气体绝热过程中绝热指数（多方反应的比例系数）保持不变。
绝热指数过程常用于描述气体在容器中的膨胀或压缩过程。
绝热过程和多方过程
n R R n CV CV 1 n n 1 n 1 1
13
多方过程曲线与四种常见基本过程曲线 ·
n R Cn n 1 1
14
例 一容器被一可移动、无摩擦且绝热的活塞分割成Ⅰ，Ⅱ 两 部分。容器左端封闭且导热，其它部分绝热。开始时在Ⅰ 、Ⅱ中各有温度为0℃，压强1.013×105 Pa 的刚性双原子分 子的理想气体。两部分的容积均为 36升。现从容器左端缓 慢地对Ⅰ中气体加热，使活塞缓慢地向右移动，直到Ⅱ中 气体的体积变为18升为止。
p
绝热线
pV C1
pV C 2
微分
dp p dV V dp p dV V
A
等温线
由于 ＞ 1 ，所以绝热线要比 等温线陡一些。
O
V
7
3. 绝热过程中功的计算
A ( E 2 E1 ) ν C V (T 2 T1 )
A
V2 V1
pdV
焦耳定律 —— 理想气体的内能仅是其温度的函数
E E (T )
3
6. 理想气体的摩尔热容 CV 、Cp 和内能的计算
1. 定体摩尔热容 CV 和定压摩尔热容 Cp
QV dE dE CV lim ( ) ( )V ΔT 0 Δ T dT dT
dE dV dV C p ( ) p( ) p CV p( ) p =CV R dT dT dT
求 (1) 该过程中气体对外所作的功； (2) 若气体经绝热过程体积膨胀至原来的3倍，气体对外所 作的功。 解 (1) 由等温过程可得
dV A pdV RT V1 V1 V V2 3 RT ln 2 .72 10 J V1
6.4 绝热过程和多方过程
R n γ = CV + = CV 1 n n 1
4.多方过程曲线与四种常见基本过程曲线 多方过程曲线与四种常见基本过程曲线
作业： 作业：P58~64页 页 4，5，19，30 ， ， ，
1 n
2.多方过程曲线 多方过程曲线 方程， 根据多方过程 方程，有
p
pd(V n ) +V ndp = 0
dP p = n dV V
越大， 可见: n 越大， 曲 线越陡 O
n =1 n =γ n >γ
V
3.多方过程中的功﹑内能﹑热量﹑摩尔热容的计算 多方过程中的功﹑内能﹑热量﹑ 多方过程中的功 功
§6.4 绝热过程
多方过程* 多方过程
1、绝热过程的内能增量与对外做功
系统与外界没有热量交换的过程称为绝热过程。 系统与外界没有热量交换的过程称为绝热过程。
(1)绝热过程的特征 (1)绝热过程的特征 绝热过程的
Q = 0, dQ = 0 dQ = dE + pdV = 0
p
dA = pdV = dE
A = E
= 2.2×103 J E =νCV (T2 T ) 1 A = 2.2×103 J
4、气体向真空的绝热自由膨胀过程(非静态过程) 非静态过程)
一绝热容器，左半部有气体，右半部为真空。抽去隔板， 一绝热容器，左半部有气体，右半部为真空。抽去隔板， 气体向真空自由膨胀。 气体向真空自由膨胀。 过程绝热， 过程绝热，
PV = c
n
（1< n < γ
)
绝热过程、等温过程、等压过程、等容过程都可以看成是 绝热过程、等温过程、等压过程、 多方过程的特殊情况。 多方过程的特殊情况。 令 n =1, 则得等温过程； 则得等温过程；
理想气体的等温过程和绝热过程
§6－5 理想气体的等温过程和绝热过程一、等温过程（Isothermal Process ）1．特点：理想气体的温度保持不变，T =const 。
2．过程曲线：在PV 图上是一条双曲线，叫等温线。
3．过程方程：P 1V 1= P 2V 24．内能、功和热量的变化系统经过等温过程，从状态()T V P ，，11变成()T V P ，，22内能 012=-=∆E E E功 ⎰=21V V T PdV W由气体状态方程 RT M m PV ＝得 VRT M m P 1＝ 12ln 121V V RT M m dV V RT M m W V V T ==⎰——用体积表示。
用压强表示为21ln P P RT M m W T = 热量：由热力学第一定律得 1221ln ln V V RT M m P P RT M m Q T ==5．特征：在等压过程中，系统从外界吸收的热量，全部用来对外作功。
注意：对于等温过程，不能定义摩尔热容；如果要定义，则∞=C 。
二、绝热过程（Adiabatic Process ）1．特点：系统与外界没有热量交换的过程，Q =0。
2．内能、功和热量的变化系统经过绝热过程，从状态()11T V P ，，变成()22T V P ，，内能 ()12,12T T C Mm E E E m V -=-=∆ 热量 Q =0由热力学第一定律 0=+∆=W E Q ，得功 ()12,T T C Mm W m V -=－ 用状态参量P ,V 表示，根据状态方程R PV T M m ＝，可知()1 22112211,－＝－γV P V P V P V P R C W mV --= 证明：由定义可知，m V m V m V m V mP C R C R C C C ,,,,,1+=+==γ 因而1,-=γm V C R 故 11,-=γR C m V 因而 12211－γV P V P W -= 3．特征：在绝热过程中，系统对外界所作的功是由于系统内能的减少来完成的。
7-3绝热过程 多方过程
故：
R n γ Cm = Cv = R n 1 (n 1)(γ 1)
讨论 n=0，Cm=Cp， n=1，Cm=∞， ∞ 等压过程； 等压过程； 等温过程; 等温过程;
为一常数
n=γ，Cm=0， 绝热过程； 绝热过程； n= ∞ ，Cm=CV， 等体过程; 等体过程;
多方过程
利用多方方程和状态方程
dA = PdV = Rdt /(n 1) ) 故 dQ = CydT RdT /(n 1 定义 Cm = dQ/ dT 为多方过程的摩尔热容，则 为多方过程的摩尔热容，
R n γ Cm = Cv = R n 1 (n 1)(γ 1)
讨论 n=0，Cm=Cp， n=1，Cm=∞， ∞ 等压过程； 等压过程； 等温过程; 等温过程; n=γ，Cm=0， 绝热过程； 绝热过程； n= ∞ ，Cm=CV， 等体过程; 等体过程; 为一常数
3
绝热过程方程的推导
例题7-3 两个绝热容器 ，体积分别是 1和V2， 用一带有活 两个绝热容器，体积分别是V 例题 塞的管子连起来。打开活塞前， 塞的管子连起来。打开活塞前，第一个容器盛有氮气温度 第二个容器盛有氩气，温度为T 为T1 ；第二个容器盛有氩气，温度为 2 ，试证打开活塞后 混合气体的温度和压强分别是
绝热过程方程的推导
解:打开活塞后，原在第一个容器中的氮气向第二个容器中 打开活塞后， 扩散，氩气则向第一个容器中扩散， 扩散，氩气则向第一个容器中扩散，直到两种气体都在两容 器中均匀分布为止。达到平衡后，氮气的压强变为p 器中均匀分布为止。达到平衡后，氮气的压强变为 1'，氩气 的压强变为p 混合气体的压强为p= 温度均为T 的压强变为 2' ，混合气体的压强为 p1' + p2' ；温度均为 在这个过程中，两种气体相互有能量交换， 。在这个过程中，两种气体相互有能量交换，但由于容器是 绝热的，总体积未变，两种气体组成的系统与外界无能量交 绝热的，总体积未变， 总内能不变， 换，总内能不变，所以
7.3 绝热过程和多方过程
程，而自由膨胀不是准静态过程，但初末状态
是平衡态。
7.3 绝热过程和多方过程
正确解法：
Q E A Q 0, A 0
M
E CV (T2 T1 ) 0
T2 T1（初末温度相同，但不是等温过程）
由状态方程 p0V0 p(2V0 ) 得： p
p0 2
7.3 绝热过程和多方过程
§7.3 绝热过程和多方过程
7.3.1 绝热过程
1. 定义 Q 0 dQ 0
2. 吸热 QQ 0 摩尔热容： CQ 0
3. 内能增量 E M i RT
2
4. 功
AQ
E
M
i 2
RT
i2
i
i 2 ( p2V2
p1V1 )
p2V2 p1V1
1
7.3 绝热过程和多方过程
5. 绝热过程方程
pV M RT dQ dE pdV 0
pdV Vdp M RdT
M
pdV dE CVdT (CV R) pdV CVVdp
7.3 绝热过程和多方过程
C p CV R， C p CV dp dV 0
O
n 1 pV C
n pV C1
n 1
n n
V
7.3 绝热过程和多方过程
·多方过程中的功﹑内能﹑热量﹑摩尔热容的计算
功
A
V2 pdV
V1
V2 V1
p1V1n
dV Vn
1 n 1 ( p1V1 p2V2 )
R
n 1 (T2 T1 )
7-3绝热过程
本节要求： 本节要求： 1、熟记绝热过程的特点和表达式。 、熟记绝热过程的特点和表达式。 2、绝热过程中 Q、A、∆E 的计算要熟练。 、 、 、 的计算要熟练。 3、上一张幻灯片的结论归纳表一定要熟记。 、上一张幻灯片的结论归纳表一定要熟记。
结束
返回
作业 P23：7-4，7-6，7-7。
结束
返回
[例1]设有 氧气，体积为 例 设有 氧气，体积为0.41×10-3 设有8g氧气 m3, 温度为 温度为300K，如氧气作绝热膨胀，膨 ，如氧气作绝热膨胀， 胀后的体积为4.10×10-3 m3。问气体作功 胀后的体积为 多少？如氧气作等温膨胀，膨胀后的体积也 多少？如氧气作等温膨胀， 问这时气体作功多少？ 是4.10×10-3 m3 ，问这时气体作功多少？ M C A = ∆E = T1 ) V ( T2 M mol pV = C
气体若作等温膨胀，所作的功为： 气体若作等温膨胀，所作的功为： M RT V2 A= M mol 1 ln V1 1 = × 8.31×300ln10 4 =1.44×103 (J)
结束
返回
一、绝热过程 M C CP γ = A = ∆ E = M mol V ( T2 T1 ) CV γ 1 γ γ 1 γ pV = C p T = C2 V T = C1 膨胀相同的体积绝热比等温压强下降得快 n p 等 绝 V n p V 温 热 V w p T 二、多方过程 pV = C
返回
泊松方程 (绝热方程 绝热方程) 绝热方程
pV = C
γ
将理想气体状态方程代入上式， 将理想气体状态方程代入上式，并从中 就可以得到另外两个泊松方程： 消去 p 或V 就可以得到另外两个泊松方程： V p
γ γ
理想气体的多方过程方程推导
理想气体的多方过程方程推导理想气体的多方过程方程推导理想气体是一个非常重要的物理模型，而多方过程是其中的一个重要概念。
本文将为大家介绍理想气体的多方过程方程推导。
1.多方过程的定义多方过程是指在系统中，压强、体积、温度这三个物理量不断变化的过程。
在实际应用中，多方过程通常以绝热过程为典型代表。
2.多方过程的方程根据热力学理论，理想气体的多方过程可以表示为以下方程：pV^n=C其中，p表示气体的压强，V表示气体的体积，n表示多方过程中的指数，C为常数（在多方过程中，C的值不断变化）。
3.多方过程方程的推导根据热力学第一定律以及绝热过程的定义，有如下公式：dU=-pdV其中，dU表示气体内能的微小变化。
当气体发生绝热过程时，系统内没有热量的输入和输出，因此dU=0。
代入上式，得到：0=-pdV由于多方过程中三个物理量的变化不止一个，因此我们需要对该方程进行变形。
根据气体状态方程pV=RT，其中R为气体常数，将其代入0=-pdV 式子中，可得：0=-\frac{RT}{V}dV整理后，得到：V^n dV +C=0同时，将多方过程方程式子中的pV^n=C带入上式中，得到：V^n dV+pV^n dV=0因此，可以将上式整理成如下形式：(dV/V)+(n/(1-n))(dp/p)=0将上式积分，得到多方过程方程。
具体地，积分过程如下：∫(dV/V)+(n/(1-n))dp/p=-∫(n/(1-n))即：ln(V)+\frac{n}{1-n}ln(p)=const整理，可得到多方过程方程：pV^n=C4.总结本文介绍了理想气体的多方过程方程推导过程，让大家了解了其数学上的基础。
对于理解理想气体在物理学、化学等科学领域的应用，也有一定的帮助。
绝热过程、多方过程
上页
下页
系统在多方过程中内能的增量：
U CV ,m (T2 T1 )
对外界所做的功：
A
n
1
1 ( P1V1
P2V2
)
从外界吸收的热量
Q Cn,m T2 T1
例题：课本P86例2-7 ；笔记P33-34例2.
上页
下页
W 0 U 0 T2 T1
上页
下页
4. 绝热线与等温线
p
绝热线
A•
等温线
O
V
上页
下页
例1 一定量氮气，其初始温度为300K，压强为
1atm。将其绝热压缩，使其体积变为初始体
积的1/5 .已知CV = 20.8J/mol·K 求：压缩后氮气的压强和温度。
解：
C p，m
CV，m
由 P1V1 P2V2
所以
pV C1 TV 1 C2 P 1T C3
绝热过程方程
上页
下页
3.关于绝热功的计算
除了借助热一律计算功外，对于准静态绝热
过程还可利用泊松公式计算如下：
将泊松公式 PV
P1V1
代入 W
V2
PdV
得
V1
W
V2 V1
PdV
V2 V1
P1V1 V
dV
P1V1
1
1 V2 1
1 V1 1
T1V1 1 T2V2 1
7R 2 5R
7 5
2p2ຫໍສະໝຸດ p1(VV12 )7
1 55
9.52 atm
T2
T1
(V1 V2
)
1
71
300 55
571K
上页
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C n, m
n CV , m n1
（ 1 ）当n 时，V 常量，等容过程， Cn, m CV，m
（ 2 ）当n 0时，P 常量，等压过程， Cn, m C p, m
（ 3 ）当n 1时，PV 常量，等温过程， Cn, m
（ 4 ）当n 时，PV 常量，绝热过程， Cn, m 0
上页 下页
由上可见， 0 C n, m
思考
Cn, m 可能取负值吗？
答案
－ Cn,m
1 n 时，Cnm 0. ①当系统在热力学过程中对 外界所作的功大于它从外界吸收的热量时，系统虽然 吸热但温度反而下降；②外界对系统所作的功大于其 放热的绝对值时，系统虽然放热但温度反而升高。
上页 下页
推导多方过程方程：
对理想气体状态方程求微分，得
PdV VdP RdT
再由热一律的微分形式，得
CV ,m dT Cn,m dT PdV
削去dT,可得 其中
PV 常量
n
n
C p,m C n,m CV , m C n , m
上页 下页
由上式可解得多方过程的摩尔热容
上页 下页
绝热过程中 ，理想气体不吸收热量。 若系统对外界做功，内能减少，温度降低； 若外界对系统做功，内能增加，温度升高。 即，因为 Q 0,
W U nCV ,m (T2 T1 ) nCV ,m (T1 T2 )
所以， W 0 U 0 T2 T1
dU dQ dW
所以：
上页 下页
dQ 0
dW dU
由 pV n RT
微分
pdV n CV，mdT
pdV Vdp n RdT
（ 1）
削去dT, 得 令
C P ,m CV , m
—— 比热比（ 大于1 )
则（1）为：
dp dV 0 p V
pV C
上页 下页
W PdV
V1 V2 V2
P1V1 V
V1
V1
dV
1 P1V1 1 1 P1V1 V1 1 1 1 1 V2 V1 1 V2 1 P1V1 P2V2 1 7 R 7 2Fra bibliotek 5 5 R 2
由 P1V1 P2V2
T1V1
1
V1 p2 p1 ( ) 1 5 9.52 atm V2
V1 1 T2 T1 ( ) 300 5 V2
上页
7 1 5
7 5
T2V2
1
571K
下页
五.多方过程: 理想气体在准静态过程中若热容C保持为常 量，则称为多方过程。前面的四种过程是多方 过程的特例。 n 1.过程方程： PV 常量 , n称为多方指数. n 1 , 等温过程 n , 绝热过程 n 0 , 等压过程 n , 等容过程 一般情况1 n ,多方过程可近似代表气体 内进行的实际过程。
四、绝热过程：
系统始终不与外界交换热量的过程。 良好绝热材料包围的系统发生的过程。 进行得较快，系统来不及和外界交换 热量的过程。
绝热壁
p
上页
下页
1.特点：
Q0
W U n CV ,m (T2 T1 )
2. 过程方程：
PV 常量
—— 泊松方程
推导： 由热一律的微分形式 对绝热过程，
上页 下页
系统在多方过程中内能的增量：
U CV , m (T2 T1 )
对外界所做的功：
1 A ( P1V1 P2V2 ) n1
从外界吸收的热量
Q Cn, m T2 T1
例题：课本P86例2-7 ；笔记P33-34例2.
上页 下页
W 0 U 0 T2 T1
上页 下页
4. 绝热线与等温线
p
绝热线
A
O
等温线
V
上页
下页
例1 一定量氮气，其初始温度为300K，压强为 1atm。将其绝热压缩，使其体积变为初始体 积的1/5 .已知CV = 20.8J/mol· K 求：压缩后氮气的压强和温度。
解：
C p，m CV，m
由 削去P,可得 削去V，可得 所以
PV nRT PV 常量
TV
P
1
常量
常量
1
T
pV C1
TV C2 1 P T C3
1
绝热过程方程
上页
下页
3.关于绝热功的计算 除了借助热一律计算功外，对于准静态绝热 过程还可利用泊松公式计算如下： V2 将泊松公式 PV P1V1 代入 W PdV 得