反比例函数的性质
实际生活中的反比例函数
实际生活中的反比例函数
实际生活中的反比例函数
主要内容：
（一）反比例函数的性质：
反比例函数（k 是常数，）
当时，图象的两个分支分别位于第一、三象限。
在每一个象限内，y 的值随x 值的增大而减小。
当时，图象的两个分支分别位于第二、四象限。
在每一个象限内，y 的值随x 值的增大而增大。
（二）能利用反比例函数及其性质解决实际问题，解释一些生活中的现象，体会数学的价值。
比如：使劲踩气球时，气球为什幺会爆炸？
因为在温度不变的情况下，气球内气体的压强p（Pa）与它的体积V
（m3）的乘积是一个常数k。
即pV＝k（k 为常数，k>0）
在温度不变的情况下，气球内气体的压强p 是气球体积V 的反比例函数，即。
根据反比例函数的性质
当k>0 时，p 随V 的减小而增大。
如果用力踩气球，气球的体积会变小，压强会变大。
当压强大到一定程度时，气球便会爆炸。
【典型例题】
例1. 某一电路中，保持电压U 不变，电流I（安培）与电阻R（欧姆）之。
反比例函数的图像及性质
解题技巧归纳
判断函数类型
通过观察函数表达式，判断其是否为反比例 函数。
利用对称性
利用反比例函数图像的对称性，可以简化一 些复杂问题的求解过程。
分析图像特征
根据 $k$ 的正负判断双曲线所在的象限， 并理解其增减性。
结合其他知识点
在解题过程中，可能需要结合一次函数、二 次函数等其他知识点进行综合分析。
表达式
反比例函数的一般表达式为y=k/x（ k≠0），其中k是比例系数，x是自变 量，y是因变量。
自变量取值范围
由于分母不能为0，因此反比例函数 的自变量x不能为0，即x的取值范围 是x≠0。
反比例函数的定义域是除去使分母为0 的点以外的所有实数。
函数值变化规律
当x>0时，随着x的增大，y的值逐渐减小，但永远不会等于0；当x<0时 ，随着x的减小，y的值逐渐增大，也永远不会等于0。
综合应用探讨
解决问题类型
反比例函数和一次函数在解决实际问题时具有广泛的应用。例如，反比例函数可用于描述速度、密度等物理量之间的 关系；一次函数则可用于描述线性增长或下降的问题，如直线运动、均匀变化等。
建模方法
在建立反比例函数和一次函数的模型时，需要根据问题的实际背景和条件，确定函数的表达式和参数。通过比较和分 析不同函数的图像和性质，可以选择最合适的函数模型来描述问题的本质和规律。
反比例函数的图像及性质
汇报人：XXX 2024-01-22
contents
目录
• 反比例函数基本概念 • 反比例函数图像特征 • 反比例函数性质分析 • 反比例函数应用举例 • 反比例函数与一次函数比较 • 总结回顾与拓展延伸
01
反比例函数基本概念
定义与表达式
反比例函数图象的特征及性质
反比例函数图象的特征及性质： 反比例函数x k y =(k ≠0)的图象是由两个分支组成的曲线。
当0>k时，图象在一、三象限，在每一象限内，y 随x 的增大而减小；当0<k 时，图象在二、四象限，在每一象限内 ，y 随x 的增大而增大。
反比例函数xk y =(k ≠0)的图象关于直角坐标系的原点成中心对称。
例1．（补充）已知反比例函数32)1(--=m x m y 的图象在第二、四象限，求m 值，并指出在每个象限内y 随x 的变化情况？1．已知反比例函数x ky -=3，分别根据下列条件求出字母k 的取值范围（1）函数图象位于第一、三象限（2）在第二象限内，y 随x 的增大而增大2．函数y ＝－ax ＋a 与x ay -=（a ≠0）在同一坐标系中的图象可能是（ ）1．若函数x m y )12(-=与xm y -=3的图象交于第一、三象限，则m 的取值范围是 2．反比例函数xy 2-=，当x ＝－2时，y ＝ ；当x ＜－2时；y 的取值范围是 ； 当x ＞－2时；y 的取值范围是 3． 已知反比例函数y a x a =--()226，当x >0时，y 随x 的增大而增大，求函数关系式例2．（补充）如图，过反比例函数xy =（x ＞0）的图象上任意两点A 、B 分别作x 轴的垂线，垂足分别为C 、D ，连接OA 、OB ，设△AOC 和△BOD的面积分别是S 1、S 2，比较它们的大小，可得（ ）（A ）S 1＞S 2 （B ）S 1＝S 2（C ）S 1＜S 2 （D ）大小关系不能确定3．在平面直角坐标系内，过反比例函数xk y =（k ＞0）的图象上的一点分别作x 轴、y 轴的垂线段，与x 轴、y 轴所围成的矩形面积是6，则函数解析式为4．5．。
反比例函数性质
反比例函数性质
一般地，如果两个变量x、y之间的关系可以表示成y=k/x (k为常数，k≠0)的形式，那么称y是x的反比例函数。
因为y=k/x是一个分式，所以自变量X的取值范围是X≠0。
而y=k/x有时也被写成xy=k或y=k·x^（-1）。
反比例函数性质
1.当k>0时，图象分别位于第一、三象限；当k<0时，图象分别位于第二、四象限.
2.当k>0时.在同一个象限内，y随x的增大而减小；当k<0时，在同一个象限，y随x的增大而增大.
k>0时，函数在x<0上为减函数、在x>0上同为减函数；k<0时，函数在x<0上为增函数、在x>0上同为增函数。
定义域为x≠0；值域为y≠0。
3.因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与x轴相交，也不可能与y轴相交.反比例函数图像会无限接近于坐标轴但不相交（坐标轴是反比例函数图像的渐近线）
4.∣k∣越大，抛物线开口越大；∣k∣越小，抛物线开口越小。
反比例函数
5. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2则S1＝S2 ,且等于|k|.
6.反比例函数的图象是双曲线，有两支，既是轴对称图形，对称轴是y=x或y=-x，又是中心对称图形，对称中心是坐标原点.
7.反比例函数图像中，|k|的值越大，图像越远离坐标轴.。
反比例函数反比例函数的图象与性质
2023-11-06
contents
目录
• 反比例函数概述 • 反比例函数的图象 • 反比例函数的性质 • 反比例函数的应用 • 反比例函数的扩展知识
01
反比例函数概述
反比例函数的定义
反比例函数定义
一般地，形如y=k/x（k为常数，k≠0）的函数称为反比例函数 。
反比例函数的积分特性
反比例函数在区间(-∞,0)和(0,+∞) 上的积分等于常数k。
VS
反比例函数在区间(-∞,x)和(x,+∞)上 的积分等于常数k乘以x。
04
反比例函数的应用
用反比例函数解决实际问题
电力分布
在电力分布问题中，常常 需要使用反比例函数来计 算电力的分布情况，以便 合理规划电力设施。
反比例函数的定义域和值域
定义域为{x|x≠0}，值域为{y|y≠0}。
反比例函数的单调性
在区间(-∞,0)和(0,∞)上单调递减。
反比例函数的基本形式
反比例函数的基本形式
01
一般地，形如y=k/x（k为常数，k≠0）的函数称为反比例函数。Biblioteka 反比例函数的解析式02
反比例函数通常被表示为y = k / x的形式，其中k是常数且不
热传导
在热传导中，可以使用反比例函数 来描述热量在介质中的传导规律。
在几何中的应用
圆的面积
在计算圆的面积时，可以使用 反比例函数来描述圆的面积与
半径之间的关系。
球的体积
在计算球的体积时，可以使用 反比例函数来描述球的体积与
半径之间的关系。
光线反射
在光线反射问题中，可以使用 反比例函数来描述光线反射的
反比例函数图像和性质ppt课件
反比例函数的定义域和值域
定义域
反比例函数的定义域是 x ≠ 0 的所有实数，即 x 可以取任何实数值，除了 0。
值域
反比例函数的值域是除了 y = 0 以外的所有实数，即 y 可以取任何实数值，但 永远不会等于 0。
02
反比例函数的性质
反比例函数的单调性
总结词
反比例函数在其定义域内并非单 调，但在各自象限内具有单调性。
表达式形式
反比例函数的一般形式为 y = k/x (k ≠ 0)，其中 x 和 y 是自变量和 因变量，k 是常数。
反比例函数图像的绘制
图像绘制方法
反比例函数的图像通常在二维坐标系 中绘制，通过选择不同的 k 值，可 以绘制出不同的反比例函数图像。
图像特性
反比例函数的图像位于 x 轴和 y 轴的 有限区域，呈现出双曲线的形状，随 着 x 的增大或减小，y 的值会无限接 近于 0 但永远不会等于 0。
积分是数学中计算面积和体积的方法，分为定积分和不定积分。
反比例函数的不定积分
反比例函数y=1/x的不定积分为ln|x|+C（C为常数），这表明反比例函数可以通过对ln|x|进行不定积分得 到。
反比例函数与复数的关系
复数的概念
复数是实数和虚数的组合，形式为a+bi（a,b为实数）。
反比例函数在复数域的表现
投资回报
投资回报与投资风险成反比，即投资风险越大，投资回报越小；反之亦然。
反比例函数在日常生活中的应用
药物剂量
在药物治疗过程中，药物剂量与药效 成反比关系，即当药物剂量增加时， 药效可能会减弱。
体育训练
在体育训练中，训练强度与训练效果 成反比关系，即当训练强度增加时， 训练效果可能会减弱。
反比例函数的图象与性质定
奇偶性
反比例函数是奇函数，因为对于所 有 x，都有 f(-x) = -f(x)。
无界性
由于反比例函数的值域为 y ≠ 0 和 y ≠ -∞，因此其图象在 x = 0 处无 界。
反比例函数的性质
01
02
03
分母不为零
反比例函数的分母不能为 零，因此其定义域为 x ≠ 0。
无界性
反比例函数的值域为 y ≠ 0 和 y ≠ -∞，因此其图象 在 x = 0 处无界。
当$x<0$时，反比例函数的图象位于 第三象限，与直线$y=kx+b$相交于 一点，这一点也是它们的切点。
与二次函数的关系
二次函数是形如 $y=ax^2+bx+c$的函数，其 中$a, b, c$是常数且$a neq 0$
。
反比例函数的图象是一个双曲 线，分布在第一和第三象限。
二次函数的图象是一个抛物线 ，可以开口向上或向下。
反比例函数的图象与性质
目 录
• 反比例函数概述 • 反比例函数的图象特点 • 反比例函数的性质分析 • 反比例函数的应用 • 反比例函数与其他函数的关系 • 反比例函数的扩展知识
01 反比例函数概述
反比例函数的定义
反比例函数定义
反比例函数的值域
反比例函数是一种数学函数，其定义 为 f(x) = k/x，其中 k 是常数且 k ≠ 0。
磁场强度与电流
在电磁学中，磁场强度与电流之间的关系可以用反比例函数 描述，通过分析反比例函数的特性，可以研究电磁感应和电 磁波的传播。
与其他数学知识的结合
代数方程
反比例函数可以与其他代数方程 结合，用于解决代数问题，例如 求解代数方程的根或解决代数不 等式问题。
反比例函数图像与性质
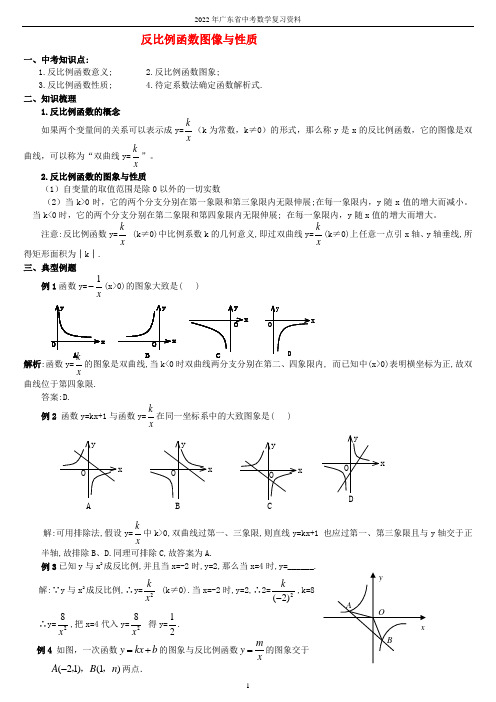
例1函数y= (x>0)的图象大致是( )
解析:函数y= 的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内,而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.
答案:D.
例2函数y=kx+1与函数y= 在同一坐标系中的大致图象是( )
解:可用排除法,假设y= 中k>0,双曲线过第一、三象限,则直线y=kx+1也应过第一、第三象限且与y轴交于正半轴,故排除B、D.同理可排除C,故答案为A.
A.y1<0<y3B.y3<0<y1;C.y2<y1<y3D.y3<y1<y2
5.已知一次函数y=x+m与反比例函数y= (m≠-1)的图象在第一象限内的交点为P(x0,3).
(1)求x0的值;
(2)求一次函数和反比例函数的解析式.
6.如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (m≠0)的图象在第一象限交于C点, CD垂直于x轴,垂足为D.若OA=OB=OD=1,
7.已知反比例函数 图象与直线 和 的图象过同一点.
（1）求这个反比例函数的解析式；
（2）当 ＞0时，这个反比例函数值 随 的增大如何变化？
8.如图，已知A(-4，2)、B(n，-4)是一次函数 的图象与反比例函数 的图象的两个交点.
(1)求此反比例函数和一次函数的解析式；
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
（1）自变量的取值范围是除0以外的一切实数
（2）当k>0时，它的两个分支分别在第一象限和第三象限内无限伸展;在每一象限内，y随x值的增大而减小。当k<0时，它的两个分支分别在第二象限和第四象限内无限伸展;在每一象限内，y随x值的增大而增大。
第六章反比例函数的概念及基本性质
反比例函数的概念及基本性质教学目标掌握反比例函数的概念、性质、图象，熟悉反比例函数与一次函数的关系 重难点分析重点：1、反比例函数的概念； 2、反比例函数的图形特征。
难点：1、求反比例函数的解析式； 2、根据图形特征比较大小。
知识点梳理1、反比例函数的概念：一般地，如果两个变量x ，y 之间的关系可以表示成xk y =(k 为常数，0≠k )的形式，那么称y 是x 的反比例函数。
一般形式：xk y = (k 为常数，)注意：（1）等号左边是函数y ，等号右边是一个分式，分子是不为零的常数k(也叫做比例系数k)，分母中含有自变量x ，且x 的指数是1，若写成1-=kx y 。
则x 的指数是－1。
（2）比例系数是反比例函数定义的一个重要组成部分。
（3）自变量x 的取值范围是的一切实数。
（4）函数y 的取值范围也是一切非零实数。
2、待定系数法求反比例函数的解析式。
3、反比例函数图象（双曲线）的画法：（1）列表；（2）描点；（3）连线。
4、反比例函数的性质：（1）当0>k 时，函数的图象在第一、三象限，在每个象限内，曲线从左向右下降，也就是说，在每个象限内，y 随x 的增大而减小；（2）当0<k 时，函数的图象在第二、四象限，在每个象限内，曲线从左向右上升．也就是说，在每个象限内，随的增大而增大。
知识点1：反比例函数的概念【例1】判断下列说法是否正确1．如果y 是x 的反比例函数，那么当x 增大时，y 就减小 【 】 2．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数 【 】 3．如果一个函数不是正比例函数，就是反比例函数 【 】 4．y 与2x 成反比例时，y 与x 并不成反比例 【 】 5．y 与x 2成反比例时，y 与x 也成反比例 【 】 6．已知y 与x 成反比例，又知当2=x 时，3=y ，则y 与x 的函数关系式是6xy = 【 】 【随堂练习】1、已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是h =__________，这时h 是a 的__________。
反比例函数的概念与性质
反比例函数在经济学中的应用
描述供求关系：反比例函数可以用来描述经济学中的供求关系，帮助分析 市场上的供需变化。
解释边际效用递减规律：反比例函数可以解释经济学中的边际效用递减规 律，即随着消费量的增加，单位消费所带来的效用逐渐减少。
反比例函数与二次函数的联系与区别
反比例函数与二次函数都是非线性函数，具有不同的函数图像和性质。
反比例函数的图像位于x轴和y轴之间，而二次函数的图像可能位于x轴上 方或下方。
反比例函数的导数在x=0处不存在，而二次函数的导数在x=0处存在。
反比例函数在x>0时单调递减，在x<0时单调递增，而二次函数在x<0时 单调递减，在x>0时单调递增。
反比例函数与幂函数的联系与区别
反比例函数与幂函数在形式上的联系：两者都是形如y=k/x（k为常数）的函数，具有反比例关 系的函数形式。
反比例函数与幂函数在性质上的区别：反比例函数的图像分布在第一、三象限，而幂函数的图 像根据幂次的不同分布在各象限；反比例函数的图像是关于原点对称的，而幂函数的图像则关 于：双曲 线，位于两轴之 间
图像位置：取决于 比例常数k，k>0 时位于一三象限， k<0时位于二四象 限
图像变化趋势： 随着x的增大或减 小，y值逐渐减小 或增大
图像与坐标轴的 交点：原点 O(0,0)和点(k,0)
反比例函数的解析式
定义：形如 y = k/x (k为常数且k≠0) 的函数称为反比例函数 解析式：y = k/x (k为常数且k≠0) 图像：双曲线，位于x轴和y轴的两侧 性质：当k>0时，图像位于第一、三象限；当k<0时，图像位于第二、四象限
反比例函数的图像和性质课件
反比例函数的图像和性质课件反比例函数是数学中的一种重要函数类型，它的图像和性质在数学学习中占据着重要的地位。
本文将从图像和性质两个方面来探讨反比例函数的特点和应用。
一、反比例函数的图像反比例函数的图像呈现出一种特殊的形状，即一条经过原点的斜线。
具体来说，反比例函数的图像是一条从左上方向右下方倾斜的直线。
这是因为反比例函数的定义域为实数集，而值域为除了0以外的实数集，因此函数的图像必然不会经过y轴上的任何点。
通过观察反比例函数的图像，我们可以发现，随着自变量的增大，函数的值会逐渐减小。
这是因为反比例函数的定义中包含有除法运算，而除法运算会使得结果随着被除数的增大而减小。
因此，反比例函数的图像呈现出一种渐近线的特点，即当自变量趋近于正无穷大时，函数的值趋近于0。
二、反比例函数的性质除了图像的特点之外，反比例函数还具有一些重要的性质。
首先，反比例函数的定义域为实数集，但值域为除了0以外的实数集。
这是因为在反比例函数中，除数不能为0，否则会导致无意义的结果。
因此，在计算反比例函数的值时，我们需要注意避免除以0的情况。
其次，反比例函数的导数为常数。
这是因为反比例函数的定义可以表示为y=k/x的形式，其中k为常数。
对该函数进行求导，我们可以得到dy/dx=-k/x^2。
可以看出，反比例函数的导数与自变量x无关，只与常数k有关。
这也意味着反比例函数的斜率在整个定义域上保持不变。
另外，反比例函数还具有一个重要的性质，即函数值的乘积为常数。
具体来说，对于反比例函数y=k/x，当x1和x2为定义域中的两个不同的实数时，有y1*y2=k。
这个性质在实际问题中有着广泛的应用，例如在电路中，电阻和电流的关系就符合反比例函数的性质。
三、反比例函数的应用反比例函数在实际问题中有着广泛的应用。
例如，在物理学中，牛顿第二定律中描述了物体的加速度与施加在物体上的力成反比的关系。
根据牛顿第二定律的表达式F=ma，我们可以得到物体的加速度a与作用力F的关系为a=k/F，其中k为常数。
数学反比例函数的图象及性质知识点归纳
数学反比例函数的图象及性质知识点归纳
数学反比例函数的图象及性质知识点归纳
店铺您整理了数学反比例函数的图象及性质知识点归纳：反比例函数的图象及性质，希望帮助您提供多想法。
和店铺一起期待学期的学习吧，加油哦!
反比例函数y=k/x的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限。
它们关于原点对称、反比例函数的图象与x轴、y轴都没有交点，即双曲线的'两个分支无限接近坐标轴，但永远不与坐标轴相交。
画反比例函数的图象时要注意的问题：
（1）画反比例函数图象的方法是描点法;
（2）画反比例函数图象要注意自变量的取值范围是k≠0，因此不能把两个分支连接起来。
k≠0
（3）由于在反比例函数中，x和y的值都不能为0，所以画出的双曲线的两个分支要分别体现出无限的接近坐标轴，但永远不能达到x 轴和y轴的变化趋势。
反比例函数的性质：
y=k/x（k≠0）的变形形式为xy=k（常数）所以：
（1）其图象的位置是：
当k﹥0时，x、y同号，图象在第一、三象限;
当k﹤0时，x、y异号，图象在第二、四象限。
（2）若点（m，n）在反比例函数y=k/x（k≠0）的图象上，则点（—m，—n）也在此图象上，故反比例函数的图象关于原点对称。
（3）当k﹥0时，在每个象限内，y随x的增大而减小;
当k﹤0时，在每个象限内，y随x的增大而增大;
【数学反比例函数的图象及性质知识点归纳】。
反比例函数的图象与性质
第17讲 反比例函数的图象与性质考点·方法·破译1．反比例函数的定义：形如k y x=（或1y kx -=，k ≠0）,y 叫做x 的反比例函数. 2．反比例函数的图象特征：反比例函数的图象是双曲线，关于y ＝x 或y ＝－x 轴对称，关于原点O 成中心对称，当k ＞0时，图象的两支分别在第一、三象限，当k ＜0时，图象的两支分别在第二、四象限，3．反比例函数的性质：当k ＞0时，在每个象限内，y 随x 增大而减小；当k ＜0时，在每个象限内，y 随x 增大而增大.经典·考题·赏析【例１】（西宁）已知函数ky x=-中，x ＞0时，y 随x 增大而增大，则y ＝kx －k 的大致图象为（ ）k ＞0，而一 次A 01．已知反比例函数a y x=（a ≠0）的图象，在每一象限内，y 的值随着x 值增大而减小，则一次函数y ＝－ax ＋a 的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 02．（龙岩）函数y ＝x ＋m 与my x=（m ≠0）在同一象限内的图象可以是（ 03（2，y 1随着x 其中正确结论的序号是 . 【例2】如图，A 、B 分别是反比例函数10y x =，6y x=图象上的点，过点A 、B 作x 轴的垂线，垂足分别为C 、D ，连接OB 、OA ，OA 交BD于E 点，△BOE 的面积为S 1，四边形ACDE 的面积为S 2，则S 2－S 1＝ .ABCDABC D【解法指导】在反比例函数kyx=中，k的几何意义为：中122121106()()22222ODE OBEk kS S S S S S∆∆-=+-+=-=-=【变式题组】01．（宁波）如图，正方形ABOC的边长为2，反比例函数kyx=过点A，则k的值是（）A．2 B．－2 C．4 D．－402．（兰州）如图，在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线3yx=（x＞0）上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小03．（牡丹江）如图，点A、B是双曲线3yx=上的点，分经过A、B两点向x轴、y轴作垂线，若S阴影＝1，则S1＋S2＝.04．（河池）如图，A、B是函数2yx=的图象上关于原点对称的任意两点，BC∥x轴，AC∥y 轴，△ABC的面积记为S，则（）A．S＝2 B．S＝4 C．2＜S＜4 D．S＞405．（泰安）如图，双曲线kyx=（k＞0）经过矩形OABC的边BC的中点E，交AB于点D，若梯形ODBC的面积为3，则双曲线的解析式为（）A．1yx=B．2yx=C．3yx=D．6yx=【例3】（成都）如图，一次函数y＝kx＋b的图象与反比例函数myx=的图象交于点A（－2，1），B（1，n）两点⑴试确定上述反比例函数和一次函数的表达式；第1题图第2题图第3题图第4题图第5题图⑵求△AOB 的面积.【解法指导】利用割补法求图形面积.解：⑴∵点A （－2，1）在反比例函数my x=的图象上， ∴m ＝(－2)×1＝－2，∴反比例函数的表达式为2y x=-.∵点 B （1，n ）也在反比例函数2y x=-图象上，∴n ＝－2，即B （1，－2）把点A （－2，1）点B （1，－2）代入一次函数y ＝kx ＋b 中，得212k b k b -+=⎧⎨+=-⎩ 解得11k b =-⎧⎨=-⎩ ∴一次函数的表达式为y ＝－x －1． ⑵在y ＝－x －1中，当y ＝0时，得x ＝－1，∴直线y ＝－x －1与x 轴的交点为C （－1，0），∵线段OC 将△AOB 分成△AOC 和△BOC ，∴1113111212222AOB AOC BOC S S S ∆∆∆=+=⨯⨯+⨯⨯=+=.【变式题组】01．（徐州）如图，已知A (n ,－2),B (1,4)是一次函数y ＝kx ＋b 的图象和反比例函数my x=的图象的两个交点，直线AB 与y 轴交于点C ．⑴求反比例函数和一次函数的关系式； ⑵求△AOC 的面积； ⑶求不等式kx ＋b mx-＜0的解集（直接写出答案）02．已知反比例函数112k y x=的图象与一次函数22y k x b =+的图象交于A 、B 点，A (1，n )，B (12-，－2). ⑴求两函数的解析式；⑵在x 轴上是否存在点P ，使△AOP 为等腰三角形？若存在，请你直接写出P 点的坐标；若不存在，说明理由. ⑶求AOB △S ；⑷若y 1＞y 2，求x 的取值范围.03．如图，A 是反比例函数1ky x=（x ＞0）上一点，AB ⊥x 轴，C 是OB 的中点，一次函数y 2＝ax ＋b 的图象经过点A 、C 两点，并交y 轴为D （0，－2），AOD S ∆＝4. ⑴求两函数的解析式；⑵在y 轴右侧，若y 1＞y 2时，求x 的取值范围.04．如图，Rt △ABO 的顶点A 是双曲线ky x=与直线y ＝－x －(k ＋1)在第二象限的交点，AB ⊥x 轴于B ，32ABO S ∆=. ⑴求这两个函数的解析式； ⑵求A 、C 两点的坐标；⑶若P 是y 轴上一动点，5PAC S ∆=，求点P 的坐标.【例4】（咸宁）两个反比例函数k y x =和1y x=在第一象限内的图象如图所示，点P 在k y x =的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x=的图象于点B ，当点P 在ky x=的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点.其中一定正确的是 （把你认为正确的序号都填上）【解法指导】∵A 、B 两点在1y x=的图象上，根 据反比例函数ky x=中k 的几何意义可知12ODB OAC S S ∆∆==，因而①正确；∵1ODB OAC PDOC PAOB S S S S k ∆∆=--=-矩形四边形，当k 不变时，若P 变动，而四边形PAOB 的面积不变．因1x =而是②正确；若设P （t ,k t ），则A （t ,1t），B （,t k k t ），∴PA ＝11k k t t t --=，PB ＝t t k -.若PA ＝PB ，则有1(1)k t k t k--=.∵k ≠1,∴2t k =,∵t ＞0,t =,∴当P时，有PA ＝PB ，并不是PA 与PB 始终相等，因而③不正确；当A 为PC 的中点时，OAC OPA OBD S S S ∆∆∆==，OPC ODP S S ∆∆=，∴ODB OPB S S ∆∆=，∴DB ＝PB ，因而④正确；故填①，②．④.【变式题组】01．（武汉）如图，已知双曲线ky x=（k ＞0）经过矩形OABC 的边AB 的中点F ，交BC 于点E ，且四边形OEBF 的面积为2，则k ＝ . 02．如图，矩形ABCD 对角线BD 中点E 与A 都在反比例函数ky x=的图象上，且3ABCD S =矩形，则k ＝ .03．如图，P 为x 轴正半轴上一点，过点P 作x 轴的垂线，交函数1y x =（x ＞0）的图象于点A ，交函数4y x=（x ＞0）的图象于点B ，过点B 作x 轴的平行线，交1y x=（x ＞0）于点C ，连接AC ，当点P 的坐标为（t ，0）时，△ABC 的面积是否随t 的变化而变化？ 04．函数2y x =（x ＞0）与8y x=（x ＞0）的图象如图所示，直线x ＝ t （t ＞0）分别与两个函数图象交于A 、C 两点，经过A 、C 分别作x 轴的平行线，交两个函数图象于B 、D两点，探索线段AB 与CD 的比值是否与t 有关，请说明理由.第1题图第3题图05．如图，梯形AOBC的顶点A、C有反比例函数的图象上，OA∥BC，上底OA在直线y＝x上，下底BC交x轴于E（2，0），求四边形AOEC的面积.演练巩固·反馈提高01．（恩施自治州）如图，一次函数y1＝x－1与反比例函数22yx=的图象点A（2，1）、B （－1，－2），则使y1＞y2的x的取值范围是（）A．x＞2 B．x＞2或－1＜x＜0C．－1＜x＜2 D．x＞2或x＜－102．（常州）若反比例函数1kyx-=的图象在其每个象限内，y随x的增大而减小，则k的值可以是（）A．－1 B．3 C．0 D．－303．（荆州）如图，直线l是经过点（1，0）且与y轴平行的直线，Rt△ABC中直角边AC＝4，BC＝3，将BC边在直线l上滑动，使A、B在函数kyx=的图象上，那么k的值是（）A．3 B．6 C．12 D．15 404．（丽水）点P在反比例函数1yx=（x＞0）的图象上，且横坐标为2，若将点P先向右第4题图平移两个单位，再向上平移一个单位后所得点为P /，则在第一象限内，经过点P /的反比例函数图象的解析式是（ ） A ． 5y x =-（x ＞0） B ． 5y x =（x ＞0） C ． 6y x =-（x ＞0） D ． 6y x=（x ＞0）05．（铁岭）如图所示，反比例函数y 1与正比例函数y 2的图象的一个交点坐标是A （2，1），若y 2＞y 1＞0，则x 的取值范围在数轴上表示为（ ）06．（泰安）函数1y x x=+图象如图所示，下列对该函数性质的论断不可能正确的是（ ） A ．该函数的图象是中心对称图形 B ．当x ＞0时，该函数在x ＝1时取得上值2C ．在每个象限内，y 随x 的增大而减小D ． y 的值不可能为1 07．（芜湖）在平面直角坐标系xOy 中，直线y ＝x 向上平移一个单位长度得到直线l , 直线l与反比例函数ky x=的图象的一个交点为A （a ,2）则k 的值等于 . 08．（广安）如图，在反比例函数4y x=-（x ＞0）的图象上有三点P 1、P 2、P 3，它们的横坐标依次为1，2，3，分别过这3个点作x 轴、y 轴的垂线，设斩中阴影部分的面积依次为S 1、S 2、S 3，则S 1＋S 2＋S 3＝ .09．（十堰）已知函数y ＝－x ＋1的图象与x 轴、y 轴分别交于点C 、B ，与双曲线ky x=交于点A 、D ，若AB ＋CD ＝BC ，则k 的值为 . 10．（遵义）如图，在平面直角坐标系中，函数ky x=（x ＞0，常数k ＞0）的图象经过点A （1，2），B （m ,n ）,(m ＞1),过点B 作y 轴的垂线，垂足为C ，若△ABC 的面积为2，则点B 的坐标为 .11．如图，点P 的坐标为（2，32），过点P 作x 轴的平行线交y 01 2 0 1 2 0 1 2 0 1 2 A B CD y x A (2,1) 0 1 2 1 Y 1 Y 2第5题图B l C1 O yx A 第3题图y x 0 1 －2 －1 第6题图2 y x0 1 2 3 第8题图P 1 P 2 P 3轴于点A，交双曲线kyx=（x＞0）于点N，作PM⊥AN，交双曲线于kyx=（x＞0）于点M．连接AM，已知PN＝4，⑴求k的值；⑵求△APM的面积.12．如图，反比例函数kyx=的图象与直线y＝x＋m在第一象限交于点P（6，2），A、B为直线上的两点，点A的横坐标为2，点B的横坐标3，D、C 为反比例函数图象上的两点，且AD、BC平行于y轴，⑴直接写出k、m的值；⑵求梯形ABCD的面积.13．如图，已知双曲线kyx=（x＞0）经过Rt△OAB斜边的中点D，与直角边AB相交于点C，若△OBC的面积为3，求k的值.14．如图，Rt△ABC的直角边BC在x轴的正半轴上，斜边AC边上的中线BD反向延长交y轴负半轴于E，双曲线kyx=（x＞0）的图象经过点A，若BECS∆＝8，求k的值.15．如图，Rt△ABC中，∠BAC＝90°，BC所在直线的解析式为42033y x=-+，AC＝3，若AB的D在双曲线ayx=（x＞0）上，将三角形向左平移，当点B 落在双曲线上时，求三角形平移的距离.16．（荆州）如图，D 为反比例函数ky x=（k ＜0）图象上一点，过D 作DC ⊥y 轴于C ，DE ⊥x 轴于E ，一次函数y x m =-+与323y x =-+的图象都经过点C ，与x 轴分别交于A 、B 两点，若梯形DCAE 有面积为4，求k 的值.17．（四川广安）如图，一次函数y kx b =+的图象与反比例函数my x=的图象相交于点A （－1，2）、点B （－4，n ）⑴求一次函数和反比例函数的解析式； ⑵求△AOB 的面积.培优升级·奥赛检测01．如图，直线l 与反比例函数m y x =与ny x=（m ＞n ＞0）的图象分别交于点A 、B ，且直线l ∥x 轴，连接PA 、PB ，小芳与小丽同学针对△PAB 面积的讨论，有以下两种意见：小芳：点P 在x 轴上移动时，△PAB 的面积总保持不变； 小丽：当直线l 上下平移时，△PAB 的面积总保持不变； 那么，你认为她们的说法中（ ）A ．只有小芳正确B ．只有小丽正确C ．两人都正确D ．两人都不正确02．（南昌市八年级竞赛题）在函数21a y x+=-（a 为常数）的图象上有三点：（－1，y 1）,(21,4y -),( 31,2y )则函数值y 1、y 2、y 3的大小关系是（ ）A．y1＜y2＜y3B．y3＜y2＜y1C．y3＜y1＜y2D．y2＜y1＜y3 03．（济南）如图，等腰直角三角形ABC位于第一象限，AB＝AC＝2，直角顶点A在直线y ＝x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线kyx=（k≠0）与△ABC有交点，则k的取值范围是（）A．1＜k＜2 B．1≤k≤3 C．1≤k≤4 D．1≤k＜404．（第十八届“希望杯”初二）直线l交反比例函数3yx=的图象于点A，交x轴于点B，点A、B与坐标原点O构等边三角形，则直线l的函数解析式为05．（成都）如图，正方形OABC的面积是4，点B在反比例函数kyx=（k＞0，x＜0）的图象上，若点R是该反比例函数图象上异于点B的任意一点，过点R分别作x轴、y轴的垂线，垂足为M、N，从矩形OMRN的面积中减去其与正方形OABC重合部分的面积，记剩余部分的面积为S，则当S＝m（m为常数，且0＜m＜4）时，点R的坐标是.（用含m的代数式表示）06．如图，已知直线12y x=与双曲线kyx=（k＞0）交于A点，且点A的横坐标为4，若双曲线kyx=（k＞0）上一点B的纵坐标为8，求△AOB的面积.07．（北京）如图，A、B两点在函数myx=（x＞0）的图象上，⑴求m的值及直线AB的解析式；⑵如果一个点的横、纵坐标均为整数，那么我们称这个点是格点，请直接写出图中阴影部分（不包括边界）所含格点的个数.08．（温州）如图，在平面直角坐标系中，直线AB与y轴和x轴分别交于点A、点B，与反比例函数myx=在第一象限的图象交于点C（1，6）点D（3，n）.过点C作CE⊥y轴于E，过点D作DF⊥x轴于点F，⑴求m、n的值；⑵求直线AB的函数解析式；⑶求证：△AEC≌△DFB．09．如图，已知正方形OABC的面积为9，点O为坐标原点，点A在x轴上，点C在y轴上，点B在函数kyx=（k＞0，x＞0）的图象上，点P（m，n）是函数kyx=（k＞0，x＞0）的图象上的任意一点，过点P作x轴、y轴的垂线，垂足分别为E、F，并设在矩形OEPF 中和正方形OABC不重合的部分面积为S.⑴求点B的坐标和k的值；⑵当92S=时，求点P的坐标；⑶写出S关于m的函数关系式.。
八年级数学反比例函数的图解和性质
声速
声速与频率和介质有关，在一定 介质中，声速与频率成反比关系。
磁场
在磁场中，磁感应强度与电流成 正比，与导线长度成反比，这是
电磁感应现象的基础。
在经济中的应用
供需关系
01
在市场经济中，商品的价格与供应量成反比关系，当需求量一
定时，供应量增加会导致价格下降。
投资回报
02
投资回报率与投资额成反比关系，当风险一定时，投资额越大，
中心对称
分布在第二和第四象限
由于k的正负性，反比例函数的图像分 布在第二和第四象限。
反比例函数的图像关于原点中心对称。
反比例函数图像的变换
k值变化
改变k的值会影响反比例函 数图像的形状和位置。
x轴和y轴的变换
通过伸缩x轴和y轴，可以 改变反比例函数图像的形 状。
图像的旋转
通过旋转反比例函数图像， 可以观察其在不同角度下 的形态。
01
02
03
确定函数表达式
首先确定反比例函数的表
达式，例如$y
=
frac{k}{x}$（其中k为常
数）。
ห้องสมุดไป่ตู้
确定坐标轴
在平面直角坐标系中，选 择适当的x和y轴范围。
绘制图像
根据反比例函数的表达式， 在坐标系中逐点绘制函数 图像。
反比例函数图像的特性
无限接近x轴和y轴
反比例函数的图像会无限接近x轴和y 轴，但不会与它们相交。
反比例函数可以看作是幂函数的一种特殊情况，即当n=-1时 的幂函数。因此，反比例函数与幂函数在性质上有一定的相 似性，例如它们的导数都与自身有关。
THANKS FOR WATCHING
感谢您的观看
反比例函数的概念的图象的性质
反比例函数的概念及图像和性质★反比例函数的概念１.反比例函数：如果两个变量ｘ、y 之间的关系可以表示成y=k x（k•为常数，k ≠０）的形式，那么称y 是ｘ的反比例函数．２.反比例函数解析式的变形:反比例函数y=k x（k ≠0）还可以写成1-=kx y (k ≠0）或k xy =(k ≠０). 注意:（１）k 为常数,ｋ≠0;（２)k x中分母x 的指数为1； (3)自变量x 的取值范围是x ≠０的一切实数;(4)因变量ｙ的取值范围是y ≠0的一切实数．例1．若函数1322)(+--=m mx m m y 是反比例函数，则m 的值是?【变式训练】１．函数122-++=m m x m y 是反比例函数，求解析式.2.已知函数122)(--+=m m x m m y .(1)若y 是x 的正比例函数，求m 的值；（2)若y 是x 的反比例函数,求m 的值，并写出此时y 与x 的函数关系式.例 2.已知y y y y 121,+=与x 2成正比例，y 2与x 成反比例，且1=x 时，1;3-==x y 时,1=y ，求当21-=x 时y 的值。
【变式训练】已知y y y 21-=,y 1与x 成反比例,y 2与2-x 成正比例,并且当3=x 时，5=y ；当1=x 时，1-=y ,求 y 与x 之间的函数关系式。
例3.在平行四边形ABCD 中，E AD AB ,6,8==为AB 上一动点（不与B A 、重合)，设DE x AE ,=的延长线交CB 的延长线于点F ,设y CF =,求y 与x 之间的函数关系,并写出自变量x 的取值范围。
【变式训练】如图，平行四边形ABCD 中,E cm BC cm AB ,1,4==是CD 边上一动点,BC AE 、的延长线交于F 点,设ycm BF xcm DE ==，.求y 与x 之间的函数关系式,并写出自变量x 的取值范围。
A DEB C F★反比例函数图像和性质利用画函数图象的方法,可以画出反比例函数的图象,它的图象是双曲线,①当0>k 时,函数的图象在第一、三象限，在每个象限内,曲线从左到右下降,也就是在每个象限内,y 随x 的增加而减小;②当0<k 时,函数的图象在第二、四象限，在每个象限内,曲线从左到右上升，也就是在每个象限内，y 随x 的增加而增大.4.画反比例函数的图象时要注意的问题：（1）画反比例函数图象的方法是描点法;（2）画反比例函数的图象要注意自变量的取值范围是0≠x ,因此,不能把两个分支连接起来;(3)由于在反比例函数中，x 和y 的值都不能为0，所以，画出的双曲线的两个分支要分别体现出无限的接近坐标轴,但永远不能达到x 轴和y 轴的变化趋势.例1.已知反比例22223-+-+=m m x m m y 的图像的两个分支分布在第二、四象限，求m 的值【变式训练】1.已知反比例函数72)2(---=m xx m y 的图像位于第一、三象限，求ｍ的值。
反比例函数图象的特征及性质
性质
当x增大时，y值减小，但xy的乘积保持不变 ，等于比例系数。
对反比例函数应用的展望
01
拓展应用领域
反比例函数作为一种基本的函 数类型，在物理、化学、工程 等领域都有广泛的应用。未来 可以进一步探索其在更多领域 的应用可能性。
02
深化理论研究
虽然反比例函数的基本性质已 经比较清楚，但是关于其更深 层次的理论研究仍然有待加强 。例如，可以进一步探讨反比 例函数与其他函数类型的复合 、变换等问题。
感谢您的观看
THANKS
性质的比较
反比例函数性质
反比例函数在其定义域内是连续的，且当x趋近于0时，y趋近于无穷大或无穷小。此外，反比例函数在其定义域 内具有单调性，即当k>0时，在每个象限内随着x的增大，y值逐渐减小；当k<0时，则相反。
一次函数性质
一次函数在其定义域内是连续的，且当x趋近于无穷大或无穷小时，y也趋近于无穷大或无穷小。此外，一次函 数的斜率决定了函数的增减性，即当斜率大于0时，函数为增函数；当斜率小于0时，函数为减函数。
反比例函数的一般形式
反比例函数的一般形式为 y = k/x（k ≠ 0），其中 k 是比例系数。
当 k > 0 时，反比例函数的图象位于 第一象限和第三象限；当 k < 0 时， 反比例函数的图象位于第二象限和第 四象限。
比例系数 k 决定了反比例函数的图象 特征和性质。
02
反比例函数的图象
图象的形状
反比例函数的图象是由两支分别位于第一、三象限和第二、四象限的双曲线组成。
当$k > 0$时，两支曲线分别位于第一、三象限内；当$k < 0$时，两支曲线分别位 于第二、四象限内。
在每个象限内，随着$x$的增大，$y$值逐渐减小，曲线从坐标轴附近向无限远处延 伸。
第1节 反比例函数的图像和性质
第二十六章反比例函数第一节反比例函数的图像和性质一、课标导航二、核心纲领1.反比例函数⑴定义：一般地，形如kyx=（k为常数，k≠0）的函数称为反比例函数，其中x是自变量，y是函数.注：①自变量x在分母上，指数为1.②比例系数k≠0.③自变量x的取值为一切非零实数，函数值的取值范围是y≠0.④反比例函数的其他形式：xy=k（k≠0）或y=kx-1（k≠0）.⑵图像：反比例函数的图像是双曲线，也称双曲线kyx=（k≠0）⑶性质（如下表所示）注：⑴y随x变化的情况必须指出“在每个象限内”或“在每一分支上”这一条件.⑵kyx=（k为常数，k≠0）中自变量x≠0，函数值y≠0，所以双曲线不经过原点，两个分支逐渐靠近坐标轴，但是永远不与坐标轴相交.2.待定系数法求反比例函数的解析式只需图像上一个点的坐标即可求出k.3.反比例函数的图像的对称性⑴中心对称：对称中心是原点.⑵轴对称：对称轴是直线y=x和直线y=—x.4.k的几何意义（如下表所示）5.数学思想⑴数形结合；⑵分类讨论.本节重点讲解：一个定义，一个性质，一个对称性，一个几何意义.三、全能突破基础演练1.如果y 是m 的反比例函数，m 是x 的正比例函数，那么y 是x 的（ ）A. 反比例函数B. 正比例函数C.一次函数D. 反比例或正比例函数 2.若反比例函数22(21)m y m -=-的图像在第二、四象限，则m 的值是（ ）A.-1或1B.小于12的任意实数 C.-1 D.不能确定 3.如图26-1-1所示，矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，点C 在反比例函数221k k y x++=的图像上.若点A 的坐标为（-2，2）则k 的值为（ ）A. 1B.-3C.4D.1或-34.若函数1mm y x-=为反比例函数，则m =______.5.三个反比例函数y 1，y 2，y 3的图像的一部分如图26-1-2所示，则k 1，k 2，k 3的大小关系为______.6. 反比例函数2k y x-=的图像一个分支经过第一象限，对于给出的下列说法： ①常数k 的取值范围是k ＞2；②另一个分支在第三象限；③在函数图像上取点A （a 1，b 1）和点B （a 2，b 2），当a 1＞a 2时，则b 1＜b 2；④在函数图像的某一分支上取点A （a 1，b 1）和点B （a 2，b 2），当a 1＞a 2时，则b 1＜b 2； ⑤函数的图像是中心对称图形但不是轴对称图形. ⑥一元二次方程x 2—（2k —1）x +k 2—1=0无实数根. 其中正确的是______（在横线上填出正确的序号）7.已知y =y 1+y 2，而y 1与x +1成反比例，y 2与x 2成正比例，并且x =1时，y =2；x =0时，y =2. 求y 与x 的函数关系式.3y图26-1-18.如图26-1-3所示，定义：若双曲线kyx=（k＞0）与它的其中一条对称轴y=x相交于A、B两点，则线段AB的长度为双曲线kyx=（k＞0）的对径.⑴求双曲线1yx=的对径；⑵若双曲线kyx=（k＞0）的对径为k的值；⑶仿照上述定义，定义双曲线kyx=（k＜0）的对径.能力提升9.已知二次函数y=ax2+bx+c的图像如图26-1-4所示，那么一次函数y=bx+c和反比例函数ayx=在同一平面直角坐标系中的图像大致是（）10.下列选项中，阴影部分面积最小的是（）BACD11.根据图26-1-5（a ）所示的程序，得到了y 与x 的函数图像如图26-1-5（b ），过点M 作PQ ∥x 轴交图像于点P 、Q ，连接OP 、OQ .则以下结论：①x ＜0时，2y x=；②△OPQ 的面积为定值；③x ＞0时，y 随x 的增大而增大；④MQ =2PM ；⑤∠POQ 可以等于90°. 其中正确的结论是（ ）A.①②④B.②④⑤C.③④⑤D.②③⑤12.⑴正比例函数y =k 1x (k 1≠0)和反比例函数2k y x=(k 2≠0)的一个交点为（1，-2），则另一个交点为______.（2）直线y=ax （a ）0）与双曲线y=x3交于A ()11,y x 、B ()22,y x 两点，则122134y x y x -= .13.如图26-1-6所示，在直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点P （3a ，a ）是反比例函数()0>=k xky 的图像上与正方形的一个交点，若图中阴影部分的面积等于9，则这个反比例函数的解析式为 .（a ）（b ）图26-1-5A14. 如图26-1-7所示，点A 、B 是函数y=x 与y=x1的图像的两个交点，作AC ⊥x 轴于C ，作BD ⊥x 轴于D ，则四边形ABCD 的面积为 .15. 如图26-1-8所示，已知双曲线()0>=k xky 经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ，若△OBC 的面积为6，则k= .16. 如图26-1-9所示，正方形OABC 的面积是4，点B 在反比例函数()0,0>>=x k xky 的图像上.若点R 是该反比例函数图像上异于点B 的任意一点，过点R 分别作x 轴、y 轴的垂线，垂足为M 、N ，从矩形OMRN 的面积中减去其与正方形OABC 重合部分的面积，记剩余部分的面积为S ，则当S=m （m 为常数，且0<m<4）时，反比例函数解析式为 ，点R 的坐标是 （用含m 的代数式表示）.17. 如图26-1-10所示，在平行四边形AOBC 中，对角线交与点E ，双曲线()0>=k xky 经过A 、E 两点，若平行四边形AOBC 的面积为18，则k = .18. 如图26-1-11所示，△AOB 为等边三角形，点B 的坐标为（-2，0），过点C （-2，0）作直线l交AO 于D ，交AB 于E ，点E 在某反比例函数图像上，当△ADE 和△DCO 的面积相等时，那么该反比例函数解析式为 . 19.（1）两个反比例函数xy x y 63==、在第一象限内的图像如图26-1-12所示，点321P P P 、、、…、2013P 在反比例函数xy 6=的图像上，它们的横坐标分别是321x x x 、、、…、2013x ，纵坐标分别是1、3、5、…共2013个连续奇数，过点分别作y 轴的平行线与的图像交点依次是()111,y x Q 、()222,y x Q 、()333,y x Q 、…、()201320132013,y x Q ，则2013y = .（2）如图26-1-13所示，在函数()08>=x xy 的图像上有点321P P P 、、、…、n P 、1+n P ，点1P 的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点321P P P 、、、…、n P 、1+n P 分别作x 轴、y 轴的垂线段，如图所示，将图中阴影部分的面积从左至右依次记为321S S S 、、、…、n S ，则1S ，n S .（用含n 的代数式表示）20.（1）①如图26-1-14（a ）所示，一个正方形的一个顶点在函数()01>=x xy 的图像上，则点1P 的坐标是（ ， ）.②如图26-1-14（b ）所示，若有两个正方形的顶点1P 、2P 都在函数()01>=x xy 的图像上，则点2P 的坐标是（ ， ）.（2）如图26-1-14（c ）所示，若将两个正方形改为两个等腰直角三角形，直角顶点在函数()04>=x xy 的图像上，斜边1OA 、21A A 都在x 轴上， ①求点的坐标；②求点2P 的坐标.（3）如图26-1-14（d ）所示，若有两个等边三角形的顶点都在函数()034>=x xy 的图像上，点1A 、1A 在x 轴上，直接写出点2P 的坐标.21.（1）探究：如图26-1-15（a ）所示，已知△ABC 和△ABD 的面积相等，试判断AB 与CD 的位置关系，并说明理由.（2）应用：①如图26-1-15（b ）所示，点M 、N 在反比例函数()0>=k xky 图像上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E 、F ，试证明：MN ∥EF .②若①中其它条件不变，只改变点M 、N 的位置，如图26-1-15（c ）所示，请判断MN 与EF 是否平行，直接写出结论。
反比例函数图像与性质知识点
反比例函数是一种数学函数，它通常对应于反对比关系，即如果某个量越大，另一个量就越小，反之亦然。
一般地，一个反比例函数形式为y=k/x，其中k是一个未知的常数。
从定义看，即使x为0，y也能被赋以有限的值，它们的变化关系也不同于线性函数的变化关系。
反比例函数的图像为连续递减的弧形，它以y轴为对称轴，反比例函数在图像上表现为从原点（0，0）出发的一条弯曲的曲线，曲线的弧度越来越小，直至无穷远时与x轴垂直，当x=0时，y值可以被给定，这也是为什么反比例函数和线性函数不同的原因。
此外，反比例函数的基本特性还有，点（a，b）处的导数是负值；它仅当x的值小于k的值的时候才有可能产生拐点；可以通过倒数的非零多项式来求反比例函数的函数值；求反比例函数的定积分时，一般使用其定义域上的积分变量将函数值单调映射到［0,1］端点之间，然后再使用不同的奇偶性求对应此定积分。
总之，反比例函数在数学理论中具有重要的地位，它是一种常用的函数形式，也有着与线性函数不同的曲线图形和相应的参数特性。
这提醒我们，在令人兴奋的数学探索之旅中，要秉承科学的态度紧紧依靠量化的思维方式来深入探讨数学物理的规律。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
反比例函数定义
一般的，如果两个变量x,y之间的关系可以表示成y=k/x(k为常数，k≠0），其中k叫做反比例系数，x是自变量，y是自变量x的函数，x的取值范围是不等于0的一切实数,且y也不能等于0。
k大于0时，图像在一、三象限。
k小于0时，图像在二、四象限.k 的绝对值表示的是x与y的坐标形成的矩形的面积。
反比例函数图像及性质
反比例函数图像：
1.反比例函数的图像是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或
第二、四象限，它们关于原点对称。
由于反比例函数中自变量x≠0，函数值y≠0，所以，它的图像与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
2.反比例函数的图像属于以原点为对称中心的中心对称的双曲线，反比例函数图像中每
一象限的每一支曲线会无限接近x轴、y轴，但不会与坐标轴相交（y≠0）。
反比例函数性质：
1.[增减性]当k>0时，图象分别位于第一、三象限，同一个象限内，y随x的增大
而减小；当k<0时，图象分别位于二、四象限，同一个象限内，y随x的增大而增大。
2.k>0时，函数在x<0上同为减函数、在x>0上同为减函数；k<0时，函数在x<0上为
增函数、在x>0上同为增函数。
定义域为x≠0；值域为y≠0。
3.因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与
x轴相交，也不可能与y轴相交。
4. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x轴，y轴的平行线，与
坐标轴围成的矩形面积为S1，S2则S1=S2=|K|
5. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴 y=x y=-x
（即第一三，二四象限角平分线），对称中心是坐标原点。
6.若设正比例函数y=mx与反比例函数y=n/x交于A、B两点（m、n同号），那么A B
两点关于原点对称。
7.设在平面内有反比例函数y=k/x和一次函数y=mx+n，要使它们有公共交点，则
n^2+4k·m≥（不小于）0。
8.反比例函数y=k/x的渐近线：x轴与y轴。
9.反比例函数关于正比例函数y=x,y=-x轴对称,并且关于原点中心对称。
10.反比例上一点m向x、y分别做垂线，交于q、w，则矩形mwqo（o为原点）的面积为
|k|
11.k值相等的反比例函数重合，k值不相等的反比例函数永不相交。
12.|k|越大，反比例函数的图象离坐标轴的距离越远。
13.[对称性]反比例函数图象是中心对称图形，对称中心是原点；反比例函数的图像也
是轴对称图形，它的对称轴是x轴和y轴夹角的角平分线。
反比例函数知识点汇总
若k为常数，则函数y=k/x就是反比例函数，自变量和自变量的函数分别是x和y，又因为反比例函数式本身是一个分数，所以x可以是任意不等于0的实数。
同时，函数式有时候也写成y=k·x^（-1）或者k=xy.
1、反比例函数的表达式
X是自变量，Y是X的函数
y=k/x=k·1/x
xy=k
y=k·x^（-1）（即：y等于x的负一次方，此处X必须为一次方）
y=k\x(k为常数且k≠0，x≠0）若y=k/nx此时比例系数为：k/n
2、函数式中自变量取值的范围
①k≠0；②在一般的情况下，自变量x的取值范围可以是不等于0的任意实数；③函数y的取值范围也是任意非零实数。
解析式y=k/x其中X是自变量，Y是X的函数，其定义域是不等于0的一切实数y=k/x=k·1/x
xy=k
y=k·x^（-1）
y=k\x(k为常数(k≠0），x不等于0）
3、反比例函数图象
反比例函数的图像属于以原点为对称中心的中心对称的双曲线（hyperbola），反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（K≠0）。
4、反比例函数中k的几何意义是什么？有哪些应用？
过反比例函数y=k/x（k≠0），图像上一点P（x，y），作两坐标轴的垂线，两垂足、原点、P点组成一个矩形，矩形的面积S=x的绝对值*y的绝对值=（x*y）的绝对值=|k|
研究函数问题要透视函数的本质特征。
反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数。
从而有k的绝对值。
在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题带来很多方便。
（注：文档可能无法思考全面，请浏览后下载，供参考。
可复制、编制，期待你的好评与关注）。