基本初等函数图像及性质大全(初中-高中)
(完整版)六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。
b.2. 4.a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m a a a +=⋅(2)nm n m aa a -=÷b.y(1)()a a nn= ； (2)当n 为奇数时，a a nn=当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
九种基本初等函数图像及性质
九种基本初等函数图像及性质基本初等函数包括一次函数、平方函数、立方函数、根号函数、指数函数、对数函数、正弦函数、余弦函数和正切函数等9种函数。
下面简单介绍它们的图像及性质。
一次函数的图像是一条直线，表达函数的形式为：y=ax+b(a≠0)，其中a表示斜率，b表示函数的截距，函数的性质是其增减性由斜率a决定。
平方函数的图像为一条凹凸不平的抛物线，表达函数的形式为：y=ax2+bx+c，其中a、b、c为实数，a≠0，此函数的性质是其单调性由a的正负决定，是增函数当a>0时，是减函数当a<0时。
立方函数的图像是一条弯曲的曲线，表达函数的形式为：y=ax3+bx2+cx+d，其中a、b、c、d为实数，a≠0，函数的性质是其单调性由a的正负决定，是增函数当a>0时，是减函数当a<0时。
根号函数的图像是一条弯曲的曲线，表达函数的形式为：y=a√x+b，其中a、b为实数，a>0，此函数的性质是常数变动，函数的解析式在a变动时它的单调性也由正负变化。
指数函数的图像是一条右倾的曲线，表达函数的形式为：y=axb，其中a、b为实数，a>0、b≠0，函数的性质是其单调性由a、b的正负决定，是增函数当a>0且b>0时，是减函数当a>0且b<0时。
对数函数的图像是一个右倾的曲线，表达函数的形式为：y=alogx + b，其中a、b为实数，a>0，此函数的性质是变数变动，函数的解析式在x变动时它的单调性也由正负变化。
正弦函数的图像是一个周期性的曲线，表达函数的形式为：y=Asin（ωx+φ），其中A、ω、φ为实数，A>0，此函数的性质是其单调性由A的正负决定，是增函数当A>0时，是减函数当A<0时。
余弦函数的图像同正弦函数，表达函数的形式为：y=Acos（ωx+φ），其中A、ω、φ为实数，A>0，此函数的性质同正弦函数一样。
正切函数的图像为一个弯曲的曲线，表达函数的形式为：y=tanx，其中x代表，函数的性质是函数的单调性变化于π/2，函数的解析式在x变动到π。
六大基本初等函数图像及其性质
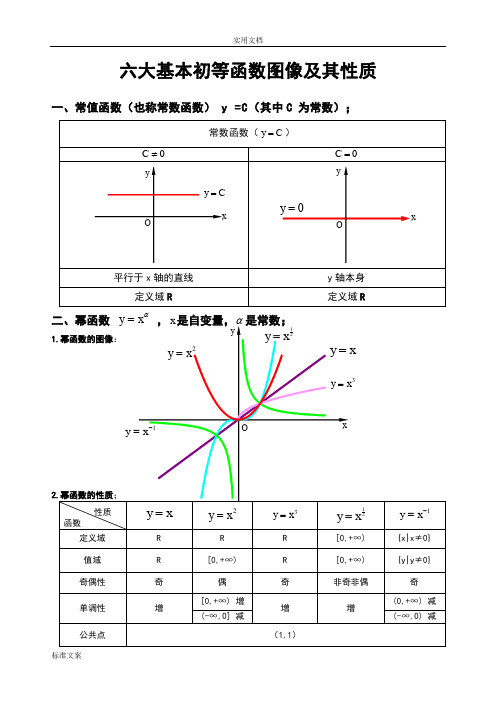
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
(完整版)六大基本初等函数图像与性质
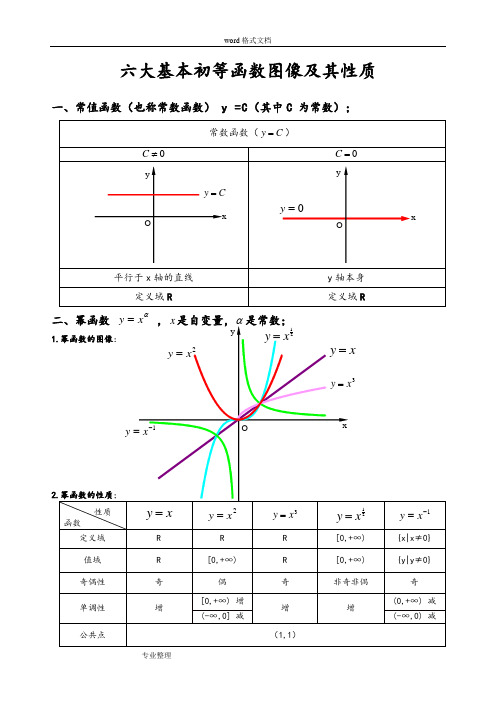
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
基本初等函数图像及性质
基本初等函数图像及性质六大基本初等函数图像及其性质一、常数函数（也称常值函数）y=C（其中C为常数）；常数函数（y=C）是平行于x轴的直线，定义域为R，值域为{C}，非奇非偶，单调性为不变，公共点为(0,C)。
二、幂函数y=x^α，x是自变量，α是常数；1.幂函数的图像：当α为正整数时，函数的图像都经过原点，并且在原点处与x轴相切。
当α为奇数时，图像关于原点对称；当α为偶数时，图像关于y轴对称。
2.幂函数的性质：函数。
定义域。
值域。
奇偶性。
单调性。
公共点y=x^2.R。
[0,+∞)。
偶。
增。
(0,0)y=x。
R。
R。
非奇非偶。
增。
(0,0)y=x^3.R。
R。
奇。
增。
(0,0)y=x^-1.{x|x≠0}。
{y|y≠0}。
奇。
(-∞,0)减。
(-1,0)∪(0,1)三、指数函数y=a^x（a>1且a≠1），定义域为R，为无界函数。
1.指数函数的图像：当a>1时，图像是单调增的曲线，经过点(0,1)；当0<a<1时，图像是单调减的曲线，也经过点(0,1)。
2.指数函数的性质：函数。
定义域。
值域。
奇偶性。
单调性。
公共点y=a^x(a>1)。
R。
(0,+∞)。
非奇非偶。
增。
(0,1)y=a^x(0<a<1)。
R。
(0,1)。
非奇非偶。
减。
(0,1)本文介绍了指数函数和对数函数的基本概念和性质。
首先，介绍了指数函数的图像和比较大小的方法。
当底数互为倒数时，两个指数函数的图像关于y轴对称。
当底数大于1时，指数函数的值随着底数的增大而增大；当底数小于1时，指数函数的值随着底数的增大而减小。
其次，介绍了指数的运算法则，包括整数指数幂的运算性质和分数指数幂的运算性质。
其中，整数指数幂的运算性质包括指数相加、相减和相乘的规律；分数指数幂的运算性质包括分数指数幂的乘方和除法的规律。
接着，介绍了对数函数的概念和性质。
对数函数是指底数为常数且大于1的指数函数的反函数。
常用对数是以10为底的对数，自然对数是以无理数e为底的对数。
（完整）六大基本初等函数图像及其性质
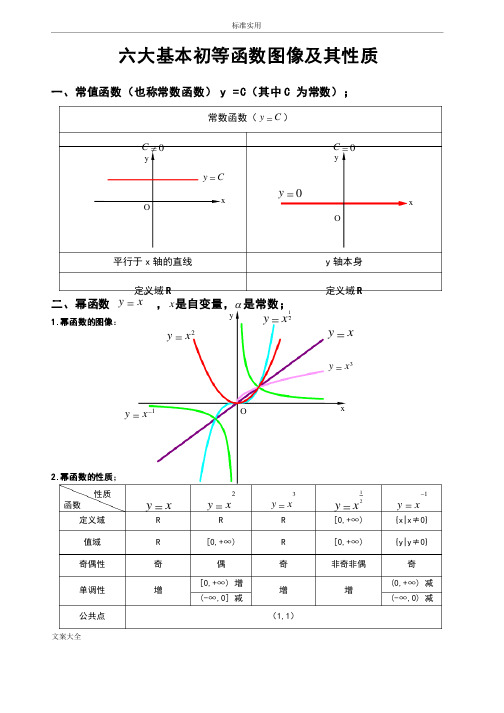
标准实用文案大全六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点（1,11,1））xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α，他们的图形都经过原点，并当α>1>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm 时，时，n n 为偶数时函数的定义域为（为偶数时函数的定义域为（0, +0, +0, +∞），∞），∞），n n 为奇数时函数的定义域为（为奇数时函数的定义域为（--∞,+,+∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（1 ,11 ,11 ,1）；）；4）如果m>n 图形于x 轴相切，如果m<n,m<n,图形于图形于y 轴相切，且m 为偶数时，还跟y 轴对称；轴对称；m m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，）当α为负有理数时，n n 为偶数时，函数的定义域为大于零的一切实数；为偶数时，函数的定义域为大于零的一切实数；n n 为奇数时，定义域为去除x=0以外的一切实数。
基本初等函数图像与性质大全初中高中资料全
①原函数 与反函数 的图象关于直线 对称．
②函数 的定义域、值域分别是其反函数 的值域、定义域．
③若 在原函数 的图象上，则 在反函数 的图象上．
④一般地，函数 要有反函数则它必须为单调函数．
六、三角函数的图像和性质
（一）正弦与余函数的图像与性质
函数
图像
定域义
R
R
值域
最值
单调性
奇偶性
③数乘： ④
⑤ ⑥换底公式：
（5）对数函数
函数名称
对数函数
定义
函数 且 叫做对数函数
图象
定义域
值域
过定点
图象过定点 ，即当 时， ．
奇偶性
非奇非偶
单调性
在定义域上是增函数
在定义域上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限， 越大图象越靠低；在第四象限， 越大图象越靠高．
五、反函数
（1）反函数的概念
奇函数
偶函数
周期性
是周期函数，2 为最小正周期
是周期函数，2 为最小正周期
对称性
对称中心 ，
对称中心 ，
2.正切与余切函数的图像与性质
函数
图像
定域义
值域
R
R
单调性
奇偶性
奇函数
奇函数
周期性
是周期函数， 为最小正周期
是周期函数， 为最小正周期
对称性
对称中心
对称中心
七、反三角函数的图像与性质
1.反正弦与反余函数的图像与性质
②正数的负分数指数幂的意义是： 且 ．0的负分数指数幂没有意义．
（3）运算性质
① ②
③
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m a a a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
(完整版)基本初等函数图像及性质大全(初中高中),推荐文档
1、一次函数与二次函数（一）一次函数（二）二次函数①一般式：2()(0)f x ax bx c a =++≠ ②顶点式：2()()(0)f x a x h k a =-+≠③两根式：12()()()(0)f x a x x x x a =--≠（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式．③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更方便．①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-顶点坐标是24(,24b ac b a a--②当0a >时，抛物线开口向上，函数在(,]2b a -∞-上递减，在[,)2ba-+∞上递增，当2b x a =-时，2min 4()4ac b f x a -=；当0a <时，抛物线开口向下，函数在(,]2b a -∞-上递增，在[,)2b a -+∞上递减，当2b x a =-时，2max 4()4ac b f x a-=．二、幂函数过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．三、指数函数（1）根式的概念：如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．①正数的正分数指数幂的意义是：0,,,m na a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：1(0,,,m m nn a a m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．（3）运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)rrrab a b a b r R =>>∈（4）指数函数函数名称指数函数四、对数函数（1）对数的定义： ①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数． ②负数和零没有对数．③对数式与指数式的互化： log (0,1,0)x a x N a N a a N =⇔=>≠>．常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．①加法：log log log ()a a a M N MN += ②减法：log log log a a aMM N N-=③数乘：log log ()naan M M n R =∈ ④log a Na N=⑤log log (0,)b n a a nM M b n R b =≠∈⑥换底公式：log log (0,1)log b a b N N b b a =>≠且（5）对数函数五、反函数设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x 是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．①确定反函数的定义域，即原函数的值域；②从原函数式()y f x =中反解出1()x f y -=；③将1()x fy -=改写成1()y f x -=，并注明反函数的定义域．①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称．②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．六、三角函数的图像和性质（一）正弦与余函数的图像与性质函数xy sin =xy cos =图像定域义R R值域[]1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时，时，2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时，时，单调性[2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2]Zk k k k k ππππππ-++∈在每个上递增在每个上递减奇偶性奇函数偶函数周期性是周期函数，2为最小正周期π是周期函数，2为最小正周期π对称性对称中心(,0)k π，:,()2x k k Z ππ=+∈对称轴对称中心(,0)2k ππ+，:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数x y tan =xy cot =图像定域义{|,}2x x R x k k Z ππ∈≠+∈且{|,}x x R x k k Z ππ∈≠+∈且值域RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,)Zk k k πππ+∈在每个上递减奇偶性奇函数奇函数周期性是周期函数，为最小正周期π是周期函数，为最小正周期π对称性对称中心(,0)2k π对称中心(,0)2k π七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦，的反函数反余弦函数arccos y x=是[]cos 0,y x x π=∈，的反函数图像定域义[]1,1-[]1,1-值域,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性[1,1]-+在上递增[1,1]-+在上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质函数反正切函数arctan y x =是tan (,)22y x x ππ=∈-，的反函数反余切函数arccot y x =是()cot 0,y x x π=∈，的反函数图像定域义(,,)-∞+∞(,,)-∞+∞值域,22ππ⎛⎫- ⎪⎝⎭()0,π单调性(,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心（0，0）对称中心（0，π/2）11。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。
且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。
函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。
4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m aa a +=⋅(2)nm nmaa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。
基本初等函数图像及性质大全(初中 高中)
一、一次函数与二次函数（1）二次函数解析式的三种形式①一般式：2()(0)f x ax bx c a =++≠ ②顶点式：2()()(0)f x a x h k a =-+≠ ③两根式：12()()()(0)f x a x x x x a =--≠（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式． ③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更方便． （3①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--②当0a >时，抛物线开口向上，函数在(,]2b a -∞-上递减，在[,)2b a-+∞上递增，当2bx a =-时，2min 4()4ac b f x a -=；当0a <时，抛物线开口向下，函数在(,]2b a -∞-上递增，在[,)2b a -+∞上递减，当2b x a=-时，2max 4()4ac b f x a -=．二、幂函数（1）幂函数的定义一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数． （2）幂函数的图象过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．（1）根式的概念：如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根． （2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m na a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：1()0,,,m m nn a a m n N a -+==>∈且1)n >．0的负分数指数幂没有意义． （3）运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈（1）对数的定义： ①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数． ②负数和零没有对数．③对数式与指数式的互化： log (0,1,0)xa x N a N a a N =⇔=>≠>． （2）几个重要的对数恒等式： log 10a =，log 1a a =，log ba ab =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）． （4）对数的运算性质 如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a aM M N N-= ③数乘：log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b =≠∈ ⑥换底公式：log log (0,1)log b a bN N b b a =>≠且 （5）对数函数五、反函数（1）反函数的概念设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x 是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y fx -=．（2）反函数的求法①确定反函数的定义域，即原函数的值域； ②从原函数式()y f x =中反解出1()x f y -=；③将1()x fy -=改写成1()y f x -=，并注明反函数的定义域．（3）反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称． ②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．六、三角函数的图像和性质（一）正弦与余函数的图像与性质 函数 x y sin =x y cos =图像定域义 RR值域 []1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时，时，2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时，时， 单调性[2,2]223[2,2]22k k k k ππππππππ-++++在每个上递增在每个上递减[2,2][2,2] k k k k ππππππ-++在每个上递增在每个上递减奇偶性 奇函数偶函数周期性 是周期函数，2π为最小正周期 是周期函数，2π为最小正周期 对称性对称中心(,0)k π，:,()2x k k Z ππ=+∈对称轴 对称中心(,0)2k ππ+，:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且 {|,}x x R x k k Z ππ∈≠+∈且值域 RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数，π为最小正周期 是周期函数，π为最小正周期 对称性对称中心(,0)2k π 对称中心(,0)2k π七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦，的反函数反余弦函数arccos y x =是[]cos 0,y x x π=∈，的反函数图像定域义 []1,1-[]1,1-值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π 单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无 无对称性对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质 函数反正切函数arctan y x = 是tan (,)22y x x ππ=∈-，的反函数反余切函数arccot y x = 是()cot 0,y x x π=∈，的反函数图像定域义 (,,)-∞+∞(,,)-∞+∞值域 ,22ππ⎛⎫- ⎪⎝⎭ ()0,π单调性 (,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心（0，0）对称中心（0，π/2）。
基本初等函数图像及性质大全(初中-高中)
（3）二次函数图象的性质
图像
定义域
对称轴
顶点坐标
值域
单调区间
递减
递增
递增
递减
①.二次函数 的图象是一条抛物线，对称轴方程为 顶点坐标是
②当 时，抛物线开口向上，函数在 上递减，在 上递增，当 时， ；当 时，抛物线开口向下，函数在 上递增，在 上递减，当 时， ．
二、幂函数
（1）幂函数的定义
一般地，函数 叫做幂函数，其中 为自变量， 是常数．
（2）幂函数的图象
过定点：所有的幂函数在 都有定义，并且图象都通过点 ．
1、一次函数与二次函数（一）一次Fra bibliotek数一次
函数
，
符号
图象
性质
随 的增大而增大
随 的增大而减小
（二）二次函数
（1）二次函数解析式的三种形式
①一般式： ②顶点式：
③两根式：
（2）求二次函数解析式的方法
①已知三个点坐标时，宜用一般式．
②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
、一次函数与二次函数
(1)二次函数解析式的三种形式
①一般式：f ( x) ax2 bx c(a 0) ②顶点式：f (x) a( x h) 2 k (a 0)
③两根式：f (x) a(x x1)( x x2)(a 0)
(2)求二次函数解析式的方法
①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时，常使用顶点式．③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求f ( x) 更方便．
(3)二次函数图象的性质
过定点：所有的幂函数在 (0, ) 都有定义，并且图象都通过点 (1,1)．
①. 二次函数 f ( x) ax 2 bx
c(a 0) 的图象是一条抛物线， 对称轴方程为 x
b
, 顶点坐标 2a
是(
b
, 4 ac b 2 )
2a 4a
②当 a 0 时，抛物线开口向上，
函数在 (
2b a ] 上递减，在 [
b , 2a ,
) 上递增，当
b 2a
时， f min ( x)
4ac b 2 ；当
a
4a
0时，抛物线开口向下，
函数在 (
b 2a
] 上递增，在 [ b 2a
上递减，当 x
b
时， f max (x)
2 a
max
4ac b 2 4a
、幂函数
1) 幂函数的定义
一般地，函数 y x 叫做幂函数，其中 x 为自变量， 是常数．
2) 幂函数的图象
三、指数函数
（1）根式的概念：如果x n a,a R,x R,n 1，且n N ，那么x 叫做a的n 次方根．
（2）分数指数幂的概念
m
①正数的正分数指数幂
等于0．
的意义是：a n n a m(a0,m, n N,且n1）．0 的正分数指数幂
②正数的负分数指数幂的意义是：
mm
1
a n (1)n
n (1a)m (a0,m,n N ,且n 1）．0的负
a a
分数指数幂没有意义．
（3）运算性质
① a r a s a r s( a 0,r, s R)②（r s rs a ) a ( a0,r,s R)
③ (ab)r a r b r (a 0,b 0,r R)
四、对数函数
x
x log a N a x N(a 0,a 1,N 0) ．
2）几个重要的对数恒等式： log a 1 0，log a a 1，log a a b b ．
1）对数的定义：
①若 a N
（a 0,
且
a 1）
，则x 叫做以 a 为底 N 的对数，记作 x log a N ，
其中 a 叫做底数， N 叫做真数．
②负数和零没有对数．
③ 对数式与指数式的互化： 3）常用对数与自然对数
常用对数： lg N ，即 log 10 N ；自然对数：
4）对数的运算性质 如果 a 0, a 1, M
lnN ，即log e N (其中 e 2.71828⋯)．
0, N 0，那么
①加法： log a M log a N log a (MN ) ②减法： log a M log a N log a
③数乘： nlog a M log a M n (n R) ④a
log a N
⑤log a b M n n log a M(b 0,n R) a b a
⑥换底公式： log a N
log
b N
(b 0,且 b 1) log b a
五、反函数
(1)反函数的概念
设函数y f (x)的定义域为A，值域为C，从式子y f(x)中解出x，得式子x (y) ．如果对于y 在C中的任何一个值，通过式子x (y) ，x在A中都有唯一确定的值和它对应，那么式子x (y) 表示x 是y 的函数，函数x ( y)叫做函数y f (x)的反函数，记作x f 1(y)，
习惯上改写成y f 1(x) ．
(2)反函数的求法
①确定反函数的定义域，即原函数的值域；
②从原函数式y f(x) 中反解出x f 1(y)；
③将x f 1(y)改写成y f 1(x) ，并注明反函数的定义域．
(3)反函数的性质
1
①原函数y f (x)与反函数y f (x)的图象关于直线y x对称．
②函数y f (x ) 的定义域、值域分别是其反函数y f 1 (x) 的值域、定义域．
③若P(a,b) 在原函数y f ( x)的图象上，则P'(b,a)在反函数y f 1(x) 的图象上．
④一般地，函数y f (x) 要有反函数则它必须为单调函数．
六、三角函数的图像和性质
一)正弦与余函数的图像与性质
2.
七、反三角函数的图像与性质
1.。