指数对数比大小高考试题汇编
高考指数对数运算比较大小专练

姓名1 .三个数a二60.7函数专练得分A. b V c V aB.2 .三个数a二60.7A. b V c V aB.3.已知 a = log! 6 , b2A. b V c V aB.4 .已知a 二0.3 1、12A. a b c66,b =0.76,c二60的大小顺序是(C. c V a V bD.c二log6,7的大小顺序是1og10.1 ,20.32,C. c V a V bD.c 二1og]0.9,则(2c C. c V a V b D.C =log 1 2 ,则a,b,c的大小关系是25. a = log°.34,b= log^cJ.S2则(A. a c : bB. c b a c. D.6 .设a=lgeb=(lge)2,cTg7e 贝VA. a b cB. c. cab D.7 .三个数0.76,607,0.67的大小关系为A 6 7 ^0.7. 0.7 <0.6 <6 B. 6 ^0.7 70.7 <6 £0.6C. 0.67<60.7<0.76D. 0.67 :::0.76::60.78.已知二032C = log1 2,则a,b,c的大小关系是2A.9 .设 a 二log i 3 ,2 ⑴。
.3<3丿 c Tn「,则(A. a b cB. a c bC. c a bD. b a cA . a b cBC . a c b DA. a b cB. b c aC. c b aD. a c b12.函数y = eln>1—x —1的图像大致是( )14.已知a 是实数,贝V 函数f(x) =1 asi nax 的图象不可能 是 (♦ ♦ ♦10 .设 a = log 12 ,c=( 3)2,则a,b,c的大小关系是(3511 .设 a=(3)5,b 5 2”(5)5 则a,b,c 的大小关系是 2(x-b)的图像可能是(15.设f (x)是函数f(x)的导函数,将y 二f(x)和y = f (X )的图象画在同一个16.函数y“og 2 口的图象(2 +x(A )关于原点对称 (C )关于y 轴对称17.函数f(X)=1 |og 2X 与g(x)才在同一直角坐标系下的图像大致y 」ky 」1二・O■ =xO ■ xA .B .直角坐标系中,不可能正确的是ACD (B )关于直线y 「-x 对称 (D )关于直线y 二x 对称18.函数y =―: 19. 函数f (x)二 20. 若 f (x ) = loj21.函数f(x)二22. 函数f (x)二 23. 已知函数- 于设f (x)=彳 24. 12的定义域是—x — x1H 1g(1x)的定义域是,则f (x )的定义域为x + 1)1— + J 4 - X 2的定义域为ln(x 1)1 - 2log 6 X 的定义域为f(x)= F ,x >0, 若 f(a) + f(1) = 0,则实数 a 的值等l x + 1, x < 0.1gx, x 〉0 mrf 1gx ,x ,0,则 Mg25. 设函数f(x) = ]—x x 乞 02,_,若 f(a)=4,则实数 a =x , x > 026. 已知函数f(x )」2, x > 2, 若关于x 的方程f (皆k 有两个不 〔(x — 1 f , x v 2.同的实根,则实数k 的取值范围是27.曲线y = e x在点A(0,1)处的切线斜率为 28.曲线 y=-x 3 + 3x 2在点(1,2)处的切线方程为_____________________ .29. 曲线y=x(3lnx+1)在点(1,1)处的切线方程为________________________30. 曲线y=x3在点(1,)处的切线与x轴、直线x=2所围成的三角形的面积为________ .30. 函数f(x)= “ x—cosx在[0 , )内有 __________ 个零点.31. 方程|x| = cosx在(— 3,+^ )内由_____________________ 个根.32. 求下列函数的导数.2 2(1)f(x)=sinx (2)f(x)=sinx (3)f(x)=cosx (4) f (x) = cos(x - x)(5) f (x) = In x (6) f (x) = ln(x22x) (7) f (x)二丄x (8)f(x)二ln xx(9) f(x) =e2x 2x(10)f (x) =e - ln(2x 4) 2 x(11) f (x) = (-x ax)e33.已知函数f(x)=x_2lnx求曲线y=f(x)在点A(1,f(1))处的切线方程;。
指、对、幂数比较大小问题【八大题型】(举一反三)(新高考专用)(解析版)2025年新高考数学一轮复习

指、对、幂数的大小比较问题【八大题型】【题型1 利用函数的性质比较大小】....................................................................................................................2【题型2 中间值法比较大小】................................................................................................................................3【题型3 特殊值法比较大小】................................................................................................................................4【题型4 作差法、作商法比较大小】....................................................................................................................6【题型5 构造函数法比较大小】............................................................................................................................7【题型6 数形结合比较大小】................................................................................................................................9【题型7 含变量问题比较大小】..........................................................................................................................12【题型8 放缩法比较大小】. (14)1、指、对、幂数的大小比较问题指数与对数是高中一个重要的知识点,也是高考必考考点,从近几年的高考情况来看,指、对、幂数的大小比较是高考重点考查的内容之一,是高考的热点问题,主要考查指数、对数的互化、运算性质,以及指数函数、对数函数和幂函数的性质,一般以选择题或填空题的形式考查.这类问题的主要解法是利用函数的性质与图象来求解,解题时要学会灵活的构造函数.【知识点1 指、对、幂数比较大小的一般方法】1.单调性法:当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较,具体情况如下:①底数相同,指数不同时,如1x a 和2x a ,利用指数函数x y a =的单调性;②指数相同,底数不同时,如1ax 和2ax ,利用幂函数a y x =单调性比较大小;③底数相同,真数不同时,如1log a x 和2log a x ,利用指数函数log a x 单调性比较大小.2.中间值法:当底数、指数、真数都不同时,要比较多个数的大小,就需要寻找中间变量0、1或者其它能判断大小关系的中间量,然后再各部分内再利用函数的性质比较大小,借助中间量进行大小关系的判定.3.作差法、作商法:(1)一般情况下,作差或者作商,可处理底数不一样的对数比大小;(2)作差或作商的难点在于后续变形处理,注意此处的常见技巧与方法.4.估算法:(1)估算要比较大小的两个值所在的大致区间;(2)可以对区间使用二分法(或利用指对转化)寻找合适的中间值,借助中间值比较大小.5.构造函数法:构造函数,观察总结“同构”规律,很多时候三个数比较大小,可能某一个数会被可以的隐藏了“同构”规律,所以可能优先从结构最接近的的两个数来寻找规律,灵活的构造函数来比较大小.6、放缩法:(1)对数,利用单调性,放缩底数,或者放缩真数;(2)指数和幂函数结合来放缩;(3)利用均值不等式的不等关系进行放缩.【题型1 利用函数的性质比较大小】【例1】(2024·湖南衡阳·模拟预测)已知a=30.3,b=0.33,c=log0.33,则a,b,c的大小关系是()A.a>b>c B.b>a>c C.c>b>a D.c>a>b【解题思路】利用指数函数、对数函数的单调性可得答案.【解答过程】a=30.3>30=1,0<b=0.33<1=0.30,c=log0.33<log0.31=0,∴a>b>c.故选:A.,b=1.20.2,c=0.52.1,则a,b,c的大小关系是【变式1-1】(2024·四川自贡·三模)已知a=log213()A.a<c<b B.c<a<b C.c<b<a D.a<b<c【解题思路】根据对数函数和指数函数的单调性即可判断.【解答过程】因为y=log2x在x∈(0,+∞)上单调递增,<log21=0即a<0;所以a=log213因为y=1.2x为增函数,故b=1.20.2>1.20=1即b>1;因为y=0.5x为减函数,故0<0.52.1<0.50=1即0<c<1,综上a<c<b.故选:A.【变式1-2】(2024·贵州贵阳·三模)已知a=40.3,b=(log4a)4,c=log4(log4a),则()A.a>b>c B.a>c>b C.b>c>a D.c>a>b【解题思路】利用指数函数单调性得到a>1,利用指对运算和指数函数单调性得到0<b<1,利用对数函数单调性得到c<0,则比较出大小.【解答过程】因为a=40.3>40=1,b=(log4a)4=0.34<1,且0.34>0,则0<b<1,c=log4(log4a)=log40.3<0,所以a>b>c,故选:A.【变式1-3】(2024·山东泰安·模拟预测)已知a=log0.20.3,b=ln a,c=2a,则a,b,c的大小关系为()A.c>b>a B.a>b>c C.b>a>c D.c>a>b【解题思路】利用对数函数的单调性求得a,b的范围,根据指数函数的单调性得c的范围,即可比较大小.【解答过程】因为y=log0.2x在(0,+∞)上单调递减,所以log0.21<log0.20.3<log0.20.2,即0<a<1,因为y=ln x在(0,+∞)上单调递增,所以ln a<ln1,即b<0,因为y=2x在R上单调递增,所以2a>20,即c>1,综上,c>a>b.故选:D.【题型2 中间值法比较大小】【例2】(23-24高三上·天津南开·阶段练习)已知a=e0.1,b=1―2lg2,c=2―log310,则a,b,c的大小关系是()A.b>c>a B.a>b>c C.a>c>b D.b>a>c【解题思路】根据指、对数函数单调性,结合中间值0,1,分析判断即可.【解答过程】由题意可得:a=e0.1>e0=1,b=1―2lg2=1―lg4,且0=lg1<lg4<lg10=1,则0<b<1,因为log310>log39=2,则c=2―log310<0,故选:B.【变式2-1】(2024·陕西铜川·模拟预测)已知a=―12,b=log65,c=log56,则()A.a<b<c B.c<b<a C.b<c<a D.a<c<b【解题思路】取两个中间值1和32,由a =>32,b <log 66=1,1=log 55<c <32即可比较三者大小.【解答过程】a =―12=>=32,b =log 65<log 66=1,1=log 55<log 56=c <log =32,因此b <c <a .故选:C .【变式2-2】(2024·山东潍坊·二模)已知a =e ―1,b =lg a ,c =e 0,则( )A .b <a <c B .b <c <a C .a <b <cD .c <b <a【解题思路】根据对数函数和指数函数单调性并结合中间量0和1即可比较大小.【解答过程】a =e ―1∈(0,1),b =lg a =lge ―1=―lge <0,c =e 0=1,所以b <a <c ,故选:A.【变式2-3】(2024·天津北辰·三模)已知a =0.53.1,b =log 0.90.3,c =log 1312,则a ,b ,c 的大小关系为( )A .c <b <aB .c <a <bC .b <a <cD .a <c <b【解题思路】根据指、对数函数单调性,结合中间值“12,1”分析大小即可.【解答过程】因为y =0.5x 在R 上单调递减,则0.53.1<0.51=12,即a <12;又因为y =log 0.9x 在(0,+∞)上单调递减,则log 0.90.3>log 0.90.9=1,即b >1;可得c =log 1312=log 32,且y =log 3x 在(0,+∞)上单调递增,则12=log <log 32<log 33=1,即12<c <1;综上所述:a <c <b .故选:D.【题型3 特殊值法比较大小】【例3】(2024·陕西商洛·模拟预测)设a =log 0.50.6,b =0.49―0.3,c =0.6―0.6,则a ,b ,c 的大小关系是( )A .c >b >aB .b >a >cC .b >c >aD .c >a >b【解题思路】利用幂函数、指数函数、对数函数的单调性,结合特殊值判定即可.【解答过程】因为y =log 0.5x 在(0,+∞)上单调递减,所以log 0.51<log 0.50.6<log 0.50.5,即0<a <1.因为y =x 0.6在(0,+∞)上单调递增,又0.49―0.3=0.7―0.6=,0.6―0.6=,又53>107>1>>10.6,故c >b >1,所以c >b >a .故选:A.【变式3-1】(23-24高二下·云南玉溪·期中)已知实数a,b,c 满足2a +a =2,2b +b =c =log 163,则( )A .c <a <bB .a <b <cC .a <c <bD .b <c <a【解题思路】由对数函数单调性得c <12,构造函数f(x)=2x +x,x ∈R ,由函数的单调性得12<a <b 及,即可得出判断.【解答过程】由对数函数单调性得,c =log 163<log 164=log 161612=12,构造函数f(x)=2x +x,x ∈R ,则f(a)=2a +a =2,f(b)=2b +b =因为y =2x 和y =x 单调递增,所以f(x)单调递增,因为2<f(a)<f(b),所以a <b ,又f(12)=212+12=<2,所以f(a)>f(12),即a >12,所以c <a <b ,故选:A .【变式3-2】(2024·宁夏银川·二模)若a =log 1314,b =(13)14,c =log 314,d =14则( )A .a >b >d >cB .a >b >c >dC .b >d >a >cD .a >d >b >c【解题思路】根据指数函数和对数函数的单调性判断即可.【解答过程】因为a =log 1314=log 34>log 33=1<<⇒13<b <1,log 314<log 31=0⇒c <0,所以a >b >d >c .故选:A .【变式3-3】(2024·天津和平·=2,b =log 123―log 129,c =―13,则有( )A .a <b <cB .a <c <bC .b <c <aD .b <a <c【解题思路】根据指数函数与对数函数的性质,借助特殊值0,可得a 最小,再利用b 3>c 3得出b,c 大小.=2可得a =log 132<log 131=0,b =log 123―log 129=log 1213=log 23>1,c =―13=213=>0,下面比较b,c ,因为32>=8,所以3>232,所以b =log 23>log 2232=32,而c 3=3=2<=278,故c <32,所以c <b ,综上,b >c >a .故选:B.【题型4 作差法、作商法比较大小】【例4】(2023·四川成都·一模)若a =3―14,b =―13,c =log 1225,则a ,b ,c 的大小关系为( )A .a >b >cB .b >c >aC .c >a >bD .c >b >a【解题思路】先根据指对函数的单调性可得0<a <1,0<b <1,c >1,再作商比较a,b 的大小,从而可求解.【解答过程】因为0<a =3―14<30=1,0<b =―13<=1,令a b=3―14―13=3―14+13×2―13=3112×―1,而3112×2=3×2=3×2―4=316<1,即3112×2―13<1,所以a <b ,又因为c =log 1225=log 12410>log 12510>log 1212=1,所以c >b >a .故选:D.【变式4-1】(2023·贵州六盘水·模拟预测)若a =ln22,b =ln33,c =ln55,则( )A .a <b <cB .c <b <aC .c<a<bD .a <c <b【解题思路】利用作差法,再结合对数函数y =ln x 的单调性分别判断a,b 和a,c 的大小关系,即可判断出a,b,c 的大小关系.【解答过程】因为b ―a =ln33―ln22=2ln3―3ln26=ln9―ln86>0,所以b >a ;又因为c ―a =ln55―ln22=2ln5―5ln210=ln25―ln3210<0,所以a >c ;综上所述:c <a <b .故选:C.【变式4-2】(2024·四川成都·二模)若a =ln 26,b =4ln2⋅ln 3,c =(1+ln3)2,则a,b,c 的大小关系是( )A .c <a <bB .a <b <cC .c <b <aD .b <a <c【解题思路】作差法比较a,b 的大小,利用对数的性质比较a,c 的大小.【解答过程】a =ln 26=(ln2+ln3)2,c =(lne +ln3)2因为ln2+ln3<lne +ln3,所以(ln2+ln3)2<(lne +ln3)2,即a <c ,a =ln 26=(ln2+ln3)2,b =4ln2⋅ln3,则a ―b =(ln2+ln3)2―4ln2⋅ln3=(ln2―ln3)2>0,即b <a ,所以b <a <c .故选:D.【变式4-3】(2024·全国·模拟预测)若a =20.4,b =30.25,c =log 0.70.5,则a,b,c 的大小关系为( )A .a <b <cB .b <a <cC .b <c <aD .c <a <b【解题思路】利用指数函数的单调性以及对数函数单调性可判断a,c 范围,比较它们的大小;利用作商法比较a,b 的大小,即可得答案.【解答过程】因为函数y =2x 在R 上单调递增,所以a =20.4<20.5=又a b=20.430.25===>1,所以b <a <因为0.52=0.25<0.343,故0.5<=0.732,y =log 0.7x 在(0,+∞)上单调递减,所以log 0.70.5>log 0.70.732=32>a <c ,所以实数a,b,c 的大小关系为b <a <c ,故选:B .【题型5 构造函数法比较大小】【例5】(2024·全国·模拟预测)已知a =ln 72,b =ln7×ln2,c =ln7ln2,则( )A .b <c <aB .b <a <cC .a <b <cD .a <c <b【解题思路】根据0<ln2<1得到c 的值最大,然后构造函数f (x )=(1―ln2)ln x ―ln2,根据f (x )的单调性和f (8)<0得到a <b .【解答过程】因为0<ln2<1,所以a =ln7―ln2<ln7,b <ln7,c >ln7,故c 的值最大.下面比较a ,b 的大小.构造函数f (x )=ln x ―ln2―ln x ⋅ln2=(1―ln2)ln x ―ln2,显然f (x )在(0,+∞)上单调递增.因为f (8)=ln8―ln2―ln8⋅ln2=ln2(2―ln8)=ln2(lne 2―ln8)<0,所以a ―b =f (7)<f (8)<0,所以a <b ,所以a <b <c .故选:C .【变式5-1】(2024·全国·模拟预测)设a =514,b =54,c =log 45,则a ,b ,c 的大小关系为( )A .a >b >cB .a >c >bC .b >a >cD .b >c >a【解题思路】利用常见函数的单调性比较大小即可.【解答过程】先比较a 和b ,构造函数y =x 4在上(0,+∞)单调递增,∵5=5>625256=,∴514>54,即a >b ;又∵4b =5,4c =4log 45=log 454,且45=4×256>54=625,∴ 4c =log 454<log 445=5=4b ,∴b >c ,∴a >b >c .故选:A.【变式5-2】(2024·天津和平·一模)已知a =log 0.20.3,b =log 0.30.2,c =log 23,则a,b,c 的大小关系为( )A .b <c <aB .c <b <aC .a <b <cD .a <c <b【解题思路】利用对数函数的单调性结合二次函数的性质即得.【解答过程】∵0<a =log 0.20.3<1,b =log 0.30.2>1,c =log 23>1,又b c=log 0.30.2⋅log 32=lg2―1lg3―1⋅lg2lg3=lg 22―lg2lg 23―lg3,因为函数f (x )=x 2―x =x―14,在0,f (0)=0,又因为12>lg3>lg2>0,所以f (lg3)<f (lg2)<0,所以f (lg2)f (lg3)<1,即lg 22―lg2lg 23―lg3<1,所以bc <1,∴b <c ,即a <b <c .故选:C .【变式5-3】(2023·河南·校联考模拟预测)已知实数a,b,c 满足a 2+log 2a =0,2023―b =log 2023b,c =log 7)A .a <b <cB .c <a <bC .b <c <aD .c <b <a【解题思路】利用构造函数法,结合函数的单调性确定正确答案.【解答过程】设f(x)=x 2+log 2x , f(x)在(0,+∞)上单调递增,又=―34<0,f(1)=1>0,所以12<a <1;设g(x) =―log 2023x , g(x)在(0,+∞)上单调递减,又g(1)=12023>0,g(2023)=―1<0,所以1< b <2023,因为c =log <log =12,所以c <12.综上可知,c <a <b .故选:B.【题型6 数形结合比较大小】【例6】(2024·河南·模拟预测)已知a =ln π,b =log 3π,c =,则a,b,c 的大小关系是( )A .b <a <cB .a <b <cC .c <b <aD .b<c<a【解题思路】利用对数函数和指数函数,幂函数的性质求解.【解答过程】∵e <3<π,∴a =log e π>log 3π=b >log 33=1,即a >b >1,∵a =ln π=2, c ==ln2下面比较2与 y =x 2与y =2x ,由指数函数y =2x 与幂函数y =x 2的图像与单调性可知,当x ∈(0,2)时,x 2<2x ;当x ∈(2,4)时,x 2>2x由x =(0,2),故2 <ln π<a < c ,所以b <a <c ,故选:A.【变式6-1】(2023·江西赣州·二模)若log 3x =log 4y =log 5z <―1,则( )A .3x <4y <5zB .4y <3x <5zC .4y <5z <3xD .5z <4y <3x【解题思路】设log 3x =log 4y =log 5z =m <―1,得到x =3m ,y =4m ,z =5m ,画出图象,数形结合得到答案.【解答过程】令log 3x =log 4y =log 5z =m <―1,则x =3m ,y =4m ,z =5m ,3x =3m +1,4y =4m +1,5z =5m +1,其中m +1<0,在同一坐标系内画出y =3x ,y =4x ,y =5x ,故5z <4y <3x 故选:D.【变式6-2】(2024·全国·模拟预测)已知a ==log a b,a c =log 12c ,则实数a,b,c 的大小关系为( )A .a <b <cB .a <c <bC .c <b <aD .c <a <b【解题思路】由函数单调性,零点存在性定理及画出函数图象,得到a,b,c ∈(0,1),得到log a b <1=log a a ,求出b >a ,根据单调性得到c =c<=a ,从而得到答案.【解答过程】令f (x )=―x ,其在R 上单调递减,又f (0)=1>0,f (1)=12―1=―12<0,由零点存在性定理得a ∈(0,1),则y =log a x 在(0,+∞)上单调递减,画出y 1=与y =log a x 的函数图象,可以得到b ∈(0,1),又y 2=a x 在R 上单调递减,画出y 2=a x 与y 3=log 12x 的函数图象,可以看出c ∈(0,1),<=1,故log a b <1=log a a ,故b >a ,因为a,c ∈(0,1),故a c >a 1=a ,由a c=log 12c 得,c =c<=a .综上,c <a <b .故选:D .【变式6-3】(2024·广东茂名·统考一模)已知x,y,z 均为大于0的实数,且2x =3y =log 5z ,则x,y,z 大小关系正确的是( )A .x >y >zB .x >z >yC .z >x >yD .z >y >x【解题思路】根据题意,将问题转化为函数y =2x ,y =3x ,y =log 5x 与直线y =t >1的交点的横坐标的关系,再作出图像,数形结合求解即可.【解答过程】解:因为x,y,z 均为大于0的实数, 所以2x =3y =log 5z =t >1,进而将问题转化为函数y =2x ,y =3x ,y =log 5x 与直线y =t >1的交点的横坐标的关系,故作出函数图像,如图,由图可知z >x >y 故选:C.【题型7 含变量问题比较大小】【例7】(23-24高三上·天津滨海新·阶段练习)设a 、b 、c 都是正数,且4a =6b =9c ,则下列结论错误的是( )A .c <b <aB .ab +bc =acC .4b ⋅9b =4a ⋅9cD .1c =2b ―1a【解题思路】首先根据指对运算,利用对数表示a,b,c ,再利用换底公式和对数运算,判断选项.【解答过程】设4a =6b =9c =k >1,所以a =log 4k =1log k 4,b =log 6k =1log k 6,c =log 9k =1log k 9,A.由对数函数的单调性可知,0<log k 4<log k 6<log k 9,可知c <b <a ,故A 正确;B.b (a +c )==1log k6⋅log k 36logk 4⋅log k 9=1log k6⋅2log k 6logk 4⋅log k 9=2logk 4⋅log k 9=2ac ,故B 错误;C.4a ⋅9c =(6b )2=36b =(4⋅9)b =4b ⋅9b ,故C 正确.D.1a +1c =log k 4+log k 9=log k 36=2log k 6=2b ,则1c =2b ―1a ,故D 正确.故选:B.【变式7-1】(2024·江西·模拟预测)若a e a =b ln b (a >0),则( )A .a <bB .a =bC .a >bD .无法确定【解题思路】令a e a =b ln b =k ,k >0,构造函数,作出函数图象,即可比大小.【解答过程】因为a >0,所以a e a >a >0,因为a e a=b ln b,所以b ln b>0,可得b>1,令a e a=b ln b=k,k>0,所以e a=ka ,ln b=kb,设f(x)=e x,g(x)=ln x,ℎ(x)=kx,作出它们的图象如图:由图可知a<b.故选项A正确.故选:A.【变式7-2】(2023·全国·模拟预测)已知a,b,c均为不等于1的正实数,且ln c=a ln b,ln a=b ln c,则a,b,c的大小关系是()A.c>a>b B.b>c>aC.a>b>c D.a>c>b【解题思路】分析可知,ln a、ln b、ln c同号,分a、b、c∈(0,1)和a、b、c∈(1,+∞)两种情况讨论,结合对数函数的单调性可得出a、b、c的大小关系.【解答过程】∵ln c=a ln b,ln a=b ln c且a、b、c均为不等于1的正实数,则ln c与ln b同号,ln c与ln a同号,从而ln a、ln b、ln c同号.①若a、b、c∈(0,1),则ln a、ln b、ln c均为负数,ln a=b ln c>ln c,可得a>c,ln c=a ln b>ln b,可得c>b,此时a>c>b;②若a、b、c∈(1,+∞),则ln a、ln b、ln c均为正数,ln a=b ln c>ln c,可得a>c,ln c=a ln b>ln b,可得c>b,此时a>c>b.综上所述,a>c>b.故选:D.【变式7-3】(2024·全国·模拟预测)已知正实数a,b,c满足e c+e―2a=e a+e―c,b=log23+log86,c+log2c=2,则a,b,c的大小关系为()A.a<b<c B.a<c<b C.c<a<b D.c<b<a【解题思路】根据e c+e―2a=e a+e―c可得e c―e―c=e a―e―2a,由此可构造函数f(x)=e x―e―x,根据f(x)的单调性即可判断a和c的大小;根据对数的计算法则和对数的性质可得b与2的大小关系;c+log2c=2变形为log2c=2―c,利用函数y=log2x与函数y=2―x的图象可判断两个函数的交点的横坐标c的范围,从而判断b与c的大小.由此即可得到答案.【解答过程】e c+e―2a=e a+e―c⇒e c―e―c=e a―e―2a,故令f(x)=e x―e―x,则f(c)=e c―e―c,f(a)=e a―e―a.和y=e x均为(0,+∞)上的增函数,故f(x)在(0,+∞)为增函数.易知y=―e―x=―1e x∵e―2a<e―a,故由题可知,e c―e―c=e a―e―2a>e a―e―a,即f(c)>f(a),则c>a>0.易知b=log23+log=log2>2,log2c=2―c,作出函数y=log2x与函数y=2―x的图象,如图所示,则两图象交点横坐标在(1,2)内,即1<c<2,∴c<b,∴a<c<b.故选:B.【题型8 放缩法比较大小】【例8】(2024·陕西西安·模拟预测)若a=0.311.5,b=log312,c=log26,d=)A.a>b>c B.b>a>dC.c>a>b D.b>c>a【解题思路】由题意首先得0<a<1,d=<0,进一步b=log312=1+log34>2,c=log26=1+log23>2,从而我们只需要比较log34,log23的大小关系即可求解,两式作商结合基本不等式、换底公式即可比较.【解答过程】a =0.311.5<0.310=1,所以0<a <1,d =<0,b =log 312=1+log 34>2,c =log 26=1+log 23>2,又因为log 34log 23=ln4⋅ln2ln3⋅ln3<=<1,所以b <c ,即d <a <b <c .故选:B.【变式8-1】(2023·河南郑州·模拟预测)已知a =log 35,b =c =3log 72+log 87,则( )A .a >b >cB .c >b >aC .b >a >cD .c >a >b【解题思路】根据指数函数、对数函数的性质及基本不等式判断即可.【解答过程】因为a =log 35=12log 325<12log 327=32,34=<=b =>32且b <2,c =3log 72+log 87=log 78+log 87>=2,所以c >b >a .故选:B.【变式8-2】(2023上·安徽·高二校联考阶段练习)已知a ==6―34,c =log 53―29log 35,则( )A .a <b <cB .b<c<aC .b <a <cD .c<a<b【解题思路】采用放缩法和中间值比较大小,得到a <b <c .【解答过程】因为a ==<=14,b =6―34=>=<=13,故b ∈c =log 53―29log 35=13log 527―19log 325>13log 525―19log 327=23―13=13,所以a <b <c .故选:A.【变式8-3】(2024·全国·模拟预测)已知a =log 8.14,b =log 3.1e ,c =ln2.1,,则( )A .a <c <bB .a <b <cC .c<a<bD .b<c<a【解题思路】先证明b >0,c >0,利用比商法结合基本不等式证明c <b ,再根据对数运算性质,结合对数函数性质证明a <c 即可得结论.【解答过程】因为b =log 3.1e >0,c =ln2.1>0,所以c b=ln2.1log 3.1e=ln2.1×ln3.1<==,又e 2≈7.389<e ,所以<lne =1,所以cb <1,故c <b ,因为a =log8.14=ln4ln8.1=2ln2ln8.1=又e 2≈7.389,所以8.1>e 2,所以>1,所以a <ln2,又ln2<ln2.1=c ,所以a <c ,所以a <c <b ,故选:A.一、单选题1.(2024·全国·模拟预测)设a =log 62,b =log 123,c =log 405,则( )A .a <b <cB .b <a <cC .c <a <bD .a <c <b【解题思路】取到数计算得1b =1+2lg2lg3,1c=1+3lg2lg5,作差法比较1b ,1c的大小,即可得到b,c 大小,利用中间值25即可比较a,c 大小.【解答过程】∵1b =log 312=1+log 34=1+lg4lg3=1+2lg2lg3,1c=log 540=1+log 58=1+lg8lg5=1+3lg2lg5,∴1b ―1c =2lg2lg3―3lg2lg5=2lg2×lg5―3lg2×lg3lg3×lg5=lg2(2lg5―3lg3)lg3×lg5=lg2(lg25―lg27)lg3×lg5<0,∴1b <1c ,又b >0,c >0,∴b >c .∵1c =1+log 58<1+log =1+log 5532=52,∴c >25;∵1a =log 26=1+log 23>1+log =1+log 2232=52,∴a <25,∴a <c .∴a <c <b .故选:D.2.(2024·安徽宿州·一模)已知3m =4,a =2m ―3,b =4m ―5,则( )A .a >0>bB .b >0>aC .a >b >0D .b >a >0【解题思路】由作差法,结合对数换底公式、对数运算性质、基本不等式比较得log 23>log 34>log 45,即可判断大小.【解答过程】由3m =4⇒m =log 34,log 23―log 34=lg3lg2―lg4lg3=lg 23―lg2⋅lg4lg2⋅lg3>=4lg 23―lg 284lg2⋅lg3=lg 29―lg 284lg2⋅lg3>0,log 34―log 45=lg4lg3―lg5lg4=lg 24―lg3⋅lg5lg3⋅lg4>=4lg 24―lg 2154lg3⋅lg4=lg 216―lg 2154lg3⋅lg4>0,∴log 23>log 34>log 45,∴b =4m ―5>4log 45―5=0,a =2m ―3<2log 23―3=0,∴b >0>a .故选:B.3.(2024·贵州毕节·一模)已知a =3log 83,b =―12log 1316,c =log 43,则a ,b ,c 的大小关系为( )A .a >b >cB .c >a >bC .b >c >aD .b >a >ca,b,c ,并判断范围,采用作差法结合基本不等式可判断a >b ,即可得答案.【解答过程】由题意可得a =3log 83=3×log 23log 223=log 23>1,b =―12log 1316=―12×log 316log 313=log 34>1,0<c =log 43<1,又log 23―log 34=lg3lg2―lg4lg3=(lg3)2―lg2lg4lg2lg3,由于lg2>0,lg4>0,lg2≠lg4,∴lg2lg4<(lg2+lg42)2=2<(lg3)2,故log 23―log 34>0,∴a >b ,综合可得a >b >c ,故选:A.4.(2023·内蒙古赤峰·模拟预测)设a =,b =,c =log 34(log 34),则( )A .c <b <aB .a <b <cC .c <a <bD .a <c <b【解题思路】利用指数函数,对数函数的单调性,找出中间值0,1,让其和a,b,c 进行比较,从而得出结果.【解答过程】由指数函数的单调性和值域,y =在R 上单调递增,故a =>=1;由y =的值域,且在R 上单调递增可知,0<b =<=1;根据对数函数的单调性,y =log 3x 在(0,+∞)上单调递增,故log 34>log 33=1,由y =log 34x 在(0,+∞)上单调递减,故c =log 34(log 34)<log 341=0.结合上述分析可知:c <0<b <1<a .故选:A.5.(2024·云南昆明·模拟预测)已知a =e 13,b =ln2,c =log 32,则a,b,c 的大小关系为( )A .a >c >bB .a >b >cC .b >c >aD .c >b >a【解题思路】引入中间变量1,再利用作差法比较b,c 的大小,即可得答案;【解答过程】∵ a =e 13>e 0=1,b =ln2<lne =1,c =log 32<log 33=1∴ a 最大,∵ b ―c =ln2―log 32=lg2lge―lg2lg3=lg2⋅>0,∴ b >c ,∴ a >b >c ,故选:B.6.(2024·陕西宝鸡·一模)已知实数a,b,c 满足e 2a 2=e 3b 3=e 5c 5=2,则( )A .a >b >cB .a <b <cC .b >a >cD .c >a >b【解题思路】先应用指对数转换求出a,b,c ,再转化成整数幂比较即可.【解答过程】因为e 2a2=e 3b 3=e 5c 5=2,所以e 2a =4,e 3b =6,e 5c =10,即得2a =ln 4,3b =ln 6,5c =ln10得a =ln 2,b ==因为y =ln x 是(0,+∞)上的增函数,比较a,b,c ,的大小关系 ,15次幂,因为幂函数y =x 15在(0,+∞)上是单调递增的,比较215,65,103即可,因为215=524288,65=7776,103=1000 所以215>103>65即2>>a >b >c .故选:A.7.(2023·湖南永州·一模)已知a =log 3π,b =1log 3π―1,c =12―log 3π,则( )A .a <b <cB .b <c <aC .c <a <bD .a <c <b【解题思路】先利用对数函数单调性求出a ∈(1,1.5),从而确定b >2,c ∈(1,2),作差法判断出a <c ,从而求出答案.【解答过程】a =log 3π>log 33=1,因为332=>π,所以a =log 3π<log 3332=1.5,所以a ∈(1,1.5),log 3π―1∈(0,0.5),故b =1log3π―1>2,2―log 3π∈(0.5,1),故c =12―log 3π∈(1,2),令a ―c =log 3π―12―log 3π=2log 3π―(log 3π)2―12―log 3π=―(log 3π―1)22―log 3π<0所以a <c <b .故选:D.8.(2023·陕西西安·一模)已知函数f(x)=―2x ,若2a =log 2b =c ,则( )A .f(b)<f(c)<f(a)B .f(a)<f(b)<f(c)C .f(a)<f(c)<f(b)D .f(c)<f(b)<f(a)【解题思路】在同一坐标系中作y =c,y =2x ,y =log 2x,y =x 的图像,得到a <c <b ,借助f(x)=―2x 的单调性进行判断即可.【解答过程】f(x)=―2x 在R 上单调递减,在同一坐标系中作y =c,y =2x ,y =log 2x,y =x 的图像,如图:所以a <c <b ,故f(b)<f(c)<f(a),故选:A.二、多选题9.(2024·河南洛阳·模拟预测)下列正确的是( )A.2―0.01>2―0.001B.log>log2π―1C.log1.85<log1.75D.log33.01>e―0.01【解题思路】利用指数函数的性质判断A;由对数函数的性质判断B,C;由对数函数的性质可得log3 3.01>1,由指数函数的性质可得e―0.01<1,即可判断.【解答过程】解:对于A,因为―0.01<―0.001,所以2―0.01<2―0.001,所以A错误;对于B,因为log>log2π2=log2π―1,所以B正确;对于C,因为log1.85>0,log1.75>0,所以log1.85=ln5ln1.8<ln5ln1.7=log1.75,所以C正确;对于D,因为log33.01>log33=1,e―0.01<e0=1,所以log33.01>e―0.01,所以D正确.故选:BCD.10.(2024·重庆·模拟预测)若b>c>1,0<a<1,则下列结论正确的是()A.b a<c a B.log b a>log c aC.cb a<bc a D.b log c a>c log b a【解题思路】由已知可得,由幂函数性质可判断A; 由对数函数性质可判断B; 由幂函数性质可判断C;由不等式的性质可判断D.【解答过程】对于A:∵0<a<1,幂函数y=x a在(0,+∞)上单调递增,且b>c>1,∴b a>c a,故选项A错误;对于B:∵0<a<1,∴函数y=log x在(0,+∞)上单调递减,又∵b>c>1,∴log a b<log a c<log a1=0,∴0>1log b c >1log c a,即0>log b a>log c a,故B正确;对于选项C:∵0<a<1,则a―1<0,∵幂函数y=x a―1在(0,+∞)上单调递减,且b>c>1,∴b a―1<c a―1,∴cb a<bc a,故选项C正确;对于选项D:由选项B可知:0>log b a>log c a,∴0<―log b a<―log c a,∵b>c>1,∴c(―log b a)<b(―log c a),∴b log c a<c log b a,故D错误.故选:BC.11.(2024·重庆·一模)已知3a=5b=15,则下列结论正确的是()A.lg a>lg b B.a+b=abC>D.a+b>4【解题思路】根据指对互化与运算以及指数函数、对数函数单调性即可判断ABC,利用基本不等式即可判断D.【解答过程】由题意得a=log315>log31>0,b=log515>log51=0,0<1a =log153,0<1b=log155,则0<1a<1b,则a>b>0,对A,根据对数函数y=lg x在(0,+∞)上单调递增,则lg a>lg b,故A正确;对B,因为1a +1b=log153+log155=1,即a+bab=1,则a+b=ab,故B正确;对C,因为a>b>0,根据指数函数y=在R<,故C错误;对D,因为a>b>0,1a +1b=1,a+b=(a+b=2+ba +ab≥2+=4,当且仅当a=b时等号成立,而显然a≠b,则a+b>4,故D正确;故选:ABD.三、填空题12.(2023·北京昌平·二模)3―2,213,log25三个数中最大的数是log25.【解题思路】利用特殊值1和2作为“桥梁”比较大小即可.【解答过程】∵1<213=<23―2==19<1,log25>log24=2,∴log25>213>3―2,即三个数中最大的数是log25.故答案为:log25.13.(2024·北京通州·三模)已知a=2―1.1,b=log1413,c=log23,则三者大小关系为a<b<c(按从小到大顺序)【解题思路】根据指数函数和对数函数的性质确定出a,b,c的范围,即可求解.【解答过程】因为a=2―1.1<2―1=12,b=log1413=log43>log42=12,且b=log1413=log43<1,c=log23>log22=1,故a<b<c,故答案为:a <b <c .14.(2023·吉林长春·模拟预测)已知a =b =,c =a ,b ,c 的大小关系为c <a <b .【解题思路】由对数函数及指数函数单调性得到a ∈(0,1),b >1,c =―12,从而得到大小关系.【解答过程】因为y =在(0,+∞)上单调递减,1>>故a =<=1且a =>=0,所以a ∈(0,1),因为y =在R 上单调递减,<0,所以b =>=1,c ==lne―12=―12,故c <a <b .故答案为:c <a <b .四、解答题15.(23-24高一·全国·随堂练习)已知x =lnπ,y =log 52,z =e ―12.(1)比较x ,y 的大小;(2)比较y ,z 的大小.【解题思路】(1)利用对数函数的单调性,x,y 和中间值1比较大小,即可判断;(2)利用对数函数的单调性,以及对数式的运算,y,z 和中间值12比较大小,即可判断.【解答过程】(1)因为π>e ,所以lnπ>lne =1,即x =lnπ∈(1,+∞)因为1<2<5,所以0=log 51<log 52<log 55=1,即log 52∈(0,1),所以x >y ;(2)y =log 52<log =12,且log 52>0,所以log 52∈0,z =e ―12=>=12,所以e ―12∈+∞,所以y <z .16.(23-24高三·全国·对口高考)(1)比较a a b b 与b a a b (a >0,b >0)的大小;(2)已知a >2,比较log (a―1)a 与log a (a +1)大小【解题思路】(1)利用作商法,分类讨论即可;(2)利用做差法、换底公式以及不等式的性质分析即可.【解答过程】(1)因为a>0,b>0,所以a a b bb a a b=,所以①当a=b>0时,a a b bb a a b==1,所以a a b b=b a a b,②当a>b>0时,ab>1,a―b>0,>1,所以a a b b>b a a b,③当b>a>0时,0<ab<1,a―b<0,>1,所以a a b b>b a a b,综上所述:当a>0,b>0,a a b b≥b a a b.(2)log(a―1)a―log a(a+1)=lg alg(a―1)―lg(a+1)lg a=lg2a―lg(a+1)lg(a―1)lg a lg(a―1),因为a>2,所以lg(a+1)>0,lg(a―1)>0,lg a>0,所以lg a lg(a―1)>0,由lg(a+1)lg(a―1)<=<=lg2a,所以lg2a―lg(a+1)lg(a―1)>0,所以lg2a―lg(a+1)lg(a―1)lg a lg(a―1)>0,即log(a―1)a―log a(a+1)>0,故log(a―1)a>log a(a+1).17.(23-24高一·湖南·课后作业)比较a,b,c的大小:(1)已知1<x<2,a=(log2x)2,b=log2x2,c=log2(log2x);(2)已知a=log36,b=log510,c=log714.【解题思路】(1)根据1<x<2,求出log2x的范围,由此判断c<0,0<a<b;(2)a=1+log32,b=1+log52,c=1+log72,由换底公式比较log32,log52,log72大小即可.【解答过程】(1)∵1<x<2,∴0=log21<log2x<log22=1,即log2x∈(0,1),∴c=log2(log2x)<log21=0,a=(log2x)2<(log2x)1=log2x,∴0<a<log2x,∴b=log2x2=2log2x>log2x>a,∴c<0<a<b,∴c<a<b;(2)∵a=log36=log3(3×2)=1+log32,b=log510=log5(5×2)=1+log52,c=log714=log7(7×2)=1+log72,又∵0<lg3<lg5<lg7,∴lg2lg3>lg2lg5>lg2lg7,∴log32>log52>log72,∴1+log32>1+log52>1+log72,即a>b>c﹒18.(23-24高一上·广东江门·阶段练习)已知正实数x,y,z满足3x=4y=6z.(1)求证:1z ―1x=12y;(2)比较3x,4y,6z的大小.【解题思路】(1)令3x=4y=6z=m,利用指数式和对数式的互化求出x,y,z,再利用对数的运算即可的证得结果;(2)因为正实数x,y,z,利用作商法可证明大小关系.【解答过程】(1)证明:令3x=4y=6z=m,利用指数式和对数式的互化知x=log3m,y=log4m,z=log6m则1x =log m3,1y=log m4,1z=log m6∴1z ―1x =log m 6―log m 3=log m 2=12y .(2)3x <4y <6z证明:因为正实数x ,y ,z ,∴3x >0, 4y >0, 6z >0,∴3x 4y =3log 3m 4log 4m =3lg m lg34lg m lg4=34×lg4lg3=34log 34=log<3,∴log <1,∴3x <4y∴4y 6z =4log 4m 6log 6m =4lg m lg46lg m lg6=23×lg6lg4=23log 46=log<2,∴log <1,∴4y <6z ∴3x <4y <6z .19.(23-24高一上·广东广州·阶段练习)已知函数f(x)=x 2x 2+1(1)判断并证明函数f(x)在区间(0,+∞)上的单调性;(2)已知a =f (20.5),b =f (log 25),c =f (0.25),试比较三个数a ,b ,c 的大小,并说明理由.【解题思路】(1)根据函数单调性的定义判断和证明即可;(2)先比较20.5,log 25,0.25三个数的大小,再利用函数f (x )的单调性即可比较a ,b ,c 的大小.【解答过程】(1)函数f(x)=x 2x 2+1=1―1x 2+1,任取x 1,x 2∈(0,+∞),且x 1<x 2则f(x1)―f(x 2)=1―1x 21+1―1―=1x 22+1―1x 21+1 =22=因为x 1,x 2∈(0,+∞),且x 1<x 2,所以x 22+1>0,x 21+1>0,x 1―x 2<0,x 1+x 2>0所以f(x 1)―f(x 2)<0,即f(x 1)<f(x 2),所以函数f (x )在区间(0,+∞)上是增函数.(2)因为20.5>20=1,2=log 24<log 25<log 28=3,0<0.25<0.20=1,所以0<0.25<20.5<log 25,由(1)可知函数f (x )在区间(0,+∞)上是增函数,所以f (0.25)<f (20.5)<f (log 25),即c <a <b .。
指数、对数比较大小练习题(1+2+3+8=250)

指数、对数比拟大小1.以下图是指数函数〔1〕x y a =,〔2〕x y b =,〔3〕x y c =,〔4〕x y d =的图象,那么a ,b ,c ,d 与1的大小关系是〔 〕A .1a b c d <<<<B .1b a d c <<<<C .1a b c d <<<<D .1a b d c <<<<2.图中曲线是对数函数y =log a x 的图象,a取4313,,,3510四个值,那么相应于C 1,C 2,C 3,C 4的a 值依次为〔 〕A .101,53,34,3B .53,101,34,3C .101,53,3,34D .53,101,3,343.()log a f x x =,()log b g x x =,()log c r x x =,()log d h x x =的图象如下图那么a ,b ,c ,d 的大小为〔 〕A .c d a b <<<B .c d b a <<<C .d c a b <<<D .d c b a <<<4.如果01a <<,那么以下不等式中正确的选项是〔 〕 A .1132(1)(1)a a -<- B .1(1)1a a +-> C .(1)log (1)0a a -+> D .(1)log (1)0a a +-<5.假设log 2log 20n m >>时,那么m 与n 的关系是〔 〕A .1m n >>B .1n m >>C .10m n >>>D .10n m >>> 6.log 5log 50m n <<,那么m ,n 满足的条件是〔 〕A .1m n >>B .1n m >>C .01n m <<<D .01m n <<< 7.设5.1348.029.0121,8,4-⎪⎭⎫ ⎝⎛===y y y ,那么〔 〕A .213y y y >>B .312y y y >>C .321y y y >>D .231y y y >> 8.以下四个数中的最大者是〔 〕y x1O (4)(3)(2)(1)A .2(ln 2)B .ln(ln 2) C. D .ln 2 9.假设a =2log π,b =7log 6,c =2log 0.8,那么〔 〕A .a >b >cB .b >a >cC .c >a >bD .b >c >a 10.设32log ,log log a b c π===〔 〕 A .a b c >>B .a c b >>C .b a c >>D .b c a >>11.设3.02131)21(,3log ,2log ===c b a ,那么〔 〕A .a b c >>B .a c b >>C .b a c >>D .b c a >>12.设232555322555a b c ===(),(),(),那么a ,b ,c 的大小关系是〔 〕A .a b c >>B .a c b >>C .b a c >>D .b c a >>13.设2log 3P =,3log 2Q =,23log (log 2)R =,那么〔 〕 A .R Q P <<B .P R Q <<C .Q R P <<D .R P Q <<14.设2554log 4,(log 3),log 5a b c ===,那么〔 〕 A .a b c >>B .a c b >>C .b a c >>D .b c a >>15.函数()lg f x x =,0<a <b ,且()()f a f b >,那么〔 〕A .1ab >B .1ab <C .1ab =D .(1)(1)0a b --> 16.设11333124log ,log ,log ,,,233a b c a b c ===则的大小关系是 A .a b c <<B .c b a <<C .b a c <<D .b c a <<17.设c b a ,,均为正数,且a a21log 2=,b b21log 21=⎪⎭⎫ ⎝⎛,c c2log 21=⎪⎭⎫⎝⎛.那么〔 〕A .c b a <<B .a b c <<C .b a c <<D .c a b <<18.ln 2ln 3ln 5,,235a b c ===,那么有〔 〕 A .a>b>c B .c<b<a C .c<a<b D .b<a<c“六法〞比拟指数幂大小对于指数幂的大小的比拟,我们通常都是运用指数函数的单调性,但很多时候,因幂的底数或指数不相同,不能直接利用函数的单调性进行比拟.这就必须掌握一些特殊方法.1.转化法例1 比拟12(322)-+与23(21)-的大小.解:∵22322(21)(21)-+=+=-, ∴11222(322)[(21)]21---+=-=-.又∵0211<-<,∴函数(21)x y =-在定义域R 上是减函数. ∴2321(21)-<-,即2132(322)(21)-+<-.评注:在进行指数幂的大小比拟时,假设底数不同,那么首先考虑将其转化成同底数,然后再根据指数函数的单调性进行判断.2.图象法例2 比拟0.7a与0.8a的大小.解:设函数0.7x y =与0.8x y =,那么这两个函数的图象关系如图.当x a =,且0a >时,0.80.7a a >;当x a =,且0a <时,0.80.7a a <;当0x a ==时,0.80.7a a=.评注:对于不同底而同指数的指数幂的大小的比拟,利用图象法求解,既快捷,又准确. 3.媒介法例3 比拟124.1-,345.6,1313⎛⎫- ⎪⎝⎭的大小.解:∵1313004215.6 5.61 4.1 4.103-⎛⎫>==>>>- ⎪⎝⎭,∴13134215.6 4.13-⎛⎫>>- ⎪⎝⎭. 评注:当底数与指数都不相同时,选取适当的“媒介〞数〔通常以“0〞或“1〞为媒介〕,分别与要比拟的数比拟,从而可间接地比拟出要比拟的数的大小.4.作商法例4 比拟a ba b 与b aa b 〔0a b >>〕的大小.解:∵a b a b a ba b b a a b a b a a a a b b a b b b --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,又∵0a b >>,∴1ab>,0a b ->. ∴1a ba b -⎛⎫> ⎪⎝⎭,即1a bb a a b a b>.∴a b b a a b a b >.评注:当底数与指数都不同,中间量又不好找时,可采用作商比拟法,即对两值作商,根据其值与1的大小关系,从而确定所比值的大小.当然一般情况下,这两个值最好都是正数.5.作差法例5 设0m n >>,0a >,且1a ≠,试比拟m m a a -+与n na a -+的大小.解:()()m m n n m m n n a a a a a a a a ----+-+=+--()()m n m n a a a a --=-+-(1)(1)(1)()n m n m m n m n n m a a a a a a a -----=-+-=--.〔1〕当1a >时,∵0m n ->,∴10m na -->.又∵1na >,1ma -<,从而0n m a a -->.∴(1)()0m n n m aa a ---->.∴m m n n a a a a --+>+.〔2〕当01a <<时,∵1m na-<,即10m n a --<.又∵0m n >>,∴1na <,1ma ->,故0n m a a -<.∴(1)()0m nn m aa a ---->.∴m m n n a a a a --+>+.综上所述,mmn n a aa a --+>+.评注:作差比拟法是比拟两个数值大小的最常用的方法,即对两值作差,看其值是正还是负,从而确定所比值的大小. 6.分类讨论法 例6 比拟221xa +与22xa +〔0a >,且1a ≠〕的大小.分析:解答此题既要讨论幂指数221x +与22x +的大小关系,又要讨论底数a 与1的大小关系. 解:〔1〕令22212x x +>+,得1x >,或1x <-.①当1a >时,由22212x x +>+,从而有22212xxa a ++>;②当01a <<时,22212x x aa++<.〔2〕令22212x x +=+,得1x =±,22212xxa a ++=.〔3〕令22212x x +<+,得11x -<<.①当1a >时,由22212x x +<+,从而有22212xxa a ++<;②当01a <<时,22212x xaa ++>.评注:分类讨论是一种重要的数学方法,运用分类讨论法时,首先要确定分类的标准,涉及到指数函数问题时,通常将底数与1的大小关系作为分类标准.。
(完整版)指数函数与对数函数高考题及答案
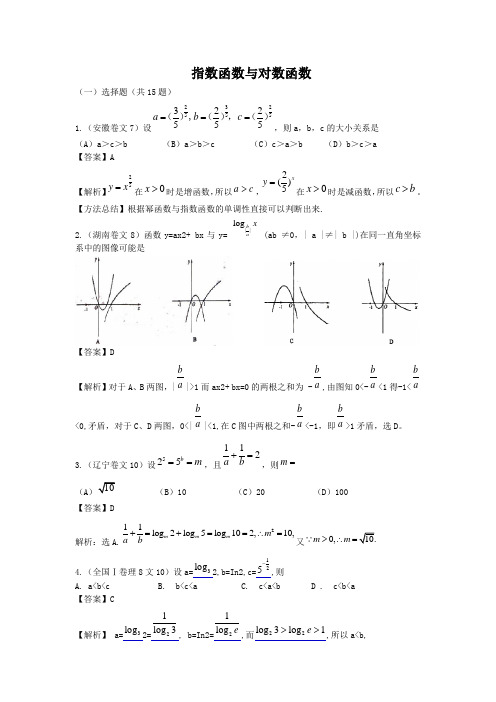
指数函数与对数函数(一)选择题(共15题)1.(安徽卷文7)设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a【答案】A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾,对于C 、D 两图,0<|b a |<1,在C 图中两根之和-b a <-1,即ba >1矛盾,选D 。
3.(辽宁卷文10)设525bm ==,且112a b +=,则m =(A(B )10 (C )20 (D )100 【答案】D解析:选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.(全国Ⅰ卷理8文10)设a=3log 2,b=In2,c=125-,则A. a<b<cB. b<c<aC. c<a<b D . c<b<a 【答案】C【解析】 a=3log 2=21log 3, b=In2=21log e ,而22log 3log 1e >>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.(全国Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a +又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.(山东卷文3)函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>,所以()()22log 31log 10x f x =+>=,故选A 。
高考指数对数运算比较大小专练

函 数 专 练姓名__________ 得分__________1.三个数7.06=a ,66=b ,06=c 的大小顺序是 ( )A.b <c <aB. b <a <cC.c <a <bD. c <b <a2.三个数7.06=a ,67.0=b ,67,0log =c 的大小顺序是 ( )A.b <c <aB. b <a <cC.c <a <bD. c <b <a 3. 已知6121og a =,1.0121og b =,9.0121og c =,则 ( )A.b <c <aB. b <a <cC.c <a <bD. c <b <a4.,20.3b -=,则,,a b c 的大小关系是( ) A .a b c >> B .a c b >> C .c b a >> D .b a c >>5.20.34log 4,log 3,0.3a b c -===,则( ) A .a c b << B .c b a << C .a b c << D .b a c <<6 ( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >>7.三个数60.770.760.6,,的大小关系为( ) A. 670.70.70.66<< B.60.770.760.6<< C. 70.760.660.7<< D.760.70.60.76<<8.,20.3b -=,则,,a b c 的大小关系是( )A .a b c >>B .a c b >>C .c b a >>D .b a c >>9,πln =c ,则 ( )A.a b c <<B.a c b <<C.c a b <<D.b a c <<10,则c b a ,,的大小关系是( )A .c b a <<B .a c b <<C .b c a <<D .a b c <<11则c b a ,,的大小关系是 ( )A. c b a >>B.a c b >>C.a b c >>D.b c a >> 12. 函数1ln --=x e y x的图像大致是( )13. 设)()(,2b x a x y b a --=<函数的图像可能是( )14. 已知a 是实数,则函数)(x f ax a sin 1+=的图象不可能...是( )15. 设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个16. 函数xx y +-=22log 2的图象( )(A )关于原点对称 (B )关于直线x y -=对称(C )关于y 轴对称(D )关于直线x y =对称17. 函数x x f 2log 1)(+=与x x g -=12)(在同一直角坐标系下的图像大致是( )A .B .C .D .18. 函数y =16-x -x 2的定义域是 . 19. 函数)1(111)(x g xx f ++-=的定义域是 .20. 若f ()x =1log 12()2x +1,则f ()x 的定义域为.21. 函数1()ln(1)f x x =++的定义域为_____________. 22. 函数x x f 6log 21)(-=的定义域为 ___________ . 23. 已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >0,x +1,x ≤0.若f (a )+f (1)=0,则实数a 的值等于 . 24. 设⎩⎨⎧≤>=0,100,1)(x x gx x f x ,则))2((-f f.25. 设函数⎩⎨⎧>≤-=0,0,)(2x x x x x f ,若4)(=a f ,则实数=a .26. 已知函数f (x )=⎩⎪⎨⎪⎧2x ,x ≥2,(x -1)3,x <2.若关于x 的方程f (x )=k 有两个不同的实根,则实数k 的取值范围是 .27. 曲线y =e x 在点A (0,1)处的切线斜率为 . 28.曲线y =-x 3+3x 2在点(1,2)处的切线方程为 .29. 曲线)1ln 3(+=x x y 在点)1,1(处的切线方程为 . 30. 曲线3y x =在点(11),处的切线与x 轴、直线2x =所围成的三角形的面积为 .30. 函数f (x )=x -cos x 在[0,+∞)内有 个零点. 31. 方程|x |=cos x 在(-∞,+∞)内由 个根. 32.求下列函数的导数.x x f sin )()1(= 2sin )()2(x x f = x x f cos )()3(= )cos()()4(2x x x f -=x x f ln )()5(= )2ln()()6(2x x x f += x x f 1)()7(=x xx f ln )()8(=22)()9(+=x e x f )42ln()()10(+-=x e x f xx e ax x x f )()()11(2+-=33.已知函数x(-=求曲线()2)f lnxxA f处的切线方程;y f x=在点(1,(1))。
历届高考中的“指数函数和对数函数”试题汇编大全

历届高考中的“指数函数和对数函数〞试题汇编大全一、选择题:〔2006年〕1.〔2006XX 文〕函数1()x y ex R +=∈的反函数是〔 〕A .1ln (0)y x x =+>B .1ln (0)y x x =->C .1ln (0)y x x =-->D .1ln (0)y x x =-+>2.〔2006理〕已知⎩⎨⎧≥<+-=1,log 1,4)13()(x x x a x a x f a 是(,)-∞+∞上的减函数,那么a 的取值范围是〔A 〕(0,1) 〔B 〕1(0,)3〔C 〕11[,)73〔D 〕1[,1)73.〔2006文〕已知(3)4,1()log ,1a a x a x f x x x --⎧=⎨≥⎩<,是〔-∞,+∞〕上的增函数,那么a 的取值范围是〔A 〕(1,+∞) 〔B 〕(-∞,3) (C)⎪⎭⎫⎢⎣⎡3,53 (D)(1,3) 4.〔2006XX 理〕函数y=㏒21-x x(x ﹥1)的反函数是 A.y =122-x x (x >0) B.y = 122-x x(x <0)C.y =x x 212- (x >0)D. .y =xx 212- (x <0) 5.〔2006XX 文〕已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设63(),(),52a f b f ==5(),2c f =则〔A 〕a b c << 〔B 〕b a c << 〔C 〕c b a << 〔D 〕c a b <<6、〔2006湖北文、理〕设f(x)=x x -+22lg ,则)2()2(xf x f +的定义域为 A. ),(),(-4004 B.(-4,-1) (1,4) C. (-2,-1) (1,2) D. (-4,-2) (2,4)7.〔2006湖南文〕函数x y 2log =的定义域是A .(0,1]B . (0,+∞) C. (1,+∞) D . [1,+∞) 8.〔2006湖南理〕函数y =( )A.(3,+∞)B.[3, +∞)C.(4, +∞)D.[4, +∞)9.〔2006XX 文、理〕与方程221(0)xx y ee x =-+≥的曲线关于直线y x =对称的曲线的方程为〔 〕A.ln(1)y x =+ B.ln(1)y x =- C.ln(1)y x =-+D.ln(1)y x =--10、〔2006全国Ⅰ卷文、理〕已知函数xy e =的图象与函数()y f x =的图象关于直线y x =对称,则A .()22()x f x e x R =∈B .()2ln 2ln (0)f x x x =>C .()22()x f x e x R =∈D .()2ln ln 2(0)f x x x =+>11.〔2006全国Ⅱ卷文、理〕已知函数()ln 1(0)f x x x =+>,则()f x 的反函数为〔A 〕1()x y e x R +=∈〔B 〕1()x y e x R -=∈ 〔C 〕1(1)x y e x +=>〔D 〕1(1)x y e x -=> 12.〔2006全国Ⅱ卷理〕函数y =f (x )的图像与函数g (x )=log 2x (x >0)的图像关于原点对称,则f (x )的表达式为(A )f (x )=1log 2x (x >0) (B )f (x )=log 2(-x )(x <0)(C )f (x )=-log 2x (x >0) (D )f (x )=-log 2(-x )(x <0)13.〔2006XX 文、理〕函数y=1+a x (0<a <1)的反函数的图象大致是〔A 〕 〔B 〕 〔C 〕 〔D 〕14.〔2006XX 文、理〕设f (x )=1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩则不等式f (x )>2的解集为 (A)〔1,2〕⋃〔3,+∞〕 (B)〔10,+∞〕 (C)〔1,2〕⋃〔10,+∞〕(D)〔1,2〕15.〔2006陕西文〕设函数f (x )=log a (x +b )(a >0,a ≠1)的图象过点〔0,0〕,其反函数过点〔1,2〕,则a +b 等于A .3B .4C .5D .616. 〔2006陕西理〕设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( )A.6B.5C.4D.317.〔2006四川文〕函数ln(1)(1)y x x =->的反函数是 〔A 〕1()1()x f x e x R -=+∈〔B 〕1()101()x fx x R -=+∈〔C 〕1()1(1)x f x e x -=+> 〔D 〕1()1(1)x f x e x -=+>18.〔2006XX 文〕如果函数2()(31)(01)xxf x a a a a a =-->≠且在区间[)0+,∞上是增函数,那么实数a的取值范围是〔 〕A.203⎛⎤ ⎥⎝⎦, B.13⎫⎪⎪⎣⎭C.(D.32⎡⎫+⎪⎢⎣⎭,∞19、〔2006XX 理〕已知函数)(x f y =的图象与函数xa y =〔0>a 且1≠a 〕的图象关于直线x y =对称,记]1)2(2)()[()(-+=f x f x f x g .若)(x g y =在区间]2,21[上是增函数,则实数a 的取值范围是〔 〕 A .),2[+∞B .)2,1()1,0( C .)1,21[ D .]21,0(20.〔2006XX 文〕设2log 3P =,3log 2Q =,23log (log 2)R =,则〔 〕 A.R Q P << B.P R Q << C.Q R P << D.R P Q <<21.〔2006XX 文〕已知1122log log 0m n <<,则(A) n <m <1 (B) m <n <1 (C)1<m <n (D)1<n <m22.〔2006XX 理〕已知0<a <1,log 1m <log 1n <0,则(A)1<n <m (B) 1<m <n (C)m <n <1 (D) n <m <123、〔2006广东〕函数2()lg(31)f x x ++的定义域是 A.1(,)3-+∞ B.1(,1)3- C.11(,)33- D.1(,)3-∞-〔2005年〕1.(2005全国卷Ⅰ理、文)设10<<a ,函数)22(log )(2--=xx a a a x f ,则使0)(<x f 的x 的取值范围是〔 〕A .()0,∞-B .()+∞,0C .()3log ,a ∞-D .()+∞,3log a2.(2005全国卷Ⅲ理、文)若ln 2ln 3ln 5,,235a b c ===,则〔 〕 A .a <b<c B .c<b<a C .c<a <bD .b<a <c3.(2005全国卷Ⅲ文科)设713=x,则 〔 〕 A .-2<x<-1 B .-3<x<-2 C .-1<x<0D .0<x<14.(2005XX 理科)若函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是 〔 〕A .)1,41[B . )1,43[C .),49(+∞D .)49,1( 5.(2005XX 理科)设)(1x f-是函数)1( )(21)(>-=-a a a x f x x的反函数,则使1)(1>-x f 成立的x 的取值范围为〔 〕A .),21(2+∞-a aB .)21,(2a a --∞C . ),21(2a aa -D . ),[+∞a 6.(2005XX 文科)若函数)1,0( )2(log )(2≠>+=a a x x x f a 在区间)21,0(内恒有f (x )>0,则f (x )的单调递增区间为()A .)41,(--∞B .),41(+∞-C .(0,∞)D .)21,(--∞ 7.(2005XX 文)已知c a b 212121log log log <<,则( )A .ca b 222>>B .cba222>>C .abc222>> D .bac222>>8.(2005XX 理、文)若函数121)(+=x x f ,则该函数在()+∞∞-,上是〔〕A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值9.(2005湖南理、文)函数f (x )=x21-的定义域是〔 〕A .(-∞,0]B .[0,+∞)C .〔-∞,0〕D .〔-∞,+∞〕10.(2005春考理科)函数y=|log 2x|的图象是 〔 〕11.(2005XX 理、文)函数bx ax f -=)(的图象如图,其中a 、b 为常数,则下列结论正确的是〔 〕 A .0,1<>b aB .0,1>>b aC .0,10><<b aD .0,10<<<b a12.(2005XX 卷)函数1ln(2++=x x y 〕的反函数是〔〕A .2x x e e y -+=B .2xx e e y -+-=C .2x x e e y --=D .2xx e e y ---=13.(2005XX 卷)若011log 22<++aa a,则a 的取值范围是 〔 〕A .),21(+∞B .),1(+∞C .)1,21(D .)21,0(14.(2005XX 理、文)已知实数a ,b 满足等式,)31()21(ba=下列五个关系式①0<b <a ②a <b <0③0<a <b ④b <a <0⑤a =b 其中不可能...成立的关系式有 〔 〕A .1个B .2个C .3个D .4个15.(2005XX 文科)函数)34(log 1)(22-+-=x x x f 的定义域为 〔 〕A .〔1,2〕∪〔2,3〕B .),3()1,(+∞⋃-∞C .〔1,3〕D .[1,3]16.(2005重庆文科)不等式组⎩⎨⎧>-<-1)1(log ,2|2|22x x 的解集为 ( )A .)3,0(B .)2,3(C .)4,3(D .)4,2(17、〔2005XX 〕函数)(321R x y x∈+=-的反函数的解析表达式为〔 〕A .32log 2-=x y B .23log 2-=x y C .23log 2x y -= D .xy -=32log 2 18.(2005湖北卷理、文)函数|1|||ln --=x e y x 的图象大致是〔 〕A 1 x y OB 1 x y OC 1 xy O D1xyO19.(2005湖北理、文)在x y x y x y y x2cos ,,log ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是〔 〕 A .0B .1C .2D .320.〔2005XX 文、理〕下列函数中既是奇函数,又是区间[]1,1-上单调递减的是〔A 〕()sin f x x = (B) ()1f x x =-+ (C) 1()()2x x f x a a -=+ (D)2()2xf x lnx-=+ 21.(2005XX 理、文)函数⎪⎩⎪⎨⎧≥<<-=-0,01,)sin()(12x ex x x f x π,若2)()1(=+a f f ,则a 的所有可能值为〔 〕 A.1 B.1,22-C.22- D. 1,22 22.(2005XX 理科) 01a <<,下列不等式一定成立的是〔 〕A .(1)(1)log (1)log (1)2a a a a +--++>B .(1)(1)log (1)log (1)a a a a +--<+C .(1)(1)log (1)log (1)a a a a +--++<(1)(1)log (1)log (1)a a a a +--++D .(1)(1)log (1)log (1)a a a a +---+<(1)(1)log (1)log (1)a a a a +---+23.(2005XX 文科)下列大小关系正确的是〔 〕A .20.440.43log 0.3<<; B .20.440.4log 0.33<<;C .20.44log 0.30.43<<;D .0.424log 0.330.4<<〔2004年〕1.〔2004XX 文、理〕已知函数y=log 2x 的反函数是y=f -1(x),则函数y= f -1(1-x)的图象是2.〔2004湖南文科〕函数)11lg(xy -= 的定义域为〔 〕A .{}0|<x xB .{}1|>x xC .{}10|<<x xD .{}10|><或x x3.〔2004湖南理科〕设)(1x f-是函数)1(log )(2+=x x f 的反函数,若8)](1)][(1[11=++--b fa f,则f(a —b)的值为(A) 1 (B)2 (C)3 (D)3log 2 4.〔2004XX 〕若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1,0)和(0,1),则 ( )(A)a=2,b=2 (B)a= 2 ,b=2 (C)a=2,b=1 (D)a= 2 ,b= 2 5.〔2004XX 文科〕若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则 f(x)=( )(A)10x -1. (B) 1-10x . (C) 1-10-x . (D) 10-x -1.6、〔2004XX 理科〕若函数y=f(x)的图象可由函数y=lg(x+1)的图象绕坐标原点O 逆时针旋转2π得到,则 f(x)=( )(A) 10-x -1. (B) 10x -1. (C) 1-10-x . (D) 1-10x . 7.(2004XX 文、理) 函数123==x y )01(<≤-x 的反函数是(A))31(log 13≥+=x x y (B))31(log 13≥+-=x x y(C))131(log 13≤<+=x x y (D))131(log 13≤<+-=x x y8.(2004XX 理科)若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a=A.42B. 22C. 41D. 21 9.(2004XX 文科)若函数)1,0)(1(log )(≠>+=a a x x f a 的定义域和值域都是[0,1],则a=〔A 〕31〔B 〕 2 〔C 〕22〔D 〕2 10.〔2004重庆文、理〕函数12log (32)y x =-的定义域是:〔〕A [1,)+∞B 23(,)+∞C 23[,1]D 23(,1]11.〔2004湖北文科〕若,111ba <<则下列结论中不.正确的是 〔 〕A .a b b a log log >B .2|log log |>+a b b aC .1)(log 2<a bD .|log log ||log ||log |a b a b b a b a +>+12.〔2004湖北文科〕若函数的图象经过第二且)10(1)(≠>-+=a a b a x f x、三、四象限,则一定有〔 〕A .010><<b a 且B .01>>b a 且C .010<<<b a 且D .01<>b a 且13.〔2004湖北理科〕函数)1(log,)(2++=x a x f 在[0,1]上的最大值与最小值之和为a,则a 的值为 〔A 〕41 〔B 〕21〔C 〕2 〔D 〕414.〔2004XX 〕对于10<<a ,给出下列四个不等式 ①)11(log )1(log a a a a +<+②)11(log )1(log aa a a +>+ ③aaaa111++<④aaaa111++>其中成立的是 A .①与③B .①与④C .②与③D .②与④15.〔2004全国卷Ⅰ文科〕已知函数=-=+-=)(,21)(,11lg )(a f a f x x x f 则若 〔 〕A .21B .-21 C .2D .-216.〔2004全国卷Ⅰ理科〕已知函数=-=+-=)(.)(.11lg )(a f b a f x xx f 则若〔 〕A .bB .-bC .b 1D .-b117.〔2004全国卷Ⅱ理、文〕函数y =-e x 的图象〔A 〕与y =e x 的图象关于y 轴对称 〔B 〕与y =e x 的图象关于坐标原点对称〔C 〕与y =e -x 的图象关于y 轴对称 〔D 〕与y =e -x 的图象关于坐标原点对称 18.〔2004全国卷Ⅲ理科〕函数)1(log 221-=x y 的定义域为〔 〕A .[)(]2,11,2 --B .)2,1()1,2( --C .[)(]2,11,2 --D .)2,1()1,2( --19.〔2004全国卷Ⅲ文科〕 记函数13xy -=+的反函数为()y g x =,则(10)g =〔 〕A . 2B . 2-C . 3D . 1-20.〔2004全国卷Ⅳ文、理〕函数)(2R x e y x∈=的反函数为 〔 〕A .)0(ln 2>=x x yB .)0)(2ln(>=x x yC .)0(ln 21>=x x y D .)0(2ln 21>=x x y 21.〔2004全国卷Ⅳ文科〕为了得到函数xy )31(3⨯=的图象,可以把函数xy )31(=的图象 〔 〕 A .向左平移3个单位长度 B .向右平移3个单位长度 C .向左平移1个单位长度D .向右平移1个单位长度22.〔2004全国卷Ⅳ文科〕已知函数kx y x y ==与41log 的图象有公共点A ,且点A 的横坐标为2,则k 〔 〕 A .41-B .41 C .21-D .21〔2003--2000年〕1.〔2003全国文科〕已知5()lg ,(2)f x x f ==则〔 〕 〔A 〕lg 2 〔B 〕lg32 〔C 〕1lg 32 〔D 〕1lg 252.〔2003文理〕设5.1344.029.01)21(,8,4-===y y y ,则〔 〕A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 23.〔2003全国、广东、XX 、XX 、XX 〕设函数0021,1)(0,,0,12)(x x f x x x x f x 则若>⎪⎩⎪⎨⎧>≤-=-的取值范围是 〔A 〕〔-1,1〕〔B 〕(1,)-+∞〔C 〕〔-∞,-2〕∪〔0,+∞〕 〔D 〕〔-∞,-1〕∪〔1,+∞〕4.〔2003XX 、XX 、XX 文理〕函数),1(,11ln+∞∈-+=x x x y 的反函数为〔 〕A .),0(,11+∞∈+-=x e e y xx B .),0(,11+∞∈-+=x e e y xxC .)0,(,11-∞∈+-=x e e y xx D .)0,(,11-∞∈-+=x e e y xx 5.〔2003XX 文科〕在P 〔1,1〕、Q 〔1,2〕、M 〔2,3〕和N )41,21(四点中,函数xa y =的图象与其反函数的图象的公共点只可能是点〔 〕A .P .B .Q.C .M.D .N.6.〔2002春招XX 〕设A>0,a ≠1,函数y =xy x a a 1log log =的反函数和的反函数的图象关于〔 〕(A)x 轴对称(B)y 轴对称(C)y =x 对称(D)原点对称7. (2002广东、XX 、河南,XX 理,全国文)已知0<x <y <a <1,则有 〔A 〕0)(log <xy a 〔B 〕1)(log 0<<xy a 〔C 〕2)(log 1<<xy a 〔D 〕2)(log >xy a8.〔2002全国文科〕函数xa y =在]1,0[上的最大值与最小值这和为3,则a =〔A 〕21 〔B 〕2 〔C 〕4 〔D 〕419.〔2001春招、XX 、XX 卷文理〕函数)10()(≠>=a a a x f x且对于任意的实数y x ,都有〔A 〕)()()(y f x f xy f = 〔B 〕)()()(y f x f xy f +=〔C 〕)()()(y f x f y x f =+〔D 〕)()()(y f x f y x f +=+10.〔2001春招、XX 、XX 卷文理〕已知x x f 26log )(=,那么)8(f 等于〔A 〕34 〔B 〕8 〔C 〕18 〔D 〕21 11.(2001全国、XX 、XX 、XX 文理,广东)若定义在区间〔-1,0〕内的函数)1(log )(2+=x x f a满足f〔x〕>0,则a的取值范围是 〔A 〕)21,0(〔B 〕]21,0(〔C 〕),21(+∞〔D 〕),0(+∞12.(2001全国文科,广东)函数)0(12>+=-x y x的反函数是〔A 〕)2,1(,11log 2∈-=x x y 〔B 〕)2,1(,11log 2∈--=x x y〔C 〕]2,1(,11log 2∈-=x x y 〔D 〕]2,1(,11log 2∈--=x x y13。
指数、对数比较大小练习题(1+2+3+8=250)

指数 【2 】.对数比较大小1.下图是指数函数(1)x y a =,(2)x y b =,(3)x y c =,(4)x y d =的图象,则a ,b ,c ,d 与1的大小关系是( )A .1a b c d <<<<B .1b a d c <<<<C .1a b c d <<<<D .1a b d c <<<<2.图中曲线是对数函数y =log a x 的图象,已知a 取4313,,,3510四个值,则响应于C 1,C 2,C 3,C 4的a 值依次为( )A .101,53,34,3B .53,101,34,3C .101,53,3,34D .53,101,3,343.已知()log a f x x =,()log b g x x =,()log c r x x =,()log d h x x =的图象如图所示则a ,b ,c ,d 的大小为( )A .c d a b <<<B .c d b a <<<C .d c a b <<<D .d c b a <<<4.假如01a <<,那么下列不等式中精确的是( ) A .1132(1)(1)a a -<- B .1(1)1a a +-> C .(1)log (1)0a a -+> D .(1)log (1)0a a +-< 5.若log 2log 20n m >>时,则m 与n 的关系是( )A .1m n >>B .1n m >>C .10m n >>>D .10n m >>> 6.已知log 5log 50m n <<,则m ,n 知足的前提是( )A .1m n >>B .1n m >>C .01n m <<<D .01m n <<< 7.设5.1348.029.0121,8,4-⎪⎭⎫ ⎝⎛===y y y ,则( )y x1O(4)(3)(2)(1)A .213y y y >>B .312y y y >>C .321y y y >>D .231y y y >> 8.以下四个数中的最大者是( )A .2(ln 2)B .ln(ln 2) C.ln .ln 2 9.若a =2log π,b =7log 6,c =2log 0.8,则( )A .a >b >cB .b >a >cC .c >a >bD .b >c >a 10.设323log ,log log a b c π===则( ) A .a b c >>B .a c b >>C .b a c >>D .b c a >>11.设3.02131)21(,3log ,2log ===c b a ,则( )A .a b c >>B .a c b >>C .b a c >>D .b c a >>12.设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是( )A .a b c >>B .a c b >>C .b a c >>D .b c a >>13.设2log 3P =,3log 2Q =,23log (log 2)R =,则( ) A .R Q P <<B .P R Q <<C .Q R P <<D .R P Q <<14.设2554log 4,(log 3),log 5a b c ===,则( ) A .a b c >>B .a c b >>C .b a c >>D .b c a >>15.已知函数()lg f x x =,0<a <b ,且()()f a f b >,则( ) A .1ab > B .1ab < C .1ab = D .(1)(1)0a b --> 16.设11333124log ,log ,log ,,,233a b c a b c ===则的大小关系是 A .a b c << B .c b a <<C .b a c <<D .b c a <<17.设c b a ,,均为正数,且a a21log 2=,b b21log 21=⎪⎭⎫ ⎝⎛,c c2log 21=⎪⎭⎫⎝⎛.则( )A .c b a <<B .a b c <<C .b a c <<D .c a b <<18.ln 2ln 3ln 5,,235a b c ===,则有( ) A .a>b>c B .c<b<a C .c<a<b D .b<a<c“六法”比较指数幂大小对于指数幂的大小的比较,我们平日都是应用指数函数的单调性,但许多时刻,因幂的底数或指数不雷同,不能直接应用函数的单调性进行比较.这就必须控制一些特别办法.1.转化法例1 比较12(322)-+与23(21)-的大小.解:∵22322(21)(21)-+=+=-,∴11222(322)[(21)]21---+=-=-.又∵0211<-<,∴函数(21)xy =-在界说域R 上是减函数.∴2321(21)-<-,即2132(322)(21)-+<-.评注:在进行指数幂的大小比较时,若底数不同,则起首斟酌将其转化成同底数,然后再依据指数函数的单调性进行断定.2.图象法例2 比较0.7a 与0.8a的大小.解:设函数0.7xy =与0.8xy =,则这两个函数的图象关系如图.当x a =,且0a >时,0.80.7a a >;当x a =,且0a <时,0.80.7a a <;当0x a ==时,0.80.7a a=.评注:对于不同底而同指数的指数幂的大小的比较,应用图象法求解,既快捷,又精确. 3.序言法例3 比较124.1-,345.6,1313⎛⎫- ⎪⎝⎭的大小.解:∵13134215.6 5.61 4.1 4.103-⎛⎫>==>>>- ⎪⎝⎭,∴13134215.6 4.13-⎛⎫>>- ⎪⎝⎭. 评注:当底数与指数都不雷同时,拔取恰当的“序言”数(平日以“0”或“1”为序言),分离与要比较的数比较,从而可间接地比较出要比较的数的大小.4.作商法例4 比较a ba b 与b aa b (0a b >>)的大小.解:∵a b a ba ba b b a a b a b a a a a b b a b b b --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,又∵0a b >>,∴1ab>,0a b ->. ∴1a ba b -⎛⎫> ⎪⎝⎭,即1a bb a a b a b>.∴a b b a a b a b >.评注:当底数与指数都不同,中央量又不好找时,可采用作商比较法,即对两值作商,依据其值与1的大小关系,从而肯定所比值的大小.当然一般情形下,这两个值最好都是正数.5.作差法例5 设0m n >>,0a >,且1a ≠,试比较m ma a -+与n na a-+的大小.解:()()mmn n m m n n a aa a a a a a ----+-+=+--()()m n m n a a a a --=-+-(1)(1)(1)()n m n m m n m n n m a a a a a a a -----=-+-=--.(1)当1a >时,∵0m n ->,∴10m na -->.又∵1n a >,1ma -<,从而0n m a a -->.∴(1)()0m nn m aa a ---->.∴m m n n a a a a --+>+.(2)当01a <<时,∵1m na-<,即10m n a --<.又∵0m n >>,∴1na <,1ma ->,故0n m a a -<.∴(1)()0m nn m aa a ---->.∴m m n n a a a a --+>+.综上所述,m mn n a aa a --+>+.评注:作差比较法是比较两个数值大小的最常用的办法,即对两值作差,看其值是正照样负,从而肯定所比值的大小.6.分类评论辩论法 例6 比较221x a+与22x a+(0a >,且1a ≠)的大小.剖析:解答此题既要评论辩论幂指数221x +与22x +的大小关系,又要评论辩论底数a 与1的大小关系.解:(1)令22212x x +>+,得1x >,或1x <-. ①当1a >时,由22212x x +>+, 从而有22212x xaa ++>;②当01a <<时,22212x xaa ++<.(2)令22212x x +=+,得1x =±,22212x xaa ++=.(3)令22212x x +<+,得11x -<<. ①当1a >时,由22212x x +<+,从而有22212xxaa ++<;②当01a <<时,22212x xaa ++>.评注:分类评论辩论是一种主要的数学办法,应用分类评论辩论法时,起首要肯定分类的标准,涉及到指数函数问题时,平日将底数与1的大小关系作为分类标准.。
高考中的 指数函数和对数函数 试题汇编大全

历届高考中的“指数函数和对数函数”试题汇编大全一、选择题:(2006年)1.(2006安徽文)函数1()x y ex R +=∈的反函数是( )A .1ln (0)y x x =+>B .1ln (0)y x x =->C .1ln (0)y x x =-->D .1ln (0)y x x =-+>2.(2006北京理)已知⎩⎨⎧≥<+-=1,log 1,4)13()(x x x a x a x f a 是(,)-∞+∞上的减函数,那么a 的取值范围是(A )(0,1) (B )1(0,)3(C )11[,)73(D )1[,1)73.(2006北京文)已知(3)4,1()log ,1a a x a x f x x x --⎧=⎨≥⎩<,是(-∞,+∞)上的增函数,那么a 的取值范围是(A )(1,+∞) (B )(-∞,3) (C)⎪⎭⎫⎢⎣⎡3,53 (D)(1,3) 4.(2006福建理)函数y=㏒21-x x(x ﹥1)的反函数是 A.y =122-x x (x >0) B.y = 122-x x(x <0)C.y =x x 212- (x >0)D. .y =xx 212- (x <0) 5.(2006福建文)已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设63(),(),52a f b f ==5(),2c f =则(A )a b c << (B )b a c << (C )c b a << (D )c a b <<6、(2006湖北文、理)设f(x)=x x -+22lg ,则)2()2(xf x f +的定义域为 A. ),(),(-4004Y B.(-4,-1)Y (1,4) C. (-2,-1)Y (1,2) D. (-4,-2)Y (2,4)7.(2006湖南文)函数x y 2log =的定义域是A .(0,1]B . (0,+∞) C. (1,+∞) D . [1,+∞) 8.(2006湖南理)函数y =( )A.(3,+∞)B.[3, +∞)C.(4, +∞)D.[4, +∞)9.(2006辽宁文、理)与方程221(0)xx y ee x =-+≥的曲线关于直线y x =对称的曲线的方程为( )A.ln(1)y x =+ B.ln(1)y x =- C.ln(1)y x =-+D.ln(1)y x =--10、(2006全国Ⅰ卷文、理)已知函数xy e =的图象与函数()y f x =的图象关于直线y x =对称,则A .()22()x f x e x R =∈B .()2ln 2ln (0)f x x x =>gC .()22()x f x e x R =∈D .()2ln ln 2(0)f x x x =+>11.(2006全国Ⅱ卷文、理)已知函数()ln 1(0)f x x x =+>,则()f x 的反函数为 (A )1()x y e x R +=∈ (B )1()x y e x R -=∈(C )1(1)x y e x +=> (D )1(1)x y e x -=> 12.(2006全国Ⅱ卷理)函数y =f (x )的图像与函数g (x )=log 2x (x >0)的图像关于原点对称,则f (x )的表达式为(A )f (x )=1log 2x (x >0) (B )f (x )=log 2(-x )(x <0)(C )f (x )=-log 2x (x >0) (D )f (x )=-log 2(-x )(x <0)13.(2006山东文、理)函数y=1+a x (0<a <1)的反函数的图象大致是(A ) (B ) (C ) (D )14.(2006山东文、理)设f (x )= 1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩ 则不等式f (x )>2的解集为 (A)(1,2)⋃(3,+∞) (B)(10,+∞) (C)(1,2)⋃ (10 ,+∞) (D)(1,2)15.(2006陕西文)设函数f (x )=log a (x +b )(a >0,a ≠1)的图象过点(0,0),其反函数过点(1,2),则a +b 等于A .3B .4C .5D .616. (2006陕西理)设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( )A.6B.5C.4D.317. (2006四川文)函数ln(1)(1)y x x =->的反函数是 (A )1()1()x f x e x R -=+∈ (B )1()101()x f x x R -=+∈ (C )1()1(1)x f x e x -=+>(D )1()1(1)x fx e x -=+>18.(2006天津文)如果函数2()(31)(01)xxf x a a a a a =-->≠且在区间[)0+,∞上是增函数,那么实数a 的取值范围是( )A.203⎛⎤ ⎥⎝⎦, B.13⎫⎪⎪⎣⎭C.(D.32⎡⎫+⎪⎢⎣⎭,∞19、(2006天津理)已知函数)(x f y =的图象与函数xa y =(0>a 且1≠a )的图象关于直线x y =对称,记]1)2(2)()[()(-+=f x f x f x g .若)(x g y =在区间]2,21[上是增函数,则实数a 的取值范围是( ) A .),2[+∞ B .)2,1()1,0(Y C .)1,21[ D .]21,0(20.(2006天津文)设2log 3P =,3log 2Q =,23log (log 2)R =,则( ) A.R Q P << B.P R Q << C.Q R P << D.R P Q <<21.(2006浙江文)已知1122log log 0m n <<,则(A) n <m < 1 (B) m <n < 1 (C) 1< m <n (D) 1 <n <m22.(2006浙江理)已知0<a <1,log 1m <log 1n <0,则 (A)1<n <m (B) 1<m <n (C)m <n <1 (D) n <m <123、(2006广东)函数2()lg(31)f x x ++的定义域是 A.1(,)3-+∞ B. 1(,1)3- C. 11(,)33- D. 1(,)3-∞-(2005年)1.(2005全国卷Ⅰ理、文)设10<<a ,函数)22(log )(2--=xx a a a x f ,则使0)(<x f 的x 的取值范围是( )A .()0,∞-B .()+∞,0C .()3log ,a ∞-D .()+∞,3log a2.(2005全国卷Ⅲ理、文)若ln 2ln 3ln 5,,235a b c ===,则( ) A .a <b<c B .c<b<a C .c<a <bD .b<a <c3.(2005全国卷Ⅲ文科)设713=x,则 ( ) A .-2<x<-1 B .-3<x<-2 C .-1<x<0D .0<x<14.(2005天津理科)若函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是 ( )A .)1,41[B . )1,43[C .),49(+∞D .)49,1(5.(2005天津理科)设)(1x f-是函数)1( )(21)(>-=-a a a x f x x的反函数,则使1)(1>-x f 成立的x 的取值范围为( )A .),21(2+∞-a aB . )21,(2a a --∞C . ),21(2a aa - D . ),[+∞a 6.(2005天津文科)若函数)1,0( )2(log )(2≠>+=a a x x x f a 在区间)21,0(内恒有f (x )>0,则f (x )的单调递增区间为 ( )A .)41,(--∞B .),41(+∞-C .(0,∞)D .)21,(--∞7.(2005天津文)已知c a b 212121log log log <<,则( )A .ca b 222>>B .cba222>> C .abc222>> D .bac222>>8.(2005上海理、文)若函数121)(+=x x f ,则该函数在()+∞∞-,上是( )A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值9.(2005湖南理、文)函数f (x )=x21-的定义域是( )A .(-∞,0]B .[0,+∞)C .(-∞,0)D .(-∞,+∞)10.(2005春考北京理科)函数y=|log 2x|的图象是 ( )11.(2005福建理、文)函数bx ax f -=)(的图象如图,其中a 、b 为常数,则下列结论正确的是( ) A .0,1<>b aB .0,1>>b aC .0,10><<b aD .0,10<<<b a12.(2005辽宁卷)函数1ln(2++=x x y )的反函数是( )A .2xx e e y -+= B .2x x e e y -+-=C .2xx e e y --= D .2x x e e y ---=13.(2005辽宁卷)若011log 22<++aa a,则a 的取值范围是 ( )A .),21(+∞B .),1(+∞C .)1,21(D .)21,0(14.(2005江西理、文)已知实数a , b 满足等式,)31()21(ba=下列五个关系式①0<b <a ②a <b <0 ③0<a <b ④b <a <0 ⑤a =b 其中不可能...成立的关系式有 ( )A .1个B .2个C .3个D .4个15.(2005江西文科)函数)34(log 1)(22-+-=x x x f 的定义域为 ( ) A .(1,2)∪(2,3) B .),3()1,(+∞⋃-∞C .(1,3)D .[1,3]16.(2005重庆文科)不等式组⎩⎨⎧>-<-1)1(log ,2|2|22x x 的解集为 ( )A .)3,0(B .)2,3(C .)4,3(D .)4,2(17、(2005江苏)函数)(321R x y x∈+=-的反函数的解析表达式为( )A .32log 2-=x y B .23log 2-=x y C .23log 2x y -= D .xy -=32log 2 18.(2005湖北卷理、文)函数|1|||ln --=x e y x 的图象大致是( )A 1 x y OB 1 x y OC 1 xy O D1xyO19.(2005湖北理、文)在x y x y x y y x 2cos ,,log ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是( ) A .0B .1C .2D .320.(2005山东文、理)下列函数中既是奇函数,又是区间[]1,1-上单调递减的是(A )()sin f x x = (B) ()1f x x =-+ (C) 1()()2x x f x a a -=+ (D) 2()2xf x lnx-=+ 21.(2005山东理、文)函数⎪⎩⎪⎨⎧≥<<-=-0,01,)sin()(12x ex x x f x π,若2)()1(=+a f f ,则a 的所有可能值为( ) A.1 B.1,22-C.22- D. 1,22 22.(2005山东理科) 01a <<,下列不等式一定成立的是 ( )A .(1)(1)log (1)log (1)2a a a a +--++>B .(1)(1)log (1)log (1)a a a a +--<+C .(1)(1)log (1)log (1)a a a a +--++<(1)(1)log (1)log (1)a a a a +--++D .(1)(1)log (1)log (1)a a a a +---+<(1)(1)log (1)log (1)a a a a +---+23.(2005山东文科)下列大小关系正确的是( )A .20.440.43log 0.3<<; B .20.440.4log 0.33<<;C .20.44log 0.30.43<<;D .0.424log 0.330.4<<(2004年)1.(2004安徽文、理)已知函数y=log 2x 的反函数是y=f -1(x),则函数y= f -1(1-x)的图象是2.(2004湖南文科)函数)11lg(xy -= 的定义域为( )A .{}0|<x xB .{}1|>x xC .{}10|<<x xD .{}10|><或x x3.(2004湖南理科)设)(1x f-是函数)1(log )(2+=x x f 的反函数,若8)](1)][(1[11=++--b fa f,则f(a —b)的值为(A) 1 (B)2 (C)3 (D)3log 2 4.(2004江苏)若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1,0)和(0,1),则 ( )(A)a=2,b=2 (B)a= 2 ,b=2 (C)a=2,b=1 (D)a= 2 ,b= 2 5.(2004上海文科)若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则 f(x)=( )(A)10x -1. (B) 1-10x . (C) 1-10-x . (D) 10-x -1.6、(2004上海理科)若函数y=f(x)的图象可由函数y=lg(x+1)的图象绕坐标原点O 逆时针旋转2π得到,则 f(x)=( )(A) 10-x -1. (B) 10x -1. (C) 1-10-x . (D) 1-10x . 7.(2004天津文、理) 函数123==x y )01(<≤-x 的反函数是(A))31(log 13≥+=x x y (B))31(log 13≥+-=x x y(C))131(log 13≤<+=x x y (D))131(log 13≤<+-=x x y8.(2004天津理科)若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a=A.42 B.22 C.41 D.21 9.(2004浙江文科)若函数)1,0)(1(log )(≠>+=a a x x f a 的定义域和值域都是[0,1],则a=(A )31(B ) 2 (C )22(D )2 10.(2004重庆文、理)函数12log (32)y x =-的定义域是:( )A [1,)+∞B 23(,)+∞C 23[,1]D 23(,1]11.(2004湖北文科)若,111ba <<则下列结论中不.正确的是( )A .a b b a log log >B .2|log log |>+a b b aC .1)(log 2<a bD .|log log ||log ||log |a b a b b a b a +>+12.(2004湖北文科)若函数的图象经过第二且)10(1)(≠>-+=a a b a x f x、三、四象限,则一定有( )A .010><<b a 且B .01>>b a 且C .010<<<b a 且D .01<>b a 且13.(2004湖北理科)函数)1(log,)(2++=x a x f 在[0,1]上的最大值与最小值之和为a,则a 的值为 (A )41 (B )21(C )2 (D )414.(2004辽宁)对于10<<a ,给出下列四个不等式 ①)11(log )1(log aa a a +<+ ②)11(log )1(log aa a a +>+ ③aaaa111++<④aaaa111++>其中成立的是 A .①与③B .①与④C .②与③D .②与④15.(2004全国卷Ⅰ文科)已知函数=-=+-=)(,21)(,11lg )(a f a f x x x f 则若 ( )A .21B .-21 C .2D .-216.(2004全国卷Ⅰ理科)已知函数=-=+-=)(.)(.11lg )(a f b a f x xx f 则若 ( )A .bB .-bC .b 1D .-b117.(2004全国卷Ⅱ理、文)函数y =-e x 的图象(A )与y =e x 的图象关于y 轴对称 (B )与y =e x 的图象关于坐标原点对称(C )与y =e -x 的图象关于y 轴对称 (D )与y =e -x 的图象关于坐标原点对称 18.(2004全国卷Ⅲ理科)函数)1(log 221-=x y 的定义域为( )A .[)(]2,11,2Y -- B .)2,1()1,2(Y --C .[)(]2,11,2Y --D .)2,1()1,2(Y --19.(2004全国卷Ⅲ文科) 记函数13xy -=+的反函数为()y g x =,则(10)g =( )A . 2B . 2-C . 3D . 1-20.(2004全国卷Ⅳ文、理)函数)(2R x e y x∈=的反函数为 ( )A .)0(ln 2>=x x yB .)0)(2ln(>=x x yC .)0(ln 21>=x x y D .)0(2ln 21>=x x y 21.(2004全国卷Ⅳ文科)为了得到函数xy )31(3⨯=的图象,可以把函数xy )31(=的图象 ( ) A .向左平移3个单位长度 B .向右平移3个单位长度 C .向左平移1个单位长度D .向右平移1个单位长度22.(2004全国卷Ⅳ文科)已知函数kx y x y ==与41log 的图象有公共点A ,且点A 的横坐标为2,则k ( ) A .41-B .41 C .21-D .21(2003--2000年)1.(2003全国文科)已知5()lg ,(2)f x x f ==则( )(A )lg 2 (B )lg32 (C )1lg 32(D )1lg 252.(2003北京文理)设5.1344.029.01)21(,8,4-===y y y ,则 ( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 23.(2003全国、广东、天津、江苏、辽宁)设函数0021,1)(0,,0,12)(x x f x x x x f x 则若>⎪⎩⎪⎨⎧>≤-=-的取值范围是 (A )(-1,1)(B )(1,)-+∞(C )(-∞,-2)∪(0,+∞)(D )(-∞,-1)∪(1,+∞)4.(2003辽宁、江苏、天津文理)函数),1(,11ln+∞∈-+=x x x y 的反函数为( )A .),0(,11+∞∈+-=x e e y xx B .),0(,11+∞∈-+=x e e y xxC .)0,(,11-∞∈+-=x e e y xx D .)0,(,11-∞∈-+=x e e y xx 5.(2003上海文科)在P (1,1)、Q (1,2)、M (2,3)和N )41,21(四点中,函数xa y =的图象与其反函数的图象的公共点只可能是点( )A .P .B .Q.C .M.D .N.6.(2002春招上海)设A>0,a ≠1,函数y =xy x a a 1log log =的反函数和的反函数的图象关于( )(A)x 轴对称(B)y 轴对称(C)y =x 对称(D)原点对称7. (2002广东、江苏、河南,天津理,全国文)已知0<x <y <a <1,则有 (A )0)(log <xy a (B )1)(log 0<<xy a (C )2)(log 1<<xy a (D )2)(log >xy a8.(2002全国文科)函数xa y =在]1,0[上的最大值与最小值这和为3,则a =(A )21 (B )2 (C )4 (D )419.(2001春招北京、内蒙古、安徽卷文理)函数)10()(≠>=a a a x f x且对于任意的实数y x ,都有(A ))()()(y f x f xy f = (B ))()()(y f x f xy f +=(C ))()()(y f x f y x f =+(D ))()()(y f x f y x f +=+10.(2001春招北京、内蒙古、安徽卷文理)已知x x f 26log )(=,那么)8(f 等于(A )34 (B )8 (C )18 (D )21 11.(2001全国、江西、山西、天津文理,广东)若定义在区间(-1,0)内的函数)1(log )(2+=x x f a满足f(x)>0,则a的取值范围是 (A ))21,0((B )]21,0((C )),21(+∞(D )),0(+∞12.(2001全国文科,广东)函数)0(12>+=-x y x的反函数是(A ))2,1(,11log 2∈-=x x y (B ))2,1(,11log 2∈--=x x y(C )]2,1(,11log 2∈-=x x y (D )]2,1(,11log 2∈--=x x y13。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数对数比大小高考试题汇编
指数函数与对数函数比大小
已知 $a>b$,则下列不等式中成立的是()
A。
$\ln(a-b)>0$
B。
$3a<3b$
C。
$a^3-b^3>0$
D。
$|a|>|b|$
解析:取 $a=2,b=1$,满足 $a>b$,$\ln(a-b)=\ln(2-
1)=\ln1=0$,知 A 错,排除 A;因为 $9=3a>3b=3$,知 B 错,排除 B;取 $a=1,b=-2$,满足 $a>b$,$1=ab$,所以
$a^3>b^3$,故选 C。
已知 $a=\log_5 2$,$b=\log_{0.5} 0.2$,$c=0.5^{0.2}$,则 $a,b,c$ 的大小关系为()
A。
$a<c<b$
B。
$a<b<c$
XXX<c<a$
D。
$c<a<b$
解析:$a=\log_5 2\log_{0.5} 0.25=2$,
$c=0.5^{0.2}<0.5^{0.1}<0.5=\dfrac{1}{2}$,故 $a<c<b$,选 A。
已知 $a,b,c$ 均为正实数,且 $ab<c^2$,则下列不等式中
成立的是()
A。
$a+b<c$
B。
$a+c<b$
XXX<a$
D。
$a+b+c<\sqrt{2c(a+b)}$
解析:由 $ab\sqrt{ab}$,故 $a+b<c+\sqrt{ab}$,即 $a+b-
c<\sqrt{ab}$。
两边平方得 $a^2+b^2+2ab-2ac-2bc+c^2<ab$,即$a^2+b^2+c^2<2ac+2bc$,再次平方得
$(a^2+b^2+c^2)^2<4c^2(a^2+b^2)$,即
$(a^2+b^2+c^2)^2<4c^2(a^2+b^2)+4a^2b^2$。
左边为正,右边
为正,两边开根号得 $a^2+b^2+c^2<\sqrt{2c(a^2+b^2)}$,即
$a+b+c<\sqrt{2c(a+b)}$,故选 D。
已知 $a,b,c$ 均为正实数,且 $a+b+c=1$,则 $a,b,c$ 的大
小关系为()
A。
$a<b<c$
B。
$a<c<b$
XXX<a<c$
D。
$b<c<a$
解析:由于$a+b+c=1$,故$a,b,cc$。
同理可得$a+c>b$,$b+c>a$,故 $a,b,c$ 互相比较没有大小关系,选 D。
设 $a,b,c$ 均为正实数,且 $ab<\dfrac{1}{4}$,
$bc<\dfrac{1}{9}$,则下列不等式中成立的是()
A。
$a+b+c<1$
B。
$a+b+c>\dfrac{11}{12}$
C。
$a+b+c>\dfrac{7}{8}$
D。
$a+b+c>\dfrac{3}{4}$
解析:由 $ab\dfrac{1}{4ab}$,代入上式得
$a+b+c<\dfrac{1}{2}\cdot\dfrac{3a+c}{3ac}\leq\dfrac{1}{2}\cdo t\dfrac{3a+\dfrac{1}{4ab}}{3a\cdot\dfrac{1}{4ab}}=\dfrac{11}{ 12}$,故选 B。
a),q=f(b),r=f(a)+f(b),则()
A.p>q,q>r,r>p
B.p<q,q<r,r<p
XXX<q,q>r,r<p
D.p>q,q<r,r>p
答案】C
解析】由题意得:
p=f(a)=lna。
q=f(b)=lnb。
r=f(a)+f(b)=lna+lnb=ln(ab)。
a<b。
XXX<lnb。
p<q。
又因为lnx为增函数。
ln(ab)>lnb。
即r>q。
又因为lnx为增函数。
ln(ab)>lna。
即r<p。
综上可得,选C。
又y=5x是增函数,∴a>b,而log23.4>log2,∴a>c,
故a>c>b.
2011•重庆文6】设a=4,则b=log3>log23﹣1,c=log34
﹣1=log45,故a>c>b,选B。
2010天津文6】设a=log54,b=(log53)2,c=log45,则
a>b,c>a,故选D。
2010全国卷1文10】设a=log32,b=ln2,c=52,则a<b,c<a,故选C。
2010安徽文7】设a=()5,b=()2,c=()5,则a>c >b,选A。
2009全国卷2文7】设a=lge,b=(lge),c=lge,则a>b,
c=a,故选B。
2009天津文5】设a=log1,则b=log20,故a>c>b,选A。
2.根据已知的对数函数和指数函数图像,可以得出a<1<c,而b=log(2/3)<0,因此选B。
3.根据指数函数的图像可知,a>1,b<1,c<0.因此可以将
其改写为:a=ln(x),b=2ln(x),c=ln(x)。
由于x∈(e,1),因此-
1<ln(x)<0,即b<a<c。
因此选C。
4.将题目中的式子展开,可得x=log(a)+log(a)=2log(a),
y=log(a)+log(5),z=log(a)-(log(a)+log(a))=-log(a)。
由于00.又因为ax>z,选C。
5.将a、b、c的值代入,可得a=log(1/3)0.因此可以将其改
写为:a=log(1/3),b=log(1/3^2),c=log(3^2/2^3)。
由于
log(1/3)<log(1/9)<log(8/9),因此有a<b<c。
因此选A。
6.将P、Q、R的值代入,可得P=log(2/3)>0,Q=log(3/2)1,因此log(log(3)-log(2))<0,即R<Q<P。
因此选A。
