大学物理03-2力矩 转动惯量 定轴转动定律
合集下载
大学物理刚体力学基础-文档资料

用右手螺旋法则确定。
2)力矩的单位、 牛·米(N·m)
3)力矩的计算: M 的大小、方向均与参考点的选择有关
MFsrin
※在直角坐标系中,其表示式为
M rF ( x i y j z k ) ( F x i F y j F z k )
ri
fij fji
M i0M j0(ri rj)fji
0
rij
rj
f ij
ri jfji 0
二、刚体定轴转动的转动定律:
刚径体r绕i 的定圆轴周转运动动,,在作刚用体在上质取点一上质的元合力m i矩,绕轴作半
M ir iF ifi r iF i r ifi
( y z z F y ) i F ( z x F x z ) j F ( x y y F x ) k F
M x i M yj M zk
i jk
Mx yFz zFy
M x y z
My zFx xFz
Fx Fy Fz
Mz xFy yFx
2、力对轴的矩:
i
Fi
由牛顿第二定律可知
ri m i
Fifi miai
则质点所受力矩
Mi miri2
对刚体所受所有力矩求和得:
riF i rifi m iri2
由于刚体各质点相对轴距离不变,令
J miri2
2、刚体定轴转动的转动定理
M J
作定轴转动的刚体,其转动角加速度与外力对该轴的力矩之 和成正比,与刚体对该轴的转动惯量成反比。 其在定轴转动中的地位与牛顿定律在质点运动中地位相当。
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的转动惯量为
2)力矩的单位、 牛·米(N·m)
3)力矩的计算: M 的大小、方向均与参考点的选择有关
MFsrin
※在直角坐标系中,其表示式为
M rF ( x i y j z k ) ( F x i F y j F z k )
ri
fij fji
M i0M j0(ri rj)fji
0
rij
rj
f ij
ri jfji 0
二、刚体定轴转动的转动定律:
刚径体r绕i 的定圆轴周转运动动,,在作刚用体在上质取点一上质的元合力m i矩,绕轴作半
M ir iF ifi r iF i r ifi
( y z z F y ) i F ( z x F x z ) j F ( x y y F x ) k F
M x i M yj M zk
i jk
Mx yFz zFy
M x y z
My zFx xFz
Fx Fy Fz
Mz xFy yFx
2、力对轴的矩:
i
Fi
由牛顿第二定律可知
ri m i
Fifi miai
则质点所受力矩
Mi miri2
对刚体所受所有力矩求和得:
riF i rifi m iri2
由于刚体各质点相对轴距离不变,令
J miri2
2、刚体定轴转动的转动定理
M J
作定轴转动的刚体,其转动角加速度与外力对该轴的力矩之 和成正比,与刚体对该轴的转动惯量成反比。 其在定轴转动中的地位与牛顿定律在质点运动中地位相当。
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的转动惯量为
定轴转动刚体的转动定律度力矩角动量转动惯量

Iz Ix Iy
z
定理证明:
对于质量平面分布的刚体, 绕 x 轴的转动惯量为:
o
yy
Ix y2dm
x
dm
绕 y 轴的转动惯量为:
I y x2dm
x
绕 z 轴的转动惯量为:
19
z
Iz z2dm (x 2 y2 )dm
y2dm x 2dm I x I y 证毕
o
yy
x z dm
0
M
绕圆环质心轴的转动惯量为
dm
oR
I MR2
例2:在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的 质点,可绕 o 轴转动,求:质点系的转动惯量I。
解:由转动惯量的定义
I
2
mi ri 2
2mb 2
m
(3b)2
11mb 2
i 1
9
例3: 如图所示,一质量为m、长为l的均质空心圆柱
体(即圆筒圆筒)其内、外半径分别为R1和R2。试求
的质元受阻力矩大,
细杆的质量密度 m
l
质元质量 dm dx
o
xl dm m dx
x
质元受阻力矩:
dM 阻 dmgx
细杆受的阻力矩
m l
M阻
dM
阻
0l
gxdx
1 2
gl 2
1 2
mgl
4
二、定轴转动刚体的角动量
1 .质点对点的角动量
L
r
P
r
mv
作圆周运动的质点的角动量L=rmv;
l
x2dm
L
x2dx
1 L3
0
1 mL2
0
3
A
力矩转动定律转动惯量

PB y
31
第32页/共42页
a
mB g
mA mB mC 2
解 得
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
A mA
mC 0时: FT1 FT2
32
第33页/共42页
C mC
mB B
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
的角加速度和角速度. M J
35
第36页/共42页
36
解: 受力分析,力矩(O)分析
重力对O点的力矩
M mgd
J
d L sin
2
有: 1 mgl sin J
2
m,l
O
θ
FN
mg
d
式中 J 1 ml2 3
得 3g sin
2l
第37页/共42页
由角加速度的定义
dω dω dθ ω dω
F
F
Fi 0 , Mi 0
M rF
M Frsin Fd
3
第4页/共42页
4、一对力偶的力矩
M Fd
F
F
ol
F 0 M 0
F'
ro
F
F 0 M 0
M F l F l Fl
22
M Fr Fr 0
4
第5页/共42页
讨论
(1)若力 F 不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
如令 mC 0 ,可得
A mA
FT1
FT2
《大学物理》3.2转动定理
3.2 转动定理
一、力矩
F
力的作用线通过转轴或是 平行于转轴,无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置,是 决定转动效果的几个重要 因素。
F
F
1.定义:
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示,一不能伸长的轻绳跨过一轴承光滑的定 滑轮,滑轮视为圆盘,绳的两端分别悬有质量为m1和m2 的物体,且m1<m2,设滑轮的质量为M,半径为R,绳与 轮之间无相对滑动,求物体的加速度和绳中张力。
解:将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等,但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体,其角加速度与它所 受合外力矩成正比,与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
一、力矩
F
力的作用线通过转轴或是 平行于转轴,无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置,是 决定转动效果的几个重要 因素。
F
F
1.定义:
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示,一不能伸长的轻绳跨过一轴承光滑的定 滑轮,滑轮视为圆盘,绳的两端分别悬有质量为m1和m2 的物体,且m1<m2,设滑轮的质量为M,半径为R,绳与 轮之间无相对滑动,求物体的加速度和绳中张力。
解:将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等,但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体,其角加速度与它所 受合外力矩成正比,与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
刚体定轴转动的转动定律力矩

力矩平衡的条件
静平衡
刚体在转动过程中,如果合力矩 为零,则刚体保持静止状态。
动平衡
刚体在转动过程中,如果合力矩为 零,则刚体保持匀速转动状态。
平衡状态
无论是静平衡还是动平衡,刚体的 平衡状态都满足合力矩为零的条件。
力矩平衡的应用
机械平衡
在机械设计中,通过调整刚体的质量 分布或添加平衡装置,使刚体在转动 过程中满足力矩平衡条件,以保证机 械设备的稳定性和可靠性。
刚体的定轴转动
定轴转动:刚体绕某一固定轴线作旋 转运动。
在定轴转动中,刚体的角速度和角加 速度是矢量,其方向沿固定轴线,而 力矩是改变刚体转动状态的唯一物理 量。
刚体定轴转动的特点
角速度矢量、角加速度矢量和力 矩矢量都与固定轴线平行。
刚体定轴转动时,其上各点的速 度方向与该点到轴线的垂直线段 相垂直,各点的加速度方向与该
实例三:旋转木马的旋转
总结词
旋转木马的旋转是刚体定轴转动的又一实例,通过外力矩的作用,使旋转木马绕轴转动。
详细描述
旋转木马在外力矩的作用下开始转动,当旋转木马转动时,由于摩擦阻力和空气阻力的作用,旋转木 马会逐渐减速并最终停止。
实例四:陀螺的稳定旋转
总结词
陀螺的稳定旋转是刚体定轴转动的最后一个实例,陀螺通过自转保持稳定的旋转状态。
在日常生活和工业生产中,转动 定律也广泛应用于各种旋转运动
的分析和设计。
04
刚体定轴转动的力矩平衡
力矩平衡的概念
力矩平衡
刚体在转动过程中,受到 的力矩之和为零,即合力 矩为零。
力矩
力对转动轴的力矩等于力 和力臂的乘积,其中力臂 是从转动轴到力的垂直距 离。
转动轴
刚体转动的中心轴,可以 是固定的点或线。
力矩 刚体定轴转动的转动定律
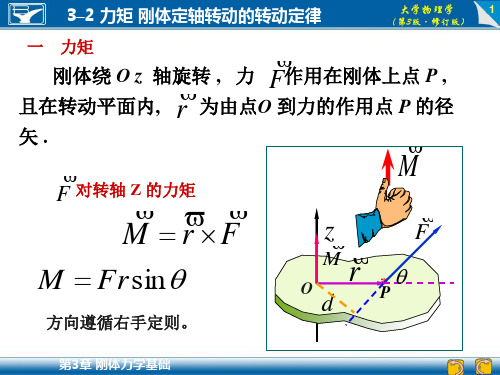
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的 转动惯量为
解 (1) M k 2 ,故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
3-第3章 刚体力学基础

大学物理学(第5版)
二、定轴转动定律
把刚体看作一个质点系
Fi
f i Δ m i a i
ri Fi ri f i Δ m i ri a i
加速度: a i a i a in
§3-2力矩 刚体定轴转动的转动定律
Mi
z M iz
Fi
Fi //
ri
mi Fi
(ri Fi ) (ri fi ) Δmi ri ai Δmi ri ai Δmi ri ain
§3-2力矩 刚体定轴转动的转动定律
M外z Miz ( mi ri 2 ) ( mi ri 2 )
i
i
i
若令
J z (mi ri 2 )
i
M 外z J z
绕定轴转动的刚体的角加速度与作用于刚体上的合外力矩成正比,与刚体的转
动惯量成反比。
注意:
——刚体定轴转动中的转动定律
(1)M和J均对于同一转轴而言;
1
2
合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。 ——刚体定轴转动时的动能定理
章目录 节目录 上一页 下一页
“十二五”普通高等教育本科国家级规划教材
大学物理学(第5版)
§3-3 刚体定轴转动的动能定理
四、机械能守恒定律
1、刚体的势能
EP mghc
m为刚体的总质量; hc为刚体质心的高度。
dm dx m dx O
r2 x2
l
dm x dx
l
x
J l x2 m dx 1 m x3 l
J 1 ml 2
J=
0
1 ml 2 3
l
1 12
3l
ml 2 m
0
l2 4
二、定轴转动定律
把刚体看作一个质点系
Fi
f i Δ m i a i
ri Fi ri f i Δ m i ri a i
加速度: a i a i a in
§3-2力矩 刚体定轴转动的转动定律
Mi
z M iz
Fi
Fi //
ri
mi Fi
(ri Fi ) (ri fi ) Δmi ri ai Δmi ri ai Δmi ri ain
§3-2力矩 刚体定轴转动的转动定律
M外z Miz ( mi ri 2 ) ( mi ri 2 )
i
i
i
若令
J z (mi ri 2 )
i
M 外z J z
绕定轴转动的刚体的角加速度与作用于刚体上的合外力矩成正比,与刚体的转
动惯量成反比。
注意:
——刚体定轴转动中的转动定律
(1)M和J均对于同一转轴而言;
1
2
合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。 ——刚体定轴转动时的动能定理
章目录 节目录 上一页 下一页
“十二五”普通高等教育本科国家级规划教材
大学物理学(第5版)
§3-3 刚体定轴转动的动能定理
四、机械能守恒定律
1、刚体的势能
EP mghc
m为刚体的总质量; hc为刚体质心的高度。
dm dx m dx O
r2 x2
l
dm x dx
l
x
J l x2 m dx 1 m x3 l
J 1 ml 2
J=
0
1 ml 2 3
l
1 12
3l
ml 2 m
0
l2 4
3_2转动定律 转动惯量 平行轴定理

平行轴定理 质量为m的刚体,如果对 其质心轴的转动惯量为JC ,则 对任一与该轴平行,相距为d 的转轴的转动惯量
d
C
m
O
J O J C md
JP 1 2 mR mR
2 2
2
圆盘对P 轴的转动惯量 P
R
O m
四 转动定律应用举例 对平动的物体应用牛顿定律;对转动的物体应 用转动定律;建立平动与转动之间的关系。
对质量面分布的刚体: d m
dS
:质量面密度
对质量体分布的刚体:d m
dV
:质量体密度
第三章 刚体的转动
3 – 2 转动定律 转动惯量 平行轴定理
例3-1 一质量为m、长为l的均匀细长棒,求通 过棒中心并与棒垂直的轴的转动惯量。
O r
l 2
O
dr
l 2
r
dr
O
O´
l
解: 设棒的线密度为,取一距离转轴 OO 为r 处的质量元dm=dr . d J r 2 d m r 2 d r
(m A m C 2)m B g mA mB mC 2
A
mA
FT1
C
F T1
F T2
mC F T2
mB B
如令 m C 0,可得
F T1 F T2
mAmBg mA mB
第三章 刚体的转动
3 – 2 转动定律 转动惯量 平行轴定理
F T1 F T2
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
M
rj
j
d
ji
iF ri ij
F ji
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对质量面分布的刚体:dm dS , :质量面密度。
上页 下页 返回 退出
例题3-1 求质量为m、长为l 的均匀细棒对下面三种 转轴的转动惯量: (1)转轴通过棒的中心并和棒垂直; (2)转轴通过棒的一端并和棒垂直; (3)转轴通过棒上距中心为h的一点并和棒垂直。
m m 单位长度质量(线密度): ,因此 dm dx dx l l l 2 2 2 m J x dm x dx l 2 l x 1 o dx ml 2(公式) x 12
说明:平行轴定理适用于任意形状刚体,无论一维、二维 还是三维。另外,轴线可以在刚体内,也可以在刚体外。
上页 下页 返回 退出
例题 3-2 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R,质量为m,密度均匀。
dr
r
R
解:设圆盘的质量面密度为,在圆盘上取一半径为r、 宽度为dr 的圆环(如图),环的面积为2rdr,环的质 量dm= 2rdr。可得 4
其体积:
2 2 2
X
dV πr dz π( R z )dz
其质量:dm dV π( R2 z 2 )dz
1 2 1 其转动惯量: dJ r dm π( R 2 z 2 ) 2 dz 2 2
上页 下页 返回 退出
X
1 2 1 dJ r dm π( R 2 z 2 )2 dz 2 2 r z dz J dJ R O Y R 1 π ( R 2 z 2 ) 2 dz R 2 8 2 5 πR mR 2 4 3 15 5 其中 m πR 3
变形,对转动无贡献; 只有 r F2 才对转动产生 贡献!此力矩方向沿转轴 ! 注:(1)在定轴转动问 题中,如不加说明,所指 的力矩是指力在转动平面 内的分力对转轴的力矩。
r F1 只能引起轴的
r F1
r F
r F2
转动 平面
r
上页 下页 返回 退出
(2) M z rF2 sin F2 d
J r dm
2
R
0
由于圆柱体是由一个个薄圆盘堆积起来的,因此
π R 1 2π r dr mR 2 2 2
3
J圆柱
1 1 2 1 2 mi R mi R m圆柱 R 2 2 i 2 i 2
上页 下页 返回 退出
平行轴定理:J JC md 2
1.角坐标 描写刚体转动位置的物理量。 在转动平面内,过O点作 一极轴,设极轴的正方向 是水平向右,则OP与极轴 之间的夹角为。
P
O
x
角称为角坐标(或角位置)。
角坐标为标量,但有正负,符号与极坐标辐角一致。
0 : 从Ox到OP是逆时针旋转 0 : 从Ox到OP是顺时针旋转
i i i
x
上页 下页 返回 退出
几种典型形状刚体的转动惯量
O' ω m O 圆环 J=mR2 细棒 R
l
1 J ml 2 12 ω
R2
L
R
R1
1 圆柱 J mR 2 2
1 2 圆筒 J m( R12 R2 ) 2
上页 下页 返回 退出
ω
R
ω
空心 R
2 2 2 薄球壳 mR J mR 2 5 3 2 1 2 想一想:圆柱 J mR 实心球 J mR 2 的原因? 5 2
0 mi i cosi mi xi mxC
m
2 i
i
O d C
P m i i'
i
x'
i
mi i2 mi d 2 mi i cos i 2d
在质心坐标 系中,质心 位于原点!
可见, JO JC md 2 ——平行轴定理
x
O
x
dx
以上说明,J 与刚体质量、质量分布、轴的位置有关!
(※)式中隐含着一个关于转动惯量的平行轴定理!
上页 下页 返回 退出
平行轴定理
定理表述:刚体绕平行于质心轴的某轴的转动惯量J, 等于绕质心轴的转动惯量 JC 加上刚体质量与两轴间 距离平方的乘积: J J md2
C
d
C
O
JO JC md
Z
上页 下页 返回 退出
例题3-3 一轻绳跨过一定滑轮,滑轮视为圆盘,绳的两 端分别悬有质量为m1和m2的物体1和2,m1<m2,如图所 示。设滑轮的质量为m,半径为r,所受的摩擦阻力矩为 Mr。绳与滑轮之间无相对滑动。试求物体的加速度和绳 的张力。 Mr 解:滑轮具有一定的转动惯 量。在转动中受到阻力矩 Mr T1 的作用,两边的张力不再相 T2 T1 T2 等,设物体 1 这边绳的张力为 a T1、T1' (T1' = T1), m a
d r sin 是转轴到F2作
用线的距离,称为力臂。 转动 平面
r F1
r
r F
r F2
(3 ) F 1 对转轴的力矩为零, 在定轴转动中不予考虑。
d
(4)在转轴方向确定后,力对转轴 的力矩方向可用+、-号表示,一般 以向上为正,即以逆时针转动方向 为正!
上页 下页 返回 退出
二、刚体转动的角量描述
上页 下页 返回 退出
2.角位移 描写刚体位置变化的物理量。 角坐标的增量: 称为刚体的角位移
3.角速度 描写刚体转动快慢和方向 的物理量。
R y
v2
P
P
v1
x
d 角速度 lim t 0 t dt
方向:满足右手定则,沿刚体转动方向右手大拇指指向。
N i 1
刚体定轴 转动定律
2 2 r m 单位: kg· m i i
上页 下页 返回 退出
d M z J J dt
刚体定轴转动定律:刚体在合外力矩的作用下,所获 得的角加速度与合外力矩的大小成正比,与刚体的转 动惯量成反比。
说明: α ,转动惯量是转动惯性 (1)Mz 一定,J 大小的量度;例如地球的转动惯量非常巨大,因此转 动惯性也非常巨大,地球的自转角速度亘古不变!
i 1 i i i i 1 i i i i 1
N
N
N
2
i i
)
根据内力性质(每 一对内力等值、反向、 共线,对同一转轴的力 矩代数和为零)得
i 1
M ij
rj
j
f ji
f ij
O
M ji
fi ri sin i 0
N
d
i ri
M ij M ji
上页 下页 返回 退出
得到:
F r sin (m r
i 1 i i i i 1
N
N
2
i i
)
上式左端为刚体所受外力对转轴的合力矩,以 Mz 表示;右端求和符号内的量与转动状态无关, 而只与刚体的质量分布有关,称为刚体转动惯量, 以J 表示。于是得到
d M z J J dt
其中转动惯量: J
上页 下页 返回 退出
解:(1)建立坐标系,分割出质量元
m (2) J x dm x dx 0 l 1 2 ml (公式) 3
2 l 2
x
O
x
h
dx
m x dx (3) J x dm l 2 h l 1 ml 2 mh 2 (※) 12
2 l 2 h 2
§3-2 力矩 转动惯量 定轴转动定律
一、力矩 F对O点的力矩: M r F M rF sin
Z
M
F
M
F
MZ
转 动 平 面
A
O r
r
M 沿Z 轴分量为 F 对Z 轴的力矩 M Z
上页 下页 返回 退出
力不在转动平面内
M r F r (F1 F2 ) r F1 r F2
上页 下页 返回 退出
J 的计算方法
质量离散分布
J mi ri 2 m1r12 m2 r22
i 1
N
2 mN rN
质量连续分布
J mi ri 2 r 2dm
i
dm :质量元
r dV
2 V
d V :体积元
dm dl , :质量线密度。 对质量线分布的刚体:
Fi sin i fi sin i mi ai mi ri
上页 下页 返回 退出
用 ri 乘以上式左右两端得
Fi ri sin i fi ri sin i mi ri 2
设刚体由N个质元构成,对每个质元可写出上述 类似方程,将这N个方程左右相加得
F r sin f r sin (m r
上页 下页 返回 退出
飞轮的质量为什么大 都分布于外轮缘?
上页 下页 返回 退出
竿 子 长 些 还 是 短 些 较 安 全 ?
质点平动的牛顿第二定律与刚体定轴转动定律的对比: 平动: 线动量 mv 转动: 角动量 J
dv 平动定律 F m dt d 转动定律 M z J dt
质量:平动中惯性大小的量度。 转动惯量:转动中惯性大小的量度。 与牛顿第二定律相似,力矩Mz与角加速度α是共 生共灭的,两者方向(符号)相同,力矩是刚体转动状 态(ω)发生变化的原因,当Mz=0时,α=0,ω保持不 变,刚体作匀角速度转动。
上页 下页 返回 退出
角速度是矢量,但对于刚体定 轴转动来说,角速度的方向只有两 个:上或下,因此用正负号就可表 示角速度的方向,而不必写成带有 箭头的矢量形式。 刚体上任一质元的速度表示为
