收集反比例函数与三角形四边形的面积等
反比例函数求面积公式大全

反比例函数求面积公式大全《反比例函数求面积公式大全》引言:反比例函数是数学中的一种特殊函数,其特点是当自变量x增加时,因变量y会以相反的趋势减小。
在数学和实际应用中,使用反比例函数可以描述许多重要的关系,尤其是与面积相关的问题。
本文将为读者提供一份反比例函数求面积的公式大全,帮助读者更好地理解和应用反比例函数。
一、长方形1. 长方形的面积与其长度(l)和宽度(w)成反比例关系,即S = k/(l×w),其中k为常数。
二、正方形1. 正方形的面积与其边长(s)的平方成反比例关系,即S = k/s²,其中k为常数。
三、圆1. 圆的面积与其半径(r)的平方成反比例关系,即S = πr²,其中π为圆周率,约等于3.14159。
四、椭圆1. 椭圆的面积与其长轴(2a)和短轴(2b)的乘积成反比例关系,即S = πab,其中a和b分别为长轴和短轴的半长。
五、三角形1. 三角形的面积与其底(b)和高(h)的乘积成反比例关系,即S = (1/2)bh。
六、平行四边形1. 平行四边形的面积与其底(b)和高(h)的乘积成反比例关系,即S = bh。
七、等腰梯形1. 等腰梯形的面积与其上底(a)、下底(b)和高(h)的关系为S = (a + b)h/2。
八、圆环1. 圆环的面积与其外半径(R)、内半径(r)和π的关系为S = π(R² - r²)。
结论:通过反比例函数求面积的公式大全,读者可以更加方便地计算各种几何形状的面积。
这些公式对于数学学习、几何推导以及实际生活中的建模和计算都具有重要意义。
希望读者能够掌握这些公式,并在实际中运用自如,提高数学应用的能力和解决问题的水平。
反比例函数与图形面积

计算定积分
利用定积分的几何意义, 计算直线与双曲线所围成 的图形面积。
注意事项
在计算过程中,需要注意 积分上下限的确定以及被 积函数的正负问题。
参数方程在面积计算中应用
参数方程表示
对于某些复杂图形,使用 参数方程表示更为方便。
面积元素计算
根据参数方程,计算面积 元素并对其进行积分。
注意事项
在使用参数方程计算面积 时,需要确保参数范围选 取合适,且要注意参数方 程的正负问题。
02
圆形面积计算:根据圆形面积公式$S = pi r^2$(其中$r$为圆形半径), 计算圆形区域的面积。
03
反比例函数图像面积计算:通过极坐 标下的定积分计算反比例函数图像在 圆形区域内的面积,即 $int_{theta_1}^{theta_2} int_{r_1(theta)}^{r_2(theta)} frac{k}{r} rdrdtheta$(其中$k$为反 比例函数的常数,$theta_1$和 $theta_2$为交点极角,$r_1(theta)$ 和$r_2(theta)$为交点极径)。
指数函数图像与 $x$ 轴围成的封闭 图形面积可以通过定积分
$int_{x_1}^{x_2} a^x dx$ 来计算, 其中 $x_1$ 和 $x_2$ 是指定的积分
上下限。
对数函数 $y = log_a x$($a > 0, a neq 1$)的图像是一个对数曲线。 当 $a > 1$ 时,曲线上升;当 $0 < a < 1$ 时,曲线下降。
在每个象限内,随着 $x$ 的增大,$y$ 的值逐渐减小。
当 $k > 0$ 时,反比例函数的图像位于 第一、三象限;当 $k < 0$ 时,反比例 函数的图像位于第二、四象限。
反比例函数求面积问题
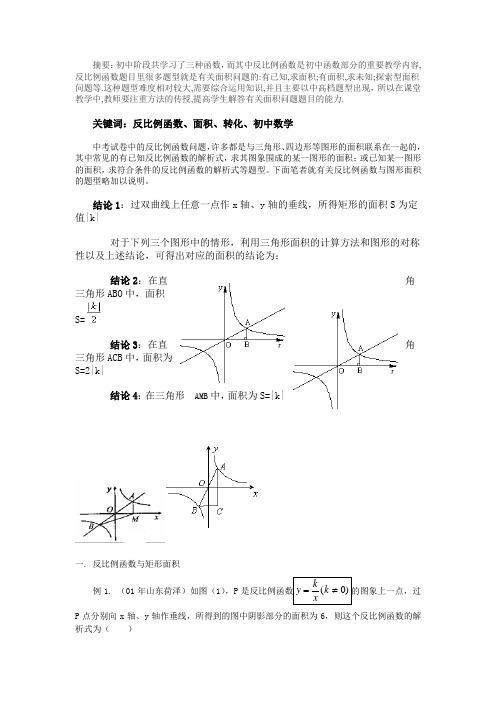
摘要:初中阶段共学习了三种函数,而其中反比例函数是初中函数部分的重要教学内容,反比例函数题目里很多题型就是有关面积问题的:有已知,求面积;有面积,求未知;探索型面积问题等.这种题型难度相对较大,需要综合运用知识,并且主要以中高档题型出现,所以在课堂教学中,教师要注重方法的传授,提高学生解答有关面积问题题目的能力.关键词:反比例函数、面积、转化、初中数学中考试卷中的反比例函数问题,许多都是与三角形、四边形等图形的面积联系在一起的,其中常见的有已知反比例函数的解析式,求其图象围成的某一图形的面积;或已知某一图形的面积,求符合条件的反比例函数的解析式等题型。
下面笔者就有关反比例函数与图形面积的题型略加以说明。
结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k|对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|一. 反比例函数与矩形面积例1. (01年山东荷泽)如图(1),P是反比例函数ykxk=≠()0的图象上一点,过P点分别向x轴、y轴作垂线,所得到的图中阴影部分的面积为6,则这个反比例函数的解析式为()图1解:设点P的坐标为(x,y)P评析:如图(2),若A AB垂直于x轴,垂足为B,AC的垂直于y轴,垂足为C图2例2. (01年福建福州)如图(3),已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B P(m,n)P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S。
(1)求B点坐标和k的值;(2P的坐标;(3)略图3解:(1点的坐标为(3,3)P在第一象限(2①②P的坐标为(66)(此种情况的求法与上述方法一样,在此不再详解)二. 反比例函数与三角形面积1. 反比例函数与直角三角形面积例3. (04年辽宁锦州)如图(4),点A AB垂直于x_____________。
反比函数图像上四种三角形的面积

反比函数图像上的四种三角形的面积函数是解决实际生活问题的重要模型,在近几年各省市的考题中,对于函数的考查比例占有相当重的份量,绝大部分是考查考生对其基本概念、图象性质的理解和应用,甚至成为中考压轴题的大类。
反比例函数的图像经常与三角形的面积联系在一起,下面就举例说明。
结论1、过反比例函数图像上一点,向x 轴作垂线,则以图像上这个点、垂足,原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。
设P (a ,b )是反比例函数y=xk(k ≠0)图像上的一点,过点P 作PA ⊥x轴,垂足为A ,三角形PAO 的面积是S ,则S k 2=结论2、过反比例函数图像上一点,向y 轴作垂线,则以图像上这个点、垂足,原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。
设P (a ,b )是反比例函数y=x k(k ≠0)图像上的一点,过点P 作PB ⊥y 轴,垂足为B ,三角形PBO 的面积是S ,则S k 2=。
结论3、正比例函数y=k 1x (k 1>0)与反比例函数y=xk(k >0)的图像交于A 、kx 襄樊市第四十七中学 熊沙 图(1)2)B 两点,过A 点作AC ⊥x 轴,垂足是C ,三角形ABC 的面积设为S ,则S=|k|,与正比例函数的比例系数k 1无关。
证明:I因为,正比例函数y=k 1x (k 1>0)与反比例函数y=x k(k >0)的图像交于A 、B 两点,所以,x k xk1=,所以,x=±111k kk k k =, 当x=11k kk 时,y= k 1x=1kk ,所以,点A 的坐标是(11k kk ,1kk ),当x =-11k kk 时,y= k 1x =-1kk ,所以,点B 的坐标是(-11k kk ,-1kk ),所以,OC 的长度是11k kk ,三角形ABC 的面积=三角形AOC 的面积+三角形BOC 的面积=21×OC ×AC+21×OC ×BD =21×11k kk ×1kk +21×11k kk ×|-1kk | =21k+21k=k 。
反比例函数中的面积问题

解得 k=2 评注:第①小题中由图形所在象限可确定k>0,应用结论可直接求k值。 第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相 等,列出含k的方程求k值。
例2(2008贵州省黔南州)如图,矩形ABOD的顶点A是函数 与函数 在第二象限的交点, 轴于B, 轴于D,且矩形ABOD的பைடு நூலகம்积为3. (1)求两函数的解析式. (2)求两函数的交点A、C的坐标.
图象上,∴
解得x=1从而所求面积为π 评注:对于较复杂的图形面积计算问题,先应观察图形的特征,若具有 对称特征,则应用对称关系可以简化解题过程。
四、 讨论与面积有关的综合问题 例8.(2008山东省)(1)探究新知:
如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由. (2)结论应用:
与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4. (1)试确定反比例函数的关系式; (2)求△AOC的面积.
.解:(1)∵点A(-2,4)在反比例函数图象上 ∴k=-8 ∴反比例函数解析式为y=
(2)∵B点的横坐标为-4, ∴纵坐标为y=2 ∴B(-4,2) ∵点A(-2,4)、 点B(-4,2)在直线y=kx+b上 ∴ 4=-2k+b 且2=-4k+b 解得 k=1 b=6 ∴直线AB为y=x+6 与x轴的交点坐标C(-6,0)
(3)若点P是y轴上一动点,且 , 求点P的坐标.
解:(1)由图象知k<0,由结论及已知条件得 -k=3 ∴
∴反比例函数的解析式为 ,一次函数的解析式为 (2)由 ,解得 ,
∴点A、C的坐标分别为(
,3),(3, ) (3)设点P的坐标为(0,m) 直线 与y轴的交点坐标为M(0,2) ∵
反比函数图像上四种三角形的面积知识点分析人教版

反比函数图像上四种三角形的面积反比例函数的图像经常与三角形的面积联系在一起,下面就举例说明。
一、三角形面积的四个结论结论1、过反比例函数图像上一点,向x 轴作垂线,则以图像上这个点、垂足,原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。
如图1所示,设P (a ,b )是反比例函数y=xk(k ≠0)图像上的一点,过点P 作PA ⊥x 轴,垂足为A , 三角形PAO 的面积是S ,则|k|=2S 。
结论2、过反比例函数图像上一点,向y 轴作垂线,则以图像上这个点、垂足,原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。
如图2所示,设P (a ,b )是反比例函数y=xk(k ≠0)图像上的一点,过点P 作PB ⊥y 轴,垂足为B , 三角形PBO 的面积是S ,则|k|=2S 。
结论3、正比例函数y=k 1x (k 1>0)与反比例函数y=xk(k >0)的图像交于A 、B 两点,过A 点作AC ⊥x 轴,垂足是C ,三角形ABC 的面积设为S ,则S=|k|,与正比例函数的比例系数k 1无关。
如图3所示。
证明1:因为,正比例函数y=k 1x (k 1>0)与反比例函数y=xk(k >0)的图像交于A 、B 两点, 所以,x k xk1=,所以,x=±111k kk k k =, 当x=11k kk 时,y= k 1x=1kk ,所以,点A 的坐标是(11k kk ,1kk ),当x=-11k kk 时,y= k 1x=-1kk ,所以,点B 的坐标是(-11k kk ,-1kk ),所以,OC 的长度是11k kk ,三角形ABC 的面积=三角形AOC 的面积+三角形BOC 的面积 =21×OC ×AC+21×OC ×BD =21×11k kk ×1kk +21×11k kk ×|-1kk | =21k+21k=k 。
反比例函数求三角形面积

反比例函数求三角形面积
三角形是广泛存在于自然界中的一种几何形状,也是许多数学问题研究中的一个重要元素。
本文通过反比例函数求解三角形的面积。
首先需要知道的是,反比例函数是一种特殊的比例函数,其关系式可以表示为y = k/x,其中k为常量,x为变量。
该函数表示的是y与x呈反比例关系,当x变大时,y会变小,当x变小时,y会变大。
三角形的面积是根据三角形的三条边长度表示的,用一般式子表示如下:
S=√(p(p-a)(p-b)(p-c))
其中,S表示三角形的面积,p为三角形的半周长,a,b,c分别表示三角形的三条边长。
由此可以看出,三角形的面积S与半周长p成正比,S与三角形的三条边长成反比例,其关系式可以表示为:
S= k/(a*b*c)
由此可以得出,三角形的面积S与三角形的三条边长成反比例,可以使用反比例函数来求解三角形面积S。
本文介绍了如何使用反比例函数求解三角形面积。
当我们需要求解三角形的面积时,可以利用该函数来计算。
因为它的工作原理是要将边长的反比例关系转换成面积与边长的正比关系,这样就可以自动计算出三角形的面积。
特别要指出的是,在求解三角形面积问题时,我们除了使用反比
例函数外,还可以使用比例函数、勾股定理等方式来求解。
然而,使用这些方法求解时需要掌握更多的公式,且求解过程较为复杂,而使用反比例函数却可以节省许多求解时间。
本文介绍了利用反比例函数求解三角形面积的方法,可以有效提高求解三角形面积问题的效率。
同时,本文也为其他求解几何图形面积问题提供了一定参考,希望能帮助读者更好地理解反比例函数的概念,从而有效提高求解几何图形问题的效率。
专题:反比例函数中的面积问题

微专题 反比例函数中的面积问题
模型一 一点一垂线
反比例函数图象上一点与坐标轴垂线、另一坐标轴上一点(含原点)围成的三 角形面积= |k|.
1
S△ABC= 2 |k|
S△ABC=12 |k|
1
S△AOC= 2 |k|
1. 如图,点A在反比例函数y=- 4 的图象上,AM⊥y轴于点M,点P是x轴上的一
方法一:S△EOF=S△EOD-S△FOD. 方法二:作EM⊥x轴于点M,交OF于点B,FA⊥x轴于点A,则S△OEB=S四边形 BMAF(划归到模型一),则S△EOF=S直角梯形EMAF.
类型一 两交点在反比例函数同一支上
Байду номын сангаас
方法一:当
BE CE
或
BFFA=m时,则S四边形OFBE=m|k|.
方法二:作EM⊥x轴于点M,
A. 1
B. m-1
C. 2
D. m
第3题图
模型四 两点两垂线
反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形 面积=2|k|.
SABC 2 | k |
易得四边形ANBM是平行四边形, ∴S四边形ANBM=AM·NM=AM·2OM=2|k|
模型四 两点两垂线 反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形
= =
1
2
1
OM·AM+12 OM·BC |k|+1 |k|=|k|
22
S△ABM=S△ADM+S△MDB
=
1 2
MD·|yB-yA|
S△ABM=S△BMO+S△AMO
=
1 2
MO·|xB-xA|
3. 如图,直线y=mx与双曲线y=k (k≠0)交于点A,B,过点A作
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数比例系数k与图形面积经典专题知识点回顾由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进行考察。
这种考察方式既能考查函数、反比例函数本身的基础知识内容,又能充分体现数形结合的思想方法,考查的题型广泛,考查方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的四种类型归纳如下:利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|类型之一k与三角形的面积k(k>0)经过直角三角形OAB斜边OB的中点D,※1、如图,已知双曲线y=x与直角边AB相交于点C.若△OBC的面积为6,则k=______.最佳答案过D点作DE⊥x轴,垂足为E,1k,由双曲线上点的性质,得S △AOC =S △DOE =2∵DE⊥x轴,AB⊥x轴,∴DE ∥ AB,∴△OAB ∽△OED,又∵OB=2OD,∴S △OAB =4S △DOE =2k,由S △OAB -S △OAC =S △OBC ,1k=6,得2k-2解得:k=4.故答案为:4.2018(x>0)的图象上任意两点A、B作2、如图1-ZT-1,分别过反比例函数y=xx轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,,比较它们的大小,可得A.S1>S2B.S1=S2C.S1<S2D.S1、S2大小不确定。
3、在下列图形中,阴影部分面积最大的是(C)k(x<0)图象上的4、如图1-ZT-3,在平面直角坐标系中,点A是函数y=x点,过点A作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为________。
5、※如图,在平面直角坐标系中,点A在函数(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k= .6、如图1-ZT-4,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,k在第一象限的图象经过点B,若OA2-AB2=8,则k的值为反比例函数y=x_______。
类型之二k与平行四边形的面积k(k<0,x<0)图象上的点,过点7、※如图,在平面直角坐标系中,点A是函数y=xA与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为___.优质解答∵AB⊥y轴,∴AB∥CD,∵BC∥AD,∴四边形ABCD是平行四边形,∴四边形AEOB的面积=AB•OE,∵S平行四边形ABCD=AB•CD=3,∴四边形AEOB的面积=3,∴|k|=3,∵<0,∴k=-3,故答案为:-3.8、如图,菱形OABC的顶点的坐标为(3,4),顶点A在x轴的正半轴上,反k(x>0)的图象经过顶点B,则k的值为()。
比例函数y=xA. 12B. 20C. 24D. 32答案:过点C 作CD ⊥OA ,∵C 的坐标为(3,4), ∴CD=4,OD=3, ∵CB ∥AO , ∴B 的纵坐标是4, ∴OC=22OD CD =5,∴AO=OC=5,∵四边形COAB 是菱形, ∴B 的横坐标是8, ∴k=8×4=32, 故选D .9、如图1-ZT-6,函数y=-x 与y=-x 4的图象相交于A 、B 两点,分别过A 、B两点作y 轴的垂线,垂足分别为C 、D ,则四边形ACBD 的面积为( )。
A. 2B. 4C. 6D. 8分析:首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=21|k|,得出S △AO C =S △ODB =2,再根据反比例函数的对称性可知:OC=OD ,AC=BD ,即可求出四边形ACBD 的面积. 解答:解:∵过函数y=-x4的图象上A ,B 两点分别作y 轴的垂线,垂足分别为点C ,D , ∴S △AOC =S △ODB =21|k|=2, 又∵OC=OD ,AC=BD ,∴S △AOC =S △ODA =S △ODB =S △OBC =2,∴四边形ABCD 的面积为:S △AOC +S △ODA +S △ODB +S △OBC =4×2=8. 故选D .点评:本题主要考查了反比例函数y=xk中k 的几何意义,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积为|k|;图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=21|k|,是经常考查的一个知识点;同时考查了反比例函数图象的对称性.10、如图1-ZT-7,点A 是反比例函数y=x2(x >0)的图象上任意一点,AB ∥x 轴交反比例函数y=-x3的图象于点B ,以AB 为边作□ABCD ,其中点C 、D 在x 轴上,则□ABCD 的面积未( )。
A. 2 B. 3 C. 4 D. 511、如图、1-ZT-8,在□ABOC 中,两条对角线交于点E ,双曲线y=xk(k <0)的一支经过C 、E 两点,若□ABOC 的面积为10,则k 的值是( )。
A. -25B. -310C. -4D.-5类型之三k与矩形的面积4上,分别过A、B两点向坐标轴作12、如图1-ZT-9,A、B两点在双曲线y=x垂线段,已知S1+S2=6,则S阴影=()。
A. 4B. 2C. 1D.无法确定13、如图1-ZT-10,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为9,则k 的值为()。
A. 1B. 2C. 3D. 4考点:反比例函数系数k的几何意义.专题:数形结合.分析:本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、矩形OABC的面积与|k|的关系,列出等式求出k值.解答:解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,∴S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则++9=4k,解得:k=3.故选C.点评:本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,本知识点是中考的重要考点,同学们应高度关注.14、如图1-ZT-11,反比例函数y=(,k >0)的图象与矩形ABCO 的两边相交于E 、F 两点,若E 是AB 的中点,S △BEF =2,则k 的值为________。
分析:设E (a ,a k ),则B 纵坐标也为a k ,代入反比例函数的y=xk ,即可求得F 的横坐标,则根据三角形的面积公式即可求得k 的值. 解:设E (a ,a k ),则B 纵坐标也为ak , E 是AB 中点,所以F 点横坐标为2a ,代入解析式得到纵坐标:ak2, BF=a k -a k 2=ak 2,所以F 也为中点, S △BEF =2=4k,k=8.故答案是:8.点评:本题考查了反比例函数的性质,正确表示出BF 的长度是关键.15、如图1-ZT-12,点P 、Q 是反比例函数y= x k图象上的两点,PA ⊥y 轴于点A ,QN ⊥x 轴于点N ,PM ⊥x 轴于点M,QBy 轴于点B ,连接PB 、QM ,△ABP 的面积记为S 1,△QMN 的面积记为S 2,则S 1____________S 2(填“>”“<”或“=”)。
16、如图1-ZT-13,在平面直角坐标系中,点O 为坐标原点,矩形OABC 的边OA 、OC 分别在x 轴和y 轴上,其中OA=6,OC=3,已知反比例函数y=(,k >0)的图象经过BC 边的中点D,交AB 于点E 。
(1)k 的值为________;(2)猜想△的面积与△的面积之间的关系,并说明理由。
答案:(1)9;(2)S△OCD=S△OBE,理由见解析.【解析】试题分析:(1)根据题意得出点D的坐标,从而可得出k的值:∵OA=6,OC=3,点D为BC 的中点,∴D(3,3).∵反比例函数(x>0)的图象经过点D,∴k=3×3=9.(2)根据三角形的面积公式和点D,E在函数的图象上,可得出S△OCD=S△OAE,再由点D为BC的中点,可得出S△OCD=S△OB...类型之四k与多边形的面积17、如图1-ZT-14所示,过点A(2,-1)分别作y轴、x轴的平行线交双曲线k于点B、C,过点C作CE⊥x轴于点E,过点B作BD⊥y轴于点D,连接y=xED,若五边形ABDEC的面积为34,则k的值为________。
18、如图1-ZT-14,点P 是反比例函数y=xk 1(k 1>0,x >0)图象上的一动点,过点P 作x 轴、y 轴的垂线,分别交x 轴、y 轴于A 、B 两点,交反比例函数y=x k2(k 2<0,且|k 2|<k 1)的图象于E 、F 两点。
(1)图1中,四边形PEOF 的面积S 1=______(用含k 1、k 2的式子表示); (2)图2中,设P 点坐标为(2,3),①点E 的坐标是(______,______),点F 的坐标是(______,______)(用含k 2的式子表示);(3)②若△OEF 的面积为38,求反比例函数y =xk2的解析式.解答:(1>0,x>0)图象上一动点,∴S=k1∴四边形PEOF的面积S1=S矩形PBOA+S△OBF+S△AOE=k1+|k2|,∵k2<0,∴四边形PEOF的面积S1=S矩形PBOA+S△OBF+S△AOE=k1+|k2|=k1-k2.(2)①∵PE⊥x轴,PF⊥y轴可知,P、E两点的横坐标相同,P、F两点的纵坐标相同,∴k1=6,∴k2=2±∵k2<0,题型之五:k与面积综合12(x 16、如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=x>0)图像上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于A、B。
(1)求证:线段AB为⊙P的直径;(2)求△AOB的面积。
