受弯构件典型例题 钢结构
例题受弯构件正截面承载力计算精选全文 (2)

Mgk=gk l02/8=13.438×62/8=60.471kN. m
简支梁在活荷载标准值作用下的跨中弯矩为: Mqk=qk l02/8=12×62/8=54kN·m
由恒载控制的跨中弯矩为 γ0 (γGMgk+γQΨcMq k) =1.0×(1.35×60.471+1.4×0.7×54)=134.556kN·m
选配4 14(As=615mm2),如图所示。
【例3.2×】某教学楼钢筋混凝土矩形截面简支 梁,安全等级为二级,截面尺寸
b×h=250×550mm , 承 受 恒 载 标 准 值 10kN/m
(不包括梁的自重),活荷载标准值12kN/m, 计算跨度=6m,采用C20级混凝土,HRB335级钢 筋。试确定纵向受力钢筋的数量。
=6.41mm<ξbh0=0.614×55=33.77mm 不属超筋梁。 As=α1fcbx/fy=1.0×9.6×1000×6.41/210=293mm2 45ft/fy =0.45×1.10/210=0.24%>0.2%,取 ρmin=0.24% ρmin bh=0.24%×1000×80=192mm2< As =293mm2
不属少筋梁。
受力钢筋选用φ8@180(As=279mm2),分布钢筋按构造要 求,选用φ6@250。
第三章 受弯构件正截面承载力计算
第六节 双筋矩形截面受弯构件 正截面承载力计算
一、双筋截面的适用情况
1) M > 1fcbo2 h b(10.5 b),但截面尺寸及材料强度
不能再增大和提高; 2)在不同荷载作用下,截面承受正、负弯矩作用 (如风荷载作用下的框架梁); 3)为提高框架梁的抗震性能,在梁中必须配置一定 比例的受压钢筋。
钢结构设计原理 第五章 受弯构件

钢结构设计原理第五章受弯构件1、第五章受弯构件51概述1、定义主要承受横向荷载作用的构件,即通常所讲的梁。
2、类型按使用功能,可分为工作平台梁、吊车梁、楼盖梁、墙梁及檩条等;按支承状况,可分为简支梁、连续梁、伸臂梁和框架梁等;按荷载作用状况,可分为单向弯曲梁和双向弯曲梁;按截面形式有型钢梁和组合梁;实腹式和格构式。
图51受弯构件的截面形式3、受弯构件梁的内力一般,仅考虑其弯矩和剪力;对于框架梁,需同时考虑M、V和N作用。
※关键词受弯构件MEMBERINBENDING梁BEAM单向受弯构件ONEWAYMEMBERINBENDING双向受弯构件TWOWAYMEMBERINBENDING52受弯构件的强度一、2、抗弯强度1、梁在弯矩作用下,当M渐渐增加时,截面弯曲应力的进展可分为三个阶段,见图52所示。
〔1〕弹性工作阶段弯矩较小时,梁截面受拉边缘?<YF,梁处于弹性工作阶段,弯曲应力呈三角形分布。
弹性极限弯矩为NEW??截面受拉边缘的?YF。
〔2〕弹塑性工作阶段弯矩继续增大,截面边缘部分进入塑性,中间部分仍处于弹性工作状态。
〔3〕塑性工作阶段当弯矩再继续增加,截面的塑性区进展至全截面,形成塑性铰,梁产生相对转动,变形大量增加。
此时为梁的塑性工作阶段的极限状态,对应的塑性极限弯矩为PNYPWFM??。
图52梁受弯时各阶段的应力分布状况问取那个阶段作为设计或计算的模型答规范中按弹性阶3、段或弹塑性阶段设计或计算。
塑性进展深度,通过塑性进展系数?来衡量。
截面样子系数NPEFWM??2、抗弯强度?单向受弯FNX????双向受弯FWNYNX???其中X?、Y截面塑性进展系数,一般状况按表61取值;?若YFTB2351>时,取X?Y10;?若直接承受动力荷载作用时,取10。
※抗弯强度不够时,可以调整截面尺寸增大NW,但以增大截面高度H最有效。
二、抗剪强度梁的抗剪强度按弹性设计,以截面的剪应力到达钢材的抗剪强度设计值作为抗剪承载力的极限状态。
受弯构件例题

M图
M
0
Fab/l Fab/l (下拉) (下拉)
0
例题
F
a
b
C
B
x1
x2
l
FB
Fb / l
Fa / l Fab / l
3.1.3 梁的内力图
解 1.求支座反力
2.列剪力方程和弯矩方程
3.画剪力图和弯矩图
A
讨论
无荷载作用区段(如AC、BC段),剪力 图为水平线(平行于梁轴线),弯矩图为 斜直线,且当剪力图为正时,弯矩图为下 斜直线(从左向右倾斜),当剪力图为负 时,弯矩图为上斜直线。
3.1.3 梁的内力图 例3.3 (教材P63例3.5)
如图所示简支梁AB,承受集
A
中荷载F作用,梁的自重不计。试
画出其剪力图和弯矩图。
例题
aF b
C
B
l
3.1.3 梁的内力图
解 1.求支座反力 方程不同时
M A(F) 0 FB l应 F分段a 列0方程FB
Fa l
MB (F) 0 FA l F b 0
(a x2 l)
M ( x2 ) M C (F外 )
A
Fb l
x2
F (x2
a)
FA
Fa l
(l
x2 )
例题
F
a
b
C
B
x1
x2
l
FB
M(x1) x1 V(x1)
aF
C x2
M(x2) V(x2)
3.1.3 梁的内力图
解
1.求支座反力
FA
Fb l
FB
钢结构受弯构件计算

钢结构受弯构件计算4.1 梁的类型和应用钢梁在建筑结构中应用广泛,主要用于承受横向荷载。
在工业和民用建筑中,最常见的是楼盖梁、墙架梁、工作平台梁、起重机梁、檩条等。
钢梁按制作方法的不同,可分为型钢梁和组合梁两大类,如图4-1所示。
型钢梁又可分为热轧型钢梁和冷弯薄壁型钢梁。
前者常用工字钢、槽钢、H 型钢制成,如图4-1(a)、(b)、(c)所示,应用比较广泛,成本比较低廉。
其中,H 型钢截面最为合理,其翼缘内外边缘平行,与其他构件连接方便。
当荷载较小、跨度不大时可用冷弯薄壁C 型钢[图4-1(d)、(e)]或Z型钢[图4-1(f)],可以有效节约钢材,如用作屋面檩条或墙面墙梁。
受到尺寸和规格的限制,当荷载或跨度较大时,型钢梁往往不能满足承载力或刚度的要求,这时需要用组合梁。
最常见的是用三块钢板焊接而成的H 形截面组合梁[图4-1(g)],俗称焊接H 型钢,其构造简单,加工方便。
当所需翼缘板较厚时,可采用双层翼缘板组合梁[图4-1(h)]。
荷载很大而截面高度受到限制或对抗扭刚度要求较高时,可采用箱形截面梁[图4-1(i)]。
当梁要承受动力荷载时,由于对疲劳性能要求较高,需要采用高强度螺栓连接的H 形截面梁[图4-1(j)]。
混凝土适用于受压,钢材适用于受拉,钢与混凝土组合梁[图4-1(k)]可以充分发挥两种材料的优势,经济效果较明显。
图4-1 梁的截面形式(a)工字钢;(b)槽钢;(c)H 型钢;(d),(e)C型钢;(f)Z型钢;(g)H 形截面组合梁;(h)双层翼缘板组合梁;(i)箱形截面梁;(j)高强度螺栓连接的H 形截面梁;(k)钢与混凝土组合梁为了更好地发挥材料的性能,钢材可以做成截面沿梁长度方向变化的变截面梁。
常用的有楔形梁,这种梁仅改变腹板高度,而翼缘的厚度、宽度及腹板的厚度均不改变。
因其加工方便,经济性能较好,目前已经广泛用于轻型门式刚架房屋中。
简支梁可以在支座附近降低截面高度,除节约材料外,还可以节省净空,已广泛应用于大跨度起重机梁中,另外,还可以做成改变翼缘板的宽度或厚度的变截面梁。
第六章受弯构件典型例题_钢结构

360
3m
3m
3m
3m 10
M图(KN·m) 1396 1446 483 468.3 V 图 ( KN) 474 465.3 163.8 155.1 1861.2 1915.8 1396 1446
155.1 155.1 163.8 465.3 474
155.1
468.3 483
【解答】 分析: (1)选择工字形焊接组合梁截面的步骤是先确定腹板高度和厚度,即 h0 和 t w ; 再确定翼缘板的宽度和厚度,即 b 和 t 。确定腹板高度时,除考虑经济要求外,还应注意满 足刚度要求;满足局部稳定要求外,还应注意满足抗剪强度要求。 (2)选择截面后,应进行强度、刚度和整体稳定的验算。强度验算时,应注意在集中 力作用的跨中截面除进行抗弯强度验算外,还应进行腹板高度处折算应力的验算。抗剪强度 和刚度,因在选择截面时已满足要求,可不再进行验算。整体稳定验算时应考虑梁跨中有侧 向支承后,受压翼缘的自由长度是实际侧向支承点的距离。 1.内力计算 跨中截面:
(200 − 8) b 96 2 (1) 翼缘: 1 = =截面满足局部稳定要求。
h0 800 = = 100 tw 8
80<
钢结构设计原理例题

h fmin =1.5t =1.5⨯10=4.74mm mm t h fm sx 77.51==,取h f =6mm 取盖板截面为260⨯6mm 2,则端缝承载力为 wt f e f B h b N ⨯⨯⨯=21 查表1-4得fwt =160 N/mm2则 kN N 8.42631616022.167.026021=⨯⨯⨯⨯⨯= 接缝一侧一条焊缝需要长度 ()mm f h N N L wt f W 58616067.0410975.40955067.0431=+⨯⨯⨯⨯-=+⨯⨯⨯-=取L W =60mm.则盖板全长为:mm L L W 130********=+⨯=+⨯=3-3.图3-73所示焊接工形截面梁,在腹板上设置一条工字对接焊缝,梁拼接处承受内力为m kN M ⋅=2500,V=500KN ,钢材为Q235钢,焊条为E43型,手工焊,二级质量标准,试验算拼接焊缝强度。
(提示:剪力V 可假定全部由腹板承担,弯矩按刚度比分配,即M II M w w =)解:查得2/215mm N f w t =,2/215mm N f w c =,2/125mm N f w v = 计算焊缝截面特征值()4237393605953601440006124021200.1121cm I =+=⨯⨯⨯+⨯⨯=431440001200.1121cm I w =⨯⨯=21201120cm A w =⨯=验算正应力m kN M I I M w w ⋅=⨯==9.4867393601440002500 2246/215/9.202600/10144000109.486mm N mm N W M w w w <=⨯⨯==σ满足 验算剪应力2223/125/7.411012010500mm N mm N A V w w <=⨯⨯==τ满足验算折算应力222222/2362151.1/4.2157.4139.2023mm N mm N w w =⨯<=⨯+=+τσ满足要求3-4.图3-74所示一柱间支撑与柱的连接节点,支撑杆承受轴拉力设计值kN N 300=,用2L80×6角钢做成,钢材均为Q235钢,焊条为E43型,手工焊。
第七章拉弯和压弯构件典型例题_钢结构精选全文
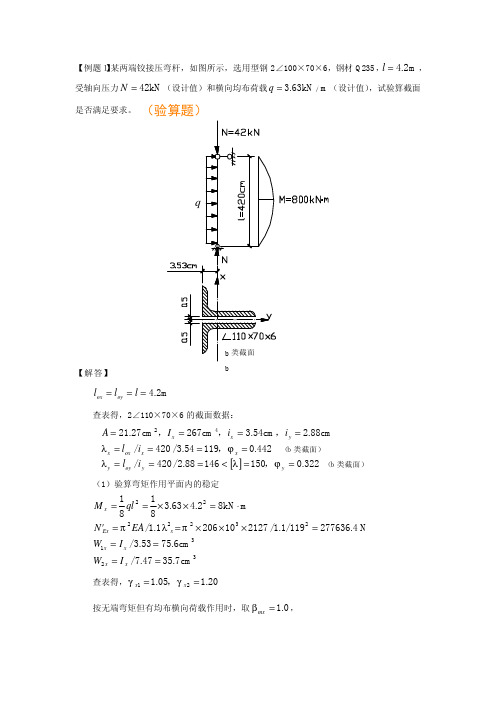
【例题1】某两端铰接压弯杆,如图所示,选用型钢2∠100×70×6,钢材Q235,m 2.4=l ,受轴向压力kN 42=N (设计值)和横向均布荷载m /kN 63.3=q (设计值),试验算截面是否满足要求。
【解答】m 2.4===l l l oy ox查表得,2∠110×70×6的截面数据:[]322.015014688.2/420/442.011954.3/420/cm 88.2cm 54.3cm 267cm 27.2142==<===========y y oy y x x ox x y x x i l i l i i I A ϕλλϕλ,,,,,(1)验算弯矩作用平面内的稳定32312322222cm 7.3547.7/cm 6.7553.3/N 277636.4119/212710206/mkN 82.463.38181=====×××==⋅=××==x x x x x Ex x I W I W EA N'ql M πλπ 查表得,20.105.121==x x γγ,按无端弯矩但有均布横向荷载作用时,取0.1=mx β,1.1/1.1(b 类截面)(b 类截面))6.277/428.01106.7505.110812127442.01042)8.01(36311×−××××+××=−+(Exx x xmx x N'N W M ANγβϕ 215N/mm 159.4114.77.442=<=+=f (满足))6.277/4225.11107.352.1108121271042)25.11(36322×−××××−×=−−(Exxx x mx N'N W M A N γβ 215N/mm 210.3230.3202=<=−=f (满足)(2)验算弯矩作用平面外的稳定7518.01460017.01235/0017.01=×−=−=y y b f λϕ3631106.757518.010*********.01042××××+××=+x b x tx y W M A N ϕβϕ 215N/mm 202141612=<=+=f (满足)实腹式截面无削弱,强度无需计算;因截面是角钢(型钢),局部稳定不用验算。
受弯构件计算例题

1.单筋矩形截面例4-1 已知矩形截面简支梁(见图4-19),混凝土保护层厚为20mm(一类环境),梁计算跨度l0=5m,梁上作用均布永久荷载(已包括梁自重)标准值g k=6kN/m,均布可变荷载标准值q k=15kN/m。
选用混凝土强度等级C20,钢筋HRB335级。
试确定该梁的截面尺寸b×h及配筋面积A s。
图4-18 例题4-1图解:(1)设计参数由附表2和附表6查得材料强度设计值,C20混凝土f c=9.6N/mm2,f t=1.1N/mm2,HRB335级钢筋f y=300N/mm2,等效矩形图形系数1=1.0。
设该梁的箍筋选用直径为φ8的HPB300钢筋。
(2)计算跨中截面最大弯矩设计值(3)估计截面尺寸b h⨯由跨度选择梁截面高度 450h mm =(111l ),截面宽度 b =200mm (12.25h ), 取简支梁截面尺寸 200450b h mm mm ⨯=⨯ (4)计算截面有效高度0h先按单排钢筋布置,取受拉钢筋形心到受拉混凝土边缘的距离a s = c+d v +d /2≈40mm ,取a s =40mm ,则梁有效高度 h 0=h -a s =450-40=410mm 。
(5)计算配筋6,max 221088.125100.2730.3991.09.6200410s s c M f bh ααα⨯===<=⨯⨯⨯ 满足适筋梁的要求。
112)1120.2730.326s ξα=--=--⨯=200.3262004109.6855300c s y f A bh mm f ξ⨯⨯⨯=== 由附表16,选用320钢筋,A s =942mm 2。
(6)验算最小配筋率min min 0.450.001659410.010*******0.002ts yf A f bh ρρρ>=====⨯>=满足要求。
(7)验算配筋构造要求 钢筋净间距为 200282203425mmd 20m 2m2mm-⨯-⨯>>==满足构造要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【题目】Q235钢简支梁如下图所示。
自重标准值0.9KN/m(荷载分项系数1.2),跨中承受悬挂集中力标准值100KN(荷载分项系数1.4),集中力作用于上翼缘。
1.梁在跨中无侧向支承,验算截面的整体稳定性;2.如改用16Mn钢,是否满足要求;3.仍用Q235,荷载悬挂于下翼缘,是否满足要求;4.仍用Q235,荷载作用位置不变,跨中增加一侧向支承点,整体稳定是否满足要求?5.验算梁翼缘和腹板的局部稳定性,并提出加强局部稳定的方法(不具体设置)。
1(2)验算工字型焊接组合梁的整体稳定性时,主要应掌握计算梁的整体稳定系数φb 的公式。
φb公式中的βb由参数ξ确定。
ξ=l1t1/b1h中的b1是梁受压翼缘的宽度。
如计算所得φb>0.6时,说明梁失稳时已进入弹塑性状态,应用相应的φb‘代替φb,进行整体稳定验算。
(3)梁的整体稳定验算不满足要求时,提高梁的整体稳定承载力的措施是很多的。
经过本题各种方法计算结果的比较,应掌握在不改变截面和荷载作用位置时,最有效的提高梁的整体稳定承载力的措施是在跨中增加侧向支承点。
(4)验算梁翼缘的局部稳定时,计算翼缘板的宽厚比b1/t(b1为受压翼缘板自由悬伸宽度);如b1/t值小于作为三边简支一边自由保证局部稳定的宽厚比限值,则翼缘的局部稳定能保证。
对于梁腹板,则计算h0/t w,根据h0/t w值的范围,设置加劲肋,以保证腹板的局部稳定。
1.验算原给定条件梁的整体稳定性(1)研究是否需要验算梁的整体稳定性查相关表可知,梁跨中无侧向支承时,荷载作用于上翼缘时,Q235钢梁不需验算整体稳定的最大l1/b值为13。
l 1/b=9000/200=45>13,应验算整体稳定。
(2)梁跨中的最大弯矩M max =1/8ql 2+1/4Fl=1/8×(0.9×1.2)×92+1/4×100×1.4×9=325.94KN·m (3)截面几何特性A=2×200×12+800×8=11200mm 2I x =1/12×(200×8243-192×8003)=1.133×109mm4 W x =I x /y=1.133×109/412=2.749×106mm 3I y =2×1/12×12×2003+1/12×800×83=1603.4×104mm4 i y 84.371012.1104.160344=××==A I Y λy =l 1/i y =9000/37.84=238(4)计算βb (或βb ‘)、φbξ=l 1t 1/b 1h=9000×12/(200×824)=0.655<2.0查相关表可知, 无侧向支承, 集中力作用于上翼缘情形: βb =0.73+0.18ξ=0.73+0.18×0.655=0.8479φb =2124.414320+h t W Ahy x y b λλβ 2773.08244.41284.237110749.2824102.1184.237432085.02632=××+×××××= (5)验算整体稳定σ=M x /(φb W x )=325.94×106/(0.2773×2.749×106)=427.58N/mm 2>215N/mm 2,不满足整体稳定要求。
2.改用16Mn 钢,重新验算改用16Mn 钢重新验算时,因f 有变化,φb 也有变化。
φb 1889.0345/2352773.02354.414320212=×= +=yy x y b f h t W Ah λλβ σ=M x /(φb W x )=325.94×106/(0.1889×2.749×106)=627.67N/mm 2>315N/mm 2由此可以看出,提高钢材强度等级,一般不能提高梁的整体稳定性。
3.将悬挂集中力作用于下翼缘时,βb 和φb 都有变化。
查相关表可知, 无侧向支承, 集中力作用于下翼缘情形: βb =2.23-0.28ξ=2.23-0.28×0.655=2.047φb 668.08244.41284.237110749.2824102.1184.2374320047.22632=××+×××××=>0.6由相关表可查得,φb ‘=0.633σ=M x /(φb ’W x )=325.94×106/(0.633×2.749×106)=187.31N/mm 2<215N/mm 2因此,整体稳定得到保证。
4.在跨中增加一侧向支承点,l 1=4500mml 1/b=4500/200=22.5>13 仍应验算整体稳定。
λy =l 1/i y =4500/37.84=118.92 ξ=l 1t 1/b 1h=4500×12/(200×824)=0.3277<2.0 查相关表可知, 跨中有一侧向支承,集中力作用。
βb =1.75φb =2124.414320+h t W Ahy x y b λλβ 93.18244.41292.118110749.2824102.1192.118432075.12632=××+×××××=>0.6应用φb ‘验算,由相关表可查得,φb ‘=0.906σ=M x /(φb ’W x )=325.94×106/(0.906×2.749×106)=130.87N/mm 2<215N/mm 2因此,整体稳定得到保证。
比较以上提高整体稳定的措施,可以看出在梁跨中增加侧向支承,减小侧向支承点距离,提高整体稳定承载力是最有效的。
5.验算翼缘、腹板的局部稳定性(1) 翼缘:81296122)8200(1==−=t b <13 翼缘截面满足局部稳定要求。
(2) 腹板:10088000==w t h 80<wt h 0<170,满足纯弯屈曲腹板的局部稳定要求,但不满足纯剪屈曲腹板的局部稳定要求,应设置横向加劲肋,保证腹板的局部稳定。
【题目】一焊接组合工字形截面主梁,其上受有次梁传来的3个集中力F 作用,F=310.2KN ,如下图(a )所示。
次梁与主梁等高连接,次梁可以作为主梁的侧向支承,材料Q235。
试设计该截面,并进行强度、刚度和整体稳定验算。
分析:(1)选择工字形焊接组合梁截面的步骤是先确定腹板高度和厚度,即0h 和w t ;再确定翼缘板的宽度和厚度,即b 和t 。
确定腹板高度时,除考虑经济要求外,还应注意满足刚度要求;满足局部稳定要求外,还应注意满足抗剪强度要求。
(2)选择截面后,应进行强度、刚度和整体稳定的验算。
强度验算时,应注意在集中力作用的跨中截面除进行抗弯强度验算外,还应进行腹板高度处折算应力的验算。
抗剪强度和刚度,因在选择截面时已满足要求,可不再进行验算。
整体稳定验算时应考虑梁跨中有侧向支承后,受压翼缘的自由长度是实际侧向支承点的距离。
1.内力计算 跨中截面:20.186132.31062.310233623max =×−××=×−×=F F M KN ·m 10.15520.310212123=×==−=F F F V KN 支座截面:3.46520.3102323max =×==F V KN2.选择截面(1)确定梁高h (腹板高度0h )需要的净截面抵抗矩:66max 10657.82151020.1861×=×==f M W nx mm 3经济高度:73.1133010657.87307333=−×=−=nx e W h cm 平台梁 [l v ]4001=,151min =l h ,8001512000min ==h mm 取腹板高12000=h mm ,初设翼缘板厚20=t mm ,则梁高1240=h mm 。
(2)腹板厚度w t 由公式 65.41251200103.4655.15.130max 1=×××==v w f h V t mm由经验公式 1111201102===h t w cm 由腹板的抗弯局部稳定,得 3w t >06.717012001700==h mm 取腹板厚度w t 10=w t mm (3)翼缘尺寸梁所需截面惯性矩: 661034.53672124010657.82×=××=×=h W I nx x mm 4 腹板的惯性矩: 8330104.1412001012112×=××==h t I w w mm 4翼缘所需惯性矩: ()661034.392710144034.5367×=×−=−=w x f I I I mm 4翼缘所需尺寸 57.6545102.11032.39272262620=×××==h I bt fmm 2 b 的选择范围: =b (51~31)=0h (51~31)2401200=×~400mm取360=b mm ,则 18.1836057.6545==t mm ≥123036030==b mm因此,翼缘尺寸为360×18,满足局部稳定要求。
截面尺寸见图(b)。
3.强度验算 (1)截面几何特性面积: 2736012120018360220=×+××=+=h t bt A w mm 2惯性矩:()[][]93330310247.612003501236360121121×=×−×=−−=h t b bt I w x mm 4 抵抗矩: 6910108.1061810247.6×=×==h I W x x mm 3截面面积矩:5011046320.392181200183602×=+××=+=t h bt S mm 3 (2)强度验算主梁自重标准值:528.281.978502.110273606=××××=−b q KN/m (式中1.2为构造系数,钢的容重为:7850kg/m 3) 则 80.1915122.1528.2812.18612max =×××+=M KN ·m 50.483122.1528.2213.465max =×××+=V KN (上二式中1.2为荷载分项系数。
