蝴蝶定理、燕尾定理——黄冈中学 周刊
蝴蝶定理

蝴蝶定理蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《男士日记》上。
由于其几何图形形象奇特、貌似蝴蝶,便以此命名,定理内容:圆O中的弦PQ的中点M,任作两弦AB,CD,弦AD与BC分别交PQ于X,Y,则M为XY之中点。
出现过许多优美奇特的解法,其中最早的,应首推霍纳在职815年所给出的证法。
至于初等数学的证法,在国外资料中,一般都认为是由一位中学教师斯特温首先提出的,它给予出的是面积证法,其中应用了面积公式:S=1/2 BCSINA。
1985年,在河南省《数学教师》创刊号上,杜锡录同志以《平面几何中的名题及其妙解》为题,载文向国内介绍蝴蝶定理,从此蝴蝶定理在神州大地到处传开。
这里介绍一种较为简便的初等数学证法。
证明:过圆心O作AD与BC垂线,垂足为S、T,连接OX,OY,OM。
SM。
MT。
∵△AMD∽△CMB,且SD=1/2AD, BT=1/2BC,∴DS/BT=DM/BM又∵∠D=∠B∴△MSD∽△MTB,∠MSD=∠MTB∴∠MSX=∠MTY;又∵O,S,X,M与O,T。
Y。
M均是四点共圆,∴∠XOM=∠YOM∵OM⊥PQ∴XM=YM二,如图1,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(o,r)(b >r>0)。
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率;x交椭圆于两点C(x1,y1),D(x2,y2)(y2>0);直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4)(y4>0)。
(Ⅱ)直线y=k求证:k1x1x2/(x1+x2)=k2x3x4/(x3+x4)(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交X轴于点P,GD交X轴于点Q。
求证:| OP | = | OQ |。
(证明过程不考虑CH或GD垂直于X轴的情形)2.解答:北京教育考试院招生考试办公室专家在公布的《2003年全国普通高等学校招生统一考试试题答案汇编》中给出的参考解答如下:(18)本小题主要考查直线与椭圆的基本知识,考查分析问题和解决问题的能力。
蝴蝶定理

CFE ADBCB E FDA 几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4 上、下部分的面积之积等于左、右部分的面积之积 2)AO ∶OC = (S 1+S 2)∶(S 4+S 3) 梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比 2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab 4)S 的对应份数为(a+b )2 定理4:相似三角形性质 1)HhC c B b A a === 2) S 1 ∶S 2 = a 2 ∶A 2 定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FC S △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD 分割成四个三角形。
高三数学二轮复习冲刺:蝴蝶定理及应用

蝴蝶定理背景下的解析几何与应用1.蝴蝶定理:AB 是二次曲线Ω的一条弦,O 是AB 的中点,过O 作Ω的两条弦CD 和EF ,其中E C ,位于AB 的同一侧,直线CF 和DE 分别交AB 于点Q P ,,则有OQ OP =.2.斜率形式结论1:B A 、分别为椭圆)(1:2222b a by a x E >=+的左、右顶点,)0,(t T 为x 轴上一定点,过M 直线交椭圆于D C ,两点,连接BD AC ,,那么ta t a k k BD AC +-=.证明:过T 作x PQ ⊥轴,交椭圆于Q P ,交BD AC ,于,,N M 由椭圆对称性可知:TQ TP =:进而据蝴蝶定理可知:TN TM =,于是可得:t a t a AT BT BTNT AT MT NBT MAT k k BD AC +-===∠∠=tan tan .结论2[1]:设抛物线)0(2:2>=p px y C 的弦AB 过定点)0)(0,(>m m M ,过点M 作非水平线l 交C 于Q P ,两点,若直线AP 与x 轴交于定点)0,(n ,直线BQ AP ,的斜率21,k k 存在且非零,则nm k k =213坎迪定理如图,过圆的弦AB 上任意一点M 引任意两条弦CD 和EF ,连接CF ED 、交AB 于P 和Q ,则MBMA MQ MP 1111-=-.坎迪定理的推广设AB 是二次曲线的任意一条弦,M 为AB 上任意一点,过M 作任意两条弦CD 和EF ,连接ED 、CF 交直线AB 于P 和Q .(1)若Q P 、位于M 两侧,则MBMA MQ MP 1111-=-;(2)若Q P 、位于M 同一侧,BM AM <,则MB MA MQ MP 1111-=+.二.典例分析例1(2020一卷)已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅= ,P 为直线x =6上的动点,PA 与E 的另一交点为C ,PB 与E 的另一交点为D .(1)求E 的方程;(2)证明:直线CD 过定点.解析:依上述蝴蝶定理的内容:由于31=PD P A k k 过E 作x MN ⊥轴,交DP AP ,与N M ,点,交椭圆于H G ,.显然E 为椭圆弦GH 的中点,由蝴蝶定理:EN EM =,3133tan tan =+-===∠∠=E E PD P A x x AE BE BENE AE NE NEB MAE k k ,23=E x 例2.在平面直角坐标系中,已知圆()22:236M x y ++=,点()2,0N ,Q 是圆M 上任意一点,线段NQ 的垂直平分线与半径MQ 相交于点P ,设点P 的轨迹为曲线E 。
蝴蝶定理

不会飞的蝴蝶——蝴蝶定理在中学平面几何中,有这样一个著名的命题:过一圆的弦AB的中点M引任意两弦CD和EF,连结CF和ED交AB于Q、P。
求证:PM=MQ。
由于题目的图形象一只蝴蝶,因此后人给它取名为“蝴蝶定理”。
这个题最早出现在公元1815年西欧的一本通俗杂志《男士日记》上,登出来是为了征求证明。
登出的当年,英国一个自学成才的中学数学教师霍纳就给出了第一个证明。
不过,霍纳的证明比较繁,使用的知识也比较深。
158年以后的1973年,又一位中学教师斯特温利用三角形面积关系,给出了一个漂亮而简捷的证明。
从这以后,这个定理限于初等数学,甚至只限于初中数学的证明象雨后春笋般脱颖而出,证法多得不枚胜举。
下面仅举四例与读者共同欣赏。
证法一:(斯特温法)如图,设AM=MB=a,MQ=x,PM=y。
又设△EPM、△CMQ、△FMQ、△DMP的面积分别为S1、S2、S3、S4。
因为∠E =∠C ,∠D =∠F ,∠CMQ =∠PMD ,∠FMQ =∠PME ,所以有14433221S S S S S S S S ⋅⋅⋅=1, 即 PMEPM AE FMQ MF MQ F FQ MF D DP DM PMD MD MP CMQ MQ MC C CQ MC E EM PE sin sin sin sin sin sin sin sin ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ =22)()(PM FQ CQ MQ DP PE ⋅⋅⋅⋅=1。
就是 PE ·DP ·(MQ )2=CQ ·FQ ·(MP )2。
由相交弦定理有CQ ·FQ =BQ ·QA=(a -x )(a+x )=a 2-x 2,PE ·DP =AP ·PB=(a -y )(a+y )=a 2-y 2,所以有 (a 2-y 2)x 2=(a 2-x 2)y 2,即 a 2y 2=a 2x 2,∵ x 、y 都是正数,∴ x=y ,即 PM =MQ 。
蝴蝶定理和燕尾定理word精品

燕尾定理燕尾定理:在三角形ABC中,AD , BE , CF相交于同一点0,那么S ABO:S AC^BD : DC .梯形中比例关系(“梯形蝴蝶定理”①S1:S3=a2:b2②S1: S3: S?: S4二a2:b2:ab:ab ;2③S的对应份数为(a+b).等积变形①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如左图S =a:b③夹在一组平行线之间的等积变形,如右上图S A ACD BCD ;反之,如果S A ACD二S A BCD,则可知直线AB平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在 △ ABC 中,D,E 分别是 AB,AC 上的点如图 上),则 S A ABC : S A ADE -(AB AC):(AD AE)如图,& =2,S 3 =4,求梯形的面积.【巩固】(2006年南京智力数学冬令营)如下图,梯形ABCD 的AB 平行于CD ,对角线AC , BD 交于O ,已知△ AOB 与厶BOC 的面积分别为 25平方厘米与35平方厘米,那么梯形 ABCD 的面积是 _______________ 平方厘米.梯形ABCD 的对角线 AC 与BD 交于点O ,已知梯形上底为 角形BOC 面积的-,求三角形 AOD 与三角形BOC 的面积之比.3(第十届华杯赛)如下图,四边形 ABCD 中,对角线AC 和BD 交于O 点,已知AO =1,并且 三角形躺积=3,那么OC的长是多少?⑴(或D 在BA 的延长线上,E 在AC2,且三角形ABO 的面积等于三CD梯形的下底是上底的1.5倍,三角形OBC的面积是9cm2,问三角形AOD的面积是多少?如下图,一个长方形被一些直线分成了若干个小块,已知三角形BCH的面积是23,求四边形EGFH的面积.【巩固】在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF 的面积为1平方厘米,那么正方形ABCD面积是______________ 平方厘米.如图面积为12平方厘米的正方形ABCD中,巳F是DC边上的三等分点,求阴影部分的面积. 如图,在长方形ABCD中,AB=6厘米,AD =2厘米,AE=EF=FB,求阴影部分的面积.如图,正方形ABCD面积为3平方厘米,A DADG的面积是11,三角形(2008年”奥数网杯”六年级试题)已知ABCD是平行四边形,BC:CE=3:2 ,三角形ODE 的面积为6平方厘米•则阴影部分的面积是 ____________________ 平方厘米.【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是_________ 平方厘米.【巩固】(2008年三帆中学考题)右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是______________ 平方厘米.如图所示,BD、CF将长方形ABCD分成4块,DEF的面积是5平方厘米,CED的面积是10平方厘米•问:四边形ABEF的面积是多少平方厘米?(2007年”迎春杯”高年级初赛)如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为_________________ 平方厘米.(98迎春杯初赛)如图,长方形ABCD中,AOB是直角三角形且面积为54, OD的长是16,OB的长是9 •那么四边形OECD的面积是 ___________ .燕尾定理应用【例1】2009年第七届希望杯五年级一试试题)如图,三角形ABC的面积是1, E是AC的中点,点D在BC上,且BD:DC=1:2 , AD与BE交于点F .则四边形DFEC的面积等于______________ .【巩固】如图,已知BD =DC , EC =2AE,三角形ABC的面积是30 ,求阴影部分面积AB D C【巩固】如图,三角形ABC的面积是200 cm2, E在AC上,点D在BC上,且AE: EC -3:5 , BD : DC =2:3 , AD与BE 交于点F .则四边形DFEC的面积等于____________【巩固】如图,已知BD =3DC , EC =2AE , BE与CD相交于点O ,则△ ABC被分成的4部分面积各占△ ABC面积的几分之几?【巩固】如图,三角形ABC的面积是1 , BD =2DC , CE =2AE , AD与BE相交于点F , 请写出这4部分的面积各是多少?【巩固】如图,E在AC上,D在BC上,且AE:EC=2:3 , BD:DC=1:2,AD与BE交于点F •四边形DFEC的面积等于22 cm2,则三角形ABC的面积_____________ •三角形ABC中,C是直角,已知AC =2 , CD =2 ,CB=3, AM=BM,那么三角形AMN (阴影部分)的面积为多少?【巩固】如图,长方形ABCD的面积是2平方厘米,EC =2DE , F是DG的中点.阴影部分的面积是多少平方厘米?平行四边形BODC的面积为__________如图所示,在四边形ABCD 中,AB=3BE ,xFxGAD=3AF,四边形AEOF的面积是12,那么ABCD是边长为12厘米的正方形,E、F分别是AB、BC边的中点,AF与CE交于G , 则四边形AGCD的面积是 __________________ 平方厘米.如图所示,在△ ABC中,BE: EC =3:1 , D是AE的中点,那么AF :FC二____________【巩固】在ABC 中,BD:DC =3:2 , AE:EC=3:1,求OB:OE 二?【巩固】在ABC 中,BD:DC=2:1 , AE:EC=1:3,求OB : OE = ?如右图,三角形ABC 中,BD:DC=4:9 , CE:EA = 4:3,求AF : FB .如右图,△ ABC中,G是AC的中点,D、E、F是BC边上的四等分点,AD与BG交于M,AF与BG交于N,已知△ ABM的面积比四边形FCGN的面积大7.2平方厘米,则△ ABC 的面积是多少平方厘米?【巩固】(2007年四中分班考试题)如图,JABC中,点D是边AC的中点,点E、F是边BC 的三等分点,若MBC的面积为1,那么四边形CDMF的面积是______________ •。
小升初平面几何常考五大模型

一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为由题知DC/GP=GC/PK,即DC/(DC-4)=(4+PK)/PK,令DC=a,PK=c,则a=4+c,则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2-c( c+4)-2(c+4)+2c+16=16。
1、图17是一个正方形地板砖示意图,在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?分析与解连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在D PC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。
蝴蝶定理

蝴蝶定理(Butterfly theorem):设M为圆内弦PQ的中点,过M作弦AB和CD.设AD和BC各相交PQ于点X和Y,则M是XY的中点.
抽屉原理:桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面至少放两个苹果.这一现象就是我们所说的“抽屉原理”.
抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一
个集合里有两个元素.”抽屉原理有时也被称为鸽巢原理.它是组合数学中一个重要的原理.
燕尾定理:因此图类似燕尾而得名,是五大模型之一,是一个关于三角形的定理(如图△ABC,D、E、F为BC、CA、AB 上点,满足AD、BE、CF 交于同一点O).
S△ABC中,S△AOB:S△AOC=S△BDO:S△CDO=BD:CD;
同理,S△AOC:S△BOC=S△AFO:S△BFO=AF:BF;
S△BOC:S△BOA=S△CEO:S△AEO=EC:AE.
证明:利用分比性质(若a/b=c/d,则(a-b)/b=(c-d)/d,[1]b≠0,d≠0,)[2]
(注:∵(a-b)/b=a/b-b/b=a/b-1,
(c-d)/d=c/d-d/d=c/d-1,
a/b=c/d
∴(a-b)/b=(c-d)/d
∵△ABD与△ACD同高
∴S△ABD:S△ACD=BD:CD
同理,S△OBD:S△OCD=BD:CD
利用分比性质,得
S△ABD-S△OBD:S△ACD-S△OCD=BD:CD
即S△AOB:S△AOC=BD:CD
命题得证.。
小学几何之蝴蝶定理大全
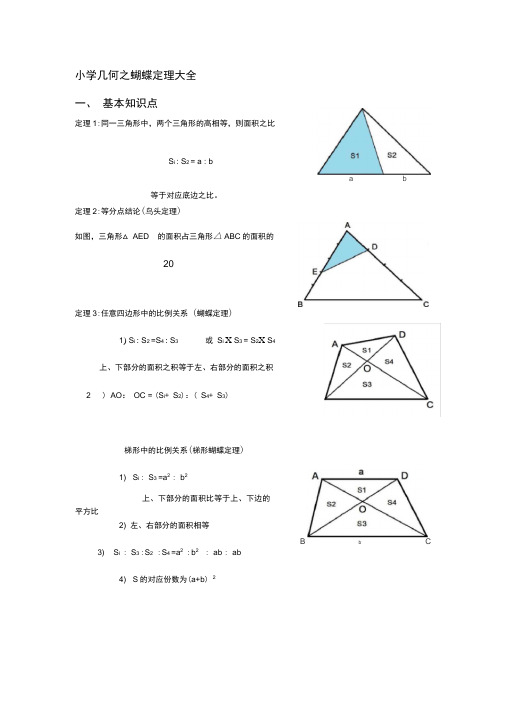
小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比S i : S2 = a : ba b等于对应底边之比。
定理2:等分点结论(鸟头定理)如图,三角形△AED的面积占三角形△ ABC的面积的20定理3:任意四边形中的比例关系(蝴蝶定理)1) S i : S2 =S4 : S3 或S i X S3 = S2X S4上、下部分的面积之积等于左、右部分的面积之积2 ) AO: OC = (S i+ S2):( S4+ S3)梯形中的比例关系(梯形蝴蝶定理)1) S i : S3 =a2: b2上、下部分的面积比等于上、下边的平方比2) 左、右部分的面积相等B b C3) S i : S3 : S2 : S4 =a2: b2: ab : ab4) S的对应份数为(a+b) 2定理4:相似三角形性质2) S i : S 2 = a 2 : A 2定理5:燕尾定理S AABG:S A AGC : =S A BGE : :S A GEC =BE : ECS A BGA : :S A BGC : =S A AGF :S A GFC =AF : FC S A AGC : :S A BCG : =S A ADG:S A DGB=AD :DB二、例题分析例1、如图,AD DB , AE EF FC ,已知阴影部分面积为 5平方厘米, 多少平方厘米?ABC 的面积是例2、有一个三角形 ABC 的面积为1,如图,且AD - AB , BE21例3、如图,在三角形 ABC 中,,D 为BC 的中点,E 为AB 上的一点,且 BE=—AB,已知四边3例4、例1如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形 ABCD 分割成四个三角形。
已知两个三角形的面积(如图所示) 另两个三角形的面积各是多少?(单位:平方厘米)例6、如下图,图中 BO=2DO 阴影部分的面积是 4平方厘米,求梯形 ABCD 勺面积是多少平三角形DEF 的面积.-BC , CF3-CA ,求 4形EDCA 勺面积是35,求三角形 ABC 的面积.,求B方厘米?例7、(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC、BD分成四个部分,△ AOB 面积为1平方千米,△ BOC面积为2平方千米,△ COD的面积为3平方千米,公园陆地的面积是6.92平方千米,求人工湖的面积是多少平方千米?例8、如图:在梯形ABCD中,三角形AOD的面积为9平方厘米25平方厘米,求梯形ABCD的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
燕尾定理
燕尾定理:
在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.
O
F
E D
C
B
A
梯形中比例关系(“梯形蝴蝶定理”):
A B
C
D
O b
a S 3
S 2
S 1S 4
①2213::S S a b =
②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2
a b +.
等积变形
①等底等高的两个三角形面积相等;
②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =
b
a
S 2S 1
D
C B
A
③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△;
反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .
④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.
二、鸟头定理
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.
如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),
则:():()ABC ADE S S AB AC AD AE =⨯⨯△△
E
D
C
B
A
E
D
C
B A
如图,22S =,34S =,求梯形的面积.
S 4
S 3
S 2
S 1
【巩固】(2006年南京智力数学冬令营)如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.
35
25O
A
B
C
D
梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三
角形BOC 面积的2
3
,求三角形AOD 与三角形BOC 的面积之比.
O
A B
C D
(第十届华杯赛)如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且3
5
ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?
A
B
C
D
O
梯形的下底是上底的1.5倍,三角形OBC 的面积是2
9cm ,问三角形AOD 的面积是多少?
A B
C
D
O
如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH 的面积是23,求四边形EGFH 的面积.
H
G F
E
D
C
B A
如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分
的面积.
G M
D
C
B
A
【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.
A B
C
D
E
F
如图面积为12平方厘米的正方形ABCD 中,,E F 是DC 边上的三等分点,求阴影部分的面积.
O
F
E
D
C
B
A
如图,在长方形ABCD 中,6AB =厘米,2AD =厘米,AE EF FB ==,求阴影部分的面积.
B
C
A
D
E
F
O
(2008年”奥数网杯”六年级试题)已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.
O
E
A
B C D
【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.
21
A
B
C
D
E
94
【巩固】(2008年三帆中学考题)右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.
16
8
2
A
B
C
D
E
如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是5平方厘米,CED ∆的面积是10平方厘米.问:四边形ABEF 的面积是多少平方厘米?
F
A
B C
D
E
10
5
(2007年”迎春杯”高年级初赛)如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.
?
8
5
2O A B
C
D E
F
(98迎春杯初赛)如图,长方形ABCD 中,AOB 是直角三角形且面积为54,OD 的长是16,OB 的长是9.那么四边形OECD 的面积是 .
A
B
C
D
E
O
燕尾定理应用 【例 1】 2009年第七届希望杯五年级一试试题)如图,三角形ABC 的面积是1,E 是AC 的
中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .
F
E
D C
B
A
【巩固】如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.
D E
F
C
B
A
【巩固】如图,三角形ABC 的面积是2
200cm ,E 在AC 上,点D 在BC 上,且
:3:5AE EC =,:2:3BD DC =,AD 与BE 交于点F .
则四边形DFEC 的面积等于 . F
E
D C
B
A
【巩固】如图,已知3BD DC =,2EC AE =,BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几?
O
E D
C
B
A
【巩固】如图,三角形ABC 的面积是1,2BD DC =,2CE AE =,AD 与BE 相交于点F ,请写出这4部分的面积各是多少?
A
B
C
D
E F
【巩固】如图,E 在AC 上,D 在BC 上,且:2:3AE EC =,:1:2BD DC =,AD 与BE 交于点F .四边形DFEC 的面积等于222cm ,则三角形ABC 的面积 .
A
B
C
D
E F
三角形ABC 中,C 是直角,已知2AC =,2CD =,3CB =,AM BM =,
那么三角形AMN (阴影部分)的面积为多少?
A
B
C
D
M N
【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部
分的面积是多少平方厘米?
x x A
B
F
G
G
F
E D C
B
A
如图所示,在四边形ABCD 中,3AB BE =,3AD AF =,四边形AEOF 的面积是12,那么平行四边形BODC 的面积为________.
O
F
E D
C
B
A
ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于G ,则四边形AGCD 的面积是_________平方厘米.
G
F
E D
C
B
A
如图所示,在ABC △中,:3:1BE EC =,D 是AE 的中点,那么:AF FC = .
F
E D
C
B
A
【巩固】在ABC ∆中,:3:2BD DC =, :3:1AE EC =,求:OB OE =?
A
B
C
D
E O
【巩固】在ABC ∆中,:2:1BD DC =, :1:3AE EC =,求:OB OE =?
A B C
D
E O
如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .
O F E
D
C
B
A
如右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?
N M G
A B
C
D E
F
【巩固】(2007年四中分班考试题)如图,ABC ∆中,点D 是边AC 的中点,点E 、F 是边BC
的三等分点,若ABC ∆的面积为1,那么四边形CDMF 的面积是_________.
F
A
B
C
D
E M
N。
