初中数学证明题经典难题集锦
初中数学经典难题(含答案)
P E
B
O
D F
C
宝剑锋从磨砺出,梅花香自苦寒来
经 典 几 何 专 题 (四)
1、已知:△ABC 是正三角形,P 是三角形内一点,PA=3,PB=4,PC=5. 求:∠APB 的度数. (初二)
A
P
B
C
2、设 P 是平行四边形 ABCD 内部的一点,且∠PBA=∠PDA. 求证:∠PAB=∠PCB. (初二) A P B C D
B
C E
3、设 P 是正方形 ABCD 一边 BC 上的任一点,PF⊥AP,CF 平分∠DCE. 求证:PA=PF. (初二) A
D A
B
P
C
E
4、如图,PC 切圆 O 于 C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线 PO 相交于 B、D.求证:AB=DC,BC=AD. (初三) A
3、 Ptolemy (托勒密) 定理: 设 ABCD 为圆内接凸四边形, 求证: AB· CD+AD· BC=AC· BD. (初三) A D
B
C
4、平行四边形 ABCD 中,设 E、F 分别是 B=∠DPC. (初二) A F P D
M
B
宝剑锋从磨砺出,梅花香自苦寒来
经 典 几 何 专 题 (二)
1、已知:△ABC 中,H 为垂心(各边高线的交点) ,O 为外心,且 OM⊥BC 于 M. A (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO. (初二) O · B
H E C
M D
2、设 MN 是圆 O 外一直线,过 O 作 OA⊥MN 于 A,自 A 引圆的两条直线,交圆于 B、C 及 D、E,直线 EB 及 CD 分别交 MN 于 P、Q. G E 求证:AP=AQ. (初二) O ·
命题与证明的难题汇编含答案

命题与证明的难题汇编含答案一、选择题1.下列命题是真命题的是( )A .若x >y ,则x 2>y 2B .若|a|=|b|,则a=bC .若a >|b|,则a 2>b 2D .若a <1,则a >1a【答案】C【解析】【分析】根据实数的乘方,绝对值的性质和倒数的意义等,对各选项举反例分析判断后利用排除法求解.【详解】A. x >y ,如x=0,y=-1,02<(-1)2,此时x 2<y 2 ,故A 选项错误;B. |a|=|b|,如a=2,b=-2,此时a≠b ,故B 选项错误;C. 若a >|b|,则a 2>b 2 ,正确;D. a <1,如a=-1,此时a=1a,故D 选项错误, 故选C.【点睛】本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,本题主要利用了实数的性质.2.下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合; ③若ABC V 与'''A B C V 成轴对称,则ABC V 一定与'''A B C V 全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )A .2B .3C .4D .5【答案】A【解析】【分析】利用轴对称的性质、等腰三角形的性质、等边三角形的判定等知识分别判断后即可确定正确的选项.【详解】解:①等腰三角形底边的中点到两腰的距离相等;正确; ②等腰三角形的底边上的高、底边上的中线、顶角的平分线互相重合;不正确: ③若ABC V 与'''A B C V 成轴对称,则ABC V 一定与'''A B C V 全等;正确; ④有一个角是60度的等腰三角形是等边三角形;不正确;⑤等腰三角形的对称轴是顶角的平分线所在的直线,不正确.正确命题为:2①③,个;故选:A【点睛】本题考查了命题与定理的知识,解题的关键是了解轴对称的性质、等腰三角形的性质、等边三角形的判定等知识,属于基础知识,难度不大.3.下列定理中,逆命题是假命题的是()A.在一个三角形中,等角对等边B.全等三角形对应角相等C.有一个角是60度的等腰三角形是等边三角形D.等腰三角形两个底角相等【答案】B【解析】【分析】先把一个命题的条件和结论互换就得到它的逆命题,再进行判断即可.【详解】解:A、逆命题为:在一个三角形中等边对等角,逆命题正确,是真命题;B、逆命题为:对应角相等的三角形是全等三角形,逆命题错误,是假命题;C、逆命题为:如果一个三角形是等边三角形,那么它是一个等腰三角形而且有一个内角等于60°,逆命题正确,是真命题;D、逆命题为:两个角相等的三角形是等腰三角形,逆命题正确,是真命题;故选:B.【点睛】本题考查了命题与定理的知识,解题的关键是能够正确的写出原命题的逆命题.4.下列命题中①等腰三角形底边的中点到两腰的距离相等②如果两个三角形全等,则它们必是关于直线成轴对称的图形③如果两个三角形关于某直线成轴对称,那么它们是全等三角形④等腰三角形是关于底边中线成轴对称的图形⑤一条线段是关于经过该线段中点的直线成轴对称的图形正确命题的个数是()A.2个B.3个C.4个D.5个【答案】A【解析】【分析】根据等腰三角形的性质、轴对称图形的定义、全等三角形的判定逐个判断即可.【详解】根据等腰三角形的三线合一可知,底边中点在顶角角平分线上,再根据角平分线的性质可知,其到两腰的距离相等,则命题①正确全等的三角形不一定是成轴对称,则命题②错误成轴对称的两个三角形一定全等,则命题③正确等腰三角形是以底边中线所在直线为对称轴的轴对称图形,则命题④错误成轴对称的图形必须是两个,一个图形只能是轴对称图形,则命题⑤错误综上,正确命题的个数是2个故选:A .【点睛】本题考查了等腰三角形的性质、轴对称图形的定义、全等三角形的判定等知识点,掌握理解各定义与性质是解题关键.5.下列命题中正确的是( ).A .所有等腰三角形都相似B .两边成比例的两个等腰三角形相似C .有一个角相等的两个等腰三角形相似D .有一个角是100°的两个等腰三角形相似【答案】D【解析】【分析】根据相似三角形进行判断即可.【详解】解:A 、所有等腰三角形不一定都相似,原命题是假命题;B 、两边成比例的两个等腰三角形不一定相似,原命题是假命题;C 、有一个角相等的两个等腰三角形不一定相似,原命题是假命题;D 、有一个角是100°的两个等腰三角形相似,是真命题;故选:D .【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.6.下列命题是假命题的是( )A .对顶角相等B .两直线平行,同旁内角相等C .平行于同一条直线的两直线平行D .同位角相等,两直线平行【答案】B【解析】解:A .对顶角相等是真命题,故本选项正确,不符合题意;B .两直线平行,同旁内角互补,故本选项错误,符合题意;C .平行于同一条直线的两条直线平行是真命题,故本选项正确,不符合题意;D .同位角相等,两直线平行是真命题,故本选项正确,不符合题意.故选B .7.下列命题中,是真命题的是( )A .若a b =,则a b =B .若0a b +>,则a ,b 都是正数C .两条直线被第三条直线所截,同位角相等D .垂直于同一条直线的两条直线平行【答案】D【解析】【分析】正确的命题是真命题,根据定义依次判断即可得到答案.【详解】A. 若a b =,则a b =±,故A 错误;B. 若0a b +>,则a ,b 中至少有一个数是正数,且正数绝对值大于负数的绝对值,故B 错误;C. 两条平行线被第三条直线所截,同位角相等,故C 错误;D. 垂直于同一条直线的两条直线平行正确,故选:D.【点睛】此题考查判断真假命题,正确掌握命题的分类并理解事件的正确与否是解题的关键.8.下列命题中,是真命题的是( )A .将函数y =12x +1向右平移2个单位后所得函数的解析式为y =12x B .若一个数的平方根等于其本身,则这个数是0和1 C .对函数y =2x,其函数值y 随自变量x 的增大而增大 D .直线y =3x +1与直线y =﹣3x +2一定互相平行【答案】A【解析】【分析】 利用一次函数的性质、平方根的定义、反比例函数的性质等知识分别判断后即可确定正确的选项.【详解】解:A 、将函数y =12x +1向右平移2个单位后所得函数的解析式为y =12x ,正确,符合题意;B 、若一个数的平方根等于其本身,则这个数是0,故错误,是假命题,不符合题意;C 、对函数y =2x,其函数值在每个象限内y 随自变量x 的增大而增大,故错误,是假命题,不符合题意; D 、直线y =3x +1与直线y =﹣3x +2因比例系数不相等,故一定不互相平行,故错误,是假命题,故选:A .【点睛】本题考查了判断命题真假的问题,掌握一次函数的性质、平方根的定义、反比例函数的性质等知识是解题的关键.9.下列命题是真命题的是()A.若两个数的平方相等,则这两个数相等B.同位角相等C.同一平面内,垂直于同一直线的两条直线平行D.相等的角是对顶角【答案】C【解析】【分析】根据平方的意义,同位角的概念,平行线的判定,对顶角的概念逐一进行判断即可得.【详解】A.若两个数的平方相等,则这两个数不一定相等,如22=(-2)2,但2≠-2,故A选项错误;B.只有两直线平行的情况下,才有同位角相等,故B选项错误;C.同一平面内,垂直于同一直线的两条直线平行,真命题,符合题意;D.相等的角不一定是对顶角,如图,∠1=∠2,但这两个角不符合对顶角的概念,故D选项错误,故选C.【点睛】本题考查了命题真假的判定,涉及了乘方、同位角、对顶角、平行线的判定等知识,熟练掌握相关知识是解题的关键.10.下列说法正确的是( )A.相等的角是对顶角B.在平面内,经过一点有且只有一条直线与已知直线平行C.两条直线被第三条直线所截,内错角相等D.在平面内,经过一点有且只有一条直线与已知直线垂直【答案】D【解析】【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.【详解】解:相等的角不一定是对顶角,故A错误;在平面内,经过直线外一点有且只有一条直线与已知直线平行,故B错误;两直线平行,内错角相等,故C错误;在平面内,经过一点有且只有一条直线与已知直线垂直,故D正确;故答案为D.【点睛】此题主要考查了命题的真假判断,掌握定理并灵活运用是解题的关键.11.下列命题是真命题的是()A.同位角相等B.对顶角互补C.如果两个角的两边互相平行,那么这两个角相等=-的图像上.D.如果点P的横坐标和纵坐标互为相反数,那么点P在直线y x【答案】D【解析】【分析】根据平行线的性质定理对A、C进行判断;利用对顶角的性质对B进行判断;根据直角坐标系下点坐标特点对D进行判断.【详解】A.两直线平行,同位角相等,故A是假命题;B.对顶角相等,故B是假命题;C.如果两个角的两边互相平行,那么这两个角相等或互补,故C是假命题;=-的图像上,故D是真命D.如果点的横坐标和纵坐标互为相反数,那么点P在直线y x题故选:D【点睛】本题考查了真命题与假命题,正确的命题称为真命题,错误的命题称为假命题.利用了平行线性质、对顶角性质、直角坐标系中点坐标特点等知识点.12.下列命题中正确的有()个①平分弦的直径垂直于弦;②经过半径的外端且与这条半径垂直的直线是圆的切线;③在同圆或等圆中,圆周角等于圆心角的一半;④平面内三点确定一个圆;⑤三角形的外心到三角形的各个顶点的距离相等.A.1 B.2 C.3 D.4【答案】B【解析】【分析】根据垂径定理的推论对①进行判断;根据切线的判定定理对②进行判断;根据圆周角定理对③进行判断;根据确定圆的条件对④进行判断;根据三角形外心的性质对⑤进行判断.【详解】①平分弦(非直径)的直径垂直于弦,错误;②经过半径的外端且与这条半径垂直的直线是圆的切线,正确;③在同圆或等圆中,同弧所对的圆周角等于圆心角的一半,错误;④平面内不共线的三点确定一个圆,错误;⑤三角形的外心到三角形的各个顶点的距离相等,正确;故正确的命题有2个故答案为:B.【点睛】本题考查了判断命题真假的问题,掌握垂径定理的推论、切线的判定定理、圆周角定理、确定圆的条件、三角形外心的性质是解题的关键.13.下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是()A.1 B.2 C.3 D.4【答案】A【解析】【分析】根据点到直线的距离,线段的性质,弧、弦、圆心角之间的关系以及垂径定理判断即可.【详解】①直线外一点到这条直线的垂线段,叫做点到直线的距离;假命题;②两点之间线段最短;真命题;③相等的圆心角所对的弧相等;假命题;④平分弦的直径垂直于弦;假命题;真命题的个数是1个;故选:A.【点睛】考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.14.下列命题属于真命题的是()A.同旁内角相等,两直线平行B.相等的角是对顶角C.平行于同一条直线的两条直线平行D.同位角相等【答案】C【解析】【分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.【详解】A、同旁内角互补,两直线平行,是假命题;B、相等的角不一定是对顶角,是假命题;C、平行于同一条直线的两条直线平行,是真命题;D、两直线平行,同位角相等,是假命题;故选C.【点睛】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.15.下列命题中,假命题是()A.平行四边形的对角线互相垂直平分B.矩形的对角线相等C.菱形的面积等于两条对角线乘积的一半D.对角线相等的菱形是正方形【答案】A【解析】【分析】不正确的命题是假命题,根据定义依次判断即可.【详解】A. 平行四边形的对角线互相平分,故是假命题;B. 矩形的对角线相等,故是真命题;C. 菱形的面积等于两条对角线乘积的一半,故是真命题;D. 对角线相等的菱形是正方形,故是真命题,故选:A.【点睛】此题考查假命题的定义,正确理解平行四边形的性质是解题的关键.16.下列命题的逆命题不正确的是()A.全等三角形的对应边相等B.两直线平行,同位角相等C.等腰三角形的两个底角相等D.矩形的对角线相等.【答案】D【解析】【分析】根据求逆命题的原则,把原命题的结论作为条件,原命题的条件作为结论得到的命题是原命题的逆命题,逐一判断逆命题的正误即可.【详解】解:A 的逆命题是:对应边相等的三角形是全等三角形,正确;B 的逆命题是:同位角相等,两直线平行,正确;C 的逆命题是:两底角相等的三角形是等腰三角形,正确;D 的逆命题是:对角线相等的四边形是矩形,错误故选:D【点睛】本题考查逆命题、全等三角形的判定、平行线的判定、等腰三角形的判定、矩形的判定,解题的关键是正确找出各选项的逆命题.17.下列命题中,是假命题的是( )A .任意多边形的外角和为360oB .在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C VC .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析.【详解】解:A. 任意多边形的外角和为360o ,是真命题;B. 在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C V ,根据HL ,是真命题;C. 在一个三角形中,任意两边之差小于第三边,是真命题;D. 同弧所对的圆周角等于圆心角的一半,本选项是假命题.故选D .【点睛】本题考核知识点:判断命题的真假. 解题关键点:熟记相关性质或定义.18.下列命题的逆命题是真命题的是( )A .直角都相等B .钝角都小于180°C .如果x 2+y 2=0,那么x=y=0D .对顶角相等【答案】C【解析】【分析】根据逆命题是否为真命题逐一进行判断即可.【详解】相等的角不都是直角,故A选项不符合题意,小于180°的角不都是钝角,故B选项不符合题意,如果x=y=0,那么x2+y2=0,正确,是真命题,符合题意,相等的角不一定都是对顶角,故D选项不符合题意,故选C【点睛】本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.19.下列四个命题中,其正确命题的个数是()①若ac>bc,则a>b;②平分弦的直径垂直于弦;③一组对角相等一组对边平行的四边形是平行四边形;④反比例函数y=kx.当k<0时,y随x的增大而增大A.1 B.2 C.3 D.4【答案】A【解析】【分析】根据不等式性质、垂径定理、平行四边形的判定、反比例函数的性质,分别进行判断,即可得到答案.【详解】解:①若ac>bc,如果c>0,则a>b,故原题说法错误;②平分弦(不是直径)的直径垂直于弦,故原题说法错误;③一组对角相等一组对边平行的四边形是平行四边,故原题说法正确;④反比例函数y=kx.当k<0时,在每个象限内y随x的增大而增大,故原题说法错误;正确命题有1个,故选:A.【点睛】本题考查了判断命题的真假,解题的关键是掌握不等式性质、垂径定理、平行四边形的判定、反比例函数的性质进行判断.20.下列命题是真命题的是()A.方程23240x x--=的二次项系数为3,一次项系数为-2B.四个角都是直角的两个四边形一定相似C.某种彩票中奖的概率是1%,买100张该种彩票一定会中奖D.对角线相等的四边形是矩形【答案】A【解析】【分析】根据所学的公理以及定理,一元二次方程的定义,概率等知识,对各小题进行分析判断,然后再计算真命题的个数.【详解】A、正确.B、错误,对应边不一定成比例.C、错误,不一定中奖.D、错误,对角线相等的四边形不一定是矩形.故选:A.【点睛】此题考查命题与定理,熟练掌握基础知识是解题关键.。
初中数学几何证明经典试题(含答案)【范本模板】
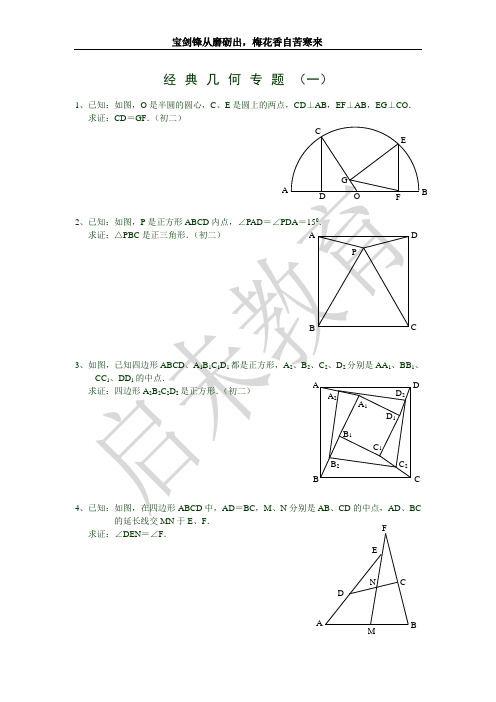
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)
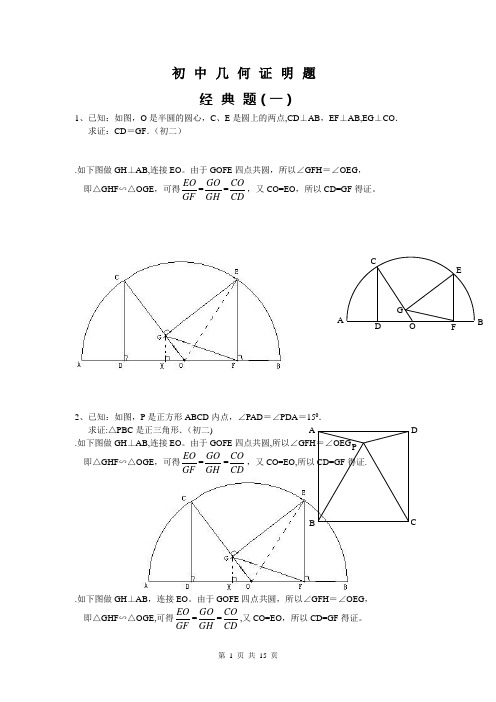
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC点P 是EF 的中点.求证:点P 到边AB 的距离等于AB的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC ,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
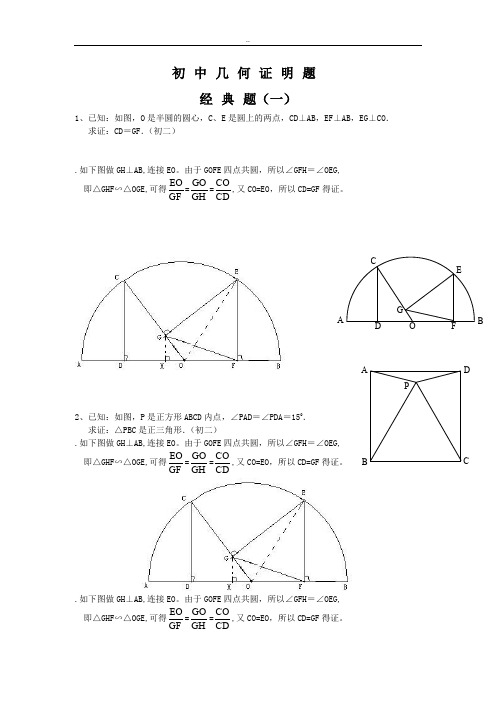
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)

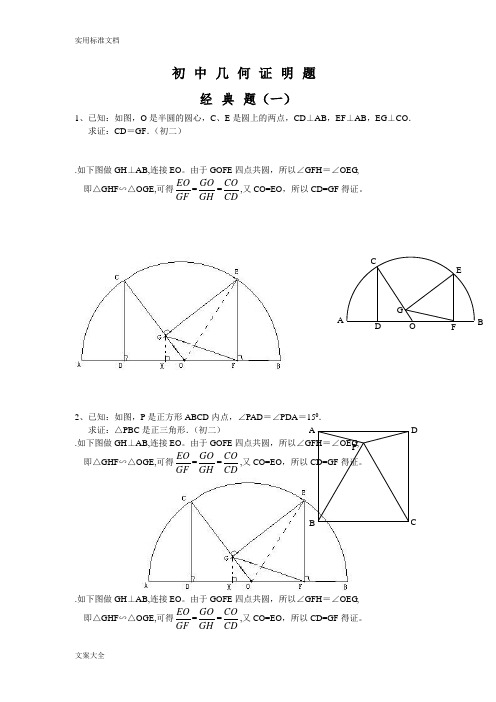
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,OM ⊥BC 于M . (1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC,BC =AD .(初三)经典题 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC=AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
(完整版)初中数学经典难题(含答案)
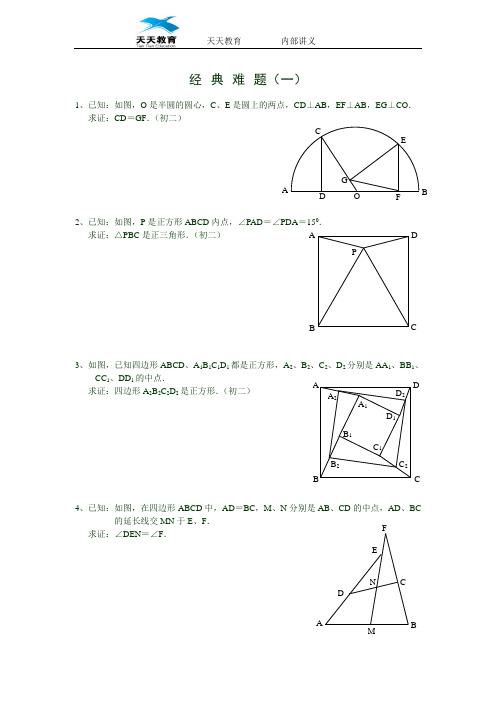
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F A E PC B A OD BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典难题(一)1、2、3、4、经典难题(二)1、2、4、经典难题(三)1、3、4、1、2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC1、2、3、3、4、。
