初中数学经典题精选
数学初中经典试题及答案
数学初中经典试题及答案一、选择题1. 下列哪个选项是方程x^2 - 5x + 6 = 0的解？A. x = 2B. x = 3C. x = 1D. x = 4答案：A2. 如果一个三角形的两边长分别为3和4，且这两边夹角的余弦值为1/2，那么第三边的长度是多少？A. √7B. √13C. √15D. √21答案：C3. 一个数的立方根是它自身的数是？A. 0B. 1C. -1D. 以上都是答案：D二、填空题4. 一个圆的直径是10厘米，那么它的半径是______厘米。
答案：55. 一个长方体的长、宽、高分别为2米、3米、4米，那么它的体积是______立方米。
答案：24三、解答题6. 已知一个等差数列的前三项分别为2，5，8，求这个数列的第10项。
答案：第10项为27。
7. 一个矩形的长是宽的两倍，如果长增加4厘米，宽增加1厘米，那么面积增加24平方厘米，求原来矩形的长和宽。
答案：原来矩形的长为8厘米，宽为4厘米。
四、证明题8. 证明：如果一个三角形的两边相等，那么这两边所对的角也相等。
答案：设三角形ABC中，AB=AC，根据等边对等角的性质，可以得出∠B=∠C，从而证明命题成立。
五、应用题9. 一个农场主有一块矩形的土地，长是宽的3倍，如果长增加20米，宽增加10米，那么面积增加600平方米。
求原来矩形土地的长和宽。
答案：原来矩形土地的长为90米，宽为30米。
10. 一个班级有40名学生，其中男生人数是女生人数的1.5倍。
求男生和女生各有多少人。
答案：男生有24人，女生有16人。
数学初中经典试题及答案
数学初中经典试题及答案一、选择题（每题3分，共30分）1. 已知一个数的平方等于36，这个数可能是：A. 6B. -6C. 6或-6D. 以上都不是2. 一个三角形的两边长分别为3和5，第三边长为：A. 2B. 4C. 6D. 83. 计算下列表达式的值：\((-3) \times (-2)\)A. 6B. -6C. 3D. -34. 一个圆的半径为5厘米，那么它的面积是：A. 78.5平方厘米B. 25平方厘米C. 78.5平方分米D. 25平方分米5. 以下哪个是等腰三角形？A. 三边长分别为3, 4, 5B. 三边长分别为5, 5, 5C. 三边长分别为2, 3, 4D. 三边长分别为1, 2, 36. 一个数的绝对值是5，这个数可能是：A. 5B. -5C. 5或-5D. 以上都不是7. 计算下列表达式的值：\((-2)^2\)A. 4B. -4C. 2D. -28. 一个直角三角形的两条直角边长分别为6和8，那么斜边长为：A. 10B. 14C. 16D. 209. 一个数的立方等于-64，这个数是：A. 4B. -4C. 2D. -210. 计算下列表达式的值：\((-1)^3\)A. 1B. -1C. 3D. -3二、填空题（每题2分，共20分）1. 一个数的相反数是-7，这个数是________。
2. 一个数的倒数是\(\frac{1}{3}\)，这个数是________。
3. 一个数的平方根是4，这个数是________。
4. 一个数的立方根是2，这个数是________。
5. 一个等差数列的首项是2，公差是3，那么第5项是________。
6. 一个等比数列的首项是3，公比是2，那么第3项是________。
7. 一个直角三角形的斜边长是10，一个直角边长是6，那么另一个直角边长是________。
8. 一个圆的直径是10厘米，那么它的周长是________厘米。
9. 一个数的绝对值是8，这个数是________或________。
初中数学教材中的经典题型
1、两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。
哪个队的施工速度快？2、从2004年5月起某列车平均提速v千米/时，用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度为多少？3、某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同，现在平均每天生产多少台机器?4、一台收割机的工作效率相当于一个农民工作效率的150倍，用这台机器收割10公顷小麦比100个农民人工收割这些小麦少用1小时，这台收割机每小时收割多少公顷小麦？5、一辆汽车开往距离出发地180千米的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后加速为原来速度的1.5倍，并比原计划提前40分钟到达目的地。
求前一小时的平均行驶速度。
6、市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室。
（1）储存室的底面积S（单位：m2）与其深度d（单位：m）有怎样的函数关系？（2）公司决定把储存室的底面积S定为500 m2，施工队施工时应该向下掘进多深？（3）当施工队按（2）中的计划掘进到地下15m时，碰上了坚硬的岩石。
为了节约建设资金，公司临时改变计划，把储存室的深改为15m，相应的，储存室的底面积应改为多少才能满足需要（保留两位小数）？7、有一个水池，水面是一个边长为10尺的正方形，在水池中央有一根芦苇，它高出水面1尺。
如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面。
这个水的深度与这根芦苇的长度分别是多少？8、如图所示，一个梯子AB长5米，顶端A靠在墙AC上，这时梯子下端B与墙角C间的距离为3米，梯子滑动后停在DE的位置上，测得DB的长为1米，则梯子顶端A下落了多少米？AEC9、已知圆柱的底面半径为6厘米，高为10厘米，蚂蚁从A点爬到B点的最短路程是多少？10、一根70cm的木棒，要放在长、宽、高分别是50cm，40cm，30cm的长方体木箱中，能放进去吗？11、一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处，折断处离地面的高度是多少？12、码头工人以每天30吨的速度往一艘轮船上装载货物，把轮船装载完毕恰好用了8天时间（1）轮船到达目的地后开始卸货，卸货速度v（单位：吨/天）与卸货时间t（单位：天）之间有怎样的函数关系？（2）由于遇到紧急情况，船上的货物必须在不超过5日内卸载完毕，那么平均每天至少要卸多少吨货物？13、（1）□ABCD中，有两个内角的度数比为1:2，则□ABCD中较小的内角是_____. B(2)菱形的周长为8cm，高为1cm。
初中数学100道最值问题经典
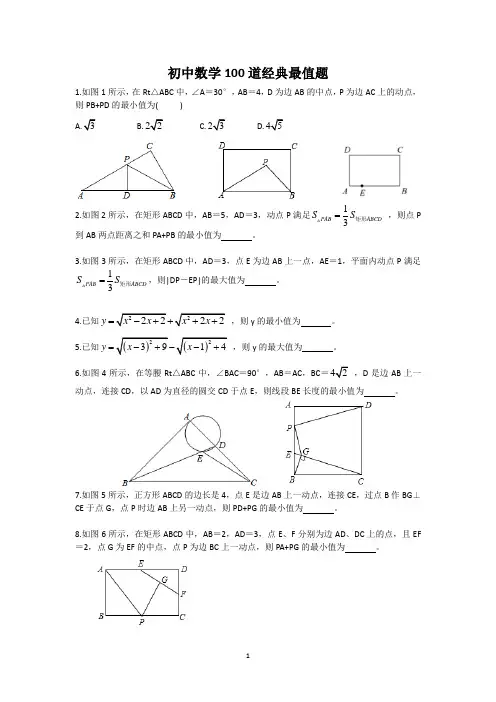
初中数学100道经典最值题1.如图1所示，在Rt △ABC 中，∠A ＝30°，AB ＝4，D 为边AB 的中点，P 为边AC 上的动点，则PB+PD 的最小值为( )B. C. D.2.如图2所示，在矩形ABCD 中，AB ＝5，AD ＝3，动点P 满足13PAB ABCD S S =矩形 ，则点P 到AB 两点距离之和PA+PB 的最小值为 。
3.如图3所示，在矩形ABCD 中，AD ＝3，点E 为边AB 上一点，AE ＝1，平面内动点P 满足13PAB ABCD SS =矩形，则|DP －EP|的最大值为 。
4.已知y ，则y 的最小值为 。
5.已知y =，则y 的最大值为 。
6.如图4所示，在等腰Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，BC ＝，D 是边AB 上一动点，连接CD ，以AD 为直径的圆交CD 于点E ，则线段BE 长度的最小值为 。
7.如图5所示，正方形ABCD 的边长是4，点E 是边AB 上一动点，连接CE ，过点B 作BG ⊥CE 于点G ，点P 时边AB 上另一动点，则PD+PG 的最小值为 。
8.如图6所示，在矩形ABCD 中，AB ＝2，AD ＝3，点E 、F 分别为边AD 、DC 上的点，且EF ＝2，点G 为EF 的中点，点P 为边BC 上一动点，则PA+PG 的最小值为 。
9.在平面直角坐标系中，A(3，0)，B(a，2)，C(0，m)，D(n，0)，且m2+n2＝4，若点E为CD 的中点，则AB+BE的最小值为。
A.3B.4C.5D.2510.如图7所示，AB＝3，AC＝2，以BC为边向上构造等边三角形BCD，则AD的取值范围为。
11.如图8所示，AB＝3，AC＝2，以BC为腰(点B为直角顶点)向上构造等腰直角三角形BCD，则AD的取值范围为。
12.如图9所示，AB＝4，AC＝2，以BC为底边向上构造等腰直角三角形BCD，则AD的取值范围为。
初中数学必做经典数学题
初中数学必做经典数学题以下是一些初中数学中的经典题目，这些题目具有一定的难度和重要性，是研究和巩固数学知识的重要素材。
1. 一元一次方程题目描述求解下列一元一次方程：a) 2x - 3 = 7b) 5(x + 2) = 25解答a) 将常数项移至等号右侧，得到：2x = 7 + 3化简得：2x = 10将方程两边同时除以2，得到：x = 5b) 将括号内的表达式进行运算，得到：5x + 10 = 25将常数项移至等号右侧，得到：5x = 25 - 10化简得：5x = 15将方程两边同时除以5，得到：x = 32. 平面几何题目描述已知三角形ABC，角A的度数为60度，边AC的长度为4 cm，边BC的长度为3 cm。
求边AB的长度。
解答根据余弦定理，可以得到下式：AB^2 = AC^2 + BC^2 - 2 * AC * BC * cos(A)将已知数据代入，得到：AB^2 = 4^2 + 3^2 - 2 * 4 * 3 * cos(60)化简得：AB^2 = 28所以，AB的长度为√28 cm。
3. 百分数和利率题目描述小明将一笔钱存入银行，年利率为5%。
如果小明存款后的第5年本金为元，求小明当初存入银行的金额是多少。
解答根据百分数和利率的计算公式，可以得到下式：本金 = 当初存入金额 / (1 + 年利率)^存款年数将已知数据代入，得到：= 当初存入金额 / (1 + 0.05)^5将方程两边同时乘以 (1 + 0.05)^5，得到：* (1 + 0.05)^5 = 当初存入金额化简得：当初存入金额≈ 7844.93元这些数学题目涵盖了初中数学中的一些重要内容，希望能够帮助你巩固和提高数学知识。
初中经典数学题
初中经典数学题
1、已知9x2-6xy+k是完全平方式，则k的值是________
答案：y2
2、某种笔记本的零售价每本2元，购买2本以上（含2本）商场推出两种优惠销售办法：第一种是一本按原价，其余七折；第二种是全部八折。
在购买相同数量的情况下，如何选择销售方法才使获得的优惠更多？
答案：设在购买x本的情况下，所花的钱一样多。
2+2（x-1）0.7=1.6x，x =3
3、一个人花8块钱买了一只鸡,9块钱卖掉了,然后他觉得不划算,花10块钱又买回来了,11块卖给另外一个人.问他赚了多少?
答案：2元
4、9a2+（________）+25b2=（3a-5b）2
答案：-30ab
5、把x4-2x2y2+y4分解因式，结果是_______
答案：（x+y）2（x-y）2
6、有只猴子在树林采了100根香蕉堆成一堆,猴子家离香蕉堆50米,猴子打算把香蕉背回家,每次最多能背50根,可是猴子嘴馋,每走一米要吃一根香蕉,问猴子最多能背回家几根香
答案：25根
7、-4x2+4xy+（_______）=-（_______）
答案：-y2；2x-y
8、已知y2+my+16是完全平方式，则m的值是_______
答案：±8
9、一栋住宅楼，爷爷从一楼走到三楼要6分钟，现在要到6楼，要走多少分钟？
答案：15分钟
10、已知a2+14a+49=25，则a的值是_________
答案：-2或-12。
初中最经典的数学题
以下是一些初中数学经典题目，这些题目对于巩固基础知识、训练解题思维和提高数学能力都很有帮助：
1. 两点之间，线段最短。
已知点A、点B，在直线L上找一点P，使得PA+PB最短。
2. 直角三角形斜边上的中线等于斜边的一半。
已知直角三角形ABC，∠ACB=90°，AD是斜边BC上的中线，求证：AD=1/2BC。
3. 等腰三角形的性质。
已知△ABC是等腰三角形，
∠B=60°，求证：AB=BC。
4. 利用三角函数测量物体的高度。
已知一个物体的高度h，在太阳光下形成的影子的长度为s，利用三角函数求太阳的高度角。
5. 利用二次函数求最值。
已知二次函数y=ax^2+bx+c，求当x取何值时，y取得最大值或最小值。
以上是一些初中数学的经典题目，希望这些题目能对你的学习有所帮助。
同时建议多练习，通过练习掌握解题思路和技巧，提高自己的数学水平。
初中经典数学题目
初中经典数学题目
1. 求解一元一次方程。
2. 计算圆的面积和周长。
3. 解析几何的基础题目。
4. 公式变化和运算。
5. 利用勾股定理解决问题。
6. 解决直角三角形的面积问题。
7. 解决等边三角形的面积和周长问题。
8. 利用坐标确定点的位置。
9. 利用二元一次方程解决问题。
10. 利用比例的定义解决问题。
11. 利用百分比解决问题。
12. 利用概率的定义解决问题。
13. 利用数据分析解决问题。
14. 利用统计中的平均数解决问题。
15. 二次函数的图象和性质问题解决。
16. 利用图形的旋转解决问题。
17. 利用图形的平移解决问题。
18. 利用数据的规律解决问题。
19. 我们使用公式a²-b²解决问题。
20. 利用方程的解集解决问题。
经典初中数学试题及答案
经典初中数学试题及答案一、选择题1. 下列哪个数是无理数？A. 3.14159B. πC. 0.33333D. √2答案：D2. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是多少？A. 5B. 6C. 7D. 8答案：A3. 一个数的平方根是它本身，这个数是：A. 0B. 1C. -1D. 2答案：A二、填空题4. 一个数的绝对值是其本身的数是________。
答案：非负数5. 如果一个多项式的次数是3，那么这个多项式被称为________。
答案：三次多项式6. 一个圆的半径是5厘米，那么这个圆的面积是________。
答案：78.5平方厘米三、计算题7. 计算下列表达式的值：(1) (-2)^3(2) √(9) + √(16)答案：(1) -8(2) 58. 解下列方程：(1) 2x + 5 = 13(2) 3y - 7 = 8答案：(1) x = 4(2) y = 5四、解答题9. 一个班级有40名学生，其中男生和女生的比例是3:2。
求这个班级有多少名男生和女生？答案：男生有24名，女生有16名。
10. 一个长方体的长、宽和高分别是10厘米、8厘米和6厘米，求这个长方体的体积。
答案：长方体的体积是480立方厘米。
五、证明题11. 证明：直角三角形的斜边的平方等于两直角边的平方和。
证明：设直角三角形的两直角边分别为a和b，斜边为c。
根据勾股定理，我们有：c^2 = a^2 + b^2六、应用题12. 某工厂生产一批零件，如果每天生产100个，需要20天完成。
现在工厂改进了生产效率，每天可以生产120个，问需要多少天可以完成？答案：需要15天可以完成。
七、综合题13. 在一个直角坐标系中，点A的坐标是(2,3)，点B的坐标是(-1,-2)，求线段AB的长度。
答案：线段AB的长度是√((2 - (-1))^2 + (3 - (-2))^2) = √(9 + 25) = √34。
初一上学期必会的40道经典数学题
初一上学期必会的40道经典数学题1. 学校春游，如果每辆汽车坐45人，则有28人没有上车;如果每辆坐50人，则空出一辆汽车，并且有一辆车还可以坐12人，问共有多少学生，多少汽车?2. 小明看书若干日，若每日读书32页，尚余31页;若每日读36页，则最后一日需要读39页，才能读完，求书的页数3. 某车间加工机轴和轴承，一个工人每天平均可加工15个机轴或10个轴承。
该车间共有80人，一根机轴和两个轴承配成一套，问应分配多少个工人加工机轴或轴承，才能使每天生产的机轴和轴承正好配套(2轴承配3机轴)?4. 某部队派出一支有25人组织的小分队参加防汛抗洪斗争，若每人每小时可装泥土18袋或每2人每小时可抬泥土14袋，如何安排好人力，才能使装泥和抬泥密切配合，而正好清场干净? 56、某印刷厂第三季度印刷了科技书籍50万册，而第四季度印刷了58万册，求季度的增长率是多少?甲、乙两厂去年完成任务的112%和110%，共生产机床4000台，比原来两厂任务之和超产400台，问甲厂原来的生产任务是多少台?5. 民航规定：乘坐飞机普通舱旅客一人最多可免费携带20千克行李，超过部分每千克按飞机票价的1.5%购买行李票。
一名旅客带了35千克行李乘机，机票连同行李费共付了1323元，求该旅客的机票票价甲、乙两人相距285米，相向而行，甲从A地每秒走8米，乙从B地每秒走6米，如果甲先走16米，那么甲出发几秒与乙相遇?6. 小明家搬了新居要购买新冰箱，小明和妈妈在商场看中了甲、乙两种冰箱.其中，甲冰箱的价格为2100元，日耗电量为1度;乙冰箱是节能型新产品，价格为2220元，日耗电量为0.5度，并且两种冰箱的效果是相同的.老板说甲冰箱可以打折，但是乙冰箱不能打折，请你就价格方面计算说明，甲冰箱至少打几折时购买甲冰箱比较合算?(每度电0.5元，两种冰箱的使用寿命均为10年，平均每年使用300天)7. 某单位急需用车，但又不需买车，他们准备和一个个体车或一国营出租公司中的一家鉴定月租车合同，个体车主的收费是3元/千米，国营出租公司的月租费为2000元，另外每行驶1千米收2元，试根据形式的`路程的多少讨论用哪个公司的车比较合算?8. 某校校长在国庆节带领该校市级“三好学生”外出旅游，甲旅行社说“如果校长买一张票，则其余学生可享受半价优惠”，乙旅行社说“包括校长在内全部按票价的6折优惠”(即按票的60%收费)。
初中数学难题精选(附答案)
经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）APCDB AFGCEBOD3、如图，已知四边形ABCD、A1B1C1D1都是正方形，A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点．求证：四边形A2B2C2D2是正方形．（初二）4、已知：如图，在四边形ABCD中，AD＝BC，M、NBC的延长线交MN于E、F．求证：∠DEN＝∠F．D2C2B2A2D1C1B1C BD AA1B经典难题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二）2、设MN是圆O外一直线，过O作OA⊥MN于A，自A及D、E，直线EB及CD分别交MN于P、Q．求证：AP＝AQ．（初二）F3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．4、如图，PC切圆O于C，AC为圆的直径，B、D．求证：AB＝DC，BC＝AD．（初三）经典难题（四）1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．求：∠APB的度数．（初二）2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD为圆内接凸四边形，求证：AB·CD＋AD·BC＝AC·BD．4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．FP DE CBAA2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC 上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典难题（一）1.如下图做GH⊥AB,连接EO。
初中数学经典题集
1.小学生小明问爷爷今年多大年龄，爷爷回答说：“我今年的岁数是你的岁数的7倍多，过几年变成你的6倍，又过几年变成你的5倍，再过若干年变成你的4倍。
”你说，小明的爷爷今年是多少岁？2. 某部队执行任务,以每小时8千米的速度前进,通信员在队伍中间接到任务后,以每小时12千米的速度把命令传到队头,然后再传到队尾,最后返回他在队中原来的位置,从离开他在队中的位置到返回共用7分12秒,问队伍长多少米?3.如图，Rt△ABC的面积为20平方厘米，在AB的同侧，分别以AB,BC,AC为直径作三个半圆，求阴影部分的面积。
4.有一个三角形满足a平方+b平方+c平方+338=10a+24b+26c，这是什么三角形？5.在平面直角坐标系中有点A(-1,0),点B(4,0),以AB为直径的半圆交y轴的正半轴于点C.(O 为原点)(1)求点C的坐标(2)求过A,B,C三点的解析式(3)在(2)的条件下,若在抛物线上有一点D,使四边形BOCD为直角梯形,求直线BD的解析式(4)设点M是抛物线上任意一点,过点M做MN垂直y轴于点N.若在线段AB上有且只有一点P,使角MPN为直角,求点M坐标.6. 边长为2的正方形ABCD内有一点P，求PA+PB+PC的最小值。
请写出过程。
7. AB，AC分别是圆O的直径和弦，D为劣弧AC上一点，DE垂直于AB于点H，交圆O 于点E，交AC于点F，P为ED延长线上一点。
问题：当点D在劣弧AC上什么位置时，才能使AD的平方=DE·DF?（要求自己画出图形）8. 已知直角三角形两条直角边长的和为根号6，斜边长为2，则这个直角三角形的面积为？9. 若满足不等式8/15<n/n+k<7/13的整数k只有一个，则正整数n的最大值为多少？请写出解答过程10. 把一个正方形切成两个长方体后，如果两者表面积之比为1:2,那么两者体积之比是多少?11. 证明两条角平分线相等的三角形是等腰三角形.12. 证明：在⊙0中，已知半径为５厘米，弦AB为５倍根号２厘米，弦AC为５厘米，求∠BAC。
初中数学经典试题100题
FG BDCBAGECDABCA初中数学经典试题荟萃1、如图，在正方形ABCD 中，6AB =，点E 在边AD 上，1=3DE AD ，连接BE ，将ABE ∆沿BE翻折，点A 落在点F 处，BF 与AC 交于点H ，点 O 是AC 中点，连接OF 并延长交CD 于点G , 求四边形GFHC 的面积。
2、如图，ABC ∆中，点D 、E 为BC 的三等分点， 点J 、K 为AC 的三等分点，若42ABC S ∆=， 求阴影部分面积S3、如图，任意凸四边形ABCD 中，E H 、三等分AD ，F G 、三等分BC ，P S 、三等分AB ，Q R 、 三等分DC ，求证：19TVNMABCD S S =4、如图，等边ABC ∆内一点P ，使得3PA =，4PB =，5PC =，求：ABC S ∆5、如图，在ABC ∆中，3AB =，2AC =， 以BC 为边在ABC ∆外作正方形BCDE ， 连接,BD CE 交于点O ， 求线段AO 的最大值。
D EFADEFABAB CDBAC6、如图，等边ABC ∆中，120BDC ∠=︒， DC GD =，AG 交CD 延长线于点E 。
求证：AE EG =7、如图，分别以锐角ABC ∆的三边为斜边 向外作等腰Rt DAB ∆、等腰Rt EBC ∆、 等腰Rt FAC ∆。
求证：①AE DF = ②AE DF ⊥8、如图，四边形ABCD 中，E F 、分别 是AB CD 、的中点，P 为对角线AC 延长线上任意一点，PF 交AD 于M ，PE 交BC 于N ，EF 交MN 于K ，求证：K 点平分线段MN9、如图，ABCD 中，E F 、分别是AB BC 、上 的点，DE 交AC 于M ，AF 交BD 于N ，若AF 平分BAC ∠，DE AF ⊥，DE 与AF 交于P ，记BE x OM =，BN y ON =，CF z BF =，试比较x y z 、、的大小关系。
初中经典数学题
初中经典数学题一、整数运算1. 求两个整数的和题目描述：已知整数a = 5，b = 3，请计算a与b的和。
解题思路：直接将a与b相加即可得到结果。
5 + 3 = 82. 求两个整数的差题目描述：已知整数a = 7，b = 4，请计算a与b的差。
解题思路：直接将a与b相减即可得到结果。
7 - 4 = 33. 求两个整数的积题目描述：已知整数a = 2，b = 6，请计算a与b的积。
解题思路：直接将a与b相乘即可得到结果。
2 * 6 = 124. 求两个整数的商题目描述：已知整数a = 15，b = 3，请计算a与b的商。
解题思路：直接将a与b相除即可得到结果。
15 / 3 = 5二、分数运算1. 分数的加法题目描述：已知分数a = 1/4，b = 2/3，请计算a与b 的和。
解题思路：将分数转换为相同的分母，然后分子相加即可得到结果。
1/4 + 2/3 = (3*1)/(3*4) + (4*2)/(4*3) = 3/12 + 8/ 12 = 11/122. 分数的减法题目描述：已知分数a = 5/6，b = 1/3，请计算a与b 的差。
解题思路：将分数转换为相同的分母，然后分子相减即可得到结果。
5/6 - 1/3 = (2*5)/(2*6) - (6*1)/(6*3) = 10/12 - 6 /12 = 4/12 = 1/33. 分数的乘法题目描述：已知分数a = 2/5，b = 3/4，请计算a与b 的积。
解题思路：将分数的分子相乘得到新的分子，分母相乘得到新的分母。
2/5 * 3/4 = (2*3)/(5*4) = 6/20 = 3/104. 分数的除法题目描述：已知分数a = 2/3，b = 4/5，请计算a与b 的商。
解题思路：将分数的分子相乘得到新的分子，分母相乘得到新的分母。
2/3 ÷ 4/5 = 2/3 * 5/4 = (2*5)/(3*4) = 10/12 = 5/6三、代数运算1. 解一元一次方程题目描述：已知方程2x + 3 = 7，请解出方程中的x的值。
初中经典数学问题
初中经典数学问题
以下是一些经典的初中数学问题：
1. 鸡兔同笼问题：一个笼子里有一些鸡和兔子，总共有35个头和94只脚，问鸡和兔子各有多少只？
2. 百钱百鸡问题：一个人用100钱买100只鸡，公鸡5钱一只，母鸡3钱一只，小鸡1钱三只，问公鸡、母鸡、小鸡各有多少只？
3. 托尔斯泰的割草问题：一个农夫用镰刀割完一片草地上的草，这片草地上的草均匀地生长。
农夫发现，他需要d天才能割完所有的草。
那么，实际上，他每天割完的草地面积是多少？
4. 欧拉的三只羊问题：一个小岛上有一只母羊和两只小羊，小羊出生后两个月就能像母羊一样能产出羊毛。
问一年后小岛上有多少只羊？
5. 费尔马大定理问题：费尔马大定理表述为：不存在整数x, y, n, 使得x^n + y^n = z^n。
这个定理经过长久的历史才被证明。
6. 勾股定理问题：直角三角形两条直角边的平方和等于斜边的平方。
这是几何学中一个非常重要的定理。
7. 概率问题：概率是描述事件发生可能性的数学工具，比如掷骰子、抽签等。
8. 代数问题：包括解方程、因式分解、不等式等。
9. 函数问题：包括一次函数、二次函数、反比例函数等。
10. 几何问题：包括线段、角、三角形、四边形、圆等图形的性质和定理。
这些问题是初中数学中常见的经典问题，通过对这些问题的学习和解决，可以提高学生的数学思维能力，为以后的数学学习打下基础。
初中数学经典题库
初中数学经典题库 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中数学经典题 库（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、点，AD 、BC 的延长线交MN 于E 、F ．APCDB A FG C E B D 2 C 2B 2 A 2 D 1C 1 B 1C B DA A 1求证：∠DEN＝∠F．经典难题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC 于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．2、设MN是圆O外一直线，过O作OA⊥MN于A，自圆于B、C及D、E，直线EB及CD分别交MN于P、求证：AP＝AQ．3、如果上题把直线MN由圆外平移至圆内，则由此可得以下命题：F设MN 是圆O 的弦，过MN 的中点A 任作两弦BC分别交MN 于P 、Q ． 求证：AP ＝AQ ．4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点． 求证：点P 到边AB 的距离等于AB经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ． 求证：PA ＝PF ．4、如图，PC 切圆O 于C ，ACPO 相交于B 、D ．求证：AB ＝DC ，BC经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5． 求：∠APB 的度数．2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ． 求证：∠PAB ＝∠PCB ．3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且AE ＝CF ．求证：∠DPA ＝∠DPC ．经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．。
初中数学200道经典题型
222初中数学易错题专题一、选择题1、A 、B 是数轴上原点两旁的点，则它们表示的两个有理数是（）A 、互为相反数B 、绝对值相等C 、是符号不同的数D 、都是负数2、有理数a 、b 在数轴上的位置如图所示，则化简|a-b|-|a+b|的结果是（）A 、2aB 、2bC 、2a-2bD 、2a+b 3、轮船顺流航行时m 千米/小时，逆流航行时(m-6)千米/小时，则水流速度（）A 、2千米/小时B 、3千米/小时C 、6千米/小时D 、不能确定4、方程2x+3y=20的正整数解有（）A 、1个B 、3个C 、4个D 、无数个5、下列说法错误的是（）A 、两点确定一条直线B 、线段是直线的一部分C 、一条直线不是平角D 、把线段向两边延长即是直线6、函数y=(m 2-1)x 2-(3m-1)x+2的图象与x 轴的交点情况是()A 、当m ≠3时，图像有一个交点B 、m ≠±1时，肯定有两个交点C 、当m =±1时，只有一个交点D 、图像可能与x 轴没有交点7、如果两圆的半径分别为R 和r （R>r ），圆心距为d ，且(d-r)2=R 2，则两圆的位置关系是（）A 、内切B 、外切C 、内切或外切D 、不能确定8、在数轴上表示有理数a 、b 、c 的小点分别是A 、B 、C 且b<a<c ，则下列数轴中正确的是（）9、有理数中，绝对值最小的数是（）A 、-1B 、1C 、0D 、不存在10、1的倒数的相反数是（）2A 、-2B 、2C 、-1D 、12211、若|x|=x ，则-x 一定是（）A 、正数B 、非负数C 、负数D 、非正数12、两个有理数的和除以这两个有理数的积，其商为0，则这两个有理数为（）A 、互为相反数B 、互为倒数C 、互为相反数且不为0D 、有一个为013、长方形的周长为x ，宽为2，则这个长方形的面积为（）A 、2xB 、2(x-2)C 、x-4D 、2·(x-2)/214、“比x 的相反数大3的数”可表示为（）A 、-x-3B 、-(x+3)C 、3-xD 、x+315、如果0<a<1，那么下列说法正确的是（）A 、a 2比a 大B 、a 2比a 小C 、a 2与a 相等D 、a 2与a 的大小不能确定16、数轴上，A 点表示-1，现在A 开始移动，先向左移动3个单位，再向右移动9个单位，又向左移动5个单位，这时，A 点表示的数是（）A 、-1B 、0C 、1D 、817、线段AB=4cm ，延长AB 到C ，使BC=AB 再延长BA 到D ，使AD=AB ，则线段CD 的长为（）A 、12cmB 、10cmC 、8cmD 、4cm 18、1-2的相反数是（）A 、1+B 、-1C 、-1-D 、-+119、方程x(x-1)(x-2)=x 的根是（）A 、x 1=1,x 2=2B 、x 1=0,x 2=1,x 3=2C 、x 1=3+25,x 2=3-52D 、x 1=0，x 2=3+25,x 3=3-522⎨x <-a20、解方程3(x 2+1)+5(x +1)-4=0时，若设x +1=y，则原方程可化为（）x 2xxA 、3y 2+5y-4=0B 、3y 2+5y-10=0C 、3y 2+5y-2=0D 、3y 2+5y+2=021、方程x 2+1=2|x|有（）A 、两个相等的实数根B 、两个不相等的实数根C 、三个不相等的实数根D 、没有实数根22、一次函数y=2(x-4)在y 轴上的截距为（）A 、-4B 、4C 、-8D 、823、解关于x 的不等式⎧x >a⎩，正确的结论是（）A 、无解B 、解为全体实数C 、当a>0时无解D 、当a<0时无解24、反比例函数y =2，当x ≤3时，y 的取值范围是（）xA 、y ≤2B 、y ≥2C 、y ≥2或y<0D 、0<y ≤2333325、0.4的算术平方根是（）A 、0.2B 、±0.2C 、10D 、±105526、李明骑车上学，一开始以某一速度行驶，途中车子发生故障，只好停车修理，车修好后，因怕耽误时间，于时就加快了车速，在下列给出的四个S-t 函数示意图象，符合以上情况的是（）27、123n x ，方差为s 2，则另一数组kx 1,kx 2,kx 3,…,kx n 的平均数与方差分别是（）A 、k x ,k 2s 2B 、x ,s 2C 、k x ,ks 2D 、k 2x ,ks 228、若关于x 的方程x -1=2有解，则a 的取值范围是（）x +aA 、a ≠1B 、a ≠-1C 、a ≠2D 、a ≠±129、下列图形中既是中心对称图形，又是轴对称图形的是（）A 、线段B 、正三角形C 、平行四边形D 、等腰梯形30、已知a =c ，下列各式中不成立的是（）b dA、a -b =a +b B 、c =a +3cC 、a =c +3aD 、ad=bcc -d c +ddb +3dbd +2b31、一个三角形的三个内角不相等，则它的最小角不大于（）A 、300B 、450C 、550D 、60032、已知三角形内的一个点到它的三边距离相等，那么这个点是（）A 、三角形的外心B 、三角形的重心C 、三角形的内心D 、三角形的垂心33、下列三角形中是直角三角形的个数有（）①三边长分别为:1:2的三角形②三边长之比为1:2:3的三角形③三个内角的度数之比为3:4:5的三角形④一边上的中线等于该边一半的三角形A 、1个B 、2个C 、3个D 、4个34、如图，设AB=1，S △OAB =4cm 2，则弧AB 长为（）A 、πcmB 、2πcmC 、πcmD 、πcm336235、平行四边形的一边长为5cm ，则它的两条对角线长可以是（）A 、4cm,6cmB 、4cm,3cmC 、2cm,12cmD 、4cm,8cm 36、如图，△ABC 与△BDE 都是正三角形，且AB<BD ，若△ABC 不动，将△BDE绕B 点旋转，则在旋转过程中，AE 与CD 的大小关系是（）A 、AE=CD B 、AE>CD C 、AE>CD D 、无法确定3328a a 2+b 20.1x325a 2+b 2122-2122-1aa 22x -1a b237、顺次连结四边形各边中点得到一个菱形，则原四边形必是（）A 、矩形B 、梯形C 、两条对角线互相垂直的四边形D 、两条对角线相等的四边形38、在圆O 中，两段弧满足AB=2CD ，那么弦AB 和弦CD 的关系是（）A 、AB=2CDB 、AB>2CDC 、AB<2CD D 、AB 与CD 不可能相等39、在等边三角形ABC 外有一点D ，满足AD=AC ，则∠BDC 的度数为（）A 、300B 、600C 、1500D 、300或150040、△ABC 的三边a 、b 、c 满足a ≤b ≤c ，△ABC 的周长为18，则（）A 、a ≤6B 、b<6C 、c>6D 、a 、b 、c 中有一个等于641、如图，在△ABC 中，∠ACB=Rt ∠，AC=1，BC=2，则下列说法正确的是（）A 、∠B=300B 、斜边上的中线长为1C 、斜边上的高线长为255D 、该三角形外接圆的半径为142、如图，把直角三角形纸片沿过顶点B 的直线BE （BE 交CA 于E ）折叠，直角顶点C 落在斜边AB 上，如果折叠后得到等腰三角形EBA ，那么下列结论中（1）∠A=300（2）点C 与AB 的中点重合（3）点E 到AB 的距离等于CE 的长，正确的个数是（）A 、0B 、1C 、2D 、343、不等式A 、x>2x +2>23x +的解是（）B 、x>-C 、x<D 、x<-44、已知一元二次方程(m-1)x 2-4mx+4m-2=0没有实数根，则m 的取值范围是（）A 、m<1/3B 、m ≤1/3C 、m ≥1/3D 、m ≥1/3且m ≠145、函数y=kx+b(b>0)和y=-k (k ≠0)，在同一坐标系中的x 图象可能是右图中的（）(注：从左到右依次为ABCD)46、在一次函数y=2x-1的图象上，到两坐标轴距离相等的点有（）A 、1个B 、2个C 、3个D 、无数个47、若点（-2，y 1）、（-1，y 2）、（1，y 3）在反比例函数y =1的图像上，则下列结论中正确的是（）xA 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 2>y 1>y 3D 、y 3>y 1>y 248、下列根式是最简二次根式的是（）A 、B 、C 、D 、49、下列计算哪个是正确的（）A 、+=B 、2+=2C 、=a +bD 、=+50、把-a（a 不限定为正数）化简，结果为（）A 、51、若a+|a|=0，则B 、+等于（）C 、-D 、-A 、2-2a B 、2a-2C 、-2D 、252、已知+=0，则x 2-2x +1的值（）A 、1B 、±1C 、1D 、-122253*、设a 、b 是方程x 2-12x+9=0的两个根，则+等于（）A 、18B 、54、下列命题中，正确的个数是（）C 、3D 、±3①等边三角形都相似②直角三角形都相似③等腰三角形都相似④锐角三角形都相似⑤等腰三角形都全等⑥有一个角相等的等腰三角形相似⑦有一个钝角相等的两个等腰三角形相似⑧全等三角形相似A 、2个B 、3个C 、4个D 、5个622a 55521a -aa-a(a -2)21-2x 62k -1二、填空题1、如果一个数的绝对值等于它的相反数，那么这个数一定是。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
37. (本小题满分6分)已知，求代数式的值；
38．(本小题满分6分) 解不等式组：，并把解集在数轴上表示出来.
39. 如图， CD切⊙O于点D，连结OC， 交⊙O于点B，过点B作弦AB⊥OD， 点E为垂足，已知⊙O的半径为10，sin∠COD=.
在同一平面内，两条线段不相交就会平行⑤有一条对角线平分一个内角
的平行四边形是菱形
A、②③ B、①②④ C、①⑤
D、②③④
4、如图，矩形ABCD中,已知AB=5,AD=12,P是AD上的动点,PE⊥AC于
E,PF⊥BD于F,则PE+PF=（ B ）
A、5 B、 C、 D、
5、在直角坐标系中，已知两点A（-8，3）、B（-4，5）以及动点
22 。（本题满分8分）（1）如图7，点O是线段AD的中点，分别以AO和 DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连
结AC和BD，相交于点E，连结BC．求∠AEB的大小；
B A O D C E 图8 C B O D 图7 A
（2）如图8，ΔOAB固定不动，保持ΔOCD的形状和大小不变，将ΔOCD 绕着点O旋转（ΔOAB和ΔOCD不能重叠），求∠AEB的大小.
第17题
15、如图，在直线y=-x+1与x轴、y轴交于点A、B，以线段AB为直角边在 第一象限内作等腰直角△ABC，∠BAC=90°，第二象限内有一点 P（a,）,且△ABP的面积与△ABC的面积相等，则a= 三、解答题
16、如图，已知矩形ABCD，延长CB到E，使CE=CA，连结AE并取中点F， 连结AE并取中点F，连结BF、DF，求证BF⊥DF。
23．如图，数轴上点A所表示的数的倒数是（ ）
第1题
A. B. 2 C.
D.
24．化简（a≠0）的结果是（ ）
A. 0 B. C. D.
25．下列判断正确的是（ ）
A. “打开电视机，正在播NBA篮球赛”是必然事件
B. “掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就必有1次反面朝
上
C. 一组数据2，3，4，5，5，6的众数和中位数都是5 D. 甲组数据的方差S甲2=0.24，乙组数据的方差S乙2=0.03，则乙组数据 比甲组数据稳定
第10题
31、⊙O是△ABC的外接圆，已知∠B=60°，则∠CAO的度数是( )
A．15° B．30° C．45° D．60°
32、二次函数
的图象如图所示，则下列关系式中错误的是、（ ） A．a＜0 B．c＞0 C．
＞0 D．
＞0 33. 已知点A（1，＋2）在双曲线上．则的值为 ．
34. 如图，已知OB是⊙O的半径，点C、D在⊙O上，∠DCB＝40°，则
C（0，n）、D(m,0)，则当四边形ABCD的周长最小时，比值为
（ ）
A、- B、- C、- D、
二、填空题
6、当x=
时，与互为倒数。9、已知x2-3x+1=0，求（x-）2 =
7、一个人要翻过两座山到另外一个村庄，途中的道路不是上山就是下
山，已知他上山的速度为v，下山的速度为v′，单程的路程为s．则这
数学试题 一、选择题 1、若一次函数y=kx+1与两坐标轴围成的三角形面积为3，则k为（ C ）
A、
B、- C、±
D、±
2、若=3，的值是（ B ）
A、1.5
B、
C、-2
D、-
3、判断下列真命题有（ C ）
①任意两个全等三角形可拼成平行四边形②两条对角线垂直且相等的四
边形是正方形③四边形ABCD，AB=BC=CD，∠A=90°，那么它是正方形④
个人往返这个村庄的平均速度为 8、将点A（4，0）绕着原点O顺时针方向旋转30°角到对应点，则点的 坐标是 9、菱形ABCD的一条对角线长为6，边AB的长是方程(X-3)(X-4)=0的解， 则菱形ABCD的周长为 10、△ABC中，∠A=90°，AB=AC，BD是△ABC的中线，△CDB内以CD为边 的等腰直角三角形周长是 11. 如图，边长为6的菱形ABCD中，∠DAB=60°，AE=AB，F是AC上一动 点，EF+BF的最小值为 12、如图，边长为3的正方形ABCD顺时针旋转30°，得上图，交DE于 D’,阴影部分面积是
（1）当x=3时，y是多少？ （2）求x与y的关系式。（注意取值范围）
20. 已知与是反比例函数图象上的两个点． （1）求、m的值；
（2）若点，则在反比例函数图象上是否存在点，使得以四点为顶点的 四边形为梯形？若存在，求出点的坐标；若不存在，请说明理由．
21直线与轴、轴分别交于A、B两点，点P从B点出发，沿线段BA匀速运 动至A点停止；同时点Q从原点O出发，沿轴正方向匀速运动 (如 图1)，且在运动过程中始终保持PO=PQ，设OQ=x. （1）试用的代数式表示BP的长. （2）过点O、Q向直线AB作垂线，垂足分别为C、D（如图2），求 证：PC=AD. （3）在（2）的条件下，以点P、O、Q、D为顶点的四边形面积为S， 试求S与的函数关系式，并写出自变量x的范围.
根据上述信息，回答下列问题： (1)这三个月中，甲品牌电脑在哪个月的销售量最大? 月份；
(2)已知该公司这三个月中销售乙品牌电脑的总数量比销售甲品牌电 脑的总数量多50台，求乙品牌电脑在二月份共销售了多少台?
（3）若乙品牌电脑一月份比甲品牌电脑一月份多销售42台，那么三
月份乙品牌电脑比甲品牌电脑多销售（少销售）多少台？
A P B Q C M 第22题图2 A P B Q C M
第22题图1
44．如图，点在⊙O上，，与相交于点，，延长到点，使，连结．
A C D O E F B
(1)证明； (2)试判断直线与⊙O的位置关系，并给出证明．
45.
如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3， BC=，直线y=经过点C，交y售公司参加社会实践活动，了解到2010年 该公司经销的甲、己两种品牌电脑在第一季度三个月(即一、二、三 月份)的销售数量情况．小明用直方图表示甲品牌电脑在第一季度每 个月的销售量的分布情况，见图①；小华用扇形统计图表示乙品牌电 脑每个月的销售量与该品牌电脑在第一季度的销售总量的比例分布情 况，见图②．
的圆心角度数是（ ）
A. 60°
B. 90°
C. 120°
D. 180°
30．一种原价均为m元的商品，甲超市连续两次打八折；乙超市一次性打
六折；丙超市第一次打七折，第二次再打九折；若顾客要购买这种商
品，最划算应到的超市是（ ）
A. 甲或乙或丙 B. 乙
C. 丙 D. 乙或丙
y x O
1 －1
第9题
A B C O E D 第19题
求：（1）弦AB的长； （2）CD的长；
40 已知正比例函数（a＜0）与反比例函数的图象有两个公共点，其中一 个公共点的纵坐标为4． （1）求这两个函数的解析式； （2）在坐标系中画出它们的图象（可不列表）； （3）利用图像直接写出当x取何值时，．
41一个不透明的布袋里装有4个大小、质地均相同的乒乓球，每个球上 面分别标有1，2，3，4．小林先从布袋中随机抽取一个乒乓球（不放回 去），再从剩下的3个球中随机抽取第二个乒乓球． （1）请你列出所有可能的结果； （2）求两次取得乒乓球的数字之积为奇数的概率．
43 如图1，点P、Q分别是边长为4cm的等边∆ABC边AB、BC上的动点，点P 从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，
（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若 变化，则说明理由，若不变，则求出它的度数；
（2）何时∆PBQ是直角三角形？ （3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线 AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不 变，则求出它的度数；
13、如图，已知四边形ABCD中，AC和BD相交于点O， 且∠AOD＝90°， 若BC＝2AD，AB＝12，CD＝9，四边形ABCD的周长是
14、有这样一组数：1，1，2，3，5…，现以这组数据的数作为正方形 边长的长度构造如下正方形；再分别从左到右取2个、3个、4个、5个正 方形拼成如下矩形记为①、②、③、④.第⑩个矩形周长是
∠OBD＝ 度. 35. 如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水
平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶 端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12 米， 那么该古城墙的高度是 米.
A B C D E O 第14题 A B P D C C 第13题图 第12题
明理由。
17、如图，已知在等腰ABCD中，AD=x，BC=y,梯形高为h（1）用含x、 y、h的关系式表示周长C （2）（AD=8，BC=12，BD=10，求证∠DCA+∠BAC=90°
18、如图，过原点的直线l1：y=3x，l2：y=x。点P从原点O出发沿x轴正 方向以每秒1个单位长度的速度运动。直线PQ交y轴正半轴于点Q，且分 别交l1、l2于点A、B。设点P的运动时间为t秒时，直线PQ的解析式为 y=―x+t。△AOB的面积为Sl(如图①)。以AB为对角线作正方形ACBD，其
A B C D G
o
第23题
（1）点C、D的坐标分别是C（
），D（
）；
（2）求顶点在直线y=上且经过点C、D的抛物
线的解析式；
（3）将（2）中的抛物线沿直线y=平移，平移后
的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。
平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？