2018年全国高考文科数学分类汇编----立体几何
高三数学-2018高考文科试题分类立体几何 精品

18 立体几何一、选择题1.(安徽3).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是省( B )A .,,αγβγαβ⊥⊥若则‖B .,,m n m n αα⊥⊥若则‖C .,,m n m n αα若则‖‖‖D .,,m m αβαβ若则‖‖‖2.(北京8)如图,动点P 在正方体1111ABCD A BC D -的对角线1BD 上,过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设B P x =,MN y =,则函数()y f x =的图象大致是( B )3.(福建6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( D ) A.223B.23C.24D.134.(广东7)将正三棱柱截去三个角(如图1所示A ,B ,C 分别是△CHI 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( A )ABC DMNP A 1B 1C 1D 1 yxA .OyxB .OyxC .Oyx D .O5.(宁夏12)已知平面α⊥平面β,l αβ=,点A α∈,A l ∉,直线AB l ∥,直线AC l ⊥,直线m m αβ∥,∥,则下列四种位置关系中,不一定...成立的是( D ) A .AB m ∥B .AC m ⊥C .AB β∥D .AC β⊥6.(湖南5)已知直线m,n 和平面βα,满足βα⊥⊥⊥,,a m n m ,则 ( D ).A n β⊥ ,//.βn B 或β⊂n α⊥n C . ,//.αn D 或α⊂n7.(湖南9)长方体1111ABCD A BC D -的8个顶点在同一个球面上,且AB=2,AD=3,11=AA ,则顶点A 、B 间的球面距离是( B )A .42π B .22πC .π2D .2π2 8.(江西9).设直线m 与平面α相交但不.垂直,则下列说法中正确的是( B ) A .在平面α内有且只有一条直线与直线m 垂直 B .过直线m 有且只有一个平面与平面α垂直 C .与直线m 垂直的直线不.可能与平面α平行 D .与直线m 平行的平面不.可能与平面α垂直 9.(辽宁12)在正方体1111ABCD A BC D -中,E F ,分别为棱1AA ,1CC 的中点,则在空间中与三条直线11A D ,EF ,CD 都相交的直线( D ) A .不存在B .有且只有两条C .有且只有三条D .有无数条10.(全国Ⅰ11)已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( B )A .13B .23C .33D .2311.(全国Ⅱ8)正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( B ) A .3 B .6 C .9 D .18 12.(全国Ⅱ12)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( C ) A .1B .2C .3D .213.(山东6) 右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( D )2A .9πB .10πC .11πD .12π 14.(上海13)给定空间中的直线l 及平面α.条件“直线l 与平面α内两条相交直线都垂直”是“直线l 与平面α垂直”的( C )A.充分非必要条件 B.必要非充分条件C .充要条件 D.既非充分又非必要条件15.(四川8)设M 是球心O 的半径OP 的中点,分别过,M O 作垂直于OP 的平面,截球面得两个圆,则这两个圆的面积比值为:( D ) (A)41 (B)12 (C)23 (D)3416.(四川10)设直线l ⊂平面α,过平面α外一点A 与,l α都成030角的直线有且只有:( B )(A)1条 (B)2条 (C)3条 (D)4条 17.(四川12)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为060的菱形,则该棱柱的体积等于( B )(A)2 (B)22 (C)32 (D)42 18.(天津5) 设a b ,是两条直线,αβ,是两个平面,则a b ⊥的一个充分条件是( C ) A .a b αβαβ⊥⊥,∥, B .a b αβαβ⊥⊥,,∥ C .a b αβαβ⊂⊥,,∥D .a b αβαβ⊂⊥,∥,19.(浙江9)对两条不相交的空间直线a 和b ,必定存在平面α,使得 ( B ) (A ),a b αα⊂⊂ (B ),//a b αα⊂ (C ),a b αα⊥⊥ (D ),a b αα⊂⊥20.(重庆11)如题(11)图,模块①-⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为 ( A )(A)模块①,②,⑤ (B)模块①,③,⑤ (C)模块②,④,⑥ (D)模块③,④,⑤21.(湖北4).用与球必距离为1的平面去截面面积为π,则球的体积为 ( D ) A.323π B.83π C.82π D. 823π22.(陕西8)长方体1111ABCD A BC D -的各顶点都在半径为1的球面上,其中1::2:1:3A B A D A A=,则两,A B 点的球面距离为( C ) A .4πB .3π C .2π D .23π 23.(陕西10) 如图,l A B A B αβαβαβ⊥=∈∈,,,,,到l 的距离分别是a 和b ,AB 与αβ,所成的角分别是θ和ϕ,AB 在αβ,内的射影分别是m 和n ,若a b >,则( D ) A .m n θϕ>>, B .m n θϕ><, C .m n θϕ<<,D .m n θϕ<>,二、填空题1.(安徽16)已知点,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =213,AC =8AD =,则,B C 两点间的球面距离是43π2.(福建15)若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是 . 9π3.(广东15)(几何证明选讲选做题)已知PA 是圆O 的切点,切点为A ,A B abl αβMA BDCOPA =2.AC 是圆O 的直径,PC 与圆O 交于B 点,PB =1,则圆O 的半径R =________.3 4.(宁夏14)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为3,底面周长为3,则这个球的体积为 .43π 5.(江西15)连结球面上两点的线段称为球的弦.半径为4的球的两条弦AB CD 、的长度分别等于27、43,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .56.(辽宁14)在体积为43π的球的表面上有A 、B ,C 三点,AB =1,BC =2,A ,C 两点的球面距离为33π,则球心到平面ABC 的距离为_________.327.(全国Ⅰ16)已知菱形ABCD 中,2AB =,120A ∠=,沿对角线BD 将ABD △折起,使二面角A BD C --为120,则点A 到BCD △所在平面的距离等于 .328.(全国Ⅱ16)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件: 充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形. 注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.9.(浙江15)已知球O 的面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA=AB=BC=3,则球O 点体积等于 。
2011年2018年新课标全国卷1文科数学分类汇编8立体几何

新课标全国卷Ⅰ文科数学分类汇编8.立体几何(含解析)一、选择题OOOO2018,5的平面截该圆柱所得的截面是面积【,】已知圆柱的上、下底面的中心分别为,过直线21218 )的正方形,则该圆柱的表面积为(为 D CA B ππ1012....π2122π82018,9216,其三视图如右图.圆柱表面上的点在正视图上的对应点为【,底面周长为】某圆柱的高为MNN的路径中,最短路径到在左视图上的对应点为,圆柱表面上的点,则在此圆柱侧面上,从BAM)的长度为(A B C D23....52217ABCD?ABCDACBBCC302?AB?BC?2018,10,则该,中,【所成的角为】在长方体与平面1111111)长方体的体积为(8 D CA B 38....282620176ABMNQ 为所在棱的中点,则在,,【为正方体的两个顶点,,,】如图,在下列四个正方体中,ABMNQ)不平行的是(与平面这四个正方体中,直接【2016,7】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂π28)直的半径.若该几何体的体积是,则它的表面积是(3π28201817πππ.D .A.B.C???A∥DCBABCD?ADCBmABCD?平面】平面过正方体,,的顶点,平面112016【,111111?nm,nABBA?平面)所成角的正弦值为(,则11.3321. D C. B .A .2233【2015,6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问其意思为:积及为米几何?”题:“今有委米依垣内角,下周八尺,高五尺,问”,米堆底部的弧长“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一)斛米的体已知15尺,米堆的体积和堆放的米各位多少?”为8尺,米堆的高为) ,估算出堆放的米有( 积约为1.62立方尺,圆周率约为3 66斛D.C.36斛斛B.22斛A.14)组成一个几何体,该几何体的三视图中的】圆柱被一个平面截去一部分后与半球(半径为r2015,11【) B r=( 正视图和俯视图如图所示,若该几何体的表面积为16+20π,则8 D..4 B1 .2 CA.】【2012,7,【201311】【2014,8】【2015,11】) 粗实线画出的一个几何体的三视图,则这个几何体是( 【2014,8】如图,网格纸的各小格都是正方形,D.四棱柱.三棱锥B.三棱柱C.四棱锥A ().【2013,11】某几何体的三视图如图所示,则该几何体的体积为16π8+D.+8πC.16+16π.A.16+8πB8 ,粗线画出的是某几何体的三视图,则此几何体的体积为】如图,网格纸上小正方形的边长为1【2012,715 D.12 B.9 C.A.6 ??2)的距离为,则此球的体积为】平面(截球O的球面所得圆的半径为1,球心O到平面,【20128????6364364.. B .C.DA 】在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【2011,8二、填空题OOSC?SABC162017面是球的直径.若平所有顶点都在球的【球,】已知三棱锥面上,的OS?ABC??SAACSBBC SCB?平面SCA_______9 .的体积为,,则球,,三棱锥的表面积为所得α2HBAB的直径上一点,AH∶=1∶,AB⊥平面,H为垂足,截球OαOH152013【,】已知是球______.的表面积为截面的面积为π,则球O】已知两个圆锥由公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面【2011,163,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为积是这个球面面积的.16三、解答题.ACM2018,18AC90?3∠ACM?ABCMAB?AC?折,为折痕将△【在平行四边形】如图,,中,以.到达点的位置,且起,使点DAD⊥ABM1 ABC⊥ACD;平面()证明:平面2Q?ABPQDABP?DQ? 2BC的体积.,求三棱锥上一点,为线段()上一点,且为线段PAD3P?ABCDCD?BAP??CDP?90?AB.,【201718】如图,在四棱锥,且中,∥PA?PD?AB?DC?APD?90?PAD?PAB,且四棱锥21()证明:平面平面;()若,8P?ABCD 的体积为,求该四棱锥的侧面积.3ABCP?6PA?P ABC内,顶点18,】如图所示,已知正三棱锥的侧面是直角三角形,在平面【2016PEAB GEDPABD在平面于点内的正投影为点..连结的正投影为点,并延长交AB G 是的中点;(1)求证:PDEFFE PAC在平面,并求四面体内的正投影的体积.)在题图中作出点(2(说明作法及理由)PEACDGB【2015,18】如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,(Ⅰ)证明:平面AEC⊥平面BED;(Ⅱ)若∠ABC=120°,AE⊥EC,三棱锥E- ACD6,求该三棱锥的侧面积.的体积为3OAO?CBCCBBCBABC?A平中,侧面且的中点为,2014,19【】如图,三棱柱为菱形,111111BBCC.面11BC?AB; 1)证明:(1 ABC?AABBCAC?的高,求三棱柱. 2()若,BC?CBB??601,11111.BAA=60°=CA=CB,ABAA,∠CA19【2013,】如图,三棱柱ABC-B中,111116的体积.BABC-ACCA2CBAB(2)CAAB(1)证明:⊥;若==,=,求三棱柱111111??90?ACB-AA,C中,侧棱垂直底面,DAC=BC=是棱AA,2012【,19】如图,三棱柱ABCBA111112的中点.C1;1()证明:平面BDC⊥平面BDC B11A BDC分此棱柱为两部分,求这两部分体积的比.(2)平面11DCBAABCD?ABCDP60??DAB AD2AB?【2011,18,中,底面】如图所示,四棱锥,为平行四边形,ABCD?PD.底面BD?PA)证明:;(1PBC?D1AD??PD(的高.)若,求棱锥2新课标全国卷Ⅰ文科数学分类汇编.立体几何(解析版)8一、选择题OOOO2018,5的平面截该圆柱所得的截面是面积】已知圆柱的上、下底面的中心分别为,过直线【,22118 )的正方形,则该圆柱的表面积为(为 D B AC π1012π....π82122π22?l?2r?28l??rl?2r,。
2018年高考题分类汇编之立体几何

2018年数学高考题分类汇编之立体几何1.【2018年浙江卷】已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ12.【2018年浙江卷】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是A. 2B. 4C. 6D. 83.【2018年文北京卷】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为A. 1B. 2C. 3D.44.【2018年新课标I卷文】在长方体中,,与平面所成的角为,则该长方体的体积为A. B. C. D.5.【2018年新课标I卷文】已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A. B. C. D.6.【2018年全国卷Ⅲ文】设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A. B. C. D.7.【2018年全国卷Ⅲ文】中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D8.【2018年全国卷II文】在正方体中,为棱的中点,则异面直线与所成角的正切值为A. B. C. D.9.【2018年天津卷文】如图,已知正方体ABCD–A1B1C1D1的棱长为1,则四棱柱A1–BB1D1D的体积为__________.10.【2018年江苏卷】如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.11.【2018年全国卷II文】已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为,若的面积为,则该圆锥的体积为__________.12.【2018年浙江卷】如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(Ⅰ)证明:AB1⊥平面A1B1C1;(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.13.【2018年天津卷文】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=,∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.14.【2018年江苏卷】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.15.【2018年江苏卷】在平行六面体中,.求证:(1);(2).16.【2018年新课标I卷文】如图,在平行四边形中,,,以为折痕将△折起,使点到达点的位置,且.(1)证明:平面平面;(2)为线段上一点,为线段上一点,且,求三棱锥的体积.17.【2018年全国卷Ⅲ文】如图,矩形所在平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面;(2)在线段上是否存在点,使得平面?说明理由.18.【2018年全国卷II文】如图,在三棱锥中,,,为的中点.(1)证明:平面;(2)若点在棱上,且,求点到平面的距离.。
2018高考数学试题分类汇编之立体几何

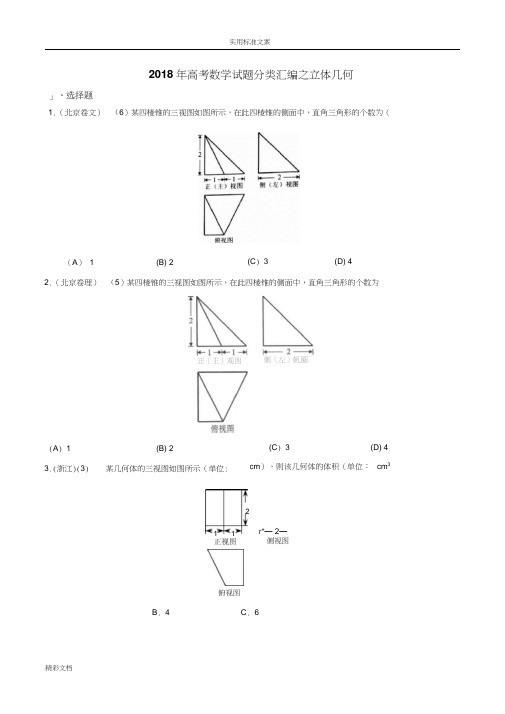
2018年高考数学试题分类汇编之立体几何一、选择题1.(北京卷文)(6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )。
(A )1(B )2 (C )3(D )42.(北京卷理)(5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(A )1 (B )2 (C )3 (D )43.(浙江)(3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是俯视图正视图A .2B .4C .6D .84.(全国卷一文)(5)已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A.B .12πC .D .10π5.(全国卷一文)(9)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为 A. B .C .3D .26.(全国卷一文)(10)在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为A .8B .C .D .7.(全国卷一理)(7)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .28.(全国卷一理)(12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C .4D9.(全国卷二文)(9)在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A B C D10.(全国卷二理)(9)在长方体1111ABCD A B C D -中,1AB BC ==,1AA ,则异面直线1AD 与1DB 所成角的余弦值为A .15B C D 11.(全国卷三文)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是12.(全国卷三文)(12)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为A .B .C .D .13.(全国卷三理)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是14.(全国卷三理)(10)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为A .B .C .D .二、填空题1.(江苏)(10)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .2.(天津文)(11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.3.(天津理)(11) 已知正方体1111ABCD A B C D -的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M EFGH -的体积为 .4.(全国卷二文)(16)已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若S A B△的面积为8,则该圆锥的体积为__________.5.(全国卷二理)(16)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若SAB △的面积为,则该圆锥的侧面积为__________.三、解答题1.(北京文)(18)(本小题14分)如图,在四棱锥P-ABCD 中,底面ABCD 为矩形,平面P AD ⊥平面ABCD ,P A ⊥PD ,P A =PD ,E ,F 分别为AD ,PB 的中点.(Ⅰ)求证:PE ⊥BC ;(Ⅱ)求证:平面P AB ⊥平面PCD ;(Ⅲ)求证:EF ∥平面PCD .2.(北京理)(16)(本小题14分)如图,在三棱柱ABC -111A B C 中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点,AB=BC ,AC =1AA =2.(Ⅰ)求证:AC ⊥平面BEF ;(Ⅱ)求二面角B-CD -C 1的余弦值;(Ⅲ)证明:直线FG 与平面BCD 相交.3.(江苏)(15)(本小题满分14分)在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥. 求证:(1)11AB A B C 平面∥;(2)111ABB A A BC ⊥平面平面.4.(浙江)(19)(本题满分15分)如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2. (Ⅰ)证明:AB 1⊥平面A 1B 1C 1;(Ⅱ)求直线AC 1与平面ABB 1所成的角的正弦值.5.(天津文)(17)(本小题满分13分)如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =BAD =90°.(Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值.6.(天津理)(17)(本小题满分13分)如图,AD BC∥且AD=2BC,AD CD⊥,EG AD∥且EG=AD,CD FG∥且CD=2FG,DG ABCD⊥平面,DA=DC=DG=2.(I)若M为CF的中点,N为EG的中点,求证:MN CDE∥平面;(II)求二面角E BC F--的正弦值;(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.7.(全国卷一文)(18)(12分)如图,在平行四边形ABCM中,3AB AC==,90ACM=︒∠,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB DA⊥.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P在线段BC上,且23BP DQ DA==,求三棱锥Q ABP-的体积.8.(全国卷一理)(18)(12分)如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.9.(全国卷二文)(19)(12分)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点. (1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.10.(全国卷二理)(20)(12分)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点. (1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.11.(全国卷三文)(19)(12分)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.12.(全国卷三理)(19)(12分)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)当三棱锥M ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.。
2018-2016三年高考真题文科数学专题分类汇编:立体几何的位置关系(解析附后)

2018-2016三年高考专题文科数学专题分类汇编:立体几何的位置关系(解析附后)考纲解读明方向1.会用平面的基本性质证明点共线、线共点、点线共面问题;会用反证法证明有关异面或共面问题.2.会判定和证明两条直线异面;会应用三线平行公理和等角定理及推论解决有关问题,会求两条异面直线所成的角;了解两条异面直线间的距离.3.高考对本节内容的考查常以棱柱、棱锥为依托,求异面直线所成的角,分值约为5分,属中档题.分析解读1.理解空间直线和平面位置关系的定义;了解直线和平面的位置关系;掌握直线与平面平行的判定定理和性质定理.2.会运用直线与平面及平面与平面的位置关系,以及它们平行的判定定理和性质定理解决简单的应用问题与证明问题.3.推理和证明要严谨、合理、充分.4.高考对本节内容的考查,一般通过对图形或几何体的认识,考查线线平行、线面平行、面面平行之间的转化思想,题型以解答题为主,分值约为5分,属中档题.2018年高考全景展示1.【2018年全国卷Ⅲ文】如图,矩形所在平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面;(2)在线段上是否存在点,使得平面?说明理由.2.【2018年全国卷II文】如图,在三棱锥中,,,为的中点.(1)证明:平面;(2)若点在棱上,且,求点到平面的距离.2017年高考全景展示1.【2017课标1,文6】如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是A .B .C .D .2.【2017课标3,文10】在正方体1111ABCD A BC D -中,E 为棱CD 的中点,则( ) A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥3.【2017课标1,文18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积. 4.【2017山东,文18】(本小题满分12分)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD , (Ⅰ)证明:1AO ∥平面B 1CD 1;(Ⅱ)设M 是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1.5.【2017江苏,15】 如图,在三棱锥A-BCD 中,AB ⊥AD , BC ⊥BD , 平面ABD ⊥平面BCD , 点E ,F (E 与A ,D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ; (2)AD ⊥AC .2016年高考全景展示1.【2016高考山东文数】已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的( )(A )充分不必要条件(B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件2. 【2016高考上海文科】如图,在正方体ABCD −A 1B 1C 1D 1中,E 、F 分别为BC 、BB 1的中点,则下列直线中与直线EF相交的是( )(A)直线AA 1(B)直线A 1B 1(C)直线A 1D 1(D)直线B 1C 13.【2016高考北京文数】(本小题14分)如图,在四棱锥ABCD P -中,⊥PC 平面ABCD ,,AB DC DC AC ⊥∥ (I )求证:DC PAC ⊥平面;(第15题)ADBEF(II )求证:PAB PAC ⊥平面平面;(III )设点E 为AB 的中点,在棱PB 上是否存在点F ,使得//PA 平面C F E ?说明理由.4. 【2016高考山东文数】(本小题满分12分) 在如图所示的几何体中,D 是AC 的中点,EF ∥DB .(I )已知AB =BC ,AE =EC .求证:AC ⊥FB ;(II )已知G ,H 分别是EC 和FB 的中点.求证:GH ∥平面ABC .解析版2018年高考全景展示1.【2018年全国卷Ⅲ文】如图,矩形所在平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面;(2)在线段上是否存在点,使得平面?说明理由.【答案】(1)证明见解析(2)存在,理由见解析【解析】分析:(1)先证,再证,进而完成证明。
2018年高考数学试的题目分类总汇编之立体几何
实用标准文案2018年高考数学试题分类汇编之立体几何(6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(B . 4C . 6(A ) 1 2.(北京卷理) (B) 2(A ) 1 3.(浙江)(3) (C ) 3 (D) 4(5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为正〔主)观图 恻(左)帆圈(B) 2(C ) 3 (D) 4某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位: cm 3俯视图r*— 2—侧视图」、选择题1.(北京卷文)4.(全国卷一文)(5)已知圆柱的上、下底面的中心分别为O i , O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积8的正方形,则该圆柱的表面积为5.(全国卷一文)(9)某圆柱的高为2,底面周长为16,其三视图如右图•圆柱表面上的点 M 在正视图上的对应点为 A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱侧面上,从 M 到N 的路径中,最短路径的长度为A . 2 17 C . 36.(全国卷一文)(10)在长方体ABCD-AB 1C 1D 1中,AB 二BC=2 , AG 与平面BBGC 所成的角为30,则该长方体的体积为 A . 8B . 6、2C . 8.2D •7 .(全国卷一理)(7)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点 M 在正视图上的对应点为A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A . 2.178 (全国卷一理)(12)已知正方体的棱长为 1,每条棱所在直线与平面 体所得截面面积的最大值为 A .二4B .二 39. (全国卷二文)(9)在正方体 ABCD -AB 1C 1D 1中,E 为棱C 。
的中点,则异面直线 AE 与CD 所成角 的正切值为12.2 nB . 12 nC .D . 10 nB . 2.5 D . 2D . 2a 所成的角相等,则 a 截此正方恵43 45 47 A• T B• T C• 2 D•210. (全国卷~理) (9)在长方体ABCD 一 AB 1C 1D 1中,AB 二BC 二1 , AA 13,则异面直线 AD 1与DB 1所成角的余弦值为11. (全国卷三文)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯 眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则 咬合时带卯眼的木构件的俯视图可以是形且其面积为 9 3,则三棱锥D-ABC 体积的最大值为13.(全国卷三理)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯 眼,图中木构件右边的小长方体是榫头•若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则 咬合时带卯眼的木构件的俯视图可以是12.(全国卷三文)(12)设 A , B , C , D 是同一个半径为 4的球的球面上四点, △ ABC 为等边三角A . 12、.3B . 183C . 24.3D . 54 36A C10)设A , B , C , D是同一个半径为4的球的球面上四点,△ ABC为等边三角形且14 .(全国卷三理)其面积为9 3,则三棱锥D - ABC体积的最大值为第(打)题图3. (天津理)(11)已知正方体 ABCD - ABC 1D 1的棱长为1,除面ABCD 夕卜,该正方体其余各面的中心分别为点E , F , G , H , M (如图),则四棱锥 M -EFGH 的体积为 ___________第(11)腔團A . 12..3B . 18.3 二、填空题1.(江苏)(10)如图所示,正方体的棱长为C . 24 3D . 54 . 32,以其所有面的中心为顶点的多面体的体积为 ____________(第1()题)2.(天津文)ABCD -\1B 1C 1D 1的棱长为1,则四棱柱 A 1 -BB 1D 1D 的体积为4. (全国卷二文)(16)已知圆锥的顶点为 S ,母线SA , SB 互相垂直,SA 与圆锥底面所成角为30,若△ SB的面积为8,则该圆锥的体积为 ____________ .5. (全国卷二理)(16)已知圆锥的顶点为 S ,母线SA ,SB 所成角的余弦值为-,SA 与圆锥底面所成角8为45°若厶SAB 的面积为5丽,则该圆锥的侧面积为 ________________ .三、解答题1.(北京文)(18)(本小题14分)如图,在四棱锥 P-ABCD 中,底面 ABCD 为矩形,平面 PAD 丄平面 ABCD ,PA 丄PD ,PA=PD ,E ,F 分别为AD ,PB 的中点.2.(北京理)(16)(本小题14 分) 如图,在三棱柱 ABC-ABG 中, CG _平面 ABC,D,E, F,G 分别为 AA, ,AC, AC 1,BB 1 的中点,AB=BC=・. 5,AC= AA =2.(I )求证:AC 丄平面BEF ; ( n )求二面角 B-CD-C 1的余弦值;(川)证明:直线 FG 与平面BCD 相交.C1(I )求证:PE 丄BC ; (H )求证:平面FAB 丄平面PCD ;(川)求证:EF //平面 PCD.B3.(江苏)(15)(本小题满分14分)《第15题)在平行六面体ABCD _A i B i CQ i 中,AA =AB, AR _ RG .求证:(1)AB//平面A i B i C ; (2)平面ABB1A1 _平面ABC .4.(浙江)(19)(本题满分15分)如图,已知多面体ABCA1B1C1, A A, B i B, C i C均垂直于平面ABC,/ ABC=120°, A1A=4, C1C=1 , AB=BC=B1B=2 .(I)证明:AB1丄平面A1B1C仁(H)求直线AC1与平面ABB1所成的角的正弦值.5.(天津文)(17)(本小题满分13分)如图,在四面体ABCD中,△ ABC是等边三角形,平面ABC丄平面ABD,点M为棱AB的中点,AB=2, AD=2 3,/ BAD=90 ° .(I )求证:AD丄BC;(H )求异面直线BC与MD所成角的余弦值;(川)求直线CD与平面ABD所成角的正弦值.(2) Q为线段AD上一点,2 P在线段BC上,且艸心严,6. (天津理)(17)(本小题满分13分)如图,AD// BC 且AD=2BC, AD _ CD , EG// AD 且EG=AD , CD// FG 且CD=2FG,DG _ 平面ABCD , DA=DC=DG=2.(I)若M为CF的中点,N为EG的中点,求证:MN //平面CDE ;(II )求二面角E — BC —F的正弦值;(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.7. (全国卷一文)(18)( 12分)如图,在平行四边形ABCM中,AB =AC =3,/ ACM =90,以AC为折痕将厶ACM折起, 使点M到达点D 的位置,且AB丄DA .(1)证明:平面ACD丄平面ABC ;A求三棱锥Q-ABP的体积.8. (全国卷一理)(18)(12分)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△ DFC折起, 使点C到达点P的位置,且PF _ BF .(1)证明:平面PEF —平面ABFD ;(2)求DP与平面ABFD所成角的正弦值.9. (全国卷二文)(19)(12分)如图,在三棱锥P - ABC 中,AB=BC=2.2,PA =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO _平面ABC ;(2)若点M在棱BC上,且MC =2MB,求点C到平面POM的距离.10. (全国卷二理)(20)(12分)如图,在三棱锥P -ABC 中,AB 二BC=2..2,PA 二PB 二PC 二AC = 4,O 为AC 的中点.(1)证明:PO _平面ABC ;(2)若点M在棱BC上,且二面角M -PA-C为30,求PC与平面PAM所成角的正弦值.11. (全国卷三文)(19)(12分)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C , D的点.(1)证明:平面AMD丄平面BMC ;(2)在线段AM上是否存在点P,使得MC //平面PBD ?说明理由.C12.(全国卷三理)(19)(12分)如图, D的点.(1)(2) 边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,证明:平面AMD丄平面BMC ;当三棱锥M —ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.。
2018年数学(文科)高考题分类 真题与模拟题 立体几何

G单元立体几何G1 空间几何体的结构5.G1[2018·全国卷Ⅰ]已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A. 12√2πB. 12πC. 8√2πD. 10π5.B[解析] 因为圆柱的轴截面是正方形,且面积为8,所以圆柱的高为2√2,底面直径为2√2,所以圆柱的表面积S=2π×√2×2√2+2×π×(√2)2=12π.故选B.16.G1[2018·全国卷Ⅱ]已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为.16.8π[解析] 如图所示,设圆锥的底面圆的圆心为O,母线长为l,则1l2=8,解得l=4,即SA=4.2连接OS,OA,因为SA与圆锥底面所成的角为30°,所以SO=2.在直角三角形SOA 中,AO=√SA2-SO2=√42-22=2√3,所以圆锥的体积V=1×π×(2√3)2×2=8π.3G2 空间几何体的三视图和直观图9.G2[2018·全国卷Ⅰ]某圆柱的高为2,底面周长为16,其三视图如图1-2所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()图1-2A. 2√17B. 2√5C. 3D. 29.B[解析] 由三视图可知圆柱表面上点M,N的位置如图①,将圆柱的侧面展开得到图②.在圆柱侧面上,从M到N的路径中,最短路径即为侧面展开图中的线段MN ,MN=√22+(164)2=2√5,故选B .3.G2[2018·全国卷Ⅲ] 中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图1-1中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )图1-1图1-23.A [解析] 卯眼的空间立体图如图,同时需要注意在三视图中,看不见的线用虚线表示,故选A .3.G2[2018·全国卷Ⅲ] 中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图1-1中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )图1-1图1-23.A[解析] 卯眼的空间立体图如图,同时需要注意在三视图中,看不见的线用虚线表示,故选A.3.G2[2018·浙江卷]某几何体的三视图如图1-1所示(单位:cm),则该几何体的体积(单位:cm3)是()图1-1A. 2B. 4C. 6D. 83.C[解析] 该几何体为直四棱柱,如图所示,底面是直角梯形,其面积为1×(1+2)×2=3,又四棱2柱的高为2,故体积为2×3=6,故选C.G3 平面的基本性质、空间两条直线17.G3、G5[2018·天津卷] 如图1-4,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB=2,AD=2√3,∠BAD=90°. (1)求证:AD ⊥BC ;(2)求异面直线BC 与MD 所成角的余弦值; (3)求直线CD 与平面ABD 所成角的正弦值.图1-417.解:(1)证明:由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD=AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC.(2)取棱AC 的中点N ,连接MN ,ND. 因为M 为棱AB 的中点,故MN ∥BC ,所以∠DMN (或其补角)为异面直线BC 与MD 所成的角. 在Rt △DAM 中,AM=1,故DM=√AD 2+AM 2=√13. 因为AD ⊥平面ABC ,故AD ⊥AC.在Rt △DAN 中,AN=1,故DN=√AD 2+AN 2=√13. 在等腰三角形DMN 中,MN=1,可得cos ∠DMN=12MN DM=√1326. 所以,异面直线BC 与MD 所成角的余弦值为√1326.(3)连接CM.因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM=√3. 又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD , 所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt△CAD中,CD=√AC2+AD2=4.在Rt△CMD中,sin∠CDM=CMCD =√34.所以,直线CD与平面ABD所成角的正弦值为√34.G4 空间中的平行关系19.G5,G4[2018·全国卷Ⅲ]如图1-5,矩形ABCD所在平面与半圆弧CD⏜所在平面垂直,M是CD⏜上异于C,D的点.(1)证明:平面AMD⊥平面BMC.(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.图1-519.解:(1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD⏜上异于C,D的点,且DC为直径,所以DM⊥CM.又BC∩CM=C,所以DM⊥平面BMC.而DM⊂平面AMD,故平面AMD⊥平面BMC.(2)当P为AM的中点时,MC∥平面PBD.证明如下:连接AC交BD于O.因为四边形ABCD为矩形,所以O为AC中点.连接OP,因为P 为AM中点,所以MC∥OP.MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.6.G4[2018·浙江卷]已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.A[解析] 因为m在平面α外,n在平面α内,所以若m∥n,则m∥α;反之,若m∥α,则m和n 可能平行或异面.故“m∥n”是“m∥α”的充分不必要条件,故选A.15.G4,G5[2018·江苏卷]在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.图1-415.证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.18.G4、G5[2018·北京卷]如图1-4,在四棱锥P-ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A⊥PD,P A=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面P AB⊥平面PCD;(3)求证:EF∥平面PCD.图1-418.证明:(1)∵P A=PD,且E为AD的中点,∴PE⊥AD.∵底面ABCD为矩形,∴BC∥AD,∴PE⊥BC.(2)∵底面ABCD为矩形,∴AB⊥AD.∵平面P AD⊥平面ABCD,∴AB⊥平面P AD,∴AB⊥PD.又P A⊥PD,∴PD⊥平面P AB,∴平面P AB⊥平面PCD.(3)如图,取PC的中点G,连接FG,GD.∵F,G分别为PB和PC的中点,∴FG∥BC且FG=1BC.2∵四边形ABCD为矩形,且E为AD的中点,∴ED∥BC,ED=1BC,2∴ED∥FG且ED=FG,∴四边形EFGD为平行四边形,∴EF∥GD.又EF⊄平面PCD,GD⊂平面PCD,∴EF∥平面PCD.G5 空间中的垂直关系18.G5,G12[2018·全国卷Ⅰ]如图1-3所示,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=2DA,求三棱锥Q-ABP的体积.3图1-318.解:(1)证明:由已知可得,∠BAC=90°,BA ⊥AC. 又BA ⊥AD ,所以AB ⊥平面ACD.又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC. (2)由已知可得,DC=CM=AB=3,DA=3√2. 又BP=DQ=23DA ,所以BP=2√2. 作QE ⊥AC ,垂足为E ,则QE 13DC.由已知及(1)可知DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE=1.因此,三棱锥Q - ABP 的体积为V Q - ABP =13×QE×S △ABP =13×1×12×3×2√2sin 45°=1.19.G5,G12[2018·全国卷Ⅱ] 如图1-4,在三棱锥P-ABC 中,AB=BC=2√2,P A=PB=PC=AC=4,O 为AC 的中点.图1-4(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC=2MB ,求点C 到平面POM 的距离.19.解:(1)证明:因为AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2√3. 连接OB.因为AB=BC=√22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB=12AC=2. 由OP 2+OB 2=PB 2知,OP ⊥OB.由OP ⊥OB ,OP ⊥AC ,OB ∩AC=O 知PO ⊥平面ABC.(2)作CH ⊥OM ,垂足为H ,又由(1)可得OP ⊥CH ,OP ∩OM=O ,所以CH ⊥平面POM , 故CH 的长为点C 到平面POM 的距离. 由题设可知OC=12AC=2,CM=23BC=4√23,∠ACB=45°, 所以OM=2√53,CH=OC ·MC ·sin ∠ACB OM=4√55, 所以点C 到平面POM 的距离为4√55.19.G5,G4[2018·全国卷Ⅲ] 如图1-5,矩形ABCD 所在平面与半圆弧CD ⏜所在平面垂直,M 是CD ⏜上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC.(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.图1-519.解:(1)证明:由题设知,平面CMD ⊥平面ABCD ,交线为CD.因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM.因为M 为CD⏜上异于C ,D 的点,且DC 为直径,所以DM ⊥CM. 又BC ∩CM=C ,所以DM ⊥平面BMC. 而DM ⊂平面AMD ,故平面AMD ⊥平面BMC. (2)当P 为AM 的中点时,MC ∥平面PBD.证明如下:连接AC 交BD 于O.因为四边形ABCD 为矩形,所以O 为AC 中点.连接OP ,因为P 为AM 中点,所以MC ∥OP .MC ⊄平面PBD ,OP ⊂平面PBD ,所以MC ∥平面PBD.19.G5,G11,G12[2018·浙江卷]如图1-3所示,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.图1-3(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.19.解: 方法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2√2,所以A1B12+A B12=A A12, 故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=√5,由AB=BC=2,∠ABC=120°得AC=2√3,由CC1⊥AC,得AC1=√13,所以A B12+B1C12=A C12,故AB1⊥B1C1.因此AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.由B1C1=√5,A1B1=2√2,A1C1=√21得cos ∠C 1A 1B 1=√6√7,sin ∠C 1A 1B 1=√7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 15.G4,G5[2018·江苏卷] 在平行六面体ABCD - A 1B 1C 1D 1中,AA 1=AB ,AB 1⊥B 1C 1. 求证:(1)AB ∥平面A 1B 1C ; (2)平面ABB 1A 1⊥平面A 1BC.图1-415.证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.18.G4、G5[2018·北京卷]如图1-4,在四棱锥P-ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A⊥PD,P A=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面P AB⊥平面PCD;(3)求证:EF∥平面PCD.图1-418.证明:(1)∵P A=PD,且E为AD的中点,∴PE⊥AD.∵底面ABCD为矩形,∴BC∥AD,∴PE⊥BC.(2)∵底面ABCD为矩形,∴AB⊥AD.∵平面P AD⊥平面ABCD,∴AB⊥平面P AD,∴AB⊥PD.又P A⊥PD,∴PD⊥平面P AB,∴平面P AB⊥平面PCD.(3)如图,取PC的中点G,连接FG,GD.∵F,G分别为PB和PC的中点,∴FG∥BC且FG=1BC.2∵四边形ABCD为矩形,且E为AD的中点,∴ED∥BC,ED=1BC,2∴ED∥FG且ED=FG,∴四边形EFGD为平行四边形,∴EF∥GD.又EF⊄平面PCD,GD⊂平面PCD,∴EF∥平面PCD.17.G3、G5[2018·天津卷]如图1-4,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2√3,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.图1-417.解:(1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2)取棱AC的中点N,连接MN,ND.因为M为棱AB的中点,故MN∥BC,所以∠DMN(或其补角)为异面直线BC与MD所成的角.在Rt△DAM中,AM=1,故DM=√AD2+AM2=√13.因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,AN=1,故DN=√AD2+AN2=√13.在等腰三角形DMN 中,MN=1,可得cos ∠DMN=12MN DM =√1326. 所以,异面直线BC 与MD 所成角的余弦值为√1326.(3)连接CM.因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM=√3. 又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD , 所以,∠CDM 为直线CD 与平面ABD 所成的角. 在Rt △CAD 中,CD=√AC 2+AD 2=4. 在Rt △CMD 中,sin ∠CDM=CM CD =√34. 所以,直线CD 与平面ABD 所成角的正弦值为√34.G6 三垂线定理 G7 棱柱与棱锥11.G7[2018·天津卷] 如图1-3,已知正方体ABCD - A 1B 1C 1D 1的棱长为1,则四棱锥A 1 - BB 1D 1D 的体积为 .图1-311.13 [解析] 点A 1到平面BB 1D 1D 的距离为√22,四边形BB 1D 1D 的面积为√2,故四棱锥A 1 - BB 1D 1D 的体积为13×√2×√22=13.G8 多面体与球12.G8[2018·全国卷Ⅲ] 设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为9√3,则三棱锥D-ABC 体积的最大值为( )A .12√3B .18√3C.24√3D.54√312.B[解析] 由题易知当点D到平面ABC的距离最大时,三棱锥D-ABC的体积最大.∵S△ABC=√34AB2=9√3,∴AB=6.设△ABC的中心为M,由等边三角形的性质得,AM=BM=CM=2√3.设球心为O,则OA=OB=OC=4,∴OM=√OB2-BM2=2,∴点D到平面ABC的距离的最大值为OM+4=6.故三棱锥D-ABC体积的最大值为13×9√3×6=18√3.G9空间向量及运算G10 空间向量解决线面位置关系G11 空间角与距离的求法9.G11[2018·全国卷Ⅱ]在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD 所成角的正切值为()A. √22B. √32C. √52D. √729.C[解析] 如图,由AB∥CD,可知∠BAE即为异面直线AE与CD所成的角.设正方体的棱长为2,连接BE,则在Rt△ABE中,AB=2,BE=√BC2+CE2=√22+12=√5,tan∠BAE=BEAB =√52,故选C.8.G11[2018·浙江卷]已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ18.D[解析] 过S作SO⊥平面ABCD,连接OE,则θ2=∠SEO,sin θ2=SOSE.取AB的中点F,连接OF,则θ3=∠SFO,sin θ3=SOSF ,∵SE≥SF,∴sin θ2≤sin θ3,又θ2,θ3∈(0,π2),∴θ2≤θ3.作GE∥BC,OG⊥GE,连接SG,则GE⊥SG,θ1=∠SEG,tan θ1=SGGE ,∵OF=GE,SO≤SG,tan θ3=SOOF,∴tanθ3≤tan θ1,∴θ2≤θ3≤θ1,故选D.19.G55,G11,G12[2018·浙江卷]如图1-3所示,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.图1-3(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.19.解: 方法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2√2,所以A1B12+A B12=A A12, 故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=√5,由AB=BC=2,∠ABC=120°得AC=2√3,由CC1⊥AC,得AC1=√13,所以A B12+B1C12=A C12,故AB1⊥B1C1.因此AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB 1⊥平面A 1B 1C 1得平面A 1B 1C 1⊥平面ABB 1, 由C 1D ⊥A 1B 1得C 1D ⊥平面ABB 1, 所以∠C 1AD 是AC 1与平面ABB 1所成的角. 由B 1C 1=√5,A 1B 1=2√2,A 1C 1=√21得 cos ∠C 1A 1B 1=√67,sin ∠C 1A 1B 1=7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913.因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 22.G11[2018·江苏卷] 如图1-8所示,在正三棱柱ABC - A 1B 1C 1中,AB=AA 1=2,点P ,Q 分别为A 1B 1,BC 的中点.(1)求异面直线BP 与AC 1所成角的余弦值; (2)求直线CC 1与平面AQC 1所成角的正弦值.图1-822.解:如图,在正三棱柱ABC - A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以{OB ⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗ }为基底,建立空间直角坐标系O - xyz. 因为AB=AA 1=2,所以A (0,-1,0),B (√3,0,0),C (0,1,0),A 1(0,-1,2),B 1(√3,0,2),C 1(0,1,2).(1)因为P 为A 1B 1的中点,所以P √32,-12,2,从而BP ⃗⃗⃗⃗⃗ =-√32,-12,2,AC 1⃗⃗⃗⃗⃗⃗ =(0,2,2), 故|cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗⃗ ·AC1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||BP ⃗⃗⃗⃗⃗⃗ |·|AC1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=√5×2√2=3√1020. 因此,异面直线BP 与AC 1所成角的余弦值为3√1020. (2)因为Q 为BC 的中点,所以Q√32,12,0,因此AQ⃗⃗⃗⃗⃗ =√32,32,0,AC 1⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗ =(0,0,2).设n=(x ,y ,z )为平面AQC 1的一个法向量,则{AQ ⃗⃗⃗⃗⃗ ·n =0,AC 1⃗⃗⃗⃗⃗⃗⃗ ·n =0,即{√32x +32y =0,2y +2z =0. 不妨取n=(√3,-1,1),设直线CC 1与平面AQC 1所成的角为θ,则sin θ=|cos <CC 1⃗⃗⃗⃗⃗⃗ ,n>|=|CC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||CC 1⃗⃗⃗⃗⃗⃗⃗⃗|·|n|=√5×2=√55, 所以直线CC 1与平面AQC 1所成角的正弦值为√55.G12 单元综合10.G12[2018·全国卷Ⅰ] 在长方体ABCD - A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为 ( ) A . 8 B . 6√2 C . 8√2D . 8√310.C [解析] 如图,连接BC 1,易知∠AC 1B 即为AC 1与平面BB 1C 1C 所成的角,由题易知∠AC 1B=30°,易得AC 1=2AB=4.设BB 1=h ,则有42=22+22+h 2, 解得h=2√2,所以该长方体的体积V=2×2×2√2=8√2.18.G5,G12[2018·全国卷Ⅰ] 如图1-3所示,在平行四边形ABCM 中,AB=AC=3,∠ACM=90°.以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB ⊥DA. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且BP=DQ=23DA ,求三棱锥Q - ABP 的体积.图1-318.解:(1)证明:由已知可得,∠BAC=90°,BA ⊥AC. 又BA ⊥AD ,所以AB ⊥平面ACD.又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC. (2)由已知可得,DC=CM=AB=3,DA=3√2. 又BP=DQ=23DA ,所以BP=2√2. 作QE ⊥AC ,垂足为E ,则QE 13DC.由已知及(1)可知DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE=1.因此,三棱锥Q - ABP 的体积为V Q - ABP =13×QE×S △ABP =13×1×12×3×2√2sin 45°=1.19.G5,G12[2018·全国卷Ⅱ] 如图1-4,在三棱锥P-ABC 中,AB=BC=2√2,P A=PB=PC=AC=4,O 为AC 的中点.图1-4(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC=2MB ,求点C 到平面POM 的距离.19.解:(1)证明:因为AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2√3. 连接OB.因为AB=BC=√22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB=12AC=2.由OP 2+OB 2=PB 2知,OP ⊥OB.由OP ⊥OB ,OP ⊥AC ,OB ∩AC=O 知PO ⊥平面ABC.(2)作CH ⊥OM ,垂足为H ,又由(1)可得OP ⊥CH ,OP ∩OM=O ,所以CH ⊥平面POM , 故CH 的长为点C 到平面POM 的距离. 由题设可知OC=12AC=2,CM=23BC=4√23,∠ACB=45°, 所以OM=2√53,CH=OC ·MC ·sin ∠ACB OM=4√55, 所以点C 到平面POM 的距离为4√55.19.G55,G11,G12[2018·浙江卷] 如图1-3所示,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC=120°,A 1A=4,C 1C=1,AB=BC=B 1B=2.图1-3(1)证明:AB 1⊥平面A 1B 1C 1;(2)求直线AC 1与平面ABB 1所成的角的正弦值. 19.解: 方法一:(1)证明:由AB=2,AA 1=4,BB 1=2,AA 1⊥AB ,BB 1⊥AB 得AB 1=A 1B 1=2√2,所以A 1B 12+A B 12=A A 12,故AB 1⊥A 1B 1.由BC=2,BB 1=2,CC 1=1,BB 1⊥BC ,CC 1⊥BC 得B 1C 1=√5, 由AB=BC=2,∠ABC=120°得AC=2√3,由CC 1⊥AC ,得AC 1=√13,所以A B 12+B 1C 12=A C 12,故AB 1⊥B 1C 1.因此AB 1⊥平面A 1B 1C 1.(2)如图,过点C 1作C 1D ⊥A 1B 1,交直线A 1B 1于点D ,连接AD.由AB 1⊥平面A 1B 1C 1得平面A 1B 1C 1⊥平面ABB 1, 由C 1D ⊥A 1B 1得C 1D ⊥平面ABB 1, 所以∠C 1AD 是AC 1与平面ABB 1所成的角. 由B 1C 1=√5,A 1B 1=2√2,A 1C 1=√21得 cos ∠C 1A 1B 1=√67,sin ∠C 1A 1B 1=7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913.因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 10.G12[2018·江苏卷] 如图1-3所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .图1-310.43 [解析] 该几何体是一个正八面体,而正八面体是由两个相同的正四棱锥组成的,由图可知一个正四棱锥的高为1,底面边长为12√22+22=√2,所以正八面体的体积V=2×13×(√2)2×1=43.1.[2018·衡阳八中月考] 如图K31-3,ABCD -A 1B 1C 1D 1为正方体,给出下列结论:①BD ∥平面CB 1D 1;②AC 1⊥BD ;③AC 1⊥平面CB 1D 1;④B 1D 1与BC 所成的角为45°.其中正确结论的个数是( )A .1B .2C .3D .4图K31-3图K31-41.D[解析]对于①,由正方体的性质得BD∥B1D1,所以BD∥平面CB1D1,故①中结论正确;对于②,连接AC,由正方体的性质得AC⊥BD,而AC是AC1在底面ABCD内的投影,可得AC1⊥BD,故②中结论正确;对于③,由正方体的性质得BD∥B1D1,由②知AC1⊥BD,所以AC1⊥B1D1,同理可证AC1⊥CB1,故AC1垂直于平面CB1D1内的两条相交直线,所以AC1⊥平面CB1D1,故③中结论正确;对于④,异面直线B1D1与BC所成的角就是直线BC与BD所成的角,故∠CBD即为异面直线B1D1与BC所成的角,在等腰直角三角形BCD中,∠CBD=45°,故B1D1与BC所成的角为45°,故④中结论正确.故选D.2.[2018·桂林、百色、梧州、崇左、北海五市联合模拟]如图K33-11,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.(1)证明:平面AEF⊥平面ACC1A1;(2)若AB=EC=2,求三棱锥C-AEF的体积.图K33-11EC=BF,又2.解:(1)证明:取线段AE的中点G,线段AC的中点M,连接MG,GF,BM,则MG=12MG∥EC∥BF,∴四边形MBFG是平行四边形,故MB∥FG.∵△ABC为正三角形,M为AC的中点,∴MB⊥AC,又平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,∴MB⊥平面ACC1A1,而MB∥FG,∴FG⊥平面ACC1A1,又∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1.(2)由(1)得FG⊥平面AEC,FG=BM=√3,所以VCAEF =VFACE=13×S△ACE·FG=13×12×2×2×√3=2√33.3.[2018·石家庄质检]如图K32-9,在四棱锥P-ABCD中,底面ABCD为正方形,且PA⊥底面ABCD,过AB的平面与侧面PCD的交线为EF,且满足S△PEF∶S四边形CDEF=1∶3(S△PEF表示△PEF的面积).(1)证明:PB∥平面ACE;(2)当PA=2AD=2时,求点F到平面ACE的距离.图K32-93.解:(1)证明:由题知四边形ABCD为正方形,∴AB∥CD,又CD⊂平面PCD,AB⊄平面PCD,∴AB∥平面PCD,又AB⊂平面ABFE,平面ABFE∩平面PCD=EF,∴EF∥AB,又AB∥CD,∴EF∥CD.又由S△PEF∶S四边形CDEF=1∶3知E,F分别为PD,PC的中点.连接BD交AC 与点G,则G为BD的中点.连接EG,在△PBD中,EG为中位线,∴EG∥PB.∵EG⊂平面ACE,PB⊄平面ACE,∴PB∥平面ACE.(2)连接AF .∵P A=2,AD=AB=1,∴AC=√2,AE=12PD=√52.∵CD ⊥AD ,CD ⊥P A ,AD ∩P A=A ,∴CD ⊥平面P AD ,∴CD ⊥PD.在Rt △CDE 中,CE=√CD 2+DE 2=32.在△ACE 中,由余弦定理知cos ∠AEC=AE 2+CE 2-AC 22AE ·CE =√55,∴sin ∠AEC=2√55,∴S △ACE =12AE ·CE ·sin ∠AEC=34.设点F 到平面ACE 的距离为h ,则V FACE =13×34×h=14h.由DG ⊥AC ,DG ⊥P A ,AC ∩P A=A ,得DG ⊥平面P AC ,且DG=√22.∵E 为PD 的中点,∴E 到平面ACF 的距离为12DG=√24,又F 为PC 的中点,∴S △ACF =12S △ACP =√22,∴V EACF =13×√22×√24=112.由V FACE =V EACF 知h=13,∴点F 到平面ACE 的距离为13.。
2018年高考数学试题分类汇编之立体几何

2018年高考数学试题分类汇编之立体几何(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年高考数学试题分类汇编之立体几何(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年高考数学试题分类汇编之立体几何(word版可编辑修改)的全部内容。
2018年高考数学试题分类汇编之立体几何一、选择题1.(北京卷文)(6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )。
(A )1(B )2 (C )3(D )42.(北京卷理)(5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(A )1(B)2 (C)3(D )43.(浙江)(3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是侧侧侧侧侧侧A .2B .4C .6D .84.(全国卷一文)(5)已知圆柱的上、下底面的中心分别为,,过直线的平面截该1O 2O 12O O 圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A .B .C .D .12π10π5.(全国卷一文)(9)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为,圆柱表面上的点在左A N 视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短B M N 路径的长度为A .B .C .D .236.(全国卷一文)(10)在长方体中,,与平面所成的角1111ABCD A B C D -2AB BC ==1AC 11BB C C 为,则该长方体的体积为30︒A .B .C .D .87.(全国卷一理)(7)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点在M 正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,A N B 从到的路径中,最短路径的长度为M NA .B .C .3D .2172528.(全国卷一理)(12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C D9.(全国卷二文)(9)在正方体中,为棱的中点,则异面直线与所1111ABCD A B C D -E 1CC AE CD 成角的正切值为A B .C D10.(全国卷二理)(9)在长方体中,,则异面直线与1111ABCD A B C D -1AB BC ==1AA =1AD 1DB 所成角的余弦值为A .BCD 1511.(全国卷三文)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是12.(全国卷三文)(12)设,,,是同一个半径为4的球的球面上四点,为等边A B C D ABC △三角形且其面积为,则三棱锥体积的最大值为D ABC -A .B .C .D .13.(全国卷三理)(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是14.(全国卷三理)(10)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为则三棱锥D ABC -体积的最大值为A .B .C .D .二、填空题1.(江苏)(10)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .2.(天津文)(11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.3.(天津理)(11) 已知正方体的棱长为1,除面外,该正方体其余各面1111ABCD A B C D -ABCD 的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥的体积为 .M EFGH -4.(全国卷二文)(16)已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为S SA SB SA 30︒,若的面积为,则该圆锥的体积为__________.SAB △85.(全国卷二理)(16)已知圆锥的顶点为,母线,所成角的余弦值为,与圆锥S SA SB 78SA 底面所成角为45°,若的面积为,则该圆锥的侧面积为__________.SAB △三、解答题1.(北京文)(18)(本小题14分)如图,在四棱锥P—ABCD 中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA ⊥PD ,PA =PD ,E ,F 分别为AD ,PB 的中点.(Ⅰ)求证:PE ⊥BC ;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证:EF ∥平面PCD 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年全国高考文科数学分类汇编——立体几何1.(北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(C)A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC=,CD=,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.2.(北京)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(Ⅰ)求证:PE⊥BC;(Ⅱ)求证:平面PAB⊥平面PCD;(Ⅲ)求证:EF∥平面PCD.【解答】证明:(Ⅰ)PA=PD,E为AD的中点,可得PE⊥AD,底面ABCD为矩形,可得BC∥AD,则PE⊥BC;(Ⅱ)由于平面PAB和平面PCD有一个公共点P,且AB∥CD,在平面PAB内过P作直线PG ∥AB,可得PG∥CD,即有平面PAB∩平面PCD=PG,由平面PAD⊥平面ABCD,又AB⊥AD,可得AB⊥平面PAD,即有AB⊥PA,PA⊥PG;同理可得CD⊥PD,即有PD⊥PG,可得∠APD为平面PAB和平面PCD的平面角,由PA⊥PD,可得平面PAB⊥平面PCD;(Ⅲ)取PC的中点H,连接DH,FH,在三角形PCD中,FH为中位线,可得FH∥BC,FH=BC,由DE∥BC,DE=BC,可得DE=FH,DE∥FH,四边形EFHD为平行四边形,可得EF∥DH,EF⊄平面PCD,DH⊂平面PCD,即有EF∥平面PCD.3.(江苏)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.4. (江苏)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.【解答】证明:(1)平行六面体ABCD﹣A1B1C1D1中,AB∥A1B1,⇒AB∥平面A1B1C;(2)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,⇒四边形ABB1A1是菱形,⊥AB1⊥A1B.在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1⇒AB1⊥BC.∴⇒AB1⊥面A1BC,且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC.5.(全国1卷)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12πB.12πC.8πD.10π【解答】解:设圆柱的底面直径为2R,则高为2R,圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,可得:4R2=8,解得R=,则该圆柱的表面积为:=10π.故选:D.6.(全国1卷)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N 的路径中,最短路径的长度为()BA.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.故选:B.7.(全国1卷)在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为()CA.8 B.6C.8D.8【解答】解:长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,即∠AC1B=30°,可得BC1==2.可得BB1==2.所以该长方体的体积为:2×=8.故选:C.8.(全国1卷)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM 折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q﹣ABP的体积.【解答】解:(1)证明:∵在平行四边形ABCM中,∠ACM=90°,∴AB⊥AC,又AB⊥DA.且AD∩AB=A,∴AB⊥面ADC,∴AB⊂面ABC,∴平面ACD⊥平面ABC;(2)∵AB=AC=3,∠ACM=90°,∴AD=AM=3,∴BP=DQ=DA=2,由(1)得DC⊥AB,又DC⊥CA,∴DC⊥面ABC,∴三棱锥Q﹣ABP的体积V==××==1.9.(全国2卷)在正方体ABCD﹣A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为()CA.B.C.D.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1棱长为2,则A(2,0,0),E(0,2,1),D(0,0,0),C(0,2,0),=(﹣2,2,1),=(0,﹣2,0),设异面直线AE与CD所成角为θ,则cosθ===,sinθ==,∴tanθ=.∴异面直线AE与CD所成角的正切值为.故选:C.10.(全国2卷)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为8π.【解答】解:圆锥的顶点为S,母线SA,SB互相垂直,△SAB的面积为8,可得:,解得SA=4,SA与圆锥底面所成角为30°.可得圆锥的底面半径为:2,圆锥的高为:2,则该圆锥的体积为:V==8π.故答案为:8π.11. (全国2卷)如图,在三棱锥P﹣ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.【解答】(1)证明:∵AB=BC=2,AC=4,∴AB2+BC2=AC2,即△ABC是直角三角形,又O为AC的中点,∴OA=OB=OC,∵PA=PB=PC,∴△POA≌△POB≌△POC,∴∠POA=∠POB=∠POC=90°,∴PO⊥AC,PO⊥OB,OB∩AC=0,∴PO⊥平面ABC;(2)解:由(1)得PO⊥平面ABC,PO=,在△COM中,OM==.S=××=,S△COM==.=V C﹣POM⇒,设点C到平面POM的距离为d.由V P﹣OMC解得d=,∴点C到平面POM的距离为.12.(全国3卷)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()AA.B.C.D.【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A.故选:A.13.(全国3卷)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D﹣ABC体积的最大值为()A.12B.18C.24D.54【解答】解:△ABC为等边三角形且面积为9,可得,解得AB=6,球心为O,三角形ABC 的外心为O′,显然D在O′O的延长线与球的交点如图:O′C==,OO′==2,则三棱锥D﹣ABC高的最大值为:6,则三棱锥D﹣ABC体积的最大值为:=18.故选:B.14.(全国3卷)如图,矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D 的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.【解答】(1)证明:矩形ABCD所在平面与半圆弦所在平面垂直,所以AD⊥半圆弦所在平面,CM⊂半圆弦所在平面,∴CM⊥AD,M是上异于C,D的点.∴CM⊥DM,DM∩AD=D,∴CD⊥平面AMD,CD⊂平面CMB,∴平面AMD⊥平面BMC;(2)解:存在P是AM的中点,理由:连接BD交AC于O,取AM的中点P,连接OP,可得MC∥OP,MC⊄平面BDP,OP⊂平面BDP,所以MC∥平面PBD.15.(上海)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设AA1是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以AA1为底面矩形的一边,则这样的阳马的个数是()CA.4 B.8 C.12 D.16【解答】解:根据正六边形的性质可得D1F1⊥A1F1,C1A1⊥A1F1,D1B1⊥A1B1,E1A1⊥A1B1,则D1﹣A1ABB1,D1﹣A1AFF1满足题意,而C1,E1,C,D,E和D1一样,故有2×6=12,故选:C.16.(上海)已知圆锥的顶点为P,底面圆心为O,半径为2.(1)设圆锥的母线长为4,求圆锥的体积;(2)设PO=4,OA、OB是底面半径,且∠AOB=90°,M为线段AB的中点,如图.求异面直线PM与OB所成的角的大小.【解答】解:(1)∵圆锥的顶点为P,底面圆心为O,半径为2,圆锥的母线长为4,∴圆锥的体积V===.(2)∵PO=4,OA,OB是底面半径,且∠AOB=90°,M为线段AB的中点,∴以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,P(0,0,4),A(2,0,0),B(0,2,0),M(1,1,0),O(0,0,0),=(1,1,﹣4),=(0,2,0),设异面直线PM与OB所成的角为θ,则cosθ===.∴θ=arccos.∴异面直线PM与OB所成的角的为arccos .17.(天津)如图,已知正方体ABCD﹣A1B1C1D1的棱长为1,则四棱锥A1﹣BB1D1D的体积为.【解答】解:由题意可知四棱锥A1﹣BB1D1D的底面是矩形,边长:1和,四棱锥的高:A1C1=.则四棱锥A1﹣BB1D1D的体积为:=.故答案为:.18.(天津)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2,∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.【解答】(Ⅰ)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,得AD⊥平面ABC,故AD⊥BC;(Ⅱ)解:取棱AC的中点N,连接MN,ND,∵M为棱AB的中点,故MN∥BC,∴∠DMN(或其补角)为异面直线BC与MD所成角,在Rt△DAM中,AM=1,故DM=,∵AD⊥平面ABC,故AD⊥AC,在Rt△DAN中,AN=1,故DN=,在等腰三角形DMN中,MN=1,可得cos∠DMN=.∴异面直线BC与MD所成角的余弦值为;(Ⅲ)解:连接CM,∵△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=,又∵平面ABC⊥平面ABD,而CM⊂平面ABC,故CM⊥平面ABD,则∠CDM为直线CD与平面ABD所成角.在Rt△CAD中,CD=,在Rt△CMD中,sin∠CDM=.∴直线CD与平面ABD所成角的正弦值为.19.(浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()CA.2 B.4 C.6 D.8【解答】解:根据三视图:该几何体为底面为直角梯形的四棱柱.如图所示:故该几何体的体积为:V=.故选:C.20.(浙江)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的()A A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:∵m⊄α,n⊂α,∴当m∥n时,m∥α成立,即充分性成立,当m∥α时,m∥n不一定成立,即必要性不成立,则“m∥n”是“m∥α”的充分不必要条件.故选:A.21.(浙江)已知四棱锥S﹣ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S﹣AB﹣C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1【解答】解:∵由题意可知S在底面ABCD的射影为正方形ABCD的中心.过E作EF∥BC,交CD于F,过底面ABCD的中心O作ON⊥EF交EF于N,连接SN,取CD中点M,连接SM,OM,OE,则EN=OM,则θ1=∠SEN,θ2=∠SEO,θ3=∠SMO.显然,θ1,θ2,θ3均为锐角.∵tanθ1==,tanθ3=,SN≥SO,∴θ1≥θ3,又sinθ3=,sinθ2=,SE≥SM,∴θ3≥θ2.故选:D.22.(浙江)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=l,AB=BC=B1B=2.(Ⅰ)证明:AB1⊥平面A1B1C1;(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.【解答】(I)证明:∵A1A⊥平面ABC,B1B⊥平面ABC,∴AA1∥BB1,∵AA1=4,BB1=2,AB=2,∴A1B1==2,又AB1==2,∴AA12=AB12+A1B12,∴AB1⊥A1B1,同理可得:AB1⊥B1C1,又A1B1∩B1C1=B1,∴AB1⊥平面A1B1C1.(II)解:取AC中点O,过O作平面ABC的垂线OD,交A1C1于D,∵AB=BC,∴OB⊥OC,∵AB=BC=2,∠BAC=120°,∴OB=1,OA=OC=,以O为原点,以OB,OC,OD所在直线为坐标轴建立空间直角坐标系如图所示:则A(0,﹣,0),B(1,0,0),B1(1,0,2),C1(0,,1),∴=(1,,0),=(0,0,2),=(0,2,1),设平面ABB1的法向量为=(x,y,z),则,∴,令y=1可得=(﹣,1,0),∴cos<>===.设直线AC1与平面ABB1所成的角为θ,则sinθ=|cos<>|=.∴直线AC1与平面ABB1所成的角的正弦值为.。
