竖曲线要素表计算
竖曲线要素及变坡点处设计高程计算

竖曲线要素及变坡点处设计高程计算 坡度计算:①坡度=高差坡长②竖曲线类型:当1n n i i +-为正值时,为凹型竖曲线; 当1n n i i +-为负值时,为凸型竖曲线。
③由厘米坐标纸上,经过反复试坡、调坡, 根据土石方填挖大致平衡和道。
设计规范中最小坡长等设计要求最后确定出变坡点: 变坡点1桩号:67.2550+K ,高程m 9404.0- 变坡点计算 ①变坡点一:桩号 67.2550+K , %150.0-i 1= %220.0i 2= R= 变坡点高程:m 9404.0- A.计算竖曲线要素:=-=1i 2i ω% 此时根据规范可知:该曲线为凹形曲线竖曲线几何要素中曲线长)(m R L 80%37.021621=⨯=⨯=ω 竖曲线几何要素中切线长m L T 402802=== 竖曲线几何要素中外距m R T E 037.062.21621240222=⨯==B.计算竖曲线起终点桩号 竖曲线起点桩号:67.2150+K竖曲线起点高程:m 8804.0-%15.0409404.0-=⨯+ 竖曲线终点桩号:67.2950+K竖曲线终点高程:m 8524.0-%22.0409404.0-=⨯+计算设计高程由110()H H T X i =-- H=H 1±hH 1:任一点切线的高程 x :计算点到起点的距离 i 1:坡度H:任一点的设计高程曲线段内各点的设计高程: K0+220X== m Rx y 0004.022== 切线高程: 设计高程:+= K0+240X= m Rx y 0137.022== 切线高程: 设计高程:+= K0+260X= m Rx y 0294.022== 切线高程: 设计高程:+= K0+280X= m Rx y 0057.022== 切线高程: 设计高程:+=直线段内各点设计高程见下表:设计高程表 桩号 高程(m )桩号高程(m )K0+000 ++ + ++++ ++ ++ ++ ++ ++ ++ ++ ++。
竖曲线运算步骤及公式讲解

1 / 2
竖曲线上高程计算
已知:①第一坡度:i 1(上坡为“+”,下坡为“-”)
②第二坡度:i 2(上坡为“+”,下坡为“-”)
③变坡点桩号:S Z
④变坡点高程:H Z
⑤竖曲线的切线长度:T
⑥待求点桩号:S
计算过程:
1、切线上任意点与竖曲线间的竖距h 通过推导可得:
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长: L = R ω
3.竖曲线切线长: T= T A =T B ≈ L/2 =
2
ωR 4、竖曲线的外距: E =R T 22
5. 竖曲线上任意点至相应切线的距离:R
x y 22
= 式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m ;
R —为竖曲线的半径,m 。
竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高,其计算步骤
如下:
(1)计算竖曲线的基本要素:竖曲线长:L ;切线长:T ;外距:E 。
(2)计算竖曲线起终点的桩号: 竖曲线起点的桩号 = 变坡点的桩号-T
(3)计算竖曲线上任意点切线标高及改正值:
切线标高 = 变坡点的标高±(x T -)⨯i ;改正值:y=R
x 22 (4)计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y
某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高- y
-----精心整理,希望对您有所帮助!。
纵断面设计——竖曲线设计

纵断面设计——竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i1 和i2,则相邻两坡度的代数差即转坡角为ω= i1-i2 ,其中i1、i2为本身之值,当上坡时取正值,下坡时取负值。
当i1- i2为正值时,则为凸形竖曲线。
当i1 - i2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:若取抛物线参数为竖曲线的半径,则有:(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距通过推导可得:2、竖曲线曲线长:L = Rω3、竖曲线切线长:T= TA =TB ≈ L/2 =4、竖曲线的外距:E =⑤竖曲线上任意点至相应切线的距离:式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R—为竖曲线的半径,m。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素(1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
因此,汽车在凸形竖曲线上行驶的时间不能太短,通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。
(3)满足视距的要求汽车行驶在凸形竖曲线上,如果竖曲线半径太小,会阻挡司机的视线。
为了行车安全,对凸形竖曲线的最小半径和最小长度应加以限制。
道路竖曲线计算

第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i 1 和i 2,则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ,其中i 1、i 2为本身之值,当上坡时取正值,下坡时取负值。
当 i 1- i 2为正值时,则为凸形竖曲线。
当 i 1 - i 2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为: 若取抛物线参数P 为竖曲线的半径 R ,则有: (二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得:2、竖曲线曲线长: L = R ω3、竖曲线切线长: T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距: E =RT 22⑤竖曲线上任意点至相应切线的距离:Rx y 22=式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m ;R —为竖曲线的半径,m 。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 (1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
因此,汽车在凸形竖曲线上行驶的时间不能太短,通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。
(3)满足视距的要求汽车行驶在凸形竖曲线上,如果竖曲线半径太小,会阻挡司机的视线。
平曲线要素计算公式
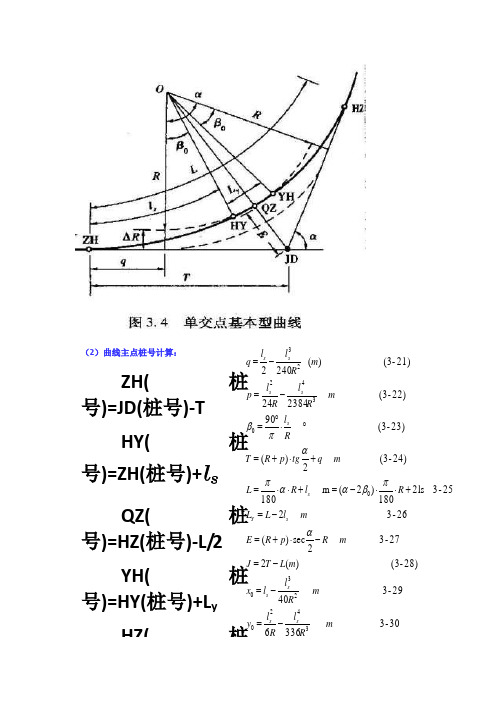
(2)曲线主点桩号计算:ZH(桩号)=JD(桩号)-T HY(桩号)=ZH(桩号)+ls QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩30-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 24023420230034223m Rl R l y m R l l x m L T J m R p R E m l L L R l R L m q tg p R T Rl m R l R l p m R l l q s s sss Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:[例1]、某山岭区二级公路,变坡点桩号为K5+030.00,高程为427.68m,i1=+5%,i2=-4%,竖曲线半径R=2000m。
试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程。
解:1.计算竖曲线要素ω= |i2-i1|= |-0.04-0.05| =0.09,为凸型。
曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=(K5+030.00)-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=(K5+030.00)+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处:横距K5x 1=(K5+ 000.00)-(K4+940.00)=60m 竖距h 1=x 12/2R=602/2×2000=0.90m 切线高程=427.68-(90-60)×0.05=426.18m 423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m 桩号K5+100.00处:横距x 2=(K5+120.00)-(K5+100.00)=20m 竖距h 2=x 22/2R=202/2×2000=0.1m切线高程=427.68-(90-20)×0.04=424.88m 设计高程=424.88-0.1=424.78m 横距x 2=(K5+100.00)-(K4+940.00)=160m 竖距h 2=x 22/2R=1602/2×2000=6.4m 切线高程=423.18+160×0.05=431.18m 设计高程=431.18-6.40=424.78m[例2]平原区某二级公路有一弯道,偏角α右=15°28′30″,半径R=600m ,缓和曲线长度Ls=70m , JD=K2+536.48。
道路竖曲线计算公式推导商榷

道路竖曲线计算公式推导商榷摘要:本文针对我国现行《道路勘测设计》教材中关于竖曲线设计公式推导存在的问题,进行了较系统的分析论证,提出了具有普通意义的计算公式和算法,可供理论教学和工程设计使用。
关键词:竖曲线;公式推导;应用在道路勘测设计中,竖曲线设计和计算是纵断面设计的重要内容。
现行的《道路勘测设计》教材对此都作了详细的阐述。
但是,不少教材在竖曲线公式的推导时存在偏差,比如竖曲线的计算方程式和竖距的公式推导等。
本文针对竖曲线计算中存在的问题进行了分析,并推导出通用的计算公式,供教学和道路工程设计使用。
现行《道路勘测设计》教材关于竖曲线计算的问题分析1.1现行《道路勘测设计》教材中竖曲线公式推导和计算方法介绍竖曲线公式推导一般先建立如图1所示的坐标系。
以竖曲线的起点作为坐标原点,以水平方向为X轴,垂直方向为Y轴,形成XOY坐标系。
通常用二次抛物线作为竖曲线的方程,设竖曲线变坡点相邻两纵坡坡度分别为i1和i2,变坡角ω用它们的代数差表示。
图1竖曲线计算公式推导示意图在图示坐标系下,二次抛物线一般方程为(1)竖曲线上任意一点P,其斜率为当X=0时,;当X=L时,,则(2)抛物线上任意一点P的曲率半径为式中知,。
代入上式得iP介于i1 、i2之间,且i1 、i2均很小,故可忽略不计,则由此可见,抛物线各点的曲率半径近乎为常数。
将式(2)代入式(1),二次抛物线竖曲线的基本方程式可表示为:或(4)一般由上述论述可得到竖曲线诸要素的计算公式如下表1:表1竖曲线的计算公式竖曲线上任意一点的设计高程,就是用该点的切线高程加上该点的竖距而得到,从而计算出整个竖曲线的设计标高。
1.2关于竖曲线公式和计算方法的问题分析在以上所推导的公式中,主要存在的问题有两个:一是竖曲线的基本方程式(公式4)表达不具有通用性。
其原因是,公式不能表达凸型竖曲线,而只能表达凹型竖曲线。
凸型竖曲线的开口应当是向下的,公式应为。
二是竖曲线上P 点的竖距计算公式(8)不具有通用性。
公路测量曲线和竖曲线要素计算方法
1.某山岭区一般二级公路,变坡点桩号为K5+030,高程为427.68m ,%51=i ,%42-=i ,竖曲线半径R =2000m 。
试计算竖曲线各要素以及桩号为k5+000和K5+100处的设计高程。
解:⑴计算竖曲线要素09.005.004.012-=--=-=i i ω,为凸形竖曲线。
曲线长20000.09180L R m ω==⨯=切线长m L T 9021802=== 外距2290 2.03222000T E m R ===⨯ ⑵计算设计高程竖曲线起点桩号=(K5+30)-90=K4+940竖曲线起点高程=427.68-90×0.05=423.18m桩号K5+000处:横距m K K x 60)9404()0005(1=+-+= 竖距m R x h 9.040006022211=== 切线高程=423.18+60×0.5=426.18m设计高程=426.18-0.9=425.28m桩号K5+100处:横距m K K x 160)9404()1005(2=+-+= 竖距m R x h 4.6400016022222=== 切线高程=423.18+160×0.05=431.18m设计高程=431.18-6.4=424.78m2.某山岭区二级公路,已知JD1、JD2、JD3的坐标分别为(40961.914,91066.103)、(40433.528,91250.097)、(40547.416,91810.392),并设JD2的R=150m ,Ls=40m ,求JD2的曲线要素。
解:⑴计算出JD2、JD3形成的方位角fwj2,︒=--=48966.11528.40433416.40547097.91250392.91810arctan 2fwj 计算出JD1、JD2形成的方位角fwj1, ︒=--=19908.289914.40961528.40433103.91066097.91250arctan1fwj 曲线的转角为α=360+fwj2-fwj1=82.29058°⑵由曲线的转角,计算出曲线的切线长T ,曲线长L 及超距J3322402019.9882240240150s s L L q R =-=-=⨯ 24243340400.444242384241502384150s s L L p R R =-=-=⨯⨯ ︒===639.7150406479.286479.280R L s β 438.151988.19229058.82tan )444.0150(2tan )(=++=++=q p R T α 0150(2)2(82.2905827.639)240290.526180180s RL L ππαβ⨯=-+=-⨯+⨯= 781.49150229058.82sec )444.0150(2sec )(=-+=-+=R p R E α下面总结范文为赠送的资料不需要的朋友,下载后可以编辑删除!祝各位朋友生活愉快!员工年终工作总结【范文一】201x年就快结束,回首201x年的工作,有硕果累累的喜悦,有与同事协同攻关的艰辛,也有遇到困难和挫折时惆怅,时光过得飞快,不知不觉中,充满希望的201x年就伴随着新年伊始即将临近。
竖曲线要素计算公式
竖曲线要素计算公式
竖曲线的要素计算公式包括以下几个要素:
1. 半径(R):竖曲线的曲线半径,可以通过以下公式计算:
R = (L^2) / (24 * A)
其中,L为曲线的长度,A为需满足的标准偏差值。
2. 起点切线长(T1):即曲线前切线的长度,可以通过以下
公式计算:
T1 = L * (1 - ((2 * R) / (3 * A)))
其中,L为曲线的长度,R为曲线半径,A为需满足的标准
偏差值。
3. 终点切线长(T2):即曲线后切线的长度,可以通过以下
公式计算:
T2 = L * (1 - ((2 * R) / (3 * A)))
其中,L为曲线的长度,R为曲线半径,A为需满足的标准
偏差值。
4. 铁路曲线中心角(θ):即曲线的转角,可以通过以下公式
计算:
θ = (L / R) * 30°
其中,L为曲线的长度,R为曲线半径。
5. 切线长(T):即曲线的切线长度,可以通过以下公式计算: T = T1 + T2
6. 过渡曲线长度(Lg):即曲线的过渡段长度,可以通过以
下公式计算:
Lg = (R / A) * 100
其中,R为曲线半径,A为需满足的标准偏差值。
需要注意的是,以上公式仅适用于标准的竖曲线计算,实际情况中可能会有一些修正或调整。
竖曲线的计算方法
竖曲线铁路线路的纵断面最理想的当然是平道,然而事实上是不可能的,为了适应地形的起伏,以减少工程量,纵断面必须用各种不同的坡面连接而成。
两相邻坡段的连续点谓之变坡点。
相邻坡段的坡度差是两相邻坡段的坡度代数差。
当相邻坡段的坡度差超过允许值时,为了保证行车平顺和安全,应在变坡点处用竖曲线连接起来。
允许不设竖曲线的坡度差允许值是根据车轮不脱轨、车钩不脱钩、列车不撞车和行车平稳等要求进行分析确定的。
一般情况下,竖曲线采用圆曲线,也可以采用抛物线,个别情况下,还可以采用连续短坡曲线。
竖曲线的计算一、圆曲线形竖曲线圆曲线形竖曲线的几何要素和各点设计标高,可按下列公式计算,如图。
R α x T TyRCα/2 BAi1i21、竖曲线的切线长度TT=R·tan(α/2)=R/2·tanα=R/2·△i‰=R/2000·△i(m) (5-1)式中 R-竖曲线半径(m);α-竖曲线转角(度);△i-相邻坡段的坡度代数差(‰)。
R=5000m时, T=2.5△i(m)R=10000m时,T=5.0△i(m)R=15000m时,T=7.5△i(m)R=20000m时,T=10.0△i(m)R=25000m时,T=12.5△i(m)2、竖曲线长度CC≈2T=R/1000·△i(m) (5-2)3、竖曲线纵距yy=x2/2R (m) (5-3)式中 x-竖曲线上计算点至竖曲线起(终)点的横距(m)。
当x=T时,变坡点的纵距Y即为竖曲线的外矢距E。
Y=E=T2/2R=1/2R(C/2)2=C2/8R (5-3.1)4、竖曲线上各点的设计标高H设h为计算点的坡度标高,则H=h±y (5-4)式中的y值,凹形取“+”,凸形取“-”。
【算例一】一凹形竖曲线i1=-4‰,i2=+2‰,△i=6‰,变坡点的里程为K235+165,标高为54.60m,R=15000m,计算竖曲线上各20m点的设计标高。
(整理)毕业设计手算稿
JD3桩号K6+747.814 R=2000m Ls=100m 计算:q=2S L -m R L L q s s 999.492000240100210024022323=⨯-=-= p =198.020002384100200024100238424342342=⨯-⨯=-R Ls R Ls ()()︒=︒⨯=︒= 1.43220001006479.286479.280R Lsβ ()()m q p R T 798.438999.49222tan 198.020002tan =+︒+=++=α()()mL R L s 634.86710022000180432.1222218020=⨯+⨯⨯︒⨯-︒=+-=ππβα()()m R 635.372000222sec198.020002secp R E =-︒+=-+=αJ=2T-L=2×438.798-867.632=9.964m ZH =K6+747.814+438.798=K7+186.612各曲线要素计算如下表:变坡点桩号K5+299.588 高程为506.284m ,%44.01=i ,i %56.12-= 1、计算竖曲线要素002.0%44.0%56.112<-=--=-=i i ω , 为凸形 曲线长:9002.04500=⨯==ωR L m切线长:452902===L T m外距:m R T E 225.04500245222=⨯==2、计算设计高程竖曲线起点桩号=(K5+299.588)-45=K5+254.588 竖曲线起点高程=506.284-45×0.44%=506.086m 竖曲线终点桩号= K5+299.588+45=K5+344.588m 竖曲线终点高程=506.284-45×1.56%=505.582m 各变坡点的竖曲线要素列入下表:变坡点桩号 ω 曲线长L 切线长T 外距E起点桩号起点 高程 终点桩号 终点 高程 K0+898.792 0.023 70.14 35.07 0.205 K0+863.722 525.717 K0+933.862 525.377 K1+770.236 0.029 130.73 65.36 0.475 K1+704.874 530.650 K1+835.599 529.645 K2+491.434 0.026 76.68 38.34 0.245 K2+453.094 515.931 K2+529.774 515.207 K3+453.014 0.023 101.34 50.67 0.286 K3+402.344 518.133 K3+503.684 517.332 K4+308.816 0.024 70.80 35.40 0.209 K4+273.416 502.577 K4+344.216 502.055 K5+299.588 0.020 90.36 45.18 0.227 K5+254.408 506.084 K5+344.768 505.577 K6+122.499 0.025 86.73 43.37 0.269 K6+079.134 494.087 K6+165.864 493.804 K6+760.069 0.027 119.21 59.60 0.395 K6+700.467 498.682 K6+819.672 498.191 K7+441.923 0.028 82.71 41.36 0.285 K7+400.568 488.107 K7+483.278 487.811 K8+075.900 0.031 139.28 69.64 0.539 K8+006.263 493.151 K8+145.538 492.418 K8+668.212 0.036 108.09 54.05 0.487 K8+614.167482.696K8+722.257482.401边坡稳定性验算已知路基高度h=6.43m 顶宽12m,其横断面初步拟定如图所示,路基填土为粘性液限粘土,土的粘聚力c=10Kpa,容重318m KN =γ,内摩擦角为35(70.0tan =ϕ),荷载为公路二级,试分析其边坡稳定性。
