最新-【数学】贵州省兴义九中2018学年高一上学期期中考试20 精品
高一数学试卷答案

兴义一中2018届高一数学第一次月考试卷答案试卷测试时间为120分钟,满分150分,答题超出密封线外无效一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项符合题目要求,请将准确答案的代号填入选择题答题表中)1、已知集合{}1,0,1-=A ,{}2,1,0=B ,则=⋃B A ( C )A. {}1,0B. {}2,0,1-C. {}2,1,0,1-D. {}1,0,1-2、若全集{}2,1,0=U ,且{}0=A C U ,则集合A 的真子集的个数为( C )A. 1B. 2C. 3D. 43、已知函数)(x f 由下表格给出,则=))2((f f ( A )A. 1B. 2C. 3D. 44、下列集合表示同一集合的是( A )A. {}012=-=x x M {}1,1-=NB. (){}1,1-=M {}1,1-=NC. (){}1,1-=M (){}1,1-=ND. {}12-==x y x M {}12-==x y y N5、设集合{}31<<=x x A ,{}02≤≥=x x x B 或,则=⋂B A ( B )A. {}32<<x xB. {}32<≤x xC. {}31<<x xD. {}21≤<x x6、下列图象中能表示为函数图象的是( C )A. B. C. D. 7、已知函数)1(-x f 的定义域为[]4,0,则函数)12(+x f 的定义域为( A )A. []1,1-B. []11,3C. []9,1D. ⎥⎦⎤⎢⎣⎡-23,218、已知偶函数)(x f 在区间)[∞+,0上为增函数,且0)3(=-f ,则满足0)12(<-x f 的x 的取值范围是( B )A. ()3,3-B. ()2,1-C. ()2,∞-D. ()+∞-,19、已知函数⎩⎨⎧>≤-=0,0,)(2x x x x x f ,且4)(=m f ,则m 等于( D ) A. 2± B. 4- C. 2 D. 24或-10、映射B A f →:,在f 的作用下A 中的元素),(y x 与B 中的元素),(y x y x -+对应,则与B 中的元素)3,1(对应的A 中的元素是( B )A. )2,1(-B. )1,2(-C. )1,2(D. )2,1(11、已知2)(3++=bx ax x f ,且7)2(=f ,则=-)2(f ( D )A. 3B. 5-C. 5D. 3-12、函数⎩⎨⎧>-≤-=1,1,1)(2x ax x x ax x f 是定义在),(+∞-∞上的增函数,则a 的取值范围是( C ) A. ]2,0( B. )2,0( C. ]1,0( D. ),0(+∞二、填空题(本大题共4小题,每小题5分,共20分)13、已知集合{}0,,2a a M =,且M ∈1,则实数a 的值为_____1-_____.14、函数41)(2--=x x x f 的定义域为_____[)()+∞⋃,22,1_______________. 15、函数322--=x x y 在区间[]2,2-的最大值为______5____.16、已知42222)1(x x x f +-=-,则函数)(x f 的解析式为_______()11)(2≤+=x x x f ____________________.三.解答题:(本大题6小题,共70分,其中17题满分10分,18--22题每小题满分12分。
兴义市黔兴中学2018-2040学年上学期期中高考数学模拟题

兴义市黔兴中学2018-2040学年上学期期中高考数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 函数()()f x x R Î是周期为4的奇函数,且在02[,]上的解析式为(1),01()sin ,12x x x f x x x ì-#ï=íp <?ïî,则1741()()46f f +=( ) A .716 B .916 C .1116 D .1316【命题意图】本题考查函数的奇偶性和周期性、分段函数等基础知识,意在考查转化和化归思想和基本运算能力.2. 已知集合,则( )ABC D3. 已知全集U R =,{|239}x A x =<≤,1{|2}2B y y =<≤,则有( ) A .A ØB B .A B B =C .()R A B ≠∅ðD .()R A B R =ð4. 已知函数(5)2()e22()2xf x x f x x f x x +>⎧⎪=-≤≤⎨⎪-<-⎩,则(2016)f -=( ) A .2e B .e C .1 D .1e【命题意图】本题考查分段函数的求值,意在考查分类讨论思想与计算能力.5. 设集合A ={x |x =2n -1,n ∈Z },B ={x |(x +2)(x -3)<0},则A ∩B =( ) A .{-1,0,1,2} B .{-1,1} C .{1}D .{1,3}6. 在复平面内,复数1zi+所对应的点为(2,1)-,i 是虚数单位,则z =( ) A .3i --B .3i -+C .3i -D .3i +7. 阅读右图所示的程序框图,若8,10m n ==,则输出的S 的值等于( )A .28B .36C .45D .1208. 如图在圆O 中,AB ,CD 是圆O 互相垂直的两条直径,现分别以OA ,OB ,OC ,OD 为直径作四个 圆,在圆O 内随机取一点,则此点取自阴影部分的概率是( )A .π1B .π21 C .π121- D .π2141- 【命题意图】本题考查几何概型概率的求法,借助圆这个载体,突出了几何概型的基本运算能力,因用到圆的几何性质及面积的割补思想,属于中等难度.9. 底面为矩形的四棱锥P -ABCD 的顶点都在球O 的表面上,且O 在底面ABCD 内,PO ⊥平面ABCD ,当四棱锥P -ABCD 的体积的最大值为18时,球O 的表面积为( ) A .36π B .48π C .60πD .72π10.已知2->a ,若圆1O :01582222=---++a ay x y x ,圆2O :04422222=--+-++a a ay ax y x 恒有公共点,则a 的取值范围为( ).A .),3[]1,2(+∞--B .),3()1,35(+∞--C .),3[]1,35[+∞-- D .),3()1,2(+∞-- 11.《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈。
最新-【数学】贵州省兴义九中2018学年高一上学期期中
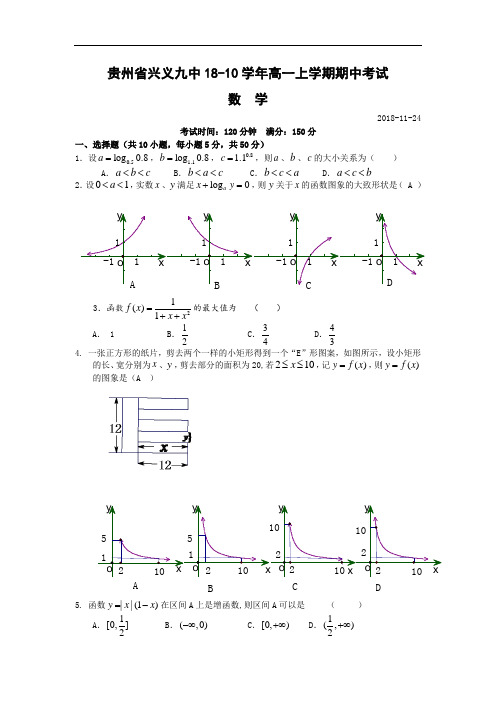
贵州省兴义九中18-10学年高一上学期期中考试数 学2018-11-24考试时间:120分钟 满分:150分一、选择题(共10小题,每小题5分,共50分)1.设0.5log 0.8a =, 1.1log 0.8b =,0.81.1c =,则a 、b 、c 的大小关系为( ) A .a b c << B .b a c << C .b c a << D .a c b << 2.设01a <<,实数x 、y 满足log 0a x y +=,则y 关于x 的函数图象的大致形状是( A )y xy xy xy xDCBA11-111-111-111-1o o o o3.函数21()1f x x x =++的最大值为 ( )A . 1B .12C .34D .434. 一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”形图案,如图所示,设小矩形的长、宽分别为x 、y ,剪去部分的面积为20,若210x ≤≤,记()y f x =,则()y f x =的图象是(A )y xy x y x yx DCBA1021021052102512210101o o o o5. 函数||(1)y x x =-在区间A 上是增函数,则区间A 可以是 ( )A .1[0,]2B .(,0)-∞C .[0,)+∞D .1(,)2+∞6.为了得到....函数x y )31(31⨯=-的图象,可以把函数1()3x y =的图象( ) A .向左平移3个单位长度 B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度7.函数32)(2--=ax x x f 在区间[]2,1上存在反函数的充要条件是( )A .(]1,∞-∈aB .[)+∞∈,2aC .(]2,1∈aD .(][)+∞⋃∞-∈,21,a8.设函数1,0()1,0x f x x - >⎧=⎨ <⎩,若,b a ≠则2)()()(b a f b a b a -⋅--+的值为( )A.aB.bC.,a b 中较大的数D.,a b 中较小的数 9.ax 2+2x+1=0至少有一个.....负的实根的充要条件是( ) A.0<a ≤1 B.a<1 C.a ≤1 D.0<a ≤1或a<010.如图,在公路MN 的两侧有四个村镇:A 1、B 1、C 1、D 1通过小路和公路相连,各路口分别是A 、B 、C 、D ,现要在公路上建一个长途汽车站,为使各村镇村民到汽车站所走的路程总和最小,汽车站应建在( )A .A 处B .D 处C .A 、B 之间的任何一处(包括A 、B )D .B 、C 间的任何一处(包括B 、C )二、填空题(共5小题,每小题5分,共25分) 11.函数y=)35(log 21-x 的定义域为_____________。
贵州高一高中数学期中考试带答案解析

贵州高一高中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.设全集,集合,则()A.B.C.D.2.等比数列中,如果则等于()A.B.C.D.13.若为实数,则下列命题正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则a2>ab>b2C.若a<b<0,则<D.若a<b<0,则>4.等差数列中,,则此数列的前20项和等于()A.90B.160C.180D.2005.方程的两个不等实根都大于2,则实数k的取值范围是()A.B.C.D.6.在△ABC中,角A,B,C所对的边分别是a,b,c,若,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形7.已知点A(1,1),B(-1,)直线过原点,且与线段AB有交点,则直线的斜率的取值范围为()A.B.C.D.8.为了得到的图象,只需将的图象()A.向右平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向左平移个长度单位9.设,则不等式的解集为()A.B.C.D.10.在锐角△ABC中,设则x , y的大小关系为( ) .A.B.C.D.11.现有数列满足:,且对任意的m,n∈N*都有:,则()A.B.C.D.二、填空题1.在平行四边形ABCD中,E和F分别是边CD和BC的中点.若=λ+μ,其中λ,μ∈R,则λ+μ=__________.2.若正数x,y满足,则的最小值是_____.3.已知函数的值域为,则的取值范围是________4.过点(1,1),且横、纵截距相等的直线方程为__________________三、解答题1.解关于的不等式.2.已知是各项均为正数的等比数列,且,(1)求的通项公式;(2)设求数列的前项和.3.已知在中,角A,B,C,的对边分别为,且(1)若的值;(2)若,求的面积.4.已知函数(1)求函数的最小正周期;(2)当时,求的最大值和最小值.5.已知数列的前项和,数列满足.(1)求数列的通项公式,并说明是否为等比数列;(2)求数列的前项和.6.已知,若对于所有的恒成立,求实数的取值范围.贵州高一高中数学期中考试答案及解析一、选择题1.设全集,集合,则()A.B.C.D.【答案】C【解析】由题意知:,,∴.【考点】集合之间的基本关系、集合运算.2.等比数列中,如果则等于()A.B.C.D.1【答案】D【解析】由等比数列的性质知:,∴.【考点】等比中项.3.若为实数,则下列命题正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则a2>ab>b2C.若a<b<0,则<D.若a<b<0,则>【答案】B【解析】当时,A错误;C选项应为;D选项应为.【考点】不等式的基本性质.4.等差数列中,,则此数列的前20项和等于()A.90B.160C.180D.200【答案】C【解析】由等差数列的性质知:,∴.【考点】等差中项、等差数列求和.5.方程的两个不等实根都大于2,则实数k的取值范围是()A.B.C.D.【答案】D【解析】由题意知:,解得.【考点】二次不等式的解法.6.在△ABC中,角A,B,C所对的边分别是a,b,c,若,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形【答案】A【解析】由正弦定理得:,即,∴.【考点】正弦定理.7.已知点A(1,1),B(-1,)直线过原点,且与线段AB有交点,则直线的斜率的取值范围为()A.B.C.D.【答案】D【解析】当直线过点时,;当直线过点时,;由图知,直线的斜率的取值范围为.【考点】直线的斜率、直线方程.8.为了得到的图象,只需将的图象()A.向右平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向左平移个长度单位【答案】B【解析】,所以向右平移个长度单位即可.【考点】三角函数的平移变换.9.设,则不等式的解集为()A.B.C.D.【答案】A【解析】当时,(舍去);当时,;综上所述,不等式的解集为.【考点】不等式的解法、等价转换思想.10.在锐角△ABC中,设则x , y的大小关系为( ) .A.B.C.D.【答案】B【解析】由题意:,在锐角中,,∴.【考点】三角恒等变换.11.现有数列满足:,且对任意的m,n∈N*都有:,则()A.B.C.D.【答案】D【解析】令,则;用累加法可求得,∴;【考点】数列通项公式的求法、数列求和.二、填空题1.在平行四边形ABCD中,E和F分别是边CD和BC的中点.若=λ+μ,其中λ,μ∈R,则λ+μ=__________.【答案】【解析】,而,∴,两式相加化简得:.【考点】向量的线性运算.2.若正数x,y满足,则的最小值是_____.【答案】5【解析】把化简得:,∴.【考点】基本不等式.3.已知函数的值域为,则的取值范围是________【答案】【解析】函数的值域为,所以的判别式,解得:.【考点】恒成立问题、二次不等式的解法.4.过点(1,1),且横、纵截距相等的直线方程为__________________【答案】或【解析】当直线经过原点时,易知直线方程为;当直线不过原点时,设直线方程为,把点(1,1)代入得,所以直线方程为.【考点】直线方程的截距式.三、解答题1.解关于的不等式.【答案】当时,不等式解集为;当时,解集为;当时,解集为.【解析】先把二次不等式看成二次方程,解出方程的两个根;再分三种情况:、、讨论两根的大小,从而可以求出不等式的解集.由得,,∵方程的两根,令得:.(1)当时,不等式解集为,(2)当时,,不等式的解集,(3)当时,,不等式的解集,【考点】二次不等式的解法、含参问题.2.已知是各项均为正数的等比数列,且,(1)求的通项公式;(2)设求数列的前项和.【答案】(1)的通项公式为;(2)数列的前项和.【解析】(1)设的公比为,易得,解得,;所以.(2)先求出数列的通项公式,再用分组求和的方法求出前项和即可.(1)设的公比为,则.由已知化简得,又,故,. 所以.(2) 由(1)知,.因此,.【考点】等比数列的通项公式、数列求和.3.已知在中,角A,B,C,的对边分别为,且(1)若的值;(2)若,求的面积.【答案】(1)边的值为;(2)的面积为.【解析】(1)由余弦定理求得;由恒等变换公式知:,从而得;再根据正弦定理可求出边的值;(2)由题意知三角形为直角三角形,的面积易求.由及余弦定理得,(1),,又故,(2),所以三角形为直角三角形∵,∴.【考点】正余弦定理综合运用、恒等变换公式.4.已知函数(1)求函数的最小正周期;(2)当时,求的最大值和最小值.【答案】(1)函数的最小正周期为;(2)的最大值为-3,最小值为-4.【解析】(1)用二倍角公式和恒等变换公式化简得,所以函数的最小正周期为;(2)当时,先求出的取值范围,结合余弦函数的图象可求的最大值和最小值.(1)(2)【考点】三角函数的图象、三角函数的最值求法.5.已知数列的前项和,数列满足.(1)求数列的通项公式,并说明是否为等比数列;(2)求数列的前项和.【答案】(1)数列的通项公式为,不是等比数列;(2)数列的前项和.【解析】(1)已知求,用即可求出数列的通项公式,由公式易知不是等比数列;(2)先求出数列的通项公式,用错位相减法求出前项和.(1),,两式相减得,故不是等比数列.(2),由错位相减得.【考点】数列通项公式的求法、数列求和.6.已知,若对于所有的恒成立,求实数的取值范围.【答案】实数的取值范围为或或.【解析】对于所有的恒成立,即的最大值都小于等于;即对于所有的恒成立,令,只要,即可解出实数的取值范围.容易得出,即的最大值为1,则对于所有的恒成立对于所有的恒成立,即对于所有的恒成立,令,只要,∴或或.【考点】恒成立问题、等价转换思想.。
兴义市高级中学2018-2019学年高三上学期11月月考数学试卷含答案

兴义市高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 已知函数f (x )=sin 2(ωx )﹣(ω>0)的周期为π,若将其图象沿x 轴向右平移a 个单位(a >0),所得图象关于原点对称,则实数a 的最小值为( )A .πB .C .D .2. 若双曲线﹣=1(a >0,b >0)的渐近线与圆(x ﹣2)2+y 2=2相切,则此双曲线的离心率等于()A .B .C .D .23. 若直线y=kx ﹣k 交抛物线y 2=4x 于A ,B 两点,且线段AB 中点到y 轴的距离为3,则|AB|=( )A .12B .10C .8D .64. 直线x+y ﹣1=0与2x+2y+3=0的距离是( )A .B .C .D .5. 设长方体的长、宽、高分别为2a 、a 、a ,其顶点都在一个球面上,则该球的表面积为( )A .3πa 2B .6πa 2C .12πa 2D .24πa 26. 函数f (x )是以2为周期的偶函数,且当x ∈(0,1)时,f (x )=x+1,则函数f (x )在(1,2)上的解析式为()A .f (x )=3﹣xB .f (x )=x ﹣3C .f (x )=1﹣xD .f (x )=x+17. 为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如由算得2()()()()()n ad bc K a b c d a c b d -=++++22500(4027030160)9.96720030070430K ⨯⨯-⨯==⨯⨯⨯附表:参照附表,则下列结论正确的是( )3.841 6.635 10.828k 2() 0.050 0.010 0.001P K k ≥①有以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别无关”; 99%②有以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别有关”;99%③采用系统抽样方法比采用简单随机抽样方法更好;④采用分层抽样方法比采用简单随机抽样方法更好;班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A .①③B .①④C .②③D .②④8. 如图,在△ABC 中,AB=6,AC=4,A=45°,O 为△ABC 的外心,则•等于( )A .﹣2B .﹣1C .1D .29. 一个多面体的直观图和三视图如图所示,点是边上的动点,记四面体的体M AB FMC E -积为,多面体的体积为,则( )1111]1V BCE ADF -2V =21V V A .B .C .D .不是定值,随点的变化而变化413121M10.将函数的图象向左平移个单位,再向上平移3个单位,得到函数的图象,)63sin(2)(π+=x x f 4π)(x g 则的解析式为( ))(x g A . B .3)43sin(2)(--=πx x g 343sin(2)(++=πx x g C .D .3123sin(2)(+-=πx x g 3)123sin(2)(--=πx x g 【命题意图】本题考查三角函数的图象及其平移变换理论,突出了对函数图象变换思想的理解,属于中等难度.11.如图甲所示, 三棱锥 的高 ,分别在P ABC -8,3,30PO AC BC ACB ===∠=o,M N BC和上,且,图乙的四个图象大致描绘了三棱锥的体积与PO (),203CM x PN x x ==∈(,N AMC -y 的变化关系,其中正确的是()A .B . C. D .1111]12.函数f (x )=ax 3+bx 2+cx+d 的图象如图所示,则下列结论成立的是()A .a >0,b <0,c >0,d >0B .a >0,b <0,c <0,d >0C .a <0,b <0,c <0,d >0D .a >0,b >0,c >0,d <0二、填空题13.设函数有两个不同的极值点,,且对不等式32()(1)f x x a x ax =+++1x 2x 12()()0f x f x +≤恒成立,则实数的取值范围是.14.计算sin43°cos13°﹣cos43°sin13°的值为 .15.(若集合A ⊊{2,3,7},且A 中至多有1个奇数,则这样的集合共有 个. 16.已知三次函数f (x )=ax 3+bx 2+cx+d 的图象如图所示,则= .17.已知△的面积为,三内角,,的对边分别为,,.若,ABC S A B C 2224S a b c +=+则取最大值时.sin cos()4C B π-+C =18.已知数列{a n }的前n 项和为S n ,a 1=1,2a n+1=a n ,若对于任意n ∈N *,当t ∈[﹣1,1]时,不等式x 2+tx+1>S n 恒成立,则实数x 的取值范围为 . 三、解答题19.已知函数f (x )=的定义域为A ,集合B 是不等式x 2﹣(2a+1)x+a 2+a >0的解集.(Ⅰ) 求A ,B ;(Ⅱ) 若A ∪B=B ,求实数a 的取值范围.20.2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t )分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.(Ⅰ)求这40辆小型车辆车速的众数及平均车速(可用中值代替各组数据平均值);(Ⅱ)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆至少有一辆的概率.21.本小题满分10分选修:不等式选讲45-已知函数.2()log (12)f x x x m =++--Ⅰ当时,求函数的定义域;7=m )(x f Ⅱ若关于的不等式的解集是,求的取值范围.x 2)(≥x f R m 22.已知圆C :(x ﹣1)2+y 2=9内有一点P (2,2),过点P 作直线l 交圆C 于A ,B 两点.(1)当l 经过圆心C 时,求直线l 的方程;(2)当弦AB 被点P 平分时,求直线l 的方程.23.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线的极坐标方程是,曲线的参数方程是1C 2=ρ2C是参数).θππθθ],2,6[,0(21sin 2,1∈>⎪⎩⎪⎨⎧+==t t y x (Ⅰ)写出曲线的直角坐标方程和曲线的普通方程;1C 2C (Ⅱ)求的取值范围,使得,没有公共点.t 1C 2C 24.(本小题满分12分)已知平面向量,,.(1,)a x =r (23,)b x x =+-r()x R ∈(1)若,求;//a b r r ||a b -r r(2)若与夹角为锐角,求的取值范围.兴义市高级中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案D B CABADABB题号1112答案AA二、填空题13.1(,1],22⎡⎤-∞-⎢⎥⎣⎦U 14. .15. 6 16. ﹣5 . 17.4π18. (﹣∞,]∪[,+∞) .三、解答题19. 20. 21.22.23.24.(1)2或2).(1,0)(0,3)-U。
高三数学-【数学】贵州省兴义九中2018届高三第一次月

贵州省兴义市第九中学2018届高三第一次月考数学一、选择题(本答题共8小题,每小题5分,满分40分在每小题.给出的四个选项中,只有一项是符合题目要求的) 1.若不等式()()222240a x a x -+--<对一切x R ∈恒成立,则a 的取值范围是( )A. (],2-∞B. ()2,2-C. (]2,2-D. (),2-∞- 2.设32:()21p f x x x mx =+++在()-∞+∞,内单调递增,4:3q m ≥,则p 是q 的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件D.既不充分也不必要条件3.函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的( )A 充分条件B 必要条件C 充要条件D 必要非充分条件4.化简)31()3)((656131212132b a b a b a ÷-的结果( )A .a 6B .a -C .a 9-D .29a5.)('x f 的图象如右图所示,则)(x f 的图象可能是 ( )6.若函数)()(2R a xax x f ∈+=,则下列结论正确的是 ( )A .∀ R a ∈,)(x f 在(0,+∞)上是增函数B .∀ R a ∈,)(x f 在(0,+∞)上是减函数C .∃ R a ∈,)(x f 是偶函数D .∃ R a ∈,)(x f 是奇函数yx+1-17. 已知函数133,(1),()log ,(1),x x f x x x ⎧≤⎪=⎨>⎪⎩则(1)y f x =-的大致图象是( )8. n S 是数列{}n a 的前n 项和,则“数列{}n S 为等差数列”是“数列{}n a 为常数列”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 二、填空题(本答题共6小题,每小题5分,共30分) 9. 函数xx f 11)(-=的定义域是______ 10.在直角坐标平面内,由直线1=x ,0=x ,0=y 和抛物线22+-=x y 所围成的平面区域的面积是________11.同时满足条件:①};5,4,3,2,1{⊆M ②若M a M a ∈∈-则6,,这样的集合M 有 个。
高三数学-【数学】贵州省兴义九中2018学年高三上学期
贵州省兴义九中18-10学年高三上学期期中考试数 学2018-11-24一、选择题(每小题5分,共60分)1.已知三角形ABC 是边长为1的等边三角形,则||AC AB + 的值为( )。
A .1B .2 C.3 D.32 2.为得到函数3cos(2)2y x π=-的图像,只需将函数3sin(22)y x =-的图像( )A .向左平移2个长度单位B .向右平移2个长度单位C .向左平移1个长度单位D .向右平移1个长度单位 3.已知集合}01|{2=-=x x A ,则下列式子表示正确的有( ) ①A ∈1②A ∈-}1{ ③A ⊆φ④A ⊆-}1,1{ A .1个B .2个C .3个D .4个4.已知方程05)2(2=++++a x a x 有两个正实数根,则实数a 的取值范围是:( )A .a<-2B .-5<a<-2C .a>-5D .-5<a 4-≤ 5.函数y=322-+x x 的单调递减区间是:( )A .(3,-∞-]B .[),3+∞-C .(1,-∞-)D .(-1,∞+) 6.函数f (x )是定义在R 上,周期为3的奇函数,已知f (1)>1,f (2)=132+-a a ,则:( )A .32<a B .132-≠<a a 且 C .321>-<a a 或 D .321<<-a 7.等比数列{n a }中,14321=a a a a ,816151413=a a a a ,则44434241a a a a = ( )A .2188B . 1024C .16D .4 8.若21tan =α,且),23,(ππα∈则sin α的值是( ) A .55-B .55C .552D .552- 9.设βα,为钝角,且55sin =α,10103cos -=β,则βα+的值为 ( )A .43π B .45π C .47π D .45π或47π10.设()833-+=x x f x ,用二分法求方程()2,10833∈=-+x x x 在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间( )A .(1,1.25)B .(1.25,1.5)C .(1.5,2)D .不能确定 11.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数a 的取值范围是( )A .),3[]3,(+∞--∞B .]3,3[-C .),3()3,(+∞--∞D .)3,3(-12.从装有2个红球和2个黒球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A .至少有一个黒球与都是黒球B .至少有一个黒球与都是黒球C .至少有一个黒球与至少有1个红球D .恰有1个黒球与恰有2个黒球二、填空题(每小题4分,共16分) 13.已知:x 、y 满足约束条件:001x y x y ≥⎧⎪≥⎨⎪+≥⎩,则(,)2f x y x y =+的最小值为__________14.在平面直角坐标系xoy 中,已知ABC ∆顶点(1,0)A -和(1,0)C ,顶点B 在椭圆22143x y +=上,则sin A sinC sin B +的值是__________15.关于x 的不等式2·32x–3x +a 2–a –3>0,当0≤x ≤1时恒成立,则实数a 的取值范围为_______ 16.设函数f (x )的图象关于点(1,2)对称,且存在反函数)(1x f -,又f(4)=0,则)4(1-f =_______三、解答题(共74分) 17.(12分)已知函数()2f x x |x a |,a R.=-∈(1)当0a ≤时,求证函数()()f x ,-∞+∞在上是增函数; (2)当a=3时,求函数()f x 在区间[0,b]上的最大值。
推荐-贵州省兴义市精华中学2018学年高一9月月考(数学) 精品
贵州省兴义市精华中学18-10学年高一9月月考数学2018-9-20(第Ⅰ卷:50分)一、选择题(每小题5分,共10题,满分50分)1.已知全集U={1,2,3,4,5,6},A={1,2,3,4},B={3,4,5,6},那么C U (A ∩B)=( )A . {3,4}B . {1,2,5,6}C . {1,2,3,4,5,6}D . Φ 2.已知集合{}1,2,3A =,那么A 的子集的个数是( )A. 3B. 7C. 8D. 93.若{|A x y =,2{|2}B y y x ==+,则A B ⋂=( )A.[1,)+∞B.(1,)+∞C.[2,)+∞D.(0,)+∞ 4.函数()1xf x x=+-的定义域为( ) A .[1,)-+∞ B .(],1-∞- C .R D .[)()1,11,-+∞5.函数22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪=-<<⎨⎪≥⎩,若()3f x =,则x 的值是( ) A . 1 B .. {}21x x -<< D6.函数1)y x =≥的反函数为( )A .y=()21x x R +∈B .y=()210x x +>C .y=()210x x +≤D .y=()210x x +≤7.已知函数()x f x a b =+的图象过(1,7),其反函数1()f x -的图象过点(4,0),则f(x)的表达式为 ( )A .43x+ B .34x+ C .52x+ D .25x+8.给出四个函数:①y=13x ⎛⎫ ⎪⎝⎭,③y=1-④y=13x 其中值域为()0,+∞的是 ( )A .①B .① ②C .②D .③ ④ 9.已知()a log 31a -恒为正数,那么实数a 的取值范围是( )A .103a <<B .1233a <<C .1a >D .1233a <<或1a > 10.已知函数27()43x f x ax ax -=++的定义域为R ,则实数a 的取值范围是 ( ) A .3,4⎛⎫-∞ ⎪⎝⎭ B .30,4⎫⎡⎪⎢⎣⎭C .30,4⎛⎫ ⎪⎝⎭D .3,4⎛⎫+∞ ⎪⎝⎭(第Ⅱ卷:100分)二、填空题 (每小题4分,共7题,满分28分)11.已知{}1|-≥x x ,{}2|<x x ,则B A = 12.已知f(x)的定义域为[0,2] , 则f(3x)的定义域为 13.若()1422+=x x f ,则()x f 的解析式为 .14.计算)142110.2541216--⎛⎫⎛⎫⨯--÷--= ⎪ ⎪⎝⎭⎝⎭.15.函数12y x =-,[3,4]x ∈的最大值为 . 16.1海里约合1852m ,根据这一关系,米数y 关于海里数x 的函数解析式为 17.已知函数y=f(x)的定义域为[-1,5], 则在同一坐标系中,函数y=f(x)的图象与直线的交点个数为三、解答题(18,19,20每小题14分,21,22每小题15,满分72分) 18.已知集合A=[-1,2] ,对于下列全集U ,分别求C U A(1){}2|≤=x x U (2) {}22|≤≤-=x x U19. 已知:函数()bf x ax c x=++(a b c 、、是常数)是奇函数,且满足517(1),(2)24f f ==,(Ⅰ)求a b c 、、的值;(Ⅱ)试判断函数()f x 在区间1(0,)2上的单调性并证明;20.若函数2()2f x x x=-+(1)判断函数的奇偶性(2)在直角坐标系画出函数图象、写出函数的单调区间,求出函数值域。
贵州省兴义九中2020至2021学年高一第一学期期中考试数学试卷
题号 一 二 三 总分 总分人 复查人得分)⎩⎨⎧ A .3 B. 8 C. 18 D .2A. 41log 2<2.02<1.02 B. 41log 2<1.02<2.02 C. 1.02<2.02<41log 2D. 1.02<41log 2<2.02 7.函数2()ln f x x x=-的零点所在的大致区间是( ) A .(1,2) B .(2,3) C .11,e ⎛⎫ ⎪⎝⎭和(3,4) D .(),e +∞8.若2log 31x =,则39xx+的值为( )A .6B .3C .52 D .129.若函数y = f (x )的定义域为[]1,2,则(1)y f x =+的定义域为( )A .[]2,3B .[]0,1C .[]1,0-D .[]3,2--10.已知函数2()2,()f x x g x x =-=。
若定义函数()min{(),()},F x f x g x =则()F x 的最大值是( )A .0 B. 1 C. 2 D. 311.定义在R 上的偶函数)(x f ,满足)()1(x f x f -=+,且在区间]0,1[-上为递增,则( )A .)2()2()3(f f f <<B .)2()3()2(f f f <<C .)2()2()3(f f f <<D .)3()2()2(f f f <<12.设S 是至少有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的,a b S ∈,对于有序实数对(),a b 在S 中有唯一确定的元素a b *与之对应)若对任意的,a b S ∈,有()*a b a b *=,则对任意的,a b S ∈,下列等式中不恒成立的是( )A. ()a b a a **=B. ()b b b b **=C. [()()a b a a b a ****=⎤⎦D. ()[()a b b a b b ****=⎤⎦第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贵州省兴义九中18-10学年高一上学期期中考试数 学2018-11-24考试时间:120分钟 满分:150分一、选择题(共10小题,每小题5分,共50分)1.设0.5log 0.8a =, 1.1log 0.8b =,0.81.1c =,则a 、b 、c 的大小关系为( ) A .a b c << B .b a c << C .b c a << D .a c b << 2.设01a <<,实数x 、y 满足log 0a x y +=,则y 关于x 的函数图象的大致形状是( A )y xy xy xy xDCBA11-111-111-111-1o o o o3.函数21()1f x x x =++的最大值为 ( )A . 1B .12C .34D .434. 一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”形图案,如图所示,设小矩形的长、宽分别为x 、y ,剪去部分的面积为20,若210x ≤≤,记()y f x =,则()y f x =的图象是(A )y xy x y x yx DCBA1021021052102512210101o o o o5. 函数||(1)y x x =-在区间A 上是增函数,则区间A 可以是 ( )A .1[0,]2B .(,0)-∞C .[0,)+∞D .1(,)2+∞6.为了得到....函数x y )31(31⨯=-的图象,可以把函数1()3x y =的图象( ) A .向左平移3个单位长度 B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度7.函数32)(2--=ax x x f 在区间[]2,1上存在反函数的充要条件是( )A .(]1,∞-∈aB .[)+∞∈,2aC .(]2,1∈aD .(][)+∞⋃∞-∈,21,a8.设函数1,0()1,0x f x x - >⎧=⎨ <⎩,若,b a ≠则2)()()(b a f b a b a -⋅--+的值为( )A.aB.bC.,a b 中较大的数D.,a b 中较小的数 9.ax 2+2x+1=0至少有一个.....负的实根的充要条件是( ) A.0<a ≤1 B.a<1 C.a ≤1 D.0<a ≤1或a<010.如图,在公路MN 的两侧有四个村镇:A 1、B 1、C 1、D 1通过小路和公路相连,各路口分别是A 、B 、C 、D ,现要在公路上建一个长途汽车站,为使各村镇村民到汽车站所走的路程总和最小,汽车站应建在( )A .A 处B .D 处C .A 、B 之间的任何一处(包括A 、B )D .B 、C 间的任何一处(包括B 、C )二、填空题(共5小题,每小题5分,共25分) 11.函数y=)35(log 21-x 的定义域为_____________。
12.设a=0.32,b=20.3,c=2log 2,试比较a 、b 、c 大小关系_________13.若函数()2x f x x =+,则11()3f -=_________。
14.方程223xx -+=的实数解的个数为_________。
MNAA 1B B 1C 1CD D 115.国家规定的个人稿酬纳税方法是:不超过800元的不纳税;超过800元而不超过4000元的按超出800元部分的14%纳税;超过4000元按全部稿酬的12%纳税.某人出版了一本书,共纳税420元,他的稿费为_______元。
三、解答题(75分)(共6小题,共75分) 16.(12分)函数2()2(0)f x ax x c a =++≠的一个零点是(1,0),另一个零点在(-1,0)之间,⑴求a 的取值范围;⑵求出()f x 的最大值或最小值,并用()g a 表示17.(12分)计算求值:(1)02163)2008()4916(4)32(--⨯-⨯-(2)(lg5)2+(lg2)(lg50)18.(12分)根据函数单调性的定义......,判断1)(2+=x axx f )0(≠a 在),1[+∞上的单调性并给..出证明...。
19.(13分)设函数)(x f =)(2112R a a xx ∈+-⋅,且对任意x ∈R ,均满足)()(x f x f -=-。
(1)求a 的值;(2)求)(x f 的值域;(3)解不等式:0<)2(2--x x f <1715.20.(12分)已知:函数2()(8)f x ax b x a ab =+---,当(3,2)x ∈-时,()0f x >;当(,3)(2,+)x ∈-∞-∞时,()0f x <.(1)求()f x 在[0,1]内的值域;(2)若20ax bx c ++≤的解集为R ,求c 的取值范围.21.(14分)已知幂函数22()()m m f x x m Z -++=∈,且(2)(3)f f <(1)求m 的值;(2)试判断是否存在正数k ,使函数()1()(21)g x k f x k x =-⨯+- 在区间[-1,2]上的值域为17[4,]8-,若存在,求出这个k 值,若 不存在,说明理由.贵州省兴义九中18-10学年高一上学期期中考试数 学 参 考 答 案一、选择题1-5 BADAA 6-10 CDCCD 二、填空题11. (3/5,4/) 12. a<b<c 13. 1 14. 2 15. 3800 三、解答题16.⑴由(1)0f =得2c a =--,∴2()22f x ax x a =+--,又另一零点在(-1,0)之间,∴(1)(0)0f f -⋅<,得2a <-⑵2a <-,∴()f x 有最大值,当1x a =-时,()f x 最大,最大值1()2g a a a=---17.(1)原式=1)74(4)32()21(262131-⨯-⨯-⨯ =22×33-7-1=100(2)原式=lg 25+(lg2)(1+lg5) =(lg5)(lg5+lg2)+lg2 =lg5+lg2=1…………12分18.在),1[+∞上任取x 1,x 2,且211x x <≤,则)1)(1()1)((11)()(2221212122221121++--=+-+=-x x x x x x a x ax x ax x f x f ∵211x x <≤,∴x 1- x 2<0,且0121<-x x .(1)当a>0时,0)()(21>-x f x f ,即)()(21x f x f >, ∴1)(2+=x axx f 是),1[+∞上的减函数;(2)当a<0时,0)()(21<-x f x f ,即)()(21x f x f <,∴1)(2+=x axx f 是),1[+∞上的增函数; 19.(1)法一: f(-x)=-f(x)∴xxx x x x x x a a a a 2121122,21122112+⋅-=+-+-⋅-=+-⋅-- 即:a-2x=1=1-a ·2x∴a+a ·2x=1+2x,∴a(1+2x)=1+2x∴a=1法二:由特殊到一般:先求出a=1可得2分,再验证)()(x f x f -=-(2)法一: )(x f =xx 2112+- ∴2x =0)(1)(1>-+x f x f 解得1)(1<<-x f ∴)(x f 的值域是(-1,1).法二:)(x f =x x x 21212112+-=+-12110,20<+<∴+∞<<xx∴121211<+-<-x,即)(x f 的值域是(-1,1).(3)法一:令21x x <,)12)(12()22(2)()(212121++-=-x x x x x f x f ∵21x x <∴2122xx<∴02221<-x x∴)()(21x f x f <∴)(x f 在R 上是增函数 原不等式即)0(f <)2(2--x x f <)4(f ∵)(x f 在R 上是增函数∴0<x 2-x-2<4解得-2<x<-1或2<x<3∴原不等式的解集是(-2,-1)U(2,3)法二:令t=x 2-x-2原不等式即171521120<+-<t t 此不等式等价于1621<<t由指数函数单调性得0<t<4即0<x 2-x-2<4解得-2<x<-1或2<x<3∴原不等式的解集是(-2,-1)U(2,3) .20.由题意可知2()(8)0f x ax b x a ab =+---=的两根分别为3,2-,且0a <,则由韦达定理可得:8323532b a aab ab a -⎧-+=-⎪=-⎧⎪⇒⎨⎨+=⎩⎪-⨯=-⎪⎩. 故22175()33183()24f x x x x =--+=-++, (1)()f x 在[0,1]内单调递减,故min max ()(1)12,()(0)18,f x f f x f ==== 故()f x 在[0,1]内的值域为[12,18].(2)22()35g x ax bx c x x c =++=-++,则要使()0g x ≤的解集为R ,只需要方程2350x x c -++=的判别式0∆≤,即25120c ∆=+≤,解得2512c ≤-. ∴当2512c ≤-时,20ax bx c ++≤的解集为R . 21.(1)∵ 22()mm f x x -++=为幂函数,且(2)(3)f f <∴220m m -++>, ∴12m -<< 又∵m z ∈ ∴0m =或1m = (2)假设存在满足条件的正数k 由题意知2()f x x =,∴2()(21)1g x kx k x =-+-+∴()g x 的对称轴为112x k=-,且开口向下, 当1112x k =-<-时,即104k <<时,min ()(2)42(21)114g x g k k ==-+-+=-≠- ∴这种情况不存在 当11112k -≤-<时,即14k ≤时, 2max4()(21)17()24()8k k g x k k ---==⇒=-此时2()231g x x x =-++,当x ∈[-1,2]时, min ()(1)2314g x g =-=--+=-∴当2k =时,()g x 的值域为17[4,]8- ∴ 存在满足条件的正数k=2。
