一元函数与二元函数在微积分学上的差异.doc
第七讲 多元函数微分学(基础班 专转本第七章)
类似地,当 x固定在 x 0,而 y 在 y 0处有改变量 y ,如 极 限 lim
y0
存在,则称此极限为函
z f ( x, y )在点( x 0 ,y 0 )处对 y 的偏导数,记为
则称二元函数 z f ( x , y) 在点 P0 ( x 0 , y 0 )处连续.如果 f ( x , y) 在区域 D 内的每一点都连续, 则称 f ( x , y) 在区域 D 上连续. 注:类似的,我们也可以定义二元函数间断点的概念 二、偏导数与全微分 引例 一定量理想气体的压强 P,体积 V,热力学 度 T 三者之间的关系为 RT P (R 为常量 ).
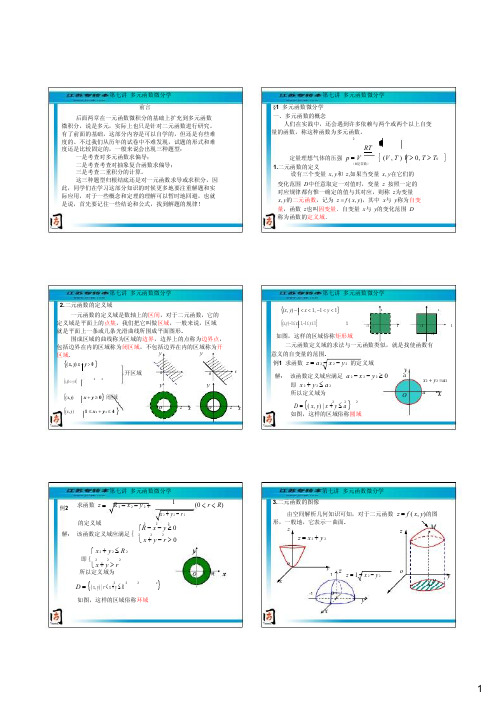
第七讲 多元函数微分学 §1 多元函数微分学 一、多元函数的概念 人们在实践中,还会遇到许多依赖与两个或两个以上自变 量的函数,称这种函数为多元函数。
2
RT
定量理想气体的压强 p V (R是常数) 1.二元函数的定义 设有三个变量 x, y和 z,如果当变量 x, y在它们的
(V , T ) V 0, T T
x 0 0 y
xy 1 1
,
f y
x 0 0 y
,zy
x 0 y 0
或f y ( x 0 , y 0 )
.
lim
lim
xy 1 1
t 11
2
lim f ( x , y ) f ( x 0 , y0 )
dPT常数
第七讲 多元函数微分学
e x cos y
x 1 o y x 2 yo 2
求 极 限 例4 求极限 lim
xy
l i m
解: 这里 就不能直 接带入 x 0, y 0
大学应用数学第四章

4.2.2二元函数的极限
我们讨论二元函数z=f(x,y),当x 点P(x,y
x0,y y0时的
极限,也就是讨论当两个自变量x、y所对应的 P0(x0,y0)时的极限.这里的P-P0表 示点P以任意地方式趋向于点P0. 为方便起见,我们把适合不等式(x-x0)2+(yy0)2<δ 2的所有点P(x,y)组成的区域称为点P0
相应的函数值记作f(x0,y0),或
4.2.1二元函数的概念
4.图形
二元函数可以视作是关于三个变量x、y、z的 三元方程,它对应的函数图形在空间直角坐 标系内表示曲面(或平面).
例如,二元函数z=Ax+By+D的图形表示平面,
函数z和两个自变量x、y之间的关系反应在图 形上就是该平面上点的竖坐标与横、0 (x0,y0)处连续.否则称该二元函数在点P0(x0,y0)处间断.
若二元函数z=f(x,y)在区域D内的每一点都连续,则称该二
元函数z=f(x,y)在区域D内连续.
4.2.3二元函数的连续性
2.连续函数的性质 性质4-1
若多元函数在有界闭区域D上连续,则该多元
函数在D上必能取得最大值与最小值.
若区域延伸到无穷远处,则该区域称为无界区
域;否则,它总可以被包围在一个以原点为中 心而半径适当大的圆内,这样的区域又称为有 界区域.围成区域的直线或曲线也称为区域的边 界;连同边界在内的区域称为闭区域;不包括 边界的区域称为开区域.
4.2.1二元函数的概念
3.函数值
对于二元函数z=f(x,y),当给定两个自变量x、 y的一组值(x0,y0)时,就可以根据该函数的 关系式z=f(x,y)来求出其相应的函数值了,其
记作
4.2.2二元函数的极限
Rolle中值定理的推广及其在解题方面的应用

Rolle中值定理的推广及其在解题方面的应用刘红玉【摘要】微分中值定理把函数在区间上的值的变化与导数联系起来,是利用导数研究函数整体性状最基本的理论依据,在数学中十分重要,内容极为丰富。
以Rolle中值定理为例,把一元函数的Rolle中值定理推广到多元函数及向量值函数的情形,并进行了几何分析,最后通过实例阐述了Rolle中值定理在解题方面的应用。
%Differential mean value theorem it's the most basic theoretical basis to study connects changes of the function the overall character of functions values on the interval with derivative, by using derivative, and also very important in mathematics , and the content is extremely rich. In this paper, taking Rolle Mean - Value theorem as an example, and extends it to the case of multi - function and the vector - valued functions, and given geometric analysis, then elaborates the mean value theorem in solving problems by example.【期刊名称】《宜春学院学报》【年(卷),期】2012(034)008【总页数】3页(P24-26)【关键词】可微;连续;Rolle中值定理;Jacobi矩阵;应用【作者】刘红玉【作者单位】陇南师范高等专科学校,甘肃成县742500 兰州大学数学与统计学院,兰州730000【正文语种】中文【中图分类】O172.1Abstract:Differential mean value theorem connects changes of the function values on the interval with derivative,it's the most basic theoretical basis to study the overall character of functions by u sin g derivative,and also very impor tan t in mathematics,and the content is extremely rich.In this paper,taking Rolle Mean-Value theorem as an example,and extendsit to the case of multi-function and the vector-valued functions,and given geometric analysis,then elaborates the mean value theoremin solving problems by example.Key words:differentiable;continuous;Rolle Mean-Value theorem;Jacobi Matrix;application导数是研究函数性态的重要工具,仅从导数概念出发并不能充分体现这种工具的作用,它需要建立在微分学的基本定理的基础之上,这些基本定理统称为“中值定理”。
函数的连续性和可微性论文

目录引言 (1)1.一元函数的连续性和可微性 (1)1.1一元函数的连续性 (1)1.1.1 定义 (1)1.1.2 定理 (2)1.1.3 间断点及其分类 (4)1.2 一元函数的可微性 (8)1.2.1 可微的定义 (8)1.2.2微分的运算法则 (9)1.2.3 可导、可微以及连续之间的关系 (9)2.二元函数的连续性和可微性 (11)2.1二元函数的连续性 (11)2.1.1 定义 (11)2.1.2 定理 (11)2.2二元函数的可微性 (13)2.2.1 二元函数可微性的定义 (13)2.2.2 偏导数的定义 (13)2.2.3 定理 (14)2.2.4 微分的几何应用 (15)2.2.5 偏导数的连续性、函数可微性、可偏导性与函数连续性的关系. (17)结束语 (24)参考文献 (25)致谢 (26)引言连续性和可微性是函数的重要特性,从几何形象上粗略地说,连续函数在坐标系上的图像是一条连续不断的曲线,下面就简单的介绍一元函数的连续性和可微性和二元函数的连续性和可微性.对一元函数,连续性和可微性是等价的,它是函数增量与自变量增量之间关系的另一种表达式,函数的微分是函数增量的线性主要部分,可微和可导是等价的,因而求一元函数的导数和微分的方法是相同的.一元函数的可导性是比连续性更强的性质,可导必连续,而连续未必可导.微积不但是数学的许多分支以及物理、化学、计算机、机械、建筑等领域的基本数学工具,在社会、经济等领域中也得到越来越广泛的应用.另一方面,微分所反映的数学思想也是日常生活与工作中认识问题、研究问题所难以或缺的.函数的连续性、可导性与可微性是高等数学中最基本、最重要的概念,这三个概念是微积分的重要组成部分,本文在对比函数连续性、可导性与可微三个概念的基础上,深入讨论了三者之间的联系与区别,为学生深入理解和学习微积分学理清了思路.一元函数连续性、可导性与可微性的概念连续函数是高等数学中重点讨论的一类函数.连续性是函数的一个重要特性,它反映了许多自然现象的一种共同特征.而多元函数是一元函数的推广,它具有比一元函数更复杂的性质.就一般的二元函数来说,连续性和可微性是不等价的,学习数学分析之后,我们知道当二元函数的两个偏导数都连续时,函数可微.首先证明了当二元函数的一个偏导数存在,另一个偏导数连续时,函数可微.然后考虑了一般的多元函数的情形,得到了当多元函数的某个偏导数连续,而其余偏导数存在时,函数可微.由此可见可微性与偏导存在性间的关系是复杂的.本文通过具体实例对多元微分学中的几个重要概念间的进行分析讨论,主要研究二元函数的连续性,偏导存在性,可微性等概念以及它们之间因果关系,在掌握了二元函数的有关理论与研究方法之后,再将它推广到一般的多元函数中去.1.一元函数的连续性和可微性1.1一元函数的连续性1.1.1 定义定义1 设函数f 在某0()U x 内有定义,若0lim ()()x x f x f x →=,则称f 在点0x 连续.由于函数在一点的连续性是通过极限来定义的,因而也可以直接用εδ-方式来叙述,即:若对任给的0ε>,使得当0x x δ-<时有0()()f x f x ε-<,则称f 在点0x 连续.若f 在区间上的每一点都连续,则称f 为上的连续函数. 定义2 设函数f 在某()()()00U x U x +-内有定义.若()()()()0000lim lim x x x x f x f x f x f x +-→→⎛⎫== ⎪⎝⎭, 则称f 在点0x 右(左)连续.1.1.2 定理定理1 函数f 在0x 连续的充要条件是:f 在点0x 既是左连续,又是右连续. 定理2(局部有界性)若函数f 在点0x 连续,则f 在某0()U x 内有界.定理3(局部保号性)若函数f 在点0x 连续,且0()0f x >(或0<),则对任何正数0()r f x <(或0()r f x <-),存在某0()U x ,使得对一切0()x U x ∈,有()(())f x r f x r ><-或.例1.1 “()f x 在x a =连续”是()f x 在点x a =处连续的( )条件 (A)必要非充分(B)充分非必要 (C)充要(D)既非充分又非必要解:()f x 在x a =连续,()f x ⇒在x a =连续,()f x 在x a =连续⇒()f x 在x a =连续,如,1,()1,x af x x a ≥⎧=⎨-<⎩,()1f x =,()f x 在x a =连续,但()f x 在x a =间断.故选(B )定理4(四则运算)若函数f 和g 在点0x 连续,则g f ±,f g ⋅,/f g (这里0)(0≠x g ) 也都在点0x 连续.定理5 若函数f 在点0x 连续,g 在点0u 连续,)(00x f u =,则复合函数f g 在点0u 连续.证 由于g 在点0u 连续,对于任给的,存在10δ>,使得当01u u δ-<时有()()0g u g u ε-< (1.1)又由()00u f x =及()u f x =在点0x 连续,故对上述10δ>,存在0δ>,使得当0x x δ-<时有()()001u u f x f x δ-=-<.联系(1)得:对任给的0ε>,存在0δ>,当01u u δ-<时有()()()()0g f x g f x ε-<.这就证明了f g 在点0u 连续.例1.2 设()f x 在x a =处连续,()g x 在x a =处间断,又()0f a ≠,则( ). (A)[]()g f x x a =在处间断, (B)[]()f g x x a =在处间断, (C)[]2()g x x a =在处间断, (D)()()g x x a f x =在处间断. 解: 分析一 连续与不连续的复合可能连续,也可能间断,故(A ),(B )不对.不连续函数的相乘可能连续,故(C )也不对,因此,选(D ).分析二 ()f x 在x a =处连续,()g x 在x a =处间断,又()0f a ≠,⇒()()g x x a f x =在处间断,若不然,⇒()(),()()g x g x f x f x =在x a =连续,与已知矛盾,选(D ). 定理6(最大、最小值定理)若函数f 在闭区间[]b a ,上连续,则f 在[]b a ,上有最大值和最小值.推论 (有界性定理)若函数f 在闭区间[]b a ,上连续,则f 在[]b a ,上有界. 定理7(介值性定理)若函数f 在闭区间[]b a ,上连续,且)()(b f a f ≠,若μ为介于)(a f 与)(b f 之间的任何实数,则至少存在一点()b a x ,0∈,使得μ=)(0x f .推论(根的存在定理)若函数f 在闭区间[]b a ,上连续,且)(a f 与)(b f 异号(即()()0f a f b <,则只是存在一点()b a x ,0∈,使得0()0f x =,即方程()0f x =在(,)a b 内至少有一个根.例1.3 证明:若0r >,n 为正整数,则存在唯一正数0x ,使得0nx r =(0x 称为 r 的n 次正根(即算术根),记作0x =). 证 先证存在性.由于当x →+∞时有n x →+∞,故必存在正数a ,使得n a r >,因()n f x x =在[]0,a 上连续,并有(0)()f r f a <<,故由介值性定理,至少存在着一点()00,x a ∈,使得00()nf x x r ==.再证唯一性.设正数1x 使得1n x r =,则有()()12101010011...0n n n n n x x x x x x x x ----=-+++=.由于第二个括号内的数为正数,所以只能010x x -=,即01x x =.定理8(反函数的连续性)若函数f 在[]b a ,上严格单调并连续,则反函数1-f 在其定义域[][])(),()(),(a f b f b f a f 或上连续.例 1.4 由于sin y x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上严格单调且连续,故其反函数1sin y x -=在区间[]1,1-上连续.定理9 (一致连续性定理)若函数f 在闭区间[],a b 上连续,则f 在[],a b 上一致连续.定理10 一切基本初等函数都是其定义域上的连续函数. 定理11 任何初等函数都是在其定义区间上的连续函数.1.1.3 间断点及其分类定义 2 设函数f 在某00()U x 内有定义,若f 在点0x 无定义,或f 在点0x 有定义而不连续,则称点0x 为函数f 间断点或不连续点.若0x 为函数f 间断点,则必出现下列情形之一: (ⅰ)f 在点0x 无定义,或极限0lim ()x x f x →不存在.(ⅱ)f 在点0x 有定义,极限0lim ()x x f x →存在,但00lim ()()x x f x f x →≠.据此,我们可对函数的间断点作如下分类:(1)可去间断点 若lim ()x x f x A →=.而f 在点0x 无定义,或有定义但0()f x A ≠,则称0x 为f 的可去间断点.(2)跳跃间断点 若函数f 在点0x 的左、右极限都存在,但lim ()lim ()x x x x f x f x +-→→≠. 则称0x 为f 的跳跃间断点.(3)函数的所有其他形式的间断点,即使得函数至少有一侧极限不存在的那些点,称为第二类间断点.图1.1 可去间断点 图1.2图1.3 跳跃间断点判断函数连续性的方法:(1)若是初等函数,则在它的定义域区间上处处连续. (2)用连续性运算法则.(3)分别判断左右连续性或按定义判断.例1.5 设有定义在(),-∞∞上的函数()f x :(A )1,0(),0sin x f x x x x=⎧⎪=≠⎨⎪⎩(B )sin ,0()cos 1,0x x f x x x ≤⎧=⎨->⎩(C )1(1),0()1,0x x x f x x ⎧⎪+≠=⎨⎪=⎩ (D )11(1),0()1,0x x f x xx ⎧+≠⎪=⎨⎪=⎩(1)在定义域上连续的是( ),(2)函数()f x 以0x =为第二类间断点的是( ).解 (1) 00x x <>与时上述()f x 均分别与某初等函数相同,故连续. 只需在考察哪个函数()f x 在0x =处连续.注意到(),0()(),0g x x f x h x x ≤⎧=⎨>⎩,其中()g x 在(],0-∞连续,()h x 在[)0,+∞连续,因(]()()(,0)()f x g x x f x =∈-∞⇒在0x =左连续,若又有(0)(0)g h =[)()()(0,)()f x h x x f x ⇒=∈+∞⇒在0x =右连续,因此()f x 在0x =连续.(B)的()f x 满足0sin (cos 1),x x xx ===-又sin ,cos 1x x -均连续()0f x x ⇒=在连续,因此,(B )中的()(),f x -∞+∞在连续,应选(B ).(2)关于(A ):由00sin sin lim ()lim 1,lim ()lim 1,x x x x x xf x f x x x++--→→→→====-- ⇒ 0x =是()f x 的第一类间断点(跳跃间断点).关于(C ):由1lim ()lim(1)(0)xx x f x x e f →→=+=≠,⇒ 0x =是()f x 的第一类间断点(可去间断点). 已证(B )中()f x 在0x =连续,因此选(D ),我们也可以直接考察(D ),由111ln(10001lim ()lim(1)lim =+x x x x x x f x e x++++→→→=+=∞), ⇒ 0x =是()f x 的第二类间断点.例1.6 设(),()f x g x 在0x x =均不连续,则在0x x =处( ). (A)()()f x g x +吗,()()f x g x ⋅均不连续.(B)()()f x g x +不连续,()()f x g x ⋅的连续性不确定. (C)()()f x g x +的连续性不确定,()()f x g x ⋅不连续.(D)()()f x g x +,()()f x g x ⋅的连续性均不确定.解:如:1,0()0,0x f x x ≥⎧=⎨<⎩,0,0()1,0x g x x ≥⎧=⎨<⎩,在0x =均不连续,但()()1f x g x +=.()()0f x g x ⋅=在0x =均连续.又如:1,0()0,0x f x x ≥⎧=⎨<⎩,2,0()0,0x g x x ≥⎧=⎨<⎩,在0x =均不连续,而3,0()()0,0x f x g x x ≥⎧+=⎨<⎩,2,0()()0,0x f x g x x ≥⎧⋅=⎨<⎩在0x =均不连续,因此选(D ).例1.7 讨论下列函数的连续性并判断其间断点的类型.(1)21()(1)arctan 1f x x x =++,(2)ln(1),0()10x x x f x x x +⎧>⎪⎪=⎪-≤<⎪⎩,(3) sin 201sin cos ,0()0,0xt dt x x f x x x ⎧⎪⎪≠=⎨⎪=⎪⎩⎰解:(1)这是初等函数,它在定义域(20x ≠)上连续,因此1x ≠±时均连续,1x =±时,2101lim (1)arctan()2()12x x x ππ→++=⨯-=--, 2101lim (1)arctan()2()12x x x ππ→-+=⨯+=-, 故1x =是第一类间断点(跳跃间断点),又10lim 0x y →-+=,10lim 0x y →--=,故1x =-也是第一类间断点(可去间断点).(2)在区间()0,+∞,[)1,0-上,函数y 分别与某初等函数相等,因而连续,在0x =处无定义,而ln(1)lim lim 1x x x y x++→→+==,0lim lim lim 1x x x y x---→→→===, 0x ⇒=是第一类间断点(可去间断点).(3) 记sin 20()cos x g x t dt =⎰,又变限几分的性质及复合函数的连续性,知()g x 是连续函数,再由连续函数的运算法则,知0x ≠时()1()sin g x f x x x=连续,由于 200()limlimcos(sin )cos 10x x g x x x x→→==≠,而01lim sin x x →±不存在,所以0()1limsin x g x x x→±不存在,即0x =是()f x 的第二类间断点. 1.2 一元函数的可微性1.2.1 可微的定义设函数()y f x =,当自变量0x x =有增量x ∆时,若存在于x ∆无关的常数0()A x ,使得函数的增量00()()y f x x f x ∆=+∆-可表为0()()y A x x o x ∆=∆+∆ (0)x ∆→,则称()f x 在0x x =处可微,0()A x x ∆称为()f x 在0x x =处的微分,记为00()()x x x x dyA x x dfA x x ===∆=∆或.微分的几何意义: 00()()y f x x f x ∆=+∆-是曲线()y f x =在点0x x =处相应于自变量增量x ∆的纵坐标0()f x 的增量,微分0x x dy=是曲线()y f x =在点()000,()M x f x 处的切线相应于自变量增量x ∆的纵坐标的增量.如下图所示图1.4定理1 函数f 在点0x 可微的充要条件是函数f 在点0x 可导,而且上式中0()A x 等于)(0x f ',即'()dy f x dx =.1.2.2微分的运算法则[()()]()()d u x v x du x dv x ±=± [()()]()()()()d u x v x v x du x u x dv x =+ 2()()()()()()()()u x v x du x u x dv x d v x v x -= dx x g u f x g f d )()())((''= ,其中()u g x =例1.8 求22ln cos y x x x =+的微分解:2222(ln cos )(ln )(cos )dy d x x x d x x d x =+=+ ()222ln ()ln (cos )xd x x d x d x =++ 2(2ln 12sin )x x x dx =+-.1.2.3 可导、可微以及连续之间的关系一元函数的可导性与可微性是等价的,函数的可导性是比可微性更强的性质,可导必连续,连续未必可导,例如,13y x y x ==与在0x =连续,但不可导.例1.9 设0()0f x ≠,()f x 在0x x =连续,则()f x 在0x x =可导是()f x 在0x x =可导的( ).(A)充分非必要 (B)充分必要 (C)必要非充分 (D)非充分非必要解:由0()0f x ≠00()0()0f x f x ⇒><或,因()f x 在0x x =连续,则()f x 在0x 某邻域是保号的,即0δ∃>,当0x x δ-<时,00000()()00()0()()0()0(),()0f x f x f x f x x x f x f x f x f x δ⎧>>>⎧⎪⇒-<=⎨⎨<<-<⎩⎪⎩,,时,,,因此选(B ).例1.10 设()00x f x x ≥=<,则( ).(A)()f x 在0x =处不连续 (B)(0)f '存在(C)(0)f '不存在,曲线()y f x =在点()0,0处不存在切线 (D)(0)f '不存在,曲线()y f x =在点()0,0处存在切线 解: 由()()0lim 00x f x f →==,故()f x 连续()()000limlim x x f x f x++→→-==+∞, ()()000limlim x x f x f x --→→-==-∞. ()y f x =的图形如图1.5所示,()f x 在0x =的左右极限都不存在,因此)(0f '不存在. ()y f x =存在切线0x =,选(D ). 例1.11 讨论函数2202(1cos ),0()1,01cos ,0xx x x f x x t dt x x -⎧<⎪⎪==⎨⎪⎪>⎩⎰在0x =的连续性和可导性.解:我们可先讨论函数在0x =的可导性,因为当()f x 在0x =可导或)0(+'f ,)0(-'f 均存在但不相等时,均可得()f x 在0x =连续,由()f x 分段定义的具体形式,可按定义求出)0(+'f ,)0(-'f 来讨论)(0f '是否存在. 222'020000cos 1()(0)cos 2sin (0)lim limlim lim 022xx x x x t dt f x f x x x x f xx x +++→→→→----=====⎰, 2'320000()(0)2(1cos )2(sin )2cos 1(0)lim lim lim lim 0332x x x x f x f x x x x x f x x x x---→→→→-----=====, 因此,0)0()0(='='-+f f ,即()f x 在0x =可导,因而也必连续.2.二元函数的连续性和可微性2.1二元函数的连续性2.1.1 定义设f 为定义在点集2D R ∈上的二元函数,0P D ∈(它或者是D 的聚点,或者是D 的孤立点),对于任给的正数ε,总存在相应的正数δ,只要()0;P U P D δ∈,就有0()()f P f P ε-<,则称f 关于集合D 在点0P 连续.若f 在D 上任何点都关于集合D 连续,则称f 为D 上的连续函数.2.1.2 定理定理1(复合函数的连续性)设函数(),u x y ϕ=和(),v x y φ=在xy 平面上点()000,P x y 的某邻域内有定义,并在点0P 连续;函数(),f u v 在uv 平面上点()000,Q u v 的某邻域内有定义,并在点0Q 连续,其中()000,u x y ϕ=,()000,v x y φ=.则复合函数()()(),,,,g x y f x y x y ϕφ=⎡⎤⎣⎦在点0P 也连续.证 由f 在点0Q 连续可知:任给正数ε,存在相应正数η,使得当0u u η-<,0v v η-<时有()()00,,f u v f u v ε-<,又由,ϕφ在点0Q 连续可知:对上述正数η,总存在正数δ,使得当0x x δ-<,0y y δ-<时,都有()()000,,u u x y x y ϕφη-=-<, ()()000,v v x y x y φφη-=--<,综合起来,当0x x δ-<,0y y δ-<时,便有()()()()0000,,,,g x y g x y f x y f x y ε-=-<,所以说复合函数()()(),,,,g x y f x y x y ϕφ=⎡⎤⎣⎦在点0P 连续.定理2(有界性与最大、最小值定理)若函数f 在有界闭区域2D R ∈上连续,则f 在D 上有界,且能取得最大值与最小值.定理3(一致连续性定理)若函数f 在有界闭区域2D R ∈上连续,则f 在D 上一致连续.即对任何0ε>,总存在只依赖于ε的正数δ,使得对于一切点P 、Q ,只要(),P Q ρδ<,就有()()f P f Q ε-<.定理4(介值性定理)设函数f 在有界闭区域区域2D R ∈上连续,若1P ,2P 为D 中任意两点,且()()12f P f P <,则对任何满足不等式()()12f P f P μ<<,的实数μ,必存在点0P D ∈,使得()0f Pμ=. 定理5(有界性与最大值最小值定理)若函数f 在有界闭区域区域2D R ∈上连续,则f 在D 上有界,且能取得最大值与最小值.证 先证则f 在D 上有界.倘若不然,则对每个正整数n ,必存在点n P D ∈,使得 (),1,2,n f P n n >=⋅⋅⋅ (2.1) 于是得到一个有界点列{}n P D ⊂,且总能使{}n P 中有无穷多个不同的点.由聚点定理的推论,有界无限点列{}2n P R ⊂必存在收敛子列{}k n P,设0lim k n k P P →∞=,且因D 是闭区域,从而0P D ∈.由于f 在D 上连续,当然在点0P 也连续,因此有()()0lim k n k f P f P →∞=,这与不等式(2)相矛盾,所以f 是D 上的有界函数.下面证明f 在D 上能取得最大值、最小值.为此设()()inf ,sup m f D M f D ==,可证必有一点Q D ∈,使()f Q M =(同理可证存在D Q ∈',使m Q f =')().如若不然,对任意P D ∈,都有()0M f P ->.考察D 上的连续函数()()1F P M f P =-,由前面的证明知道,在D 上有界.又因F 不能在D 上达到上确界M ,所以存在收敛点列{}n P D ⊂,使()lim n n f P M →∞=,于是有lim n →∞=+∞,这导致与F 在D 上有界的结论想矛盾.从而证得f在D 上能取得最大值.2.2二元函数的可微性2.2.1 二元函数可微性的定义设函数(),z f x y =在点()000,P x y 的某邻域()0U P 内有定义,对于()0U P 中的点()()00,,P x y x x y y =+∆+∆,若函数f 在点0P 处的全增量z ∆可表示为:()()000,,o z f x x y y f x y ∆=+∆+∆-()A x B y o ρ=∆+∆+ (2.2)其中,A B 是仅与点0P 有关的常数,ρ=()ορ是较ρ高阶的无穷小量,则称函数f 在点0P 可微,并称(1)式中关于,x y ∆∆的线性函数A x B y =∆+∆为函数f 在点0P 的全微分,记作()000,P dzdf x y A x B y ==∆+∆ (2.3)由(2.1)、(2.3)可见dz 是z ∆的线性主部,特别当,x y ∆∆充分小时,全微分dz 可作为全增量z ∆的近似值,即()()()()0000,,f x y f x y A x x B y y ≈+-+-.全微分的几何意义: 函数(),z f x y =在点()000,P x y 的全微分在几何上表示曲面(),z f x y =在点()()0000,,,x y f x y 处切平面上点的竖坐标的增量.2.2.2 偏导数的定义设函数(),z f x y =,(),x y D ∈,若()00,x y D ∈,且()0,f x y 在0x 的某邻域内有定义,则当极限()()()00000000,,,limlim x x x f x y f x x y f x y x x ∆→∆→∆+∆-=∆∆,存在时,称这个极限为函数f 在点()00,x y 关于x 的偏导数,记作()00,x f x y 或()00,x y fx∂∂.若(),z f x y =在点()000,P x y 存在()00,f x y x ∂∂与()00,f x y y∂∂,称(),z f x y =在点()000,P x y 可偏导.偏导数的几何意义:()00,f x y x∂∂即曲面(),z f x y =与平面0y y =的交线在点()()00000,,,M x y f x y 处的切线对x 轴的斜率;()00,f x y y∂∂即曲面(),z f x y =与平面0x x =的交线在点()()00000,,,M x y f x y 处的切线对y 轴的斜率.2.2.3 定理定理1(可微的必要条件)若二元函数在其定义域内一点()00,x y 处可微,则f 在该点关于每个自变量的偏导数都存在,且(1)式中的()00,x A f x y =,()00,y B f x y =.依此函数f 在点()00x y 的全微分可唯一地表示为()()()000000,,,x y x y dff x y x f x y y =⋅∆+⋅∆.与一元函数类似,由于自变量的增量等于自变量的微分,即x dx ∆=, y dy ∆=.所以全微分又可以写为()()0000,,x y dz f x y dx f x y dy =+.定理2(可微的充分条件)若函数(),z f x y =的偏导数在点()00,x y 的某邻域内存在,且x f ,y f 在点()00,x y 处连续,则函数f 在点()00,x y 处可微.证 我们把全增量z ∆写作()()0000,,z f x x y y f x y ∆=+∆+∆-()()()()00000000,,,,f x x y y f x y y f x y y f x y =+∆+∆-+∆++∆-⎡⎤⎡⎤⎣⎦⎣⎦ 在第一个括号里,它是函数()0,f x y y +∆关于x 的偏增量;在第二个括号里,则是函数()0,f x y 关于y 的偏增量.对它们分别用一元函数的拉格朗日中值定理,得()()01000212,,,0,1x y z f x x y y x f x y y y θθθθ∆=+∆+∆∆++∆∆<< (2.4)由于x f 与y f 在点()00,x y 连续,因此有()()01000,,x x f x x y y x f x y θα+∆+∆∆=+ (2.5)()()00200,,y y f x y y f x y θβ++∆=+ (2.6)其中当()(),0,0x y ∆∆→时,0,0αβ→→,将(4),(5)带入(3)式,则得()()0000,,x y z f x y x f x y y x y αβ∆=∆+∆+∆+∆,故函数f 在点()00,x y 可微.定理 3 设函数在点()00,x y 的某邻域内存在偏导数,若(),x y 属于该邻域,则存在()010x x x ξθ=+-和()020y y y ηθ=+-,120,1θθ<<,使得()()()()()()00000,,,,x y f x y f x y f y x x f x y y ξη==-+-.定理4 曲面(),z f x y =在点()()00000,,,P x y f x y 存在不平行于z 轴的切平面∏的充要条件是函数f 在点()000,P x y 可微.求分段函数在分段点的全微分1 用定义求),(00y x f x ',),(00y x f y ',即求xy x f y x x f y x f x x ∆-∆+='→∆),(),(lim),(0000000和yy x f y y x f y x f y y ∆-∆+='→∆),(),(lim),(0000000,若偏导不存在,则不可微,若存在,则2.2计算22),),(limyx yf x f y x f y y x x f pyf x f f y x y x ∆+∆∆'-∆'--∆+∆+=∆'-∆'-∆→(ρ,若极限为0,则可微,否则不可微,可微时,dy y x f dx y x f dz y x )0000,(),('+'=.2.2.4 微分的几何应用1空间曲面的且平面与法线若空间曲面S 的方程为(),,0F x y z =,()0000,,M x y z 是S 上的一点,则S 在0M 点的且平面方程为()()()()()()0000000F M F M F M x x y y z z x y z∂∂∂-+-+-=∂∂∂. 法线方程为()()()()()()000000x x y y z z F M F M F M xyz ---==∂∂∂∂∂∂.其中(),,F x y z 在点M 处有连续偏导数且()()()2220000F M F M F M x y x ∂∂∂⎛⎫⎛⎫⎛⎫++≠ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭.例2.1 试求抛物面22z ax by =+在点()0000,,M x y z 处的切平面方程与法线方程. 解 因为()000,2x f x y ax =,()000,2y f x y by =,过M 的切平面方程为()()0000022z z ax x x by y y -=-+-,由于22000z ax by =+,化简为000220ax x by y z z +--=.过M 的法线方程为00000221x x y y z z ax by ---==-. 2 空间曲线的切线去法平面若空间曲线Γ的参数方程为()x x t =,()y y t =,()z z t =()t αβ≤≤,又()()()()()0000000,,,,M x y z x t y t z t =是Γ上的一点,则Γ在点0M 的切线方程为)(()(000t z z z t y y y t x x x '-='-='-).法平面方程为0))(())(())((000000=-'+-'+-'z z t z y y t y x x t x .其中,()x t ,()y t ,()z t 在0t t =可导且0)()()020202≠'+'+'t z t y t x (.3 近似计算例2.2 求 3.961.08的近似值.解 设(),y f x y x =,令01x =,04y =,0.08x ∆=,0.04y ∆=-,则有()3.96001.08,f x x y y =+∆+∆ ()()()1,41,41,4x y f f x f y ≈+∆+∆ ()4140.081ln10.04=+⨯+⨯⨯-10.32 1.32=+=.2.2.5 偏导数的连续性、函数可微性、可偏导性与函数连续性的关系.可以从可微性的定义看出,函数在可微点处必连续,但在函数的连续点处不一定存在偏导数,更不能保证函数在该点连续.如下图所示图1.6定理5 如果函数).(y x f z =的偏导数yzx z ∂∂∂∂、在点),(y x 连续,则函数在该点可微分. 证明:因为我们只限于讨论在某一区域内有定义的函数(对于偏导数也如此),所以假定偏导数在点),(y x P 连续,就含有偏导数在该点的某一领域内必然存在的意思.设点),(y y x x ∆+∆+为这领域内任意一点,考察函数的全增量)],(),([)],(),([),(,(y x f y y x f y y x f y y x x f y x f y y x x f z -∆++∆+-∆+∆+=-∆+∆+=∆)在第一个方括号内的表达式,由于y y ∆+不变,因而可以看做是x 的一元函数),(y y x f ∆+的增量.于是,应用拉格朗日中值定理,得到xy y x x f y y x f y y x x f x ∆∆+∆+=∆+-∆+∆+),(),(),(1θ )10(<<θ又依假设,),(y x f x 在点),(y x 连续,所以上式可写为xx y x f y y x f y y x x f x ∆+∆=∆+-∆+∆+1),(),(),(ε (2.7)其中1ε为y x ∆∆、的函数,且当0,0→∆→∆y x 时,01→ε. 同理可证第二个方括号内的表达式可写为y y y x f y x f y y x f y ∆+∆=-∆+2),(),(),(ε (2.8) 其中2ε为y ∆的函数,且当002→→∆ε时,y .由(2.7)、(2.8)两式可见,在偏导数连续的假定下,全增量z ∆可以表示为y x y y x f x y x f z y x ∆+∆+∆+∆=∆21),(),(εε容易看出2121εερεε+≤∆+∆yx ,它是随着0)0,0()→→∆∆ρ即,(y x 而趋于零的.这就证明了).(y x f z =在点),(y x P 是可微分的.定理6如果函数).(y x f z =在点),(y x 可微分,那么函数在该点必定连续 证明:由全微分定义可知:函数).(y x f z =在点),(y x 的全增量)ρο(),(),(+∆+∆=∆-∆+∆+=∆y B x A z y x f y y x x f z可得0lim 0=∆→z ρ.从而),(]),([lim ),(lim 0)0,0(),(y x f z y x f y y x x f y x =∆+=∆+∆+→→∆∆ρ因此函数).(y x f z =在点),(y x 处.定理7如果函数).(y x f z =在点),(y x 可微分,则函数在点),(y x 的偏导数yzx z ∂∂∂∂、必定存在,且函数).(y x f z =在点),(y x 的全微分为y yzx x z dz ∆∂∂+∆∂∂=. 证明:设函数).(y x f z =在点),(y x P 可微分.于是,对于点P 的某个领域内的任意一点),(y y x x P ∆+∆+',式子(2.9)总成立)(ρο+∆+∆=∆y B x A z (2.9)特别当0=∆y 时,(2.9)式也应成立,这时x ∆=ρ,所以(2.9)式成为)(),(),(x x A y x f y x x f ∆+∆⋅=-∆+ο.上式两边各除以,x ∆在令0→∆x 而取得极限,就得A xy x f y x x f x =∆-∆+→∆),(),(lim,从而偏导数xz∂∂存在,且等于A.同样可证B y z =∂∂.所以该定理得证.例2.3 下列函数在()0,0处不连续的是( )(A)()()()()(),0,0,0,,0,0x y f x y x y ≠==⎩(B)()()()()()3322,,0,0,0,,0,0x y x y x yf x y x y ⎧-≠⎪+=⎨⎪=⎩(C)()()()()(),0,0,0,,0,0x y f x y x y ≠==⎩(D)()()()()()221,,0,0,0,,0,0x y x y f x y x y =+=⎪=⎩解(A )中, (),f x y x =≤=, 故有, (A )连续.(B)中,()3333222222,x y x y f x y x y x y x y x y-=≤+≤++++,则有()()()(),0,0lim,0,00x y f x y f →==,(),f x y 在点()0,0连续(C ),当(),x y 沿直线y x =趋于()0,0时,()()2,0,00f x y f ==≠=,因此,(),f x y 在点()0,0不连续.(D),221sinx y +有界,⇒ ()()()()(()22,0,0,0,01lim ,lim 00,0x y x y f x y f x y →→===+ ⇒(),f x y 在点()0,0连续.例2.4 设函数(),f x y 在点()00,P x y 的两个偏导数'x f 和'y f 都存在,则( ) (A)()0lim ,y y x x f x y →→存在(B)()00lim ,x x f x y →及()00lim ,y y f x y →都存在(C)(),f x y 在P 点必连续 (D)(),f x y 在P 点必可微解 函数()0,f x y 和()0,f x y 已成为一元函数,二元函数(),f x y 在点()00,P x y 对x 的偏导数等于一元函数()0,f x y 在0x 点倒数,因为偏导数'x f 在点P 存在,所以()0,f x y 在0x x =处必连续,从而()00lim ,x x f x y →存在,同理()00lim ,y y f x y →存在.选(B).如上例中,()()()()()22,,0,0,0,,0,0xyx y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,(),f x y 在P 点不连续.例2.5 讨论函数()()()()()22,,0,0,0,,0,0xy x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,(),f x y 在点()0,0处的连续性,并判断偏导是否存在.解 先判断(),f x y 在点()0,0处是否可偏导,由于()()()()000000,,0,00,0limlim 0x x f x x y f x y f x f x x∆→∆→+∆-+∆-==∆∆ 即()0,00fx∂=∂,同理()0,00f y∂=∂,因此偏导数都存在,考察(),f x y 在点()0,0的连续性,令y kx =,则 ()022220lim ,lim (1)(1)x y kx x kx kf x y k x k →=→==++,即当(),x y 沿不同直线y kx =趋于()0,0时(),f x y 有不同的极限,因此(),f x y 在点()0,0不连续.例2.6 设()()()()()2222,,0,0,0,,0,0x y x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,讨论(),f x y 在()0,0处的连续性和可微性,并求()0,0df.解 当()(),0,0x y ≠时,2322222222()f xy x y x x y x y ∂=-∂++,当()(),0,0x y =时,因()(),00f x x =∀,于是()0,0f x∂=∂()()0,00,0lim0x f x f x∆→+∆-=∆.同理可得,当()(),0,0x y ≠时,2232222222()f x y x y y x y x y ∂=-∂++,()0,00f y ∂=∂.考察f x ∂∂,fy∂∂在()0,0的连续性,注意到 2221x x y ≤+,2221y x y ≤+,2322222222()f xy x y x x y x y ∂=-∂++, 故4fx x ∂≤∂, 4f y y ∂≤∂,()()()0,0,0,0lim0x y f fx x →∂∂==∂∂,()()()0,0,0,0lim0x y f fy y →∂∂==∂∂即f x ∂∂,fy∂∂在点()0,0处均连续,因此(),f x y 在点()0,0可微.于是()()()0,00,00,00f f dfdx dy xy∂∂=+=∂∂例2.7证明函数z =()0,0连续但偏导数不存在. 证明 因为()((),0,0lim00,0x y z →==,所以z =()0,0连续,又()()0,00,0xz x z x x∆+∆-=∆∆,当0x ∆→时,极限不存在,因此()0,0x z 不存在.同理可得,()0,0y z 也不存在.例2.8 证明函数()222222()sin 0,0,0x y x y f x y x y ⎧++≠⎪=⎨⎪+≠⎩在点()0,0连续且偏导存在,但偏导在()0,0不连续,而f 在原点()0,0可微.证明 要证明(),f x y 在()0,0连续,即证()()()(),0,0lim,0,0x y f x y f →=,由()()()()22,0,0lim00,0x y x y f →+==,所以(),f x y 在()0,0连续.当220x y +=时 ()()()000,00,01lim lim sin 00,0x x x f x f x f x x∆→∆→+∆-=∆==∆∆ 当220x y +≠时(),2sin x f x y x = 而()(),0,0lim 20x y x →=,()(,0,0limx y →不存在,因此()()(),0,0lim,x x y f x y →不存在,从而(),x f x y 在点()0,0不连续.同理可证(),y f x y 在点()0,0不连续. 然而()(,0,00,00,0limx y f f x f y∆∆→∆-∆-∆()(22,0,0lim0x y ∆∆→==所以f 在原点()0,0可微.例2.9证明函数22220(,)0,0x y f x y x y +≠=⎪⎪+=⎩在原点两个偏导存在,但不可微.证明 由偏导数定义:000lim )0,0()0,0(lim )0,0(00=∆-=∆-∆+=→∆→∆x xf x f f x x x .同理可求得0)0,0(=x f .下面利用可微的定义来证明其不可微性. 用反证法.若函数f 在原点可微,则应是较22y x ∆+∆=ρ的高阶无穷小量,为此考察极限220limy x yx ∆+∆∆∆→ρ.当动点(,)x y 沿直线y mx =趋于(0,0)时,则(,)(0,0)2222(,)(0,0)limlim 11x y y mxx y xy m mx y m m →=→==+++. 这一结果说明动点沿不同斜率m 的直线趋于原点时,对应的极限值也不同.因此所讨论的极限不存在.故函数f 在原点不可微.结束语以上就是本文所讨论的函数的连续性和可微性,深刻的掌握其定义和用法很重要,掌握其解法能够简化或解决很多问题,这不仅可以体现在理论研究中,而且在处理许多实际问题时也别具特色.函数连续性和可微性的应用贯穿于初高等数学各部分的内容中,对其整理归纳可以提高我们分析问题和解决问题的能力.由于可微性在社会科学和自然科学的许多方面都有应用,它的解法灵活多样,因此本文的重点是能够运用初高等数学的相关知识灵活地解决实际问题;但有些题目只能用一些固定的方法来解决,这些方法有一定的局限性,因此本文的难点是掌握求积分的一些特殊的解法.本文主要是对函数连续性和可微性问题的类型和相应的解题方法进行较深入地探讨,以形成较完整的理论体系.通过本文的论述,我们可以更全面地了解连续性和可微性以及他们之间的联系,具有一定的应用价值.另外,熟练掌握此部分内容对数学的学习也大有帮助.在这一过程中,我们更系统地分析了连续性可微性问题的类型和解决方法,使我们更能体会到前人探索的艰辛,以及获得成功时的喜悦之情,从而激发了我们对数学的兴趣,当然由于多元函数连续性和可微性关系复杂,证明的方法也很多,加之我们的专业知识有限以及研究方法不成熟,文中难免出现不足之处.例如:对问题类型的讨论不够深刻和全面,由于求解解法的灵活性,本文只是归纳了部分连续性和可微性问题类型和解法,因此不能囊括所有的问题.总之,这篇论文还有很多地方值得商榷,望老师和同学们提出宝贵的意见.参考文献[1] 张禾端,高等代数(第三版),北京:高等教育出版社,1992年4月第九版[2] 马小土,硕士研究生入学考试1000题,第三版,北京:中国人民大学出版社,2000,4[3] 华东六省工科数学系列教材编委会.高等数学学习指导书[M].沈阳:辽宁科学技术出版社,1991[4] 李永乐,数学复习全书(理工类).高等数学[M].北京:国家行政学院出版社,2011[5] 徐森林,薛春华.数学分析(第二册)[M].北京:清华大学出版社,2006[6] 裴礼文.数学分析中的典型问题和解题方法[M].北京:高等教育出版社,1993[7] 清华大学数学科学系《微积分》编写组.微积分[M].北京:清华大学出版社,2004[8] 电子科技大学应用数学系编.微积分[M].成都:电子科技大学出版社,2000[9] 童武.全国硕士研究生入学考试历年试题精解(数学三)[M].北京:北京大学出版社,2004[10] 同济大学应用数学系编.高等数学[M].北京:高等教育出版社,2004,12[11] 同济大学应用数学系编.高等数学习题集[M].上海:上海财经大学出版社.2006,9[12] 童雪耐,对称区域上的积分,数学通报,1991[13] 刘玉链,数学分析讲义(下册,第三版),北京:高等教育出版社,1996[14] 张志军,熊德之.微积分及其应用[M].北京:科学出版社.2007[15] 华东师范大学数学系编.数学分析(第二版)[M]. 北京:高等教育出版社.1991致谢逝者如斯,不舍昼夜,四次春去春又来,岁月稍纵即逝.此时,回头想想这段短暂的求学路,时而喜悦,时而惆怅.在这个美丽的校园里,原本天真幼稚的我如今已蜕变成一个睿智、沉稳的青年,感谢命运的安排,让我有幸结识了许多良师益友,是他们教我如何品味人生,让我懂得如何更好的生活!人生处处是驿站,已是挥手作别之时,在此,向所有帮助过我的人献上我最诚挚的谢意!本学位论文是在我的指导老师宋强的亲切关怀与细心指导下完成的.从课题的选择到论文的最终完成,宋老师始终都给予了细心的指导和不懈的支持,并且在耐心指导论文之余,宋老师仍不忘拓展我们的文化视野,让我们感受到了‘可微性’的美妙与乐趣.值得一提的是,宋老师宅心仁厚,不慕荣利,对学生认真负责,在他的身上,我们可以感受到一个学者的严谨和务实,这些都让我们获益菲浅,并且将终生受用无穷.毕竟“经师易得,人师难求”,希望借此机会向宋老师表示最衷心的感谢!此外,本文最终得以顺利完成,也是其他同学的帮助分不开的,虽然他们没有直接参与我的论文指导,但在开题时也给我提供了不少的意见,提出了一系列可行性的建议,在此向他们表示深深的感谢!。
二元函数连续性、偏导数存在性及可微性的讨论

编号:Xxxxxxxx学校本科毕业论文二元函数连续性、偏导数存在性及可微性的讨论院系:数学科学系姓名:XXXX学号:XXX专业:XXXX年级:2008级指导教师:XXX职称:讲师完成日期:2012年5月摘要二元函数微分学是高等数学的重点之一,理清其基本概念之间的相互关系对于认识二元函数的性质有重要的意义,只有这样才能弄清楚二元函数连续、偏导数及可微之间的关系,才能更好地加以利用.本论文将重点对它们之间的关系加以总结和探讨,并给以证明和应用举例.本论文正文主要介绍了二元函数连续性、偏导数存在性及可微性的基本知识.对它们分别进行了总结证明和进一步讨论,还总结二元函数连续性、偏导数存在性及可微性的简单关系,并举出的例子加以论证支撑.关键词:二元函数;连续;偏导数;可微AbstractBinary Function Differential Calculus is one of the priorities of the higher mathematics, to clarify the basic concepts of the relationship between the significance for understanding the nature of the binary function, the only way to figure out the binary function continuous partial derivatives and differentiability the relationship between, in order to better take advantage of this paper will focus on the relationships between them to be summarized and discussed, and give proof of application example.In this thesis, the text introduces binary function continuity, partial derivatives of the Existence and differentiability of basic knowledge. Them a summary of the proof and further discussion, and also summarizes the continuity of the binary function, the partial derivatives exist and micro of simple relations, citing the examples to demonstrate support.Key words:Dual function; Continuously; Partial derivative; Differentiable目录摘要IABSTRACT II引言21 二元函数的连续、偏导数及可微三个概念的定义31.1二元函数的连续性31.2二元函数的可微性31.3二元函数的偏导数42 二元函数三个概念的结论总结及证明52.1二元函数连续性的结论总结及证明52.2二元函数可微性的结论总结及证明72.3二元函数偏导数存在性的结论总结113 二元函数三个概念之间关系的总结123.1二元函数连续性与偏导数存在性的关系及例证123.1.1 二元函数连续,但偏导不一定存在的举例证明123.1.2 二元函数偏导存在,但不一定连续的举例证明123.2二元函数可微性与偏导数存在性的关系及例证133.2.1 可微与偏导存在关系的举例证明133.2.2 偏导连续与可微关系的举例证明154 二元函数连续性、偏导数存在性及可微性关系的概图22结束语 23参考文献 24致谢 25引言二元函数微分学是一元函数微分学的推广,因此它保留了一元函数微分学的许多性质.但由于自变量由一个增加到两个,从而产生了某些本质上的新的内容.如一元函数微分学中,函数在某点可导,则它在这点可微,反之亦然.但在二元函数微分学中,函数在某点偏导数存在,推不出它在这点可微.又如,一元函数微分学中,函数在某点可导,则它在这点必连续.但在二元函数微分学中,函数在某点的偏导数都存在,却推不出它在这点连续.同时二元函数微分学是高等数学教学中的一个重难点,它涉及的内容实际上是微积分学内容在二元函数中的体现,其中有关二元函数的连续性、偏导数存在性及可微性之间的关系是学生在学习中容易发生概念模糊和难以把握的一个重要知识点.当前,二元函数的连续性、偏导数存在性及可微性之间的关系研究方面已经取得了一定的成果,但是,在国内的许多教材中只是对它们三者的定义作了说明,而对它们之间的关系很少提及或没有提到,在一般的教材中对于该部分内容的介绍比较粗略浅显,在一些学术性论文中也只是对二元函数的连续性、偏导数存在性及可微性的个别关系做了具体的说明,因此在让学生学习这方面的知识时能达到对这方面知识可以做到全面的掌握让是当前教学中的一大难题.本文具体就二元函数的连续性、偏导数存在性及可微性之间的关系通过实例作深入的探讨,就二元函数连续性、偏导数及可微性在教材相关内容的基础上进行进一步的探讨、研究,对教材内容做一些适当的补充和扩展,为后继课程的学习奠定基础.然后总结有关二元函数微分学中这关于二元函数连续性、偏导数存在性及可微性这三个概念之间的关系,并对二元函数具体的实例详细加以证明,建立他们之间的关系图.这样对有效理解和掌握多元函数微积分学知识将起到重要作用.1 二元函数的连续、偏导数及可微性概念二元函数的连续、偏导数及可微的概念都是用极限定义的,不同的概念对应不同的极限.考虑函数()y x f ,在点),(00y x 的情形,它们分别为: 1.1 二元函数的连续性定义1 设f 为定义在点集2D R ⊂上的二元函数,0P D ∈(它或者是D 的聚点,或者是D 的孤立点).对于任给的正数ε,总存在相应的正数δ,只要0(;)P U P D δ∈ ,就有 0()(),f P f P ε-<则称f 关于集合D 在点0P 连续,在不致误解的情况下,也称f 在点0P 连续.若f 在D 上任何点都关于集合D 连续,则称f 为D 上的连续函数. 由上述定义知道:若0P 是D 的孤立点,则0P 必定是f 关于D 的连续点;若0P 是D 的聚点,则f 关于D 在0P 连续等价于()()00lim P f P f DP P P =∈→1.2 二元函数的可微性与一元函数一样,在二元函数微分学中,主要讨论二元函数的可微性及其应用,我们首先建立二元函数可微性概念.定义 2 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 内有定义,对于()0P U 中的点()()y y x x y x P ∆+∆+=00,,,若函数f 在点0P 处的全增量z ∆可表示为:()()()ρο+∆+∆=-∆+∆+=∆y B x A y x f y y x x f z ,,00,其中A ,B 是仅与点0P 有关的常数,22y x ∆+∆=ρ,()ρο是较ρ高阶的无穷小量,则称函数f 在点0P 处可微,并称上式中关于x ∆,y ∆的线性函数A xB y ∆+∆为函数f 在点0P 的全微分,记作y B x A y x df dz P ∆+∆==),(|000 .由上可知dz 是z ∆的线性主部,特别当x ∆,y ∆充分小时,全微分dz 可作为全增量z ∆的近似值,即()())()(,,0000y y B x x A y x f y x f -+-+≈在使用上,有时也把()()()ρο+∆+∆=-∆+∆+=∆y B x A y x f y y x x f z ,,00写成如下形式y x y B x A z ∆+∆+∆+∆=∆βα,这里()()()()0lim lim 0,0,0,0,==→∆∆→∆∆βαy x y x1.3 二元函数的偏导数由一元函数微分学知道:若()x f 在点0x 可微,则函数增量()()()x x A x f x x f ∆++∆=-∆+ο00,其中()0x f A '=.同样,若二元函数f 在点),(00y x 可微,则f 在),(00y x 处的全增量可由()()()ρο+∆+∆=-∆+∆+=∆y B x A y x f y y x x f z 0000,,表示.现在讨论其中A 、B 的值与函数f 的关系.为此,在式子y x y B x A z ∆+∆+∆+∆=∆βα中令)0(0≠∆=∆x y ,这时得到z ∆关于x 的偏增量z x ∆,且有x x A z x ∆+∆=∆α或者α+=∆∆A xzx 现让0→∆x ,由上式得A 的一个极限表示式()()xy x f y x x f x z A x x x ∆-∆+=∆∆=→∆→∆000000,,lim lim,容易看出,上式右边的极限正是关于x 的一元函数()0,y x f 在0x x =处的导数.类似地,令)0(0≠∆=∆y x , 由yx y B x A z ∆+∆+∆+∆=∆βα又得到()()yy x f y y x f yz B y y x ∆-∆+=∆∆=→∆→∆00000,,l i mlim ,它是关于y 的一元函数()y x f ,0在0y y =处的导数.综上所述,可知函数()y x f z ,=在点),(00y x 处对x 的偏导数,实际上就是把y 固定在0y 看成常数后,一元函数()0,y x f z =在点0x 处的导数,同样,把x 固定在0x ,让y 有增量y ∆,如果极限存在,那么此极限称为函数()y x f z ,=在),(00y x 点处对y 的偏导数.记作()00,y x f y .因此,二元函数当固定其中一个自变量时,它对另一个自变量的导数称为偏导数,可定义如下:定义3 设函数()y x f z ,=,(,)x y D ∈.若00(,)x y D ∈,且()0,y x f 在0x 的某一邻域内有定义,则当极限()()()xy x f y x x f x y x f x x x ∆-∆+=∆∆→∆→∆00000000,,lim ,lim存在时,称这个极限为函数f 在点()00,y x 关于x 的偏导数,记作()00,y x f x 或),(00|y x x f∂∂ 注意 1 这里符号x ∂∂,y ∂∂专用于偏导数算符,与一元函数的导数符号dxd 相仿,但又有差别.注意 2 在上述定义中,f 在点()00,y x 存在关于x (或y )的偏导数,f 至少在{}δ<-=00,|),(x x y y y x (或{}δ<-=00,|),(y y x x y x )上必须有定义.若函数()y x f z ,=在区域D 上每一点()y x ,都存在对x (或对y )的偏导数,则得到函数()y x f z ,=在区域D 上对x (或对y )的偏导数(也简称偏导数),记作()y x f x ,或x y x f ∂∂),((()y x f y ,或yy x f ∂∂),(),也可简单地写作x f ,x z 或x f ∂∂(y f ,y z 或yf∂∂). 2 二元函数三个概念的进一步研究2.1 二元函数连续性的进一步研究一元函数若在某点存在左导数和右导数,则这个一元函数必在这点连续,但对于二元函数()y x f ,来说,即使它在某点()000,y x P 既存在关于x 的偏导数()00,y x f x ,又存在关于y 的偏导数()00,y x f y ,()y x f ,也未必在点()000,y x P 连续.不过,我们却有如下定理:定理1 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 内有定义,若()y x f ,0作为y 的一元函数在点y =0y 连续,()y x f x ,在()0P U 内有界,则()y x f ,在点()000,y x P 连续.证明 任取()y y x x ∆+∆+00,∈()0P U , 则()()0000,,y x f y y x x f -∆+∆+()()()()00000000,,,,f x x y y f x y y f x y y f x y =+∆+∆-+∆++∆- (1) 由于()y x f x ,在()0P U 存在,故对于取定的y y ∆+0, ()y y x f ∆+0,作为x 的一元函数在以0x 和0x +x ∆为端点的闭区间上可导,从而据一元函数微分学中的拉格朗日中值定理,存在θ∈(0 ,1) ,使()()()x y y x x f y y x f y y x x f x ∆∆+∆+=∆+-∆+∆+000000,,,θ将它代入(1) 式, 得()()0000,,y x f y y x x f -∆+∆+()()()000000,,,x f x x y y x f x y y f x y θ=+∆+∆∆++∆- (2)由于()∈∆+∆+y y x x 00,θ()0P U ,故()y y x x f x ∆+∆+00,θ有界,因而当()()0,0,→∆∆y x 时, 有00(,)0f x x y y x +∆+∆⋅∆→.又据定理的条件知,()y x f ,0在y =0y 连续,故当()()0,0,→∆∆y x 时, 又有0000(,)(,)0f x y y f x y +∆-→.所以, 由(2) 知, 有[]000000lim (,)(,)0x y f x x y y f x y ∆→∆→+∆+∆-=.这说明()y x f ,在点()000,y x P 连续.推论 1 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 内有定义,若()y x f ,0作为y 的一元函数在点0y y =连续,()y x f x ,在点()000,y x P 连续,则()y x f ,在点()000,y x P 连续.证明 由于()y x f x ,在点()000,y x P 连续,故()y x f x ,必在点()000,y x P 的某邻域内有界,因而据定理1 ,()y x f ,在点()000,y x P 连续.推论 2 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 内有定义. 若()y x f x ,在()0P U 有界, ()00,y x f y 存在,则()y x f , 在点()000,y x P 连续.证明 由于()00,y x f y 存在,故()y x f ,0作为y 的一元函数在点y =0y 连续,从而据定理1可得 ,()y x f ,在点()000,y x P 连续.推论 3 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 内有定义,若()y x f x ,在点()000,y x P 连续, ()00,y x f y 存在,则()y x f ,在点()000,y x P 连续.证明 由于()y x f x ,在点()000,y x P 连续,故()y x f x ,必在点()000,y x P 的某邻域内有界. 又由于()00,y x f y 存在,故()y x f ,0作为y 的一元函数在点0y y =连续,因而据定理1可得出 ,()y x f ,在点()000,y x P 连续.同理可证如下的定理2及其推论.定理 2 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 有定义,()y x f y ,在()0P U 内有界,()0,y x f 作为x 的一元函数在点x =0x 连续,则()y x f ,在()000,y x P连续.推论 1 设函数()y x f z ,=在点()000,y x P 的某邻域内()0P U 有定义, ()y x f y ,在点()000,y x P 连续, ()0,y x f 作为x 的一元函数在点0x x =连续,则()y x f ,在点()000,y x P 连续.推论 2 设函数()y x f z ,=在点()000,y x P 的某邻域内()0P U 有定义,()y x f y ,在()0P U 内有界, ()00,y x f x 存在,则()y x f ,在点()000,y x P 连续.推论 3 设函数()y x f z ,=在点()000,y x P 的某邻域()0P U 有定义, ()y x f y , 在点()000,y x P 连续, ()00,y x f x 存在,则()y x f ,在点()000,y x P 连续.2.2 二元函数可微性的进一步研究众所周知,一元函数中,可微性与可导是一回事,但在二元函数中情况就不同了.定理 3 函数(,)f x y 在点00(,)P x y 可微的充分必要条件是(,)f x y 在点00(,)P x y 的俩个偏导数都存在,且对0ε∀>,0δ∃>,当0000(,)(,)(,)(,)f x y f x y f x y f x y ε--+≤00()x x y y -+-.证明 必要性 已知函数(,)f x y 在点00(,)P x y 可微,故00(,)x f x y 与00(,)y f x y 存在,且00000000(,)(,)(,)()(,)()()x y z f x y f x y f x y x x f x y y y ορ∆=-=-+-+, 其中00()()x x y y ρ=-+-. 即0000(,)(,)(,)(,)f x y f x y f x y f x y --+[]000000(,)()(,)(,)x f x y x x f x y f x y =---+ []00000000(,)(,)()(,)(,)()y y f x y f x y y y f x y f x y ορ+---+于是,当00(,)(,)x y x y ≠时,有000000(,)(,)(,)(,)f x y f x y f x y f x y x x y y --+-+-000000(,)(,)(,)x f x y f x y f x y x x x x ρ--⋅--≤000000(,)(,)(,)()y f x y f x y f x y y y y y ορρρ--⋅--++000000(,)(,)(,)x f x y f x y f x y x x -≤--000000(,)(,)()(,)0(0)y f x y f x y f x y y y ορρρ-+-+→→-从而当0ρ→(即00(,)(,)x y x y →)时,000000(,)(,)(,)(,)0f x y f x y f x y f x y x x y y --+→-+-即0ε∀>,0δ∃>,当0x x δ-<与0y y δ-<且00(,)(,)x y x y ≠时,有000000(,)(,)(,)(,)f x y f x y f x y f x y x x y y ε--+<-+-所以,0ε∀>,0δ∃>,当0x x δ-<与0y y δ-<且00(,)(,)x y x y ≠时,有0000(,)(,)(,)(,)f x y f x y f x y f x y ε--+≤ 00()x x y y -+-.充分性 已知函数(,)f x y 在点00(,)P x y 两个偏导数存在,0ε∀>,0δ∃>,当0x x δ-<与0y y δ-<且00(,)(,)x y x y ≠时,有000000(,)(,)(,)(,)()f x y f x y f x y f x y x x y y ε--+≤-+-令00()()x x y y ρ=-+-,则当0ρ→时,有0000(,)(,)(,)(,)0f x y f x y f x y f x y ρ--+→于是当00(,)(,)x y x y ≠时,有000000(,)()(,)()x y y z f x y x x f x y f y y ∆--+-[]000000000(,)(,)(,)(,)(,)(,)()f x y f x y f x y f x y f x y f x y x x x x ⎡⎤---++-⎢⎥-⎣⎦0000000(,)(,)(,)()y f x y f x y f x y y y y y ⎡⎤-+--⎢⎥-⎣⎦从而有000000(,)()(,)()x y y z f x y x x f x y f y y ρ∆--+-=0000(,)(,)(,)(,)f x y f x y f x y f x y ρ--++0000000(,)(,)(,)()x f x y f x y x x f x y x x ρ⎡⎤---+⎢⎥-⎣⎦ 0000000(,)(,)(,)()0(0)x f x y f x y y y f x y x x ρρ⎡⎤---→→⎢⎥-⎣⎦ 所以,函数(,)f x y 在点00(,)P x y 可微.证毕.定理 4 若函数()y x f z ,=在()00,y x 点处,()y x f x ,连续()00,y x f y 存在(或()00,y x f x 存在,()y x f y ,连续),则函数()y x f z ,=在()00,y x 处可微.由此定理的条件仍有对一个偏导数(二元)连续性的要求.因而用来判断函数的可微性仍有较大的局限性.例如:对于函数2221sin (,)0,x x y f x y ⎧⎪+=⎨⎪⎩002222=+≠+y x y x , ())0(1cos )(21sin 2,2222222322≠+++-+=y x yx y x x y x x y x f x 有 ())0(1cos )(2,22222222≠+++-=y x yx y x y x y x f y ())0(1cos 21sin20,22≠-=x xx x x x f x 从而())0(21cos 21,2≠-=x xx x x f y 由于)0,(lim 0x f x x →和),(lim 0x x f y x →都不存在,因而),(y x f x 和),(y x f y 在点)0,0(都不连续.关于),(y x f 在点)0,0(的可微性,无论是根据教材中所介绍的定理,还是根据上述定理都不能给出肯定的结论.本文给出另一个可微的充分条件,它完全放弃对两个偏导数(二元)连续性的要求,因而对某些函数可微性的判定有独到的作用.为了叙述方便,引入如下概念.定义 如果对于函数),(y x f z =存在0>η,使得当η<∆y 时,),(00y y x f x ∆+存在,且当0→∆x 时,变量000000(,)(,)(,)(0),(,)0(0),x f x x y y f x y y f x y y x x y xx α+∆+∆-+∆⎧-+∆∆≠⎪∆∆=∆⎨⎪∆=⎩ 关于y ∆一直趋向于0,即对任意的0>ε,存在0>δ,当δ<∆<x 0时,对任意y ∆(y η∆<)都有(,)x y αε∆∆<成立,我们就称函数(,)z f x y =在点00(,)x y 关于y 对x 一致可导.类似地可定义),(y x f z =在点),(00y x 关于x 对y 一致可导.定理 5 若函数),(y x f z =在点),(00y x 有:),(00y x f y 存在,),(y x f 关于y 对x 一致可导,且),(y x f o x 在0y 连续,则),(y x f z =在点),(00y x 可微.证明: 因),(00y x f y 及),(00y y x f x ∆+)(η<∆y 存在,故有),(),(),(000000y x f y y x x f y x y -∆+∆+=∆),(),(),(),(00000000y x f y y x f y y x f y y x x f -∆++∆+-∆+∆+=[][]y y y x f x y x y y x f y x ∆∆++∆∆∆+∆+=)(),(),(),(0000βαy y y y x f x y x x y y x f y x ∆∆+∆+∆∆∆+∆∆+=)(),(),(),(0000βα(3)其中),(y x ∆∆α如前述定义,而0)(→∆y β()0,0→∆→∆y x ), 于是有0)(lim22=∆+∆∆⋅∆→∆→∆yx yy y x β (4)又因为),(0y x f x 在0y 连续,故有),(),(lim 000000y x f y y x f x y x x =∆+→∆→∆ (5)再由),(y x ∆∆α所具备的性质知,对任意0>ε,存在)(0ηδδ<>,当δδ<∆<∆y x ,且022≠∆+∆y x 时,有εα<∆∆),(y x 此即0),(lim 00=∆∆→∆→∆y x y x α从而0),(lim220=∆+∆∆∆∆→∆→∆yx xy x y x α (6)综合(3)——(6)式即得[]0),(),(),(lim2200000000=∆+∆∆+∆-∆→∆→∆y x yy x f x y x f y x f y x y x可见),(y x f 于),(00y x 可微.显然,调换定理条件中x f 和y f 的位置,结论仍然成立.指出,尽管定理5已完全放弃对两个偏导数的(二元)连续性要求,但它所给出的条件仍然不是可微的必要条件.因此,如何用两个偏导数所应具备的性质来等价地刻画二元函数的可微性,就需要进一步的探讨,这对以后仍是大我们还要有裨益的.1. 若果f 在点),(00y x 处不连续或偏导数不存在,则f 在点),(00y x 处不可微.2. 若果f 在点),(00y x 处连续,存在),(00y x f x 、),(00y x f y ,则f 在点),(00y x 处可微的充分必要条件是满足下列等价的任一式: (1) ),(),(0000y x f y y x x f z -∆+∆+=∆220000(),(),(y x y y x f x y x f y x ∆+∆+∆+∆=ε其中0→ε(当0,0→∆→∆y x )(2) ),(),(0000y x f y y x x f z -∆+∆+=∆y x y y x f x y x f y x ∆=∆+∆+∆=210000),(),(εε 其中120,0εε→→(当0,0→∆→∆y x 时)推论 4 若二元函数(,)z f x y =在00(,)x y 处两个偏导数00(,)x f x y ,00(,)y f x y 均存在,且00(,)xy f x y 或者00(,)yx f x y 存在,则函数(,)f x y 在00(,)x y 处可微.证明 不妨设00(,)xy f x y 存在(00(,)yx f x y 存在的情形可作类似证明).因为000000(,)(,)(,)limx x xy y y f x y f x y f x y y y →-=-所以000lim (,)(,)x x y y f x y f x y →=,即0(,)x f x y 在0y y =处连续.根据定理3可知函数(,)f x y 在00(,)x y 处连续. 2.3 二元函数偏导数存在性进一步研究二元函数()y x f ,在点),(0o y x 的两个偏导数有明显的几何意义:设)),(,,(00000y x f y x M 为曲面),(y x f z =上的一点,过0M 作平面0y y =,截此曲面得一曲线,此曲线在平面0y y =上的方程为),(0y x f z =,则导数0|),(0x x y x f dxd→, 即偏导数),(00y x f x ,就是这曲线在点0M 处的切线x T M 0对x 轴的斜率.同样,偏导数),(00y x f y 的几何意义是曲面被平面0x x =所截得的曲线在点0M 处的切线y T M 0对y 轴的斜率.我们已经知道,如果一元函数在某点具有导数,则它在该点必定连续.但对于二元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续.这是因为各偏导数存在只能保证点P 沿着平行于坐标轴的方向趋于0P 时,函数值)(p f 趋于)(0p f ,但不能保证点P 按任何方式趋于0P 时,函数值)(p f 都趋于)(0p f .3 二元函数三个概念之间关系的总结3.1 二元函数连续性与偏导数存在性的关系及例证对一元函数来说,可导必连续.但对二元函数来说,即使x f ,y f 存在但f 也不一定连续.事实上,对于二元函数来说,函数在一点处的偏导数存在和函数在该点处连续是没有必然联系的.下面加以说明这个问题. 3.1.1 二元函数连续,但偏导不一定存在的举例证明例 1 讨论函数()22,y x y x g +=在点()0,0处的连续性和偏导数是否存在? 解: 由()()()()()220,0,0,0,lim,lim y x y x g y x y x +=→→0=(0,0)g =可知函数()22,y x y x g +=在点()0,0连续. 而由偏导数定义:0(0,0)(0,0)(00)limx x g x g f x∆→+∆-=∆2001,0lim lim 1,0x x x x x x x x ∆→∆→∆>∆⎧∆===⎨-∆<∆∆⎩该极限()0,0x g 不存在,同理可证()0,0y g 也不存在. 所以函数),(y x g 在()0,0点的偏导数不存在. 由此说明,二元函数在一点连续,偏导数未必存在. 3.1.2 二元函数偏导存在,但不一定连续的举例证明例 2 函数()22,,1,x y f x y ⎧+=⎨⎩ 00≠=xy xy 在点()0,0处()0,0x f ,()0,0y f存在,但不连续.证明 由偏导数定义:()()()xf x f f x x ∆-∆+=→∆0,00,0lim 0,00 0lim x x ∆→=∆0= 同理可求得 ()0,00y f = 因为()()()()()()()22,0,0,0,0lim,lim00,01x y x y f x y x y f →→=+=≠=故函数()22,,1,x y f x y ⎧+=⎨⎩00≠=xy xy 在点()0,0处不连续.综上可见,对于二元函数()y x f ,在某点()00,y x 的连续性与偏导数存在,两者之间没有必然的联系,即()y x f ,在某点()00,y x 偏导数存在与否,与其在该点是否连续无关.但如果假定函数的各个偏导数有界,即有下面命题:命题 1 如果二元函数f 在点00(,)P x y 的某邻域()U P 内的偏导数x f ,y f 有界,则f 在()U P 内连续.证明 由x f ,y f 在()U P 内有界,设此邻域为1(,)U P δ,存在0M >,使x f M <,y f M < ,在1(,)U P δ内成立,由于12(,)(,)(,)(,)x y Z f x x y y f x y f x x y y x f x y y y M x M yθθ∆=+∆+∆-=+∆+∆∆++∆∆≤∆+∆(其中120,1θθ≤≤).所以对任意的正数ε,存在1,2(1)M εδδ⎧⎫=⎨⎬+⎩⎭,当,x y δδ∆<∆<时,有(,)(,)f x x y y f x y ε+∆+∆-<,故f 在(,)U P δ内连续.3.2 二元函数可微性与偏导数存在性的关系及例证 3.2.1 可微与偏导存在关系的举例证明定理 6 (可微的必要条件)若二元函数()y x f z ,=在其定义域内一点()000,y x P 处可微,则f 在该点关于每个自变量的偏导数都存在,且()()()000000|,,,x x d x y f x y dx f x y dy =+ ,()00,y x f A x =,()00,y x f B y =. 证明 由于()y x f ,在点),(000y x P 可微,则())(),(,0000ρο+∆+∆=-∆+∆+=∆y B x A y x f y y x x f z其中,y x ∆∆,为自变量y x ,的该变量,B A ,仅与点),(000y x P 有关,而与y x ∆∆,无关,22y x ∆+∆=ρ.若令0y y =即0=∆y ,于是x ∆=ρ,故)(x x A z ∆+∆=∆ο可见xx A x z∆∆+=∆∆)(ο,Axx A x zy x f x y x x =∆∆+=∂∂=→∆))((lim |),(0),(0000ο,即()A y x f x =00,,类似可证()B y x f y =00,.可见,对于二元函数,偏导数的存在是函数),(y x f z =可微分的必要条件.但是偏导数的存在不是函数可微分的充分条件.事实上,当一个二元函数),(y x f z =在点),(y x 处的偏导数yzx z ∂∂∂∂,都存在时,尽管形式上可以写成式子y y zx x z ∆∂∂+∆∂∂,但是它与z ∆之间可以不是22y x ∆+∆=ρ的高阶无穷小,因而由定义,此时函数),(y x f z =在点),(y x 处是不可微的.注 1:定理5的逆命题不成立.即二元函数()y x f ,在点()000,y x P 处的偏导数即使存在也不一定可微.下面用例3说明函数在一点的偏导数存在,但函数在该点却不可微.例 3 证明函数()22,,0,xy x y f x y ⎧⎪+=⎨⎪⎩002222=+≠+y x y x 在原点两个偏导数存在,但不可微.证明 由偏导数的定义:()()()xf x f f x x ∆-∆+=→∆0,00,0lim0,00=000lim0x x∆→-=∆同理可证()0,00y f =,即在原点关于x 与y 的偏导数存在. 下面利用可微的定义来证明其不可微 用反证法:若函数f 在原点可微,则())(()()00,00,00,00,0y f df f x y f f dx f dy ⎡⎤⎡⎤∆-=+∆+∆--+⎣⎦⎣⎦ 22x y x y∆∆=∆+∆应是较22y x ∆+∆=ρ的高阶无穷小量,为此考察极限2200limlimy x yx dff ∆+∆∆∆=-∆→→ρρρ当动点()y x ,沿直线mx y =趋于()0,0时, 则()()()()220,0,220,0,11lim limm mm m y x xy y x mx y y x +=+=+→=→ 这一结果说明动点沿不同斜率m 的直线趋于原点时,对应的极限值也不同,因此所讨论的极限不存在.故函数f 在原点不可微. 3.2.2 偏导连续与可微关系的举例证明定理 7 (可微的充分条件) 若二元函数()y x f z ,=的偏导在点()000,y x P 的某邻域内存在且x f 与y f 在点()000,y x P 处连续,则函数()y x f ,在点()000,y x P 可微.可微的充分条件可以改进: 如果函数()y x f z ,=满足以下条件: 1. (,)x f x y 在点00(,)x y 处存在;2. (,)y f x y 在点00(,)x y 的某个邻域内存在;3. (,)y f x y 在点00(,)x y 处连续; 则(,)f x y 在点00(,)x y 处可微.证明 由于00(,)x f x y 存在,即有:0000000(,)(,)lim (,)x x f x x y f x y f x y x ∆→+∆-=∆ 即:0000(,)(,)(,)x f x x y f x y f x y xα+∆-=+∆(其中0lim 0x α∆→=)则000000(,)(,)(,)x f x x y f x y f x y x x α+∆-=⋅∆+⋅∆由于(,)x f x y 在点00(,)x y 的某个邻域内存在,不妨设(,)y f x y 在ω={01(,)|x y x x ψ-<且02y y ψ-<}内存在设0()(,)g y f x x y =+∆并规定1x ψ∆<则()g y 在20|2y y y ψ⎧⎫-≤⎨⎬⎩⎭上每一点都存在,从而()g y 在20|2y y y ψ⎧⎫-≤⎨⎬⎩⎭上每一点都连续,规定:22y ψ∆≤则根据中值定理存在1y ,使得:001()()()g y y g y g y y +∆-=∆(其中10y y y -≤∆)即:000001(,)(,)(,)y f x x y y f x x y f x x y y +∆+∆-+∆=+∆⋅∆当220x y ∆+∆→且0y ∆→ 从而有00x x x +∆→,10y y →又由于0100(,)(,)y y f x x y f x y +∆=在点00(,)x y 处连续0100(,)(,)y y f x x y f x y β+∆=+其中220lim 0x y β∆+∆→=则000000(,)(,)(,)y f x x y y f x x y f x y y y β+∆+∆-+∆=⋅∆+⋅∆综上所述有:0000(,)(,)f x x y y f x y +∆+∆-[][]00000000(,)(,)(,)(,)f x x y y f x y f x x y y f x y =+∆+∆-++∆+∆- 0000(,)(,)x y f x y x x f x y y y αβ=∆+⋅∆+∆+⋅∆又由于2222lim0x y x yx yαβ∆+∆→⋅∆+⋅∆=∆+∆故(,)f x y 在点00(,)x y 点可微.证毕.教材中关于二元函数的微分一般只是分别给出了必要条件和充分条件,对可微的充要条件涉及比较少.偏导数的存在是函数可微的必要条件而不是充分条件,但是,如果在假设函数的各个偏导数连续,则函数是可微的.但此条件给的太强,于是我们总结了判别二元函数在某点可微的一个充分条件,可对此定理的条件进行减弱,得出:定理 8 若函数()y x f z ,=在点()000,y x P 的邻域G 内()y x f x ,连续,()00,y x f y存在,则函数f 在点()00,y x 可微.证明 全增量()),(,0000y x f y y x x f z -∆+∆+=∆[][]),(),(),(),(00000000y x f y y x f y y x f y y x x f -∆++∆+-∆+∆+=这里第一个括号是当y y y ∆+=0时函数关于x 的增量,而第二个括号则是当0x x =时函数关于y 的增量,对于它们分别应用一元函数的拉格朗日中值定理,得()y y y x f x y y x x f z y x ∆∆++∆∆+∆+=∆),(,200010θθ )1,0(21<<θθ 由于()y x f x ,,()00,y x f y 在点()00,y x 连续,因而有()αθ+=∆+∆+),(,00010y x f y y x x f x x ,()βθ+=∆+),(,00200y x f y y x f y y , 其中当)0),((→∆∆y x 时,0,0→→βα.所以()()y x y y x f x y y x f z y x ∆+∆+∆+∆=∆βα0000,, 令22y x ∆+∆=ρ,则当0→ρ时,ερρβραρβα⋅=∆+∆=∆+∆)(yxy x 是关于ρ的高阶无穷小.事实上,由于βαρβραε+≤∆+∆=yx而当0→ρ时0→ε,即)(ροερβα=⋅=∆+∆y x .这就证明了),(y x f z =在点),(00y x 是可微的.例 4 求证21sin ,0(,)0,0x e y y y f x y y ⎧≠⎪=⎨⎪=⎩在点(0,0)可微.证明 因为0(,)(,)(,)lim x f f x x y f x y x y x x∆→∂+∆-=∂∆22011sin sin limx x x x e y e y y yx+∆∆→-=∆201sin (1)limx xx e y e yx∆∆→-=∆21sin(0)x e y y y=≠0(,)(,)limy f f x y y x y x y∆→∂+∆=∂∆ 22011()sin sin limx x y e y y e y y y yy∆→+∆-+∆=∆11112sincos (2sin cos )x x x e y e e y y y y y=-=-.(0)y ≠ 00(,0)(,0)00(,0)lim lim 0x x f f x x f x x x xx ∆→∆→∂+∆--===∂∆∆同理(0,)0fy y∂=∂ 即21sin ,0(,)0,0x e y y f y x y x y ⎧≠∂⎪=⎨∂⎪=⎩ 11(2sin cos ),0(,)0,0xe y yf y y x y x y ⎧-≠∂⎪=⎨∂⎪=⎩于是(0,0)(0,0)0x y f f == 又2001lim sin0x x y e y y∆→X →=, 所以(,)x f x y 在点(0,0)连续. 但0011lim (2sincos )x x y e y y y∆→X →-不存在,即(,)y f x y 在(0,0)点不连续. 又定理8可知(,)f x y 在点(0,0)可微.显然,与传统的判别方法相比,这个充分条件更加减弱了判别条件,进一步阐明了二元函数偏导数与可微性的关系,使适用范围扩大,适用性加强.注意 这个条件是可微的充分条件并非必要条件,即()y x f z ,=在()00,y x 的邻域G 内()00,y x f y 存在但()y x f x ,不连续,但()y x f ,在点()00,y x 也可微.下面我们用例5说明函数在一点可微,但它的偏导数在该点却不连续. 例 5 求函数()()22221sin ,,0,x y x y f x y ⎧+⎪+=⎨⎪⎩ 002222=+≠+y x y x ,在原点()0,0处,(1)()0,0y f 是否存在 (2)x f 是否连续(3)是否可微.解 (1) 由定义知()()()0,0,00,0limx y f y f f y∆→∆-=∆221sinlim 0y y y y∆→∆∆==∆所以()0,0y f 存在.(2) 因为当022≠+y x 时,()y x f ,偏导数存在,故()⎪⎩⎪⎨⎧⎪⎪⎭⎫⎝⎛++-+=,0,1cos 11sin 2,222222y x y x y x x y x f x 002222=+≠+y x y x , 而()y x f x y x ,lim 00→→不存在,故()y x f ,在原点不连续.(3)法 1:因()()200,00,01(0,0)limlim sin 0x x x f x f f x x x→→-=== ()()2000,0,01(0,0)limlim sin 0y y y f y f f y y y→→-=== 则()()0,00,00x y df f dx f dy =+=()22221,(0,0)()sinf f x y f x y x y∆=-=++ 221sinρρ=(()22,:0x y x y ∀+≠)从而2221sin1limlimlim sin0f dfρρρρρρρρρ→→→∆-===即函数(),f x y 在点()0,0可微.法 2:(0,0)0x f =,(0,0)0y f =,(0,)(0,0)(0,0)lim00x x xy y f y f f y →-==-即(0,0)x f ,(0,0)y f 存在,且(0,0)xy f 存在.根据推论4可知题设所给函数(,)f x y 在(0,0)处可微.3.3 二元函数连续性与可微性的关系及例证类似于一元函数的连续性与可导性间的关系,即二元函数(),f x y 在点()000,P x y 可微,则必连续.反之不然.定理 9 若二元函数()y x f ,在其定义域内一点()y x ,可微,则f 在该点必然连续.证明 事实上()ρο+B∆+A∆=∆y x z ,0lim 0=∆→z ρ,()()[]()y x f z y x f y y x x f y x ,,lim ,lim 0=∆+=∆+∆+→→∆→∆ρ故f 在()y x ,连续.注意 函数()y x f ,在某点()y x ,可微,则()y x f ,在该点连续;但()y x f ,在某点()y x ,连续,函数在该点却不一定可微.例 6 证明函数(),||f x y xy =在点()0,0连续,但它在点()0,0不可微.证明 (1) 因为()()000lim ,lim ||00,0x x y y f x y xy f →→→→===,故函数(),||f x y xy =在点()0,0连续.(2) 因为(0,0)(0,0)||||f f x y f x y ∆=+∆+∆-=∆∆()()0,00,00x y df f dx f dy =+=所以 2200||||limlim()()x y x y f dfx y ρρ→∆→∆→∆∆∆-=∆+∆当动点(),x y 沿直线y x =趋于()0,0时,有2200||||1lim02()()x y x y x y ∆→∆→∆∆=≠∆+∆ 即0lim0f dfρρ→∆-≠,故(),f x y 在原点()0,0不可微.例 7 函数y x y x f +=),(在点)0,0(处连续,但在)0,0(点不可微. 解: 因为()()()()())0,0(0)(lim ,lim0,0,0,0,f y x y x f y x y x ==+=→→所以y x y x f +==),(在点)0,0(处连续. 又因为xx x f x f f x x x ∆∆=∆-∆+=→∆→∆00l i m )0,0()0(l i m)0,0(,此极限不存在;同理)0,0(y f 的极限也不存在.因此不能把)(ρο+∆+∆=∆y B x A z 的形式.4 二元函数连续性、偏导数存在性及可微性关系的概图如果函数(),z f x y ∆=在点(,)x y 可微分,则函数在该点必连续,反之不一定成立.如果函数(),z f x y ∆=在点(,)x y 可微分,则函数在该点的偏导数必存在,反之一定成立.如果函数(),z f x y ∆=在点(,)x y 连续,则偏导不一定存在. 如果函数(),z f x y ∆=在点(,)x y 偏导存在,则不一定连续.如果函数(),z f x y ∆=在点(,)x y 偏导连续,则函数在该点必可微,反之不一定成立.综上所述二元函数连续性、偏导数存在性及可微性的关系如下图所示.偏导连续可微连续偏导存在结束语本文对二元函数连续性、偏导数存在性及可微性之间关系的讨论,根据分析可以看出二元函数连续性、偏导数存在性及可微性之间的关系比一元函数连续、导数存在及可微之间的关系要复杂的多,究其原因主要在于二元函数极限比一元函数极限对自变量的要求更高、更复杂.如0lim ()x x f x →只要求在x 从0x 的左右俩侧趋向于0x 时,()f x 趋于同一值.而对()()()00,,lim,x y x y f x y →要求点(),x y 以任何方式趋向于点()00,x y 时,(),f x y 都趋向于同一极限,任何方式包含了x 与y 的不同关系以及趋向时的不同路径,从而导致二元函数产生了二重极限与累次极限的区别,正是由于二元函数极限的这种复杂性导致了二元函数诸多关系的复杂性.依据本文的分析得出它们三者之间的关系,不但对学习是一种积极的推动作用,有助于使学生对这方面的知识不会产生干扰,能较好地辨别它们之间的本质区别,使得原有知识更加牢固,也同时抓住了函数的本质.这方面的知识繁多,证明的方法难易悬殊,使用技巧各异,而且同一问题也可用多种不同方法来解决. 二元函数连续性、偏导数存在性及可微性之间关系的知识是人类智慧最伟大的成就之一,是数学上的伟大创造,它现在广泛影响着生产技术和科学的发展,如今已是广大科学工作者以及技术人员不可缺少的工具.以上我从比较初等的方法入手,进而对二元函数连续性、偏导数存在性及可微性的若干概念、定理、性质等内容这一方面的内容作了浅显的论述,将初等数学和高等数学的有关内容衔接起来,从而在整体上更好地理解有关这方面的知识.至于解决具体问题时个人可依据知识的储备、问题的要求来进行方法的选择.本文列举了二元函数连续性、偏导数存在性及可微性这方面的知识和证明方法,根据证明方法、举例、适用范围进行了归纳总结,力求有理论依据、有例题参考、有实用价值.从定义出发证明是最“原始”的做法,不易被人想到,但它在证明中确有其优势.证明的方法应该还有很多,对于其它新的方法有待于进一步探索与研究.为此,我们有必要学习好、掌握好二元函数连续性、偏导数存在性及可微性之间的关系这方面的知识,配以先进的管理观念和现代化的通信、网络、计算机技术,尽可能的把这些知识灵活运用推广,满足其他行业对这些知识的需要,创造更好的经济效益和社会效益.参考文献[1] 华东师范大学数学系. 数学分析(下)[M] . 北京: 高等教育出版社,2001: 100 –112[2] 吉米多维奇. 数学分析习题集[M] . 北京: 人民教育出版社, 1958: 62-78[3]马振民. 数学分析的方法与技巧选讲[M]. 兰州: 兰州大学出版社, 1999: 36-54.[4] 裴礼文. 数学分析中的典型问题与方法[M]. 北京: 北京高等教育出版社, 1993: 86-97.[5] 华东师范大学数学系. 数学分析[M] . 北京: 人民教育出版社, 1981: 137-160.[6] 李超. 有关多元函数连续性的几个新结论[J]. 韶关学院学报(自然科学版).2002,23(6): 1-6.[7] 周良正,王爱国. 偏导数存在,函数连续及可微的关系[J]. 高等函授学报(自然科学版).2005,19(5): 1-4.[8] 何鹏,余文辉,雷敏敛. 二元函数连续、可偏导、可微等诸条件间关系的研究[J]. 南昌高专学报. 2005,61(6): 1-2.[9] 黄梅英. 浅谈二元函数可微性[J]. 三名师专学报. 2000,17(1): 1-5.[10] 龚俊新. 二元函数连续、偏导、可微之间的关系[J]. 湖北师范学院学报(自然科学版).2000.23-24.[11] 同济大学数学教研室主编.高等数学(下册)(第四版)[M]. 高等教育出版社,.2000,20(3): 1-3.[12] 张郑严. 关于二元函数可微性定理的探讨[J]. 西北建筑工程学院报,.1993.4,46-48.[13] 高敏艳. 二元函数可微性定理的一个新的证明[J]. 天津师范大学学报(自然科学版),1999,19(3): 71-72.[14] 吴良森,等. 数学分析学习指导书.高等教育出版社, 2004.9.[15] 刘玉琏,傅沛仁. 数学分析讲义(三版).高等教育出版社, 2001.2.[16] 刘玉琏,等. 数学分析讲义学习辅导书(二版).高等教育出版社, 2004.7.[17] 罗炳荣. 《数学》(报考理工科研究生复习指导丛书).湖南科学技术出版社,.高等教育出版社,1985.327.。
微积分第八章

利用函数全增量的概念,连续定义可用另一种形式表述.
三、 二元函数的连续性
函数z=f(x,y)在点(x0,y0)的某邻域内有定义, 当自变量x,y分别由x0变到x0+Δx,y0变到y0+Δy时, 函数z=f(x,y)有增量
f(x0+Δx,y0+Δy)-f(x0,y0) 称其为函数z=f(x,y)在点(x0,y0)的全增量,记 为Δz,即
P0(x0,y0)处连续.
如果函数z=f(x,y)在区域D内各点都连续,则称函数
z=f(x,y)在区域D内连续.
三、 二元函数的连续性
对于闭区域上的连续函数z=f(x,y),则要求
函数z=f(x,y)在区域D内和边界上都连续.当点
P0(x0,y0)
D
中的P→P0是指P在区域D内所取的路线趋近于点
P0(x0,y0),极限中满足0<(x-x0)2+(y-y0)2<δ
图 8-7
一、多元函数的概念
定义域D就是曲面在xOy面上的投影区域. 例如,函数z=a2-x2-y2(a>0)的图形是球心在原点、 半径为a的上半球面(见图8-8).
图 8-8
二、 二元函数的极限
与一元函数情况类似,对于二元函数z=f(x,y),我们 需要考察当自变量x,y无限趋近于常数x0,y0时,即当点 P(x,y)无限逼近于点P0(x0,y0)时,对应的函数值的变化趋 势,这就是二元函数的极限问题.
微积分中的一元函数和二元函数

微积分中的一元函数和二元函数在数学学习中,微积分是一个必不可少的领域,而微积分中的一元函数和二元函数是其中的重要内容。
一元函数简单来说就是一个自变量只有一个的函数,比如y = f(x)。
而二元函数有两个自变量,比如z = f(x,y)。
这两个概念在微积分中有着不同的应用。
一元函数是微积分的基础,它的研究是微积分的起点。
一元函数在微积分中有着很大的应用,它可以用来描述许多物理现象,比如物体的移动、物流的变化等等。
同时,它也可以用来求解曲线和曲面的面积、体积以及最大值、最小值等等。
在微积分中,一元函数的导数是十分重要的概念。
通过求导,我们可以得到一元函数的图像上某一点的斜率,从而得到该点的变化趋势。
同时,导数还可以用来求函数的最大值和最小值,以及函数的增减性、凸凹性等等。
而二元函数则相对来说更加复杂一些。
它包含了两个自变量,因而带来了更多的维度、更多的变化。
二元函数在微积分中也有
着不同的应用。
它可以用来描述三维物体的表面,以及三维物体内部某一点的值等情况。
在微积分中,二元函数的偏导数是其中的重要概念。
它在二元函数的图像上描述了某一点处某一个自变量的变化对应的因变量的变化趋势。
同时,偏导数还可以用来描述二元函数的最大值、最小值以及凸凹性等等。
总的来说,微积分中的一元函数和二元函数都是其中重要的部分。
从它们的应用中可以看出,这两个概念在各自的领域中都有着重要的作用。
而在微积分中,它们则是求解问题和研究事物的基础和关键。
多元函数微分法和应用

第8章多元函数微分及其应用第一卷研究一元函数的微分方法。
利用这些知识,我们可以求出直线上质点运动的速度和加速度,也可以求出曲线切线的斜率。
还不够,因为一元函数只研究由一个因素决定的事物。
一般来说,对自然现象的研究总是离不开时间和空间。
需要三个坐标来确定空间中的点。
因此,一般物理量往往取决于四个变量。
在某些问题中,需要考虑更多的变量。
这样,就有必要研究多元函数的微分。
多元函数微分是一元函数微积分的扩展,所以多元函数微积分与一元函数微积分有很多相似之处,但也有很多不同之处。
学生在学习这部分时要特别注意他们的差异。
地方。
一、教学目标和基本要求(1)了解多元函数的概念。
(2)了解两个变量的函数的极限和连续性的概念,与有界封闭区域上的连续函数的性质有关。
(3)了解偏导数和全微分的概念,了解全微分存在的充要条件,并在近似计算中应用全微分。
(4)了解方向导数和梯度的概念,掌握它们的计算方法。
(5)掌握复合函数一阶和二阶偏导数的计算方法。
(6)找到隐函数的偏导数,包括那些由方程组确定的函数。
(7)了解曲线的切面和法线以及曲面的切面和法线,掌握它们的方程。
(8)理解多元函数极值的概念,找出函数的极值。
了解条件极值的概念,利用拉格朗日乘子法求条件极值,解决一些比较简单的最大值和最小值的应用问题。
二、教学内容及课时分配:第 1 节多元函数的基本概念 2 小时第二部分偏导数 1 学分第三个全差1学分第 4 节多元复合函数的导数规则 2 小时练习课2小时第五节隐函数2小时的推导公式第六节多元函数微积分的几何应用2学分第七节方向导数和梯度 2 学分第 8 节多元函数的极值及其方法 2 小时练习课2小时三、教学内容的重点和难点:强调:1.多元函数的极限和连续性;2.偏导数的定义;总微分的定义3.多元复合函数的推导规则;隐函数的推导规则4.方向导数和梯度的定义5.如何找到多元函数的极值和最大值困难:1.多元函数微分的几个概念,即多元函数极限的存在性、多元函数的连续性、偏导数的存在性、全微分的存在性、连续性的关系偏导数;2.在多元复合函数的求导规则中,抽象函数的高阶导数;3.由方程组确定的隐函数的推导规则;4.梯度大小和方向的重要性;5.如何找到条件极值四、教学内容的深化与拓宽:1.多元函数微积分几个概念的深厚背景;2.多元复合函数求导法则的应用;3.由方程确定的隐函数,推广到由方程组确定的隐函数4.利用多元函数微积分的知识研究空间曲线和曲面的性质;5.将偏导数的概念推广到方向导数,从而得到梯田的概念6.利用多元函数微积分的知识研究无条件极值和条件极值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元函数与二元函数在微积分学上的差异.doc
微积分学是一门研究函数变化的学科,主要包括微分和积分两部分。
在微积分学中,最基本的概念就是函数。
函数是一种将一个自变量映射到一个因变量的数学映射,很多计算问题都可以使用函数来表示、分析和求解。
在微积分学中,函数被分为两种:一元函数和二元函数。
这两种函数的差异如下:
一、定义
一元函数是只有一个自变量的函数,通常用f(x)的形式来表示,其中x代表自变量的值。
例如,f(x) = x^2是一个一元函数,它表示x的平方值。
二、求导和偏导
求导是微积分中的重点之一,它是指对于一个函数,求出它的导数,用来描述函数的变化率。
对于一元函数f(x),它的导数可以用f'(x)来表示,表示f(x)的变化率;而对于二元函数f(x,y),它的导数就被称为偏导数,用∂f(x,y)/∂x或∂f(x,y)/∂y表示,表示
f(x,y)在x或y方向上的变化率。
也就是说,对于二元函数,从一个方向变化时,它的导数可能不同,需要分别计算偏导数。
三、积分
综上所述,一元函数和二元函数在微积分学上有很大的差异。
一元函数只有一个自变量,因此求导和积分都很直观;而二元函数则需要用偏导数和重积分来描述其变化和面积体积的计算。
对于学习微积分的人来说,需要知道这两种函数之间的区别,并且能够熟练掌握其计算方法,才能够更好地应用微积分解决实际问题。
