《弹性力学》习题库

合集下载

弹性力学习题库

（2）沿与水平面成30°倾角的微面上的全应力和正应力。
l30o 1/ 2, m30o 3 / 2
px xl xym py xyl ym
px
2 2
30, py
1 2
0
y
C
0
30
O
° 0
0
B 45°
0
x
A
n l2 x m2 y 2lm xy
n
1 2
30
例 2.4.1
例2.4.1：当应变为常量时，ex =a, ey =b , gxy =c ，试求对应的位移分量。
x2 y2
f
(x)
(2)将 x代y 入平衡微分方程第二式
xy
3q0 h3l
x2 y2
f
(x)
y
y
xy
x
fy
0
y
2q0 h3l
xy3
f
(x) y
g(x)
例 2.3.1
例2.3.1：在负载结构中，某点O处的等厚平行四面体各面的受力情况如图所示（平面应力状态）。试求（1）主应力的大小及方向（2）沿与水平面成30°倾角的微面上的全应力和正应力。
先求应力分量 x , y , xy ：
y
C
0
30
O
° 0
0
B 45°
0
x
A
CB面上
y 0, xy 0
例 2.3.1
先求应力分量 x , y , xy ：
AB面上: 方向向量:
2
2
l45o 2 , m45o 2
y
C
0
30
O
° 0
n lm(σ y σx ) (l 2 m2 ) xy

弹性力学试题及答案

弹性力学试题及答案一、选择题（每题10分，共40分）1. 在弹性力学中，下列哪个物理量表示应变能密度？A. 应力B. 应变C. 位移D. 应力能密度答案：D2. 在平面应力状态下，下列哪个方程是正确的？A. σ_x + σ_y = 0B. σ_x + σ_y = σ_zC. σ_x + σ_y = τ_xyD. σ_x + σ_y = 0答案：D3. 在弹性体中，应力与应变之间的关系可以用下列哪个关系式表示？A. σ = EεB. σ = GγC. τ = μγD. σ = λε答案：A4. 在弹性力学中，下列哪个方程表示平衡方程？A. σ_x + σ_y + σ_z = 0B. ε_x + ε_y +ε_z = 0 C. τ_xy = τ_yx D. σ_x + σ_y + σ_z = F答案：D二、填空题（每题10分，共30分）1. 弹性力学中的基本假设有：连续性假设、线性假设和________假设。

答案：各向同性2. 在三维应力状态下，应力分量可以表示为：σ_x, σ_y, σ_z, τ_xy, τ_xz, τ_yz。

其中，τ_xy表示________面上的切应力。

答案：xOy3. 在弹性力学中，位移与应变之间的关系可以用________方程表示。

答案：几何方程三、计算题（每题30分，共90分）1. 已知一弹性体在平面应力状态下的应力分量为：σ_x = 100 MPa，σ_y = 50 MPa，τ_xy = 25 MPa。

弹性模量E = 200 GPa，泊松比μ = 0.3。

求应变分量ε_x, ε_y, γ_xy。

解：首先，利用胡克定律计算应变分量：ε_x = σ_x / E = 100 MPa / 200 GPa = 0.0005ε_y = σ_y / E = 50 MPa / 200 GPa = 0.00025γ_xy = τ_xy / G = 25 MPa / (E / 2(1 + μ)) = 25 MPa / (200 GPa / 2(1 + 0.3)) = 0.000375答案：ε_x = 0.0005，ε_y = 0.00025，γ_xy = 0.0003752. 一弹性体在三维应力状态下的应力分量为：σ_x = 120 MPa，σ_y = 80 MPa，σ_z = 40 MPa，τ_xy = 30 MPa，τ_xz = 20 MPa，τ_yz = 10 MPa。

弹性力学试题及答案

弹性力学试题及答案一、选择题（每题5分，共20分）1. 弹性力学中，描述材料弹性特性的基本物理量是（）。

A. 应力B. 应变C. 弹性模量D. 泊松比答案：C2. 在弹性力学中，下列哪项不是胡克定律的内容？（）A. 应力与应变成正比B. 材料是均匀的C. 材料是各向同性的D. 材料是线性的答案：B3. 弹性模量E和泊松比ν之间的关系是（）。

A. E = 2(1 + ν)B. E = 3(1 - 2ν)C. E = 3(1 + ν)D. E = 2(1 - ν)答案：D4. 根据弹性力学理论，下列哪种情况下材料会发生塑性变形？（）A. 应力小于材料的弹性极限B. 应力达到材料的弹性极限C. 应力超过材料的屈服强度D. 应力小于材料的屈服强度答案：C二、填空题（每题5分，共20分）1. 弹性力学中，应力的定义是单位面积上的______力。

答案：内2. 弹性力学的基本假设之一是______连续性假设。

答案：材料3. 弹性力学中，应变的量纲是______。

答案：无4. 弹性力学中，当外力撤去后，材料能恢复原状的性质称为______。

答案：弹性三、简答题（每题10分，共30分）1. 简述弹性力学中应力和应变的区别。

答案：应力是描述材料内部单位面积上受到的内力，而应变是描述材料在受力后形状和尺寸的变化程度。

2. 解释弹性力学中的杨氏模量和剪切模量。

答案：杨氏模量（E）是描述材料在拉伸或压缩过程中应力与应变比值的物理量，反映了材料的刚度；剪切模量（G）是描述材料在剪切应力作用下剪切应变与剪切应力比值的物理量，反映了材料抵抗剪切变形的能力。

3. 弹性力学中，如何理解材料的各向异性和各向同性？答案：各向异性是指材料的物理性质（如弹性模量、热膨胀系数等）在不同方向上具有不同的值；而各向同性则是指材料的物理性质在各个方向上都是相同的。

四、计算题（每题15分，共30分）1. 已知一圆柱形试件，其直径为50mm，长度为100mm，材料的弹性模量E=210GPa，泊松比ν=0.3。

(完整版)《弹性力学》试题参考答案

《弹性力学》试题参考答案（答题时间：100分钟）一、填空题（每小题4分）1．最小势能原理等价于弹性力学基本方程中：平衡微分方程，应力边界条件。

2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。

3．等截面直杆扭转问题中，的物理意义是杆端截面上剪应力对转轴的矩等于M dxdy D=⎰⎰2ϕ杆截面内的扭矩M 。

4．平面问题的应力函数解法中，Airy 应力函数在边界上值的物理意义为边界上某一点（基准ϕ点）到任一点外力的矩。

5．弹性力学平衡微分方程、几何方程的张量表示为：，。

0,=+i j ij X σ)(21,,i j j i ij u u +=ε二、简述题（每小题6分）1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。

圣维南原理：如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力（主矢与主矩相同），则近处的应力分布将有显著的改变，但远处的应力所受影响可以忽略不计。

作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。

（2）将次要的位移边界条件转化为应力边界条件处理。

2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数的分离变量形式。

ϕ题二（2）图（a ）（b ）⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x ⎩⎨⎧=+++= )(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比 μ 已知。

试求薄板面积的改变量。

S∆题二（3）图设当各边界受均布压力q 时，两力作用点的相对位移为。

由得，l ∆q E)1(1με-=)1(2222με-+=+=∆Eb a q b a l 设板在力P 作用下的面积改变为，由功的互等定理有：S ∆lP S q ∆⋅=∆⋅将代入得：l ∆221b a P ES +-=∆μ显然，与板的形状无关，仅与E 、、l 有关。

弹性力学教材习题及解答(供参考)

1 —1.选择题a. 下列材料中，_D_属于各向同性材料。

A. 竹材；B. 纤维增强复合材料；C. 玻璃钢；D. 沥青。

b. 关于弹性力学的正确认识是_A_。

A•计算力学在工程结构设计的中作用日益重要；B. 弹性力学从微分单元体入手分析弹性体，因此与材料力学不同，不需要对问题作假设;C. 任何弹性变形材料都是弹性力学的研究对象；D. 弹性力学理论像材料力学一样，可以没有困难的应用于工程结构分析。

c. 弹性力学与材料力学的主要不同之处在于_B_。

A. 任务；B. 研究对象；C. 研究方法；D. 基本假设。

d. 所谓完全弹性体”是指_B_。

A. 材料应力应变关系满足胡克定律；B. 材料的应力应变关系与加载时间历史无关；C. 本构关系为非线性弹性关系；D. 应力应变关系满足线性弹性关系。

2—1.选择题a. 所谓应力状态”是指_B_。

A. 斜截面应力矢量与横截面应力矢量不同；B. 一点不同截面的应力随着截面方位变化而改变；C. 3个主应力作用平面相互垂直；D. 不同截面的应力不同，因此应力矢量是不可确定的。

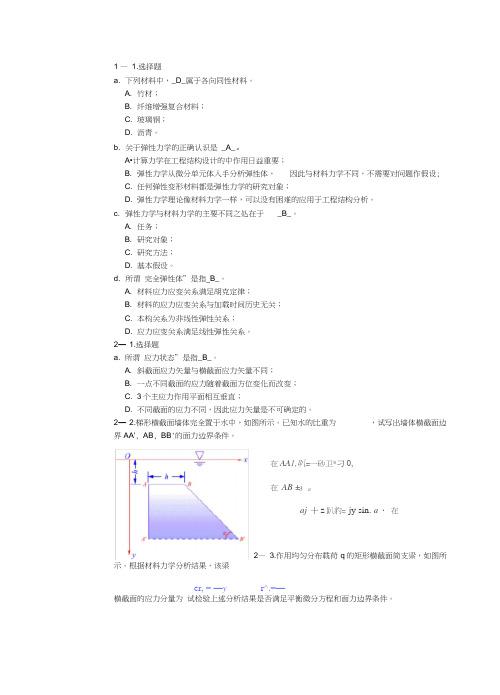
2—2.梯形横截面墙体完全置于水中，如图所示。

已知水的比重为，试写出墙体横截面边界AA', AB, BB'的面力边界条件。

在AA1,叭=一砂卫*刁0,在AB ±3 aaj十z趴豹=-jy sin. a、在2—3.作用均匀分布载荷q的矩形横截面简支梁，如图所示。

根据材料力学分析结果，该梁er, = —y r^.=—横截面的应力分量为试检验上述分析结果是否满足平衡微分方程和面力边界条件。

由此，只有当仃卩确罡.材料力学中所得轲的解答才能满足平衡方程和边界条件’即芮満足弹性力学基本方程的解. 2 - 4.单位厚度的楔形体，材料比重为，楔形体左侧作用比重为的液体，如图所示。

试~ a x cos os - sin a,~ cos tz - tr^ sin tz y^y sin a 0 cos /? - sm 0=6 厂期cos 』一 cr 尸血厅=0.2- 5.已知球体的半径为r ，材料的密度为 1,球体在密度为 i （ 1 > 1）的液体中漂浮，如沉入複体割分 yj 面力F = -p 3g （z 0 - z ） 1边界条件为舌匕一卩”严严+ @ 一厂）％ = 0-X% 十丁〔巧-51） +（z-f ）r v = 0.肚迄+严疋*（"尸）（务一耳）a 也来沉人液郎中的部分（珂 < 立< 2尸），边畀条件为开T ■*■尸欣斗仗一町％ = °, f 十十住-尸打中=①6 +y^ 十仗“门口丁 550*写出楔形体的边界条件。

弹性力学网考考试题及答案

弹性力学网考考试题及答案一、单项选择题（每题2分，共20分）1. 弹性力学中，应力状态的基本方程是（）。

A. 平衡方程B. 几何方程C. 物理方程D. 相容方程答案：A2. 弹性力学中，平面应力问题是指（）。

A. 应力分量σx、σy、τxy均不为零B. 应力分量σx、σy、τxy中有一个为零C. 应力分量σx、σy、τxy中有两个为零D. 应力分量σx、σy、τxy中有三个为零答案：C3. 在弹性力学中，圣维南原理适用于（）。

A. 静力平衡问题B. 热弹性问题C. 动力学问题D. 流体力学问题答案：A4. 弹性力学中，平面应变问题是指（）。

A. 应变分量εx、εy、γxy均不为零B. 应变分量εx、εy、γxy中有一个为零C. 应变分量εx、εy、γxy中有两个为零D. 应变分量εx、εy、γxy中有三个为零答案：B5. 弹性力学中，主应力和主应变之间的关系是（）。

A. 线性关系B. 非线性关系C. 没有关系D. 取决于材料的性质答案：A6. 弹性力学中，莫尔圆在σ-τ平面上表示的是（）。

A. 应力状态B. 应变状态C. 位移场D. 速度场答案：A7. 弹性力学中，平面应力问题和平面应变问题的区别在于（）。

A. 应力分量的数量B. 应变分量的数量C. 位移分量的数量D. 材料的性质答案：B8. 弹性力学中，三向应力状态下的应力分量不包括（）。

A. σxB. σyC. σzD. τxy答案：D9. 弹性力学中，应力集中现象通常发生在（）。

A. 光滑表面B. 尖锐转角C. 平坦区域D. 均匀区域答案：B10. 弹性力学中，弹性模量E和泊松比μ之间的关系是（）。

A. E = 2G(1+μ)B. E = 3G(1-2μ)C. E = 3G(1+2μ)D. E = 2G(1-μ)答案：A二、多项选择题（每题3分，共15分）11. 弹性力学中，下列哪些方程是基本方程？（）A. 平衡方程B. 几何方程C. 物理方程D. 相容方程答案：ABCD12. 弹性力学中，下列哪些因素会影响材料的弹性模量E？（）A. 材料种类B. 温度C. 应力状态D. 应变状态答案：AB13. 弹性力学中，下列哪些是平面应力问题的特点？（）A. 应力分量σz为零B. 应变分量εz不为零C. 位移分量w为零D. 位移分量u和v不为零答案：AC14. 弹性力学中，下列哪些是平面应变问题的特点？（）A. 应变分量εz为零B. 应力分量σz不为零C. 位移分量w不为零D. 位移分量u和v不为零答案：AD15. 弹性力学中，下列哪些是应力集中现象的影响因素？（）A. 材料性质B. 几何形状C. 载荷类型D. 边界条件答案：BCD三、判断题（每题2分，共20分）16. 弹性力学中，平衡方程是描述物体内部力的平衡状态的方程。

弹性力学期末考试试题及答案

弹性力学期末考试试题及答案一、名词解释（每题5分，共25分）1. 弹性力2. 弹簧常数3. 应力4. 应变5. 胡克定律6. 弹性模量7. 弹性体的形变8. 弹性位移9. 弹性能量10. 弹性碰撞二、选择题（每题2分，共20分）1. 以下哪种材料不属于弹性材料？A. 钢铁B. 橡胶C. 玻璃D. 水2. 在弹性限度内，弹性力与形变量之间的关系遵循哪一定律？A. 平方律B. 立方律C. 直线律D. 反比律3. 一弹簧的弹簧常数为50N/m，当一个力作用于弹簧上使其压缩0.1m时，弹簧的弹性势能为多少？A. 0.5JB. 1JC. 2JD. 5J4. 下列哪种情况下，弹簧的弹性力最大？A. 弹簧处于自然长度时B. 弹簧被压缩时C. 弹簧被拉伸时D. 弹簧被压缩或拉伸到极限时5. 两个相同的弹性球碰撞，如果它们的弹性系数不同，那么碰撞后它们的速度关系是？A. 速度大小不变，方向相反B. 速度大小不变，方向相同C. 速度大小发生变化，方向相反D. 速度大小发生变化，方向相同三、填空题（每题5分，共25分）1. 一弹性体的形变是指其_________的变化。

2. 在弹性碰撞中，两个物体的速度满足_________定律。

3. 弹簧的弹簧常数_________，表示弹簧的_________。

4. 当一个力作用于弹性体上时，该力与弹性体的_________之比称为应力。

5. 弹性模量是衡量材料_________的物理量。

四、计算题（共40分）1. 一弹簧的弹簧常数为200N/m，当一个力作用于弹簧上使其压缩0.5m时，求弹簧的弹性势能。

（5分）2. 质量为2kg的物体从静止开始沿斜面滑下，斜面与水平面的夹角为30°，斜面长度为10m，摩擦系数为0.2。

求物体滑到斜面底部时的速度。

（5分）3. 两个弹性球A和B，质量分别为m1和m2，弹性系数分别为k1和k2。

它们从静止开始相互碰撞，求碰撞后A和B的速度。

弹性力学试题及答案

2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。

3．等截面直杆扭转问题中， M dxdy D=⎰⎰2ϕ的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。

4．平面问题的应力函数解法中，Airy 应力函数ϕ在边界上值的物理意义为边界上某一点（基准点）到任一点外力的矩。

5．弹性力学平衡微分方程、几何方程的张量表示为：0,=+i j ij X σ ，)(21,,i j j i ij u u +=ε。

二、简述题（每小题6分）1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。

作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。

（2）将次要的位移边界条件转化为应力边界条件处理。

2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。

题二（2）图（a ）⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x （b ）⎩⎨⎧=+++=)(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比已知。

试求薄板面积的改变量S ∆。

题二（3）图设当各边界受均布压力q 时，两力作用点的相对位移为l ∆。

由q E)1(1με-=得，)1(2222με-+=+=∆Eb a q b a l设板在力P 作用下的面积改变为S ∆，由功的互等定理有：l P S q ∆⋅=∆⋅将l ∆代入得：221b a P ES +-=∆μ显然，S ∆与板的形状无关，仅与E 、μ、l 有关。

弹性力学题库

第一章绪论1、所谓“完全弹性体”是指（B）。

A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是（A）。

A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都是弹性力学的研究对象D、弹性力学理论像材料力学一样，可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是（D）。

A、杆件B、板壳C、块体D、质点4、弹性力学研究物体在外力作用下，处于弹性阶段的应力、应变和位移。

5、弹性力学可以解决材料力学无法解决的很多问题；并对杆状结果进行精确分析，以及验算材力结果的适用范围和精度。

与材料力学相比弹性力学的特点有哪些？答：1）研究对象更为普遍；2）研究方法更为严密；3）计算结果更为精确；4）应用范围更为广泛。

6、材料力学研究杆件，不能分析板壳；弹性力学研究板壳，不能分析杆件。

（×）改：弹性力学不仅研究板壳、块体问题，并对杆件进行精确的分析，以及检验材料力学公式的适用范围和精度。

7、弹性力学对杆件分析（C）。

A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定8、图示弹性构件的应力和位移分析要用什么分析方法？（C）A、材料力学B、结构力学C、弹性力学D、塑性力学解答：该构件为变截面杆，并且具有空洞和键槽。

9、弹性力学与材料力学的主要不同之处在于（B ）。

A 、任务B 、研究对象C 、研究方法D 、基本假设10、重力、惯性力、电磁力都是体力。

（√）11、下列外力不属于体力的是（D ）A 、重力B 、磁力C 、惯性力D 、静水压力12、体力作用于物体内部的各个质点上，所以它属于内力。

（×）解答：外力。

它是质量力。

13、在弹性力学和材料力学里关于应力的正负规定是一样的。

本科弹性力学试题及答案

本科弹性力学试题及答案一、选择题（每题2分，共20分）1. 弹性力学中，下列哪一项不是基本假设？A. 连续性假设B. 均匀性假设C. 各向异性假设D. 小变形假设答案：C2. 在弹性力学中，下列哪一项不是应力的类型？A. 正应力B. 剪应力C. 拉应力D. 弯应力答案：D3. 弹性模量E和泊松比μ之间存在以下哪种关系？A. E = 2G(1+μ)B. E = 3G(1-2μ)C. E = 3G(1+μ)D. E = 2G(1-μ)答案：C4. 弹性力学中的圣维南原理适用于以下哪种情况？A. 仅适用于平面应力问题B. 仅适用于平面应变问题C. 适用于平面应力和平面应变问题D. 不适用于任何情况答案：C5. 弹性力学中，下列哪一项不是位移场的基本方程？A. 几何方程B. 物理方程C. 运动方程D. 边界条件答案：D6. 弹性力学中，下列哪一项不是平面应力问题的特点？A. 应力分量σz=0B. 应变分量εz≠0C. 应力分量τxz=τyz=0D. 应变分量γxz=γyz=0答案：B7. 弹性力学中，下列哪一项不是平面应变问题的特点？A. 应力分量σz≠0B. 应变分量εz=0C. 应力分量τxz=τyz=0D. 应变分量γxz=γyz=0答案：A8. 弹性力学中，下列哪一项不是应力集中的类型？A. 几何不连续引起的应力集中B. 材料不连续引起的应力集中C. 载荷不连续引起的应力集中D. 温度不连续引起的应力集中答案：D9. 弹性力学中，下列哪一项不是弹性常数？A. 杨氏模量EB. 泊松比μC. 剪切模量GD. 体积模量K答案：D10. 弹性力学中，下列哪一项不是弹性体的基本性质？A. 均匀性B. 连续性C. 各向同性D. 各向异性答案：D二、填空题（每题2分，共20分）1. 弹性力学中，应力状态的基本方程包括______、______和______。

答案：几何方程、物理方程、平衡方程2. 弹性力学中，应变能密度W与应力分量和应变分量的关系为W=______。

弹性力学100题

弹性力学100题一、单项选择题1.弹性力学建立的基本方程多是偏微分方程，还必须结合（C ）求解这些微分方程，以求得具体问题的应力、应变、位移。

A相容方程 B •近似方法C •边界条件D •附加假定2.根据圣维南原理，作用在物体一小部分边界上的力系可以用（B ）的力系代替，则仅在近处应力分布有改变，而在远处所受的影响可以不计。

A.几何上等效B・静力上等效C平衡D •任意3.弹性力学平面问题的求解中，平面应力问题与平面应变问题的三类基本方程不完全相同，其比较关系为（B ）。

A •平衡方程、几何方程、物理方程完全相同B •平衡方程、几何方程相同，物理方程不同C •平衡方程、物理方程相同，几何方程不同D •平衡方程相同，物理方程、几何方程不同4.不计体力，在极坐标中按应力求解平面问题时，应力函数必须满足（A ）①区域内的相容方程；②边界上的应力边界条件；③满足变分方程；④如果为多连体，考虑多连体中的位移单值条件。

A.①②④B.②③④C.①②③D.①②③④5.如下图1所示三角形薄板，按三结点三角形单元划分后，对于与局部编码ijm对应的整体编码，以下叙述正确的是（D ）。

①I单元的整体编码为162②II单元的整体编码为426③II单元的整体编码为246④III单元的整体编码为243⑤IV单元的整体编码为564图1A.①③B.②④C.①④D.③⑤6.平面应变问题的微元体处于（C ）A.单向应力状态B.双向应力状态C.三向应力状态，且-是一主应力D.纯剪切应力状态7.圆弧曲梁纯弯时，（CA.应力分量和位移分量都是轴对称的B.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的，位移分量不是轴对称的D.位移分量是轴对称的，应力分量不是轴对称的8.下左图2中所示密度为「的矩形截面柱，应力分量为：匚x =0fy Ay B, xy 0对图（a）和图（b）两种情况由边界条件确定的常数A及B的关系是（C ）A.A 相同，B也相同B.A 不相同，B也不相同C.A 相同，B不相同D.A 不相同，B 相同图 2图39、上右图3示单元体剪应变丫应该表示为(B )◎备DA冷B10、设有平面应力状态二X =ax by, ；「y = ex dy, xy dx - ay - x，其中，a,b,c,d 均为常数，为容重。

弹性力学试题及答案

弹性力学试题及答案一、选择题（每题2分，共20分）1. 弹性力学中的胡克定律描述的是：A. 应力与位移的关系B. 应力与应变的关系C. 应变与位移的关系D. 位移与力的关系2. 以下哪个不是弹性力学的基本假设？A. 连续性假设B. 均匀性假设C. 各向同性假设D. 各向异性假设3. 弹性模量和泊松比的关系是：A. E = 2G(1+ν)B. E = 3K(1-2ν)C. E = 3K(1+ν)D. E = 2G(1-ν)4. 以下哪种材料可以看作是各向同性材料？A. 木材B. 钢筋混凝土C. 单晶硅D. 多晶硅5. 应力集中现象通常发生在：A. 均匀受力区域B. 材料的中间区域C. 材料的边缘或孔洞附近D. 材料的内部二、简答题（每题10分，共30分）6. 简述平面应力和平面应变的区别。

7. 解释什么是圣维南原理，并简述其应用。

8. 描述弹性力学中的主应力和主应变的概念及其意义。

三、计算题（每题25分，共50分）9. 一个长方体材料块，尺寸为L×W×H，受到均匀压力p作用于其顶面，求其内部任意一点处的应力状态。

10. 已知某材料的弹性模量E=200 GPa，泊松比ν=0.3，求其剪切模量G。

答案一、选择题1. 答案：B（应力与应变的关系）2. 答案：D（各向异性假设）3. 答案：A（E = 2G(1+ν)）4. 答案：D（多晶硅）5. 答案：C（材料的边缘或孔洞附近）二、简答题6. 答案：平面应力是指材料的一个方向（通常是厚度方向）的应力为零，而平面应变是指材料的一个方向（通常是厚度方向）的应变为零。

平面应力通常用于薄板或薄膜，而平面应变用于长厚比很大的结构。

7. 答案：圣维南原理指出，在远离力作用区域的地方，局部应力分布对整个结构的应力状态影响很小。

这个原理常用于简化复杂结构的应力分析。

8. 答案：主应力是材料内部某一点应力张量的最大值，主应变是材料内部某一点应变张量的最大值。

弹性力学试题及答案

2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。

3．等截面直杆扭转问题中， M dxdy D=⎰⎰2ϕ的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。

4．平面问题的应力函数解法中，Airy 应力函数ϕ在边界上值的物理意义为边界上某一点（基准点）到任一点外力的矩。

5．弹性力学平衡微分方程、几何方程的张量表示为：0,=+i j ij X σ ，)(21,,i j j i ij u u +=ε。

二、简述题（每小题6分）1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。

作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。

（2）将次要的位移边界条件转化为应力边界条件处理。

2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。

题二（2）图（a ）⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x （b ）⎩⎨⎧=+++= )(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比已知。

试求薄板面积的改变量S ∆。

题二（3）图设当各边界受均布压力q 时，两力作用点的相对位移为l ∆。

《弹性力学》试题参考答案

2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。

3．等截面直杆扭转问题中， M dxdy D=⎰⎰2ϕ的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。

4．平面问题的应力函数解法中，Airy 应力函数ϕ在边界上值的物理意义为边界上某一点（基准点）到任一点外力的矩。

5．弹性力学平衡微分方程、几何方程的张量表示为：0,=+i j ij X σ ，)(21,,i j j i ij u u +=ε。

二、简述题（每小题6分）1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。

作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。

（2）将次要的位移边界条件转化为应力边界条件处理。

2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。

题二（2）图（a ）⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x （b ）⎩⎨⎧=+++= )(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比 μ 已知。

试求薄板面积的改变量S ∆。

题二（3）图设当各边界受均布压力q 时，两力作用点的相对位移为l ∆。

弹性力学题

弹性力学题Company number：【0089WT-8898YT-W8CCB-BUUT-202108】一、单项选择题1.弹性力学建立的基本方程多是偏微分方程，还必须结合（ C ）求解这些微分方程，以求得具体问题的应力、应变、位移。

A．相容方程 B．近似方法 C．边界条件 D．附加假定2.根据圣维南原理，作用在物体一小部分边界上的力系可以用（ B ）的力系代替，则仅在近处应力分布有改变，而在远处所受的影响可以不计。

A．几何上等效 B．静力上等效 C．平衡 D．任意3.弹性力学平面问题的求解中，平面应力问题与平面应变问题的三类基本方程不完全相同，其比较关系为（ B ）。

A．平衡方程、几何方程、物理方程完全相同B．平衡方程、几何方程相同，物理方程不同C．平衡方程、物理方程相同，几何方程不同D．平衡方程相同，物理方程、几何方程不同4.不计体力，在极坐标中按应力求解平面问题时，应力函数必须满足（ A ）①区域内的相容方程；②边界上的应力边界条件；③满足变分方程；④如果为多连体，考虑多连体中的位移单值条件。

A.①②④B. ②③④C. ①②③D. ①②③④5.如下图1所示三角形薄板，按三结点三角形单元划分后，对于与局部编码ijm对应的整体编码，以下叙述正确的是（ D ）。

① I单元的整体编码为162② II单元的整体编码为426③ II单元的整体编码为246④ III单元的整体编码为243⑤ IV单元的整体编码为564图1A. ①③B. ②④C. ①④D. ③⑤6.平面应变问题的微元体处于（ C ）A.单向应力状态B.双向应力状态是一主应力 D.纯剪切应力状态C.三向应力状态，且z7.圆弧曲梁纯弯时，（ C ）A.应力分量和位移分量都是轴对称的B.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的，位移分量不是轴对称的D.位移分量是轴对称的，应力分量不是轴对称的8.下左图2中所示密度为ρ的矩形截面柱，应力分量为：0,,0=+==xy y x B Ay τσσ对图（a ）和图(b)两种情况由边界条件确定的常数A 及B 的关系是（ C ）相同，B 也相同不相同，B 也不相同相同，B 不相同不相同，B 相同图 2 图 39、上右图3示单元体剪应变γ应该表示为（ B ）10、设有平面应力状态x ay dx dy cx by ax xy y x γτσσ---=+=+=,,，其中，d c b a ,,,均为常数，γ为容重。

弹性力学试题及答案

弹性力学试题及答案题目一：弹性力学基础知识试题：1. 弹性力学是研究什么样的物体的变形与应力关系？答案：弹性力学是研究具有弹性的物体（即能够恢复原状的物体）的变形与应力关系的学科。

2. 弹性力学中的“应力”是指什么？答案：应力是物体内部相邻两部分之间的相互作用力与其接触面积之比。

3. 弹性力学中的“应变”是指什么？答案：应变是物体在受力作用下发生形变的程度。

正应变表示物体在拉伸力作用下的伸长程度与原始长度之比，负应变表示物体在压缩力作用下的压缩程度与原始长度之比。

4. 弹性力学中的“胡克定律”是什么？答案：胡克定律描述了弹簧的弹性特性。

根据胡克定律，当弹簧的变形量（即伸长或缩短的长度）与施加在弹簧上的力成正比时，弹簧的弹性变形是符合弹性恢复原状的规律的。

题目二：弹性系数计算试题：1. 弹性模量是用来衡量什么的物理量？答案：弹性模量是衡量物体在受力作用下发生弹性形变的硬度和刚度的物理量。

2. 如何计算刚体材料的弹性模量？答案：刚体材料的弹性模量可以通过应力与应变之间的关系来计算。

弹性模量E等于应力σ与应变ε之比。

3. 如何计算各向同性材料的体积弹性模量（Poisson比）？答案：各向同性材料的体积弹性模量（Poisson比）可以通过材料的横向应变与纵向应变之比来计算。

Poisson比v等于横向应变ε横与纵向应变ε纵之比。

4. 如何计算材料的剪切弹性模量？答案：材料的剪切弹性模量G（也称剪切模量或切变模量）可以通过材料的剪应力与剪应变之比来计算。

题目三：弹性体的应力分析试题：1. 弹性体的应力状态可以用什么来表示？答案：弹性体的应力状态可以用应力张量来表示。

2. 什么是平面应力状态和轴对称应力状态？答案：平面应力状态是指在某一平面上的应力分量仅存在拉伸（或压缩）和剪切，而垂直于该平面的应力分量为零的应力状态。

轴对称应力状态是指应力分量只与径向位置有关，而与角度无关的应力状态。

3. 弹性体的应力因子有哪些？答案：弹性体的应力因子包括主应力、主应力差、偏应力、平均应力、最大剪应力、最大剪应力平面等。

弹性力学题库

C )第一章绪论1、所谓“完全弹性体”是指（B ）。

A 、材料应力应变关系满足虎克定律B 、材料的应力应变关系与加载时间、历史无关C 、本构关系为非线性弹性关系D 、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是（ A ）。

A 、计算力学在工程结构设计中的作用日益重要B 、弹性力学从微分单元体入手分析弹性体，因此与材料力学不同，不需要对问题作假设C 、任何弹性变形材料都是弹性力学的研究对象D 、弹性力学理论像材料力学一样，可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是（ D ）。

A 、杆件B 、板壳C 、块体D 、质点4、弹性力学研究物体在外力作用下，处于弹性阶段的应力、应变和位移。

5、弹性力学可以解决材料力学无法解决的很多问题；并对杆状结果进行精确分析，以及验算材力结果的适用范围和精度。

与材料力学相比弹性力学的特点有哪些？答：1）研究对象更为普遍;2）研究方法更为严密；3）计算结果更为精确；4）应用范围更为广泛。

6、材料力学研究杆件，不能分析板壳；弹性力学研究板壳，不能分析杆件。

（X ）改：弹性力学不仅研究板壳、块体问题，并对杆件进行精确的分析，以及检验材料力学公式的适用范围和精度。

8、图示弹性构件的应力和位移分析要用什么分析方法？（7、弹性力学对杆件分析（ C )。

A 、无法分析 B 、得出近似的结果 C 、得出精确的结果 D 、需采用一些关于变形的近似假定yz15、按弹性力学规定，下图所示单元体上的剪应力（ C ）。

D 、静水压力C 、弹性力学D 、塑性力学解答：该构件为变截面杆，并且具有空洞和键槽。

9、弹性力学与材料力学的主要不同之处在于（ B ）。

10、重力、惯性力、电磁力都是体力。

（V ）11、下列外力不属于体力的是（ D ）A 、重力B 、磁力C 、惯性力 12、体力作用于物体内部的各个质点上，所以它属于内力。

弹性力学100题

一、单项选择题1.弹性力学建立的基本方程多是偏微分方程，还必须结合（ C ）求解这些微分方程，以求得具体问题的应力、应变、位移。

A ．相容方程B ．近似方法C ．边界条件D ．附加假定2.根据圣维南原理，作用在物体一小部分边界上的力系可以用（ B ）的力系代替，则仅在近处应力分布有改变，而在远处所受的影响可以不计。

A ．几何上等效B ．静力上等效C ．平衡D ．任意3.弹性力学平面问题的求解中，平面应力问题与平面应变问题的三类基本方程不完全相同，其比较关系为（ B ）。

A ．平衡方程、几何方程、物理方程完全相同B ．平衡方程、几何方程相同，物理方程不同C ．平衡方程、物理方程相同，几何方程不同D ．平衡方程相同，物理方程、几何方程不同4.不计体力，在极坐标中按应力求解平面问题时，应力函数必须满足（ A ）①区域内的相容方程；②边界上的应力边界条件；③满足变分方程；④如果为多连体，考虑多连体中的位移单值条件。

A. ①②④B. ②③④C. ①②③D. ①②③④5.如下图1所示三角形薄板，按三结点三角形单元划分后，对于与局部编码ijm 对应的整体编码，以下叙述正确的是（ D ）。

① I 单元的整体编码为162② II 单元的整体编码为426③ II 单元的整体编码为246④ III 单元的整体编码为243⑤ IV 单元的整体编码为564图1A. ①③B. ②④C. ①④D. ③⑤ 6.平面应变问题的微元体处于（ C ）A.单向应力状态B.双向应力状态C.三向应力状态，且z 是一主应力D.纯剪切应力状态7.圆弧曲梁纯弯时，（ C ）A.应力分量和位移分量都是轴对称的 463521I III II IVB.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的，位移分量不是轴对称的D.位移分量是轴对称的，应力分量不是轴对称的8.下左图2中所示密度为ρ的矩形截面柱，应力分量为：0,,0=+==xy y x B Ay τσσ对图（a ）和图(b)两种情况由边界条件确定的常数A 及B 的关系是（ C ）A.A 相同，B 也相同B.A 不相同，B 也不相同C.A 相同，B 不相同D.A 不相同，B 相同图 2 图 39、上右图3示单元体剪应变γ应该表示为（ B ）10、设有平面应力状态x ay dx dy cx by ax xy y x γτσσ---=+=+=,,，其中，d c b a ,,,均为常数，γ为容重。

弹性力学试卷题库原版

弹性力学试卷题库一、概念、理论公式推导（10分）06秋推导出按应力求解平面应力问题的相容方程。

07秋、07春试推导出按位移求解弹性力学问题时所用的基本微分方程。

（Lame方程）07秋02、08年考研解释下列术语，并指出他们的特征1.平面应力问题2、平面应变问题08春试导出求解平面应力问题的用应力分量表示的相容方程。

08考研试推导求解弹性力学平面问题极坐标下的平衡微分方程06考研试推导出空间（轴对称）问题的平衡微分方程。

推导平面问题的相容方程列出平面问题中的常用方程理论：圣维南定理07考研（20分）如图所示为平面应力状态下的细长薄板条，上下边接受均布力q的作用，其余边界上均无面力作用，试说明A，B，C点处的应力状态二、定界条件（10分*2）06秋、07秋、07秋02、07春、08春1、（10分）楔型体双边受对称均布剪力q 。

Oy xq qα/2α/2xy o C Bqq06秋、 2、（10分）矩形截面挡水墙的密度为ρ，厚度为h ，水的密度为γ。

07秋、08考研3、（10分）下图所示楔形体，试分别写出极坐标和直角坐标下的定解条件。

07秋02、07春4、设有矩形截面的长竖柱，密度为ρ，在一边侧面上受均布剪力q 。

γgρgxy O2h 2h08春、07考研5、（10分）楔形体在一面受有均布压力q 和楔顶受有一集中载荷P 的作用。

08考研简支梁受均布荷载q 作用，ρgyxObqP xy r θα β q o xqLqLLLy07考研悬臂梁在端部受集中力M 、F ，上面受有分布载荷xlq 0，下面受有均布剪力006考研矩形薄板，三边固定，一边受有均布压力qhlMxl q 0Oxyxboa baq如图所示为一矩形截面水坝，其左侧面受静水压力，顶部受集中力P 作用。

试写出定界条件，固定边不考虑。

图示水坝，顶面受有均布压力q ，斜面受静水压力作用，底部固定，写出定解条件。

（下载的图一中）三、平面（直角或极坐标）（20分） 06秋、08考研等厚度薄板沿周边承受均匀压力q 的作用，若O 点不能移动和转动，试求板内任意一点A(x,y)处的位移。