浙江省财政预算收入与全省生产总值数据
庞皓计量经济学 第二章 练习题及参考解答(第四版)
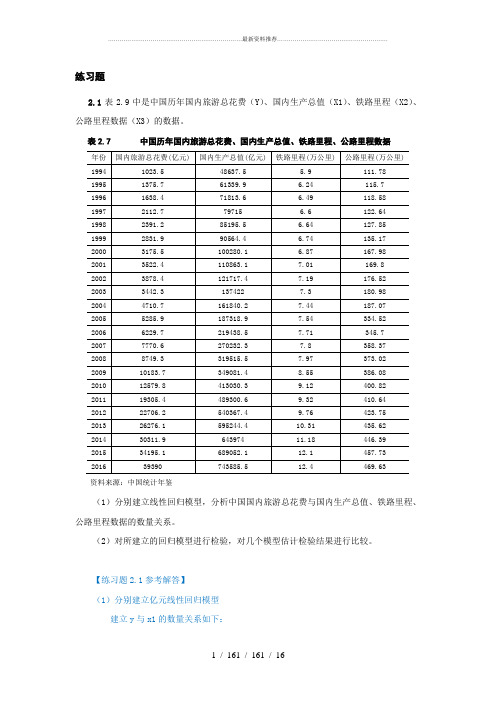
练习题2.1表2.9中是中国历年国内旅游总花费(Y)、国内生产总值(X1)、铁路里程(X2)、公路里程数据(X3)的数据。
表2.7 中国历年国内旅游总花费、国内生产总值、铁路里程、公路里程数据资料来源:中国统计年鉴(1)分别建立线性回归模型,分析中国国内旅游总花费与国内生产总值、铁路里程、公路里程数据的数量关系。
(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
【练习题2.1参考解答】(1)分别建立亿元线性回归模型建立y与x1的数量关系如下:建立y与x2的数量关系如下:建立y与x3的数量关系如下:(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
关于中国国内旅游总花费与国内生产总值模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,GDP 对中国国内旅游总花费有显著影响。
同理:关于中国国内旅游总花费与铁路里程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,铁路里程对中国国内旅游总花费有显著影响。
关于中国国内旅游总花费与公路里程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,公路里程对中国国内旅游总花费有显著影响。
2.2为了研究浙江省一般预算总收入与地区生产总值的关系,由浙江省统计年鉴得到如表2.8所示的数据。
年份一般预算总收入(亿元)地区生产总值(亿元)年份一般预算总收入(亿元)地区生产总值(亿元)Y X Y X 197827.45123.721998 401.80 5052.62 197925.87157.751999 477.40 5443.92 198031.13179.922000 658.42 6141.03 198134.34204.862001 917.76 6898.34 198236.64234.012002 1166.58 8003.67 198341.79257.092003 1468.89 9705.02 198446.67323.252004 1805.16 11648.70 198558.25429.162005 2115.36 13417.68 198668.61502.472006 2567.66 15718.47 198776.36606.992007 3239.89 18753.73 198885.55770.252008 3730.06 21462.69 198998.21849.442009 4122.04 22998.24 1990101.59904.692010 4895.41 27747.65 1991108.941089.332011 5925.00 32363.381992 118.36 1375.70 2012 6408.49 34739.13 1993 166.64 1925.91 2013 6908.41 37756.58 1994 209.39 2689.28 2014 7421.70 40173.03 1995 248.50 3557.55 2015 8549.47 42886.49 1996 291.75 4188.53 2016 9225.0747251.361997340.524686.11(1)建立浙江省一般预算收入与全省地区生产总值的计量经济模型,估计模型的参数,检验模型的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2017年,浙江省地区生产总值为52000亿元,比上年增长10%,利用计量经济模型对浙江省2017年的一般预算收入做出点预测和区间预测(3)建立浙江省一般预算收入的对数与地区生产总值对数的计量经济模型,估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义。
浙江省人民政府关于下达2024年浙江省国民经济和社会发展计划的通知

浙江省人民政府关于下达2024年浙江省国民经济和社会发展计划的通知文章属性•【制定机关】浙江省人民政府•【公布日期】2024.02.05•【字号】浙政发〔2024〕1号•【施行日期】2024.02.05•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】宏观调控和经济管理正文浙江省人民政府关于下达2024年浙江省国民经济和社会发展计划的通知浙政发〔2024〕1号各市、县(市、区)人民政府,省政府直属各单位:2024年浙江省国民经济和社会发展计划已经省十四届人大二次会议审议批准,现印发给你们,请认真组织实施。
各地、各部门在2024年计划安排和组织实施过程中,重点抓好十方面工作:一、聚焦聚力提升政策引导保障成效准确把握政策取向,加强政策工具创新和协调配合,进一步提高政策实施的精准度、实效性。
(一)迭代升级“8 4”经济政策体系。
优化8个政策包和4张要素保障清单,安排省级财政资金1023.6亿元,支持经济高质量发展。
精准落实惠企政策,为市场经营主体减负2500亿元以上。
坚持政府过紧日子,严肃财经纪律,严控一般性支出,大幅压减论坛、展会、节庆等活动,把更多财力用在帮企业、促发展、惠民生上。
(二)积极争取和用好国家政策。
统筹做好项目甄选、申报等工作,积极争取并高效用好地方政府专项债券,充分发挥其对重大项目建设的拉动作用;争取100个以上项目纳入国家用地保障范围,力争更多项目纳入国家能耗单列清单。
(三)发挥“4 1”专项基金撬动作用。
坚持市场化专业化运作,完成专项基金组建和运行机制建设,制定尽职免责细则,完善绩效评价和激励约束机制,健全投资风险防控体系,年度计划投资200亿元,撬动社会资本1000亿元,并扩大省科创母基金规模。
坚持“投早、投小、投科技”,在战略性新兴产业领域催生一批拥有核心技术和市场竞争力的高成长企业。
(四)推动金融更好服务实体经济。
坚持把金融服务实体经济作为根本宗旨,切实提升服务理念、能力和质效,力争制造业中长期贷款、普惠小微贷款增速高于各项贷款平均增速,促进社会综合融资成本稳中有降。
浙江gdp总量2023最新数据

浙江gdp总量2023最新数据浙江gdp总量2023最新数据上半年浙江实现生产总值38717亿元,按可比价格计算,同比增长6.8%,增速比一季度提高1.9个百分点。
浙江gdp2023上半年最新数据一、农业生产形势稳定,农产品供应有保障上半年,农林牧渔业增加值同比增长4.3%,增速比一季度提高0.2个百分点。
猪牛羊禽肉类总产量58.2万吨,增长10.8%。
牛奶产量增长6.8%,禽蛋产量增长11.9%。
水产品总产量244.2万吨,增长5.6%。
生猪存栏618.6万头,下降0.4%,累计出栏458.8万头,增长10.1%,其中,能繁母猪存栏66.5万头,下降0.3%。
二、工业经济稳步回升,新兴产业引领增长上半年,规模以上工业增加值同比增长4.7%,增速比一季度提高1.7个百分点。
38个工业行业大类中,25个行业增加值增速比一季度提高,回升面65.8%。
规模以上工业中,民营企业增加值增长7.0%;新能源产业、装备制造业、数字经济核心产业制造业增加值分别增长25.9%、9.4%和8.4%。
三、服务业增长贡献显著,交通物流持续恢复上半年,服务业增加值同比增长8.4%,增速比一季度加快2.0个百分点。
其中,住宿和餐饮业增加值增长18.1%,增速比一季度提高6.5个百分点;交通运输、仓储和邮政业,信息传输、软件和信息技术服务业,租赁和商务服务业,金融业,批发和零售业增加值分别增长14.6%、12.5%、12.3%、10.6%和6.6%。
交通物流持续恢复,货运量、货物周转量分别增长6.4%和12.3%;客运量、旅客周转量分别增长70.2%和111.5%。
四、有效投资稳定增长,投资结构持续优化上半年,固定资产投资同比增长9.0%。
其中,制造业投资增长17.6%,基础设施投资增长8.0%。
重点领域投资稳步推进,高新技术产业投资增长29.3%;交通、能源和水利投资增长16.2%。
制造业投资结构持续优化,数字经济核心产业制造业和装备制造业投资分别增长60.5%和36.3%。
浙江省生产总值、三大产业增加值、财政收入、公共预算支出、居民人均可支配收入及GDP目标分析

浙江省生产总值、三大产业增加值、财政收入、公共预算支出、居民人均可支配收入及GDP目标分析2016年以来,浙江省委、省政府抢抓新一轮科技革命和产业变革的历史机遇,超前谋划和布局人工智能、大数据、云计算等一批重量级未来产业,组建之江实验室、建设杭州城西科创大走廊,推动企业将迭代创新作为终身追求,抢占科技革命的制高点,正是其中之意。
从兄弟省市比较来看,浙江和广东、上海、江苏等兄弟省市同作为全国高水平发展区域,在对接国家重大战略、深化经济体制改革、实施创新驱动、推进产业转型升级等方面面临的机遇和挑战具有一定的相似性和同步性。
尤其是当前国际国内形势更趋复杂多变,各省市都在积极谋求经济社会转型升级。
浙江在主要经济指标较好增长的同时,也必须意识到在科技研发投入、服务业占比、PCT专利申请量、研究型大学培育等方面还存在差距。
未来有必要借鉴参考兄弟省市重点经济战略举措,尤其需深度研究创新引擎待增强、改革利益分配不均、社会结构多样化、公共服务提供能力提升等问题,为全国打造经济高质量发展模板,为“十三五”完美收官夯实支撑。
2018年浙江省GDP为58003亿元,人均GDP为107625元。
2019年浙江生产总值(GDP)为62352亿元(合9039亿美元),比上年增长6.8%。
其中,第一产业增加值2097亿元,增长2.0%;第二产业增加值26567亿元,增长5.9%;第三产业增加值33688亿元,增长7.8%。
2019年浙江省规模以上工业增加值16157亿元,比上年增长6.6%,农林牧渔业增加值比上年增长2.2%。
服务业增加值增速高于生产总值1.0个百分点,其中,批发零售、交通运输仓储邮政、住宿餐饮、金融、房地产业增加值分别增长6.3%、6.0%、6.2%、10.2%和5.0%,信息传输软件和信息技术等其他营利性服务业增加值增长10.1%。
2019年浙江省预计数字经济核心产业增加值占GDP的10%左右,健康、文化、金融产业增加值均增长10%以上。
计量经济学-简单线性回归模型
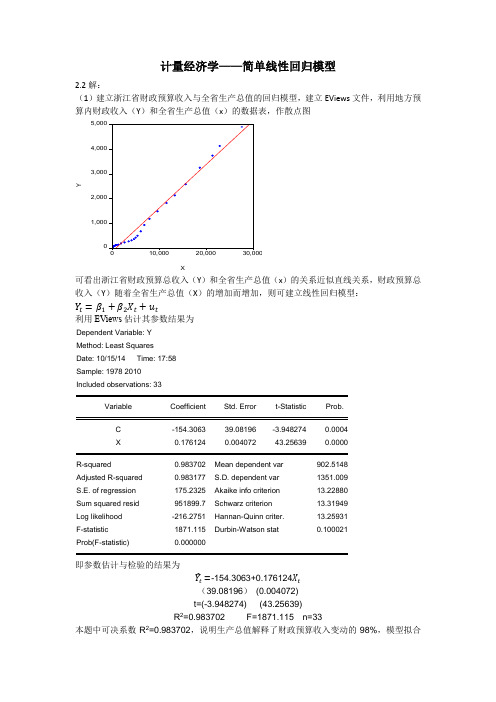
S.E. of regression
175.2325
Akaike info criterion
13.22880
Sum squared resid
951899.7
Schwarz criterion
13.31949
Log likelihood
-216.2751
Hannan-Quinn criter.
已经得到 =800, =8000, =300, (10)=2.23
则n=12, =30, =40000,
= =8000
=
650 2.23* * =650 30.1256411
即在95%的置信概率下消费支出C平均值的预测区间为(619.874359,680.125641)
2.4解:
(1)建立建筑面积与建造单位成本回归模型,建立EViews文件,利用建造单位成本(Y)和建筑面积(x)的数据表,作散点图
10071.74
Schwarz criterion
9.984610
Log likelihood
-57.42275
Hannan-Quinn criter.
9.873871
F-statistic
178.0715
Durbin-Watson stat
1.172407
Prob(F-statistic)
0.000000
Kurtosis
1.664917
2.346511
Jarque-Bera
0.898454
0.213547
Probability
0.638121
0.898729
Sum
42.28000
19432.00
庞皓计量经济学练习题及参考解答第四版

练习题2.1表2.9中是中国历年国内旅游总花费(Y)、国内生产总值(X1)、铁路里程(X2)、公路里程数据(X3)的数据。
表2.7 中国历年国内旅游总花费、国内生产总值、铁路里程、公路里程数据资料来源:中国统计年鉴(1)分别建立线性回归模型,分析中国国内旅游总花费与国内生产总值、铁路里程、公路里程数据的数量关系。
(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
【练习题2.1参考解答】(1)分别建立亿元线性回归模型建立y与x1的数量关系如下:建立y与x2的数量关系如下:建立y与x3的数量关系如下:(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
关于中国国内旅游总花费与国内生产总值模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,GDP 对中国国内旅游总花费有显著影响。
同理:关于中国国内旅游总花费与铁路里程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,铁路里程对中国国内旅游总花费有显著影响。
关于中国国内旅游总花费与公路里程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显著性检验表明,公路里程对中国国内旅游总花费有显著影响。
2.2为了研究浙江省一般预算总收入与地区生产总值的关系,由浙江省统计年鉴得到如表2.8所示的数据。
年份一般预算总收入(亿元)地区生产总值(亿元)年份一般预算总收入(亿元)地区生产总值(亿元)Y X Y X 197827.45123.721998 401.80 5052.62 197925.87157.751999 477.40 5443.92198031.13179.922000 658.42 6141.03 198134.34204.862001 917.76 6898.34 198236.64234.012002 1166.58 8003.67 198341.79257.092003 1468.89 9705.02 198446.67323.252004 1805.16 11648.70 198558.25429.162005 2115.36 13417.68 198668.61502.472006 2567.66 15718.47 198776.36606.992007 3239.89 18753.73 198885.55770.252008 3730.06 21462.69 198998.21849.442009 4122.04 22998.24 1990101.59904.692010 4895.41 27747.65 1991108.941089.332011 5925.00 32363.38 1992118.361375.702012 6408.49 34739.13 1993166.641925.912013 6908.41 37756.58 1994209.392689.282014 7421.70 40173.03 1995 248.50 3557.55 2015 8549.47 42886.49 1996 291.75 4188.53 2016 9225.07 47251.36 1997 340.52 4686.11(1)建立浙江省一般预算收入与全省地区生产总值的计量经济模型,估计模型的参数,检验模型的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2017年,浙江省地区生产总值为52000亿元,比上年增长10%,利用计量经济模型对浙江省2017年的一般预算收入做出点预测和区间预测(3)建立浙江省一般预算收入的对数与地区生产总值对数的计量经济模型,估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义。
庞皓计量经济学第三版课后习题及答案(顶配word版)
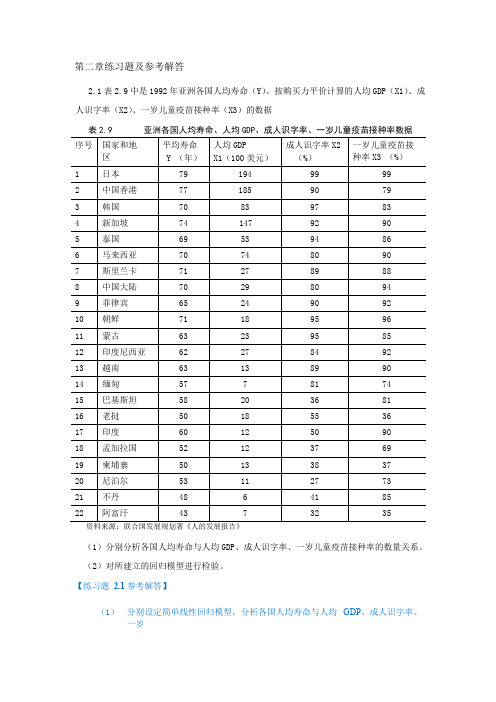
第二章练习题及参考解答2.1表2.9中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题2.1 参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于0.05,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显著影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为0.5261 人均寿命与成人识字率回归的可决系数为0.7168 人均寿命与一岁儿童疫苗接种率的可决系数为0.5379相对说来,人均寿命由成人识字率作出解释的比重更大一些2.2为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长9.0%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义【练习题2.2 参考解答】建议学生独立完成2.3 由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
计量经济学习题

计量经济学一、 单选题1、经济计量分析工作的基本步骤是( B )。
A .设定理论模型→收集样本资料→估计模型参数→检验模型B .设定模型→估计参数→检验模型→应用模型C .个体设计→总体估计→估计模型→应用模型D .确定模型导向→确定变量及方程式→估计模型→应用模型2、用一组有30个观测值的样本估计模型i 01i i Y X u ββ+=+,在0.05的显著性水平下对1β的显著性作t 检验,则1β显著地不等于零的条件是其统计量t 大于( D )。
A t 0.05(30)B t 0.025(30)C t 0.05(28)D t 0.025(28)3、计量经济学成为一门独立学科的标志是( A )。
A .1930年世界计量经济学会成立B .1933年《计量经济学》会刊出版C .1969年诺贝尔经济学奖设立D .1926年Economics 一词构造出来4、同一统计指标按时间顺序记录的数据列称为( B )。
A .横截面数据B .时间序列数据C .修匀数据D .原始数据5、横截面数据是指( A )。
A .同一时点上不同统计单位相同统计指标组成的数据B .同一时点上相同统计单位相同统计指标组成的数据C .同一时点上相同统计单位不同统计指标组成的数据D .同一时点上不同统计单位不同统计指标组成的数据6、计量经济模型的基本应用领域有( A )。
A .结构分析、经济预测、政策评价B .弹性分析、乘数分析、政策模拟C .消费需求分析、生产技术分析D .季度分析、年度分析、中长期分析7、参数β的估计量ˆβ具备有效性是指( B )。
A .ˆvar ()=0βB .ˆvar ()β为最小C .ˆ()0ββ-=D .ˆ()ββ-为最小 8、当模型存在序列相关现象时,适宜的参数估计方法是( C )A 、加权最小二乘法B 、间接最小二乘法C 、广义差分法D 、工具变量法9、产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为ˆY 356 1.5X -=,这说明( D )。
