[学习]概率论与数理统计浙大四版第五章概率论复习
概率论与数理统计浙大四版习题答案第五章

第五章 大数定理和中心极限定理1.[一] 据以往经验某种电器元件的寿命服从均值为100小时的指数分布,现在随机的抽取16只,设它们的寿命是相互独立的,求这16只元件寿命总和大于1920小时的概率。
解:设第i 只寿命为X i ,(1≤i ≤16),故E (X i )=100,D (X i )=1002(l=1,2,…,16).依本章定理1知⎪⎪⎪⎪⎪⎭⎫⎝⎛≤-=⎪⎪⎪⎪⎪⎭⎫⎝⎛⨯-≤⨯-=≤∑∑∑===8.040016001001616001920100161600)1920(1616161i i i i i i X P X P X P.7881.0)8.0(=Φ=从而.2119.07881.01)1920(1)1920(161161=-=≤-=>∑∑==i ii iXP XP3.[三] 计算机在进行加法时,对每个加数取整(取为最接近它的整数),设所有的取整误差是相互独立的,且它们都在(-0.5,0.5)上服从均匀分布,(1)若将1500个数相加,问误差总和的绝对值超过15的概率是多少? (2)几个数相加在一起使得误差总和的绝对值小于10的概率不小于0.90 解:(1)设取整误差为X i (Λ,2,1=i ,1500),它们都在(-0.5, 0.5)上服从均匀分布。
于是: 025.05.0)(=+-==p X E i 12112)]5.0(5.0[)(2=--=i X D 18.111251211500)(,0)(==⨯==i i X nD X nE ⎭⎬⎫⎩⎨⎧≤≤--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>∑∑∑===1515115115150011500115000i i i i i i X P X P X P⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤≤--=∑=18.111518.1118.1115115001i i X P1802.0]9099.01[2)]34.1(1[2)]34.1()34.1([1=-⨯=Φ-=-Φ-Φ-=8.某药厂断言,该厂生产的某种药品对于医治一种疑难的血液病的治愈率为0.8,医院检验员任意抽查100个服用此药品的病人,如果其中多于75人治愈,就接受这一断言,否则就拒绝这一断言。
(浙大四版)概率论与数理统计知识点总结(word文档物超所值)
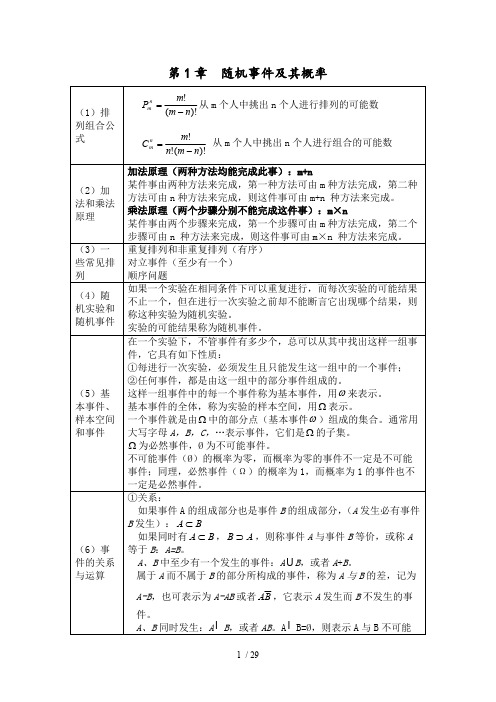
1° 1, 2 L n ,
2°
P(1 ) P( 2 ) L
P( n )
1 n
。
设任一事件 A ,它是由1, 2 L m 组成的,则有
P(A)=(1 ) U ( 2 ) UL U ( m ) = P(1 ) P( 2 ) L P( m )
P(Bi ) ,( i 1 , 2 ,…, n ),通常叫先验概率。 P(Bi / A) ,( i 1 , 2 ,…, n ),通常称为后验概率。贝叶斯公式
3 / 29
(17)伯 努利概型
反映了“因果”的概率规律,并作出了“由果朔因”的推断。 我们作了 n 次实验,且满足 每次实验只有两种可能结果, A 发生或 A 不发生; n 次实验是重复进行的,即 A 发生的概率每次均一样; 每次实验是独立的,即每次实验 A 发生与否与其他次实验 A 发生与否是互不影响的。
第 1 章 随机事件及其概率
(1)排 列组合公 式
Pmn
m! 从 (m n)!
m
个人中挑出
n
个人进行排列的可能数
C
n m
m! n!(m n)!
从 m 个人中挑出 n 个人进行组合的可能数
(2)加 法和乘法 原理
(3)一 些常见排 列 (4)随 机实验和 随机事件
(5)基 本事件、 样本空间 和事件
C Pn(k)
k n
pk qnk
,
k
0,1,2,L
,n 。
第二章 随机变量及其分布
设离散型随机变量 X 的可能取值为 Xk(k=1,2,…)且取各个值的 概率,即事件(X=Xk)的概率为
P(X=xk)=pk,k=1,2,…, 则称上式为离散型随机变量 X 的概率分布或分布律。有时也用
(浙大第四版)概率论与数理统计知识点总结.
1
概率论与数理统计 公式(全) 知识点总结
当 A=Ω 时,P( B )=1- P(B)
P ( AB) 为事件 A 发生条 P ( A) P ( AB) ( 12 ) 条 件下,事件 B 发生的条件概率,记为 P( B / A) 。 件概率 P ( A) 条件概率是概率的一种,所有概率的性质都适合于条件概率。 例如 P(Ω /B)=1 P( B /A)=1-P(B/A) 乘法公式: P( AB) P( A) P( B / A) ( 13 ) 乘 更一般地,对事件 A1,A2,…An,若 P(A1A2…An-1)>0,则有 P( A1 A2 … An ) P( A1) P( A2 | A1) P( A3 | A1 A2) …… P( An | A1 A2 … 法公式 An 1) 。
A、B 中至少有一个发生的事件:A B,或者 A+B。
属于 A 而不属于 B 的部分所构成的事件,称为 A 与 B 的差,记为
A-B, 也可表示为 A-AB 或者 A B , 它表示 A 发生而 B 不发生的事件。
1
概率论与数理统计 公式(全) 知识点总结
A、B 同时发生:A B,或者 AB。A B=Ø,则表示 A 与 B 不可能同
p
k
;
f ( x)dx
。
P(X=1)=p, P(X=0)=q
1
概率论与数理统计 公式(全) 知识点总结
二项分布
在 n 重贝努里试验中, 设事件 A 发生的概率为 p 。 事件 A 发生的次数是随机变量,设为 X ,则 X 可能取值为
0,1,2,, n 。
k k nk P( X k ) Pn(k ) Cn p q
F ( ) lim F ( x) 0 ,
浙江大学概率论与数理统计第4版课后答案及笔记

浙江⼤学概率论与数理统计第4版课后答案及笔记浙江⼤学《概率论与数理统计》(第4版)笔记和课后习题(含考研真题)详解第1章 概率论的基本概念1.1 复习笔记⼀、随机事件1事件间的关系(见表1-1-1)表1-1-1 事件间的关系2事件的运算设A,B,C为事件,则有:(1)交换律:A∪B=B∪A;A∩B=B∩A;(2)结合律:A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C;(3)分配律:A∪(B∩C)=(A∪B)∩(A∪C);A∩(B∪C)=(A∩B)∪(A∩C);(4)德摩根律:;。
⼆、频率与概率概率的性质(1)若A⊂B,则P(B-A)=P(B)-P(A)与P(B)≥P(A)(2)(逆事件的概率)P(A_)=1-P(A);(3)(加法公式)P(A∪B)=P(A)+P(B)-P(AB);推⼴:对于任意n个事件A1,A2,…,A n,三、等可能概型(古典概型)计算公式四、条件概率1乘法定理(1)乘法公式:若P(A)>0,则P(AB)=P(B|A)P(A)。
(2)若P(A1A2…A n-1)>0,则有2全概率公式和贝叶斯公式(1)全概率公式P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+…+P(A|B n)P(B n)(2)贝叶斯公式注:全概率公式和贝叶斯公式的最简单形式五、独⽴性1两个事件独⽴(1)P(AB)=P(A)P(B)(2)两个定理①若P(A)>0,A,B相互独⽴,则P(B|A)=P(B),反之同样。
②若事件A与B独⽴,则A与B_独⽴,A_与B独⽴,A_与B_独⽴。
2三个事件独⽴设A,B,C是三个事件,如果满⾜等式则称A,B,C两两独⽴,若也成⽴,则A,B,C相互独⽴。
3n个事件独⽴设A1,A2,…,A n是n(n≥2)个事件,∀1≤i<j<k<…≤n,则A1,A2,…,A n相互独⽴。
《概率论与数理统计》浙江大学第四版课后习题答案

概率论与数理统计习题答案 第四版 盛骤 (浙江大学)浙大第四版(高等教育出版社) 第一章 概率论的基本概念1.[一] 写出下列随机试验的样本空间(1)记录一个小班一次数学考试的平均分数(充以百分制记分)([一] 1)⎭⎬⎫⎩⎨⎧⨯=n n nn o S 1001, ,n 表小班人数(3)生产产品直到得到10件正品,记录生产产品的总件数。
([一] 2)S={10,11,12,………,n ,………}(4)对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。
查出合格品记为“1”,查出次品记为“0”,连续出现两个“0”就停止检查,或查满4次才停止检查。
([一] (3))S={00,100,0100,0101,1010,0110,1100,0111,1011,1101,1110,1111,} 2.[二] 设A ,B ,C 为三事件,用A ,B ,C 的运算关系表示下列事件。
(1)A 发生,B 与C 不发生。
表示为:C B A 或A - (AB+AC )或A - (B ∪C )(2)A ,B 都发生,而C 不发生。
表示为:C AB 或AB -ABC 或AB -C(3)A ,B ,C 中至少有一个发生表示为:A+B+C(4)A ,B ,C 都发生, 表示为:ABC(5)A ,B ,C 都不发生,表示为:C B A 或S - (A+B+C)或C B A ⋃⋃(6)A ,B ,C 中不多于一个发生,即A ,B ,C 中至少有两个同时不发生 相当于C A C B B A ,,中至少有一个发生。
故 表示为:C A C B B A ++。
(7)A ,B ,C 中不多于二个发生。
相当于:C B A ,,中至少有一个发生。
故 表示为:ABC C B A 或++ (8)A ,B ,C 中至少有二个发生。
相当于:AB ,BC ,AC 中至少有一个发生。
(浙大第四版)概率论与数理统计知识点总结

第1章随机事件及其概率(1)排列组合公式)!(!nmmP n m从m个人中挑出n个人进行排列的可能数)!(!!nmnmC n m从m个人中挑出n个人进行组合的可能数(2)加法和乘法原理加法原理(两种方法均能完成此事):m+n某件事由两种方法来完成,第一种方法可由m种方法完成,第二种方法可由n种方法来完成,则这件事可由m+n 种方法来完成。
乘法原理(两个步骤分别不能完成这件事):m×n某件事由两个步骤来完成,第一个步骤可由m种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m×n 种方法来完成。
(3)一些常见排列重复排列和非重复排列(有序)对立事件(至少有一个)顺序问题(4)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。
试验的可能结果称为随机事件。
(5)基本事件、样本空间和事件在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质:①每进行一次试验,必须发生且只能发生这一组中的一个事件;②任何事件,都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件,用来表示。
基本事件的全体,称为试验的样本空间,用表示。
一个事件就是由中的部分点(基本事件)组成的集合。
通常用大写字母A,B,C,…表示事件,它们是的子集。
为必然事件,?为不可能事件。
不可能事件(?)的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件(Ω)的概率为1,而概率为1的事件也不一定是必然事件。
(6)事件的关系与运算①关系:如果事件A的组成部分也是事件B的组成部分,(A发生必有事件B发生):BA如果同时有BA,AB,则称事件A与事件B等价,或称A 等于B:A=B。
A、B中至少有一个发生的事件:A B,或者A+B。
属于A而不属于B的部分所构成的事件,称为A与B的差,记为A-B,也可表示为A-AB或者BA,它表示A发生而B不发生的事件。
(完整word版)(浙大第四版)概率论与数理统计知识点总结详解

(7)概率 的公理化 定义
Ai Ai
德摩根率: i1
i1
AB AB,AB AB
设 为样本空间, A 为事件,对每一个事件 A 都有一个实数 P(A),若满足下列三个条件:
件下,事件 B 发生的条件概率,记为 P(B / A) P( AB) 。 P( A)
条件概率是概率的一种,所有概率的性质都适合于条件概率。 例如 P(Ω/B)=1 P( B /A)=1-P(B/A) 乘法公式: P(AB) P(A)P(B / A) 更一般地,对事件 A1,A2,…An,若 P(A1A2…An-1)>0,则有
P( A1A2 … An) P( A1)P( A2 | A1)P( A3 | A1A2) …… P( An | A1A2 …
An 1) 。 ①两个事件的独立性
设事件 A 、B 满足 P(AB) P(A)P(B) ,则称事件 A 、B 是相互独 立的。
若事件 A 、 B 相互独立,且 P(A) 0 ,则有
A-B,也可表示为 A-AB 或者 AB ,它表示 A 发生而 B 不发生的事件。
1
概率论与数理统计 公式(全)
知识点总结
A、B 同时发生:A B,或者 AB。A B=Ø,则表示 A 与 B 不可能同
时发生,称事件 A 与事件 B 互不相容或者互斥。基本事件是互不 相容的。
-A 称为事件 A 的逆事件,或称 A 的对立事件,记为 A 。它表示
1
概率论与数理统计 公式(全)
知识点总结
当 A=Ω时,P( B )=1- P(B)
浙江大学概率论与数理统计(盛骤第四版)——概率论部分1-90页精品文档

# 频率 反映了事件A发生的频繁程度。
15
n
Ai Ai A1 A2
n
n
An; Ai Ai=A1A2 An;
i1
i1
i1
i1
例:设A={ 甲来听课 },B={ 乙来听课 } ,则:
A B {甲、乙至少有一人来}
都不来}
A BAB{甲、乙至少有一人不来}
14
§3 频率与概率
例:
称S中的元素e为基本事件或样本点.
一枚硬币抛一次 S={正面,反面}; 记录一城市一日中发生交通事故次数
S={0,1,2,…}; 记录某地一昼夜最高温度x,最低温度y
S={(x,y)|T0≤y≤x≤T1}; 记录一批产品的寿命x S={ x|a≤x≤b }
10
(二) 随机事件
一般我们称S的子集A为E的随机事件A,当且 仅当A所包含的一个样本点发生称事件A发生。 例:观察89路公交车浙大站候车人数,S={0,1,2,…};
概率论与数理统计是研究随机现象 数量规律的一门学科。
1
第一章 概率论的基本概念
• 1.1 随机试验 • 1.2 样本空间 • 1.3 概率和频率 • 1.4 等可能概型(古典概型) • 1.5 条件概率 • 1.6 独立性
第二章 随机变量及其分布
• 2.1 随机变量 • 2.2 离散型随机变量及其分布 • 2.3 随机变量的分布函数 • 2.4 连续型随机变量及其概率密度 • 2.5 随机变量的函数的分布
记 A={至少有10人候车}={10,11,12,…} S, A为随机事件,A可能发生,也可能不发生。
如果将S亦视作事件,则每次试验S总是发生, 故又称S为必然事件。 为方便起见,记Φ 为不可能事件,Φ 不包含
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将 FY ( y) 关于 y 求导数得到Y 的概率密度为
fY
(
y)
2
1
y
[
f
X
(
y) fX (
y )],
0,
0 y 4, 其他.
当 0 y 1时, 0 y 1, 1 y 0,
于是
fX (
y) 1, 3
fX (
y) 1; 3
当 1 y 4 时, 1 y 2, 2 y 1,
0, 其他.
fY X ( y x)
f (x, y) fX (x)
e x y , 0 x y ,
0,
其他.
(4) P{ X 1Y 2} P{ X 1,Y 2} P{Y 2}
1
2
f (x, y)d xd y
2
fY ( y)d y
解:设 Bi ={箱中恰好有i件次品},i=0,1,2.
A={顾客买下所查看的一箱}
由题设可知:P(B0 )=0.8, P(B1 )=0.1; P(B2 )=0.1.
P(A∣B0 )=1;
P(A∣ B1
)= C149 C240
4 5
;
P(A∣B2)=
C148 C240
12 19
2
1)由全概率公式:P(A)= P( A Bi )P(Bi ) ≈0.94
概率论复习课
例1 设玻璃杯整箱出售,每箱20个,各箱含0,1,2个 次品的概率分别为0.8,0.1,0.1,某顾客欲购买一 箱玻璃杯,由售货员任取一箱,经顾客开箱随机查看 4个。若无次品,则买一箱玻璃杯,否则不买。
求:1)顾客买此箱玻璃杯的概率; 2)在顾客买的此箱玻璃杯中,确实没有次品的 概率。
(5) 求 ( X ,Y ) 的联合分布函数 ;
(6) 求 Z X Y 的密度函数 ;
(7) 求 P{X Y 1}.
解 (1) 由 f ( x, y)d x d y 1 ,得
1
dy
y cxe y d x c
y2ey d y分部积分c,
例3 设随机变量( X ,Y ) 的联合概率密度为
cxe y , 0 x y ,
f (x, y)
(1) 求常数 c; 0.
其他.
(2) X 与Y 是否独立?为什么?
(3) 求 f X Y (x y), fY X ( y x); (4) 求 P{X 1Y 2}, P{X 1Y 2};
1
dx
2 xe y d y
0
x
2 1 y2e y d y 02
1 2e1 1 e2
2 1 5e2
.
又由条件密度的性质知
1
P{ X 1Y 2} fX Y ( x 2)d x,
而
f
X
Y
(
x
2)
x 2
,
0 x 2,
0, 其他.
从而有
P{ X 1Y 2} 1 x d x 1 .
因 0 Y X 2 4, 故当 y 0 时, FY ( y) 0,
当 y 4 时, FY ( y) 1,
当 0 y 4 时, FY ( y) P{Y y} P{X 2 y}
P{ y X y}
FX ( y) FX ( y).
i0
2)由贝叶斯公式:P(B0
A)
P( A B0 )P(B0 ) P( A)
≈0.85
例2 设 X 在区间(2,1) 上服从均匀分布,求 Y X 2
的概率密度. 解 X 的概率密度为
fX ( x) 13 ,
2 x 1,
先求 Y 的分布函数 FY ( y).
0, 其他.
0
0
20
c 1.
(2)
fX ( x)
f
( x,
y)d
y
x 0,
xe y
d
y,
xex , x 0,
0, x 0.
x0 x 0.
fY ( y)
f (x, y)d x
y 0
xe y d
x,
y0
0,
02
4
(5) 由于 F ( x, y) P{ X x,Y y}, 故有 :
当 x 0 或 y 0 时, 有 F ( x, y) 0.
当0 y x 时, 有
F(x, y) P{X x,Y y}
y
dv
v uev d u 1
y v2ev d v
故得 0,
x 0 或 y 0,
F ( x,
y)
1
(
y2 2
y
1)e y ,
0 y x ,
1 ( x
1)e x
1 2
x2e y ,0
x
y
.
(6)
根据 fZ (z)
f (x,z x)d x,
由于要被积函数 f (x,z x) 非零 ,只有当
于是 因此
f X ( y) 0,
fX (
y) 1. 3
2
1
y
1 3
1 3
,
fY
(
y)
2
1
y
0
13,
0,
0 y 1, 1 y 4, 其他.
即
3
1
y
,
fY
(
y)
6
1
y
,
0,
0 y 1, 1 y 4, 其他.
0 x z x, 即 0 x z 时, 从而有: 2
当 z 0 时, fZ (z) 0;
y 0.
12 y2e y , y 0,
0,
y 0.
由于在 0 x y 上, f ( x, y) f X ( x) fY ( y), 故 X 与Y 不独立.
(3)
fX Y (x y)
f (x, y) fY ( y)
2x y2
,
0 x y ,
0
0
20
1 ( y2 y 1)e y . 2
当0 x y 时, 有
F( x, y) P{X x,Y y}
x
du
y uev d v
0
u
x u(eu e y )d u 0
1 ( x 1)e x 1 x2e y . 2
