Smith预估器控制设计要点
Smith预估控制原理
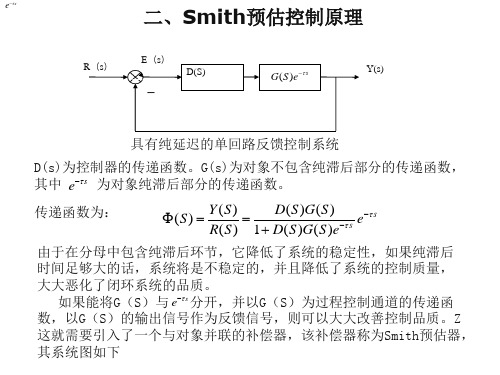
R(S)
这样,引入了Smith预估器后,系统 中等效对象的传递函数就不含纯滞 s 后环节 e 部分
_
D(S)
G(s)
e s
显然,经Smith预估补偿后,已消除了纯滞后部分对控制系统的影响,而受控制对象的纯 滞后部分在等效系统的闭环控制回路之外,不影响系统的稳定性。所以对任何纯滞后时 间,系统都是稳定的。
u (t ) K P e(t ) TI
e(t )d (t ) T
0
D
dt
式中u(t)-控制器的输出; e(t)-控制器的输入,它是给定值和被控对象输出的差,称为偏差 信号;
K P -控制器的比例系数;
TI
TD
-控制器的积分时间; -控制器的微分时间。
PID控制器各控制规律的作用如下: (1)比例控制(P):比例控制是一种最简单的控制方式。其控制器的输 出与输入误差信号成比例关系,能较快克服扰动,使系统稳定下来。但当仅 有比例控制时系统输出存在稳态误差 (2)积分控制(I):在积分控制中,控制器的输出与输入误差信号的积分 成正比关系。对一个自动控制系统,如果在进入稳态后存在稳态误差,则称 此控制系统是有差系统。为了消除稳态误差,在控制器中必须引入“积分项” 积分项对误差的累积取决于时间的积分,随着时间的增加,积分项会越大。 这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输 出增大使稳态误差进一步减小,直到等于零。但是过大的积分速度会降低系统 的稳定程度,出现发散的振荡过程。比例+积分(PI)控制器,可以使系统在进 入稳态后无稳态误差。 (3)微分控制(D):在微分控制中,控制器的输出与输入误差信号的微分 (即误差的变化率)成正比关系。自动控制系统在克服误差的调节过程中可能 会出现振荡甚至失稳。其原因是由于存在有较大惯性环节或有滞后环节,具有 抑制误差的作用,其变化总是落后于误差的变化。解决的办法是使抑制误差的 作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。
斯密斯预估控制器

施密斯预估控制姓名:学号:班级:1 实验目的对大多数控制系统,采用常规的控制技术均可以达到满意的控制效果,但对于复杂及特殊要求的控制系统,采用常规的控制室技术很难达到目的,在这种情况下,就需要采用复杂控制技术,其中Smith 预估控制算法是常用的一种,通过本实验加深对Smith 预估控制算法的理解和掌握。
2 实验原理图1为被控对象具有纯滞后特性的单回路反馈控制系统,D (s )是控制器,被控对象的传递函数为etss -)(G p ,其中,)(G p s 为被控对象中不包含纯滞后部分的传递函数,ts-e为被控对象纯滞后部分的传递函数。
)(t r )(t e )(t u )(t y_施密斯预估原理:与D (s )并接一补偿环节,用来补偿被控对象中的纯滞后部分,这个补偿环节称为预估器,其传递函数为)1)((G p tse s --,t 为纯滞后时间,补偿后的系统结构如图2所示。
)(t r )(t e )(t u )(t y_ _)(t y τ由施密斯预估控制器)1)((G p tses --和控制器D (s )组成的回路陈伟纯滞后补偿器,)(s Ds e s τ-)(G p)(s Ds e s τ-)(G p)1)((G p ts e s --其传递函数为:)1)(()(1)()(D m s p e s G s D s D s τ--+=经过补偿后的系统闭环传递函数为:s p p sp m sp m e s G s D s G s D es G s D e s G s D τττ---+=+=Φ)()(1)()()()(1)()(s )(该式说明,进过补偿后,消除了之后部分对控制系统的影响,因为式中ts-e 在闭环控制回路之外,不影响系统的稳定性。
设广义被控对象为:1011()()()1Ts s se e H s G s G s es T sττ----==⋅+取T=1、τ=2、T 1=2.88,经采样(T=1s )保持后,其广义对象z 传递函数为00.2934()0.7066G z z =-,而2se -转换为2个单位迟延。
Smith预估补偿控制策略

组员: 蔺潇 刘杭 赵全红 齐宝喆 张谦 史绍杨
Smith 预估补偿控制策略在转炉煤气回收 2-1 도형 系统中的应用 目录
工业背景 工业原理 控制方案设计
控制算法研究
2 / 12
工业背景
在转炉炼钢生产过程中,炉口会产生大量的高温烟气,其主要成分为C O,如果不进行回收处理和控制排放,不仅污染大气环境,还会造成能 源浪费 。工艺分析表明 :转炉煤气回收与烟气减排的效果关键存于炉 口的压差控制。目前,工业生产中普遍采用的仍然是传统的PID控制方 法。但由于PID调节器增益参数是固定的,故对于诸如转炉煤气回收这 样的非线性、纯滞后复杂系统,采用它来设计位置伺服控制器,经常会
工业原理
目前转炉煤气回收系统主要采用的是文氏管湿法除尘回收技术(OG),基本工艺 流程如图1所示,主要有转炉活动烟罩、汽化烟道、一文脱水、二文喉口调节、 回收汽柜、放散塔几个部分组成,分别具有输送烟气、降温除尘、流量调节、 煤气收集、放散排空的功能 。罩在炉口上的活动炯罩与炉口问的缝隙处,存在 着烟罩内、外气体之间的压差。压差负值较大,将导致炉外空气被吸入烟罩, 促使CO燃烧,使煤气回收量和热值降低,反之,压差正值较大,将造成炉口烟 气外溢,同样使煤气回收量和热值减少,并污染大气环境。由于在转炉钢水冶 炼过程中,炉内烟气的生成量在不断变化,炉口压差也随之改变,因此,通过 压差的测量来实时调节二文喉口的开度,控制烟气输出流量,使风机的抽风量 与烟气的生成量保持一致,即可使炉口压差趋近于零,就可避争烟气外溢或向 罩内吸入空气,从而达到较好的烟气减排及煤气回收效果。
工艺原理
控制方案设计
根据上述工艺要求,可设计图2所示的炉口差压控制原理框图。通过安置在活动 烟罩顶部的取压管,从炉口取出压差信号后,经差压变送器转换,再根据压差设 定值,由Smith预估补偿控制器进行调节量输出计算,然后通过电动执行机构驱 动二文喉口的流量调节阀(RD阀)。由于工业现场环境十分恶劣,作用于RD阀的 各种干扰会导致其定位不准确,如:由外部设备引起的机械振动以及被控流体和 内部润滑介质流动造成的振动都会导致执行器产生振荡;此外由于脏物或油污使 传动机构卡涩,引起执行器的机械连接阀体等传动机构之间的磨损程度产生变化。 为此,通常在执行机构与调节机构环节设置闭环控制,即采用安装在调节机构上 的角位移传感器发出反馈信号与调节信号相比较,直至电动执行机构的伺服放大 器的输出为零,RD阀转动停止,从而实现RD阀的准确定位。由于冶炼过程中, 需要对转炉实施加料、降罩等工艺操作,这将导致炉内化学反应加剧,烟气生成 量骤然变化,使得炉内烟气压力波动较大。为保持炉口压差为设定值,必须使喉 口开度的控制速度能跟上烟气压力变化的速度,并满足无级调节要求,才能达到 炉口压差的自动控制的目的。
实验三Smith预估

实验三S m i t h预估 The following text is amended on 12 November 2020.实验报告||实验名称Smith预估控制算法设计实验课程名称计算机控制技术与系统||实验三 Smith 预估控制算法设计实验1、实验目的在控制算法学习的基础上,根据给定对象特性设计Smith 预估控制器算法,并利用Matlab 软件进行仿真实验,同时与PID 算法控制算法进行比较,加深对该控制算法的掌握和理解。
2、系统结构框图Smith 预估控制系统框图为:3、实验过程及分析设广义被控对象为要求一:取τ=2、T 1=,取采样时间T=1s ,采用零阶保持器,使用Matlab 函数求取出广义对象的z 传递函数;实验过程:使用matlab 求z 传函的函数:clc;clear all;close all;T=1;T1=;tao=2;G0=tf([1],[T1 1],'inputdelay',tao)sysd=c2d(G0,T,'zoh')上述函数将s 传函210(s) 2.881s G e s -=+转化为z 传函20.29340(z)0.7066G z z -=-。
要求二:通过对象阶跃响应曲线,整定PID 参数,采用常规PID 进行给定值扰动和外部扰动响应实验,并绘制控制器输出P 和系统输出y 响应曲线; 实验过程:借助matlab 软件中的simulink 搭建系统仿真模型。
首先将外部扰动置零,利用阶跃响应曲线来整定PID 参数。
利用试凑法整定PID 参数。
PID 控制器的数学描述如下。
首先只给比例作用,调节系统使其稳定;其次加入积分作用消除系统静差;最后加入微分作用。
最后合理调整各个参数,使系统品质达到最优。
经过整定,最终选取P=,I=,D=0,N=100,系统可以相对较好的稳定下来。
输出的曲线如下在30T 的时候在对象之前加入的阶跃干扰,在50T 的时候在对象之后加入幅值为的阶跃扰动,得到的系统的输出曲线如下。
内模控制和Smith预估器

第五节 Smith 预估控制Smith 预估控制方法是在1957年由Smith 提出来的,其特点是预先估计被控系统在基本扰动下的动态特性,然后用预估器进行补偿,力图使被延迟的被控制量超前反映到控制器中,使控制器提前动作,从而显著地减小系统的超调量,同时加速系统的调节过程。
一、Smith 预估控制原理预估控制系统原理图如图7-24所示。
(a) 预估控制系统原理框图 (b) Smith 预估器图7-24 预估控制系统原理图 图中,s e s G τ−)(p 为具有时滞为τ的对象传递函数,其中)(p s G 为被控对象;)(m s G 为内部模型(又称为对象的标称或名义模型),即Smith 预估器的传递函数,()s e s G s G τ−−=1)()(p m ;)(s D 为(前馈)内模控制器;)(s d 为扰动;)(s R 为参考输入;)(s Y 为被控对象输出;)(m s Y 为内部模型输出。
由图7-24可知,将Smith 预估器与控制器(或被控对象)二者并联。
在理论上可以使被控对象的时间滞后得到完全补偿,控制器的设计就不必再考虑对象的时滞作用了。
现在,系统中假设没有补偿器(预估器),则控制器输出与被控量之间的传递函数便为 s e s G s U s Y τ−=)()()(p (7-50) 上式表明,受到)(s U 控制作用的被控量)(s Y 要经过纯滞后时间τ之后才能反馈到系统控制器输入端。
若采用预估补偿器,则控制量)(s U 与反馈到控制器输入端的反馈信号)(s Y ′之间的传递函数乃是两个并联通道之和,即)()()()(m p s G e s G s U s Y s +=′−τ (7-51) 为使反馈信号)(s Y ′不发生时间滞后τ,则要求(7-51)式满足)()())(()()(p m p s G s G e s s G s U s Y s =+=′−τ (7-52) 于是,就导出了Smith 预估补偿器的传递函数为()s e s G s G τ−−=1)()(p m (7-53) 在系统中设置了Smith 预估器的情况下,可以推导出系统的闭环传递函数为)()(1)()()1)(()(1)()(1)1)(()(1)()()()(p p p p p p s G s D e s G s D e s G s D e s G s D e s G s D e s G s D s R s Y s s s s+=−++−+=−−−−−ττττ (7-54) 由上式可以明显看出,在系统的特征方程中,已经不含有s e τ−项。
Smith预估
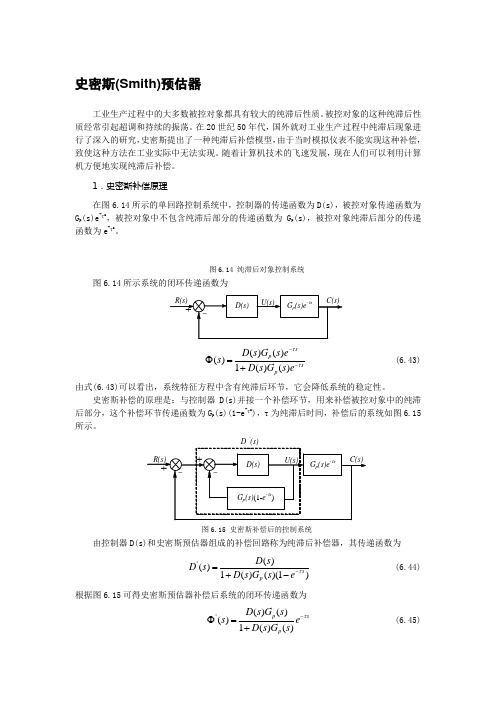
史密斯(Smith)预估器工业生产过程中的大多数被控对象都具有较大的纯滞后性质。
被控对象的这种纯滞后性质经常引起超调和持续的振荡。
在20世纪50年代,国外就对工业生产过程中纯滞后现象进行了深入的研究,史密斯提出了一种纯滞后补偿模型,由于当时模拟仪表不能实现这种补偿,致使这种方法在工业实际中无法实现。
随着计算机技术的飞速发展,现在人们可以利用计算机方便地实现纯滞后补偿。
1.史密斯补偿原理在图6.14所示的单回路控制系统中,控制器的传递函数为D(s),被控对象传递函数为G p (s)e -τs ,被控对象中不包含纯滞后部分的传递函数为G p (s),被控对象纯滞后部分的传递函数为e -τs 。
图6.14 纯滞后对象控制系统图6.14所示系统的闭环传递函数为()()()1()()sp s p D s G s e s D s G s e ττ--Φ=+ (6.43)由式(6.43)可以看出,系统特征方程中含有纯滞后环节,它会降低系统的稳定性。
史密斯补偿的原理是:与控制器D(s)并接一个补偿环节,用来补偿被控对象中的纯滞后部分,这个补偿环节传递函数为G p (s)(1-e -τs ),τ为纯滞后时间,补偿后的系统如图6.15所示。
‘图6.15 史密斯补偿后的控制系统由控制器D(s)和史密斯预估器组成的补偿回路称为纯滞后补偿器,其传递函数为'()()1()()(1)s p D s D s D s G s e τ-=+- (6.44) 根据图6.15可得史密斯预估器补偿后系统的闭环传递函数为 '()()()1()()p s p D s G s s e D s G s τ-Φ=+ (6.45)由式(6.45)可以看出,经过补偿后,纯滞后环节在闭环回路外,这样就消除了纯滞后环节对系统稳定性的影响。
拉氏变换的位移定理说明e -τs仅仅将控制作用在时间座标上推移了一个时间τ,而控制系统的过渡过程及其它性能指标都与对象特性为G p (s)时完全相同。
Smith预估器控制设计

《计算机控制》课程设计报告题目: Smith预估器控制设计姓名:《计算机控制》课程设计任务书指导教师签字:系(教研室)主任签字:2012年7月5 日Smith 预估器控制设计一、实验目的通过混合仿真实验,学习并掌握用于具有纯滞后系统的纯滞后补偿(Smith预估器控制)的设计及其实现。
二、实验内容被控对象为-512()2se G s s =+, 1.0s T =画出系统框图,设计Smith 数字预估器。
三、控制系统仿真 1.方案设计已知纯滞后负反馈控制系统,其中图1.其中D(s)为调节器传递函数,-512()2se G s s =+为对象传递函数,其中-5()sO G s e 包含纯滞后特性,纯滞后时间常数5τ=。
系统的特征方程为:5121()()1()02se D s G s D s s -+=+=+由于闭环特征方程中含有-5s e 项,产生纯滞后现象,/5/150.5m T τ==≥,采用常规的PID 控制会使系统稳定性变差,甚至产生振荡。
为了改善系统特性,引入Smith 预估器,使得闭环系统的特征方程中不含有-5s e 项。
Smith 纯滞后补偿的计算机控制系统:图 2.上图所示ZOH 为零阶保持器,传递函数为:se s G Tsh --1)(=,并且有:lT =τ(l为大于1的整数,T 为采样周期)。
由已知可知, 1.0T s =,则551l Tτ===。
2.负反馈调节器D(z)的确定D(z)为负反馈调节器,通常使用PID 控制规律。
使用扩充响应曲线法对数字PID 控制器进行参数整定。
扩充响应曲线法是在模拟PID 控制器响应曲线法的基础上推广应用到数字PID 控制器参数整定的方法。
扩充响应曲线法是用于具有纯滞后的一阶对象,由前面分析和已知: 1.0T s =,5τ=,5l =,1m T =,因此依据课本128页表4.2扩充响应曲线法整定PID 参数表选择数字PID 参数计算公式,由于1=0.25Tτ=,则选择控制度为1.20,控制规律为PI 控制,因此选定PI 参数为:0.78()pmK T τ=3.60iT τ=所以有:0.156p K = 18i T = 则控制器的传递函数为:i 110.1560.00867()(1)0.156(1)T 18p s D s K s s s+=+=+=⋅ 将得到的模拟控制器用一阶后向差分法离散化得到:1-1-1--1-10.7-717.0)-1(1|)()(1-z z z T T K s D z D i p Tz s =⋅+===】【 3.Smith 补偿器)z D (τ的确定Smith 纯滞后补偿的计算机控制系统的框图:图 3.sT Ks G m O ⋅+=1)( lT ≈τ spes G s G τ-)()(=s m Tsso h e s T s e K e s G s G s G ττ---)1()-1()()()(+==)-1)(()(-s p e s G s D ττ=)-11--11)(-1)(z -K(1 ])1(1[)-1)(z -K(1 )]-1()1()-1([)]([)(1--1--1--1---z ezz s T s Z z e s T s e K Z s D Z z D mT T lm ls m Ts =+=+==τττ令mT -T ea =,)-1(-mT T eK b =则有1--1--1)-1()(az z bz z D l =τSmith 预估器(纯滞后补偿器)的框图:图 4.)-1()()(-1l z z C z C =)()()az -(1)()z -(1c(k)1-11-1-l k u bz k c k c ==最后解得)1-()1-()()-(-)()(1111k ac k bu k c l k c k c k c +==由上一步所得的数据: 1.0T s =,5τ=,5l =,1m T =,12K =解得如下数据:1---110.368mT T a ee e ====1--1(1-)12(1-)7.584mT T b K e e ==⨯=则-1-5-17.584(1-)()1-0.368z z D z zτ=1111()()-(-5)()7.584(-1)0.368(-1)c k c k c k c k u k c k ==+由此可得到:11()7.584(-1)0.368(-1)-(-5)c k u k c k c k =+由此可见,Smith 补偿器的差分方程有1(-5)c k 项,即存在滞后5拍的信号,因此产生纯滞后信号对纯滞后补偿控制是至关重要的。
带Smith预估器的预测PID控制器的设计

预测PID控制算法仿真[J].系统仿真学报.2004, 16(3): 495-499. [3] Vega P, Prada C, Aleixandre V. Self-tuning predictive PID controller [J].IEEE Proc. Part D,1991,138(3):303-311. [4] 邵惠鹤,认正云. 预测PID控制算法的基本原理及研 究现状[J]. 世界仪表与自动化. 2004, (6):17-21. [5] KATAYAMA M, YAMAMOTO T, MADA Y. A practical design of multiloop robust PIDcontrol systems[J]. Electrical Engineering in Japan,2004, 147(3): 330-337. [6] 吴刚. 预测控制研究及在工业锅炉自动控制中的应 用[D]. 合肥: 中国科学技术大学, 1989. [7] 邵惠鹤.工业过程高级控制[M].上海:上海交通大学
矩阵求逆,计算量大,且不能保证矩阵可逆,计算中还
会出现数值病态问题,在实际应用中存在着较大的安全
隐患。
为避免传统GPC中的矩阵求逆问题,在算法中引入阶
梯式策略[6]。令
其中,
,此时的目标函数变为:
(9) 其中,
得到的控制律为:
1.3 整定结果 由式(4)与式(14)的对应关系,我们可以比较得到 PID控制器各参数(其中 为采样周期)如下:
文中控制器采用I-PD型结构,该控制律在改变设定 值时,控制器输出不至于有太大的变化,增强了系统的 抗扰动能力[7],另外可以很方便地得到此I-PD控制律与 GPC控制律之间的联系,从而可以依据GPC思想来进行PID 参数的整定[5]。其具体形式为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计算机控制》课程设计报告题目: Smith预估器控制设计姓名:《计算机控制》课程设计任务书指导教师签字:系(教研室)主任签字:2012年7月5 日Smith 预估器控制设计一、实验目的通过混合仿真实验,学习并掌握用于具有纯滞后系统的纯滞后补偿(Smith预估器控制)的设计及其实现。
二、实验内容被控对象为-512()2se G s s =+, 1.0s T =画出系统框图,设计Smith 数字预估器。
三、控制系统仿真 1.方案设计已知纯滞后负反馈控制系统,其中图1.其中D(s)为调节器传递函数,-512()2se G s s =+为对象传递函数,其中-5()sO G s e 包含纯滞后特性,纯滞后时间常数5τ=。
系统的特征方程为:5121()()1()02se D s G s D s s -+=+=+由于闭环特征方程中含有-5s e 项,产生纯滞后现象,/5/150.5m T τ==≥,采用常规的PID 控制会使系统稳定性变差,甚至产生振荡。
为了改善系统特性,引入Smith 预估器,使得闭环系统的特征方程中不含有-5s e 项。
Smith 纯滞后补偿的计算机控制系统:图 2.上图所示ZOH 为零阶保持器,传递函数为:se s G Tsh --1)(=,并且有:lT =τ(l为大于1的整数,T 为采样周期)。
由已知可知, 1.0T s =,则551l Tτ===。
2.负反馈调节器D(z)的确定D(z)为负反馈调节器,通常使用PID 控制规律。
使用扩充响应曲线法对数字PID 控制器进行参数整定。
扩充响应曲线法是在模拟PID 控制器响应曲线法的基础上推广应用到数字PID 控制器参数整定的方法。
扩充响应曲线法是用于具有纯滞后的一阶对象,由前面分析和已知: 1.0T s =,5τ=,5l =,1m T =,因此依据课本128页表4.2扩充响应曲线法整定PID 参数表选择数字PID 参数计算公式,由于1=0.25Tτ=,则选择控制度为1.20,控制规律为PI 控制,因此选定PI 参数为:0.78()pmK T τ=3.60iT τ=所以有:0.156p K = 18i T = 则控制器的传递函数为:i 110.1560.00867()(1)0.156(1)T 18p s D s K s s s+=+=+=⋅ 将得到的模拟控制器用一阶后向差分法离散化得到:1-1-1--1-10.7-717.0)-1(1|)()(1-z z z T T K s D z D i p Tz s =⋅+===】【 3.Smith 补偿器)z D (τ的确定Smith 纯滞后补偿的计算机控制系统的框图:图 3.sT Ks G m O ⋅+=1)( lT ≈τ spes G s G τ-)()(=s m Tsso h e s T s e K e s G s G s G ττ---)1()-1()()()(+==)-1)(()(-s p e s G s D ττ=)-11--11)(-1)(z -K(1 ])1(1[)-1)(z -K(1 )]-1()1()-1([)]([)(1--1--1--1---z ezz s T s Z z e s T s e K Z s D Z z D mT T lm ls m Ts =+=+==τττ令mT -T ea =,)-1(-mT T eK b =则有1--1--1)-1()(az z bz z D l =τSmith 预估器(纯滞后补偿器)的框图:图 4.)-1()()(-1l z z C z C =)()()az -(1)()z -(1c(k)1-11-1-l k u bz k c k c ==最后解得)1-()1-()()-(-)()(1111k ac k bu k c l k c k c k c +==由上一步所得的数据: 1.0T s =,5τ=,5l =,1m T =,12K =解得如下数据:1---110.368mT T a ee e ====1--1(1-)12(1-)7.584mT T b K e e ==⨯=则-1-5-17.584(1-)()1-0.368z z D z zτ=1111()()-(-5)()7.584(-1)0.368(-1)c k c k c k c k u k c k ==+由此可得到:11()7.584(-1)0.368(-1)-(-5)c k u k c k c k =+由此可见,Smith 补偿器的差分方程有1(-5)c k 项,即存在滞后5拍的信号,因此产生纯滞后信号对纯滞后补偿控制是至关重要的。
纯滞后信号可以用存储单元法近似产生。
4.采用Matlab 系统仿真本系统采用PI 控制算法,用matlab 下的Simulink 工具箱搭建闭环系统结构,加以1V 的阶跃信号,PI 控制器系数0.156p K = ,18i T =,取反馈系数为1.使用Smith 预估补偿器的仿真结构得到输出曲线分别如图所示: 系统仿真结构框图为:图 5. 系统仿真波形图为:图 6.2.使用不带Smith预估补偿器的仿真结构得到输出曲线分别如图所示:系统仿真结构框图为:图 7.系统仿真波形图为:图8.分析:通过比较前后两次仿真的波形图可以看出,采用带Smith预估器控制的设计与传统的PID控制设计相比,大大的减少了响应曲线的超调,同时也加快了系统的响应过程,增加了系统的稳定性,使系统逐渐趋于稳定,达到了预期控制的目的。
四、电路设计及元件选型控制器部分需要AD转换器,DA转换器,反相器,运算放大器,单片机。
1.AD转换器AD转换器选择ADC0809, ADC0809是一种逐次逼近式的8路模拟输入,8路数字输出的A/D转换器,可以与单片机直接连接。
逐次逼近式速度较高,比较简单,而且价格也不是很高,因此是微型计算机应用系统中最为常用的一种A/D转换器。
AD转换器的电路设计:(1) 由于只需要一路信号,只选择IN-0输入,三根地址线固定接地,选择IN-0通道。
(2) 由于ADC0809需要500KHz的时钟源,利用单片机AT89S52的ALE引脚输出的脉冲信号其频率为单片机工作晶振的六分之一,此处单片机采用12MHz的晶振,则需经过4分频后供给ADC0809的CLK端。
(3)START脚为AD转换启动信号,高电平有效,由程序控制,故与单片机的P2.0脚通过非门相连。
(4)AD采样值为系统的偏差信号,有正负两种情况,故选择ADC0809的参考电压为正负5V。
(5)AD转换结束后,EOC脚输出高电平,此时单片机接收EOC信号,读取AD 转换的结果,将EOC脚经反相器与单片机的INT0脚相连。
AD转换结果由P0口读入,故将AD转换器的输出与单片机P0口相连,高低位依次相连经以上分析,设计AD转换器的接口电路如图所示:图9.注意:ADC0809对输入模拟量要求信号单极性,电压范围是0-5V,若信号太小,必须进行放大;输入模拟量在转换过程中应保持不变,若模拟量变化太快则需在输入前加采样保持电路。
2.DA转换器DA转换器选择DAC0832,DAC0832是具有两个输入数据寄存器的8位DAC,它能直接与51单片机相连,其主要特性为:a)分辨率为8位b)电流输出,稳定时间为1sc)可双缓冲输入,单缓冲输入或直接数字输入,单一电源供电DA转换器的电路设计:(1)参考电压选择+5V,直接与供电电源相连。
(2)选择DAC为单缓冲方式,即输入寄存器工作于受控状态,DAC寄存器处于直通状态,由DAC0832的引脚特性,将DAC0832的引脚接发如下:CS:片选端,低电平有效,直接接低电平ILE:数据锁存允许控制端,高电平有效,直接接高电平。
WR2:DAC寄存器写选通控制端,低电平有效,由于其处于直通状态,故直接接低。
XFER:数据传送控制,低电平有效,故直接接地。
WR1;第一级输入寄存器写选通控制,低电平有效。
其输入为上升沿时,将输入数据锁存到DAC寄存器,故将该脚与单片机P2.1口相连,由程序控制DA转换的时间。
(3) DA的八路输入,与单片机的P1口相连,高低位依次对应。
经以上分析,设计DA转换器的接口电路如图所示:图10.3.控制器设计控制器选择AT89C51单片机,根据ADC0809和DAC0832的特性,及上述分析,设计单片机与AD、DA的接口电路如下图所示:图 11.总控制电路图如下图所示:图 12.五、采用直接程序法1.单片机程序算法1.将带Smith 预估器控制的控制器的传递函数转化为差分方程: 11()7.584(-1)0.368(-1)-(-5)c k u k c k c k =+由于已求得110.1650.156()1z D z z ---=-根据)]()([)()(z C z E z D z U -⨯= 可得()(1)0.165()0.156(1)0.165()0.156(1)u k u k e k e k c k c k =-+---+- 则控制器的算法为:(1),11()7.584(-1)0.368(-1)-(-5)c k u k c k c k =+(2),()(1)0.165()0.156(1)0.165()0.156(1)u k u k e k e k c k c k =-+---+-2.由于系统的采样周期 1.0T s =在52单片机通过选用定时器T0工作在方式1下来实现,即16位定时计数器。
单片机采用12M 晶振,则其机器周期为1us 。
由公式ms us X 501-216=⨯)( 得初值03015536CB X X ==再通过20次循环实现 1.0T s =的采样延时。
2.程序流程图图13. 主程序流程图图 14. 中断服务程序流程图3.AT89C51的单片机C语言程序51单片机C语言程序代码:#include<reg51.h>#include<math.h>#define uchar unsigned char#define uint unsigned int#define ADC0809 P0;//AD0809的端口部分,P0为AD的数据接口;sbit AD_Start=P2^0;//开始转换信号有T0定时来控制;sbit DA_WR=P2^1;#define DAC0832 P1;//DAC0832的端口部分;P1为DA的数据接口;uchar C1K0,C1K1,C1K2,C1K3,C1K4,C1K5;uchar CK0,CK1;//分别为k,k-1时刻smith预估器的输出uchar UK0,UK1;//分别为k,k-1时刻的控制器的输出uchar EK0,EK1;//分别为k,k-1时刻的AD的输入uint i=0;main(){C1K0=C1K1=C1K2=C1K3=C1K3=C1K4=C1K5=0;UK0=UK1=0;CK1=0;EK1=0;DA_WR=0;TMOD=0X01; //定时器0控制方式1,16位的定时器计数器TL0=0XE0; //定时器初始化;TH0=0XB1;TR0=0; //关闭T0计时;ET0=1;PT0=1; //T0中断允许优先级;EX0=1;IT0=1; //触发方式,跳沿触发;P1=0X00; //先清零DA;TR0=1; //定时器开始计时,20ms转换一次;EA =1; //总中断开;while(1); //等待中断}void int_0(void) interrupt 0 //单片机中断处理程序;{EA=0;AD_Start=1;P0=EK0;C1K0=7.584*UK1+0.368*C1K1;CK0=C1K0-C1K5 ;C1K5= C1K4;C1K4= C1K3;C1K3= C1K2;C1K2= C1K1;C1K1= C1K0;UK0=UK1+0.165*EK0-0.156*EK1-0.165*CK0+0.156*CK1;UK1=UK0;CK1=CK0;EK1=EK0;UK0=P1;EA=1;}void inter_timer0()interrupt 1 //定时器0溢出中断;{EA=0;i=20; //循环20次实现1.0S采样for(i;i>0;i--){TL0=0XB0;TH0=0X3C; //延时50ms}AD_Start=0; //启动AD;EA=1;}六、设计工作总结及心得体会七、参考文献1.刘建昌等主编计算机控制系统科学出版社20092.张晋格主编控制系统CAD—基于MATLAB语言机械工业出版社2004.63.张毅刚主编单片机原理及应用高等教育出版社2003.12。
