版第5章定积分及其利用单元自测题答案
高等数学第05章 定积分及其应用习题详解

0
x 1 sin tdt 0dt 1 , 2
b a
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) , 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时,f ( x) 0, 则 b f ( x)dx 在几何 a
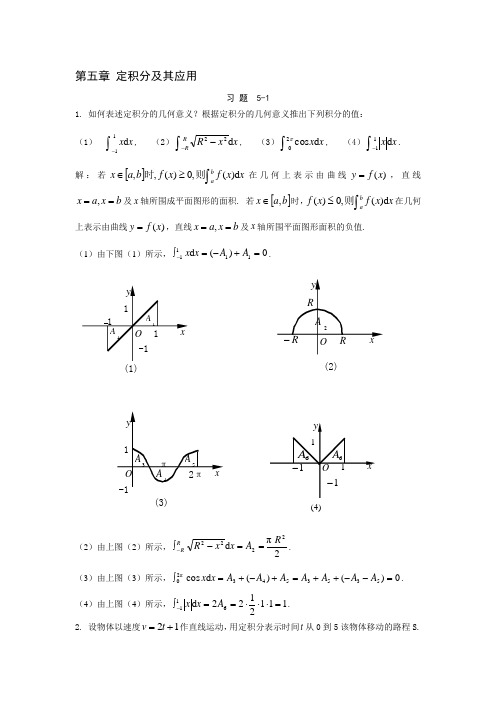
上表示由曲线 y f ( x) ,直线 x a, x b 及 x 轴所围平面图形面积的负值. (1)由下图(1)所示, 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 (即 n 时 ) ,由定积分的定义得: x d x = . 0 3
= 5. 利用定积分的估值公式,估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式:
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ,求 y 的极小值
解: 当 y x 1 0 ,得驻点 x 1 , y '' 1 0. x 1 为极小值点, 极小值 y (1)
( x 1)dx - 2
大学高等数学第五章 定积分及其应用答案
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
微积分 北京大学出版社 第5章 定积分--答案

1
−1
∫ ( x + x )e
−1
−x
dx =
1 1 1 −x 1 0 1 1
解法 1:原式=
0
∫
1
xe dx + ∫ xe dx = 2∫ xe dx + 0 = −2∫ xde = −2 x e
−x −x −x −x −1 0 0
+ 2∫ e− x dx = −2e−1 − 2 e− x = 2 −
1 1 8(07) ∫ 3 e x dx = x 1
1 1 1 1 1 1 1 1 1 1 1 x x x x 2 = e2 解原式= − ∫ de = − e + ∫ e d = − e + 1 + e x x x 2 2 1 1 1 1 2 2 2 2
2
9(02)设 F ( x) =
x2 f ( t )dt ,其中 f ( x) 为连续函数,则 lim F ( x) = ( x →a x−a ∫ a
2
π
2
; x = 0, t = 0
π
2
π
2
1 + cos 2t ⎛1 1 ⎞2 π 原式= ∫ cos t cos tdt = ∫ dt = ⎜ t + sin 2t ⎟ = 4 2 ⎝2 4 ⎠0 0 0
(注:该题利用几何意义积分比变量替换积分简单)
+∞
π
7(00)
∫e
1
x
1 dx = + e 2− x
6.(00)
⎛1⎞ f⎜ ⎟ ⎝ x⎠
∫
0
1
2 x − x 2 dx =
2019年第五章 定积分及其应用习题.doc

第五章 定积分及其应用【内容提要1.定积分的概念和性质(1)定积分的定义设 )(x f 是定义在 [,]a b 上的函数,在区间 [,]a b 内任意插入 1n - 个 分点0121,n n a x x x x x b -=<<<<<=将其分成 n 个小区间。
记1(1,2,,)i i i x x x i n -∆=-=,max{}i x λ=∆,在每个小区间上任取一点 1[,]i i i x x ξ-∈,下列和式的极限01lim()niii f x λξ→=∆∑存在,且与小区间的划分及 iξ 的选取无关,则称函数)(x f 在 [,]a b 上可积,并称该极限值为 )(x f 在 [,]a b 上的定积分 ,记作() d baf x x ⎰,即01() d l i m() d nbiiai f x x f x x λξ→==∆∑⎰,其中 )(x f 称为被积函数,() d f x x称为被积表达式,x 称为积分变量,a 称为积分下限,b 称为积分上限,[,]a b 称为积分区间。
(2)定积分的性质1)常数因子可以提到积分号外()d ()d bbaakf x x k f x x =⎰⎰ (k 为常数)。
2)函数代数和的积分等于它们积分的代数和。
[()()]d ()d ()d b bbaa a f x g x x f x x g x x ±=±⎰⎰⎰3)对任意单个实数 ,,,a b c 恒有()d ()d ()d bcb aacf x x f x x f x x =+⎰⎰⎰。
4)若在区间 [,]a b 上,被积函数 ()f x K ≡,那么()d d d ()bb baaaf x x K x K x K b a ===-⎰⎰⎰特别地,当 1K = 时,()d d bbaaf x x K x b a ==-⎰⎰5)如果在区间 [,]a b 上, ()()f x g x ≤,则()d ()d bbaaf x xg x x ≤⎰⎰ (a b <)。
高数第五章广义积分、定积分应用课堂练习题及参考答案

ab.
2
y
b
O
ax
1
4
(2)
四.求下列平面图形分别绕 x 轴、y 轴旋转产生的立体的体积.
1. 由椭圆 x2 y2 1围成的平面图形 a2 b2
解:如图,该旋转体可视为由上半椭圆 y b a2 x2 及 x 轴所围成的图形,绕 x 轴旋转而成 a
的立体,故
Vx
a
dV
a
a
a
b2 a2
解: Vx
2 (x3 )2 dx
0
7
x7
|02
128 7
Vy
2
8 0
x
x3dx
2
1 ( 5
x5 )
|80
64 5
(或者 Vy
8 (22 3
0
y2
)dy
(4 y
3 5
5
y3
)
|80
64 5
(3)
4. 曲线 y x3 与直线 x 0, y 1所围成的图形
解: Vy
1
(3
0
y )2 dy
;当
p 1时,发散
3.
11 1 x2
dx 1 x
1 1
2
( “对”,“错” )
11 1 x2 dx
解:错,无界函数的积分,瑕积分,瑕点为 0,
1
1 dx
01 dx
11 dx
1 x2
1 x2
0 x2
0
1
1 0 dx
lim (1 1) ,(或者
1 x2
x 1
x x 0
2
3
3
x2
x3 3
1
0
定积分及其应用习题详解

第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰AA A A A A A x x .(4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x .2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故∑∑∑===∆=∆=∆n i i i n i i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰10 d x e x≥⎰10 d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
版第5章定积分及其应用单元自测题答案-8页文档资料
第五章 定积分及其应用主要内容内容提要:一、定积分的定义 二、定积分的简单性质⎰⎰⎰±=±bab ab adx x g dx x f dx x g x f )()()]()([⎰⎰=bab a dx x f k dx x kf )()(0)(=⎰a a dx x f⎰⎰-=ba ab dx x f dx x f )()(⎰⎰⎰+=bcc ab adx x f dx x f dx x f )()()(当)(x f 是奇函数时,0)(=⎰-a a dx x f ;当)(x f 是偶函数时,⎰⎰=-aa adx x f dx x f 0)(2)(.三、微积分基本公式C x F dx x f +=⎰)()( ⇒)()()()(a F b F x F dx x f ba b a-==⎰.四、定积分的计算:方法与不定积分相同. 1.换元积分法(1)定积分的凑微分法⎰⎰='bab ax d x f dx x x f )())(()())((ϕϕϕϕ⎰=)()()()(b a du u f x u ϕϕϕ)()()(b a u F ϕϕ=(2)定积分的第二类换元法 令)(a ϕα=,)(b ϕβ=,则⎰⎰'=b adt t t f t x dx x f )())(()()(ϕϕϕβα2.分部积分法⎰⎰='bab ax dv x u dx x v x u )()()()(⎰-=b aba x du x v x v x u )()()]()([⎰'-=b aba dx x u x v x v x u )()()]()([五、积分上限函数的导数:(1))()(x f dt t f xa ='⎪⎭⎫ ⎝⎛⎰ (2))())(()()(x u x u f dt t f dx d x u a '=⎰(3))('))(()('))(()()()(x x f x x f dt t f dx d x x ϕϕψψψϕ-=⎰六、反常积分 1、⎩⎨⎧≤>⎰∞+1,1,1p p x dx p 发散收敛; 2、⎩⎨⎧≥<-⎰1p ,1p ,)a x (dxba p 发散收敛 七、定积分的应用(微元法) 1.平面图形的面积.2.体积:只要求旋转体的体积. 3.弧长第五章 定积分及其应用单元自测题一、填空题: 1.=⎰-xdx x sin 4ππ0 。
高等数学:第5章定积分(自测题答案)
《高等数学》单元自测题答案 第五章 定积分及其应用一、填空题: 1、0; 2、≤; 3、65; 4、)sin(362x x ; 5、2+e . 二、选择题:1、D ; 2 、C ; 3、B ; 4、C ; 5、D 。
三、计算题:1、解 令t x sin 2=,则tdt dx cos 2=,且 当0=x 时,0=t ;当2=x 时,2π=t 。
所以,⎰⎰⋅-=-20232023cos 2sin 44sin 84πtdt t t dx x x⎰⎰⋅-=⋅⋅=2022203cos cos )1(cos 32cos 2cos 2sin 8ππttd t tdt t t1564)cos 31cos 51(322035=-=πt t 。
2、解⎰⎰⎰⎰+=+=+---20322322223cos 20cos )cos (πππππππxdx xdx xdx dx x x34)sin 31(sin 2sin )sin 1(2203202=-=-=⎰ππt x x d x 。
3、解⎰⎰⎰--=-⋅=210221021021112arcsin )arcsin (arcsin dx xx x xd x x xdx π123121221121)1(211221022122-+=-⋅+=--+=⎰πππxx x d 。
4、解31)11lim (31)131(31314=--=⋅-=+∞→+∞∞+⎰xx x dx x 。
5、解 2)arcsin(ln )(ln 1ln )(ln 111212π==-=-⎰⎰ee e x x x d x x dx 。
四、应用题:1、已知函数)(x f 在 12=x 的某邻域内可导,且0)(lim 12=→x f x ,1004)(lim 12='→x f x ,求3121212)12(])([limx dtdu u tf x tx -⎰⎰→。
解 []2121231212123121212)12(3)(lim )12(])([lim )12(])([lim x du u xf x dt du u tf x dt du u tf x x xt x xt x --='-'⎥⎦⎤⎢⎣⎡=-⎰⎰⎰⎰⎰→→→ [])12(6)]([)(lim )12(3)(lim 121221212x x f x du u f x du u f x x x x x --+='--'⎥⎦⎤⎢⎣⎡=⎰⎰→→ 20086)()(2lim 6)]()([)(lim 1212='+=-'+--=→→x f x x f x f x x f x f x x 。
《高等数学教程》第五章 定积分 习题参考答案-推荐下载
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
第5章定积分及其应用
第5章 定积分及其应用§5.1 定积分的概念习 题 5-11.填空题:(1)函数()f x 在区间[,]a b 上的定积分是积分和的极限,即()baf x dx ⎰=( ).(2)定积分的值只与( )及( )有关,而与( )的记法无关. (3)区间[,]a b 的长度的定积分的表示是( ). (4)被积函数()f x 在区间[,]a b 上连续是定积分()baf x dx ⎰存在的( ).(5)定积分的几何意义( ). 2.利用定积分的定义计算下列积分: (1)2baxdx ⎰; (2)1x e dx ⎰.3.利用定积分的定义计算由抛物线21y x =+,直线x a =、x b =(b a >)及x 轴所围成的图形的面积.4.利用定积分的几何意义,证明下列等式: (1)1310x -=⎰; (2)sin 0xdx ππ-=⎰;(3)4π=⎰; (4)11arctan 0xdx -=⎰;(5)11124x dx xdx -=⎰⎰ ; (6)2202cos 2cos xdx xdx πππ-=⎰⎰.5.利用定积分的几何意义求a⎰(0)b >的值.6. 将下列极限表示成定积分: (1)()201lim3nii i i x λξξ→=-∆∑,λ是[]7,5-上的分割;(2)01limni i x λ→=,λ是[]0,1上的分割.7.将下列和式的极限表示成定积分:(1)111lim 12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; (2)112lim p p p p n n n +→∞+++(0p >);(3))221limn n n →∞+; (4)n .8.有一河,宽为200米,从一岸到正对岸每隔20米测量一次水深,测得数据如下(图5-1-8).试用梯形公式求此河横截面积的近似值.图5-1-8§5.2 定积分的性质习 题 5-21. 证明定积分的性质: (1)()()bb aakf x dx k f x dx =⎰⎰ (k 为常数); (2)1b baadx dx b a ⋅==-⎰⎰. 2. 估计下列积分值:(1)421(2)x dx +⎰; (2)3244(1sin )x dx ππ+⎰; (3)arctan x xdx ;(4)21x edx ⎰; (5)2211x dx x +⎰; (6)20sin x dx x π⎰. 3. 设()f x 及()g x 在[],a b 上连续,证明: (1) 若在[],a b 上,()0f x ≥,且()0baf x dx =⎰,则在[],a b 上,()0f x ≡;(2)若在[],a b 上,()0f x ≥,且()f x 不恒等于零,则()0baf x dx >⎰;(3)若在[],a b 上,()()f x g x ≤,且()()bbaaf x dxg x dx =⎰⎰,则在[],a b 上,()()f x g x ≡.4. 根据定积分性质及第3题的结论,比较下列每组积分的大小:(1)320sin xdx π⎰,220sin xdx π⎰; (2)221x dx ⎰,231x dx ⎰;(3)21ln xdx ⎰,221(ln )x dx ⎰; (4)10x e dx ⎰,21x e dx ⎰;(5)1xe dx ⎰,()101x dx +⎰; (6)20xdx π⎰,20sin xdx π⎰;(7)20sin xdx π⎰,02sin xdx π-⎰; (8)2cos xdx π-⎰,20cos xdx π⎰;(9)10xdx ⎰,()01ln 1x dx +⎰ (10)()01ln 1x dx +⎰,011xdx x+⎰;. 5. 利用积分中值定理求下列极限: (1)sin limn pnn x dx x+→∞⎰; (2)120lim 1nn x dx x →∞+⎰; (3)10lim 1n xx n x e dx e →∞+⎰.6. 设()f x 在[],a b 上连续,()0baf x dx =⎰.证明:()f x 在[],a b 上在[],a b 内至少存在一个零点.7. 设()f x 在[]0,1上连续,在()0,1内可导,且1233()(0)f x dx f =⎰.证明:在()0,1内至少存在一点ξ,使得()0f ξ'=.8. 设()f x 在[],a b 上连续,在(),a b 内可导,且存在(),c a b ∈,使得()()()caf x dx f b c a =-⎰.证明:在(),a b 内至少存在一点ξ,使得()0f ξ'=.§5.3 微积分基本公式习 题 5-31. 设0()cos xx t tdt ϕ=⎰,求(0)ϕ',4πϕ⎛⎫' ⎪⎝⎭. 2.求下列函数的一阶导数: (1)0()sin xtx e dt ϕ=⎰; (2)223()t xx e dt ϕ-=⎰;(3)2()x x ϕ=⎰; (4)2x y =;(5)32x xy =⎰; (6)()cos 2sin ()cos xxx t dt ϕπ=⎰;(7)22x txy t e dt -=⎰; (8)2()xe xy f t dt =⎰.3. 求下列函数的二阶导数:(1)()330sin xy t x tdt =-⎰; (2)258sin ()xy t f x dt dy t ⎛⎫= ⎪⎝⎭⎰⎰.4. 利用洛必达法则,求下列极限:(1)20cos limxx t dt x→⎰; (2)201lim arctan xx tdt x+→⎰;(3)202limsin 2x t x x e dt x x→-⎰; (4)()2202002sin limln 1x x xt dtt t dt→⎡⎤+⎣⎦⎰⎰;(5)121ln 1lim (1)xx tdtt x →-⎰+; (6)232lim(sin )x x x t dtt t t dt→-⎰⎰;(7)22201lim ()x t x x t t edt x -→+∞+⎰; (8)()222020lim xt xx t e dt te dt→⎰⎰.5. 设函数()y y x =由方程00cos 0y xte dt tdt +=⎰⎰所确定,求dydx. 6. 设函数()y y x =由方程20cos y x x y tdt -+=⎰所确定,求dy dx.7. 设0sin t x udu =⎰,0cos t y udu =⎰,求dydx.8.设20()(1)xt f x t t e dt -=-⎰,问x 为何值时,()f x 有极值?9. 求函数0()(4)xF x t t dt =-⎰在[1,5]-上的最大值与最小值.10. 计算下列各定积分: (1)24211()x dx x+⎰; (2)()13213x x dx --⎰; (3)332(21)x dx --⎰; (4)1(21)xe dx +⎰; (5)12111dx x -+⎰; (6)240tan xdx π⎰;(7)10⎰; (8)21201x dx x +⎰; (9)20cos 2x dx π⎛⎫ ⎪⎝⎭⎰; (10)41dx ⎰; (11)420213311x x dx x -+++⎰; (12)211e dx x ---+⎰; (13)20sin x dx π⎰; (14)设21,01()1,10x x f x x x ⎧+ ≤≤=⎨+ -≤<⎩,求11()f x dx -⎰. 11. 设()f x 连续,若()f x 满足1()()x f xt dt f x xe =+⎰,求()f x .12. 设13201()()1f x x f x dx x =++⎰,求()f x 与10()f x dx ⎰. 13. 设0ln(1)()(0)xt f x dt x t+=>⎰,求1()f x f x ⎛⎫+ ⎪⎝⎭. 14. 设1sin ,0()20,0x x f x x x ππ⎧ ≤≤⎪=⎨⎪ <>⎩或,求0()()x x f t dt ϕ=⎰在(,)-∞+∞内的表达式.§5.4 定积分的换元积分法与分部积分法习 题 5-41. 用换元积分法求下列定积分: (1)122(115)dxx --+⎰; (2)101xx e dx e +⎰; (3)220sin cos x xdx π⎰; (4)022122dx x x -⎰++; (5)1⎰; (6)2120t te dx -⎰; (7)1221xe dx x ⎰; (8)35201x dx x +⎰; (9)2502353x x dx x +-+⎰;(10)6e e⎰; (11)21e ⎰; (12)320sin cos d πθθθ⎰;(13)1(14);(15)ax ⎰;(16)3⎰(17)⎰;(18)0;(19) 0⎰; (20); (21)3122(1)xdx -+⎰;(22)1;(23)41⎰;(24)1⎰-;(25)⎰; (26)2⎰; (27)-⎰; (28)()223min 2,x dx -⎰(29)2sin sin cos xdx x xπ+⎰;(30)0π⎰. 2. 用分部积分法求下列定积分: (1)ln 2x xe dx ⎰; (2)1ln e x xdx ⎰;(3)41⎰; (4)1arctan x xdx ⎰; (5)220sin x xdx π⎰; (6)324sin xdx xππ⎰; (7)220cos x xdx π⎰; (8)1530ln x xdx ⎰ ;(9)230x e dx ;(10)22(1)x - ; (11)220cos x e xdx π⎰; (12)1sin(ln )ex dx ⎰ ;(13)22ln (1)e exdx x -⎰; (14)12(1)ln (1)e x x dx -++⎰;(15)221log x xdx ⎰;(16)20sin x x dx π⎰; (17)1ln eex dx ⎰ ; (18)()242sec 1tan x xdx x π+⎰;(19)161⎰; (20)122(1)m xdx -⎰(m 为自然数).3. 利用积分区间的对称性以及函数的奇偶性,计算下列定积分:(1)22sin cos 2x xdx ππ-⎰;(2)22ππ-⎰;(3)6sin x xdx ππ-⎰;(4)1⎰; (5)x dx ; (6)221cos xdx x ππ-+⎰;(7)522cos xdx ππ-⎰; (8)325425sin 21x xdx x x -+⎰+; (9))sin x x dx ππ-⎰+.(10)244cos 1x xdx e ππ--+⎰.4.已知()f x 是连续函数,证明 (1)1()()[()]baf x dx b a f a b a x dx =-+-⎰⎰;(2)200()[()(2)]aaf x dx f x f a x dx =+-⎰⎰;(3)()2321()2aa x f x dx xf x dx =⎰⎰(0a >).5. 设()f x 是连续函数,证明 (1) 当()f x 是偶函数时,则0()()xx f t dt ϕ=⎰为奇函数;(2)当()f x 是奇函数时,则0()()xx f t dt ϕ=⎰为偶函数.6. 证明:220()2()aaax dx x dx ϕϕ-=⎰⎰,其中()x ϕ为连续函数.7. 证明:110(1)(1)m n n m x x dx x x dx ϕϕ-=-⎰⎰.8. 证明:20sin 2sin nn xdx xdx ππ=⎰⎰.9. 证明:112211111xx dx dx x x =++⎰⎰(0x >). 10. 设31sin ()x t f x dt t =⎰,求120()x f x dx ⎰.若1sin ()n x t f x dt t=⎰,求110()n x f x dx -⎰.11. 若()f x ''在[0,]π连续,(0)2f =,()1f π=,证明:[()()]sin 3f x f x xdx π''+=⎰.12. 当0x >时,()f x 可导,且满足方程11()1()xf x f t dt x=+⎰, 求()f x .§5.5 广义积分习 题 5-51 计算下列瑕积分.(1)41dx x +∞⎰; (2)0e +∞⎰; (3)2122dx x x +∞-∞++⎰; (4)211(1)dx x x +∞+⎰; (5)1+∞⎰; (6) 0sin px e xdx ω+∞-⎰(0,0p ω>>);(7)21arctan xdx x+∞⎰;(8) 1⎰(9)1e⎰(10)10⎰;(11)21⎰;(12)()22011dx x -⎰.2. 求当k 为何值时,瑕积分()21ln kdx x x +∞⎰收敛?当k 为何值时,该瑕积分发散?又当k 为何值时,该瑕积分取得最小值?3. 计算瑕积分0n x n I x e dx +∞-=⎰(n 为自然数).4. 求c 为何值时,使2lim xc tx x c te dt x c -∞→+∞+⎛⎫= ⎪-⎝⎭⎰. 5.求2+∞⎰.6. 计算下列式子:(1)(7)2(4)(3)ΓΓΓ; (2)3(3)()29()2ΓΓΓ; (3)40x x e dx +∞-⎰; (4)2220x x e dx +∞-⎰. 7. 用Γ函数表示下列积分,并指出积分的收敛范围.(1)nxe dx +∞-⎰(0n >); (2)101ln pdx x ⎛⎫⎪⎝⎭⎰; (3)22x dx +∞--∞⎰;(4)mn x x edx +∞-⎰; (5)10⎰; (6)311dx x +∞+⎰. §5.6 定积分的几何应用习题5-61. 求由下列各组曲线所围成平面图形的面积:(1)1xy =,y x =,2x =; (2)x y e =,xy e -=,1x =; (3)2y x =,2x y +=; (4)3y x =,1y =,2y =,0x =;(5)0y =,1y =,ln y x =,0x =; (6)22x y =,228x y +=;(7) ln y x =,y 轴,ln y a =,ln y b =( 0b a >>);(8) 23y x =+,2y x =. 2. 直线x k =平分由2y x =,0y =,1x =所围之面积,求k 之值. 3. 求抛物线243y x x =-+-及在点(0,3)-和(3,0)处切线所围成图形的面积. 4. 求抛物线22y px =及其在点,2p p ⎛⎫⎪⎝⎭处的法线所围成的图形的面积. 5. 求曲线33cos ,sin x a t y a t ==,).0(>a 所围成图形的面积. 6. 求曲线2cos r a θ=).0(>a 所围成图形的面积.7. 求曲线2(2cos r a θ=+)).0(>a 所围成图形的面积. 8. 求对数螺线r ae θ=(0a >,πθπ-≤≤)及射线θπ=所围成图形的面积.9. 计算阿基米德螺线r a θ= (0a >)上相应于θ从0到2π的一段弧与极轴所围成的图形(如图5-6-22)的面积.图5-6-22 图5-6-2310.求由下列各曲线所围成图形的公共部分的面积. (1) 3cos r θ=及1cos r θ=+;(2) r θ=及2cos 2r θ=.11. 圆1r =被心形线1cos r θ=+分割成两部分,求这两部分的面积. 12.设sin y x =,02x π≤≤.问:为t 何值,图5-6-23中阴影部分的面积1s 与2s 之和最小?最大?13.求由下列已知曲线围成的平面图形绕指定的轴旋转而成的旋转体的体积.(1)2xy a =,0y =,x a =,2x a =(0a >),绕x 轴. (2)22(2)1x y +-=,绕x 轴.(3)ln y x =,0y =,x e =,绕x 轴和y 轴. (4)224x y +=,24(1)x y =--,0y >,绕x 轴. (5)5xy =,6x y +=,绕x 轴.(6)cos y x =,0x =,x π=,x 轴,绕y 轴.14. 求摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩(02t π≤≤,0a >)的一拱与0y =所围成的图形绕直线2y a =旋转而成的旋转体的体积.15. 由心形线4(1cos )ρθ=+和直线0θ=及2πθ=所围成图形绕极轴旋转而成的旋转体的体积.16. 一个棱锥体的底面是长为2a 的正方形,高为h ,求此棱锥体的体积 (如图5-6-24).图5-6-24 图5-6-2517.设直线y ax b =+(0a >,0b >)与直线0x =,1x =及0y =所围成的梯形面积等于A ,试求a 、b ,使这个梯形绕x 轴旋转所得旋转体的体积最小.18.在由椭圆域2214y x +≤绕y 轴旋转而成的椭球体上,以y 轴为中心轴打一个圆孔,使剩下的部分的体积恰好等于椭球体体积的一半,求圆孔的直径.19.设有一锥体,其高为h ,上、下底都为椭圆,椭圆的轴长分别为2a 、2b 与2A 、2B ,求这锥体的体积.20.作半径为r 的球的外切正圆锥,问此圆锥的高h 为何值时,其体积V 最小?求出此最小值(如图5-6-25).21.把星形线232323x y a +=所围成的图形绕x 轴旋转(图5-6-26),计算所得旋转体的体积.图5-6-26 图5-6-27 22.用积分的方法证明图5-6-27所示球缺的体积为2()3H V H R π=-. 23.求圆盘222x y a +≤绕x b =-(0b a >>)旋转而成的旋转体的体积.24.证明:由平面图形x a =,x b =,0a b ≤<,0()y f x ≤≤绕y 轴旋转而成的旋转体的体积为2()baV xf x dx π=⎰.25.利用24题的结论,计算sin y x =(0x π≤≤)和x 轴所围成的图形绕y 轴旋转所成的旋转体的体积.习题5-71. 已知边际成本'2()25309C q q q =+-,固定成本为55,试求总成本()C q ,平均成本与变动成本.2. 已知边际收入为'()30.2R q q =-,q 为销售量,求总收入函数()R q ,并确定最高 收入的大小.3. 某产品生产q 个单位是总收入R 的变化率为'()200100qR q =-,求: (1)生产50个单位时的总收入;(2)在生产100个单位的基础上,再生产100个单位时总收入的增量.4. 已知某商品每周生产q 个单位时,总成本变化率为'()0.412C q q =-(元/单位),固 定成本500,求总成本()C q . 如果这种商品的销售单价是20元,求总利润()L q ,并问每周生产多少单位时才能获得最大利润?图5-7-56. 设某城市人口总数为F ,已知F 关于时间t (年)的变化率为dF dt =,假设在计算的初始时间(0)t =,城市人口数为100(万),试求t 年中该城市人口总数.7. 若边际消费倾向在收入为Y 时为1232Y -,且当收入为零时总消费支出070c =.(1)求消费函数()c Y ;(2)求收入由100增加到196时消费支出的增加数.8. 设储蓄边际倾向(即储蓄额S 的变化率)是收入y 的函数 '()0.3S y =, 求收入从100元增加到900元时储蓄的增加额.9. 如果需求曲线为2()500.025D q q =-,并已知需求量为20个单位,试求消费者剩余CS .10. 假设某国某年洛伦兹曲线近似地由3y x =(01x ≤≤)表示,试求该国的基尼系数.11. 某投资项目的成本为100万元,在10年中每年可收益25万元,投资率为5%,试 求这10年中该项投资的纯收入的贴现值.12. 一位居民准备购买一栋别墅,现价为300万元,如果以分期付款的方式,要求每年 付款21万元,且20年付清,而银行贷款的年利率为4%,按连续复利计息,请你帮这位购5. 某新产品的销售率由下式给出()10090x f x e -=-,式中x 是产品上市的天数,前四天的销售总数是曲线()y f x =与x 轴在之间的面积(如图5-7-5),求前四天总的销售量.房者作一决定:是采用一次付款合算还是分期付款合算?总习题五1.求下列极限:(1) limnn k →∞=. (2) 21lim inni n i nen ne→∞=+∑;(3)11lim n n i n →∞= (4)112lim p p p p n n n +→∞+++(0p >); (5)lim n →∞2.利用积分中值定理求下列极限: (1)sin lim0n pnn xdx x +→∞=⎰; (2)222lim n x n n x dx e+→∞⎰.3.求下列极限:(1)101lim (1sin 2)xtx t dt x →+⎰; (2)lim ()x a x a x f t dt x a →-⎰(其中()f x 连续);(3)()2arctan lim xx t dt→+ (4) ()2210limxt t x e dt→+∞⎰.4.(已知[]02()1()1xf t dt f x -=-⎰,求(0)f '.5. 已知()2021,0()0,x t e dtx f x x x ⎧-⎪≠=⎨⎪=0⎩⎰,求(0)f '. 6.设()f t 在0t ≤≤+∞上连续,若220()(1)x f t dt x x =+⎰,求(2)f .7. 求函数0()(3)xF x t t dt =-⎰在[1,5]-上的最大值与最小值.8. 证明:111ln(1)11ln 23n n n+=++++<+. 9. 设()f x 、()g x 在区间[,]a b 上均连续,证明:(1)()222()()()()bbbaaaf xg x dxf x dxg x dx ≤⋅⎰⎰⎰(柯西-施瓦茨不等式);(2)[]()()()111222222()()()()bbba aaf xg x dxf x dxg x dx +≤+⎰⎰⎰(闵可夫斯基不等式).10. 设函数()f x 在区间[,]a b 上连续,且()0f x >,证明:11ln ()ln ()b b a a f x dx f x dx b a b a ⎡⎤≥⎢⎥--⎣⎦⎰⎰. 11. 设()f x 在[0,]a (0a >)上有连续导数,且(0)0f =,证明:2()2aMa f x dx ≤⎰,其中0max ()x aM f x ≤≤'=.12. 设()f x 在[0,1]上连续且单调减少,试证:对任何(0,1)a ∈,有1()()af x dx a f x dx ≥⎰⎰.13. 设()x ϕ在[,]a b 上连续,()()()xaf x x b t dt ϕ=-⎰,证明:必存在(,)a b ξ∈,使得()f ξ'=0.14.设()f x 在区间[,]a b 上连续,()g x 在区间[,]a b 上连续且不变号.证明至少存在一点[,]a b ξ∈,使下式成立()()()()bbaaf xg x dx f g x dx ξ=⎰⎰(积分第一中值定理).15. 计算下列定积分:(1)3(1sin )x dx π-⎰; (2)e ;(3)⎰; (4)0ax ⎰ (0a >);(5)20sin 1cos x xdx xπ++⎰; (6)40ln(1tan )x dx π+⎰;(7)a⎰(0a >); (8);(9)121(21)x x dx -++⎰; (10)sin )x x dx ππ-⎰(11)42213||||1x x dx x -⎛⎫-+ ⎪+⎝⎭⎰; (12)设2,01()2,12x x f x x x ⎧ ≤≤=⎨-<<⎩,求20()f x dx ⎰.16.利用函数的奇偶性计算定积分121(x dx -+⎰. 17. 利用函数的周期性计算定积分2(sin 2)(tan 1)a ax x dx π++⎰.18. 设函数()f x 在(,)-∞+∞内连续,并满足条件()sin xu f x u e du x -=⎰,求()f x .19. 计算下列各题: (1)设(5)2f =,5()3f x dx =⎰,求5()xf x dx '⎰.(2)已知2()tan f x x =,求40()()f x f x dx π'''⎰.20. 证明()[()()]aaaf x dx f x f x dx -=+-⎰⎰,并求下列定积分:(1)441sin dx x ππ-+⎰; (2)244sin 1x x dx e ππ--+⎰; (3)244cos 1nxx dx e ππ--+⎰(n 为正整数). 21. 设()f x 在区间[,]a b 上连续,且()f x 关于2a bx +=对称的点处取相同的值.证明: 2()2()a b baaf x dx f x dx +=⎰⎰.22. 证明:112211111xx dt dt t t =++⎰⎰(0x >). 23. 判断下列瑕积分的敛散性:(1)1+∞⎰;(2)2+∞⎰;(3)2cos ln xdx x+∞⎰;(4) 0+∞⎰;(5)3(1)(2)dxx x x +∞--⎰;(6)1+∞⎰;(7)120ln 1xdx x -⎰; (8)1ln 11eex dx x --⎰.24. 已知sin 2x dx x π+∞=⎰,求220sin x dx x+∞⎰. 25. 求介于直线0x =,2x π=之间由曲线sin y x =和cos y x =所围成的平面图形的面积.26. 求椭圆22113x y +=和22113x y +=的公共部分的面积. 27. 求曲线x y e =及该曲线的过原点的切线和x 轴的负半轴所围成的平面图形的面积. 28. 设曲线21:1L y x =-(01)x ≤≤、及x 轴和y 轴所围成的区域被曲线21:L y ax =分为面积相等两部分,其中a 是大于零的常数,试确定a 的值.29. 求由柱体222x y a +≤与222x z a +≤(0a >)的公共部分所围成图形的体积.30.将曲线r =绕x 轴旋转而成的旋转体的体积. 31. 将抛物线2y x ax =-在横坐标0与c (0c a >>)之间的弧段绕x 轴旋转,问c 为 何值时,所得旋转体体积V 等于弦OP (P 为抛物线与x c =的交点)绕x 轴旋转所得锥体体积.32. 设抛物线2y ax bx c =++通过点(0,0),且当[0,1]x ∈时,0y ≥.试确定a b c 、、 的值,使得该抛物线与直线1x =,0y =所围成图形的面积为13,且使该图形绕x 轴旋转而成的旋转体的体积最小.33.一位居民准备购买一栋别墅价值为300万元,若首付为50万元,以后分期付款,每年付款数目相同,10年付清,而银行贷款的年利率为6%,按连续复利计息,每年应付款多少?(0.60.5448e-≈)34. 某公司投资2000万建成一条生产线,投产后,在t 时刻的追加成本和追加收益分别为23()52g t t =+ (百万/年)23()17t t ϕ=- (百万/年)试确定该生产线在何时停产可获得最大利润?最大利润是多少?.35.生产某种产品的固定成本为50万元,边际成本与边际收益分别为216100=-+(万元/单位产品)MC Q Q=-(万元/单位产品)MR Q894试确定工厂应将产量定为多少个单位时,才能获得最大利润?并求最大利润.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、定积分的定义
二、定积分的简单性质
b
[ f (x) g(x)]dx f (x)dx g(x)dx
a
a
b
kf (x)dx k f (x)dx
a
a f (x)dx 0
a
b f (x)dx a f (x)dx
b
a
c
b
b
a f (x)dx a f (x)dx c f (x)dx
F(x) b
a
F (b) F (a) .
a
b
u
(
x)v
(
x)dx
[u(x)v(x)] b
[u(x)v(x)] b
五、积分上限函数的导数:
(1)
d
(2)
d
(3)
x a
dx a
dx (x)
六、反常积分
1、
1
f
(t
)dt
a
当 f (x) 是奇函数时, f (x)dx 0 ;
a
a
b
a
当 f (x) 是偶函数时, f (x)dx 2 f (x)dx .
三、微积分基本公式
f (x)dx F (x) C
a
四、定积分的计算:方法与不定积分相同.
1.换元积分法
(1)定积分的凑微分法
a
b f ((x)) (x)dx b f ((x))d(x)
u ( x )
(2)定积分的第二类换元法
令 (a) , (b) ,则
f (x)dx
2.分部积分法
x (t)
aLeabharlann F( aa
u
第五章 定积分及其应用
(b )
)( a )
b f ((t)) (t)dt
b
a
主要内容
b
b
f (x)dx
0
(b )
f ( u )du
(a )
a
第 1 页 共 8 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
a
f (x)
u( x ) f ( t )dt f ( u( x ))u( x )
b
u ( x)dv( x)
(x) f (t)dt f ( (x)) '(x) f ((x))'(x)
dx 收敛, p 1
xp
发散,
b dx 发发 , p 1
2、 a ( x a ) p 发发 , p 1
七、定积分的应用(微元法) 1.平面图形的面积. 2.体积:只要求旋转体的体积. 3.弧长
;
p 1
a
a
b
v( x)du ( x)
a
b
v(
a
x)u
(
x)dx
第 2 页 共 8 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
