画出下列有限自动机的状态转换图
第三章有穷自动机
例：将图示的DFA M最小化。
a
b
6
4
a
a
a
b
a
1
ab
5a
7
b3
b
b
2 b
1、将M状态分为两个子集： P0=({1,2,3,4},{5,6,7})
2、{1,2,3,4}读入a后划为： P1=({1,2},{3,4},{5,6,7})
3、进一步划分： P2=({1,2},{3},{4},{5,6,7})
对M的状态集S进行划分的步骤：
①把S的终态与非终态分开，分成两个子集， 形成基本划分，属于这两个不同子集的 状态是可区别的。
②假定某个时候已含m个子集，记={I(1) , I(2) , …,I(m) }且属于不同子集的状态是可 区别的，再检查中的每个I能否进一步划 分，对于某个I(i) ，令I(i) ={S1,S2,…,Sk}， 若存在一个输入字符使得move(I(i) ,a)不包 含在现行的某一子集I(i)中，则将I(i)一分 为二。
若M的某些结既是初态结，又是终态结，
或者存在一条从某个初态结到某个终态结 的道路，则空字可为M所接受。
例： NFA M=({0,1,2,3,4},{a,b},f,{0},{2,4})
f(0,a)={0,3} f(2,b)={2} f(0,b)={0,1}
f(3,a)={4} f(1,b)={2} f(4,a)={4}
M’=(K, ,f,S,Z)
一个含有m个状态和n个输入字符的NFA 可表示为一张状态转换图，该图含有m个 状态结，每个结可射出若干条 箭弧与别的 结点相连接，每条弧用*中的一个字（不 一定要不同的字，且可以为空字）作标记 （称输入字），整个图至少含有一个初态 结以及若干个终态结。
2017年11月软件设计师上午真题及答案
2017年11月软件设计师上午真题1.在程序执行过程中，Cache与主存的地址映射是由（）完成的。
A.操作系统B.程序员调度C.硬件自动D.用户软件2.某四级指令流水线分别完成取指、取数、运算、保存结果四步操作。
若完成上述操作的时间依次为8ns、9ns、4ns、8ns，则该流水线的操作周期应至少为（）ns。
A.4B.8C.9D.333.内存按字节编址。
若用存储容量为32Kx8bit的存储器芯片构成地址从AOOOOH到DFFFFH的内存，则至少需要（）片芯片。
A.4B.8C.16D.324.计算机系统的主存主要是由（）构成的。
A.DRAMB.SRAMD.EEPROM5.以下关于海明码的叙述中，正确的是（）。
A.海明码利用奇偶性进行检错和纠错B.海明码的码距为1C.海明码可以检错但不能纠错D.海明码中数据位的长度与校验位的长度必须相同6.计算机运行过程中，CPU需要与外设进行数据交换。
采用（）控制技术时，CPU与外设可并行工作。
A.程序查询方式和中断方式B.中断方式和DMA方式C.程序查询方式和DMA方式D.程序查询方式、中断方式和DMA方式7.与HTTP相比，HTTPS协议对传输的内容进行加密，更加安全。
HTTPS 基于（）安全协议，其默认端口是（）。
A.RSAB.DESC.SSLD.SSHA.1023B.443C.809.下列攻击行为中，属于典型被动攻击的是（）。
A.拒绝服务攻击B.会话拦截C.系统干涉D.修改数据命令10.（）不属于入侵检测技术。
A.专家系统B.模型检测C.简单匹配D.漏洞扫描11.以下关于防火墙功能特性的叙述中，不正确的是（）。
A.控制进出网络的数据包和数据流向B.提供流量信息的日志和审计C.隐藏内部IP以及网络结构细节D.提供漏洞扫描功能12.某软件公司项目组的程序员在程序编写完成后均按公司规定撰写文档，并上交公司存档。
此情形下，该软件文档著作权应由（）享有。
A.程序员B.公司与项目组共同C.公司D.项目组全体人员13.我国商标法规定了申请注册的商标不得使用的文字和图形，其中包括县级以上行政区的地名（文字）。
编译原理之有限自动机
b
4
5
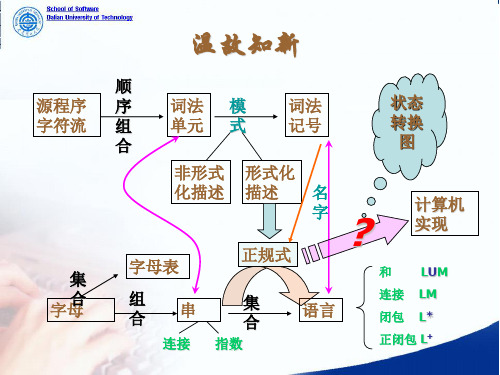
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8}
状态 A
输入符号 ab B
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8}
识别器：是一个程序，取串x作为输入，当 x是语言的句子时，它回答“是”，否则回 答“不是”。 状态转换图（有限自动机）识别器 确定/不确定有限自动机——时空权衡问题
确定有限自动机：快，空间大
2.3 有 限 自 动 机
2.3.1 不确定的有限自动机（简称NFA）
一个数学模型，它包括: 状态集合S；
缺点：1、输入字 符包括
NFA能到达的所有状态：s1, s2, …, sk，则 DFA到达状态{s1, s2, …, sk}
2.3 有 限 自 动 机
输入符号
状态 a
b
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7}
状态 A
输入符号 ab
a
2
3
开始
0
1
a
b
6
7
8
9
输入符号 ab BC BD
a
2
3
开始
2.2 词法记号的描述与识别
编译原理 3.2正规文法和状态转换图
2020/6/18
第30页/共24页
一个简单的词法分析器示例
1 C语言子集的单词符号表示 2 C语言子集对应的状态转换图的设计 3 状态转换图的实现
2020/6/18
第31页/共24页
1 C语言子集的单词符号表示
大多数程序语言的单词符号都可用 状态转换图予以识别。下面构造一个C 语言子集的简单词法分析器，该C语言 子集的所有单词符号及其种别编码和内 码值如下表所示。
开始符号S作为初始状态； S 设一符号F不属于V作为终止状态； F
2020/6/18
第7页/共24页
形如A→aB的规则：从结点A引一条矢线到结
点B，并用符号a标记这条矢线；
a
A
B
形如A→a的规则：从结点A引一条矢线到终态
结点F，并用符号a标记这条矢线；
a
A
F
2020/6/18
第8页/共24页
则有：S=> a1A1=> a1 a2A2=> a1 a2 a3A3=> … => a1 a2 a3 … an-1An-1=> a1a2a3…an
事实上，在利用状态转换图M对符号串ω进行识别的 过程中，M中的每一次状态转换都模拟了G中的一步 直接推导，所以，上述方法是一个自顶向下的分析
方法。
2020/6/18
a
R
A
2020/6/18
第16页/共24页
例如：G[Z]：Z→U0∣V1 U →Z1∣1 V →Z0∣0
1
2020/6/18
1
U
初态 R
0
V
0
Z
1
0
第17页/共24页
二、状态图的使用——识别句子
编译原理 第3章习题解答
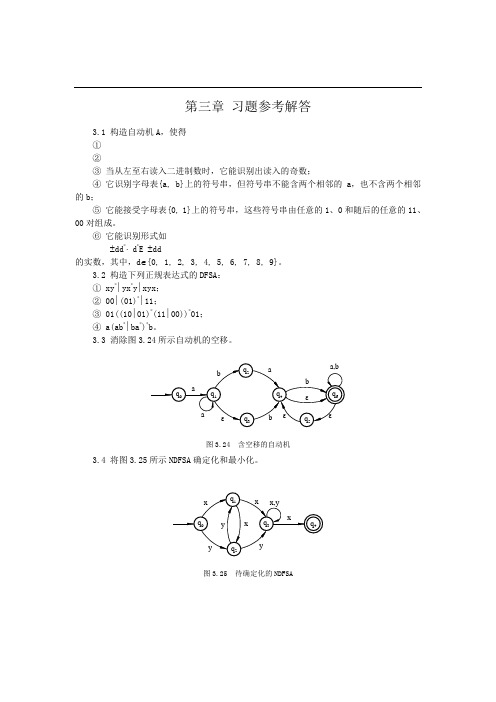
第三章习题参考解答3.1 构造自动机A，使得①②③当从左至右读入二进制数时，它能识别出读入的奇数；④它识别字母表{a, b}上的符号串，但符号串不能含两个相邻的a，也不含两个相邻的b；⑤它能接受字母表{0, 1}上的符号串，这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数，其中，d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA：① xy*∣yx*y∣xyx；② 00∣(01)*∣11；③ 01((10∣01)*(11∣00))*01；④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式，试证明① e∣e=e；② {{e}}={e}；③ {e}=ε∣e{e}；④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机，指明该自动机是不是确定的，并写出它相应的语言： G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中，f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]：〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。
编译原理1-3章作业
（b）已是DFA，只需最少化
b
=> 0
b 2
3
b
a
a
8、令文法为 E->T|E+T|E-T T->F|T*F|T/F F->(E)|I
(1)给出i+i*i、i*(i+i)的最左推导和最右推导； (2)给出i+i+i、 i+i*i和i-i-i的语法树。
9、证明下面的文法是二义性的： S->iSeS|iS|i
证明：该文法存在一个句子iiiei有两棵不同语法分析树，如下所示， 因此该文法是二义的。
第三章
7、构造下列正规式相应的DFA 1(0|1)*101 0*10*10*10* 9、对下面情况给出DFA及正规表达式 （1）{0,1}上的含有子串010的所有串； 12、将图3.18的(a)和(b)分别确定化和最少化。
1(0|1)*101 (1) 构造NFA：
(2) 确定化
构造状态转换矩阵如下：
8、令文法为 E->T|E+T|E-T T->F|T*F|T/F F->(E)|I
(1)给出i+i*i、i*(i+i)的最左推导和最右推导； (2)给出i+i+i、 i+i*i和i-i-i的语法树。 答：(1) 最左推导： E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*i E=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F) =>i*(i+i) 最右推导： E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*i E=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i) =>F*(i+i)=>i*(i+i)
软件设计师上午基础知识考试选择题专项强化真题试卷9(题后含答案及解析)
软件设计师上午基础知识考试选择题专项强化真题试卷9(题后含答案及解析)题型有：1.1．某确定性有限自动机(DFA)的状态转换图如下图所示，令d=0｜1｜2｜…｜9，则以下字符串中，能被该DFA接受的是(49)。
A．3857B．120000C．-123.67D．5760000000正确答案：C解析：本题程序语言翻译基础知识。
翻译高级语言源程序的第一步工作是进行词法分析，即将源程序中的单词(记号)识别出来，该过程可用有限自动机描述。
自动机M识别一个字符串的过程是从开始状态出发，根据字符串中的字符依次进行状态转移，若能到达终态且字符串结束，则该字符串可被自动机M识别。
考查题目中的选项，3857的识别过程是状态0→状态1→状态1→状态1，状态1不是终态；字符串 1.2E+5中的“+”不能识别；字符串0.576E10的识别过程是状态0→状态1→状态5→状态6→状态6，在状态6下不能识别E。
字符串-123.67的识别过程是状态0→状态4→状态1→状态1→状态5→状态6→状态6，因此该字符串可被题中的自动机识别。
2．一个算法是对某类给定问题求解过程的精确描述，算法中描述的操作都可以通过将已经实现的基本操作执行有限次来实现，这句话说明算法具有(62)特性。
A．有穷性B．可行性C．确定性D．健壮性正确答案：B解析：本题考查算法基本概念。
一个算法是对某类给定问题求解过程的精确描述，算法有5个基本特性：有穷性、确定性、可行性、有输入和输出。
其中，有穷性是指对于任意一组合法输入值，在执行有穷步骤之后一定能结束，即算法中的每个步骤都能在有限时间内完成。
确定性是指对于每种情况下所应执行的操作，在算法中都有确切的规定，使算法的执行者或阅读者都能明确其含义及如何执行，并且在任何条件下，算法都只有一条执行路径。
可行性是指算法中的所有操作都必须足够基本，都可以通过已经实现的基本操作运算有限次实现之。
题目中的描述说明的是算法的可行性。
正规式与有限自动机
正规式与有限自动机正规式与有限自动机之间的转换1）有限自动机转换为正规式对于S上的NFAA/,可以构造一个S上的正规式/?,使得切⑷。
拓广状态转换图的概念，令每条弧可用一个正规式作标记。
为S上的NFA Af构造相应的正规式及，分为如下两步。
（1）在M的状态转换图中加两个节点，一个x节点，一个y节点。
从x节点到NFAM 的初始状态节点引一条弧并用e标记，从NFAM的所有终态节点到y节点引一条弧并用e 标记。
形成一个与A/等价的MS AT只有一个初态jc和一个终态少。
（2）按下面的方法逐步消去中除x和；；的所有节点。
在消除节点的过程中，用正规式来标记弧，最后节点jc和；；之间弧上的标记就是所求的正规式。
消除节点的规则如图2-12所示。
2）正规式转换为有限自动机同样地，对于S上的每个正规式/?,可以构造一个S上的NFAAf,使得L（A0=Z（及）。
（1）对于正规式i,可用图>13所示的拓广状态图表示。
R o（1）通过对正规式/?进行分裂并加入新的节点，逐步把图转变成每条弧上的标记是E上的一个字符或e,转换规则如图2-14所示。
最后所得的图即为一个NFAM,JC为初态节点，少为终态节点。
显然，L（A0=I（及）。
【试题2-24】2011年11月真题48下图所示为一个有限自动机（其中，A是初态、C是终态），该自动机识别的语言可用正规式（48）表示。
A. (0|1)*01B. 1*0*10*1C. 1*(0)*01D. 1*(0|10)*1*分析：在正规式中，符号*表示重复若干次（包括0次），符号|表示“或”。
在状态A，可以输入1或0，如果输入1还可以回到状态A，如果输入0直接到达状态B；在状态B，可以输入0或1，如果输入0则还回到状态B，而输入1，则进入到状态C；在状态C可以输入0或1，输入0到达状态B，输入1到达状态A，但由于C是终态，自动机可识别的语言是由0、1构成的字符串的集合，但该集合必须以01结果，因此选项A正确。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题3
3-1 画出下列有限自动机的状态转换图，并说明它所识别或接受的语言是什么？
①M＝({S，A，B，C}，{0，1}，f，S，{S})，其转换函数为：
f(S，0)=B f(B，0)= S
f(S，1)=A f(B，1)= C
f(A，0)=C f(C，0)= A
f(A，1)=S f(C，1)= B
参考答案：有限自动机的状态转换图
它所识别或接受的语言是：
L(M)={ε,00,11,0101,0110,1001,1010,0011,0000,1111,…,}
由偶数个0或偶数个1组成的二进制串。
②M＝({0，1，2}，{a，b}
解答：有限自动机M的状态转换图：
有限自动机M所识别或接受的语言是：
L(M)={a,aaa,abaa,ba,baaa,babaa,…}
3-2设计字母表∑={a,b}上的确定有限自动机，使它能识别或接受下列语言：①以aa为首的所有符号串集合；
解答：
正则式e=aa(a | b)*
NFA：
最小化：
2
②以aa结尾的所有符号串集合；
e=(a|b)*aa
{X}为0
{X,A}为1
③含有相继两个a或相继两个b的所有符号串集合。
e=(a|b)*(aa|bb)(a|b)*
3-3 试把下述NFA变换为DFA。
解答：
最基本的方法是子集法：
重命名：
{0}为0，{1}为1，{1，2}为2，包含原终态2的{1，2}为新终态，于是所求DFA为：
解：最基本的方法：子集法：
重命名：
3-4 试把下列εFA变换为非εFA。
参考答案：
用子集法：
3-5 试把下列FA确定化(若需要的话)和最小化。
参考答案：
2,4状态是死状态，应删除。
只有一个状态的FA肯定是确定化的和最小化的。
此FA是DFA，不需要确定化。
最小化：
首先按终态与非终态划分：{0，1}，{2，3，4，5}；然后计算：
对于输入a，b，{0，1}1等价。
对于输入a，{2，4}后继属于同一集合{0，1}，{3，5}后继属于同一集合{3，5}，故可继续划分为：{2，4}，{3，5}。
进一步计算：
3，5等价。
合并等价状态，最小化为：
3-6 构造下列正则表达式对应的确定有限自动机。
①a(b | a)*aba
②a(abab* | a(bab)*a)*b
3-7 写出下列FA所对应的正则表达式。
①在FA M的转换图上加进一个初态结X和一个终态结Y。
消去(0,1,b)这条弧：
e=(a(b+a)*)*
②消去(2,1,a)这条弧：e=ab(ab|ba|a)*
3-8 构造正则文法GLsl
·S‘mBI m
B?’mB nSlm
所对应的有限白动机。
3-9 给出下面的确定有限自动机所对应的正则文法。
3-11 用某种高级语言写出：
①非确定有限自动机确定化的算法；
②有限自动机简化的算法；
③把正则表达式转换为有限自动机的算法。