反比例函数图象上的动点问题
反比例函数动点问题

反比例函数动点问题通常涉及到一些几何和代数的知识。
以下是一个典型例题的分析:
已知A、B是反比例函数y=k/x(k>0,x≠0)的图像上的两点,当点A在第一象限时,与坐标轴围成的矩形AEOF的面积为3,则点B 与坐标轴围成的矩形的面积是()。
A. 3
B. -3
C. 6
D. 无法确定
我们可以根据题意进行推理。
由于点A在第一象限,所以矩形AEOF 的面积可以表示为|k| = 3。
同时,由于点B在反比例函数的图像上,与x轴和y轴围成一个矩形,其面积也为|k|。
但是这个矩形的面积的具体数值无法确定,因为它与点A的坐标有关。
因此,正确答案是D. 无法确定。
希望这个例子能够帮助你理解反比例函数动点问题的一般思路和方法。
如果你有更多的例题需要分析,欢迎继续提问。
北师大初三数学上册反比例函数难题带答案解析

初三数学上册反比例函数一.选择题(共20小题)1.如图,点A、B是反比例函数y=(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为()A.﹣12B.﹣10C.﹣9D.﹣62.如图,A、B、C是反比例函数y=(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有()A.4条B.3条C.2条D.1条3.如图,正方形ABCO和正方形CDEF的顶点B、E在双曲线y=(x>0)上,连接OB、OE、BE,则S△OBE的值为()A.2B.2.5C.3D.3.54.如图,点A是函数y=的图象上的点,点B,C的坐标分别为B(﹣,﹣),C(,).试利用性质:“函数y=的图象上任意一点A都满足|AB﹣AC|=2”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=的图象上运动时,点F总在一条曲线上运动,则这条曲线为()A.直线B.抛物线C.圆D.反比例函数的曲线5.如图,在平面直角坐标系中,△ABO的顶点A在x轴上,反比例函数y=(x<0)的图象与△OAB的边OB、AB 分别交于点C,点D.若BC:BO=2:3,BD:BA=3:4,S△ABO=,则k的值为()A.﹣8B.﹣6C.D.﹣6.如图,点A在反比例函数y=(k≠0)的图象上,且点A是线段OB的中点,点D为x轴上一点,连接BD交反比例函数图象于点C,连接AC,若BC:CD=2:1,S△ADC=.则k的值为()A.B.16C.D.107.如图,点A是双曲线y=上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为,tan∠ABD=,则k的值为()A.﹣2B.﹣3C.﹣D.8.如图所示,已知双曲线y=(x<0)和y=(x>0),直线OA与双曲线y=交于点A,将直线OA向下平移与双曲线y=交于点B,与y轴交于点P,与双曲线y=交于点C,S△ABC=6,=,则k=()A.﹣6B.﹣4C.6D.49.如图,已知A,B为反比例函数y1=图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且=时,k的值为()A.﹣B.﹣3C.﹣4D.﹣10.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=上,过点C作CE∥x轴交双曲线于点E,则CE的长为()A.B.C.3.5D.511.如图,已知A1,A2,A3,…A n,…是x轴上的点,且OA1=A1A2=A2A3=…=A n﹣1A n…=1,分别过点A1,A2,A3,…,A n,…作x轴的垂线交反比例函数y=(x>0)的图象于点B1,B2,B3,…,B n,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△B n P n B n+1的面积为S n,则S1+S2+S3+…+S n等于()A.B.C.D.12.如图,O为坐标原点,点C在x轴上.四边形OABC为菱形,D为菱形对角线AC与OB的交点,反比例函数y=在第一象限内的图象经过点A与点D,若菱形OABC的面积为24,则点A的坐标为()A.(1,6)B.(,5)C.(2,4)D.(3,3)13.如图,点A,B分别在y轴正半轴、x轴正半轴上,以AB为边构造正方形ABCD,点C,D恰好都落在反比例函数y=(k≠0)的图象上,点E在BC延长线上,CE=BC,EF⊥BE,交x轴于点F,边EF交反比例函数y=(k ≠0)的图象于点P,记△BEF的面积为S,若S=+12,则△CEP的面积是()A.2+2B.2﹣2C.+2D.﹣214.如图,平面直角坐标系中,矩形OABC的边与函数y=(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于()A.4B.6C.8D.不能确定15.如图,直线AD分别与x轴,y轴交于A,D两点,与反比例函数y=的图象交于B,C两点,连接OB,OC,若AB=BC,S△BOC=4,则k的值为()A.4B.C.D.16.如图,以矩形OABC的顶点O为坐标原点建立平面直角坐标系,使点A、C分别在x轴、y轴的正半轴上,双曲线y=(x>0)的图象经过BC的中点D,且与AB交于点E.过OC边上一点F,把△BCF沿直线BF翻折,使点C 落在点C′处(点C′在矩形OABC内部),且C′E∥BC,若点C′的坐标为(2,3),则k的值为()A.B.C.D.17.如图,点A是反比例函数y=(x>0)的图象上一点,过点A作直线y=﹣x的垂线,垂足为点B,再过点A作AC⊥AB交y=(x>0)的图象于点C,若△ABC是等腰三角形,则点B的坐标是()A.(﹣,)B.(﹣,)C.(﹣2,2)D.(﹣3,3)18.如图,菱形四边形ABCD的四个顶点分别在反比例函数y=,y=﹣的图象上,若该菱形的面积为78,则这个菱形的边长为()A.B.C.13D.1319.反比例函数y=的图象向右平移个单位长度得到一个新的函数,当自变量x取1,2,3,4,5,…,(正整数)时,新的函数值分别为y1,y2,y3,y4,y5,…,其中最小值和最大值分别为()A.y1,y2B.y43,y44C.y44,y45D.y2014,y201520.如图,△ABC是等边三角形,顶点C在y轴的负半轴上,点A(1,),点B在第一象限,经过点A的反比例函数y=(x>0)的图象恰好经过顶点B,则△ABC的边长为()A.3B.2C.4D.3二.填空题(共10小题)21.如图,在平面直角坐标系中,经过点A的双曲线y=(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为.22.如图,函数y=(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则k=2+;④若MF=MB,则MD=2MA.其中正确的结论的序号是.(只填序号)23.已知如图,直线y=x分别与双曲线y=(m>0,x>0)、双曲线y=(n>0,x>0)交于点A,点B,且=,将直线y=x向左平移6个单位长度后,与双曲线y=交于点C,若S△ABC=4,则mn的值为.24.如图,等边△OBA和等边△AFE的一边都在x轴上,双曲线y=(k>0)经过OB的中点C和AE的中点D,已知OB=16,则点F的坐标为.25.如图,直角坐标系xOy中,直线y=﹣x+b分别交x,y轴的正半轴于点A,B,交反比例函数y=﹣的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若,则CD的长为.26.如图,直线y=x﹣8交x轴于点A,交y轴于点B,点C是反比例函数y=的图象上位于直线AB上方的一点,CD∥/x轴交AB于点D,CE⊥CD交AB于点E,若AD•BE=4,则k的值为.27.如图,△OBC的边BC∥x轴,过点C的双曲线y=(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为.28.如图,一次函数y=x与反比例函数y=(k>0)的图象在第一象限交于点A,点C在以B(7,0)为圆心,2为半径的⊙B上,已知AC长的最大值为7,则该反比例函数的函数表达式为.29.如图,C、D是双曲线y=(x>0,k>0)上两点,延长CD交x轴于点E,DB⊥x轴于点B,点F是线段DE的中点,延长FB交y轴于点S,连接SE,若S△SBE=,则k=30.如图,已知动点A在函数y=(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD =AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于.三.解答题(共10小题)31.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.(1)求一次函数与反比例函数的解析式;(2)根据所给条件,请直接写出不等式k1x+b>的解集;(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.32.如图,反比例函数y=的图象与一次函数y=x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△P AB的面积;(2)设直线P A、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠P AQ与∠PBQ 的大小,并说明理由.33.如图1,已知点A(a,0),B(0,b),且a、b满足,▱ABCD的边AD与y轴交于点E,且E为AD中点,双曲线经过C、D两点.(1)求k的值;(2)点P在双曲线上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.34.平面直角坐标系xOy中,点A、B分别在函数y1=(x>0)与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(1)若AB∥x轴,求△OAB的面积;(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD 边与函数y1=(x>0)的图象都有交点,请说明理由.35.如图1所示,已知y=(x>0)图象上一点P,P A⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M 是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.(1)如图2,连接BP,求△P AB的面积;(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为2,求此时P点的坐标;(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.36.如图,直线y1=﹣x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.(1)求y与x之间的函数关系式;(2)直接写出当x>0时,不等式x+b>的解集;(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.37.如图1,在平面直角坐标系中,四边形AOBC是矩形,点C的坐标为(4,3),反比例函数y=(k>0)的图象与矩形AOBC的边AC、BC分别相交于点E、F,将△CEF沿EF对折后,C点恰好落在OB上.(1)求证:△AOE与△BOF的面积相等;(2)求反比例函数的解析式;(3)如图2,P点坐标为(2,﹣3),在反比例函数y=的图象上是否存在点M、N(M在N的左侧),使得以O、P、M、N为顶点的四边形是平行四边形?若存在,求出点M、N的坐标;若不存在,请说明理由.38.如图,直线y=k1x(x≥0)与双曲线y=(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.(1)求k1与k2的值;(2)求直线PC的表达式;(3)直接写出线段AB扫过的面积.39.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x >0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b﹣>0的解集.40.如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).(1)求反比例函数的解析式;(2)反比例函数的图象与线段BC交于点D,直线过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.参考答案与试题解析一.选择题(共20小题)1.【分析】设A(m,),C(0,n),则D(m,0),E(m,0),由AB=BC,推出B(,),根据点B在y =上,推出•=k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2•S△AEB=14,根据S△AEC=S△AEO+S△ACO﹣S△ECO,构建方程即可解决问题;【解答】解:设A(m,),C(0,n),则D(m,0),E(m,0),∵AB=BC,∴B(,),∵点B在y=上,∴•=k,∴k+mn=4k,∴mn=3k,连接EC,OA.∵AB=BC,∴S△AEC=2•S△AEB=14,∵S△AEC=S△AEO+S△ACO﹣S△ECO,∴14=•(﹣m)•+•n•(﹣m)﹣•(﹣m)•n,∴14=﹣k﹣+,∴k=﹣12.故选:A.2.【分析】如解答图所示,满足条件的直线有两种可能:一种是与直线BC平行,符合条件的有两条,如图中的直线a、b;还有一种是过线段BC的中点,符合条件的有两条,如图中的直线c、d.【解答】解:如解答图所示,满足条件的直线有4条,故选:A.3.【分析】连接CE.只要证明CE∥OB,推出S△OBE=S△OBC,即可解决问题;【解答】解:连接CE.∵四边形ABCO,四边形DEFC都是正方形,∴∠ECF=∠BOC=45°,∴CE∥OB,∴S△OBE=S△OBC,∵BC=OC,点B在y=上,∴BC=OC=2,∴S△OBE=×2×2=2,故选:A.4.【分析】如图:延长AC交BF的延长线于G,连接OF.只要证明OF是△BCG的中位线,可得OF=CG=,即可解决问题.【解答】解:如图:延长AC交BF的延长线于G,连接OF.∵AF⊥BG,∴∠AFB=∠AFG=90°,∴∠BAF+∠ABF=90°,∠G+∠GAF=90°,∵∠BAF=∠F AG,∴∠ABF=∠G,∴AB=AG,∵AF⊥BG,∴BF=FG,∵B(﹣,﹣),C(,),∴OB=OC,∴OF=CG,∵|AB﹣AC|=2,AB=AG,∴CG=2,∴OF=,∴点F在以O为圆心为半径的圆上运动.故选:C.5.【分析】设B(m,n),想办法求出A,D,C的坐标,构建方程求出mn的值即可解决问题.【解答】解:设B(m,n),∵BC:BO=2:3,∴C(m,n),∵BD:AB=3:4,∴点D的纵坐标为n,∵C,D在y=的图象上,∴D(m,),∴直线BD的解析式为y=x﹣n,令y=0,得到x=m,∴A(m,0),∵S△ABO=,∴×(﹣m)×n=,∴mn=﹣,∴k==﹣×=﹣,故选:C.6.【分析】作AE⊥OD于E,CF⊥OD于F.首先证明S△AOC=S△AOE+S梯形AEFC﹣S△OCF=S梯形AEFC,由此构建方程即可解决问题;【解答】解:作AE⊥OD于E,CF⊥OD于F.连接AC,AD.∵BC:CD=2:1,S△ADC=,∴S△ACB=,∵OA=AB,∴B(2m,2n),S△AOC=S△ACB=,∵A、C在y=上,BC=2CD,∴C(m,n),∵S△AOC=S△AOE+S梯形AEFC﹣S△OCF=S梯形AEFC,∴•(n+n)×m=,∴mn=16,故选:B.7.【分析】如图作BH⊥OD于H.延长BA交y轴于E.由tan∠ABD=tan∠BDH=,设DH=5m,BH=9m,则BH =BE=9m,OD=4m,推出C(﹣6m,m),推出A(﹣m,9m),由△ABD的面积为,推出×m×9m=,可得m2=,推出k=﹣6m×m=﹣2;【解答】解:如图作BH⊥OD于H.延长BA交y轴于E.∵AB∥DH,∴∠ABD=∠BDH,∴tan∠ABD=tan∠BDH=,设DH=5m,BH=9m,则BH=BE=9m,OD=4m,∴C(﹣6m,m),∴A(﹣m,9m),∵△ABD的面积为,∴×m×9m=,∴m2=,∴k=﹣6m×m=﹣2,故选:A.8.【分析】设A(x a,y a),B(x b,y b),C(x c,y c),则有x a y a=x b y b=5,x c y c=k,由OA∥BC可得:=,过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,由图可得:S△ABC=S梯形AFEB+S梯形BEDC﹣S梯形AFDC,代入坐标可得到:(y a+y b)(x b﹣x a)+(y b+y c)(x c﹣x b)﹣(y a+y c)(x c﹣x a)=6,整理得到:y a x b﹣x a y b+y b x c ﹣y c x b﹣y a x c+x a y c=6,综上得到y b x c﹣y c x b=12,已知=,可得=,y b==,综合以上式子可得:10+x c y c=12,所以x c y c=4,即k=4.【解答】解:设A(x a,y a),B(x b,y b),C(x c,y c),则有x a y a=x b y b=5,x c y c=k,∵OA∥BC∴=,整理得到:y a x b﹣y a x c=x a y b﹣x a y c①过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,∵S△ABC=S梯形AFEB+S梯形BEDC﹣S梯形AFDC=6∴(AF+BE)×EF+(BE+CD)×DE﹣(AF+CD)×DF=6代入坐标可得到:(y a+y b)(x b﹣x a)+(y b+y c)(x c﹣x b)﹣(y a+y c)(x c﹣x a)=6,整理得:y a x b﹣x a y b+y b x c﹣y c x b﹣y a x c+x a y c=6,②①②联立得:y b x c﹣y c x b=12,③由=,可得:=,即x b=x c,∴y b==,代入③得:10+x c y c=12,解得:x c y c=4,即k=﹣4.解法二:如图连接OB,OC,作BE⊥OP于E,CF⊥OP于F.∵OA∥BC,∴S△OBC=S△ABC=6,∵PB:PC=1:2,∴S△OPB=2,S△OPC=4,∵S△OBE=,∴S△PBE=,∵△BEP∽△CFP,∴S△CFP=4×=2,∴S△OCF=2,∴k=﹣4.故选:B.9.【分析】如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出=()2,因为CA:AB=5:8,AO=OB,推出CA:OA=5:4,推出CO:OA=3:4,可得=()2=,因为S△AOE =2,可得S△COF=,延长即可解决问题;【解答】解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.∵A、B关于原点对称,∴OA=OB,∵AC=BC,OA=OB,∴OC⊥AB,∴∠CFO=∠COA=∠AEO=90°,∵∠COF+∠AOE=90°,∠AOE+∠EAO=90°,∴∠COF=∠OAE,∴△CFO∽△OEA,∴=()2,∵CA:AB=5:8,AO=OB,∴CA:OA=5:4,∴CO:OA=3:4,∴=()2=,∵S△AOE=2,∴S△COF=,∴=,∵k<0,∴k=﹣,故选:A.10.【分析】证明△DHA≌△CGD(AAS)、△ANB≌△DGC(AAS)得到:AN=DG=1=AH,而AH=﹣1﹣m=1,解得:m=﹣2,即可求解.【解答】解:设点D(m,),如图所示,过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,∵∠GDC+∠DCG=90°,∠GDC+∠HDA=90°,∴∠HDA=∠GCD,又AD=CD,∠DHA=∠CGD=90°,∴△DHA≌△CGD(AAS),∴HA=DG,DH=CG,同理△ANB≌△DGC(AAS),∴AN=DG=1=AH,则点G(m,﹣1),CG=DH,AH=﹣1﹣m=1,解得:m=﹣2,故点G(﹣2,﹣5),D(﹣2,﹣4),H(﹣2,1),则点E(﹣,﹣5),GE=,CE=CG﹣GE=DH﹣GE=5﹣=,故选:B.11.【分析】由OA1=A1A2=A2A3=…=A n﹣1A n=1可知B1点的坐标为(1,y1),B2点的坐标为(2,y2),B3点的坐标为(3,y3)…B n点的坐标为(n,y n),把x=1,x=2,x=3代入反比例函数的解析式即可求出y1、y2、y3的值,再由三角形的面积公式可得出S1、S2、S3…S n的值,故可得出结论.【解答】解:∵OA1=A1A2=A2A3=…=A n﹣1A n=1,∴设B1(1,y1),B2(2,y2),B3(3,y3),…B n(n,y n),∵B1,B2,B3…Bn在反比例函数y=(x>0)的图象上,∴y1=1,y2=,y3=…y n=,∴S1=×1×(y1﹣y2)=×1×(1﹣)=(1﹣);S2=×1×(y2﹣y3)=×(﹣);S3=×1×(y3﹣y4)=×(﹣);…S n=(﹣),∴S1+S2+S3+…+S n=(1﹣+﹣+﹣+…+﹣)=.故选:C.12.【分析】作AE⊥OC于E,DF⊥OC于F.设A(a,b).想办法证明OE=EF=CF即可解决问题;【解答】解:作AE⊥OC于E,DF⊥OC于F.设A(a,b).∵四边形ABCO是菱形,∴AD=DC,∵AE∥DF,∴EF=FC,∴DF=AE=b∵反比例函数y=在第一象限内的图象经过点A与点D,∴D(2a,b),∴OE=EF=FC=a,∴OA=OC=3a,∴AE==2a,∵OC•AE=24,∴3a•2a=24,∴a2=4,∵a>0,∴a=2,∴A(2,4),故选:C.13.【分析】如图作DM⊥y轴于M,CN⊥x轴于N.设OA=b,OB=a.首先利用全等三角形的性质求出D、C两点坐标,再证明a=b,再构建方程求出a、k,再求出直线EF的解析式,利用方程组确定点P坐标即可解决问题;【解答】解:如图作DM⊥y轴于M,CN⊥x轴于N.设OA=b,OB=a.∵四边形ABCD是正方形,∵AD=AB=BC,∠DAB=∠ABC=90°,易证△AOB≌△BNC≌△DMA,∴DM=OA=BN=b,AM=OB=CN=a,∴D(b,a+b),C(a+b,a),∵点C,D恰好都落在反比例函数y=(k≠0)的图象上,∴b(a+b)=a(a+b),∵a+b≠0,∴a=b,∴OA=OB,∴∠ABO=45°,∠EBF=45°,∵BE⊥EF,∴△BEF是等腰直角三角形,∵BC=EC,∴可得E(3a,2a),F(5a,0),∴×4a×2a=+12,∵D(a,2a),∴2a2=k,∴a=2,k=8,∴E(6,4),F(10,0),∴直线EF的解析式为y=﹣x+10,由,解得或,∴p(5+,5﹣),∴PE=﹣,∴S△ECP=•EC•EP=•(﹣)×2=2﹣2,故选:B.14.【分析】连接OF、OB、OE.首先证明EF是△BAC的中位线,利用相似三角形的性质即可解决问题.【解答】解:连接OF、OB、OE.∵四边形ABCO是矩形,∴S△ABO=S△BCO,∵BF=CF,∴S△CFO=S△BFO,∵E、F在y=(x>0)上,∴S△AEO=S△FCO=S△ABO,∴AE=EB,∵BF=CF,∴EF∥AC,∴△BEF∽△BAC,∴=,∵S矩形ABCO=16,∴S△BEF=×8=2,∴S四边形ACFE=8﹣2=6,故选:B.15.【分析】首先证明CD=BC=AB,设C的横坐标为x,则B的横坐标为2x,根据S△OBC=S△OBD﹣S△OCD,构建方程,即可求得k的值;【解答】解:作BE⊥x轴于E,CF⊥x轴于F,∴BE∥CF,∴=,∵AC=BC,∴CF=2BE,∵S△COF=S△OBE,∴CF•OF=OE•BE,∴OE=2OF,∵OD∥CF∥BE,∴DC=BC=AB,∴设C的横坐标为x,则B的横坐标为2x,∴C的纵坐标为,B的纵坐标为,∴CF=,BE=,OA=3x∵S△OBC=S△OAC﹣S△OAB,△OBC的面积为4,∴OA•CF﹣OA•C=4,∴•3x•﹣•3x•=4,∴k=故选:B.16.【分析】首先证明点E是线段AB的中点,设BC=BC′=m,则EC′=m﹣2.在Rt△BEC′中,根据BC′2=BE2+EC′2,构建方程求出m即可解决问题;【解答】解:连接OD、OE.设BC=BC′=m,则EC′=m﹣2.∵CD=BD,∴S△CDO==S矩形ABCD,∵S△AOE==S△CDO=S矩形ABCD,∴AE=EB,∵C′(2,3),∴AE=EB=3,在Rt△BEC′中,∵BC′2=BE2+EC′2,∴m2=32+(m﹣2)2,∴m=,∴E(,3),∵点E在y=上,∴k=,故选:D.17.【分析】由题意,△ABC是等腰直角三角形,BC∥x轴,设B(a,﹣a),想办法证明A(﹣a,﹣3a),利用待定系数法求出a即可.【解答】解:由题意,△ABC是等腰直角三角形,BC∥x轴,设B(a,﹣a),∵AC∥OB,∴AC⊥直线y=x,∴A、C关于直线y=x对称,作OH⊥AC于H,则四边形ABOH是矩形,∴AH=HC=OB,AB=2OB,∴A(﹣a,﹣3a),∴3a2=6,∴a2=2,∵a<0,∴a=﹣,∴B(﹣,),故选:A.18.【分析】据对称性可知,反比例函数y=,y=﹣的图象是中心对称图形,菱形是中心对称图形,推出菱形ABCD 的对角线AC与BD的交点即为原点O.如图:作DM⊥x轴于M,CN⊥x轴于N.连接OD,OC.由△DOM∽△OCN,S△DOM=2,S△OCN=,推出()2=,可以假设OD=2k,OC=3k,根据菱形的面积公式构建方程即可解决问题;【解答】解:根据对称性可知,反比例函数y=,y=﹣的图象是中心对称图形,菱形是中心对称图形,∴菱形ABCD的对角线AC与BD的交点即为原点O.如图:作DM⊥x轴于M,CN⊥x轴于N.连接OD,OC.∵DO⊥OC,∴∠DOM+∠CON=90°,∠CON+∠OCN=90°,∴∠DOM=∠OCN,∵∠DMO=∠CNO=90°,∴△DOM∽△OCN,∵S△DOM=2,S△OCN=,∴()2=,∴可以假设OD=2k,OC=3k,∵S菱形ABCD=4••2k•3k=78,∴k=,∴CD==k=,故选:B.19.【分析】图象y=向右平移个单位长度得到一个新的函y=,因为44<<45,结合图形可知:当x<44时,y<0,y随x的增大而减小,x=44时,得到y的最小值y44,当x>45时,y>0,y随x的增大而增大,x=45时,得到y的最大值y45;【解答】解:图象y=向右平移个单位长度得到一个新的函y=,∵44<<45,∴当x<44时,y<0,y随x的增大而减小,x=44时,得到y的最小值y44,当x>45时,y>0,y随x的增大而增大,x=45时,得到y的最大值y45,故选:C.20.【分析】如图延长AB到D,使得AB=BD,连接CD,作AH⊥y轴于H,DE⊥y轴于E.设C(0,c).由△ACH ∽△CDE,推出===,由A(1,),推出AH=1,CH=﹣c,推出EC=,DE=﹣c,推出D(﹣c,c﹣),根据BA=BD,可得B(,),因为A、B在y=上,可得=×,解方程求出点C坐标即可解决问题;【解答】解:如图延长AB到D,使得AB=BD,连接CD,作AH⊥y轴于H,DE⊥y轴于E.设C(0,c).∵△ABC是等边三角形,∴AB=AC=BC,∵AB=BD,∴BA=BC=BD,∴△ACD是直角三角形,∵∠CAD=60°,∴DC=AC,∵∠ACD=∠AHC=∠DEC=90°,∴∠ACH+∠DCE=90°,∵∠ECD+∠CDE=90°,∴∠ACH=∠CDE,∴△ACH∽△CDE,∴===,∵A(1,),∴AH=1,CH=﹣c,∴EC=,DE=﹣c,∴D(﹣c,c﹣),∵BA=BD,∴B(,),∵A、B在y=上,∴=×,整理得:4c2﹣16c﹣11=0,解得c=﹣或(舍弃),∴C(0,﹣),∴AC==2,故选:B.二.填空题(共10小题)21.【分析】过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,由等腰三角形的判定与性质得出OA=BA,∠OAB=90°,证出∠AOM=∠BAN,由AAS证明△AOM≌△BAN,得出AM=BN,OM=AN,即可得到求出B的坐标,代入反比例函数即可得出一元二次方程,解方程即可得到k的值.【解答】解:如图所示,过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,则OD=MN,DN=OM,∠AMO=∠BNA=90°,∴∠AOM+∠OAM=90°,∵∠AOB=∠OBA=45°,∴OA=BA,∠OAB=90°,∴∠OAM+∠BAN=90°,∴∠AOM=∠BAN,∴△AOM≌△BAN,∴AM=BN=1,OM=AN=k,∴OD=1+k,BD=OM﹣BN=k﹣1∴B(1+k,k﹣1),∵双曲线y=(x>0)经过点B,∴(1+k)•(k﹣1)=k,整理得:k2﹣k﹣1=0,解得:k=(负值已舍去),故答案为:.22.【分析】①设点A(m,),M(n,),构建一次函数求出C,D坐标,利用三角形的面积公式计算即可判断.②△OMA不一定是等边三角形,故结论不一定成立.③设M(1,k),由△OAM为等边三角形,推出OA=OM=AM,可得1+k2=m2+,推出m=k,根据OM=AM,构建方程求出k即可判断.④如图,作MK∥OD交OA于K.利用平行线分线段成比例定理解决问题即可.【解答】解:①设点A(m,),M(n,),则直线AC的解析式为y=﹣x++,∴C(m+n,0),D(0,),∴S△ODM=n×=,S△OCA=(m+n)×=,∴△ODM与△OCA的面积相等,故①正确;∵反比例函数与正比例函数关于原点对称,∴O是AB的中点,∵BM⊥AM,∴OM=OA,∴k=mn,∴A(m,n),M(n,m),∴AM=(m﹣n),OM=,∴AM不一定等于OM,∴∠BAM不一定是60°,∴∠MBA不一定是30°.故②错误,∵M点的横坐标为1,∴可以假设M(1,k),∵△OAM为等边三角形,∴OA=OM=AM,1+k2=m2+,∵m>0,k>0,∴m=k,∵OM=AM,∴(1﹣m)2+=1+k2,∴k2﹣4k+1=0,∴k=2,∵m>1,∴k=2+,故③正确,如图,作MK∥OD交OA于K.∵OF∥MK,∴==,∴=,∵OA=OB,∴=,∴=,∵KM∥OD,∴==2,∴DM=2AM,故④正确.故答案为①③④.23.【分析】先求出直线y=x向左平移6个单位长度后的解析式为y=x+4,那么直线y=x+4交y轴于E(0,4),作EF⊥OB于F.根据互相垂直的两直线斜率之积为﹣1得出直线EF的解析式为y=﹣x+4,再求出F(,),EF==,根据S△ABC=4,求出AB=,那么OA=AB=,进而求出A、B 两点坐标,求出m、n即可解决问题.【解答】解:直线y=x向左平移6个单位长度后的解析式为y=(x+6),即y=x+4,∴直线y=x+4交y轴于E(0,4),作EF⊥OB于F.可得直线EF的解析式为y=﹣x+4,由,解得,即F(,).∴EF==,∵S△ABC=4,∴•AB•EF=4,∴AB=,∵=,∴OA=AB=,∴A(3,2),B(5,),∴m=6,n=,∴mn=100.故答案为100.24.【分析】过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用待定系数法求反比例函数解析式;过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解.【解答】解:过点C作CG⊥OA于点G,过点D作DH⊥AF于点H,∵点C是等边△OAB的边OB的中点,∴OC=8,∠AOB=60°,∴OG=4,CG=OG•tan60°=4,∴点C的坐标是(4,4),∴k=4×4=16,∴该双曲线所表示的函数解析式为y=,设AH=a,则DH=a.∴点D的坐标为(16+a,a),∵点D是双曲线y=上的点,∴a×(16+a)=16,即:a2+16a﹣16=0,解得:a1=﹣8+4,a2=﹣8﹣4(舍去),∴AD=2AH=﹣16+8,∴AF=2AD=﹣32+16,∴OF=AO+AF=16﹣32+16=16﹣16,即点F的坐标为(16﹣16,0).故答案为:(16﹣16,0).25.【分析】由题意B(0,b),A(b,0),推出OA=OB=b,因为直线y=﹣x+b关于直线y=x对称,反比例函数y =﹣关于y=x对称,推出BC=AD,设BC=AD=a,则C(﹣a,b+a),D(b+a,﹣a),想办法构建方程求出a、b的关系,求出点D的坐标(用b表示),再利用待定系数法即可解决问题;【解答】解:由题意B(0,b),A(b,0),∴OA=OB=b,∵直线y=﹣x+b关于直线y=x对称,反比例函数y=﹣关于y=x对称,∴BC=AD,设BC=AD=a,则C(﹣a,b+a),D(b+a,﹣a),∵,∴=,整理得:12a2+17ab﹣14b2=0,解得a=b或a=﹣b(舍弃),∴D(b,﹣b),∵D在y=﹣的图象上,∴b×(﹣b)=﹣4,解得b=3或﹣3(舍弃),∴D(4,﹣1),C(﹣1,4),∴CD==5,故答案为5.26.【分析】过D作DF⊥AO于F,过EG⊥OB于G,则DF∥OB,GE∥AO,设C(x,y),则GE=x,DF=﹣y,由△ADF∽△ABO,可得AD=﹣y,由△BEG∽△BAO,可得BE=2x,再根据AD•BE=4,即可得到k=xy=.【解答】解:如图,过D作DF⊥AO于F,过EG⊥OB于G,则DF∥OB,GE∥AO,由直线y=x﹣8,可得A(,0),B(0,﹣8),∴AO=,BO=8,AB=,设C(x,y),则GE=x,DF=﹣y,由△ADF∽△ABO,可得,即=,∴AD=﹣y,由△BEG∽△BAO,可得,即=,∴BE=2x,∵AD•BE=4,∴﹣y×2x=4,∴xy=﹣,∴k=xy=﹣,故答案为:﹣.27.【分析】延长BC交y轴于点E,过点D作DF⊥x轴于点FBA⊥x轴于A.由矩形与反比例函数的性质,可得S四边=S△OBC=8,易证得△ODF∽△OBA,又由OD:DB=1:2,即可得S△ODF=S四边形ABDF=×4=,则形ABDF可求得答案.【解答】解:延长BC交y轴于点E,过点D作DF⊥x轴于点F,BA⊥x轴于A.∵梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,∴四边形OABE是矩形,∴S△OBE=S△OAB,∵过点C的双曲线y=交OB于点D,∴S△OCE=S△ODF,∴S四边形ABDF=S△OBC=8,∵DF∥AB,∴△ODF∽△OBA,∵OD:DB=1:2,∴OD:OB=1:3,∴S△ODF:S△OAB=1:9,∴S△ODF:S四边形ABDF=1:8,∴S△ODF=S四边形ABDF=×8=1,∴k=2.故答案为:2.28.【分析】设A(m,m),因为点C在以B(7,0)为圆心,2为半径的⊙B上,已知AC长的最大值为7,可得AB =5,由此构建方程即可解决问题.【解答】解:设A(m,m),∵点C在以B(7,0)为圆心,2为半径的⊙B上,已知AC长的最大值为7,∴AB=5,∴m2+(7﹣m)2=25,解得m=3或4,∴A(3,3)或(4,4),∵点A在y=上,∴k=9或16,∴反比例函数的解析式为y=或y=,故答案为y=或y=.29.【分析】连接OD.设D(m,n),只要证明△SBO∽△DEB,可得=,推出DB•OB=OS•BE,因为S△SBE =,可得•BE•SO=,推出BE•SO=,推出DB•OB=,即可解决问题;【解答】解:连接OD.设D(m,n)∵DB⊥OE,∴∠DBE=90°,∵DF=FE,∴BF=FE,∴∠FEB=∠FBE,∵∠FBE=∠SBO,∴∠SBO=∠DEB,∵∠SOB=∠DBE=90°,∴△SBO∽△DEB,∴=,∴DB•OB=OS•BE,∵S△SBE=,∴•BE•SO=,∴BE•SO=,∴DB•OB=,∵D(m,n)在y=上,∴k=mn=DB•OB=,故答案为.30.【分析】作DF⊥x轴于点F,EG⊥y轴于G,得到△QEG∽△PDF,于是得到,设EG=9t,则PF=25t,然后根据△ADE∽△FPD,据此即可得到关于t的方程,求得t的值,进而求解.【解答】解:作DF⊥x轴于点F,EG⊥y轴于G,∴△QEG∽△DPF,∴,设EG=9t,则PF=25t,∴A(9t,),由AC=AEAD=AB,∴AE=9t,AD=,DF=,PF=25t,∵△ADE∽△FPD,∴AE:DF=AD:PF,9t:=:25t,即t2=,图中阴影部分的面积=×9t×9t+××=,故答案为:.三.解答题(共10小题)31.【分析】(1)把A、B的坐标代入反比例函数解析式求出m=﹣n,过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,求出梯形BCAD的面积和△BDA的面积,即可得出关于n的方程,求出n的值,得出A、B 的坐标,代入反比例函数和一次函数的解析式,即可求出答案;(2)根据A、B的横坐标,结合图象即可得出答案;(3)分为两种情况:当点P在第三象限时和当点P在第一象限时,根据坐标和图象即可得出答案.【解答】解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,即m=﹣n,则A(2,﹣n),过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,∵A(2,﹣n),B(n,﹣2),∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,∵S△ABC=•BC•BD∴×2×(2﹣n)=5,解得:n=﹣3,即A(2,3),B(﹣3,﹣2),把A(2,3)代入y=得:k2=6,即反比例函数的解析式是y=;把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,解得:k1=1,b=1,即一次函数的解析式是y=x+1;(2)∵A(2,3),B(﹣3,﹣2),∴不等式k1x+b>的解集是﹣3<x<0或x>2;(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是p≤﹣2,当点P在第一象限时,要使y1≥y2,实数p的取值范围是p>0,即P的取值范围是p≤﹣2或p>0.32.【分析】(1)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,如图1,可根据条件先求出点B的坐标,然后把点B的坐标代入反比例函数的解析式,即可求出k,然后求出直线AB与反比例函数的交点A的坐标,从而得到OA=OB,由此可得S△P AB=2S△AOP,要求△P AB的面积,只需求△P AO的面积,只需用割补法就可解决问题;(2)过点P作PH⊥x轴于H,如图2.可用待定系数法求出直线PB的解析式,从而得到点N的坐标,同理可得到点M的坐标,进而得到MH=NH,根据垂直平分线的性质可得PM=PN,即△PMN是等腰三角形;(3)过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),运用待定系数法求出直线AQ的解析式,即可得到点D的坐标为(c﹣4,0),同理可得E(c+4,0),从而得到DT=ET,根据垂直平分线的性质可得QD=QE,则有∠QDE=∠QED.然后根据对顶角相等及三角形外角的性质,就可得到∠P AQ=∠PBQ.【解答】解:(1)k=4,S△P AB=15.提示:过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,如图1,把x=4代入y=x,得到点B的坐标为(4,1),把点B(4,1)代入y=,得k=4.解方程组,得到点A的坐标为(﹣4,﹣1),则点A与点B关于原点对称,∴OA=OB,∴S△AOP=S△BOP,∴S△P AB=2S△AOP.设直线AP的解析式为y=mx+n,把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,求得直线AP的解析式为y=x+3,则点C的坐标(0,3),OC=3,∴S△AOP=S△AOC+S△POC=OC•AR+OC•PS=×3×4+×3×1=,∴S△P AB=2S△AOP=15;(2)过点P作PH⊥x轴于H,如图2.B(4,1),则反比例函数解析式为y=,设P(m,),直线P A的方程为y=ax+b,直线PB的方程为y=px+q,联立,解得直线P A的方程为y=x+﹣1,联立,解得直线PB的方程为y=﹣x++1,∴M(m﹣4,0),N(m+4,0),∴H(m,0),∴MH=m﹣(m﹣4)=4,NH=m+4﹣m=4,∴MH=NH,∴PH垂直平分MN,∴PM=PN,∴△PMN是等腰三角形;(3)∠P AQ=∠PBQ.理由如下:过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),直线AQ的解析式为y=px+q,则有,解得:,∴直线AQ的解析式为y=x+﹣1.当y=0时,x+﹣1=0,解得:x=c﹣4,∴D(c﹣4,0).同理可得E(c+4,0),∴DT=c﹣(c﹣4)=4,ET=c+4﹣c=4,∴DT=ET,∴QT垂直平分DE,∴QD=QE,∴∠QDE=∠QED.∵∠MDA=∠QDE,∴∠MDA=∠QED.∵PM=PN,∴∠PMN=∠PNM.∵∠P AQ=∠PMN﹣∠MDA,∠PBQ=∠NBE=∠PNM﹣∠QED,∴∠P AQ=∠PBQ.33.【分析】(1)先根据非负数的性质求出a、b的值,故可得出A、B两点的坐标,设D(1,t),由DC∥AB,可知C (2,t﹣2),再根据反比例函数的性质求出t的值即可;(2)由(1)知k=4可知反比例函数的解析式为y=,再由点P在双曲线上,点Q在y轴上,设Q(0,y),P(x,),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标;(3)连NH、NT、NF,易证NF=NH=NT,故∠NTF=∠NFT=∠AHN,∠TNH=∠TAH=90°,MN=HT,由此即可得出结论.【解答】解:(1)∵+(a+b+3)2=0,且≥0,(a+b+3)2≥0,∴,解得:,∴A(﹣1,0),B(0,﹣2),∵E为AD中点,∴x D=1,设D(1,t),又∵四边形ABCD是平行四边形,∴C(2,t﹣2),∴t=2t﹣4,∴t=4,∴k=4;(2)∵由(1)知k=4,∴反比例函数的解析式为y=,∵点P在双曲线上,点Q在y轴上,∴设Q(0,y),P(x,),①当AB为边时:如图1所示:若ABPQ为平行四边形,则=0,解得x=1,此时P1(1,4),Q1(0,6);如图2所示;若ABQP为平行四边形,则=,解得x=﹣1,此时P2(﹣1,﹣4),Q2(0,﹣6);②如图3所示;当AB为对角线时:AP=BQ,且AP∥BQ;∴=,解得x=﹣1,∴P3(﹣1,﹣4),Q3(0,2);故P1(1,4),Q1(0,6);P2(﹣1,﹣4),Q2(0,﹣6);P3(﹣1,﹣4),Q3(0,2);(3)连NH、NT、NF,∵MN是线段HT的垂直平分线,∴NT=NH,∵四边形AFBH是正方形,∴∠ABF=∠ABH,在△BFN与△BHN中,,∴△BFN≌△BHN,∴NF=NH=NT,∴∠NTF=∠NFT=∠AHN,四边形ATNH中,∠ATN+∠NTF=180°,而∠NTF=∠NFT=∠AHN,所以,∠ATN+∠AHN=180°,所以,四边形ATNH内角和为360°,所以∠TNH=360°﹣180°﹣90°=90°.∴MN=HT,∴=.34.【分析】(1)如图1,AB交y轴于C,由于AB∥x轴,根据k的几何意义得到S△OAC=2,S△OBC=2,所以S△OAB =S△OAC+S△OBC=4;(2)根据函数图象上点的坐标特征得A、B的纵坐标分别为、﹣,根据两点间的距离公式得到OA2=a2+()2,OB2=b2+(﹣)2,则利用等腰三角形的性质得到a2+()2=b2+(﹣)2,变形得到(a+b)(a﹣b)(1﹣)=0,由于a+b≠0,a>0,b<0,所以1﹣=0,易得ab=﹣4;(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1=(x>0)的图象一定有交点,设直线CD与函数y1=(x>0)的图象交点为F,由于A点坐标为(a,),正方形ACDE的边长为3,则得到C 点坐标为(a﹣3,),F点的坐标为(a﹣3,),所以FC=﹣,然后比较FC与3的大小,由于3﹣FC =3﹣(﹣)=,而a≥4,所以3﹣FC≥0,于是可判断点F在线段DC上.【解答】解:(1)如图1,AB交y轴于C,∵AB∥x轴,∴S△OAC=×|4|=2,S△OBC=×|﹣4|=2,∴S△OAB=S△OAC+S△OBC=4;(2)∵A、B的横坐标分别为a、b,∴A、B的纵坐标分别为、﹣,∴OA2=a2+()2,OB2=b2+(﹣)2,∵△OAB是以AB为底边的等腰三角形,∴OA=OB,∴a2+()2=b2+(﹣)2,∴a2﹣b2+()2﹣()2=0,∴a2﹣b2+=0,∴(a+b)(a﹣b)(1﹣)=0,∵a+b≠0,a>0,b<0,∴1﹣=0,∴ab=﹣4;(3)∵a≥4,而AC=3,∴直线CD在y轴的右侧,直线CD与函数y1=(x>0)的图象一定有交点,设直线CD与函数y1=(x>0)的图象交点为F,如图2,∵A点坐标为(a,),正方形ACDE的边长为3,∴C点坐标为(a﹣3,),∴F点的坐标为(a﹣3,),。
反比例函数上的点平移规律

反比例函数上的点平移规律我们来简单了解一下反比例函数的定义。
反比例函数可以表示为y = k/x,其中k是常数,通常被称为比例常数。
该函数的图像是一个以原点为中心的对称图形,当x不等于0时,y的值与x成反比例关系。
在反比例函数中,当我们将点(x, y)沿x轴或y轴方向进行平移时,点的坐标也会发生相应的变化。
具体来说,当点(x, y)沿x轴方向平移h个单位时,其新的坐标为(x + h, y);而当点(x, y)沿y轴方向平移k个单位时,其新的坐标为(x, y + k)。
这种平移规律使得反比例函数在坐标平面上的图像发生了移动。
举个例子来说明这个平移规律。
假设有反比例函数y = 2/x,其中k = 2。
现在考虑点(2, 1)在x轴方向平移3个单位,我们可以根据平移规律计算出新的坐标为(5, 1)。
同样地,如果将点(2, 1)在y轴方向平移2个单位,新的坐标将为(2, 3)。
通过这个例子,我们可以看到反比例函数上的点在平移过程中,其坐标发生了相应的变化。
这种变化是根据平移规律而产生的,可以用简单的加减法来实现。
这个规律在解决实际问题时非常有用,例如在物理学中,我们可以利用反比例函数来描述两个物体之间的关系。
除了在坐标平面上进行平移,反比例函数上的点还可以进行其他类型的变换,如旋转和缩放。
这些变换可以通过对坐标进行适当的计算来实现。
例如,如果我们要将点(2, 1)绕原点逆时针旋转90度,可以根据旋转公式计算出新的坐标为(-1, 2)。
总结起来,反比例函数上的点在平移过程中会发生相应的变化,这种变化遵循平移规律。
通过对坐标进行合适的加减运算,我们可以实现点在坐标平面上的平移、旋转和缩放等变换。
这些变换可以帮助我们更好地理解和应用反比例函数,从而解决实际问题。
在数学中,反比例函数是一种重要的函数类型,具有广泛的应用。
通过理解和掌握反比例函数上的点平移规律,我们可以更好地理解函数的性质和特点,为解决实际问题提供有力的工具。
中考数学反比例函数-经典压轴题

,解得
,
∴ 一次函数解析式为 y=2x+2,
∵ 点 A 的横坐标是 1,
∴ 当 x=1 时,y=4,即 A(1,4),
把 A(1,4)代入反比例函数 y= ,可得 k=4,
∴ 反比例函数解析式为 y=
(2)解:解方程组
,可得
或
,
∴ B(﹣2,﹣2),
又∵ A(1,4),BH⊥y 轴,
∴ △ ABH 面积= ×2×(4+2)=6. 【解析】【分析】(1)先由 tan∠ CDO=2 可求出 C 坐标,再把 D 点坐标代入直线解析式, 可求出一次函数解析式,再由直线解析式求出 A 坐标,代入双曲线解析式,可求出双曲线 解析式;(2)△ ABH 面积可以 BH 为底,高=yA-yB=4-(-2)=6.
5.函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决 下面的问题.
(1)分别求出当 2≤x≤4 时,三个函数:y=2x+1,y= ,y=2(x﹣1)2+1 的最大值和最小 值;
(2)若 y= 的值不大于 2,求符合条件的 x 的范围;
(3)若 y= ,当 a≤x≤2 时既无最大值,又无最小值,求 a 的取值范围; (4)y=2(x﹣m)2+m﹣2,当 2≤x≤4 时有最小值为 1,求 m 的值. 【答案】 (1)解:y=2x+1 中 k=2>0, ∴ y 随 x 的增大而增大, ∴ 当 x=2 时,y 最小=5;当 x=4 时,y 最大=9.
联立
,解得直线 PA 的方程为 y= x+ ﹣1,
联立
,解得直线 PB 的方程为 y=﹣ x+ +1,
∴ M(m﹣4,0),N(m+4,0),
2020上海市八年级数学第二学期期末压轴题一(解析版)

例2020年上海市宝山区初二下学期期末第24题如图1,反比例函数4yx=的图像与过原点的直线y=kx(k≠0)相交于点A、B,点A的横坐标是-4.点P是第一象限内反比例函数图像上的动点,且在直线AB的上方.(1)求k的值和点B的坐标;(2)若点P的坐标是(1, 4),且以点P、A、B、C为顶点的四边形为矩形时,写出点C 的坐标以及此时的矩形面积;(3)设点Q是动点P关于x轴的对称点,直线P A、PB与x轴分别交于点M、N,试用数学方法判断四边形PMQN是怎样的特殊四边形.图1动感体验打开几何画板文件名“20宝山24”,拖动点P在双曲线上运动,可以体验到,当点P的坐标为(1, 4)时,以A、P、B、Q为顶点的矩形只存在一种情况.点击屏幕左下方的按钮“第(3)题”,拖动点P在双曲线上运动,可以体验到,四边形PMQN始终保持菱形的形状.满分解答(1)将x=-4代入4yx=,得y=-1.所以A(-4,-1).将A(-4,-1)代入y=kx,得-1=-4k.解得k=14.因为点B与点A关于原点对称,所以B(4, 1).(2)如图2,已知A(-4,-1)、B(4, 1)、P(1, 4),所以AP2=52+52=50,BP2=32+32=18,AB2=82+22=68.所以AP2+BP2=AB2.所以△ABP是直角三角形,∠APB=90°.因此以点P、A、B、C为顶点的矩形,只存在一种情况,点C与点P关于原点对称,所以C(-1,-4).所以S矩形P ACB=AP∙PB=5232=30.图2(3)如图3,设P(m,4m),那么Q(m,4-m).设MN与PQ交于点G.由P(m,4m)、A(-4,-1),得直线AP的解析式为141=+-y xm m.所以M(m-4, 0).由P(m,4m)、B(4, 1),得直线AP的解析式为141=-++y xm m.所以N(m+4, 0).所以MG=NG=4.所以PQ垂直平分MN.又因为P、Q两点关于x轴对称,所以MN垂直平分PQ.所以四边形PMQN是菱形.图3例2020年上海市宝山区初二下学期期末第25题如图1,在梯形ABCD中,AD∥BC,∠B=90°,如果AD=4,BC=10,点E在线段AB上,将△BCE沿CE翻折,线段CB恰好和线段CD重合.(1)求梯形ABCD的高以及点E与点B之间的距离;(2)如图2,EF⊥CE交CD的延长线于点F,过点F作FG⊥BA于点G,求梯形ADFG 的中位线的长度;(3)动点M在线段CE上,当△DEM为等腰三角形时,求线段CM的长.图1 图2动感体验打开几何画板文件名“20宝山25”,可以体验到,△BCE与△DCE全等,△GEF与△DEF 全等.点击屏幕左下方的按钮“第(3)题”,拖动点M在EC上运动,可以体验到,△DEM 的三个顶点各有一次机会落在对边的垂直平分线上.满分解答(1)如图3,过点D作DH⊥BC于H.在Rt△DHC中,DC=BC=10,CH=BC-AD=10-4=6,所以DH=8.如图4,在Rt△AED中,AD=4,设AE=x,那么ED=EB=AB-AE=8-x.由勾股定理,得AE2+AD2=ED2.所以x2+42=(8-x)2.解得x=3.所以EB=8-x=5.图3 图4(2)如图5,因为EF⊥CE,所以∠2+∠3=90°.所以∠1+∠4=90°.又因为∠1=∠2,根据等角的余角相等,得∠3=∠4.又因为∠FGE=∠FDE=90°,EF=EF,所以△GEF≌△DEF.所以EG=ED=5.所以GA=GE-AE=5-3=2.如图6,过点F作FN⊥BC于N.在Rt△FNC中,FN=GA+AB=2+8=10,设FD=FG=m,那么FC=FD+DC=m+10,NC=BC-FG=10-m.由勾股定理,得FN2+NC2=FC2.所以102+(10-m)2=(10+m)2.解得m=52.所以梯形ADFG的中位线=1()2FG AD+=15(4)22⨯+=134.图5 图6(3)如图7,在Rt△BCE中,BE=5,BC=10,所以CE=55.分三种情况讨论等腰三角形DEM.①如图7,当EM=ED=5时,CM=CE-EM=555.②如图8,当MD=ME时,可证得DM是Rt△DEC斜边上的中线.所以CM=EM=12CE=55.③如图9,当DE=DM时,可证得DN//AN,CM是Rt△MNC的斜边.在Rt△MNC中,MN=DN-DM=8-5=3,NC=BC-AD=10-4=6,所以CM=35.图7 图8 图9上面第②、③两种情况的解题过程如下:如图8,当MD=ME时,∠MDE=∠MED.根据等角的余角相等,得∠MDC=∠MCD.所以DM=CM.所以CM=EM=12CE55.如图9,当DE=DM时,∠2=∠5.又因为∠1=∠2,所以∠1=∠5.所以DM//AB.所以∠MNC=∠B=90°.在Rt△MNC中,MN=DN-DM=8-5=3,NC=BC-AD=10-4=6,所以CM=35例2020年上海市崇明区初二下学期期末第24题如图1,在平面直角坐标系中,已知点A(2, 0)、B(0, 4),点C为线段AB的中点,点D为x轴上的动点.(1)求直线AB的函数表达式;(2)当直线CD与直线AB互相垂直时,求点D的坐标;(3)以A、C、D三点为顶点的三角形能否成为等腰三角形?若能,请直接写出D点的坐标;若不能,请说明理由.图1动感体验打开几何画板文件名“20崇明24”,拖动点D在x轴上运动,可以体验到,△ACD的顶点C、D各有一次机会落在对边的垂直平分线上,顶点A有两次机会落在对边的垂直平分线上.满分解答(1)设直线AB的函数表达式为y=kx+4(k≠0).将A(2, 0)代入,得2k+4=0.解得k=-2.所以直线AB的函数表达式为y=-2x+4.(2)如图2,因为CD垂直平分AB,所以DA=DB.设点D(x, 0),根据DA2=DB2列方程,得(x-2)2=x2+42.解得x=-3.所以D(-3, 0).(3)如图3,在Rt△AOB中,OA=2,OB=4,所以AB=25.图2因为点C为线段AB的中点,所以AC=5,C(1, 2).分三种情况讨论等腰三角形ACD.①如图3,当AD=AC=5时,点D坐标为(2+5, 0)或(2-5, 0).②如图4,当DA=DC时,根据DA2=DC2列方程,得(x-2)2=(x-1)2+22.解得x=12-,所以D(12-, 0).③如图5,当CA=CD时,点C在AD的垂直平分线上,所以D(0, 0),此时点D与点O重合.图3 图4 图5例2020年上海崇明区初二下学期期末第25题如图1,在矩形ABCD中,AB=6,BC=8,点P为边AD上一动点,把△ABP沿BP翻折后得到△EBP.(1)当点E恰好落在矩形对角线BD上时,求线段AP的长;(2)当直线PE与边BC相交于点F时,△FBP是否一定是等腰三角形?请给出你的结论,并证明你的结论;(3)当直线PE与边BC相交于点F,且点E在线段PF上时,设AP=x,BF=y,求y 关于x的函数解析式,并写出函数定义域.图1 备用图动感体验打开几何画板文件名“20崇明25”,拖动点P在AD上运动,观察左图,可以体验到,当点E落在矩形对角线BD上时,△DPE是直角三角形.观察中间图,可以体验到,△FBP 始终保持等腰三角形的形状不变.观察右图,可以体验到,当点E、F两点重合时,四边形ABFP是正方形.满分解答(1)如图2,在Rt△ABD中,AB=6,AD=8,所以BD=10.在Rt△DPE中,DE=BD-BE=10-6=4,设AP=EP=x,那么PD=8-x.由勾股定理,得EP2+DE2=PD2.所以x2+42=(8-x)2.解得x=3.所以AP=3.(2)△FBP一定是等腰三角形.理由如下:如图3,因为AD//BC,所以∠1=∠3.又因为∠1=∠2,所以∠2=∠3.所以PF=BF,△FBP是等腰三角形.(3)如图4,在Rt△BEF中,BE=AE=6,BF=y,EF=PF-PE=y-x,由勾股定理,得BE2+EF2=BF2.所以62+(y-x)2=y2.整理,得y=2362+xx.定义域是827-≤x≤6.当F、C两点重合,y=8,解得x=827-;当E、F两点重合时,x=6.图2 图3 图4例2020年上海市奉贤区初二下学期期末第25题如图1,在平面直角坐标系xOy中,直线y=-3x+15交x轴于点A,交y轴于点B,点C在直线AB上,点D与点C关于原点对称,联结AD,过点C作CE∥AD交x轴于点E.(1)求点A、B坐标;(2)当点C的横坐标为2时,求点E坐标;(3)过点B作BF∥AD交直线DE于点F,如果四边形ABFD是矩形,求点C的坐标.图1动感体验打开几何画板文件名“20奉贤25”,拖动点C在直线AB上运动,可以体验到,四边形ACED和四边形ABFD始终保持平行四边形的形状不变,矩形ABFD只存在一种情况,此时△ACD是直角三角形.满分解答(1)由y=-3x+15,当x=0时,y=15;当y=0时,x=5.所以A(5, 0),B(0, 15).(2)如图2,因为点D与点C关于原点对称,所以OC=OD.因为CE∥AD,所以∠OCE=∠ODA.又因为∠COE=∠DOA,所以△COE≌△DOA.所以OE=OA=5.所以E(-5, 0).也就是说,不论点C在直线AB上什么位置,点E 的位置都是确定的.(3)如图2,因为OC=OD,OE=OA,所以四边形ACED是平行四边形.所以AC//ED.如图3,又因为BF∥AD,所以四边形ABFD是平行四边形.如果四边形ABFD是矩形,那么∠CAD=90°.所以AO是Rt△ACD斜边上的中线,所以OA=OC=OD=5.设C(m,-3m+15),那么OC2=m2+(-3m+15)2=52.整理,得m2-9m+20=0.解得m1=4,或m2=5(此时点C与点A重合,舍去).所以点C的坐标为(4, 3).图2 图3例2020年上海市奉贤区初二下学期期末第26题如图1,四边形ABCD中,AD∥BC,∠A=90°,AD=4,DC=5,过点C作CE∥BD 交AD延长线于点E,联结BE交CD于点F.(1)当AB=AD时,求BC的长;(2)设BC=x,四边形BCED的面积为y,求y关于x的函数关系式,并写出定义域;(3)当△BDF为直角三角形时,求BC的长.图1动感体验打开几何画板文件名“20奉贤26”,拖动点C运动,可以体验到,点C的运动轨迹是以点D为圆心,半径为5的圆,四边形BCED始终保持平行四边形的形状不变.点击按钮“∠DFB=90°”,可以体验到,四边形BCED是菱形.点击按钮“∠BDF=90°”,可以体验到,△BDC 是直角三角形.满分解答(1)如图2,作DH⊥BC于H,得到矩形ABHC和直角三角形DHC.在Rt△DHC中,DH=AB=AD=4,DC=5,所以HC=3.所以BC=BH+HC=AD+HC=4+3=7.(2)如图2,在Rt△DHC中,DC=5,HC=BC-BH=x-4.由勾股定理,得DH2=DC2-HC2=52-(x-4)2.整理,得DH=289-++x x.如图3,因为AE∥BC,CE∥BD,所以四边形BCED是平行四边形.所以y=S四边形BCED=BC∙DH=289-++x x x.定义域是0<x<9.当点C落在AD的延长线上时,A、B两点重合,此时x=BC=AD+DC=4+5=9.图2 图3(3)分两种情况讨论直角三角形BDF.①如图4,当∠BFD=90°时,BE垂直DC.所以四边形BCED是菱形.所以BD=BC=x.在Rt△DBH中,DH2=DB2-BH2=x2-42.在Rt△DCH中,DH2=DC2-CH2=52-(x-4)2.所以x2-42=52-(x-4)2.整理,得2x2-8x-25=0.解得1466+=x,或2466-=x(舍去).所以BC 466+.②如图5,当∠BDC=90°时,△BDC也是直角三角形.在Rt△DBH中,DB2=DH2+BH2=52-(x-4)2+42.在Rt△BDC中,由勾股定理,得BC2=DB2+DC2.所以x2=52-(x-4)2+42+52.整理,得x2-4x-25=0.解得1229 =+x,或2229 =-x(舍去).所以BC=229+.图4 图5例2020年上海市虹口区初二下学期期末第24题如图1,一次函数y=2x+4的图像与x、y轴分别相交于点A、B,以AB为边作正方形ABCD,点C、D在直线AB的下方.(1)求点A、B、C的坐标;(2)求直线CD的表达式;(3)设直线CD与x轴交于点E,点F为直角坐标平面xOy内一点,当四边形AECF 为等腰梯形时,请直接写出所有符合条件的点F的坐标.图1动感体验打开几何画板文件名“20虹口24”,可以体验到,四个直角三角形都全等,正方形ABCD 的外接矩形MNPQ也是正方形.点击屏幕左下方的按钮“第(3)题”,可以体验到,以A、E、C、F为顶点的四边形为等腰梯形存在三种情况.满分解答(1)由y=2x+4,得A(-2, 0),B(0, 4).如图2,构造正方形ABCD的外接正方形MNPQ.因为∠1+∠2=90°,∠2+∠3=90°,所以∠1=∠3.又因为∠M=∠N=90°,AB=BC,所以△ABM≌△BCN.所以CN=BM=OA=2,BN=AM=OB=4.所以C(4, 2).(2)因为CD//AB,设直线CD的表达式为y=2x+b.代入点C(4, 2),得8+b=2.解得b=-6.图2所以直线CD的表达式为y=2x-6.(3)由y=2x-6,得E(3, 0).分两种情况讨论四边形AECF为等腰梯形.①如图3,当FC//AE时,设等腰梯形的对称轴与x轴交于点H,与FC交于点G.由A(-2, 0)、E(3, 0),得对称轴GH为直线x=12.所以点C(4, 2)关于直线x=12的对称点F的坐标为(-3, 2).②如图4,当AF//CE时,点F在直线AB上.设F(m, 2m+4 ).根据FC2=AE2列方程,得(m-4)2+(2m+4-2)2=52.解得m1=1,或m2=-1(此时四边形AECF为平行四边形,舍去).所以F(1, 6).图3 图4 图5拓展延伸第(3)题,问题若改为以A、E、C、F为顶点的四边形为等腰梯形,则还有一种情况.如图5,EF//AC.由A(-2, 0)、C(4, 2),得直线AC的表达式为1233=+y x.设直线EF的解析式为13=+y x b,代入E(3, 0),得1+b=0.解得b=-1.所以直线EF的解析式为113=-y x.设F(n,113-n).根据AF2=CE2列方程,得(n+2)2+(113-n)2=12+22.整理,得2101093+=n n.解得n1=0,或n2=-3(此时四边形AECF为平行四边形,舍去).所以F(0,-1).例2020年上海市虹口区初二下学期期末第25题如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=4,点D是射线CB上一点(点D与点C不重合),以AD为边作等边△ADE,且点E与点C在直线AD的异侧,过点E作EF⊥AB于点F.(1)求证:△ACD≌△AFE;(2)联结BE,设CD=x,BE=y,当点D在线段CB上时,求y关于x的函数关系式,并写出定义域;(3)当△ADB为等腰三角形时,求△ADB的面积.图1 备用图动感体验打开几何画板文件名“20虹口25”,拖动点D在CB上运动,可以体验到,△ACD与△AFE 始终保持全等.点击屏幕左下方按钮“第(3)题”,拖动点D在射线CB上运动,可以体验到,△ADB是等腰三角形存在两种情况.满分解答(1)如图2,在Rt△ABC中,∠ABC=30°,AB=4,所以AC=2,∠BAC=60°.因为△ADE是等边三角形,所以AD=AE,∠DAE=60°.所以∠BAC=∠DAE.所以∠BAC-∠DAF=∠DAE-∠DAF,即∠1=∠2.又因为EF⊥AB,所以∠AFE=∠C=90°.所以△ACD≌△AFE(AAS).图2(2)如图2,由△ACD≌△AFE,得AF=AC=2,FE=CD=x.所以FB=AB-AF=4-2=2.在Rt△BEF中,由勾股定理,得BE2=FE2+FB2.所以y2=x2+22.整理,得24y x.=+定义域是0<x≤23.(3)分两种情况讨论等腰三角形ADB.①如图3,当点D在线段CB上时,∠ADB是钝角,只存在DA=DB的情况,所以∠3=∠B=30°.因此∠1=30°.在Rt△ACD中,AC=2,设CD=m,那么AD=2m.由勾股定理,得m2+22=(2m)2.解得m=23±(舍去负值).所以BD=CB-CD=2323-=43.此时S△ADB=12⋅BD AC=43.②如图4,当点D在线段CB的延长线上时,∠ABD是钝角,只存在BA=BD=4的情况.此时S△ADB=12⋅BD AC=4.图3 图4。
中考数学专题:反比例函数与三角形(难题)(题目含详细答案)

《反比例函数—三角形》难度题【典型例题1】如图,已知点A 是双曲线y =x4在第一象限的分支上的一个动点,连结AO 并延长交另一分支于点B ,以AB 为边作等边△ABC ,点C 在第四象限.随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线xky =(k <0)上运动,则k 的值是 ﹣12 .【类型训练1】(2016眉山)如图,已知点A 是双曲线6y x=在第三象限分支上的一个动点,连结AO 并延长交另一分支于点B ,以AB 为边作等边三角形ABC ,点C 在第四象限内,且随着点A 的运动,点C 的位置也在不断变化,但点C 始终在双曲线ky x=上运动,则k 的值是 。
解:∵双曲线6y =∴点A 与点B 关于原点对称.∴OA =OB .连接OC ,如图所示.∵△ABC 是等边三角形,OA =OB ,∴OC ⊥AB .∠BAC =60°.∴3OCtan OAC OA∠==.∴,3OC OA =,过点A 作AE ⊥y 轴,垂足为E ,过点C 作CF ⊥y 轴,垂足为F ,∵AE ⊥OE ,CF ⊥OF ,OC ⊥OA ,∴∠AEO =∠OFC ,∠AOE =90°-∠FOC =∠OCF .∴△OFC ∽△AEO .相似比3OCOA=,∴面积比3OFC AEOS S = .∵点A 在第一象限,设点A 坐标为 (a ,b ),∵点A 在双曲线6y x =上,∴S △AEO =12ab =62,∴S △OFC =12FC OF ⋅= 362.∴设点C 坐标为(x ,y ),∵点C 在双曲线ky x =上,∴k =xy ∵点C 在第四象限,∴FC =x ,OF =-y .∴FC•OF =x•(-y )=-xy =-36 6.∴xy =-36..故答案为:-36.【类型训练2】如图,已知点A 是双曲线xy 4=在第一象限的分支上的一个动点,连结AO 并延长交另一分支于点B ,以AB 为斜边作等腰直角△ABC ,点C 在第四象限.随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线xky =(k <0)上运动,则k 的值是 ﹣4 .【解答】解:连接OC ,过点A 作AE ⊥y 轴于点E ,过点C 作CF ⊥x 轴于点F ,如图所示.∵线段AB 过原点O ,且反比例函数图象关于原点对称,∴点O 为线段AB 的中点. ∵△ACB 为等腰直角三角形,∴OC ⊥AB ,OC=OA .∵∠AOE+∠AOF=90°,∠COF+∠AOF=90°,∴∠AOE=∠COF .在△AOE 和△COF 中,有,∴△AOE ≌△COF ,∴S △AOE =S △COF .∵点A 在反比例函数x y 4=的图象上,点C 在反比例函数xky =的图象上, ∴有×4=|k|,解得:k =±4.∴点C 在第四象限,∴k =﹣4.【典型例题2】如图,等腰直角三角形OAB 和BCD 的底边OB 、BD 都在x 轴上,直角顶点A 、C 都在反比例函数y =kx图象上,若D (-8,0),则k =___8-_______.【方法】利用特殊形的角度、长度与坐标的关系,巧设坐标,联立方程求值 A (-a , a ),C (-4-a , 4-a ) 82-=-=a k【类型题训练2】如图,等边三角形OAB 和BCD 的底边OB 、BD 都在x 轴上,直角顶点A 、C 都在反比例函数y =kx图象上,若D (-12,0),则k =__________.【典型例题3】如图,Rt △AOB 中,O 为坐标原点,∠AOB =90°,∠B =30°,如果点A 在反比例函数xy 1=(x >0)的图象上运动,那么点B 在函数xy 3-=(填函数解析式)的图象上运动.x【方法】A 、B 两点分别向y 轴作垂线段,利用相似直角三角形的比例关系,用A 点坐标表示B 点坐标 设A )1,(00x x , B (x ,y ),得:B )3,3(00x x -【类型题练习3A 】如图,Rt △ABO 中,∠AOB =90°,点A 在第一象限、点B 在第四象限,且AO :BO =1:2,若点A ),(00y x 的坐标0x 、0y 满足001x y =,则点B (x ,y )的坐标x ,y 所满足的关系式为 xy 2-=【类型题练习3B 】已知点A ,B 分别在反比例函数x y 2=(x >0),xy 8-=(x >0)的图象上且OA ⊥OB ,则tanB 为21AOBxyAOBxy【解】相似比【典型例题4】如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 9【解】∵点D 为△OAB 斜边OA 的中点,且点A 的坐标(﹣6,4), ∴点D 的坐标为(﹣3,2), 把(﹣3,2)代入双曲线)0(<=k xky ,可得k =﹣6,即双曲线解析式为x y 6-=,∵AB ⊥OB ,且点A 的坐标(﹣6,4), ∴C 点的横坐标为﹣6,代入解析式xy 6-=,y=1, 即点C 坐标为(﹣6,1),∴AC=3,又∵OB=6,∴S △AOC =×AC×OB = 9. 故答案为:9.【类型题训练4A 】如图,已知双曲线)0(>k xky =经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =_____2_____A BOxy DCABOx y DC【方法】设D ),(a k a , 则B )2,2(a k a , C )2,2(ak a【类型题训练4B 】(2014•孝感)如图,Rt △AOB 的一条直角边OB 在x 轴上,双曲线x ky(x >0)经过斜边OA 的中点C ,与另一直角边交于点D .若S △OCD =9,则S △OBD 的值为 6 .【类型题训练4C 】如图,等腰直角三角形ABC 顶点A ,C 在x 轴上,∠BCA =90°,AC =BC =22,反比例函数y =x3(x >0)的图象分别与AB ,BC 交于点D ,E .当△BDE ∽△BCA 时,点E 的坐标为 )2,223(【方法】设坐标;联立方程【类型题训练4D 】(2014•浙江湖州)如图,已知在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数xky =(k ≠0)在第一象限的图象经过OA 的中点B ,交AC 于点D ,连接OD .若△OCD ∽△ACO ,则直线OA 的解析式为解:设OC =a ,∵点D 在xky =上,∴CD =, ∵△OCD ∽△ACO ,∴=,∴AC ==,∴点A (a ,),∵点B 是OA 的中点,∴点B 的坐标为(,),∵点B 在反比例函数图象上,∴=,解得,a 2=2k ,∴点B 的坐标为(,a ),设直线OA 的解析式为y =mx ,则m •=a ,解得m =2,所以,直线OA 的解析式为y =2x . 故答案为:y =2x【类型题训练4E 】如图,Rt △AOC 的直角边OC 在x 轴上,∠ACO=90o ,反比例函数xky =经过另一条直角边AC 的中点D ,3=∆AOC S ,则k = 3【典型例题5】如图,A 、B 是双曲线)0(>=k xky 上的点, A 、B 两点的横坐标分别是a 、2a ,线段AB 的延长线交x 轴于点C ,若S △AOC = 6.则k= 4【方法】向坐标轴作垂线段,将坐标与长度、角度建立等量关系 C(3a , 0)【类型题训练5A 】(2014•重庆)如图,反比例函数xy 6-=在第二象限的图象上有两点A 、B ,它们的横坐标分别为﹣1,﹣3,直线AB 与x 轴交于点C ,则△AOC 的面积为( )A .8B .10C .12D .24【类型题训练5B 】yxOBCA如图,点A 、B 在反比例函数(0,0)ky k x x=>>的图像上,过点A 、B 作x 轴的垂线,垂足分别为M 、N ,延长线段AB 交x 轴于点C ,若OM MN NC ==,AOC ∆的面积为6,则k 的值为 4.【类型题训练5C 】如图,点A 、B 在反比例函数y = kx的图象上,且点A 、B 的横坐标分别为a 、2a (a <0),若S △AOB=3,则k 的值为____-4____.【方法】等面积法设A(a , 2b ), B(2a, b ) 梯形AFEB 面积为3 4-=∴k】如图,若双曲线y =kx与边长为5的等边△AOB 的边OA ,AB 分别相交于C ,D 两点,且OC =3BD ,则实数k 的值为 .OABxyO AB xyEF 934【典型例题6】已知点A 是双曲线y =4x上一动点,且OA =4,OA 的垂直平分线交x 轴于点B ,过A 作AC ⊥x轴于点C ,则△ABC 的周长为________62________,∠ABC =____︒30_____【方法】设而不求,求比例;勾股定理;AB = 21AC【类型题训练6A 】如图,点A 在双曲线6y x=上,且OA =4,过A 作AC ⊥x 轴,垂足为C ,OA 的垂直平分线交OC 于B ,则△ABC 的周长为_______7OCA BxyM【变式训练1】如图,点P 1(x 1,y 1),点P 2(x 2,y 2),…,点P n (x n ,y n )在函数xy 1=(x >0)的图象上,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…,△P n A n ﹣1A n 都是等腰直角三角形,斜边OA 1、A 1A 2、A 2A 3,…,A n ﹣1A n 都在x 轴上(n 是大于或等于2的正整数),则点P 3的坐标是)23,23(-+ ;点P n 的坐标是 )1,1(---+n n n n (用含n 的式子表示).【变式训练2】如图,点P 是反比例函数y =x34 (x >0)图象上的动点, 在y 轴上取点Q ,使得以P ,O ,Q 为顶点的三角形是一个含有30°的直角三角形,则符合条件的点Q 的坐标是 (0,2), (0,8),(0,23),(0,338) . OC A B x yM【变式训练3】如图,点A (m ,6),B (n ,1)在反比例函数图象上,AD ⊥x 轴于点D ,BC ⊥x 轴于点C ,DC =5.线段DC 上有一点E ,当△ABE 的面积等于5时,点E 的坐标为 (5,0) .【解】由题意得:,解得:,∴A (1,6),B (6,1),设反比例函数解析式为xk y ,将A (1,6)代入得:k =6,则反比例解析式为y =; 设E (x ,0),则DE =x ﹣1,CE =6﹣x ,∵AD ⊥x 轴,BC ⊥x 轴,∴∠ADE =∠BCE =90°,连接AE ,BE ,则S △ABE =S 四边形ABCD ﹣S △ADE ﹣S △BCE=(BC +AD )•DC ﹣DE •AD ﹣CE •BC =×(1+6)×5﹣(x ﹣1)×6﹣(6﹣x )×1【变式训练4】如图,以原点O 为顶点的等腰直角三角形ABO 中,∠BAO =90°,反比例函数k y x = 过A 、B 两点,若点A 的横坐标为2,则k = 252- .【变式训练5】(2015•眉山)如图,A 、B 是双曲线xk y =上的两点,过A 点作AC ⊥x 轴,交OB 于D 点,垂足为C .若△ADO 的面积为1,D 为OB 的中点,则k 的值为【变式训练6】如图,已知点A 在反比例函数)0(<=x xk y 上,作RT ⊿ABC ,点D 为斜边AC 的中点,连DB 并延长交y 轴于点E ,若⊿BCE 的面积为8,则k = 16【解】由题意,12BCE S BC OE ==8【变式训练7】 (2010•长春)如图,平面直角坐标系中,OB 在x 轴上,∠ABO=90°,点A 的坐标为(1,2),将△AOB 绕点A 逆时针旋转90°,点O 的对应点C 恰好落在双曲线xk y =(x >0)上,则k 的值为 3解答:解:易得OB=1,AB=2,∴AD=2,∴点D 的坐标为(3,2),∴点C 的坐标为(3,1),∴k =3×1=3.【变式训练8】如图,△AOB 和△ACD 均为正三角形,顶点B 、D 在双曲线x y 4=(x >0)上,则S △OBP = 4 .【解】过A 作AF ⊥OB ,作P 作PG ⊥OB ,∵△OAB 与△ADC 都为等边三角形,∴∠BOA=∠DAC=60°,∴AD ∥OB ,∴AF=PG (平行线间的距离处处相等),∵OB 为△OBA 和△OBP 的底,∴OBAF=OBPG ,即S △OBP =S △OAB (同底等高的三角形 面积相等),过B 作BE ⊥x 轴,交x 轴于点E ,可得S △OBE =S △ABE =S △OBA ,∵顶点B 在双曲线y=(x >0)上,即k=4,∴S △OBE ===2,则S △OBP =S △OBA =2S △OBE =4,故答案为:4【变式训练9】如图,点A 是反比例函数xk y =的图象上的一点,过点A 作AB ⊥x 轴,垂足为B .点C 为y 轴上的一点,连接AC ,BC .若△ABC 的面积为3,则k 的值是 ﹣6【解】连结OA ,如图,∵AB ⊥x 轴,∴OC ∥AB ,∴S △OAB =S △C AB =3, 而S △OAB =|k|,∴|k|=3,∵k <0,∴k=﹣6.【变式训练10】 如图在反比例函数x y x y 32=-=和的图象上分别有A 、B 两点,若AB ∥x 轴且OA ⊥OB,则=OB OA 36 .【变式训练11】如图,A 、B 是函数xy 2=的图象上关于原点对称的任意两点,BC ∥x 轴,AC ∥y 轴, △ABC 的面积记为S ,则S= ( ).(A)S =2(B)S =4 (C)2<S <4 (D)S >4【变式训练12】如图,等腰直角△POA 的直角顶点P 在反比例函数xy 4=)0(>x 的图象上,A 点在x 轴正半轴上,则A 点坐标为 . 第15题O B A y x【变式训练13】如图,已知点A ,B 在双曲线)0(>=x xk y 上,AC ⊥x 轴于点C ,BD ⊥y 轴于点D ,AC 与BD 交于点P ,P 是AC 的中点,若△ABP 的面积为3,则k 的值为 .【变式训练14】如图,过点C (1,2)分别作x 轴、y 轴的平行线,交直线y=-x +6于A 、B 两点,若反比例函数k y x=(x >0)的图像与△ABC 有公共点,则k 的取值范围是( ) A .2≤k ≤9 B. 2≤k ≤8 C. 2≤k ≤5 D. 5≤k ≤8答案:A【变式训练15】如图,在平面直角坐标系xOy 中,直线x y 23=与双曲线xy 6=相交于A ,B 两点,C 是第一象限内双曲线上一点,连接CA 并延长交y 轴于点P ,连接BP ,BC .若△PBC 的面积是24,则点C 的坐标为 (6,1).【解答】设BC 交y 轴于D ,如图,设C 点坐标为(a ,) 解方程组得或,∴A 点坐标为(2,3),B 点坐标为(﹣2,﹣3),设直线BC 的解析式为y=kx+b ,把B (﹣2,﹣3)、C (a ,)代入得,解得,∴直线BC 的解析式为y=x+﹣3,当x=0时,y=x+﹣3=﹣3,∴D 点坐标为(0,﹣3)设直线AC 的解析式为y=mx+n ,把A (2,3)、C (a ,)代入得,解得,∴直线AC 的解析式为y=﹣x++3,当x=0时,y=﹣x++3=+3,∴P 点坐标为(0, +3)∴PD=(+3)﹣(﹣3)=6,∵S △PBC =S △PBD +S △CPD ,∴×2×6+×a×6=24,解得a=6,∴C 点坐标为(6,1).【变式训练16】 如图,在平面直角坐标系中,双曲线3y x =(x >0)上的一点C 过等边三角形OAB 三条高 的交点,则点B 的坐标为____________.答案: (3,3)【变式训练17】如图,A 、B 是双曲线xk y =上的两点,过A 点作AC ⊥x 轴,交OB 于D 点,垂足为C .若△ADO 的面积为1,D 为OB 的中点,则k 的值为【变式训练18】(2012武汉)如图,点A 在双曲线y =x k 的第一象限的那一支上,AB 垂直于x 轴与点B ,点C 在x 轴正半轴上,且OC =2AB ,点E 在线段AC 上,且AE =3EC ,点D 为OB 的中点,若△ADE 的面积为3,则k 的值为___316_____. 【方法】等面积法,设A (a , 2b ), 则C (2a ,0)4=∆ACD S ACD COD ABD ABCD S S S S ∆∆∆++=梯形【变式训练19】(2014山东济南)如图,OAC ∆和BAD ∆都是等腰直角三角形, 90=∠=∠ADB ACO ,反比例函数xk y =在第一象限的图象经过点B ,若1222=-AB OA ,则k 的值为________. 【变式训练20】(2013浙江省)如图,已知动点A 在函数4(0)y x x=>的图象上,AB x ⊥轴于点B ,AC y ⊥轴于点C ,延长CA 至点D ,使AD=AB ,延长BA 至点E ,使AE=AC 。
专题66 反比例函数中的动点最值问题(解析版)-中考数学解题大招复习讲义

例题精讲【例1】.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为________解:当x=0时,y=×0+4=4,∴点B的坐标为(0,4);当y=0时,x+4=0,解得:x=﹣6,∴点A的坐标为(﹣6,0).∵点C、D分别为线段AB、OB的中点,∴点C的坐标为(﹣3,2),点D坐标为(0,2).作点C关于x轴的对称点C′,连接C′D交x轴于点P,此时PC+PD的值最小,如图所示.∵点C的坐标为(﹣3,2),∴点C′的坐标为(﹣3,﹣2).设直线C′D的解析式为y=kx+b(k≠0),将C′(﹣3,﹣2),D(0,2)代入y=kx+b得:,解得:,∴直线C′D的解析式为y=x+2.当y=0时,x+2=0,解得:x=﹣,∴点P的坐标为(﹣,0),即点P的坐标为(﹣1.5,0).变式训练【变1-1】.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB 的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小解:设点P的坐标为(x,),∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,∴四边形OAPB是个直角梯形,∴四边形OAPB的面积=(PB+AO)•BO=(x+AO)•=+=+•,∵AO是定值,∴四边形OAPB的面积是个减函数,即点P的横坐标逐渐增大时四边形OAPB的面积逐渐减小.故选:C.【变1-2】.如图,一次函数y=2x与反比例函数y=(k>0)的图象交于A,B两点,点M在以C(2,0)为圆心,半径为1的⊙C上,N是AM的中点,已知ON长的最大值为,则k的值是.解:方法一、联立,∴,∴,∴A(),B(),∴A与B关于原点O对称,∴O是线段AB的中点,∵N是线段AM的中点,连接BM,则ON∥BM,且ON=,∵ON的最大值为,∴BM的最大值为3,∵M在⊙C上运动,∴当B,C,M三点共线时,BM最大,此时BC=BM﹣CM=2,∴(,∴k=0或,∵k>0,∴,方法二、设点B(a,2a),∵一次函数y=2x与反比例函数y=(k>0)的图象交于A,B两点,∴A与B关于原点O对称,∴O是线段AB的中点,∵N是线段AM的中点,连接BM,则ON∥BM,且ON=,∵ON的最大值为,∴BM的最大值为3,∵M在⊙C上运动,∴当B,C,M三点共线时,BM最大,此时BC=BM﹣CM=2,∴=2,∴a1=或a2=0(不合题意舍去),∴点B(,),∴k=,故答案为:.【例2】.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x 轴上,则PM+PN的最小值是2.解:∵正方形OABC 的边长是6,∴点M 的横坐标和点N 的纵坐标为6,∴M (6,),N (,6),∴BN =6﹣,BM =6﹣,∵△OMN 的面积为10,∴6×6﹣×6×﹣×6×﹣×(6﹣)2=10,∴k =24,∴M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,∵AM =AM ′=4,∴BM ′=10,BN =2,∴NM ′===2,故答案为2.变式训练【变2-1】.已知在平面直角坐标系中有两点A (0,1),B (﹣1,0),动点P 在反比例函数y =的图象上运动,当线段PA 与线段PB 之差的绝对值最大时,点P 的坐标为(1,2)或(﹣2,﹣1).解:如图,设直线AB的解析式为y=kx+b,将A(0,1)、B(﹣1,0)代入,得:,解得:,∴直线AB的解析式为y=x+1,直线AB与双曲线y=的交点即为所求点P,此时|PA﹣PB|=AB,即线段PA与线段PB 之差的绝对值取得最大值,由可得或,∴点P的坐标为(1,2)或(﹣2,﹣1),故答案为:(1,2)或(﹣2,﹣1).【变2-2】.如图,一次函数y1=mx+n(m≠0)的图象与双曲线y2=(k≠0)相交于A(﹣1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.(1)求双曲线的解析式;(2)经研究发现:在y轴负半轴上存在若干个点P,使得△CPB为等腰三角形.请直接写出P点所有可能的坐标.解:(1)∵点A(﹣1,2)在双曲线y2=(k≠0)上,∴k=﹣1×2=﹣2,∴反比例函数解析式为y2=﹣,(2)∵点B在双曲线y2=﹣上,∴2b=﹣2,∴b=﹣1,∴B(2,﹣1),将点A(﹣1,2),B(2,1)代入一次函数y1=mx+n(m≠0)中,得,∴,∴一次函数的解析式为y=﹣x+1;令x=0,则y=1,∴C(0,1),设P(0,p)(p<0),∵B(2,﹣1),∴BC==2,BP=,CP=1﹣p,∵△CPB为等腰三角形,∴①当BC=BP时,2=,∴p=1(舍)或p=﹣3,∴P(0,﹣3),②当BC=CP时,2=1﹣p,∴p=1﹣2,∴P(0,1﹣2),③当BP=CP时,=1﹣p,∴p=﹣1,∴P(0,﹣1),故满足条件的点P的坐标为(0,﹣3)或(0,1﹣2)或(0,﹣1).1.如图,点N是反比例函数y=(x>0)图象上的一个动点,过点N作MN∥x轴,交直线y=﹣2x+4于点M,则△OMN面积的最小值是()A.1B.2C.3D.4解:设点N的坐标为(,m),则点M的坐标为(2﹣m,m)(m>0),∴MN=﹣(2﹣m)=m+﹣2,=MN•m=m2﹣m+3=(m﹣2)2+2,∴S△OMN∴当m=2时,△OMN面积最小,最小值为2.故选:B.2.如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为()A.B.C.D.解:∵AB=AC=a,∠BAC=18°,∴∠ABC=∠ACB=(180°﹣18°)=81°,∴∠ABC=∠APB+∠PAB=81°,∵∠PAQ=99°,∠BAC=18°,∴∠PAB+∠QAC=99°﹣18°=81°,∴∠APB=∠QAC,同理可得∠PAB=∠AQC,∴△APB∽△QAC,∴=,即=,整理得,y=,∵x、y都是边的长度,是正数,∴y与x之间的函数关系用图象表示是反比例函数在第一象限内的部分,纵观各选项,只有A符合.故选:A.3.如图,已知A、B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM ⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为()A.B.C.D.解:①点P在AB上运动时,此时四边形OMPN的面积S=K,保持不变,故排除B、D;②点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为a,则S=OC×CP=OC×(l﹣at),因为l,OC,a均是常数,所以S与t成一次函数关系.故排除C.故选:A.4.已知点A是双曲线y=在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边△ABC.随着点A的运动,点C的位置也不断变化,但始终在一个函数的图象上运动,则这个函数的表达式为y=﹣.解:设A(a,),∵点A与点B关于原点对称,∴OA=OB,∵△ABC为等边三角形,∴AB⊥OC,OC=AO,∵AO=,∴CO=,过点C作CD⊥x轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即=,解得:y=﹣a2x,在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+,将y=﹣a2x代入,(a4+1)x2=3×可得:x2=,故x=,y=﹣a2x=﹣a,则xy=﹣3,故可得:y=﹣(x>0).故答案为:y=﹣(x>0).5.如图,点P是双曲线C:y=(x>0)上的一点,过点P作x轴的垂线交直线AB:y=x﹣2于点Q,连接OP,OQ.当点P在曲线C上运动,且点P在Q的上方时,△POQ面积的最大值是3.解:∵PQ⊥x轴,∴设P(x,),则Q(x,x﹣2),∴PQ=﹣x+2,=(﹣+2)•x=﹣(x﹣2)2+3,∴S△POQ∵﹣<0,∴△POQ面积有最大值,最大值是3,故答案为3.6.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,则点P到直线AB距离最短时的坐标为(,).解:(1)设直线AB的解析式为y=ax+b,将点A(1,0),点B(0,2)代入得,解得,∴直线AB为y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=OB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,∴﹣2x2+hx﹣3=0,当△=h2﹣24=0时,h=2或﹣2(舍弃),此时点P到直线AB距离最短,解方程﹣2x2+2x﹣3=0得x==,∴P(,),故答案为P(,).7.如图,在平面直角坐标系中,点A,B在反比例函数y=(k≠0)的图象上运动,且始终保持线段AB=4的长度不变.M为线段AB的中点,连接OM.则线段OM长度的最小值是(用含k的代数式表示).解:如图,因为反比例函数关于直线y=x对称,观察图象可知:当线段AB与直线y=x 垂直时,垂足为M,此时AM=BM,OM的值最小,∵M为线段AB的中点,∴OA=OB,∵点A,B在反比例函数y=(k≠0)的图象上,∴点A与点B关于直线y=x对称,∵AB=4,∴可以假设A(m,),则B(m+4,﹣4),∴(m+4)(﹣4)=k,整理得k=m2+4m,∴A(m,m+4),B(m+4,m),∴M(m+2,m+2),∴OM===,∴OM的最小值为.故答案为.8.如图,点A是反比例函数y=在第一象限的图象上的一点,过点A作AB⊥y轴于点B.连接AO,以点A为圆心,分别以AB,AO为半径作直角扇形BAC和OAD,并连接CD,则阴影部分面积的最小值是2π+2.解:如图,过点D作DE垂直于CA的延长线于点E,则∠AED=90°,由题意可知,AB=AC,AO=AD,∠BAC=∠DAO=90°,∵AB⊥y轴,∴∠ABO=90°,∴∠BAO+∠OAE=90°,∠DAE+∠OAE=90°,∴∠BAO=∠DAE,∴△BAO≌△EAD(AAS),∴DE=OB.∵点A是反比例函数y=在第一象限的图象上的一点,∴OB•AB=4,∴S△AOB=OB•AB=2,∴S△ACD=AC•DE=OB•AB=2,∴S阴影=S△ACD+S扇形OAD=2+=2+∵(AB﹣OB)2≥0,∴AB2﹣2AB•OB+OB2≥0,∴AB2+OB2≥2AB•OB,∴S阴影≥2+×2AB•OB=2+2π.故答案为:2+2π.9.如图,点A是反比例函数y=(k>0)图象第一象限上一点,过点A作AB⊥x轴于B 点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连接CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,连接BC,△ACB是等腰直角三角形,则若S1﹣S2的值最大为1,则k的值为4+4.解:如图连接BC、O′C,作CH⊥x轴于H.由题意⊙O′与反比例函数图象均关于直线y=x对称,∴点A、C关于直线y=x对称,设A(m,2m)则C(2m,m),∴BO′=CH=m,BO′∥CH,∴四边形BHCO′是平行四边形,∵BH=CH,∠BHC=90°,∴四边形BHCO′是正方形.∴∠ABC=45°,∴△ACB是等腰直角三角形,∵S1﹣S2=S△DBC﹣S△ACB,△ABC的面积是定值,∴△DBC的面积最大时,S1﹣S2的值最大,∴当DO′⊥BC时,△DBC的面积最大,∴m•(m+m)﹣•2m•m=1,∴m2=2(+1),∵k=2m2,∴k=4+4,故答案为:等腰直角三角形,4+4.10.如图,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P的坐标.解:(1)设A点的坐标为(a,b),则由,得ab=2=k,∴反比例函数的解析式为;(2)由条件知:两函数的交点为,解得:,,∴A点坐标为:(2,1),作出A点关于x轴对称点C点,连接BC,P点即是所求则点C(2,﹣1),∵B(1,2),设直线BC的解析式为:y=kx b,解得:,∴直线BC的解析式为:y=﹣3x+5,当y=0时,x=,∴点P(,0).11.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若△ABC面积为2.(1)求k的值(2)x轴上是否存在一点D,使△ABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由.解:(1)∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=2÷2=1,又∵A是反比例函数y=图象上的点,且AC⊥x轴于点C,∴△AOC的面积=|k|,∴|k|=1,∵k>0,∴k=2.故这个反比例函数的解析式为y=;(2)x轴上存在一点D,使△ABD为直角三角形.将y=2x与y=联立成方程组得:,解得:,,∴A(1,2),B(﹣1,﹣2),∵△ABD是以AB为斜边的直角三角形∴∠ADB=90°,如图3,∵O为线段AB的中点,∴OD=AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA==,∴OD=,∴D(,0).根据对称性,当D为直角顶点,且D在x轴负半轴时,D(﹣,0).故x轴上存在一点D,使△ABD以AB为斜边的直角三角形,点D的坐标为(,0)或(﹣,0).12.如图,一次函数y=x+2的图象与反比例函数y=的图象交于点A(1,a),B两点.(1)求反比例函数的解析式及点B的坐标;(2)在x轴上找一点C,使|CA﹣CB|的值最大,求满足条件的点C的坐标及△ABC的面积.解:(1)∵直线y=x+2经过点A(1,a),∴a=3,∵反比例函数y=经过A(1,3),∴k=3,∴y=,由,解得或,∴B(﹣3,﹣1).(2)作点B关于x轴的对称点B′,连接AB′,延长AB′交x轴于点C,点C即为所求;∵A(1,3),B′(﹣3,1),∴直线AB′的解析式为y=x+,∴C(﹣5,0),=S△CBB′+S△BB′A=×2×2+×2×4=6.∴S△ABC13.如图,一次函数y=2x﹣3的图象与反比例函数y=的图象相交于点A(﹣1,n),B 两点.(1)求反比例函数的解析式与点B的坐标;(2)连接AO、BO,求△AOB的面积;(3)点D是反比例函数图象上的一点,当∠BAD=90°时,求点D的坐标.解:(1)∵点A(﹣1,n)在一次函数y=2x﹣3的图象上,∴n=﹣5,∴点A(﹣1,﹣5),∵点A(﹣1,﹣5)在反比例函数的图象上,∴k=﹣1×(﹣5)=5,∴;联立,解得:,,∴点;(2)设y=2x﹣3与y轴的交点为点E,则点E(0,﹣3),∴OE=3,=S△AOE+S△BOE=×3×1+×3×=;∴S△AOB(3)设点,如图,分别过点D,B作y轴的平行线DM,BN,过点A作MN⊥DM于M,交BN于N,则MN⊥BN,∴∠M=∠N=90°,∴∠DAM+∠ADM=90°,∵∠BAD=90°,∴∠BAN+∠DAM=90°,∴∠BAN=∠ADM,∴△BAN∽△ADM,∴=,即=,解得:a1=﹣10,a2=﹣1(舍),∴.14.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).(1)求反比例函数的解析式;(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴在直线y=2x+3中,当x=1时,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,∴反比例函数的解析式为:y=;(2)将点D(a,1)代入y=,得:a=5,∴点D坐标为(5,1)设点D(5,1)关于x轴的对称点为D′(5,﹣1),过点B(1,5)、点D′(5,﹣1)的直线解析式为:y=kx+b,可得:,解得:,∴直线BD′的解析式为:y=﹣x+,根据题意知,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣x+=0,解得:x=,故点P的坐标为(,0).15.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<的解集.(3)当k为何值时,△AEF的面积最大,最大面积是多少?解:(1)∵四边形OABC为矩形,OA=3,OC=2,∴AB=2,BC=3,∵F为AB的中点,∴点F坐标为(3,1),∵点F在反比例函数y=(x>0)的图象上,∴k=3×1=3,∴反比例函数解析式为y=,∵点E在BC上,∴E点纵坐标为2,在y=中,令y=2,可求x=,∴E点坐标为(,2);(2)不等式ax+b<的解集即直线在反比例函数下方时对应的自变量的取值范围,由(1)可知点E、F两点的横坐标分别为、3,∴不等式ax+b<的解集为:0<x<或x>3;(3)由题意可知点E的纵坐标为为2,点F的横坐标为3,且E、F在反比例函数y=(x>0)的图象上,∴可设E(,2),F(3,),∴AF=,CE=,∴BE=BC﹣CE=3﹣,=AF•BE=••(3﹣)=﹣k2+=﹣(k﹣3)2+,∴S△AEF∵﹣<0,是关于k的开口向下的抛物线,∴S△AEF有最大值,最大值为,∴当k=3时,S△AEF即当k的值为3时,△AEF的面积最大,最大面积为.16.如图,直线OA:y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.解:(1)设点A的坐标为(a,b),则,解得:k=2.∴反比例函数的解析式为y=.(2)联立直线OA和反比例函数解析式得:,解得:.∴点A的坐标为(2,1).设A点关于x轴的对称点为C,则C点的坐标为(2,﹣1),连接BC较x轴于点P,点P即为所求.如图所示.设直线BC的解析式为y=mx+n,由题意可得:B点的坐标为(1,2),∴,解得:.∴BC的解析式为y=﹣3x+5.当y=0时,0=﹣3x+5,解得:x=.∴P点的坐标为(,0).17.已知:如图,一次函数y=﹣2x+10的图象与反比例函数y=的图象相交于A、B两点(A在B的右侧),点A横坐标为4.(1)求反比例函数解析式及点B的坐标;(2)观察图象,直接写出关于x的不等式﹣2x+10﹣>0的解集;(3)反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)把x=4代入y=﹣2x+10得y=2,∴A(4,2),把A(4,2)代入y=,得k=4×2=8.∴反比例函数的解析式为y=,解方程组,得,或,∴点B的坐标为(1,8);(2)观察图象得,关于x的不等式﹣2x+10﹣>0的解集为:1<x<4或x<0;(3)存在,理由:①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=﹣2x+10,当y=0时,﹣2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5﹣4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴,即,∴MH=4,∴M(0,0),可设直线AP的解析式为y=mx,则有4m=2,解得m=,∴直线AP的解析式为y=x,解方程组,得,,∴点P的坐标为(﹣4,﹣2).②若∠ABP=90°,同理可得:点P的坐标为(﹣16,﹣).综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,﹣).18.反比例函数(k为常数.且k≠0)的图象经过点A(1,3),B(3,m).(1)求反比例函数的解析式及B点的坐标;(2)在x轴上找一点P,使PA+PB的值最小,①求满足条件的点P的坐标;②求△PAB的面积.解:(1)把A(1,3)代入y=得,k=3,∴反比例函数的关系式为:y=;把B(3,m)代入y=得,m=1,∴点B的坐标为(3,1);(2)①如图所示,作点B关于x轴的对称点B′,则B′(3,﹣1),连接AB′交x轴于点P,此时PA+PB最小.设直线AB′的关系式为y=kx+b,把A(1,3),B′(3,﹣1)代入得,,解得,,∴直线AB′的关系式为y=﹣2x+5,当y=0时,x=,即:P(,0),也就是,OP=,②S△P AB=S梯形ABNM﹣S△AMP﹣S△BPN=(1+3)×2﹣(﹣1)×3﹣(3﹣)×1=.19.如图,一次函数y=﹣x+4的图象与反比例y=(k为常数,且k≠0)的图象交于A (1,a),B两点.(1)求反比例函数的表达式及点B的坐标;(2)①在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;②在x轴上找一点M,使|MA﹣MB|的值为最大,直接写出M点的坐标.解:(1)把点A(1,a)代入一次函数y=﹣x+4,得a=3,∴A(1,3),把点A(1,3)代入反比例y=,得k=3,∴反比例函数的表达式y=,解得或,故B(3,1).(2)作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小∴D(3,﹣1)设直线AD的解析式为y=mx+n,则,解得,∴直线AD的解析式为y=﹣2x+5,令y=0,则x=,∴P点坐标为(,0);(3)直线y=﹣x+4与x轴的交点即为M点,此时|MA﹣MB|的值为最大,令y=0,则x=4,∴M点的坐标为(4,0).20.如图,四边形ABCD是正方形,点A的坐标是(0,1),点B的坐标是(0,﹣2),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过A、C两点,两函数图象的另一个交点E的坐标是(m,3).(1)分别求出一次函数与反比例函数的解析式.(2)求出m的值,并根据图象回答:当x为何值时,一次函数的值大于反比例函数的值.(3)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求点P坐标.解:(1)∵点A的坐标为(0,1),点B的坐标为(0,﹣2),∴AB=1+2=3,∵四边形ABCD为正方形,∴BC=AB=3,∴C(3,﹣2),把C(3,﹣2)代入y=,得k=3×(﹣2)=﹣6,∴反比例函数解析式为y=﹣;把C(3,﹣2),A(0,1)代入y=ax+b,得,解得,∴一次函数解析式为y=﹣x+1;(2)∵反比例函数y=﹣的图象过点E(m,3),∴m=﹣2,∴E点的坐标为(﹣2,3);由图象可知,当x<﹣2或0<x<3时,一次函数落在反比例函数图象上方,即当x<﹣2或0<x<3时,一次函数的值大于反比例函数的值;(3)设P(t,﹣),∵△AOP的面积恰好等于正方形ABCD的面积,∴×1×|t|=3×3,解得t=18或t=﹣18,∴P点坐标为(18,﹣)或(﹣18,).21.如图,点A是反比例函数y=(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连接AB、BC、CD、DA.设点A的横坐标为m.(1)求点D的坐标(用含有m的代数式表示);(2)判断四边形ABCD的形状,并说明理由;(3)当m为何值时,四边形ABCD是正方形?并求出此时AD所在直线的解析式.解:(1)∵点A的横坐标为m,∴点A的纵坐标为,∵E是AC的中点,AC⊥x轴,∴E(m,),∵BD⊥AC,AC⊥x轴,∴BD∥x轴,∴点B,E,D的纵坐标相等,为,∴点D的横坐标为2m,∴D(2m,);(2)四边形ABCD是菱形,∵B(0,),E(m,),D(2m,),∴EB=ED=m,∵AE=EC,∴四边形ABCD是平行四边形,∵BD⊥AC,∴平行四边形ABCD是菱形;(3)∵平行四边形ABCD是菱形,∴当AC=BD时,四边形ABCD是正方形,∴2m=,∴m=2,或m=﹣2(舍),∴A(2,4),D(4,2),设直线AD的解析式为y=kx+b,∴,∴,∴直线AD解析式为y=﹣x+6,∴当m=2时,四边形ABCD是正方形,此时直线AD解析式为y=﹣x+6.22.如图,一次函数y=﹣x+2的图象与两坐标轴分别交于A,B两点,与反比例函数y=交于点C、D,且点C坐标为(﹣2,m).(1)求反比例函数的解析式;(2)若点M在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,求点M的坐标.(3)点P在第二象限的反比例函数图象上,若tan∠OCP=3,求点P的坐标.解:(1)∵点C(﹣2,m)在一次函数y=﹣x+2的图象上,∴m=﹣(﹣2)+2,解得:m=4,∴C(﹣2,4),将C(﹣2,4)代入y=,得k=﹣8,∴反比例函数为y=﹣;(2)如图1,过点C作CH⊥y轴于H,在直线y=﹣x+2中,当x=0时,则y=2,∴B(0,2),由(1)知,C(﹣2,4),∴BC==2,当BM=BC=2时,OM=2+2,∴M(0,2+2),当BC=MC时,点C在BM的垂直平分线,∴M(0,6),综上所述,点M的坐标为(0,2+2)或(0,6)(3)作OQ⊥PC于Q,过Q作HG⊥x轴于G,CH∥x轴,交HG于H,则△CHQ∽△QGO,∴,∵tan∠OCP=3,∴,设CH=x,则GQ=3x,HQ=4﹣3x,∴OG=3HQ=12﹣9x=x+2,解得x=1,∴Q(﹣3,3),∴直线CQ的解析式为y=x+6,∴x+6=﹣,解得x1=﹣2,x2=﹣4,∵点P与C不重合,∴P(﹣4,2).。
反比例函数动点问题训练
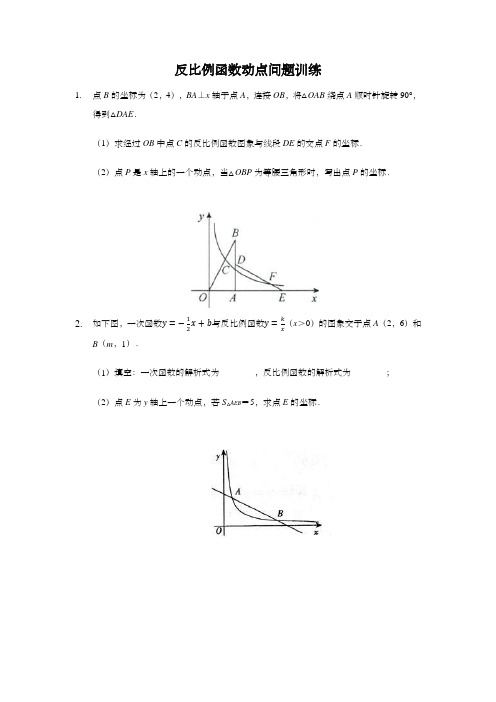
反比例函数动点问题训练1.点B的坐标为(2,4),BA⊥x轴于点A,连接OB,将△OAB绕点A顺时针旋转90°,得到△DAE.(1)求经过OB中点C的反比例函数图象与线段DE的交点F的坐标.(2)点P是x轴上的一个动点,当△OBP为等腰三角形时,写出点P的坐标.2.如下图,一次函数y=−12x+b与反比例函数y=kx(x>0)的图象交于点A(2,6)和B(m,1).(1)填空:一次函数的解析式为________,反比例函数的解析式为________;(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.第2页,共10页3. 如图,直线y =12x +2与x 轴交于点A ,与反比例函数y =kx (x >0)的图象交于点B ,BC⊥x 轴于C 点,且S △ABC =9. (1)求反比例函数的解析式;(2)若点P 是反比例函数图象上的一动点,且位于直线BC 的右侧,过P 点作y 轴的平行线,交直线AB 于点M ,交x 轴于点N .①若BC MN =35,在直线y =12x +2上有一点Q ,在x 轴上有一点D ,使得△DPQ 周长最小,请求出Q 点坐标以及此时△DPQ 的周长;②是否存在这样的P 点,使得△BPM 为PM 为底边的等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.4. 如图,在平面直角坐标系中,O 为坐标原点,△ABO 的边AB 垂直x 轴于点B ,反比例函数y =kx (x >0)的图象经过AO 的中点C ,与边AB 相交于点D ,若D 的坐标为(4,m ),AD =3.(1)求反比例函数y =kx 的解析式;(2)经过C 、D 两点的直线的解析式是______;(3)设点E 是线段CD 上的动点,过点E 且平行y 轴的直线与反比例函数的图象交于点F ,则△OEF 面积的最大值是______.5.如图,双曲线y=kx (x>0)与直线y=−12x+b相交于A(2,m),B(6,n)两点.(1)直接写出:关于x的不等式12x+kx>b的解集是________,k=________,b=________;(2)把点A绕平面内的某一点M顺时针旋转90°,恰好与点B重合,已知点M关于点A的对称点为M′,求证:点M′在双曲线y=kx上;(3)如图,点P是双曲线y=kx(x>0)上的一个动点,PE⊥y轴于点E,过点P的直线l:y=k1x+b1交x轴的正半轴于点F,当点P向右运动时,四边形OEPF的面积S 如何变化?给出你的结论并说明理由.6.如图,一次函数y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,2),与双曲线y=k交第二象限于点C,点C的横坐标为−2.x的解析式;(1)求一次函数y=ax+b和反比例函数y=kx(2)点D为反比例函数y=k第四象限图象上一个动点,DE⊥y轴于点E,连接AE,xOD,当▵ABE的面积是▵OED面积的4倍时,求点D的坐标.第4页,共10页7.如图,在平面直角坐标系中,已知RtΔABC中,∠C=90°,AC=4,BC=3,点A(6,5),B(2,8),反比例函数y=k(x>0)过点C,过点A作AD // y轴交双曲线于点D.x的表达式;(1)求反比例函数y=kx(2)动点P在y轴正半轴运动,当线段PC与线段PD的差最大时,求P点的坐标;(3)将RtΔABC沿直线CO方向平移,使点C移动到点O,求线段AB扫过的面积.第6页,共10页8. 矩形AOBC 中,OB =4,OA =3.分别以OB ,OA 所在直线为x 轴,y 轴,建立如图1所示的平面直角坐标系.F 是BC 边上一个动点(不与B ,C 重合),过点F 的反比例函数y =kx (k >0)的图象与边AC 交于点E .(1)当点F 运动到边BC 的中点时,求点E 的坐标; (2)连接EF ,求∠EFC 的正切值;(3)如图2,将△CEF 沿EF 折叠,点C 恰好落在边OB 上的点G 处,求此时反比例函数的解析式.9. 如图,已知直线y =12x +b 与y 轴交于点B (0,-3),与反比例函数y =kx (x >0)的图象交于点A ,与x 轴交于点C ,BC =3AC . (1)求反比例函数的解析式;(2)若P 是y 轴上一动点,M 是直线AB 上方的反比例函数y =kx (x >0)的图象上一动点,直线MN ⊥x 轴交直线AB 于点N ,求△PMN 面积的最大值.(k>0,x>0)的图象经过▵OABC 10.如图,平面直角坐标系xOy中,点C(3,0).函数y=kx的顶点A(m,n)和边BC的中点D.(1)求m的值;(2)若的面积等于6,求k的值;(3)在第(2)问的基础上,过点D作直线l平行于直线AB,点P为直线l的上一个动点,点Q为平面内一动点,若以A、P、O、Q为顶点的四边形为矩形,求点P的坐标.11.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,3),将线段AB绕点A顺时针旋转(k≠0,x>0)的图象经过点C.90°得到线段AC,反比例函数y=kx(1)求直线AB和反比例函数y=k(k≠0,x>0)的解析式;x(2)已知点P是反比例函数y=k(k≠0,x>0)图象上的一个动点,求点P到直线AB最x短距离时的坐标.12.如图,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x−4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=k也经过A点.连接BC.x(1)求k的值;(2)判断△ABC的形状,并求出它的面积.(3)若点P为x正半轴上一动点,在点A的右侧的双曲线上是否存在一点M,使得△PAM是以点A为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.13.如图, 直线y=kx+b(k≠0)与双曲线y=m(m≠0)在第一象限交于点A、B,且该直线与x轴正x半轴交于点C, 过A、B分别作x轴的垂线, 垂足分别为E、D.已知A(4,1).(1)求双曲线的表达式;(2)若CD=4CE.求k,b的值;(3)在(2)的条件下, 若点M为直线AB上的动点,则OM长度的最小值为 .(x>0)14.如图,直线y=﹣x+1与x,y轴分别交于A、B两点,P(a,b)为双曲线y=12x 上的一动点,PM⊥x轴与M,交线段AB于F,PN⊥y轴于N,交线段AB于E(1)求E、F两点的坐标(用a,b的式子表示);第8页,共10页(2)当a=3时,求△EOF的面积.4(3)当P运动且线段PM、PN均与线段AB有交点时,探究:BE、EF、FA这三条线段是否能组成一个直角三角形?说明理由;的图象交于A、B两点,其中A(1,n),15.如图,已知直线y1=3x与反比例函数y2=kx点C是反比例函数在第一象限图象上不同于A的一动点(C在A右侧),BC交y轴于点F.(1)直接写出:①k的值为______;点B的坐标为______;②当y1>y2时,x的取值范围是______;(2)若∠BAC=90°,求点C的坐标;(3)如图2,延长CA交y轴于点E,直接写出EF的长为______.的图像和一次函数y2=ax+b的图像交于A(3,4)、B(-6,n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数图像上的动点问题
——反比例函数复习
一、开门见山揭示课题 二、复习过程演绎
(一)问题1教学
出示右图:如图,坐标系内有一点A (2,4),有一反比例函数图像经过A 点。
则它的函数关系式是什么?(学生口答)
变:过A 作AD ⊥x 轴于D ,连结OA ,则S △AOD =___. 学生口答。
(预设两种:S △AOD =12OD ×AD =4, S △AOD =12×8)
师:你是怎么知道的?
总结:①把点的坐标转化为线段的长,往往是解决直角坐标系中有关图形计算的手段(预设1);
变1:若C 是图像上的一个动点,也构造这样的直角三角形COF ,则面积为多
少?你的理由?S △AOD =1
2︳k ︳(根据学生回答,引出C 为动点)
师:提问:连结AC ,在这个图形中,你还能找出其他面积相等的部分吗?(学生在工作单上试做)
学生回答:(1)S △AOM =S 梯MDFC ;S △AOC =S △ADFC 板书 (移动几何画板观看)
变2:若C 点坐标为(4,2),求S △AOC 生说师写过程(板书转化思想) 变3:S △AOC =6,求C 点坐标 学生试做。
优生板演。
毕。
师:请大家仔细看黑板上同学所做题目。
请给与评价。
有哪些地方值得你欣赏的?哪些地方你觉得要修正的?
(老师根据学生所言,共同规范书写过程)板书分类思想 阶段评价 (二)出示问题2
变4:延长AO 交图像于点B ,则B 点坐标为多少?(口答) 师:你的理由?(中心对称图形)
延长CO 、AO 交图像的另一分支于点E 、B ,连结AF 、BF ,四边形AEBC 是什么
C
F
O
y
O
x
A (2,4)
D
特殊四边形?理由?
提问:四边形AEBC 还有可能是其他特殊平行四边形吗? (教师用几何画板拖动点的位置,让学生感知点的运动)
变5:点C 是该反比例函数图像第一象限上的一个动点,若连结BC 恰好经过点D ,
求此时点C 的坐标;
追问:是矩形吗?
有可能是菱形吗?你有理由吗?
三、总结:谈谈本节课的收获。
“三二一”
三种数学思想:数形结合思想、分类讨论思想、转化思想 两种解题方法: 转化
求面积,一般性图形 特殊性图形 动点问题要抓住其不变的地方
一个学习建议:经常思考一题多变、一题多法
8
6
4
2
-2
-4
-5
5
10
(2,4)
A O
B
C
E
F。
