振型分解反应谱法

结构设计系列之振型分解反应谱法苏义前言我国规范对于常规结构设计有两个方法：底部剪力法和振型分解反应谱法。

其中，底部剪力法视多质点体系为等效单质点体系，且其地震作用沿高度呈倒三角形分布，当结构层数较高或体系较复杂时，其计算假再用，因部剪时，其计算假定不再适用，因此规范规定底部剪力法仅适用于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构。

因此，一般结构均采用振型分解反应谱法。

振型分解反应谱法的基本步骤：通过体系的模态分析，求出多自由度体系的振型通过体系的模态分析求出多自由度体系的振型向量、参与系数等等；然后把每个振型看作单自由度体系，求出其在规定反应谱的地震加速度作用下产生的地震效应；最后把所有振型的地震效应式进行叠，得到体系震应应按一定方式进行叠加，就会得到体系地震效应的解。

注意注意：振型分解反应谱法只适用于弹性分析，对于弹塑性体系，由于力与位移不再具有对应关系，性体系，由于力与位移不再具有一一对应关系，该法不再适用。

目录一模态分析二反应谱分析三振型组合方法四方向组合方法一、模态分析模态分析也被称作振型叠加法动力分析，是线性体系地震分析中最常用且最有效的方法。

它最主要的优势在于其计算一组正交向量之后，可以将大型整体平衡方程组缩减为相对数量较少的解耦二阶平解阶微分方程，这样就明显减少了用于数值求解这些方程的计算时间。

模态分析为结构相关静力分析提供相关结构性能，包括结构静力地震作用分析和静力风荷载分析。

模态分析是其它动力分析的基础，包括反应谱分析和时程分析。

一、模态分析特征向量分析用于确定体系的无阻尼自由振动的模态和频率，分析这些自振模态是理解结构性能很好的工具。

下面我们以不考虑阻尼的高层建筑为例，了解一下关下面我们以不考虑阻尼的高层建筑为例，了解下关于无阻尼自由振动的一些基本概念。

一、模态分析对于一般的高层建筑，我们可以将其看作多自由度体系。

根据每个质点的力学平衡条件，建立每个质点的振动平衡方程式，联立这些方程式，即为多自由度体系的振动平衡方程组。

平一、模态分析对于一个自由度个数为n的体系，设下列符号分别表示：一、模态分析如果体系有n个自由度，当不考虑阻尼时，体系自由振动的平衡方程组为：自由度个数越多，上式就会越复杂。

为了简化表达方式，我们常常将上式用矩阵形式来表达：一、模态分析式中：一、模态分析上述矩阵及向量可以具体表述为：一、模态分析设该方程组的通解为：{Φ}即为振型向量（又称特征向量），其表达式为：将上式代入平衡方程组，则有：满足上式，并且振型向量{Φ}具有非零解的条件为：这是个以圆频率为未知数的次联立方程组，这个这是一个以圆频率ωn方程组中只包含质量矩阵[M ]和刚度矩阵[K ]，因此其解只跟体系本身的性质有关，跟所施加的外荷载（地震作用、风荷载等）无关，故称作体系的特征方程。

一、模态分析令λ＝ω2，λ称作体系的特征值（eigenvalue）。

求解式，可以得到n个由小到大排可以得到n个由小到大排列的特征值λ ：λ1、λ2、λ3、··· 、λn及圆频率ω值（开根号后取正数）：ω1、ω2、ω3、 、ωn、···、ω，把求得的每个ω值代入式（2.2.1-5），就可以求得每个值应向{1}{2}{3}每个ω值对应的振型向量{Φ}、{Φ}、{Φ}、··· 、{Φn}，我们称其为体系的第1振型向量、第2振型向量、第3振型向量、··· 、第n振型向量（也叫特征向量），或者简称为振型。

一、模态分析各个振型可表示为下列形式：各个振型向量可合并为一个振型矩阵：该值为某一振型中各质点之间比值的大小，并不表示该值为某一振型中各质点之间比值的大小并不表示振幅的大小，只是表示体系的振动形状。

一、模态分析多自由度体系的各个振型均有不同的形状，如下图：一、模态分析在多自由度体系中，振型的总个数与体系的总自由度数相等。

对于层数为N层的单塔高层建筑，按串联刚片系层模型考虑时，每层有X向平动、Y向平动、Rz转动三个自由度，总共有3N个自由度，那么体系个，有个，那总共就应该有3N个振型。

前求由到排列圆率值，体根据前面求出的由小到大排列的圆频率ω值，可知体系的自振频率由小到大依次为：体系的自振周期由大到小依次为：其中T称为第1振型的自振周期也叫基本周期T 其中，T1称为第1振型的自振周期，也叫基本周期，T2称为第2振型的周期，T n称为第n振型的自振周期。

一、模态分析对体系进行模态分析之后，为了计算简化，可根据质量矩阵[M ]对振型矩阵进行归化：量矩阵[M]对振型矩阵进行归一化：式中，[E ]为单位对角矩阵。

式中[E]为单位对角矩阵对其进行矩阵变换（过程略）之后，可得：将上式的矩阵展开，即成为下面的非矩阵表达式：在加速度为的地震作用下体系振动平衡方程式为：向量{I }为方向向量，其与加速度对应方向的元素向量{I}为方向向量，其与加速度为1，其余为0。

一、模态分析通过振型矩阵[Φ] 对位移矩阵进行下列变换：式中：{ q}――振型坐标中的位移向量上式的实质就是对体系按振型进行分解，即把体系的上式的实质就是对体系按振型进行分解即把体系的位移分割成各个振型的位移。

反过来讲，体系的位移也等于各个振型产生的位移之和。

移也等于各个振型产生的位移之和将上式代入可得：得对上式两边均左乘第j振型向量{Φj }T( j＝1,2,3,…,n)，并利振型的交（上式左边除第振型外并利用振型的正交性（即上式左边除了第j振型以外的项均为零），可得：一、模态分析令：则体系的振动就分解为n个独立的单自由度体系的振动平衡方程：上式两边同时除以，则变化为：一、模态分析令：我们把γj 称作体系第j振型的参与系数（participation 称作体系第j振型的参与系数（participation factor），如果体系有n个自由度，那么就对应有n个、…、从大到小排列的振型参与系数γ1、γ2、γ3、、γn。

参与系数的大小表示在地震作用下，体系振动时该振型所占比例的大小，参与系数越大，说明该振型所占例，参与系越，出现的几率越多。

对于串并联刚片系层模型，方向向量{}等于{}，则对于串并联刚片系层模型，方向向量{I }等于{1}，则上式的矩阵展开后即成为下面的非矩阵表达式：对应抗规()对应《抗规》(5.2.2-2)由于振型矩阵[Φ]已根据质量矩阵[M ] 进行了归一化处理，即：则有：一、模态分析将式两边乘以第jj T 振型的参与向量γj {Φj }，可得：上式右侧即为在加速度为的地震作用下第j振型的的地震作用下，第j振型的基底总剪力。

根据Edward L. Wilson 教授的定义，第j振型的振型参与质量为一个特定方向上的单位基第j振型的振型参与质量为个特定方向上的单位基底加速度引起的基底剪力，即：对于串并联刚片系层模型，，因此：对应第j振型的参与质量系数为：一、模态分析当计算时所取的总振型数k个与体系的自由度n相等时，那么各振型参与质量之和等于总质量。

但体系的自由度n往往很大，让所有振型都参与组合并不现实且无此必要。

我国《高规》第5.1.13条规定：“抗第震设计时，B级高度的高层建筑结构、混合结构和本工程第10章规定的复杂高层建筑结构，尚应符合下列规定：宜考虑平扭耦联计算结构的扭转效应，振型数不应小于15，对多塔楼结构的振型数不应小于塔楼数的9倍，且计算振型数应使各振型参与质塔楼数的倍且计算振型数应使各振型参与质量之和不小于总质量的90%”。

即累计振型质量参与系数（也叫质量参与比）不小于90%。

与系数（也叫质量参与比）不小于90%一、模态分析对于计算振型数为k个的体系，其累计振型质量参与系数为：我国规范要求为：从上述推导过程可知，结构的周期、频率、振型质量从上述推导过程可知结构的周期频率振型质量参与系数等等特性都与外加作用（地震烈度或基本风压）无关，均为体系的自振特性。

风压）无关均为体系的自振特性二、反应谱分析反应谱是指具有不同周期和一定阻尼的单质点结构在地震地面运动影响下最大反应与结构自震周期的关系曲线。

反应谱中各点的值，可以看作是在一个臂个共同基础上的一系列逐步加长的悬臂摆承受横向震动下的反应。

二、反应谱分析虽然目前结构分析软件的发展水平允许我们基于振型叠加法或其它方法在地震作用的整个过程对结构响应进行完整的计算（即对结构进行时程分析），但是它需要提供详尽的场地信息，这一点并不，详，是所有实际工程都能做到，并且时程分析会输出地震作用每个时刻的位移及内力响应，对这些信息的统计会耗费大量的工时，且难以形成直接用于指导结构设计的信息。

地震作用反应谱分析本质上是一种拟动力分析，它首先使用动力方法计算出各质点的地震响应，并使用统计的方法绘成反应谱曲线，然后再使用静力计的方法绘成应谱曲线然后使静力方法进行结构分析。

结构反应谱分析避免了对整个时间范围内的响应进行处理，给出的信息可以个时间范围内的响应进行处理给出的信息可以很方便的用于结构设计。

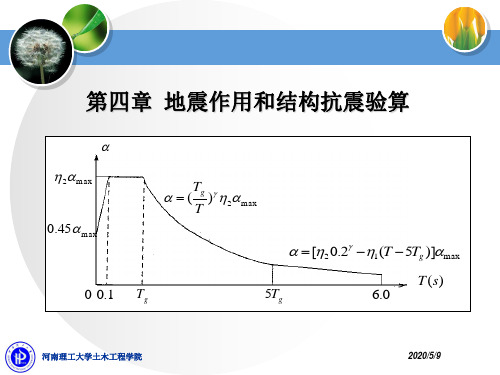
二、反应谱分析我国规范的设计反应谱是以地震影响系数的形式给出，见下图：前面我们已求出第j振型自振周期T j、振型参与系数γj 、振型坐标Φji等等，根据每一振型的自振周期，可求得其相应的地震影响系数α值。

求得其相应的地震响系数值二、反应谱分析设αj为相应于第j振型自振周期的影响系数、g为重力加速度。

对于不考虑扭转耦联振动影响的结构，第j振型中第i质点的地震作用为：对应《抗规》(5.2.21)对应《抗规》(5.2.2-1)将上式求出的地震作用加到结构上，进而求解出n个单自由度体系在地震作用下产生的效应（弯矩、剪力、轴力及变形等等），然后把所有振型的效应按一定方式进行叠加，就会得到体系反应位移应按定方式进行叠，会得到体系反应位移的解。

三、振型组合方法振型叠加的方法主要有以下几种：1.ABS法（Absolute Sum Method）1ABS法（Absolute Sum Method）这种方法假设所有振型的最大模态值都发生在同一个时间点上，通过求它们的绝对值之和来进行振型时间点上通过求它们的绝对值之和来进行振型叠加。

实际上，最大模态值发生在同一时刻的可能性基本不存在，因此，这方法是用于计算结能性基本不存在因此这一方法是用于计算结构位移或内力峰值的最保守方法。

三、振型组合方法2.SRSS法（Square Root of Sum Square）这种方法假设所有最大模态值都是相互独立的，通过这种方法假设所有最大模态值都是相互独立的通过求参与组合的各个振型的平方和的平方根（Square Root of Sum Square）来进行组合。

它没有考虑各Root of Sum Square）来进行组合。