振型分解反应谱法求位移例题3.2.2
计算水平作用的振型分解反应谱法
计算水平作用的振型分解反应谱法水平作用的振型分解反应谱法是一种用于结构地震响应分析的方法。
它通过将结构的地震响应分解为多个模态响应，并结合每个模态的频率、阻尼和模态形态，计算出结构在不同地震波作用下的反应谱。
水平作用的振型分解反应谱法的基本原理是基于结构的振型分解理论。
振型分解理论认为，结构的地震响应可以看作是一系列模态振型的叠加效应。
每个模态都代表了结构在不同频率下的振动行为。
根据模态分解的原理，可以将结构的振动方程简化为模态响应方程。
在计算水平作用的振型分解反应谱时，首先需要确定结构的振型特性，包括结构的固有周期、振型形态和阻尼比。
通常可以通过有限元分析或振动试验等方法来确定这些特性。
然后，需要确定地震波的加速度谱。
地震波的加速度谱描述了地震波在不同频率下的强度。
可以通过查阅地震动数据库或根据地震动参数进行计算来获取。
接下来，可以根据结构的振型特性和地震波的加速度谱，计算每个模态下的反应谱。
对于每个模态，可以首先计算出结构的频率响应函数。
频率响应函数描述了结构在单一频率下的响应特性，包括振幅和相位。
然后，将频率响应函数和地震波的加速度谱进行卷积积分，得到模态响应谱。
模态响应谱描述了结构在单个模态下的振动响应特性，包括最大位移、最大加速度和最大应变等。
最后，将每个模态的响应谱按照其中一种组合规则进行叠加，得到整个结构的反应谱。
常见的组合规则包括将每个模态响应谱按照线性叠加或主应力法进行组合。
线性叠加方法适用于结构的线性响应范围，主应力法适用于结构的非线性响应范围。
通过计算水平作用的振型分解反应谱，可以获得结构在地震作用下的振动响应特性。
这些特性可以用于评估结构的抗震性能，指导结构的设计和加固，以增强结构的地震抗力。
《振型分解反应谱法》课件
振型分解反应谱法的应用前景
支撑结构的设计和评估
结构设计师和工程师可以利用振 型分解反应谱法，解决实际工程 中的动力响应问题。
工程抗震加固
对已经存在的结构进行加固和改 造时，可以使用振型分解反应谱 法进行更加精细的工程分析，在 不拆除原有结构的同时，提高结 构抗震能力。
地震灾害对策和减灾措施
应用振型分解反应谱法，制定防 灾预案，提高灾害应对和减灾能 力。
振型分解反应谱法
综合振型分解法和反应谱法的优势，识别结构响应来源并计算其动力响应。在大型和复杂结 构抗震分析中应用广泛。
振型分解反应谱法的步骤
数据采集和准备
收集地震动数据，进行处理和筛 选。
滤波处理
去除噪音，提取有效信息。
振型识别和分离
根据振动理论进行振型分解，分 离出不同频率的振型组合。
反应谱计算
振型分解反应谱法的总结和展望
1 现有研究进展
当前振型分解反应谱法的应用领域已经涵盖了建筑、桥梁、风电、海洋、地基、地铁等 众多领域。
2 未来研究方向
应用人工智能技术优化振型分解反应谱法的分析精度和速度，以及开发更加智能化的分 析工具。
3 机遇和挑战
随着大型基础设施建设和城市更新进程加快，结构的抗震设计和评估的需求日益增长。 振型分解反应谱法将有广阔的市场前景，也面临着挑战。
根据结构振型组合和地震动谱计 算每个组合的动力响应。
振型分解反应谱法的数学基础
1
谱分解定理的定义和原理
将一个线性有界算符分解成一组特征向量和特征值，用于结构振动分析。
2
单自由度系统的反应谱
单自由度结构的动力响应，是地震加速度历时曲线和结构自振响应的乘积。
3
多自由度系统的反应谱
振型分解反应谱法
如何解j振型对应的广义坐标方程
Dj (t)
2
j
j
Dj
2 j
D
j
(t)
j
xg (t)
已知：对于单自由度体系
x 2x 2x xg (t)
x(t) 1
d
t 0
xg (
)e
(t
)
sin
d
(t
)d
对于j振型折算体系（右图）
j
(t
)
1
j
t 0
xg (
)e
j
j
(t
)
sin
j
(t
)d
D
j
(t
)
j j
其中： Fji (t) mi[x ji jj (t) x ji j xg (t)]
---t时刻第j振型i质点的水平地震作用
Fji (t) mi[x ji jj (t) x ji j xg (t)]
---t时刻第j振型i质点的水平地震作用
体系j振型i质点水平地震作用标准值为：
Fji Fji (t) max mi x ji j j (t) xg (t) max
0.55 0.75
第三组 0.35
0.45
0.65 0.90
例：试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组。
解：（1）求体系的自振周期和振型
0.334
0.667
4.019
X 1 0.667 X 2 0.666 X 3 3.035
F1n
F2n
F jn
Fnn
mi
F1i
F2i
F ji
Fni
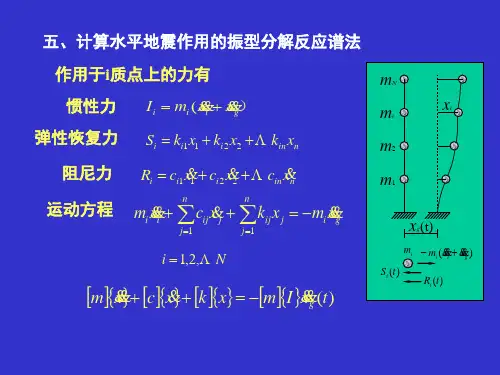
计算水平地震作用的振型分解反应谱法
& & & Ri = ci1x1 + ci2 x2 +Lcinxn
xi
& mi &&i + ∑cij xi + ∑kij xi = mi &&g x x
j =1 j =1
n
n
i =1,2,LN
xg(t) Ri (t)
i质点相对于基础的位移与加速度为
xi (t) = ∑xji Dj (t)
j =1
N
职业技学院
---体系j振型i质点水平地震作用标准值计算公式 ---体系j振型i 体系
α j ---相应于j振型自振周期的地震影响系数； ---相应于j振型自振周期的地震影响系数； 相应于
xji --- j振型i质点的水平相对位移； 振型i质点的水平相对位移；
一般只取2-3个振型， 一般只取 个振型， 个振型 当基本自振周期大于1.5s 当基本自振周期大于 或房屋高宽比大于5时 或房屋高宽比大于 时， 振型个数可适当增加。 振型个数可适当增加。
3 3
2 270×(0.667) + 270×(0.666) +180×1 = 0.428 第二振型 γ 2 = ∑mi x2i / ∑mi x2i = 2 2 2 i =1 i=1
3
3
270×(0.667) + 270×(0.666) +180×1
第三振型 γ 3 = ∑mi x3i / ∑m x
V23 = 120.8
职业技学院
17 . 8
17 .8 kN 80 .9 kN
63 . 1 44 . 1 3振型
107 .2 kN
第三振型
（5）计算各振型的地震作用效应（层间剪力） 计算各振型的地震作用效应（层间剪力）
振型分解反应谱法
附录一 振型分解反应谱法振型分解反应谱法作为弹性多自由体系的主要分析方法，很有必要对振型分解反应谱法有充分的了解。
本文仅作为大家参考之用，如有理解上的错误或者不当，敬请谅解。
1、单自由度体系在地震作用下的运动 如图（1）所示，根据达朗贝尔原理有： 0=++s I c f f f （1）也即：g u m ku u c um -=++ （2） 方程两边同时除以m ，可化为：g u u u u-=++22ωξω （3） 式中，2/k m ω= ，令ωξm c2=，为体系阻尼比。
2、多自由度体系在地震作用下的运动类似于单自由度体系分析过程，体系运动方程为：g u m u k u c u m ][}]{[}]{[}]{[-=++ （4）无阻尼体系自由振动时，0=g u，0=c ，上式即为： }0{}]{[}]{[=+u k um （5） 根据方程解的特征，设其解的形式为：)sin(}{}{ϕωφ+=t u （6）代入（5）式有：}0{)sin(}]){[]([2=+⋅-ϕωφωt m k （7）由于0)sin(≠+ϕωt则}0{}]){[]([2=-φωm k （8）另外，}0{}{≠φ，故特征方程为：0][][2=-m k ω （9）由（9）式可以求出2ω，进而可以求得各阶振型对应的圆频率2i ω，再代入（8）式可求对应于各个2i ω的特征向量}{i φ，即为振型。
振型φ：多自由度体系自由振动时，各质点在任意时刻位移比值是一定的，不随时间变化，即体系自由振动过程中形状保持不变。
振型是结构形状保持不变的振动形式，振型的形状是唯一的。
N 个自由度的体系具有N 个振型。
则结构的变形总可以表示成这N 个振型的线性组合：{}∑==Ni i i q u 1φ （10）其中i q 称为正则坐标。
3、振型的正交性由于}0{}]{[}]{[2=-φωφm k （11） 则}0{}]{[}]{[2=-r r r m k φωφ （12）（12）式两边同时左乘T n }{φ，)(r n ≠，得到：}]{[}{}]{[}{2r T n r r T n m k φφωφφ= （13）同理，}]{[}{}]{[}{2n Tr n n T r m k φφωφφ=，该式两边同时转置一次，得到：}]{[}{}]{[}{2r T n n r T n m k φφωφφ= （14）（13），（14）两式左右对应相减，得到：0}]{[}){22=-r T n n r m φφωω（ )(n r ≠ （15）因为22n r ωω≠所以 0}]{[}{=r Tn m φφ )(n r ≠ （16） 同理亦有 0}]{[}{=r Tn k φφ )(n r ≠ （17）即所说的振型关于质量和刚度矩阵满足正交性质。
振型分解反应谱法题库
振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。
该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。
振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。
适用条件（1）高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。
（此为底部剪力法的适用范围）（2）除上述结构以外的建筑结构，宜采用“振型分解反应谱法”。
（3）特别不规则的建筑、甲类建筑和规范规定的高层建筑，应采用时程分析法进行补充计算。
刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。
因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规范限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规范限值较多时，可采用削弱刚度的方法。
同样，对刚重比的调整也可能影响周期比。
特别是当结构的周期比接近规范限值时，应采用加强结构外围刚度的方法规范上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。
见高规5.4.1和5.4.2及相应的条文说明。
刚重比不满足规范上限要求，说明重力二阶效应的影响较大，应该予以考虑。
规范下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，避免结构的失稳倒塌。
见高规5.4.4及相应的条文说明。
刚重比不满足规范下限要求，说明结构的刚度相对于重力荷载过小。
但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。
第三章 计算水平地震作用的振型分解反应谱法(第9节课讲义)
地震特征周期分组的特征周期值（s）
场地类别
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一组 0.25
0.35
0.45 0.65
第二组 0.30
0.40
0.55 0.75
第三组 0.35
0.45
0.65 0.90
（2）计算各振型的地震影响系数
查表得 max 0.16
Tg 0.4s
第一振型 Tg T1 5Tg
第二振型 0.1s T2 Tg
---t时刻第j振型i质点的水平地震作用
Fji Fji (t) max mi x ji j j (t) xg (t) max
---体系j振型i质点水平地震作用标准值
单自由度体系水平地震作用：
F
F (t ) max
m x(t) xg (t) max
G
多自由度体系j振型i质点水平地震作用：
mx cx kx m1xg (t)
mN
mi
xi
m2
m1
xg(t)
mi mi (xi xg )
Si (t)
Ri (t)
D j
(t )
2
j
j
D j
2 j
D
j
(t )
X
T j
M
1
X
T j
M
X
j
xg
(t )
n
j
X
T j
M
1
X
T j
M
X
j
mi x ji
i 1
n
mi
x
2 ji
i 1
---j振型的振型参与系数
335.8 671.6 845.8
组合后各层地震剪力
振型分解反应谱法
振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。
该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。
振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。
适用条件（1）高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。
（此为底部剪力法的适用范围）（2）除上述结构以外的建筑结构，宜采用“振型分解反应谱法”。
（3）特别不规则的建筑、甲类建筑和规范规定的高层建筑，应采用时程分析法进行补充计算。
刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。
因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规范限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规范限值较多时，可采用削弱刚度的方法。
同样，对刚重比的调整也可能影响周期比。
特别是当结构的周期比接近规范限值时，应采用加强结构外围刚度的方法规范上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。
见高规5.4.1和5.4.2及相应的条文说明。
刚重比不满足规范上限要求，说明重力二阶效应的影响较大，应该予以考虑。
规范下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，避免结构的失稳倒塌。
见高规5.4.4及相应的条文说明。
刚重比不满足规范下限要求，说明结构的刚度相对于重力荷载过小。
但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。
振型分解反应谱法
q1 (t ) 和
q2 (t )
确定后，质点的位移
u1 (t )
和
u2 (t )
也将随之确定。
2019/2/6
第8讲 振型分解反应谱法
3
式（3-55）也可以这样理解：体系的位移可看作是由 各振型向量乘以相应的组合系数和后叠加而成的。换句 话讲，这种方法是将实际位移按振型加以分解，故称为 振型分解法。另外，由于和是随时间变化的，因此，同 一振型在不同时刻对总位移“贡献”的大小是不一样的。
第
8讲
振型分解反应谱法
考虑两个自由度的体系。将质点和在水平向地震作用 下任一时刻的位移和用其两个振型的线性组合表示， 即：
u1 (t ) 11q1 (t ) 21q2 (t )
u2 (t ) 12 q1 (t ) 22 q2 (t )
(3-55a)
（3-55b）
2019/2/6
0.05
例：试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组。 解： （1）求体系的自振周期和振型 m 180t
型组合公式，称为完全二次项组合法，简称CQC法：
S
ij S i S j i 1 j 1
m
m
（3-65）
式中 ,s-----水平地震作用效应； m-----参与振型组合的振型数，一般可取2～3个振型, 当基本自振周期 T1>1.5s
或房屋高宽比大于5时，振型个数可适当增加；
2019/2/6
一般的多自由度线弹性体系，式（3-55）可写成如下形式
{u(t )} { j }q j (t ) [ ]{q(t )} 3-56
j 1
n
振型分解反应谱法
n
j
ij 1 ，下面证明它是成立的：
1 as is (i 1, 2,3, , n)
即：
s 1
(1)
式中： ij
1 a111 a212 an 1n 1 a2 21 a2 22 an 2 n (2) 1 a1 n1 a2 n 2 an nn 为振型矩阵的元素：a j 为常系数，由式（1）可唯一确定。
多质点弹性体系在地面水平运动影响下，质点 i 上的总惯性力是：
Fi (t ) mi [ xg (t ) xi (t )]
为了推导简便，将 xg (t) 写成如下形式：
xg (t ) xg (t ) j ij
j 1
n
振型分解反应谱法
使上式成立的唯一可能是 将1按振型展开：
n
sin j (t )d
第 i 质点相对于结构底部的位移可求出如下：
xi (t ) T i ,:q q j . ij j . j (t ). ij
j 1 j 1
n
n
振型分解反应谱法
利用振型矩阵关于刚度矩阵和质量矩阵的正交性将多质点体系分解为 一个一个单质点体系来考虑，从而使问题得以简化。下面说明如何利 用单质点弹性体系水平地震作用的反应谱来确定多质点弹性体系的地 震作用问题，即所谓的振型分解反应谱法。
振型分解反应谱法
广义模态位移可用杜哈美积分写出：
j qj j
或
t
0
xg ( )e
j j ( t )
sin j (t )d
q j (t ) j . j (t )
j (t ) 1
振型分解反应谱法求结构的最大位移和底部最大剪力_概述说明以及解释
振型分解反应谱法求结构的最大位移和底部最大剪力概述说明以及解释1. 引言1.1 概述本文讨论的是振型分解反应谱法在求解结构的最大位移和底部最大剪力方面的应用。
在工程设计和结构分析中，了解结构的抗震性能是至关重要的，因为地震荷载可能会对结构造成巨大影响。
因此，准确估计结构在地震作用下的位移和剪力变化对于设计可靠、安全稳定的建筑物至关重要。
1.2 文章结构本文共分为五个部分进行详细介绍。
首先，在引言部分我们将概述本文的主题和研究目的。
然后，我们将详细讨论振型分解反应谱法的理论基础、求解过程以及其应用范围与限制。
接着，在第三部分中，我们将探讨如何使用等效静力法原理来求解结构的最大位移，并给出相应的求解步骤和计算公式。
第四部分将重点研究底部最大剪力的求解，包括底部剪力分布特点、剪力计算方法及公式导出过程，并通过数值模拟和实验验证结果对比来进行进一步分析。
最后，我们将在结论与展望部分总结主要研究结论，并对存在问题提出改进方向的展望。
1.3 目的本文的主要目的是介绍和解释振型分解反应谱法在求解结构最大位移和底部最大剪力中的应用。
通过阐述相关理论基础、求解过程以及实例分析，旨在为工程师和研究人员提供一种有效的方法来评估建筑物在地震作用下的抗震性能。
此外，本文还将探讨该方法存在的限制，并提出改进方向，以促进该领域未来的研究和应用发展。
2. 振型分解反应谱法2.1 理论基础振型分解反应谱法是结构动力学中常用的一种分析方法，通过将结构的地震作用响应按照不同振型进行分解，进而求解结构在各个振型下的最大位移和底部最大剪力。
该方法基于以下两个理论基础：首先是振型理论。
振型是描述结构在地震激励下的运动状态的数学函数形式。
结构可通过特征向量与自由振荡频率确定其对应的振型形态。
其次是反应谱理论。
反应谱是一种表征动力响应强度与频率关系的曲线。
通过将地震输入转化为加速度-频率坐标系上的曲线，可以获取到某个特定周期（频率）下结构对地震作用响应的峰值。
振型分解反应谱法
3104
50
2
0
0.00003 4 0.058 2 15 0
12 307.6 1 17.54rad / s
22 1625.8 2 40.32rad / s
X12 X11
m112 k11
k12
60307.6 8104 3104
n i 1
j 1
j x ji
Gi G
n
式中 G Gi （结构总重量）
i 1
FEK 则结构总的水平地震作用（底部剪力）
n
nn
FEK
V
2 jo
1G
(
x ) j
Gi 2
1 j ji G
j 1
j1 i1
1cG
其中
nn
c
(
) i
Gi 2
0
0 m2
x1 x2
0 0
k11 k21
k12 k22
2
m1
0
0
m2
0
k11
k21
2m1
k22
k12
2
m2
0
8104 60 2 3104
3104
m1 270t m1 270t
解：（1）求T1,T2,T3(方法后面要讲实用方法）
T1 0.467s T2 0.208s T3 0.134s
X
T 1
0.334
0.667
abaqus振型分解反应谱法
一、引言abaqus是一种常用的仿真软件，在工程实践中被广泛应用。
振型分解反应谱法是abaqus中用于地震工程分析的一种方法，通过该方法可以有效地对结构在地震作用下的动力响应进行分析，为工程设计和安全评估提供重要参考。
二、振型分解反应谱法的基本原理1. 振型分解振型分解是指将结构的动力响应分解为一系列基本的振型模态的叠加。
在地震工程中，结构的动力响应可以通过对振型模态的分解来进行分析，这一过程对于确定结构的峰值加速度和位移响应具有重要意义。
2. 反应谱法反应谱法是一种结构动力分析的常用方法，它以结构的加速度、速度或位移等动力响应为基础，通过建立相应的反应谱曲线来描述结构在地震激励下的响应特性。
在abaqus中，可以使用反应谱法来模拟结构在地震作用下的响应情况。
三、abaqus中的振型分解反应谱法实现1. 模态分析在进行振型分解反应谱法分析之前，首先需要进行结构的模态分析，通过abaqus可以求解结构的振型频率和模态形状等信息。
2. 地震加载在模态分析之后，需要进行地震加载，abaqus可以根据不同的地震波形数据对结构进行加载，并求解结构在地震作用下的动力响应。
3. 振型分解通过abaqus可以进行振型分解，将结构的动力响应分解为一系列振型模态的叠加。
4. 反应谱计算根据振型分解的结果，可以利用abaqus中的反应谱分析功能，绘制结构在地震激励下的反应谱曲线，从而全面地了解结构的响应特性。
四、案例分析下面通过一个简单的案例来演示abaqus中振型分解反应谱法的实现过程。
1. 结构模型假设我们考虑一个简单的砖混结构，在abaqus中建立其有限元模型，并进行模态分析。
2. 地震加载选择适当的地震波形数据，对结构进行地震加载，求解结构的动力响应。
3. 振型分解对结构的动力响应进行振型分解，得到结构的振型频率和模态形状等信息。
4. 反应谱计算利用abaqus中的反应谱分析功能，绘制结构在地震作用下的反应谱曲线，分析结构的响应特性。
计算水平地震作用的振型分解反应谱法
例：试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8 类场地，设计地震分组为第二组。 抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组。 解： 1）求体系的自振周期和振型 （ m = 180t
3
职业技学院
K 3 = 98MN/m
职业技学院
（6）计算地震作用效应（层间剪力） 计算地震作用效应（层间剪力）
2 2 V = V 2 +V21 +V31 = 845.8kN 1 11
334 . 2
2 2 V2 = V 2 +V22 +V32 = 671.6kN 12
120 . 8 0 .1
120 . 8
2振型
668 . 6 836
γ j --- j振型的振型参与系数； 振型的振型参与系数；
Gi --- i质点的重力荷载代表值。 质点的重力荷载代表值。
F1n
mi
F2 n F2i F22 F21
F jn
Fnn Fni
Fn 2
地震作用效应 弯矩、位移等） （弯矩、位移等）
SEK =
F1i
m2 m1
F ji
Fj 2 F j1
j振型
F12 F11
0.1 < T3 < Tg s α3 =η2αmax = 0.16
α =[η20.2γ η1(T5Tg )] max α
T(s)
5Tg
6.0
0.05 ξ 0.05 ξ γ = 0.9 + η2 =1+ 0.5 + 5ξ 0.06 +1.7ξ
职业技学院
（3）计算各振型的振型参与系数