振型分解反应谱法和底部剪力法
底部剪力振型分解

SHANGHAI UNIVERSITY工程中的数值分析方法课程论文COURSE (THESIS)题目:底部剪力法和振型分解反应谱法比较分析学院土木工程系专业建筑与土木工程学号 15722学生姓名芮指导教师朱杰江日期 2016年 3月5日底部剪力法和振型分解反应谱法比较分析朱杰江,(上海大学,上海,200000)摘要:工程中,多自由度弹性体系水平地震作用的计算一般采用振型分解反应谱法,在一定的条件下还可以采用简化的振型分解反应谱法即底部剪力法。
为验证抗震设计规范对底部剪力法和振型分析法的适用条件和范围的规定,用C++编写Jocabi 法程序,对五层均匀、五层非均匀、八层均匀、八层非均匀、十层均匀和十层均匀结构进行了比较分析,证实了规范的正确性,并给出了新的规律。
关键词:抗震;底部剪力法;振型分解法;C++;Jocabi法中图分类号:TU 443文献标识码:AComparative analysis between equivalent base shear method and modal analysismethodZHUJiejiang,Rui Zheng Qing(Shanghai university,200000)Abstract: In engineering, the calculation of multi degree of freedom elastic system generally adopts horizontal seismic action model analysis method,under certain conditions can also be simplified by using the model analysis method--bottom shear method.In order to vertify the rule of application conditions and range about bottom shear method and modal analysis method in earthquake resistant design code, this article has compared and analysed five-storey uniform, five-storey nonuniform, eight-storey uniform, eight-storey nonuniform, ten-storey uniform and ten-storey nonuniform structure by Jocabi method through c++ program. The result has confirmed correctness of earthquake resistant design code. And it also give some new regularity.Key words:seismic resistance; bottom shear method; model analysis method; C++; Jocabi method0引言进行建筑结构地震反应分析时,首先要确定结构的计算简图,除少数结构可以简化成单质点体系外,大多数建筑结构(如多、高层建筑,多跨不等高厂房)质量分布比较分散,则应简化为多质点体系进行分析。
振型分解反应谱法

结构设计系列之振型分解反应谱法苏义前言我国规范对于常规结构设计有两个方法:底部剪力法和振型分解反应谱法。
其中,底部剪力法视多质点体系为等效单质点体系,且其地震作用沿高度呈倒三角形分布,当结构层数较高或体系较复杂时,其计算假再用,因部剪时,其计算假定不再适用,因此规范规定底部剪力法仅适用于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构。
因此,一般结构均采用振型分解反应谱法。
振型分解反应谱法的基本步骤:通过体系的模态分析,求出多自由度体系的振型通过体系的模态分析求出多自由度体系的振型向量、参与系数等等;然后把每个振型看作单自由度体系,求出其在规定反应谱的地震加速度作用下产生的地震效应;最后把所有振型的地震效应式进行叠,得到体系震应应按一定方式进行叠加,就会得到体系地震效应的解。
注意注意:振型分解反应谱法只适用于弹性分析,对于弹塑性体系,由于力与位移不再具有对应关系,性体系,由于力与位移不再具有一一对应关系,该法不再适用。
目录一模态分析二反应谱分析三振型组合方法四方向组合方法一、模态分析模态分析也被称作振型叠加法动力分析,是线性体系地震分析中最常用且最有效的方法。
它最主要的优势在于其计算一组正交向量之后,可以将大型整体平衡方程组缩减为相对数量较少的解耦二阶平解阶微分方程,这样就明显减少了用于数值求解这些方程的计算时间。
模态分析为结构相关静力分析提供相关结构性能,包括结构静力地震作用分析和静力风荷载分析。
模态分析是其它动力分析的基础,包括反应谱分析和时程分析。
一、模态分析特征向量分析用于确定体系的无阻尼自由振动的模态和频率,分析这些自振模态是理解结构性能很好的工具。
下面我们以不考虑阻尼的高层建筑为例,了解一下关下面我们以不考虑阻尼的高层建筑为例,了解下关于无阻尼自由振动的一些基本概念。
一、模态分析对于一般的高层建筑,我们可以将其看作多自由度体系。
根据每个质点的力学平衡条件,建立每个质点的振动平衡方程式,联立这些方程式,即为多自由度体系的振动平衡方程组。
底部剪力法与振型分解反应谱法的比较分析

底部剪力法与振型分解反应谱法的比较分析在研究了多、高层规则的钢筋混凝土-框架结构的水平地震作用中,通过刚度、高度、层数、层高、平面尺寸的变化对底部剪力法与振型分解反应谱法之间的比较分析。
标签:底部剪力法;振型分解反应谱法;等效系数引言底部剪力法[1]适用于基本振型主导的规则和高宽比很小的结构,此时结构的高阶振型对于结构剪力的影响有限,而对于倾覆弯矩则几乎没有什么影响,因此采用简化的方式也可满足工程设计精度的要求。
底部剪力法尚有一个重要的意义就是我们可以用它的理念,简化的估算建筑结构的地震响应,从而在静力的概念上把握结构的抗震能力。
但是在底部剪力法的计算条件上,研究的还不够具体。
通过以振型分解法的计算结果为依据来比较分析底部剪力法的计算条件。
1 工程概况钢筋混凝土-框架结构,层高适中,梁板柱均为现浇柱网布置,混凝土强度C30,结构规则[2-3],设计地震分组为第一组[4],设防烈度7度取0.15g,多遇地震,场地类别为1类,周期折减系数取0.6,结构阻尼比为0.05,活载折减系数0.5,等效系数[5]取0.852 刚度影响在刚度的不同分布情况中,除顶层地震剪力偏差较大外,其余各层地震剪力偏差相对较小,总地震剪力偏差在工程计算中还是可以使用的。
以上数据表明:以剪切变形为主(一般轴压比大于0.5),在刚度随高度递减时,其层间位移偏差较小些,一般偏差在20%-30%之间;在刚度随高度分布比较均匀时,层间位移偏差相对要大很多。
3 层数影响采用以剪切变形为主,刚度随高度递减(或均匀型)分布。
通过5、7、10、12、15、20、25、30层来讨论。
底部剪力法计算的顶层地震剪力往往比振型分解法的大,底部剪力法计算的各层地震作用主体是呈倒三角形状,但顶层地震作用明显增大,并且随着层数的增加,顶层地震作用偏差逐渐增大的趋势。
(其主要原因是底部剪力法的理论基础是地震作用竖向呈倒考虑顶部附加地震作用,然而在自振周期过大时(一般为0.75s),此时结果偏大,即附加地震作用偏大,)。
底部剪力法和振型分解反应谱法的异同

底部剪力法和振型分解反应谱法是两种常用的结构地震响应分析方法,用于计算结构在地震作用下的受力和变形。
它们在原理和应用上有一些异同之处:
底部剪力法(Base Shear Method):
原理:底部剪力法是一种力的平衡方法,基于结构总质量和地震力之间的平衡关系,将地震力按照结构的刚度和相对刚度分配到各个层面或支撑点上,进而计算出结构的受力和变形。
特点:
利用地震力按刚度分配的方法,将地震力分布到结构各层面或支撑点上。
简化了地震响应分析,适用于常规的结构体系。
结构刚度和地震力分配的假设对结果影响较大,需要合理选择地震力分配系数和抗侧刚度分布。
振型分解反应谱法(Mode Superposition Response Spectrum Method):
原理:振型分解反应谱法是基于振型分解和叠加原理,将结构的地震响应分解为各个振型的响应,并利用振型反应谱进行叠加计算得到总体响应。
特点:
将结构的振动特性和地震激励的频谱特性相结合,通过模态分析计算各个振型的响应,然后叠加得到总体响应。
能够考虑结构的多个振型对地震响应的贡献,更加准确地分析结构的动力特性。
需要进行模态分析和振型选择,计算较为复杂,适用于复杂结构和对动力特性分析较为关注的工程。
总体上,底部剪力法是一种力的平衡方法,基于结构刚度和地震力进行分配,适用于常规结构;而振型分解反应谱法则是基于振动特性和频谱分析的方法,适用于复杂结构和对动力特性分析较为关注的工程。
两种方法在实际工程应用中,根据结构类型和分析需求的不同,可灵活选择使用。
振型反应谱分析法和底部剪力法例题
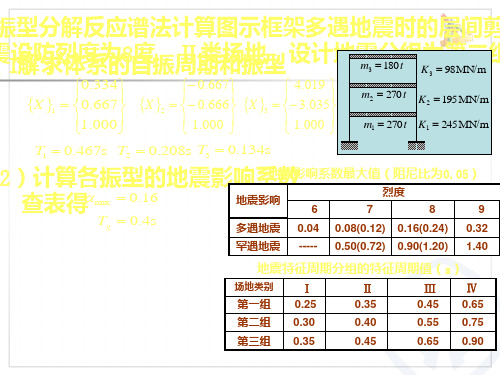
m1 270t K1 245 MN/m
T1 0.467s T2 0.208s T3 0.134s
(2)计算各振型的地震影响系数
查表得max 0.16
Tg 0.4s
第一振型Tg T1 5Tg
1
(Tg T
) 2 max
0.139
2 m ax 0.45 m ax
(Tg T
)
2 m ax
振型分解反应谱法计算图示框架多遇地震时的层间剪
(震1设解)防:求烈体度系为的8自度振,周Ⅱ期类和场振地型,设计地震m3 分180t组K为3 第98MN二/m 组
0.334
0.667
4.019
X 1 0.667 X 2 0.666 X 3 3.035 m2 270t K2 195MN/m
第二振型V21 120.9 120.7 120.8 120.8kN
80.9kN
V22 120.7 120.8 0.1kN
107.2kN
V23 120.8
第三振型
振型分解反应谱法计算图示框架多遇地震时的层间剪
(震1设解)防:求烈体度系为的8自度振,周Ⅱ期类和场振地型,设计地震m3 分180t组K为3 第98MN二/m 组
0.063
振型分解反应谱法计算图示框架多遇地震时的层间剪
(震1设解)防:求烈体度系为的8自度振,周Ⅱ期类和场振地型,设计地震m3 分180t组K为3 第98MN二/m 组
0.334
0.667
4.019
X 1 0.667 X 2 0.666 X 3 3.035 m2 270t K2 195MN/m
120.8kN
120.7kN
120.9kN
第二振型
17.8kN 80.9kN 107.2kN
底部剪力法--反应谱法--时程分析法概念及分析

底部剪⼒法--反应谱法--时程分析法概念及分析底部剪⼒法/反应谱法/时程分析法⼀些有⽤的概念从传统的观点来看,底部剪⼒法,反应谱法和时程分析法是三⼤最常⽤的结构地震响应分析⽅法。
那么正确的认识它们的⼀些关键概念,对于建筑结构的抗震设计具有⾮常重要的意义。
HiStruct在此简单的总结⼀些,全当抛砖引⽟。
1. 底部剪⼒法⾼规规定:⾼度不超过40m、以剪切变形为主且质量和刚度沿⾼度分布⽐较均匀的⾼层建筑结构,可采⽤底部剪⼒法。
底部剪⼒法适⽤于基本振型主导的规则和⾼宽⽐很⼩的结构,此时结构的⾼阶振型对于结构剪⼒的影响有限,⽽对于倾覆弯矩则⼏乎没有什么影响,因此采⽤简化的⽅式也可满⾜⼯程设计精度的要求。
底部剪⼒法尚有⼀个重要的意义就是我们可以⽤它的理念,简化的估算建筑结构的地震响应,从⽽⾄少在静⼒的概念上把握结构的抗震能⼒,它还是很有⽤的。
2. 反应谱⽅法⾼规规定:⾼层建筑结构宜采⽤振型分解反应谱法。
对质量和刚度不对称、不均匀的结构以及⾼度超过100m的⾼层建筑结构应采⽤考虑扭转耦联振动影响的振型分解反应谱法。
反应谱的振型分解组合法常⽤的有两种:SRSS和CQC。
虽然说反应谱法是将并⾮同⼀时刻发⽣的地震峰值响应做组合,仅作为⼀个随机振动理论意义上的精确,但是从实际上它对于结构峰值响应的捕捉效果还是很不错的。
⼀般⽽⾔,对于那些对结构反应起重要作⽤的振型所对应频率稀疏的结构,并且地震此时长,阻尼不太⼩(⼯程上⼀般都可以满⾜)时,SRSS 是精确的,频率稀疏表⾯上的反应就是结构的振型周期拉的⽐较开;⽽对于那些结构反应起重要作⽤的振型所对应的频率密集的结果(⾼振型的影响较⼤,或者考虑扭转振型的条件下),CQC是精确的。
这是因为对于建筑⼯程上常⽤的阻尼⽽⾔,振型相关系数(见⾼规3.3.11-6)在很窄的范围内才有显著的数值。
3.反应谱分析的精确性对于采⽤平均意义上的光滑反应谱进⾏分析⽽⾔,其峰值估计与相应的时程分析的平均值相⽐误差很⼩,⼀般只有百分之⼏,因此可以很好的满⾜⼯程精度的要求,正是在这个平均(普遍性)意义上,我们认为反应谱分析⽅法是精确的。
底部剪力法和振型分解反应谱法的异同

底部剪力法和振型分解反应谱法的异同介绍如下:
相同点:
1.都是计算结构地震响应的方法,能够提供结构的地震反应最大
值。
2.都能够考虑结构的非线性特性。
3.都是基于结构自振的响应理论。
不同点:
1.计算方法不同:底部剪力法是一种强迫振动法,采用结构的等
效单自由度体系,通过对结构的受力分析计算结构的动力特性参数,然后将地震荷载转化为等效水平力,计算结构的最大底部剪力。
而振型分解反应谱法则是一种自由振动法,采用结构的振型分解分析,通过对结构的振型响应进行叠加,计算结构的最大位移、加速度和应力等。
2.基本假设不同:底部剪力法基于结构的等效单自由度体系,假
设结构在地震作用下的振动全部由一个等效的质量块完成,而振型分解反应谱法假设结构在地震作用下的振动是由各个振型独立完成的。
3.能够考虑的因素不同:底部剪力法主要考虑结构的刚度、阻尼
和质量等因素,而振型分解反应谱法则主要考虑结构的振型、频率和阻尼等因素。
综上所述,虽然底部剪力法和振型分解反应谱法都是用于计算结构地震响应的方法,但它们的计算方法、基本假设和能够考虑的因素等方
面存在很大的不同。
在实际工程中,应根据具体情况选择合适的方法进行分析。
3—5 多自由度弹性体系的最大地震反应与水平地震作用

3.5.2 底部剪力法
再将余下的部分 (1−δn )FEK 进行分配。因此, 进行分配。因此,在 考虑了上述调整后, 考虑了上述调整后,顶点的水平地震作用为 GnHn Fn = n (1−δn )FEK +δnFEK ∑ H jGj (3-135b) 135b) j=1 而其余各质点的水平地震作用为
αj Gi Vjo = ∑ Fji = ∑α jγ jφjiGi = α1G∑ γ j X ji i=1 i=1 i=1α G 1
n n n
5-3)
αj Gi 2 FEK = ∑V = α1G ∑( ∑ γ j X ji ) = α1Gξ j=1 j=1 i=1α G 1
n 2 jo n n
(3-
3.5.2 底部剪力法
式中, 为高振型影响系数, 式中,ξ为高振型影响系数,其表达式为
αj Gi 2 ξ = j∑1(i∑ γ j X ji ) = =1α G 1
n n
计算资料的统计分析表明, 计算资料的统计分析表明 , 当结构体系各质点重量 相等,并在高度方向均匀分布时, 相等,并在高度方向均匀分布时, , ξ =1.5( n为质点数n +1) /(2n +1) 为质点数。如为单质点体系(即单层建筑 即单层建筑), 为质点数。如为单质点体系 即单层建筑 , ,如 ξ =1 为无穷多质点体系, 抗震规范》取中间值, 为无穷多质点体系, 。《抗震规范》取中间值, ξ = 0.75 故式(3-5-3) ξ = 0.85 即 。故式 n n n αj Gi 2 2 FEK = ∑Vjo = α1G ∑( ∑ γ j X ji ) = α1Gξ j=1 j=1 i=1α G 1 改写为
3.5.2 底部剪力法
FEK = α1Geq
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振型分解反应谱法可以考虑多阶振型互相耦合的作用,尤其是扭转振型的耦联,如果只是单阶振型,则振型分解反应谱法和底部剪力法应该是一致的。
所以底部剪力法一般用在低层的、简单的、规则的、对称的结构中,如砌体结构住宅楼或者多层框架(新规范要求加上楼梯就又麻烦了)之类。
此外,振型分解反应谱法计算出来的地震剪力都是绝对值,没有方向,在这一点上,底部剪力法算出不同方向地震作用所引起的剪力的方向,比较有物理意义。
振型分解反应谱法:
也称规范法,适用于大量的工程计算,该法有侧刚及总刚两种计算方法,分别对应侧刚模型及总刚模型,其主要区别是侧刚模型采用刚性楼板假定的简化刚度矩阵模型。
总刚模型是采用弹性楼板假定的真实结构模型转化成的刚度矩阵模型。
振型分解反应谱法先计算结构的自振振型,选取若干个振型分别计算各个振型的水平地震作用,将各振型水平地震作用于结构上,求其结构内力,最后将各振型的内力进行组合,得到地震作用下的结构内力和变形。
其基本原理就是用“规范”反应谱,先求得各振型的对应的“最大”地震力,组合后得到结构的组合地震作用。
这里面有一个求“广义特征值”而得出结构前几阶振型和频率的重要步骤,在这个过程中程序按力学和数学的法则进行繁多的中间计算,而不输出中间资料,仅将结果值告知设计人。
底部剪力法:
底部剪力法(拟静力法)(Equivalent Base Shear Method) 根据地震反应谱理论,以工程结构底部的总地震剪力与等效单质点的水平地震作用相等,来确定结构总地震作用的方法。
一种用静力学方法近似解决动力学问题的简易方法,它发展较早,迄今仍然被广泛使用。
其基本思想是在静力计算的基础上,将地震作用简化为一个惯性力系附加在研究对象上,其核心是设计地震加速度的确定问题。
该方法能在有限程度上反映荷载的动力特性,但不能反映各种材料自身的动力特性以及结构物之间的动力响应,更不能反映结构物之间的动力耦合关系。
但是,拟静力法的优点也很突出,它物理概念清晰,与全面考虑结构物动力相互作用的分析方法相比,计算方法较为简单,计算工作量很小、参数易于确定,并积累了丰富的使用经验,易于设计工程师所接受。
但是,应该严格限定拟静力法的使用范围:它不能用于地震时土体刚度有明显降低或者产生液化的场合,而且只适用于设计加速度较小、动力相互作用不甚突出的结构抗震设计。
