电路理论习题答案 第四章
上海交通大学研究生入学考试488基本电路理论基本电路答案4

图中:
图a电路属于翻转对称,其等效电路如图c所示。图b属于旋转对称,其等效电路如图d所示。
题6.6图(c)题6.6图(d)
由图c
图d可简化为图e
题6.6图(e)
4-40试求如图所示网络中的电压v0。
解:
题6.7图
题中网络可等效为图a所示网络,如上题,电路a的解可分解为具有翻转对称网络和具有旋转对称网络两钟情况迭加。这两种情况的等效网络分别示于图b和c。
4.5解:
题4.5图
把点路图重画,去掉虚支路,并以节点4为参考节点。
根据电路图可得:
则根据系统步骤可得:
两个电源放出功率:电压源 ,电流源 。
4-6如图所示的电路中,R1=R2=R3=R4=30,R5=R6=R7=50,Vs1=Vs2=Vs3=200V,is4=10A。试用视察法列出该电路的节点方程,并求出电流i1,i2,i3和i4。
解:
题6.5图
连接于A、B两点的1A电流源可以用分别连接于A与B点至无限远处的两个1A电流源来代替,如下图所示:
然后分别求出与,由于对称的原因,每个电流单独作用时,流过R的电流为0.25A,
根据迭加定理:
4-39试求如图所示的网络中的电压v1和电流i1,设R=1Ω。
解:
题6.6图
根据迭加定理,电路解可分解为下列两种情况之和:
题6.9图(a)题6.9图(b)题6.9图(c)
入端电阻
所以,戴维宁电路如图b所示,并由此得诺顿电路如图c所示,图中:
4-43试求出如图所示网络的戴维宁等效电路。
解:
题6.10图
理想变压器的性能方程为
, ,
入端电阻由图a求得。为试验电压,有
电路理论_(4)

例:电路如图(a), 电路响应
i2 i2 iS 0 i2 uS 0 i2(1) i2(2)
u1 u1 iS 0 u1 uS 0 u1(1) u1(2)
电路等效为下图
i (1)
2
uS R1 R2
i(2)
2
R1iS R1 R2
u (1) 1
R1uS R1 R2
u(2) 1
R1R2iS R1 R2
18
二、 诺顿定理
诺顿定理:任何一个线性含源二端网络,对外电路来讲,可 以用一个电流源和电导的并联组合等效变换。其电流源的电 流 iS = isc 为网络端口的短路电流;电导Geq=(1/ Req )为网络 内部电源均为0时的端口的输入电导。
含源一端 口网络
戴维宁等效电路 诺顿等效电路
两种等效电路共有3个参数: uoc , isc ,Req 其关系为: uoc = isc Req 戴维宁等效电路和诺顿等效电路统称为一端口的等效发电机。
33
4-6 对偶原理
注意以下关系式:u Ri, i Gu 对于CCVS: u2 ri1, 对于VCCS: i2 gu1
对偶元素:电压与电流;电阻与电导;CCVS与VCCS;r与g
n
R Rk k 1
i u R
uk
Rk R
u
两个电路互为对偶
n
G Gk k 1
u i G
ik
Gk G
i
显然,在上式中将对偶元素互 换,则对应关系式彼此转换
+
6
例:4-2 求图示电路中的电压 u3 。
+
7
例:4-3 求图示电路中的电压 u3 。
+
8
线性电路的齐性定理:当所有激励(独立电压源和独立电流源) 都同时增大或减小K倍时,响应(电压或电流)也将同样增大或 减小。 例:4-4 求图示电路中的各支路电流。
电路理论基础第四章习题解答西安电子科技大学出版社
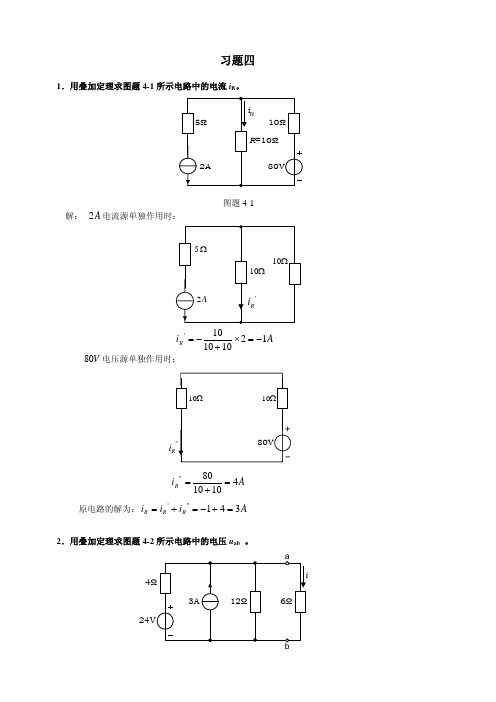
习题四1.用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解: A 2电流源单独作用时:A i R 12101010'−=×+−=V 80电压源单独作用时:i A i R 4101080''=+=原电路的解为:A i i i R R R 341'''=+−=+=2.用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解:V 24电压源单独作用时:Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时:Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为:V u u u ab ab ab 18612'''=+=+=3.用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解: A 6电流源单独作用时:ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时:Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为:()()A i i i 624'''−=−+−=+=4.图题4-4所示电路中,R =6Ω,求R 消耗的功率。
图题4-4解: 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u :12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻:eqRΩ=++×=426363eq R 原电路简化为:Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5.图题4-5所示电路中, R 1=1.5Ω R 2=2Ω,求(a )从a、b 端看进去的等效电阻;(b )i 1与i s 的函数关系。
大学电路习题第4章
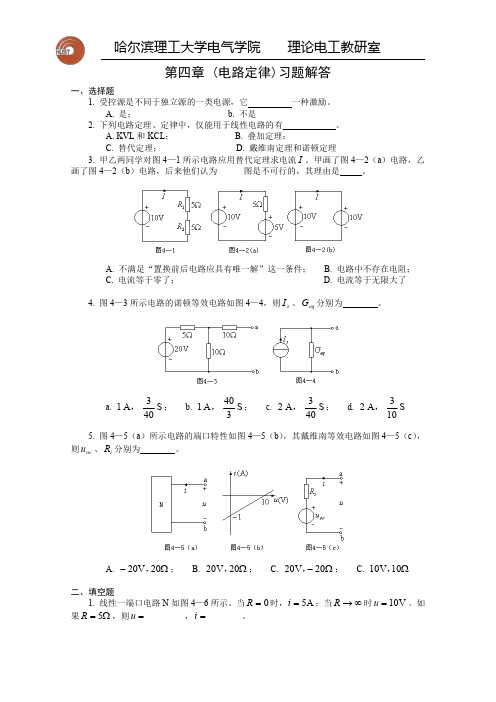
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源,它一种激励。
A.是; b.不是2.下列电路定理、定律中,仅能用于线性电路的有。
A.KVL 和KCL ; B.叠加定理;C.替代定理; D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。
甲画了图4—2(a )电路,乙画了图4—2(b )电路,后来他们认为图是不可行的,其理由是。
A.不满足“置换前后电路应具有唯一解”这一条件;B.电路中不存在电阻;C.电流等于零了;D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4,则s I 、eq G 分别为。
a.S 403A 1,;b.S 340A 1,;c.S 403A 2,;d.S 103A 2,5.图4—5(a )所示电路的端口特性如图4—5(b ),其戴维南等效电路如图4—5(c ),则oc u 、i R 分别为。
A.Ω-20V 20,;B.Ω20V 20,;C.Ω-20V 20,; C.Ω10V 10,二、填空题1.线性一端口电路N 如图4—6所示。
当0=R 时,A 5=i ;当∞→R 时V 10=u 。
如果Ω=5R ,则=u ,=i 。
2.图4—7所示电路中,N 为线性电路,且Ω=10R 。
当0=s u ,0=s i 时,V 5=u ;当A 2=s i ,0=s u 时,V 8=u ;当0=s i ,V 10=s u 时,V 6=u 。
那么,当A 6=s i ,V 4=s u 时,=i 。
3.图4—8(a )所示电路的戴维南等效电路如图4—8(b ),那么=s U ,=eq R 。
4.图4—9(a )所示电路的戴维南等效电路如图4—9(b ),则=s U ,=eq R 。
5.在图4—10(a )所示的电路中,i u 1024-=(i 的单位用安培时,u 的单位为伏特),其戴维南等效电路如图4—10(b ),则=s u ,=0R 。
三、计算题1.用叠加定理计算图4—11所示电路中的u 。
电路理论复习思考题期末复习题及答案

第1章复习思考题1-1.图1-1所示电路,试写出各电路所标出的未知电压和电流的数值。
图1-11-2.根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是电源还是负载。
(a) (b) (c)图1-21-3.直流电路如图1-3所示,求电感电流和电容电压。
图1-31-4.如图1-4所示,电路中包含的各个元件的电压和电流参考方向如图所示,其中100P 1=W ,10P 2-=W ,50P 3=W ,20P 4=W ,求5P ,元件5是电源还是负载?图1-41-5.求图1-5所示电路中的电压1u 和1i 。
图1-51-6.求图1-6所示电路中的电压u 。
3Ω2Ω4Ωi10 V图1-61-7.求图1-7所示电路中的电压U 。
2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8.图1-8所示电路中,已知5u ab -=V ,求电压源电压s u 。
图1-81-9.电路如图1-9所示,试求电压U X 。
图1-91-10.如图1-10所示的图,如果选1、2、3、4、8支路为树,则其基本回路组是什么?如果选择自然网孔为基本回路组,则其对应的树由哪些支路组成?②⑤1 2 3 4610 ④89 ⑥57 ③图1-10第2章复习思考题2-1.写出题2 1图所示各电路的端口电压电流的伏安特性方程。
(a) (b)图2-12-2.电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示,试计算a、b两端的电阻,其中电阻R=8。
(a) (b)(c)(d)(e) (f)图2-22-3. 利用电源等效变换,化简图2-3(a)和(b)的一端口网络。
(a) (b)图2-32-4.利用电源的等效变换求图示2-4电路中的电流I 。
图2-42Ω6V+I2Ω 2A7Ω6A2Ω2-5.求图2-5电路中的受控电流源的功率。
图2-5 2-6.求图2-6各电路的输入电阻R in。
图2-6第3章复习思考题3-1.用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。
电路理论基础第四版 孙立山 陈希有主编 第4章习题答案详解

教材习题4答案部分(p126)答案解:将和改写为余弦函数的标准形式,即电压、电流的有效值为初相位相位差;与同相;与正交,超前于答案答案解:(a)利用正弦量的相量表示法的线性性质得:(b)磁通相量通常用最大值表示,利用正弦量的相量表示法的微分性质得:(c) 利用正弦量的相量表示法的线性性质与微分性质得:答案解:电压表和电流表读数为有效值,其比值为阻抗模,即将已知条件代入,得联立方程,解得答案解:(a) RC串联电路中电阻电压与电容电压相位正交,各电压有效值关系为电流的有效值为(b)RC并联电路中电阻电流与电容电流相位正交,总电流有效值为(c)由并联电容、电感上电流相位相反,总电流为电阻电压与电容电压相位正交,总电压为:答案略答案解:设,则所求电流有效值为。
答案解:电压源和电流源的相量分别为对节点①和②列相量形式节点电压方程由图可知受控源控制量解得受控电流源的电压为答案解:相量模型如图(b)所示。
对节点①、②列节点电压方程:(1)(2)联立解得又因为所以即越前于的相位差为。
答案解:对含运算放大器的电路宜列写节点电压方程:(1)(2)由端口特性得(3)将式(2)(3)代入(1)得输出电压瞬时值为答案解:图示电路容抗,列节点电压方程(1)将代入(1)式解得电流答案解:由阻抗的串、并联等效化简规则得当时,由上式得,且与频率无关。
答案解:(1)求开路电压对图(a)电路列节点电压方程受控源控制量即为节点电压,即(3)将式(3)代入式(2)再与式(1)联立解得,(2)求等效阻抗在ab端外施电压源,求输入电流,与的比值即为等效阻抗。
由节点②得又答案解:对图(a)电路做戴维南等效,如图(b)所示。
(1)(2)由图(b)可知,当时,电阻两端电压与电阻无关,始终等于。
由式(1)解得将式(3)代入式(2)得答案解:先对图(a)电路ab端左侧电路作戴维南等效,如图(b)所示。
令得等效阻抗由知,欲使电流有效值为最大,电容的量值须使回路阻抗虚部为零,即:等效后电路如图(b)所示。
电路理论试题及答案
分析本电路有两处接“地”,可以将这两处的“地”用短路线相连,如图2.2(a)中虚线所示。应用电阻并联等效、电压源互换为电流源等效,将图2.2(a)等效为图2.2 (b);再应用电阻并联等效与电流源并联等效,将图2.2 (b)等效为图2.2(c)由图图2.2(c)即可简便地求得Vb。
分析若能求得N两端子上的电流、电压,即可求得PN。设
电流I,电压U的参考方向如图中所标。由KCL,KVL,和OL,求得I,U,从而便求得PN。
[评注]吸收一25w功率即是产生(供出)25w的功率。由此可判断网络N内部一定包含有电源。但不能说若PN为正值,N内就不含电掠。
例1.8图1.12所示电路,求电压u。
例1.2一确定电路,若如图1.6(a)所示所设电流I的参考方向,选b点位参考点,试计算电流I;电位Va,Vb,Vc;电压Uab,Ubc。若再如图1.6(b)所示所设电流I的参考方向,选c点位参考点,再计算电流I;电位Va,Vb,Vc;电压Uab,Ubc。
分析本问题由欧姆定律及KVL很容易计算得结果,但通过计算所要表述的有关电流、电位、电压探层次的概念是重要的。
(3)电路中任意两点之间的电压数值与参考点选在何处无关。
例1.3图1.7所示电路,求电流源IS产生的功率PS。
[评注]独立电流源不是理想电流表,不能想当然的把独立电流源两端的电压当作零。对电流源两端的电压的参考方向亦可设成与图中所标参考方向相反,那样,求得的电压值为负值,就要套用电压、电流参考方向关联情况产生功率的公式,求得其产生的功率也是100W。
解:列写图2.9(d)所示回路KVL方程,有
解得 A
[评注]在用各种电路等效方法求解含有受控源的电路时,注意,不要把控制量所在支路变化掉。本问题中,不要把控制量i所在支路即2Ω串联9V电压源支路互换等效为电流源。
电路理论 第4章
B
B
24
A
第 4 章
+ 20V _ 5Ω
+ _ 15V R3 5 Ω 3Ω
R4 4Ω B
I
有源二端网络等效为电 流源模型 ——诺顿定理 有源二端网络等效为电 压源模型—— 戴维南定理
有 源 二 端 网 络
R4 4Ω
I
等 效 电 源
R4 4Ω
第四章
第 4 章
电路分析方法之三
--电路定理法
叠加原理 等效电源定理 特勒根定理 互易定理
教学重点:替代定理
难点:线性电路的线性关系 戴维南定理 特勒根定理 运用多个定理的综合解题
1
§4-2 替代定理或置换定理
第 4 章
替代定理(又称置换定理): 在具有唯一解的线性网络中,若某条支路的电压UK (或电流IK)为已知,则这条支路可以用一个电压值为 UK的独立电压源(或用一个电流值为IK的独立电流源) 来替代,若替代后电路仍具有唯一解,则该网络所有支 路的电压和电流均保持不变。 说明: 1. 替代定理适用于线性、非线性电路、定常和时变电路。 2. 替代定理的应用必须满足的条件: 1) 原电路和替代后的电路必须有唯一解。 2) 被替代的K支路必须是独立的、和电路其它 部分应无耦 合及受控关系。
I1 2Ω I2 10A I 3 1Ω I4 4Ω 5Ω + 10V _
原电路 根据叠加定理
I1’’ 2Ω I2’’ I3’’ 1Ω I4’’ 4Ω 5Ω + 10V _
11
I 1 = I 1 ′ − I 1 ″, I 2 = I 2 ′ − I 2 ″ I3 = I3′ + I3 ″, I4 = I4 ′ + I4 ″
US"= 10I1 " + U1" =10×1.6 + 9.6 =25.6V US= US' +US"=-6+25.6=19.6V
电路理论第4章-电路定理
本章主要内容
一、叠加定理
四、戴维南定理和诺顿定理 五、最大功率传输定理
第四章、电路定理
一、叠加定理
几个概念 (1)线性电阻:电阻的伏安特性曲线为线性。
R为常数,符合u=iR 。
(2)激励:独立电源又称为激励,由于它的存在, 电路中能够产生电流或电压。
(3)响应:由激励在电路中产生电流或电压称 为响应。
(3)、有源二端网络:二端网络中含有电源。
有源二端网络:
第四章、电路定理 四、戴维南定理和诺顿定理 说明有源一端口网络,其对外的最简等效电路是一
个电压源与电阻的串联.
等效
第四章、电路定理
四、戴维南定理和诺顿定理
1. 戴维宁定理
任何一个线性含源一端口网络,对外电路来说,
总可以用一个电压源和电阻的串联组合来等效置
+-+-UUoocc
66
66
bb 10V
44
+–
+ Req Uoc
–
Ia Rx b
①求开路电压
Uoc = U1 - U2 = -104/(4+6)+10 6/(4+6) = 6-4=2V
②求等效电阻Req
Req=4//6+6//4=4.8
③ Rx =1.2时,
I= Uoc /(Req + Rx) =0.333A
u(2) (6i(2) 6) (21) 8V u u(1) u(2) 9 8 17V
3A
+ - 6 i (2)
+ u(1)
6 3
1
- 6V
+
3+u(2) - +
12V -
1 2A
电路理论 第4章习题答案
解:1)U = 10∠15° V ( ɺ
−
C
电路吸收功率最大, 电路发生谐振 . 电路吸收功率最大,即 1 1 ∵ω = ⇒ 2500 = ⇒ L = 0.02 Η LC 8 × 10 −6 × L U2 U 2 10 2 ∵P = ∴R = = = 1Ω R P 100
ωL 2500 × 0 .02 ∴Q = = = 50 R 1
时电路发生谐振, 如当 ω = 1000rad / s时电路发生谐振,求电 路 谐振时电容 C的值和电流源的端电压 U . 的值和电流源的端电压
解:
ɺ IS
+ ɺ U −
R1
C
L
R2
jωL = j1000 × 0.2 = j 200Ω
R2 ⋅ jωL 100× j200 Z2 = = = 80 + j40Ω R2 + jωL 100 + j200
图示电路, 4-13 图示电路,试确定方框内最简单的等效串联 组合的元件值。 组合的元件值。
+ u=100cos2tV i=10cos(2t+60o)A
解:
ɺ ɺ (a ) U m = 100∠ 0° V, I m = 10∠ 60° A
ɺ Um 100∠0° Z= = = 10∠ − 60° = 5 − j8.66Ω ɺ Im 10∠60° 1 ∴ R = 5Ω , = 8.66 ⇒ C = 0.0577 F ωC
∴ZL = 1.943∠ .88° = 1.86 + j0.564 16
2 UOC 7.7632 P = = = 8.10W max 4Ri 4×1.86
4 − 41 u S = 2 cos 10 t V, r = 1 , 问负载阻抗 Z L为多少时
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ch4电路定理习题、电路如图4-51所示,若电压源的电压若电压源的电压U s>1V V ,则电路的功率情况是怎样的?解:211i A i =+21S U i =Ω111S U i ∴=+1S U V >1101S U i =->10US S P U i ∴=-⋅<20R S P U i =⋅>110S SP A U A U =-⋅⨯=-<若则(产生)(吸收)(产生)4.5、图4-54,求a,b 两点间的电压.解:()1110i A⇒=---=Ω()2213i A A=--=由KCL 定理则2A 流过525328220ab U i A V A ∴-++⨯-+⨯=45332817ab U V∴=+⨯+⨯-=3i 2i 1i4.9、电路如图4-58所示。
求结点①与结点②之间的电压u 12。
()13434831U U +-=--⨯()34515825SU U A A-++=-3122211,0U V U V U V=⇒==121211U U U V∴=-=参考点选在②点:对④点,解:对①点:4.10、已知线性含源单口网络与外电路相连,如图4-59所示,且已知ab 端口电压,而ab 端口的短路电流,试求出单口网络N 的戴维南等效电路。
线性含源单口网络Na b+U5k Ω2.5K Ω20V +-解:1204052553OC V U V=⨯=+⇒40540312.55333OCO U V VR -=-⨯Ω++12403103OC SC O U I I I mAS R =+=+=10OC U V ⇒=05RK =Ω0152.5//53R K K =ΩΩ=Ω设ab 的左边等效为01R 1OC U 和的串联:OCU o R 网络N 也用和等效当端口短路时:由①、②+_1OCU 01R +-oR OCU 10sc I mA =4.10、已知线性含源单口网络与外电路相连,如图4-59所示,且已知ab 端口电压,而ab 端口的短路电流,试求出单口网络N 的戴维南等效电路。
线性含源单口网络Na b+U5k Ω2.5K Ω20V +-解:40540312.5(2)5333OCO U V VR -=-⨯Ω++10OC U V⇒=05R K =Ω当端口短路时:由①、②+_1OCU 01R +-oR OCU 403V 53Ω1240310(1)3SC OC O I I I U mA S R =+=+=SCI SCI 1I 2I scI 10sc I mA =、已知线性电阻网络如图所示,当2A 电流源没接入时,3A 电流源对网络提供功率54W,且知U2=12V;当3A 电流源没接入时,2A 电流源对网络提供28W 功率,且知U3=8V 。
﹙1﹚求两电源同时接入时,各电源的功率。
﹙2﹚试确定网络N 最简单的一种结构和元件参数值。
3A22’+-2AU 3+-U 211’解:3A22’+-2AU 3+-U 211’()()1123,U U ()133541833P A U V A ===()1212U V=当3A 作用,分量用表示()()2223,U U ()222281422P A U V A ===()238U V=当2A 单独作用时,分量用表示当两电源共同作用时,()()12222121426U U U V V V =+=+=()()1233318826U U U V V=+=+=()22222652A P A U w =-⨯=-⨯=-()33332678A P A U w =-⨯=-⨯=-3A22’+-2AU 3+-U 211’2)23U U ≠ 用如下网络代替235i A A A =+=22526(1)Z R R AU V⨯+⨯==R ⨯ZR Y R 且已知当2A 单独作用时:()()222314, 8U V U V==()()()()22231481322xU U R --∴===Ω同理3A 单独作用时:()()112312, 18U V U V==()()11321812233Y U U R A --∴===Ω4Z R ∴=Ω将Rx=13代入(1)式,得:4.13、No 为无源线性电阻网络,R1可调,R2固定,当US=8V 时,R1=0时,I2=0.2A ;当逐渐增大R1值时,使I2=0.5A 时,R1端电压U1=5V ,如图4-62(a)所示,当US=20V 时,变化R1值,使I2=2A ,如图4-62(b)所示,试问此时R1端电压U1为何值。
可用替代定理将R1用U1电压源替代,解:2121S I K U K U =⋅+⋅1211122112210.2,8,000.2804030.5,8,50.58550S S K I A U V R U V K K I A U V U V K K K ====⇒=⇒=⨯+⨯⎫⇒⎬===⇒=⨯+⨯⎭=时时2121S I K U K U =⋅+⋅211122112120.2,8,000.2800.5,8,50.585140350S S I A U V R U V K K I A U V U V K K K K ===⇒=⇒=⨯+⨯⎫⎬===⇒=⨯+⨯⎭=⇒=时时21211120,22032202254050S U V I A A K K U U U V∴==⇒=⨯+⋅⇒=+⇒=时4.14、已知图中非线性电阻为流控电阻,其伏安关系为U=-2i +12,试用代文宁定理求出电压U 。
i +-U2Ω2A2Ω4Ω5V4V1)先求a ,b 右边的戴维南等效电路。
2Ω2A2Ω4Ω5V 4VAB+-+-2Ω2A2Ω4Ω4V AB+-+-5V +-)先求a ,b 右边的戴维南等效电路。
2Ω2A2Ω4Ω4V AB+-+-5V 0R 01202R V =Ω+=Ω求2Ω2A2Ω4Ω4V AB+-+-5V OCU 2240OC U V V=-⨯+=求,2)0i A=221212u i i U V=-+⇒=4.15、已知图4-64所示电路,补充,电阻获得的最大功率=5W,试求:和。
55R =ΩS U m g 。
I-14V +-R 53ΩU S +-g m U 22Ω1Ω1ΩU2+-解:OCU 1)先求12m i g U =-列网孔方程:()211131S i i U ++-⋅=-i2i1()225(1)m Si g U U ∴⋅--=-OC U +-补充方程:221(2)U i =-⨯(2)代入①25Sm U i g ⇒=-()122421425SOCm m U U V i i V g U g =++⨯=+⨯-+-245S m S m U g U g +=+-4.15、已知图4-64所示电路,补充,电阻获得的最大功率=5W,试求:和。
55R =ΩS U m g 。
I-14V +-R 53ΩU S +-g m U 22Ω1Ω1ΩU2+-I2I1U +-补充方程:②求0R 令内部独立源为0,a,b 端加U I3()()()()3213211212111310I I I U I I I +--⨯-=--⨯-+++-⨯=()2321U I I =⨯-列网孔方程:1465m mg UR UsI g +∴==-1465m mg UR UsI g +∴==-245S m Sm U g U UOC g +=+-最大功率定理知0551m R R g ==Ω⇒=2200max005105ccc U U P W U V R =⇒=⇒=±21410818.671.5S SS S U U V U V U V+⨯⨯∴+=±⇒=-=或。
