流体管路流动阻力系数的测定
化工原理实验~流体流动阻力系数的测定实验报告
流体流动阻力系数的测定实验报告一、实验目的：1、掌握测定流体流动阻力实验的一般实验方法。
2、测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。
3、验证湍流区内摩擦阻力系数λ为雷诺系数Re和相对粗糙度的函数。
4、将所得光滑管的λ—Re方程与Blasius方程相比较。
二、实验器材：流体阻力实验装置一套三、实验原理：1、直管摩擦阻力不可压缩流体（如水），在圆形直管中做稳定流动时，由于黏性和涡流的作用产生摩擦阻力；流体在流过突然扩大、弯头等管件时，由于流体运动的速度和方向突然变化，产生局部阻力。
影响流体阻力的因素较多，在工程上通常采用量纲分析方法简化实验，得到在一定条件下具有普遍意义的结果，其方法如下。
流体流动阻力与流体的性质，流体流经处的几何尺寸以及流动状态有关，可表示为△P=f (d, l, u,ρ,μ,ε)引入下列无量纲数群。
雷诺数Re=duρ/μ相对粗糙度ε/ d管子长径比l / d从而得到△P/(ρu2)=ψ(duρ/μ，ε/ d， l / d)令λ=φ（Re，ε/ d）△P/ρ=（l / d）φ（Re，ε/ d）u2/2可得摩擦阻力系数与压头损失之间的关系,这种关系可=△P/ρ=λ（l / d）u2/2用试验方法直接测定。
hf——直管阻力，J/kg式中，hfl——被测管长，md——被测管内径，mu——平均流速，m/sλ——摩擦阻力系数。
当流体在一管径为d的圆形管中流动时，选取两个截面，用U形压差计测出这两个截面间的静压强差，即为流体流过两截面间的流动阻力。
根据伯努利方程找出静压强差和摩擦阻力系数的关系式，即可求出摩擦阻力系数。
改变流速可测出不同Re下的摩擦阻力系数，这样就可得出某一相对粗糙度下管子的λ—Re关系。
（1）、湍流区的摩擦阻力系数在湍流区内λ=f（Re，ε/ d）。
对于光滑管，大量实验证明，当Re在3×103~105范围内，λ和Re的关系遵循Blasius关系式，即λ=0.3163 / Re0.25对于粗糙管，λ和Re的关系均以图来表示。
流体流动阻力的测定实验报告2
1.93 0.00054 1.31 1.477 32322 0.0172
2.24 0.00062 1.61 1.715 37513 0.0157
2.61 0.00073 2.01 1.998 43710 0.0145
3.00 0.00083 2.51 2.297 50241 0.0137
查表得：21.3℃下水的密度 998.2kg/m³，粘度为 0.981mpa*s 以第三组数据为例： 流量：q=0.93m³/h=0.00026m³/s 流速：u=q/A= 雷诺数：Re= 由 hf
突然扩大管的局部阻力系数数据表 水流量（m ³ / h ) 1.99 3 4.04 压降（k P a ) 1.04 2.35 4.44 流速u 2 （m / s ) 0.3992 0.6018 0.8104 流速u 1 （m / s ) 2.7507 4.1468 5.5843 局部阻力系数ζ 1.2544 1.2528 1.2643
局部阻力数据记录表
扩 大 管 水流量/ m .h 压降/kPa
3 -1
1.99 1.06
3.00 2.37
4.04 4.46
管径：由 Φ(22×3) mm 扩大到 Φ(48×3) mm(23.2℃，初始压降 0.02kpa)
层流管数据记录表 时间/s 体积/ml 压降 /kpa 温度/℃ 180 118 0.44 24.5 120 162 0.94 24.3 120 208 1.34 24.6 90 202 1.48 24.9 60 163 1.84 25.1 60 200 2.46 25.6 层流管 径 Φ(6×1.5) 长 1.5m,
0.87 1.05 2.42E-04 2.92E-04 0.698 0.843 0.58 0.77 15379 18561 0.0334 0.0304
流体流动阻力的测定实验报告
流体流动阻力的测定实验报告一、实验目的1、掌握流体流经直管和管件时阻力损失的测定方法。
2、了解摩擦系数λ与雷诺数 Re 之间的关系。
3、学习压强差的测量方法和数据处理方法。
二、实验原理流体在管内流动时，由于黏性的存在，必然会产生阻力损失。
阻力损失包括直管阻力损失和局部阻力损失。
1、直管阻力损失根据柏努利方程，直管阻力损失可表示为：＼（h_f ＝＼frac{＼Delta p}｛ρg}＼）其中，＼（h_f\）为直管阻力损失，＼（＼Delta p\）为直管两端的压强差，＼（ρ\）为流体密度，＼（g\）为重力加速度。
摩擦系数\（λ\）与雷诺数\（Re\）及相对粗糙度\（＼frac{＼epsilon}｛d}＼）有关，其关系可通过实验测定。
当流体在光滑管内流动时，＼（Re ＜ 2000\）时，流动为层流，＼（λ ＝＼frac{64}｛Re}＼）；＼（Re ＞ 4000\）时，流动为湍流，＼（λ\）与\（Re\）和\（＼frac{＼epsilon}｛d}＼）的关系可由经验公式计算。
2、局部阻力损失局部阻力损失通常用局部阻力系数\（＼zeta\）来表示，其计算式为：＼（h_f' ＝＼frac{＼zeta u^2}｛2g}＼）其中，＼（h_f'＼）为局部阻力损失，＼（u\）为流体在管内的流速。
三、实验装置1、实验设备本实验使用的主要设备包括：离心泵、水箱、不同管径的直管、各种管件（如弯头、三通、阀门等）、压差计、流量计等。
2、实验流程水箱中的水经离心泵加压后进入实验管路，依次流经直管和各种管件，最后流回水箱。
通过压差计测量直管和管件两端的压强差，用流量计测量流体的流量。
四、实验步骤1、熟悉实验装置，了解各仪器仪表的使用方法。
2、检查实验装置的密封性，确保无泄漏。
3、打开离心泵，调节流量至一定值，稳定后记录压差计和流量计的读数。
4、逐步改变流量，重复上述步骤，测量多组数据。
5、实验结束后，关闭离心泵，整理实验仪器。
流体流动阻力测定实验指导书
化工原理实验辅助讲义化工原理实验指导书姜少华编五邑大学化工与环境基础实验教学中心2006年9月实验一流体流动阻力的测定一、实验目的1．把握测定流体流经直管、管件和阀门时阻力损失的一样实验方式。
2．测定直管摩擦系数λ与雷诺准数Re的关系，验证在一样湍流区内λ与Re的关系曲线。
3．测定流体流经管件、阀门时的局部阻力系数。
4．学会无纸记录仪和涡连番量计的利用方式。
5．识辨组成管路的各类管件、阀门，并了解其作用。
二、大体原理流体通过由直管、管件（如三通和弯头等）和阀门等组成的管路系统时，由于粘性剪应力和涡流应力的存在，要损失必然的机械能。
流体流经直管时所造成机械能损失称为直管阻力损失。
流体通过管件、阀门时因流体运动方向和速度大小改变所引发的机械能损失称为局部阻力损失。
1．直管阻力摩擦系数λ的测定流体在水平等径直管中稳固流动时，阻力损失为：（1）即，（2）式中：λ —直管阻力摩擦系数，无因次；d —直管内径，m；—流体流经l米直管的压力降，Pa；—单位质量流体流经l米直管的机械能损失，J/kg；ρ —流体密度，kg/m3；l —直管长度，m；u —流体在管内流动的平均流速，m/s。
滞流(层流)时，（3）（4）式中：Re —雷诺准数，无因次；μ —流体粘度，kg/(m·s)。
湍流时λ是雷诺准数Re和相对粗糙度（ε/d）的函数，须由实验确信。
由式（2）可知，欲测定λ，需确信l、d，测定、u、ρ、μ等参数。
l、d为装置参数（装置参数表格中给出），ρ、μ通过测定流体温度，再查有关手册而得，u通过测定流体流量，再由管径计算取得。
例如本装置采纳涡连番量计测流量，V，m3/h。
(5)可用U型管、倒置U型管、测压直管等液柱压差计测定，或采纳差压变送器和二次仪表显示。
（1）当采纳倒置U型管液柱压差计时(6)式中：R－水柱高度，m。
（2）当采纳U型管液柱压差计时(7)式中：R－液柱高度，m；－指示液密度，kg/m3。
流体管路阻力系数的测定
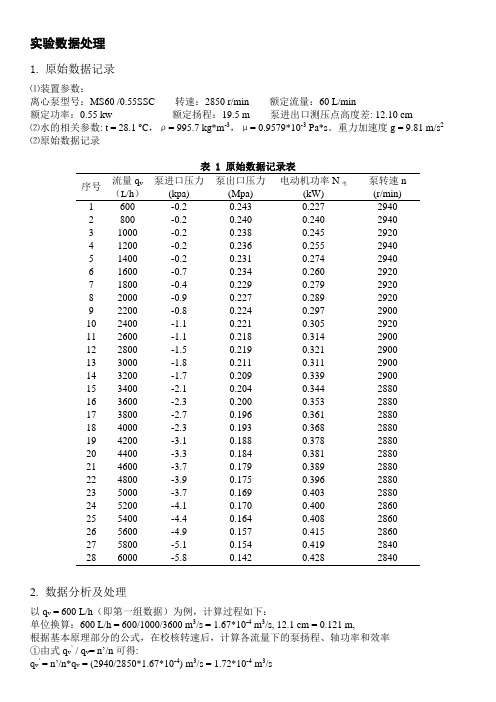
实验数据处理1.原始数据记录⑴装置参数：离心泵型号：MS60 /0.55SSC 转速：2850 r/min 额定流量：60 L/min额定功率：0.55 kw 额定扬程：19.5 m 泵进出口测压点高度差: 12.10 cm⑵水的相关参数: t = 28.1 o C，ρ= 995.7 kg*m-3，μ= 0.9579*10-3 Pa*s。
重力加速度g = 9.81 m/s2⑵原始数据记录表 1 原始数据记录表序号流量q v（L/h）泵进口压力(kpa)泵出口压力(Mpa)电动机功率N电(kW)泵转速n(r/min)1 600 -0.2 0.243 0.227 29402 800 -0.2 0.240 0.240 29403 1000 -0.2 0.238 0.245 29204 1200 -0.2 0.236 0.255 29405 1400 -0.2 0.231 0.274 29406 1600 -0.7 0.234 0.260 29207 1800 -0.4 0.229 0.279 29208 2000 -0.9 0.227 0.289 29209 2200 -0.8 0.224 0.297 290010 2400 -1.1 0.221 0.305 292011 2600 -1.1 0.218 0.314 290012 2800 -1.5 0.219 0.321 290013 3000 -1.8 0.211 0.311 290014 3200 -1.7 0.209 0.339 290015 3400 -2.1 0.204 0.344 288016 3600 -2.3 0.200 0.353 288017 3800 -2.7 0.196 0.361 288018 4000 -2.3 0.193 0.368 288019 4200 -3.1 0.188 0.378 288020 4400 -3.3 0.184 0.381 288021 4600 -3.7 0.179 0.389 288022 4800 -3.9 0.175 0.396 288023 5000 -3.7 0.169 0.403 288024 5200 -4.1 0.170 0.400 286025 5400 -4.4 0.164 0.408 286026 5600 -4.9 0.157 0.415 286027 5800 -5.1 0.154 0.419 284028 6000 -5.8 0.142 0.428 28402.数据分析及处理以q v = 600 L/h（即第一组数据）为例，计算过程如下：单位换算：600 L/h = 600/1000/3600 m3/s = 1.67*10-4 m3/s, 12.1 cm = 0.121 m,根据基本原理部分的公式，在校核转速后，计算各流量下的泵扬程、轴功率和效率①由式q v’ / q v= n’/n可得:q v’= n’/n*q v = (2940/2850*1.67*10-4) m3/s = 1.72*10-4 m3/s②扬程H = H0 + (p2 –p1)/（ρg）= 0.121+( 0.243*1000000+0.2*1000)/(9.81*995.7) = 25.02 m由式H’ / H = (n’/n)2可得:H’ = (n’/n)* H = [(2850/2940)2*23.26] m = 23.51 m③轴功率N = N电*0.95 = (0.227*0.95) = 0.216 kw由式N’ / N = (n’/n)3可得:N’= (n’/n)3*N = [(2850/2940)3*0.216] kw = 0.196 kwη= (q v Hρg/N) *100% = (1.67*10-4*25.02*995.7*9.81/0.216/1000)*100% = 18.93% η’ = (q v’H’ρg/N’) = (1.72*10-4*23.51*995.7*9.81/0.196/1000)*100% = 20.11%按此方法，对后面几组数据实施同样的计算，列出表格如下：表2 离心泵特性曲线数据处理表序号q v×10-4（m3/s)q v’×10-4（m3/s)H（m）H’（m）N（kW）N’（kW）η/% η/’%1 1.67 1.62 25.02 23.51 0.216 0.196 18.93 20.112 2.22 2.15 24.71 23.22 0.228 0.208 17.68 18.783 2.78 2.71 24.51 23.35 0.233 0.216 17.18 18.124 3.33 3.23 24.30 22.84 0.242 0.221 16.36 17.395 3.89 3.77 23.79 22.36 0.260 0.237 14.91 15.846 4.44 4.34 24.15 23.00 0.247 0.230 15.95 16.837 5.00 4.88 23.61 22.49 0.265 0.246 14.53 15.338 5.56 5.42 23.45 22.34 0.275 0.255 13.93 14.709 6.11 6.01 23.14 22.34 0.282 0.268 13.38 14.0210 6.67 6.51 22.86 21.78 0.290 0.269 12.87 13.5811 7.22 7.10 22.55 21.78 0.298 0.283 12.33 12.9212 7.78 7.64 22.70 21.92 0.305 0.289 12.14 12.7213 8.33 8.19 21.91 21.16 0.295 0.280 12.10 12.6814 8.89 8.74 21.69 20.95 0.322 0.306 10.99 11.5115 9.44 9.35 21.22 20.78 0.327 0.317 10.59 11.0216 10.00 9.90 20.83 20.40 0.335 0.325 10.13 10.5517 10.56 10.45 20.46 20.04 0.343 0.332 9.73 10.1318 11.11 11.00 20.12 19.70 0.350 0.339 9.39 9.7719 11.67 11.55 19.69 19.28 0.359 0.348 8.94 9.3120 12.22 12.09 19.30 18.90 0.362 0.351 8.70 9.0521 12.78 12.64 18.83 18.44 0.370 0.358 8.31 8.6522 13.33 13.19 18.44 18.05 0.376 0.365 7.99 8.3223 13.89 13.74 17.80 17.43 0.383 0.371 7.58 7.8924 14.44 14.39 17.94 17.82 0.380 0.376 7.70 7.9625 15.00 14.95 17.36 17.24 0.388 0.384 7.31 7.5526 15.56 15.50 16.70 16.58 0.394 0.390 6.91 7.1427 16.11 16.17 16.41 16.52 0.398 0.402 6.72 6.9028 16.67 16.73 15.25 15.36 0.407 0.411 6.12 6.28注：t是水的温度，q v是水的流量，N电是电动机功率，p1 是泵进口压力，p2是泵出口压力，n 是泵转速，ρ是水的密度，q V’是校核流量，H是扬程，H’是校核扬程，N是轴功率，N’是校核轴功率，η是效率，η’是校核效率。
流体流动阻力的测定(化工原理实验报告)
流体流动阻力的测定（化工原理实验报告）流体流动阻力的测定（化工原理实验报告）摘要：本实验研究了流体流动阻力的测定方法，以了解流阻比数据和参数对流体流动特性的影响。
实验中采用了空心管实验装置，在一定的压差试验条件下，通过压力表和熨斗流量计测量压力和流量，计算出流阻比系数。
通过实验，研究了流阻比系数随着实验参数（流量、温度、压力）变化的规律，从而获得一定规律性的微观流动特性数据。
关键词：流阻比；熨斗流量计；实验；流动阻力1 前言流体流动阻力是研究流体流动特性的一项重要参数。
它决定了流体在管道内流动时会受到什么样的阻力，直接影响着流体在设备内的流动性能和传热特性。
因此，准确测量流体流动阻力是研究管道流动的关键问题。
本实验旨在研究空心管装置测量的流阻比数据对流体流动特性的影响，以便获得微观流动特性数据，并用于管道设计、传热学的研究中。
2 实验目的1）研究在空心管实验装置内测量流阻比系数的变化规律：2）利用测量的流阻比系数，得出瞬态流体流动特性曲线，即流量与压力的变化规律； 3）通过实验有规律地分析，获得实验流体的微观流动特性参数。
3 实验装置本实验主要采用空心管实验装置（见图1），由电磁阀控制罐内的液体，带动空心管内的流体循环，保持流量一定，从而实现实验的要求。
该装置由如下几个部分组成：（1）空心管；（2）球阀；（3）高低压罐；（4）汽缸和气缸；（5）液体泵；（6）电磁阀；（7）水箱；（8）熨斗流量计；（9）压力表；（10）温度计。
4 实验方法1）确定实验条件：根据实验任务，确定温度、压力、流量等参数，以及电磁阀的控制时间；2）进行实验：根据实验条件，控制电磁阀的开启和关闭，实现空心管内的液体流动，同时调节实验参数，测量压力及流量；3）根据压力和流量，绘出流量-压力曲线，计算出对应的流阻比系数；4）根据实验数据，进行实验数据分析，探究实验参数变化时，流阻比系数变化规律，得出流体的微观流动特性参数。
5 实验数据在实验中，调节不同的参数，实现不同的实验条件，测量得到流量和压力的数据，根据测量的实验数据，画出Flow-Pressure曲线，结果如下表1所示：实验条件实测压力(MPa) 实测流量（M3/h）流阻比(MPa/m3/h)条件1 0.39 0.159 0.80条件2 0.51 0.159 1.06条件3 0.62 0.159 1.29条件4 0.68 0.159 1.41条件5 0.80 0.159 1.64表1 实验结果图2 Flow-Pressure曲线图6 结论1）根据上述的实验结果，可以发现，随着压力和流量的增加，流阻比也相应地增大；2）通过分析实验数据，可以获得一定的规律性的微观流动特性数据，即通过把不同的实验参数变量并入方程式中，可以根据需要精确地预测不同条件下，流体流动时的压力和流量变化规律；3）该测试结果可以作为设计管路时流体传热特性和流动特性的参考，更好地掌握管路中流体的流动特性。
流体管路流动阻力系数的测定
流体管路流动阻力系数的测定1 绪论流体基本理论为物理设计工程提供了基本的设计和分析方法，而流体管路流动阻力系数是求解流体传动系统、蒸汽系统、水喷射柴油发动机系统等的基本模型，已广泛地用于工程设计和实验测试的方法中。
应用阻力系数来分析流体流动在管路系统中的分布特性及流动状态，对工程设计中的管路系统有重要的导向作用，其精确的测试对工程实际应用至关重要。
2 流体管路流动阻力系数的测定主要从两个方面考虑，即实验测定管路内部阻力系数和实验测定管路外部阻力系数。
实验参数主要包括管路外表面断面积、流体性能参数、流体流量和管路弯曲参数等，其中流体性能参数对实验结果影响最大。
（1）内部阻力系数测试管路内部阻力基本理论分析公式是：f = 0.0775(N/D)(ρ/μ)0.5。
其中f是管道内部阻力系数，N为流体质量流量，D为管径，ρ为流体密度，μ为流体粘度。
另外，直管情况下，管路内部阻力系数计算公式f = 0.0225(N/D2)(ρ/μ)0.5，弯曲情况下，管路内部阻力系数计算公式f = 0.075(N/D2)(ρ/μ)0.5。
管路内部阻力系数测试一般采用内部试验管路，通过在里头装压力表，测量管路端部压力差，得到阻力系数f。
流体流动在管路系统中的外部阻力系数的近似计算公式是：f = k/D，其中f是管道外部阻力系数，k是摩擦係数，D为管径。
外部阻力系数测试一般采用蒙特卡洛试验，一般原理是通过在不同管路中改变流体流量，来获得不同的阻力表达式，从而求取摩擦係数。
3 结论流体管路流动阻力系数是求解流体传动系统、蒸汽系统、水喷射柴油发动机系统等的基本模型，精确的测试对工程实际应用至关重要。
管路内部阻力系数的测试主要通过在管路内安装压力表，测量压降求出；外部阻力系数测试一般采用蒙特卡洛法，通过获得不同的阻力表达式求取摩擦係数。
管路流体流动阻力的测定(华南师范大学)
实验四管路流体流动阻力的测定一、实验目的1、掌握流体流动阻力的测定方法2、测定流体流过直管时的摩擦阻力，并确定摩擦系数λ与雷诺数Re 的关系3、测定流体流过管件的局部阻力，并求出阻力系数。
二、实验原理流体在管路中流动时，由于粘性剪应力和涡流的存在，不可避免地会引起压力损耗。
这种损耗包括流体经过直管的沿程阻力以及因流体流动方向改变或因管子大小形状改变所引起的局部阻力。
1、直管阻力损失的测定不可压缩流体连续稳定地在直管中流动时，相距l 米的任意两个截面1-1和2-2间的机械能恒算可以用下式来表示：2211221222fp u p u gz gz h ρρ++=+++（4-1）或者2211221222fp u p u z z H g g g gρρ++=+++（4-2）式中：1z ，2z ——截面1-1和截面2-2距基准面的高度，m1p ，2p ——流体在截面1-1和截面2-2处的绝对压强，Pa ；1u ，2u ——流体在截面1-1和截面2-2处的流速，m ·s -1；ρ——流体的密度，kg ·m -3f h ——单位质量流体流过l 米距离时的直管阻力损失，J ·kg -1f H ——单位重量流体流过l 米距离时的直管阻力损失，m。
当两个截面管径相等，并处于同一水平面时，则有12z z =，12u u u==分别代入式（4-1）和式（4-2）得：12f p p ph ρρ-==（4-3）以及12f p p pH g gρρ-== （4-4）应用上述两式均可计算出流体的直管阻力损失，其大小主要体现在所取两截面的压差12p p -上。
因此，只需测得所取截面的压差，便可得到直管阻力损失。
2、直管摩擦系数λ和雷诺数Re 的测定当流体在圆形直管内流动时，直管的阻力损失可通过范宁（Fanning ）公式进行计算：22f l u h d λ=⋅（4-5）或22f l u H d g λ=⋅（4-6）式中：λ——直管的摩擦系数，无量纲；l ——直管的长度，m ；d ——直管的内径，m ；大量实验研究表明，摩擦系数λ与流体的密度ρ、粘度μ、管径d 、流速u 和管壁粗糙度e 有关应用因次分析的方法，可以得出摩擦系数与雷诺数和管壁相对粗糙度e/d 存在函数关系，即：(Re,ef dλ=（4-7）通过实验测得λ和Re 数据，可以在双对数坐标上标绘出实验曲线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
五、数据处理
1、局部阻力管的原始数据以及相关处理数据
局部阻力管（不锈钢+闸阀） 18℃水的密度：ρ=998.2kg/m3
管内径：20 mm 18℃水的粘度：1.0559×10-3 Pa·s
测量段长度：1000mm
2、光滑管的原始数据以及相关处理数
光滑管（不锈钢） 18℃水的密度：ρ=998.2kg/m3
管内径：20 mm 18℃水的粘度：1.0559×10-3 Pa·s 测量段长度：1000mm
序 号 体积流量
（m 3/h)
左 （cmH 2O ）
右 （cmH 2O ）
差 值 （Pa)
流
速 （m/s)
雷 诺 数
(Re)
摩
擦
阻 力 系 数
(λ)
Blasius 公 式 下
算出的λ 绝对误差 相对误差
1 0.5 72.5 74 147.13 0.44 8287.73 0.0305 0.0287 0.001751 6.10%
2 1 70.5 74.5 392.35 0.88 16575.45 0.020
3 0.0279 -0.00357 -14.95% 3 1.5 68 77 882.79 1.33 25051.53 0.0200 0.0251 -0.00139 -6.49%
4 2 64.
5 78.5 1373.23 1.77 33339.2
6 0.0176 0.0234 -0.00226 -11.38% 5 2.5 59.5 81.5 2157.94 2.21 41626.98 0.017
7 0.0222 -0.0009
8 -5.24% 6 3 53.5 84.5 3040.73 2.65 49914.71 0.0174 0.0212 -0.00045 -2.54% 7 3.5 46 88 4119.70 3.1 58390.7
9 0.0172 0.0204 0.000102 0.60% 8
4 39
91
5100.58
3.54
66678.52
0.0163
0.0197
-0.00017
-1.05%
3、粗糙管的原始数据以及相关数据处理
粗糙管（镀锌铁管） 18℃水的密度：ρ=998.2kg/m 3
管内径：20 mm 18℃水的粘度：1.0559×10-3 Pa·s 测量段长度：1000mm
y = 0.3022x - 0.266
R² = 0.8749
0 0.005
0.01 0.015 0.02 0.025 0.03 0.035 0
20000
40000
60000 80000
-
序
号 体积流量 （m 3/h) 左 （cmH 2O ）
右 （cmH 2O ）
差值
（Pa)
流
速
（m/s)
雷诺数
(Re) 摩擦阻力系
数 (λ)
1 0.5 7
2 74 196.18 0.44 8331.45 0.0402 2 1 69.5 75.5 588.5
3 0.88 16662.90 0.0301 3 1.5 65 79 1373.23 1.33 24994.35 0.0313
4 2 58 83.
5 2501.25 1.77 33325.79 0.0320 5 2.5 50 89 3825.44 2.21 41657.24 0.0313 6
3
39
97.5
5738.15
2.65
49988.69
0.0326
4、根据计算所得的粗糙管和光滑管的实验结果，在同一对数坐标上绘制曲线：
对照《化工基础》教材上的曲线图（如下）,估算出两管的相对粗糙度和绝对粗糙度
y = 0.092x - 0.102
R² = 0.4247
y = 0.3022x - 0.266
R² = 0.8749
0 0.005
0.01 0.015 0.02 0.025 0.03 0.035 0.04 0
20000
40000
60000
80000
光滑管、粗糙管在同一坐标轴上的λ-Re 曲线
-
光滑管 粗糙管 乘幂 ( 粗糙管 ) 乘幂 ( 光滑管 )
已知光滑管和粗糙管的管内径都为20mm,将光滑管和粗糙管的λ和Re值代入上图可估算为粗糙管的相对
粗糙度为0.004，绝对粗糙度约为0.00008；光滑管的相对粗糙度约为0.0001，绝对粗糙度约为
0.000002。
5、数据方法示例：
（1）湍流时流量、流速、以及摩擦力系数的计算取光滑管第一组的数据示例
已知:
光滑管（不锈钢）18℃水的密度：ρ=998.2kg/m3管内径：20 mm
18℃水的粘度：1.0559×10-3 Pa·s
测量段长度L：1000mm,其中，λ为光滑管阻力摩擦系数，无因次d为光滑管内径，
∆p为流体流经 L m 光滑管两端的压力
又有：
流量q v =0.5m3/h
流速 u=q v / A = 4 q v / ∏d2 = 4×0.5/3600×3.14×0.022 m/s = 0.4423≈0.44 m/s
雷诺数 Re=dup /μ=(0.02*0.44*998.2)/0.0010599=8287.73
摩擦阻力系数由∆p =ρLλl u2 / 2d得
λ=2d ∆p/ρLu2 = 2×0.02×147.13÷(998.2×1×0.442) = 0.03045357 ≈ 0.3045
其中，λ为光滑管阻力摩擦系数，无因次d 为光滑管内径∆p 为流体刘晶L m 光滑管两端的压力
① 局部阻力ξ的计算以局部阻力管中第一组的数据为例
由 h f = ∆p f /ρg =ξu 2/2g 故
ξ=2 g h f / u 2 = 2∆p f /ρ u 2
= 2×147.1321394÷(998.2×0.4423213022 )= 1.50676065 ≈ 1.5068
② 光滑管中 Blasius 公式下算出的λ的计算
在光滑管中（ε=0）中
q v = 0.5 m 3/h 时，雷诺数为 Re=
q v =4 m 3/h 时，雷诺数为 Re=
由上计算可知该流体在光滑管中的 3000﹤Re ﹤105，因此可以采用本次实验条件下拟合出来的
柏拉修斯公式（Blasius ）λ= 0.3022Re -0.266 来计算真值，再与实验值比较计算出绝对误差和相对误差。
以光滑管第一组数据（q v = 0.5 m 3/h 时）为例
λ= 0.3022× 8287.725257-0.266= 0.036084672 ≈ 0.0361
然后根据公式：（绝对误差=测量值-真值；相对误差=绝对误差÷真值） ，计算绝对误差和相对误差即可。
y = 0.3022x - 0.266
R² = 0.8749
0 0.005
0.01 0.015 0.02 0.025 0.03 0.035 0
20000
40000
60000
80000
光滑管的 -
六、思考题：
1、实验是以水为介质测得的关系曲线，它是否适用于其它流体？
答：可以。
Re反映了流体的性质，虽然其它流体黏度和密度与水的不同，但最终都在Re上反映出来了，所以可以引用。
2、在不同设备上，不同水温下测定的λ-Re数据能否关联在同一曲线上？
答：管径不同，温度不同，导致即使在同一流速下Re都不相同。
这样关联出来没有任何实际意义。