三年级下册数学试题-竞赛专题:第九讲-行程问题-追及问题(含答案)人教版
追及问题及参考答案

追及问题及参考答案追及问题是一种常见的问题,它涉及到两个或多个物体之间的相对速度和距离。
在这种问题中,一个物体追赶另一个物体,需要找出何时能够追上或者两者之间的距离。
解决追及问题需要理解相对速度的概念,以及如何应用速度和距离的关系。
问题:一辆汽车以速度v1行驶,另一辆汽车以速度v2行驶,两辆汽车在同一道路上同向行驶,v1>v2。
两辆汽车之间的初始距离为d,问两辆汽车何时能够相遇?我们需要找出两辆汽车之间的相对速度。
因为它们同向行驶,所以相对速度为v1-v2。
我们需要考虑两辆汽车相遇时它们所走的总距离。
因为它们同向行驶,所以当它们相遇时,它们所走的总距离为d。
现在,我们可以使用公式:时间t =总距离 /相对速度 = d / (v1-v2)来计算它们相遇的时间。
根据上述公式,我们可以得出答案:t = d / (v1-v2)。
答案:两辆汽车将在时间t = d / (v1-v2)时相遇。
通过这种方法,我们可以解决各种追及问题。
需要注意的是,在解决追及问题时,我们需要考虑物体的相对速度和距离,以及物体的初始位置和速度。
只有理解了这些因素,我们才能正确地解决追及问题。
答案参考:选择A或B者,属于工作满足感不足。
选择C或D者,则除了寻求更好的发展机会外,可能还意味着没有通过工作与同事或客户建立起良好的人际关系。
最好的策略是:如果目前的处境不是很好,先踏实地干好本职工作,再设法爬到相邻的较高层。
答案参考:对公司的了解程度,决定了今后工作的适应程度。
仅仅了解一些表面情况的人,必须加强了解,否则可能成为最后一个知道公司倒闭的人。
D.我在以前的工作中,总能够很快地掌握新的技能。
答案参考:选择A者,有经验固然好,但雇主更希望你能带来新的经验和方法。
选择B者,很好,符合面试的自我定位。
选择C者,表明了强烈的求职愿望,但空洞,缺乏事实支撑。
选择D者,掌握了快速学习能力当然好,但最好能提供证明你能力的学习业绩或证明参照系。
三年级下册数学试题-奥数:行程问题—追及(练习含答案)全国通用
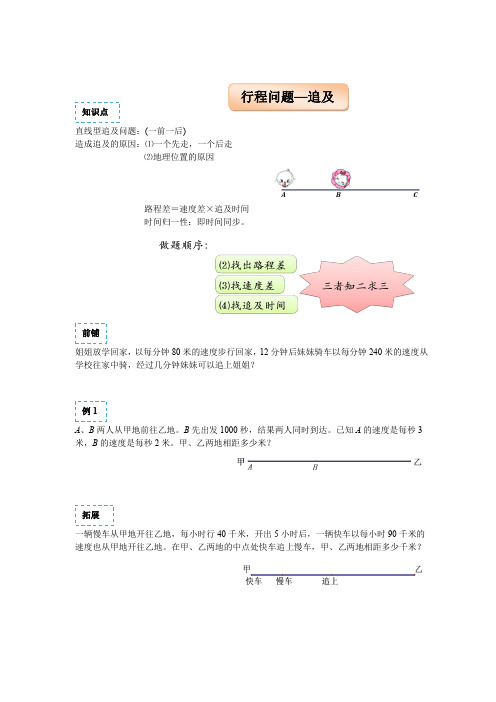
直线型追及问题:(一前一后)造成追及的原因:⑴一个先走,一个后走⑵地理位置的原因路程差=速度差×追及时间时间归一性:即时间同步。
姐姐放学回家,以每分钟80米的速度步行回家,12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑,经过几分钟妹妹可以追上姐姐?A、B两人从甲地前往乙地。
B先出发1000秒,结果两人同时到达。
已知A的速度是每秒3米,B的速度是每秒2米。
甲、乙两地相距多少米?一辆慢车从甲地开往乙地,每小时行40千米,开出5小时后,一辆快车以每小时90千米的速度也从甲地开往乙地。
在甲、乙两地的中点处快车追上慢车,甲、乙两地相距多少千米?拓展例1前铺知识点行程问题—追及甲、乙二人练习跑步,若甲让乙先跑10米,则甲跑5秒钟可追上乙;若甲让乙先跑2秒钟,则甲跑4秒钟就能追上乙。
问:甲、乙二人的速度各是多少?兄弟两人骑自行车同时从学校出发回家。
哥哥每小时行15千米,弟弟每小时行10千米。
出发半个小时后哥哥因事返回学校,到学校后又耽搁了1小时,然后动身去追弟弟。
当哥哥追上弟弟时,距学校多少千米?两人在环形跑道中同时同地同向而行1.两个人每追及一次,路程差增加一个周长;反之,两个人路程差每增加一周,必定追及一次。
2.两个人每追及一次,每次所需要的时间均相等,即每次增加t。
幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米,晶晶每秒钟跑4米,问冬冬第2次追上晶晶时两人各跑了多少圈?在周长为400米的圆形跑道的一条直径的两端,甲、乙两人分别以每秒6米和每秒4米的速例5例4知识点例3例2度骑自行车同时同向出发(顺时针)沿圆周行驶,经过多长时间,甲第二次追上乙?测试题1.甲、乙两地相距240千米,一列慢车从甲地出发,每小时行60千米.同时一列快车从乙地出发,每小时行90千米。
两车同向行驶,快车在慢车后面,经过多少小时快车可以追上慢车?A.6 B.8 C.10 D.122.小红和小蓝练习跑步,若小红让小蓝先跑20米,则小红跑5秒钟就可追上小蓝;若小红让小蓝先跑4秒钟,则小红跑6秒钟就能追上小蓝、小红、小蓝二人的速度各是多少?A.10,6 B.6,10 C.6,8 D.8,63.王芳和李华放学后,一起步行去体校参加排球训练,王芳每分钟走110米,李华每分钟走70米,出发5分钟后,王芳返回学校取运动服,在学校又耽误了2分钟,然后追赶李华。
行程问题(追及问题)专题训练(完整资料).doc

【最新整理,下载后即可编辑】行程问题(追及问题)专题训练知识梳理:1、两物体在同一直线上运动所涉及的追及、相遇、相撞的问题,通常归为追及问题。
2、追及路程=速度差×追及时间速度差=追及路程÷追及时间追及时间=追及路程÷速度差3、“追及路程”是指在相同的时间内两个运动物体速度快的比速度慢的多行的路程;“追及时间”是指速度快的物体从出发到追上速度慢的物体所经历的时间。
例题精讲:1、哥哥以每分钟50米的速度从学校步行回家,12分钟后弟弟从学校出来骑车追哥哥,结果在距学校800米处追上哥哥。
求弟弟骑车的速度。
分析:当弟弟追上哥哥时,距学校800米。
这800米是哥哥两次所行路程的和,一次是12分钟内行的路程,另一次是弟弟从出发到追上哥哥所用时间内(追及时间)哥哥行的路程。
解:解答:弟弟追上哥哥的时间(追及时间)(800-12×50)÷50=(800-600)÷50=200÷50=4(分)弟弟的速度800÷4=200(米)答:弟弟骑车每分钟行200米2、两辆汽车从甲地运送货物到乙地。
大货车以每小时行36千米的速度先出发2小时后,小货车以每小时48千米的速度追赶。
当小货车追上大货车时,大货车已开出多远?分析:求大货车开出多远必须先求出追及时间,再乘上小货车的速度就求出大货车开出的路程。
解:追及时间为:(36×2)÷(48-36)=6(小时);大货车开出的路程为:48×6=288(千米)。
3、一辆货车以每小时65千米的速度前进,一辆客车在它的后面1500米处,以每小时80千米的速度同向行驶,客车在超过货车前2分钟,两车相距多少米?分析:客车超过货车的一瞬间,也就是客车追上货车,这时两车所行的路程是相等的。
客车超过货车前2分钟两车相距的路程即客车与货车2分钟内的路程差。
解:解答:客车与货车1小时的路程差80-65=15(千米)客车与货车2分钟的路程差15×1000÷60×2=500(米)答:客车在超过货车前2分钟,两车相距500米专题训练:1、两匹马在相距50米的地方同时同向出发,出发时黑马在前白马在后,如果黑马每秒跑10米,白马每秒跑12米,几秒后两马相距70米?2、李明和张强绕周长为1200米的环形广场竞走。
小学数学《行程问题之相遇与追击》练习题(含答案)

小学数学《行程问题之相遇与追击》练习题(含答案)内容概括我们把研究路程、速度、时间以及这三者之间关系的一类问题,总称为行程问题.在对小学数学的学习中,我们已经接触过一些简单的行程应用题,行程问题主要涉及时间(t )、速度(v )和路程(s )这三个基本量,它们之间的关系如下:(1)速度×时间=路程 可简记为:s = vt(2)路程÷速度=时间 可简记为:t = s ÷v(3)路程÷时间=速度 可简记为:v = s ÷t显然,知道其中的两个量就可以求出第三个量.涉及到两个或两个以上物体运动的问题,其中最常见的是相遇问题和追及问题.相遇问题:速度和×相遇时间=路程和 t v S 和和=追及问题:速度差×追及时间=路程差 t v S 差差=对于上面的公式大家已经不陌生了,在下面的学习中我们将和小朋友们一起复习回顾以前的相关知识,而后拓展提高!相遇问题【例1】 两地相距400千米,两辆汽车同时从两地相对开出,甲车每小时行40千米,乙车每小时比甲车多行5千米,4小时后两车相遇了吗?【例2】 大头儿子的家距离学校3000米,小头爸爸从家去学校,大头儿子从学校回家,他们同时出发,小头爸爸每分钟比大头儿子多走24米,50分钟后两人相遇,那么大头儿子的速度是每分钟走多少米?【例3】 甲乙两车同时从A 、B 两地出发相向而行,6小时相遇.相遇后甲车继续行驶4小时到达B 地.乙车每小时行30千米,A 、B 两地相距多少千米?【例4】南辕与北辙两位先生对于自己的目的地S城的方向各执一词,于是两人都按照自己的想法驾车同时分别往南和往北驶去,二人的速度分别为50千米/时,60千米/时,那么北辙先生出发5小时他们相距多少千米?【例5】夏夏和冬冬同时从两地相向而行,夏夏每分钟行50米,冬冬每分钟行60米,两人在距两地中点50米处相遇,求两地的距离是多少米?【例6】甲、乙两列火车同时从东西两镇之间的A地出发向东西两镇反向而行,它们分别到达东西两镇后,再以同样的速度返回,已知甲每小时行60千米,乙每小时行70千米,相遇时甲比乙少行120千米,东西两镇之间的路程是多少千米?【例7】甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离.追击问题【例8】龟兔赛跑同时出发,全程7000米,乌龟以每分30米的速度爬行,兔子每分钟跑330米.兔子跑了10分钟就停下来睡了200分钟,醒来后立即以原速往前跑.当兔子追上乌龟时,离终点的距离是多少千米?【例9】小明步行上学,每分钟行70米.离家12分钟后,爸爸发现小明的文具盒忘在家中,爸爸带着文具盒,立即骑自行车以每分钟280米的速度去追小明.问爸爸出发几分钟后追上小明?【例10】小新和正南在操场上比赛跑步,小新每分钟跑250米,正南每分钟跑210米,一圈跑道长800米,他们同时从起跑点出发,那么小新第一次超过正南需要多少分钟?第三次超过正南需要多少分钟?【例11】两名运动员在湖的周围环形道上练习长跑。
初三年级奥数行程问题试题及答案

初三年级奥数行程问题试题及答案导读:本文初三年级奥数行程问题试题及答案,仅供参考,如果觉得很不错,欢迎点评和分享。
1.羊跑5步的时间马跑3步,马跑4步的距离羊跑7步,现在羊已跑出30米,马开始追它。
问:羊再跑多远,马可以追上它?解:根据“马跑4步的距离羊跑7步”,可以设马每步长为7x米,则羊每步长为4x米。
根据“羊跑5步的时间马跑3步”,可知同一时间马跑3*7x米=21x米,则羊跑5*4x=20米。
可以得出马与羊的速度比是21x:20x=21:20根据“现在羊已跑出30米”,可以知道羊与马相差的路程是30米,他们相差的份数是21-20=1,现在求马的21份是多少路程,就是30÷(21-20)×21=630米2.甲乙辆车同时从ab两地相对开出,几小时后再距中点40千米处相遇?已知,甲车行完全程要8小时,乙车行完全程要10小时,求ab两地相距多少千米?答案720千米。
由“甲车行完全程要8小时,乙车行完全程要10小时”可知,相遇时甲行了10份,乙行了8份(总路程为18份),两车相差2份。
又因为两车在中点40千米处相遇,说明两车的路程差是(40+40)千米。
所以算式是(40+40)÷(10-8)×(10+8)=720千米。
3.在一个600米的环形跑道上,兄两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次,若两个人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4分钟相遇一次,两人跑一圈各要多少分钟?答案为两人跑一圈各要6分钟和12分钟。
解:600÷12=50,表示哥哥、弟弟的速度差600÷4=150,表示哥哥、弟弟的速度和(50+150)÷2=100,表示较快的速度,方法是求和差问题中的较大数(150-50)/2=50,表示较慢的速度,方法是求和差问题中的较小数600÷100=6分钟,表示跑的快者用的时间600/50=12分钟,表示跑得慢者用的时间。
行程问题训练(追及问题)

追及问题两个运动着的物体从不同的地点出发,同向运动。
慢的在前,快的在后,经过若干时间,快的追上慢的。
有时,快的与慢的从同一地点同时出发,同向而行,经过一段时间快的领先一段路程,我们也把它看作追及问题。
解答这类问题要找出两个运动物体之间的距离和速度之差,从而求出追及时间。
解题的关键是在互相关联、互相对应的距离差、速度差、追及时间三者之中,找出两者,然后运用公式求出第三者来达到解题目的。
基本公式有:追及(或领先)的路程÷速度差=追及时间速度差×追及时间=追及(或领先)的路程追及(或领先)的路程÷追及时间=速度差要正确解答有关“行程问题”,必须弄清物体运动的具体情况。
如:运动的方向(相向、相背、同向),出发的时间(同时、不同时),出发的地点(同地、不同地)、运动的路线(封闭、不封闭),运动的结果(相遇、相距多少、追及)。
常用公式:行程问题基本恒等关系式:速度×时间=路程,即S=vt.行程问题基本比例关系式:路程一定的情况下,速度和时间成反比;时间一定的情况下,路程和速度成正比;速度一定的情况下,路程和时间成正比。
相遇追及问题中符号法则:相向运动,速度取和;同向运动,速度取差。
流水行船问题中符号法则:促进运动,速度取和;阻碍运动,速度取差。
行程问题常用比例关系式:路程比=速度比×时间比,即S1/S2=v1/v2×t1/t2电梯运行规律:能看到的电梯级数=(人速+电梯速度)×顺电梯运动所需时间能看到的电梯级数=(人速—电梯速度)×逆电梯运动所需时间2v1v2往返运动问题核心公式:往返平均速度= ------- (其中v1和v2分别表示往返的速度)v1+v23S1+S2两次相遇问题核心公式:单岸型S= -------;两岸型 S=3S1-S2 (S表示两岸的距离)2相向而行:相遇时间=距离÷速度之和相背而行:相背距离=速度之和×时间注意:同向而行追及时速度慢的在前,快的在后。
小学数学《行程问题之相遇与追击》练习题(含答案)

小学数学《行程问题之相遇与追击》练习题(含答案)内容概括我们把研究路程、速度、时间以及这三者之间关系的一类问题,总称为行程问题.在对小学数学的学习中,我们已经接触过一些简单的行程应用题,行程问题主要涉及时间(t )、速度(v )和路程(s )这三个基本量,它们之间的关系如下:(1)速度×时间=路程 可简记为:s = vt(2)路程÷速度=时间 可简记为:t = s ÷v(3)路程÷时间=速度 可简记为:v = s ÷t显然,知道其中的两个量就可以求出第三个量.涉及到两个或两个以上物体运动的问题,其中最常见的是相遇问题和追及问题.相遇问题:速度和×相遇时间=路程和 t v S 和和=追及问题:速度差×追及时间=路程差 t v S 差差=对于上面的公式大家已经不陌生了,在下面的学习中我们将和小朋友们一起复习回顾以前的相关知识,而后拓展提高!相遇问题【例1】 两地相距400千米,两辆汽车同时从两地相对开出,甲车每小时行40千米,乙车每小时比甲车多行5千米,4小时后两车相遇了吗?【例2】 大头儿子的家距离学校3000米,小头爸爸从家去学校,大头儿子从学校回家,他们同时出发,小头爸爸每分钟比大头儿子多走24米,50分钟后两人相遇,那么大头儿子的速度是每分钟走多少米?【例3】 甲乙两车同时从A 、B 两地出发相向而行,6小时相遇.相遇后甲车继续行驶4小时到达B 地.乙车每小时行30千米,A 、B 两地相距多少千米?【例4】南辕与北辙两位先生对于自己的目的地S城的方向各执一词,于是两人都按照自己的想法驾车同时分别往南和往北驶去,二人的速度分别为50千米/时,60千米/时,那么北辙先生出发5小时他们相距多少千米?【例5】夏夏和冬冬同时从两地相向而行,夏夏每分钟行50米,冬冬每分钟行60米,两人在距两地中点50米处相遇,求两地的距离是多少米?【例6】甲、乙两列火车同时从东西两镇之间的A地出发向东西两镇反向而行,它们分别到达东西两镇后,再以同样的速度返回,已知甲每小时行60千米,乙每小时行70千米,相遇时甲比乙少行120千米,东西两镇之间的路程是多少千米?【例7】甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离.追击问题【例8】龟兔赛跑同时出发,全程7000米,乌龟以每分30米的速度爬行,兔子每分钟跑330米.兔子跑了10分钟就停下来睡了200分钟,醒来后立即以原速往前跑.当兔子追上乌龟时,离终点的距离是多少千米?【例9】小明步行上学,每分钟行70米.离家12分钟后,爸爸发现小明的文具盒忘在家中,爸爸带着文具盒,立即骑自行车以每分钟280米的速度去追小明.问爸爸出发几分钟后追上小明?【例10】小新和正南在操场上比赛跑步,小新每分钟跑250米,正南每分钟跑210米,一圈跑道长800米,他们同时从起跑点出发,那么小新第一次超过正南需要多少分钟?第三次超过正南需要多少分钟?【例11】两名运动员在湖的周围环形道上练习长跑。
行程问题(追及问题)专题训练

行程问题(追及问题)专题训练知识梳理:1、两物体在同一直线上运动所涉及的追及、相遇、相撞的问题,通常归为追及问题。
2、追及路程=速度差×追及时间速度差=追及路程÷追及时间追及时间=追及路程÷速度差3、“追及路程”是指在相同的时间内两个运动物体速度快的比速度慢的多行的路程;“追及时间”是指速度快的物体从出发到追上速度慢的物体所经历的时间。
例题精讲:1、哥哥以每分钟50米的速度从学校步行回家,12分钟后弟弟从学校出来骑车追哥哥,结果在距学校800米处追上哥哥。
求弟弟骑车的速度。
分析:当弟弟追上哥哥时,距学校800米。
这800米是哥哥两次所行路程的和,一次是12分钟内行的路程,另一次是弟弟从出发到追上哥哥所用时间内(追及时间)哥哥行的路程。
解:解答:弟弟追上哥哥的时间(追及时间)(800-12×50)÷50=(800-600)÷50=200÷50=4(分)弟弟的速度800÷4=200(米)答:弟弟骑车每分钟行200米2、两辆汽车从甲地运送货物到乙地。
大货车以每小时行36千米的速度先出发2小时后,小货车以每小时48千米的速度追赶。
当小货车追上大货车时,大货车已开出多远?分析:求大货车开出多远必须先求出追及时间,再乘上小货车的速度就求出大货车开出的路程。
解:追及时间为:(36×2)÷(48-36)=6(小时);大货车开出的路程为:48×6=288(千米)。
3、一辆货车以每小时65千米的速度前进,一辆客车在它的后面1500米处,以每小时80千米的速度同向行驶,客车在超过货车前2分钟,两车相距多少米?分析:客车超过货车的一瞬间,也就是客车追上货车,这时两车所行的路程是相等的。
客车超过货车前2分钟两车相距的路程即客车与货车2分钟内的路程差。
解:解答:客车与货车1小时的路程差80-65=15(千米)客车与货车2分钟的路程差15×1000÷60×2=500(米)答:客车在超过货车前2分钟,两车相距500米专题训练:1、两匹马在相距50米的地方同时同向出发,出发时黑马在前白马在后,如果黑马每秒跑10米,白马每秒跑12米,几秒后两马相距70米?2、李明和张强绕周长为1200米的环形广场竞走。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教新课标三年级数学下册行程问题(二)知识概述1、追及问题的意义:两个物体同方向运动,在后面的速度较快的物体赶上前面速度较慢的物体称为追及。
2、追及问题的特点:①追及者的速度比被追及者的速度要快;②两人同时出发时,从出发到追上,两人所经历的时间相同;③从开始追到追上,两人所行路程差等于他们追及发生时相距的路程。
3、追及问题的基本量:速度差:两个运动物体在单位时间(秒、分、时)所走的路程差(快速-慢速);追及时间:速度快的运动物体从开始追到追上速度慢的物体所用的时间;追及路程(路程差):速度快的运动物体开始追时和速度慢的物体相距的距离。
4、追及问题的基本数量关系:追及路程(路程差)=速度差×追及时间小红在小明前面100米,两人同时出发朝相同的方向行走。
(试着画一画)(1)小明要想追上小红,必须具备什么条件?(2)当小明追上小红时,他们两人所走的路程有什么关系?时间呢? 【解析】(1)小明要追上小红,必须比小红的速度快,并且同向行驶在同一路线上。
(2)画线段图:发现追上小红时,他们各自走的路程,小明比小红多了100米,而时间必须在同一时间同时开始行程才可。
这样追上小红后,他们所走的时间相等。
甲、乙两人相距150米,甲在前,乙在后,甲每分钟走60米,乙每分钟走75米,两人同时向南出发,几分钟后乙追上甲?【解析】 追及时间=路程差÷速度差 =150÷(75-60) =150÷15 =10(分钟)甲、乙两人练习跑步,如果甲让乙先跑10米,那么甲跑5秒钟可以追上乙。
已知甲的速度是6米/秒,求乙的速度? 【解析】行程问题是反映物体匀速运动的应用题。
由于变化较多,而且又纷繁复杂,所以对于学习者而掌握涉及基本数量关系的追及行程问题,理解较复杂数量关系的追及行程问题;通过追及问题的学习掌握简单追及问题的解题思路和方法,培养学生分析解决问题的能力,提高思维能力;通过行程中追及问题的学习,培养学生学以致用的应用意识。
名师点题乙的速度=甲的速度-速度差速度差=路程差÷追及时间=10÷5=2米/秒乙的速度=5-2=3米/秒【巩固拓展】1、姐姐放学回家,以每分钟80米的速度步行回家,12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑,经过几分钟妹妹可以追上姐姐?【解析】先求出路程差。
80×12=960(米)960÷(240-80)=6(分钟)2、早晨小胖去上学,5分钟后小胖的爸爸发现小胖忘带铅笔盒,立即出门去追小胖,已知小胖每分钟走60米,爸爸每分钟走110米。
几分钟后,爸爸追上小胖?【解析】当爸爸出发时,小胖与爸爸的距离是60×5= 300米;爸爸每分钟比小胖多走110 -60=50米,即每分钟爸爸与小胖间的距离缩短50米,即速度差,所以300米里面有几个50米就是几分钟。
60×5÷(110-60)=6(分钟)3、甲乙两架飞机同时从一个机场起飞,向同一方向飞行,甲机每小时行300千米,乙机每小时行340千米,飞行4小时后它们相隔多少千米?这时候甲机提高速度用2小时追上乙机,甲机每小时要飞行多少千米?【解析】4小时后它们相隔的距离就是它们的路程差(340-300)×4=160(千米)速度差=路程差÷追及时间=160÷2=80(千米/小时)甲飞机的速度:80+340=(420千米/小时)小明以每分钟50米的速度从学校步行回家,12分钟后小强从学校出发骑自行车去追小明,结果在距学校1000米处追上小明,求小强骑自行车的速度?【解析】画线段图来帮助理解先从所问的出发,要求速度,必须先知道速度差,而速度差=路程差÷追及时间追及时间为1000÷50-12=8分钟,从而去思考路程差:路程差也就是小明先走的路程:50×12=600米速度差=600÷8=75那么小强骑自行车的速度:75+50=125(米/分钟)【巩固拓展】小智和小慧从学校到森林公园去春游,小智步行,每小时走5千米。
他出发后4小时,小慧骑自行车,每小时行15千米。
小慧追上小智时,正好到达森林公园,学校离森林公园有多少千米?【解析】路程差:4×5=20千米追及时间:20÷(15-5)=2小时而学校到公园的路程是路程差+小智后2小时的路程,或者是小慧2小时骑车的路程20+2×5=30(千米)妈妈以每分钟80米的速度从家步行到单位上班,10分钟后,小华跑步从家追赶妈妈,结果在距家1200米的地方追上妈妈。
小华每分钟跑多少米?【解析】10分钟妈妈走了80×10=800(米),在小华追上妈妈的过程中,妈妈又走了1200-800=400(米),妈妈走这一段的时间是:400÷80=5(分钟),即是小华追上妈妈的时间。
又知道小华跑的路程是1200米,然后根据速度=路程÷时间,就可以求出小华每分钟跑多少米,即:小华的速度:1200÷5=240(米)。
【巩固拓展】小聪和小明从学校到相距2400米的电影院去看电影。
小聪每分钟行60米,他出发后10分钟小明才出发,结果俩人同时到达影院,小明每分钟行多少米?【解析】60×10=600米小聪还离电影院1800米,也就是要走1800÷60=30分钟那么小明30分钟就追上了小明到达电影院所以小明的速度:2400÷3=80米/分钟一支部队排成1200米长的队伍行军,在队尾的通讯员要与最前面的营长联系,他用6分钟时间跑步追上了营长,为了回到队尾,在追上营长的地方等待了24分钟.如果他从最前头跑步回到队尾,那么只需多长时间?【解析】通讯员与队伍的速度差1200÷6=200米队伍的速度1200÷24=50米通讯员跑步回到队尾的时间1200÷(200+50+50)=4(分钟)答:需4分钟。
【巩固拓展】小李骑自行车每小时行13千米,小王骑自行车每小时行15千米。
小李出发后2小时,小王在小李的出发地点前面6千米处出发,小李几小时可以追上小王?【解析】画线段图理解关键是路程差=13×2-6=20千米追及时间=路程差÷速度差=20÷(15-13)=10小时两名运动员在湖的周围环形道上练习长跑, 甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙;如果两人同时同地反向出发,经过多少分钟两人相遇? 【解析】画环形图理解,甲在追上乙时,甲正好比乙多行了一圈的路程路程差=速度差×追及时间 =(250-200)×45 =2250米所以一圈的距离是2250米 相遇时间=总路程÷速度和 =2250÷(250+200) =5(分钟)【巩固拓展】一条环形跑道长400米,甲骑自行车每分钟骑450米,乙跑步每分钟250米,两人同时从同地同向出发,经过多少分钟两人第一次相遇? 【解析】追及时间=路程差÷速度差 =400÷(450-250) =2(分钟)(第9届中环杯决赛)下图为一圆形跑道,甲从A 点出发,乙从B 点出发,都按顺时针方向跑.A 、B 正好在圆的一条直径上,圆周长为20米,甲每秒跑4米,乙每秒跑3米,则当甲第一次追上乙时,甲跑了( )圈。
【解析】AB相距10米,也就是路程差为10米追及时间=路程差÷速度差=10÷(4-3)=10秒甲10秒跑来10×4=40米跑了2圈甲乙两辆汽车同时从A地出发去B地,甲车每小时行50千米,乙车每小时行40千米。
途中甲车出故障停车修理了3小时,结果甲车比乙车迟到1小时到达B地。
A、B两地间的路程是多少?【解析】假设一开始甲的车就坏掉了,修了3小时,加上迟到的1小时,就是时间共差了4小时本题相当于乙先出发4小时,然后甲在B地追上乙那么路程差=乙先开走的距离=40×4=160千米追及时间=160÷(50-40)=160÷10=16小时A、B两地路程=16×50=800千米甲、乙两车同时从A、B两地沿相同的方向行驶,甲车如果每小时行驶60千米,则5小时后可以追上前方的乙车;如果每小时行驶70千米,则3小时后可以追上前方的乙车。
由此可知,乙车每小时行驶_____千米。
【解析】画线段图,通过观察发现两种情况下的甲和乙所跑的路程甲①60×5=300千米甲②70×3=210千米而乙的速度不变,所以两种情况下乙的路程差为:300-210=90千米时间差:5-3=2乙的速度=路程差÷时间差=90÷2=45千米/小时(第13届中环杯初赛)—列队伍长600米,以每秒钟2米的速度行进。
一战士因事要从排尾赶到排头,并立即返回排尾。
若他每秒钟走3米,那么往返共行()米。
【解析】在300米的环形跑道上,田奇和王强同学同时同地起跑,如果同向而跑2分30秒相遇,如果背向而跑则半分钟相遇,求两人的速度各是多少?【解析】数量关系为:路程差÷速度差=追及时间,由题意,得知路程差为300米,追及时间为2分30秒,即150秒,因此两人速度差为300÷150=2(米/秒)。
背向而跑即所谓的相遇问题,数量关系为:路程和÷速度和=相遇时间,由题意,可以求得两人的速度和为300÷30=10(米/秒)。
有了两人的速度和与速度差,即可求得两人的速度:慢者:(10-2)÷2=4(米/秒),快者:10-4=6(米/秒)。
(小机灵杯初赛)上午8时8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上他,然后爸爸立刻回家,到家后又立即回头追小明,再追上他的时候,离家正好是8千米,问这时是几点几分? 【解析】此题是一道行程问题,就是在爸爸追上小明时然后回头,在8千米处追上小明,说明在相等的时间内,小明走了4千米,爸爸走了4+8=12(千米),爸爸的速度是小明速度的3倍。
再回到第一次追及,走了相等的路程,小明的时间是爸爸的时间的3倍. 8÷(3-1)=4(分钟),说明爸爸用了4分钟追上小明。
8+4=12(分钟),说明小明用了12分钟行了4千米,然后又行了4千米,一共用了12+12=24(分钟) 所以最后的时间是8:32.1、熊猫胖胖和乐羊羊同地同方向出发,熊猫胖胖每小时走7千米,乐羊羊每小时走5千米。
乐羊羊先走2小时后,熊猫胖胖才开始走,熊猫胖胖追上乐羊羊需要几小时? 【解析】 2×5÷(7-5) =10÷2 =5(小时)2、甲、乙两人同时从A 地到B 地,乙出发3小时后甲才出发,甲走了5小时后,已超过乙2千米。
