直线及其投影
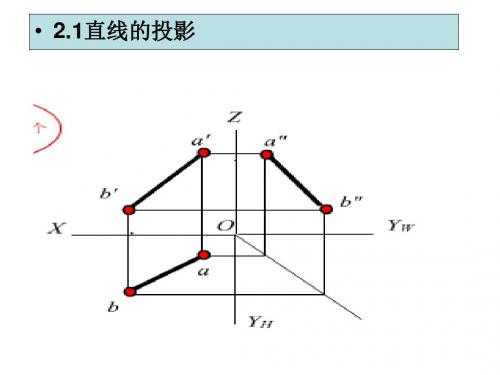
第二章 直线的投影
2.已知直线 AB 平行直线 CD,试完成直线
例:已知直线AB平行直线CD,试完成直线AB
AB 和 CD 的三面投影。 和CD的三面投影。
题解: c′〝
c
NEW
c
c
b
点C的投影在直线的同面投影上,并 符合点的投影规律。
二、D点不在 直线AB上。
a A d b a b
NEW
a b
D
d
B
d
例:判断点M是否在直线CD 上 解法1:
NEW
点M的投影不符合点在直线上的投影规律, 故M点不在直线CD上。
例:判断点M是否在直线CD 上
直线 水 平 线
直观图
投影图
投影特征 1、水平投影ab 反映实长 及直线的倾角β 和γ 。 2、正面投影a b //o x轴, 侧面投影a"b "//oy w 轴,且 均短于实长。 1、正面投影e f 反映实长 及直线的倾角α 和γ 。 2、水平投影ef //o x轴,侧 面投影e"f "//oz 轴,且均 短于实长。 1、侧面投影e"f" 反映实 长及直线的倾角α 和β 。 2、水平投影e f//oy H 轴,正 面投影e f //oz 轴,且均 短于实长。
• 1. 直线上的点,其投影必在该直线的同面投影上。 • 2. 直线上的点,分割线段之比,在投影后保持不变。
三.直线上的点 (一) 直线上点的投影特性
点C在直线上 AB上
1.直线上的点,
其投影必在该 直线的同面投 影上。
2.直线上的点,
直线的投影
例1.判断下列几组直线是否垂直:
b′
b′
a′
c′
a′
c′
a c
b
(a)
a′
c′ b′
b
c
bc
a ( b ) a′
c′ b′ b c
a
(d)
a
a′ (b′ c′ )
d′
b
c
d
a
(c)
d′
d (e)
例2 .已知侧平线AC为菱形对角线,B点在Z轴上,试完成菱形的三面投影。
z
分析:
d’
作图:
① 作出a′′c′′,过中 点o′′作中垂线交OZ 于b′′
(2)在这条投影连线上,从新投影轴 向新投影面一侧,量取点的被更换的 投影与更换的投影轴之间的距离,就 得到该点所求的新投影。
非机类
b1’ V1 a1’
X1
a’ XV
H a
思考: 变换H面?
a1’ α
实长
b’
X1∥ab
b b1’
例4 求一般位置线段AB的实长及其对W面的倾角γ, 并AB上截取一点E,使AE长为10mm。
非机类
六 一边平行于投影面的直角的投影
a′
b′
a’
b’
c’
A
c′
x
X
C
OB a
a
o
c
b
b
c
证 结明论::
⑴已当知直A角B⊥的A一C边, 平AB行∥于H投,影则面A时B⊥, 该Aa投,影则面A上B⊥的平投面影A反ac映C直; 角 ; 反之 , 两直线之一平行于投影面且在该面两直线投影成直角 , 则 ⑵ 两因直a线b∥在A空B间,的故夹ab角⊥也平一面定Aa是cC直,角则。ab⊥ac 。
直线的投影

图2-19 判别C点是否在线段AB上 作图:首先过a作一辅助线ab1,使ab1=a'b',ac1=a'c';然后连接b1b,过c1作b1b的 平行线使与ab相交,如果交点与C点的水平投影c重合,则表明C点对AB的分段符合定比 分段法,此时C点在直线段AB上;反之不在直线段AB上。 1.3两直线的相对位置 空间两直线的相对位置有三种情况:平行、相交和交叉。其中平行和相交两直线均在同一 平面上,交叉两直线不在同一平面上,因此,又称为异面直线。 1. 两直线平行: 相同;反之,若两直线的同面投影都平行,则空间两直线互相平行。如图2-20(a)所示, 因为AB∥CD,则ab∥cd、a'b'//c'd',且ab:cd= a'b':c'd'。
1.水平投影积聚为一点 2.正面投影和侧面投影都 平行于Z轴,并反映实长
1.正面投影积聚为一 点2.水平投影和侧面 投影都平行于Y轴,并 反映实长
1.侧面投影积聚为一
侧
点
垂 线
2.正面投影和水平投 影都平行于X轴,并
反映实长
(3) 一般位置直线 一般位置直线与三个投影面都倾斜,因此在三个投影面上的投影都不反映实长,投 影与投影轴之间的夹角也不反映直线与投影面之间的倾角,见图2-17。
影的夹角仍为直角;如果两直线都不平行于某一投影面时,则两直线在该投影面上的投影 不反映直角。如果两直线相交成直角、且其中有一条直线平行于某一投影面,则两直线在 该投影面上的投影仍然反映直角关系。通常称之为直角投影原理。
2-28所示,AB、BC为相交成直角的两直线,其中BC平行于H面(即水平线), AB为一般位置直线。现证明两直线的水平投影ab和bc仍相互垂直,即bc垂直于ab。
4-5投影原理-线的投影

1.投影面垂直线的投影
在三投影面体系中,当直线垂直于某一个 A
投影面时,则必同时平行于另两个投影面,
这样的直线称为投影面垂直线。 共有三种投影面垂直线: 直线⊥投影面 H:铅垂线 B
P
a( b )
直线⊥投影面 V:正垂线
直线⊥投影面 W:侧垂线
(1)铅垂线— 垂直于水平投影面的直线
z a
a
A
b
a
b
b
a
X
O
YW
B
b
a
a b 投影特性:1.ab OX ; ab OYW 2. ab=AB 3.反映、 角的真实大小
b
YH
(2)正平线—只平行于正面投影面的直线
Z b a B b
b
a
a
b a
O
A
X
YW
a
b
a
b YH
2.4 线的投影
一、直线在单一投影面上的投影
A C D B P
a( b )
E F
P c
P
e
f
d
• 直线垂直于投影面:直线在该投影面上的投影积聚为点 • 直线平行于投影面:直线在该投影面上的投影反映实长 • 直线倾斜于投影面:直线在该投影面上的投影缩短
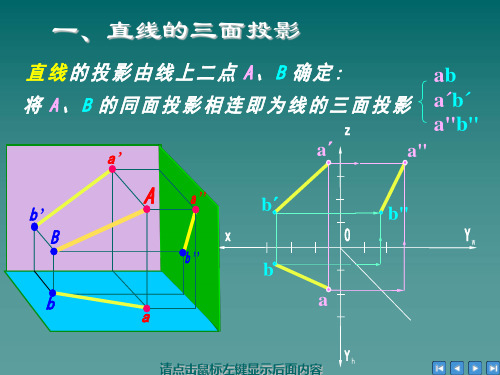
二、直线在三投影面体系中的投影
直线与投影面夹角的规定名称
(1). 求直线的实长及对 水平投影面的倾角角
AB
|zA-zB|
|zA-zB|
ab
|zA-zB |
AB
AB |zA-zB| ab
第3章 直线的投影【画法几何】.

a
b
2、正面投影a´b´//OX轴, 侧面投影a˝b˝//OYw轴
正平线的投影
c´d´反映CD实长
d′ c′ C
D
d˝ c˝
c˝d˝//OZ轴
c
d
cd //OX轴
d´
d˝ c˝
c´
正平线的投影特 性
1、正面投影c´d´反映实 长,并反映倾角α ,γ
二、 投影面平行线
( 一 ) 含义:仅平行于某一个投影面 的直线,称为投影面平行线。
平行于H面的直线称为水平线 平行于V面的直线称为正平线 平行于W面的直线称为侧平线
水平线的投影
a´b´ //OX轴
a´ A
β
b´ a˝
γ
a˝b˝//OY轴
B
b˝
a
β
γ
b
ab 反映AB的实长
a´
b´
a˝
b˝
(二) 投影面平行线 的投影特性: 水平线
e
f
投影面垂直线的投影特性
1 、 直 线 在 所 垂 直 的 投 影 面 上 积 聚为 一 点 (即有积聚性)
2 、其它两个投影垂直于相应的投影轴,并
且反映实长(即有显实性)。
例3-2:判断AB、CD、DE直线的空间位置,并找出其第三投影
d’ e’
a’ b’ c’
e”
d”
a” c”
b”
正垂线
e
a´
α
b´
B
b´ a´
m
C
b
X
A
O b
α α
a
基本要素的投影-直线的投影

●
a●
●
a
●
b
一般情况下, 直线对一个投影面的投影特性
A
●
b 直线的投影
●
仍然为直线,特殊情况为一 α M A A B个点。
B ●
● ● ● ●
●
B
●
a≡b≡m
●
●
b
a●
b
a●
直线垂直于投影面 投影重合为一点 积 聚 性
直线平行于投影面 投影反映线段实长 ab=AB
直线倾斜于投影面 投影比空间线段短 ab=ABcosα
a X A a
b a X b a Y a YH O
O b
b YW
|XA-XB|
直角三角形的作图要点: 直角三角形中,斜边为线段的实长,两直角边分别为线 段的投影及坐标差,如图
α
△Z
AB
β
△Y
AB
γ
△X
ab
a ' b'
a ' ' b' '
每个直角三角形中,三条边和直线对投影面的倾角 共四个参数,只要知道其中任意两个,就能求出其余两个
例1: α角的正确求法是(
b′
)图
b′ b′
α
a′
a′ a′
a
α
a
a
α
b (a)
b
b
(b)
(c)
例题2 已知 线段的实长AB,求它的水平投影。 AB b |zA-zB|
AB |zA-zB|
a X
ab b
ab
a
例3 已知直线AB的水平投影ab及a′,且α=30°,用直角三角 形法完成其正面投影。
《机械制图》第二章 直线的投影

1.cd积聚成一点 2.c′d′⊥OX
c″d″⊥OYW 3.c′d′=c″d″=CD
1.e″f″积聚成一点 2.ef⊥OYH
e′f′⊥OZ 3.ef=e′f′=EF
一般位置直线(投影特点:三条斜线)
b a a
b
b a
投影特性:
三个投影都缩短。 即: 都不反映空间 线段的实长及与三 个投影面夹角的实 大,且与三根投影
1. ab∥OX
影
a″b″∥OZ
特
2. a′b′=AB 3. 反映α 、γ 倾角
性
βγ
1. c′d′∥ OX c″d″∥OYW
2. cd=CD 3. 反映β 、γ 倾角
β α
1.e′f′∥OZ ef∥OY H
2. e″f″=EF 3. 反映α 、β 倾角
2.投影面垂直线
由两点到两个投影面距离相等时的两 点连线构成。该直线垂直于某一投影 面,对另外两个投影面都平行 。
YW
Y
YH
• 在直线所平行的投影面上,投影反映实长,且该投影与相邻 投影轴的夹角反映该直线对另外两个投影面的倾角大小。
• 在另外两个投影面上,线段的投影为缩短的线段,且分别 平行于直线一斜二平)
名称
直 观 图
正平线
水平线
侧平线
投
γ
影
α
图
投
第二章 直线的投影
第三节 直线的投影
一、各种位置直线及投影特性
1.一般位置直线
由一般位置的两点连线构成。 该直线与三个投影面都倾斜。
β
γ
YW
α
Y YH
投影特性: 三个投影都倾斜于投影轴,每个投影既不直接
反映线段的实长,也不直接反映倾角的大小。
各种位置直线地投影特性
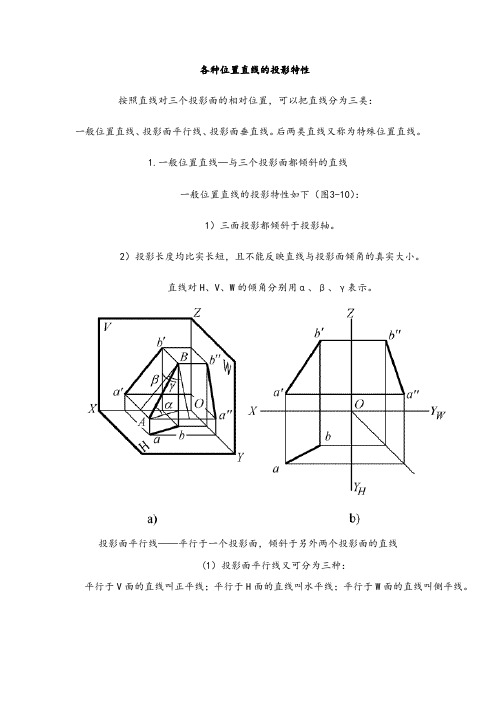
各种位置直线的投影特性按照直线对三个投影面的相对位置,可以把直线分为三类:一般位置直线、投影面平行线、投影面垂直线。
后两类直线又称为特殊位置直线。
1.一般位置直线—与三个投影面都倾斜的直线一般位置直线的投影特性如下(图3-10):1)三面投影都倾斜于投影轴。
2)投影长度均比实长短,且不能反映直线与投影面倾角的真实大小。
直线对H、V、W的倾角分别用α、β、γ表示。
投影面平行线——平行于一个投影面,倾斜于另外两个投影面的直线(1)投影面平行线又可分为三种:平行于V面的直线叫正平线;平行于H面的直线叫水平线;平行于W面的直线叫侧平线。
图3-11 正平线的投影特性(2)正平线的投影特性(图3-11):1)直线平行于V面,则V面投影与直线本身平行且等长,a'b'=AB;2)正平线上各点到V面的距离即Y坐标都相等,则a b∥OX, a"b"∥OZ。
3)AB与H面的倾角为α,由于AB平行V面,所以AB与V面的倾角为0。
又因为AB ∥a'b',a b∥OX轴,所以,a'b'与OX轴的夹角为α,同理a'b'与OZ轴的夹角即为AB与W面的倾角γ。
表3-1为投影面平行线的投影特性。
表3-1 投影面平行线的投影特性名称轴测图投影图投影特性正平线(1)a'b'=AB, 反映α、γ角(2)a b//OX轴, a"b"//OZ轴水平线(1) cd=CD ,反映β、γ角(2)c'd'//OX轴,c"d"//O YW轴侧平线(1) e"f"=EF, 反映α、β角(2)e'f'//OZ轴,ef//O YH轴投影面平行线的投影特性:1.直线在与其平行的投影面上的投影,反映该线段的实长和与其他两个投影面的倾角2.直线在其他两个投影面上的投影分别平行于相应的投影轴,且比线段的实长短投影面垂直线——垂直于一个投影面,平行于另外两个投影面的直线1)投影面垂直线又可分为三种:垂直于V面的直线叫正垂线;垂直于H面的直线叫铅垂线;垂直于W面的直线叫侧垂线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线及其投影
直线的确定――两点或一点加方向。
直线对投影面的相对位置
直线在三面投影体系中位置,可分为三种情况:
一:投影面垂直线――垂直于一个投影面的直线
垂直线分三种铅垂线――⊥H面
正垂线――⊥V面
侧垂线――⊥W面
投影特性--以铅垂线为例。
见图1,投影见图2
(1)有积聚性
(2)a¹b¹∥OZ,a¹¹b¹¹∥OZ,反映实长。
判别:有积聚性
二:投影面平行线――平行于一个投影面,但倾斜于另外两个投影面的直线。
(如平行于另
外两个投影面,则成为投影面垂直线)
平行线分三种水平线――∥H面
正平线――∥V面
侧平线――∥W面
投影特性--以水平线为例。
见图3,投影见图4
(1)a¹b¹∥OX水平,a¹¹b¹¹∥OYW
(2)ab倾斜反映实长,既ab=AB
(3)反映β、γ角实形
判别:有一个投影平行于投影轴,另一个
投影倾斜于投影轴。
三:一般位置直线――对三个投影面都倾斜的直线。
见图5
投影特性
(1)由于倾斜于投影面,故投影小于实长,
大于零。
满足ab=ABcosα,a¹b¹=
ABcosβ,a¹¹b¹¹=ABcosγ
(2)α、β、γ在投影图中都不反映实形,
既不互补,又不互余。
(3)各投影面上的投影都倾斜于投影轴。
见图6
判别:二面投影倾斜于投影轴的直线一定是一般线。
(第三投影也一定倾斜于投影轴)。
例:判别下列直线对投影面的相对位置,并画出第三投影,反映倾角实形处用αβγ表示。
直线上的点
性质――直线上点的投影一定该直线的同面投影上,且满足定比关系:AB:CD=ab:cd= a¹b¹:c¹d¹见图8,投影见图9
例1:已知线段AB的投影,试将AB分成2:3段,求点K的投影。
见图10
例2:求直线AB上点C的H投影。
(用二种方法)
线段的实长和倾角
一般线不反映线段的实长和倾角,如图1,a¹b¹和a¹¹b¹¹都
不反映实长,∠b¹a¹c¹≠α。
用直角三角形法求实长和倾角
如图2所示,三角形ABC构成直角三角形,其中直角边AC为直线的H投影,BC为AB的高差,斜边为线段AB的实长,高差BC对应的角∠BAC为直线AB对H面的夹角α的实形。
规律:
对H投影而言,缺少高度差,则以高度差为另一直角边,对应为α角,斜边为实长。
见图3对V投影而言,缺少宽度差,则以宽度差为另一直角边,对应为β角,斜边为实长。
见图4对W投影而言,缺少长度差,则以长度差为另一直角边,对应为γ角,斜边为实长。
见例1
例:在线段AB上求一点K,使AK长度为定长L
例:已知线段RS的长度为L,求水平投影rs
提示:求出宽度差即可
例4:已知如图,且α=30,补全V投影
分析:α对应高差,求出高差
注意:本题有两解
两直线的相对位置
空间两直线的相对位置有:相交、平行、异面(交叉)三种。
一:相交二直线
性质:相交二直线在同一投影面上的投影也相交,见图1,投影见图2
注意:在两直线中有一条为投影面平行线时,则在判断它们是否相交时应特别注意。
可考虑侧面投影或比例。
见图3
例1:给出平面四边形ABCD的V投影及其二边的H的H投影,完成整个H投影。
例2:已知正平线CD与直线AB相交于K,AK长度为20,且CD与H面夹角为60°,试完成CD的投影。
二:平行二直线
性质:平行直线的投影仍平行,反之,若投影都互相平行,则这二直线平行
注意:若两直线同时平行于某一投影面,则在判断它
们是否平行时应用另外方法。
方法1:考察它们在第三投影上是否互相平行。
见图
8
方法2:连结AC、BD,判断AC、BD是否相交
例:求直线AB,使与已知直线CD、EF相交,且平行于GH
分析:相交难以着手,先考察平行
三:交叉二直线――既不平行,又不相交的
直线
交叉二直线的同面投影可能平行,见图
1、图2,但不可能同时对三面投影都互相
平行,否则为平行线。
交叉二直线的同面投
影也可能相交,但这个交点只不过是二直线
上位于同一条投影线上而又分别属于二直
线上的一对重影点的投影。
见图3
利用重合投影,可以判断两直线的相对位置,见图3
一边平行于投影面的直角投影
一般来说,要使一个角不变形地投射在某一投影面上,必须使此角的两边都平行于投影面。
直角投影定理:对直角来说,只要有一边平行于投影面,则直线在该面上的投影的夹角仍旧是直角。
见图1
逆定理:两直线中,如果有一条线为投影面平行线,且投影的夹角为直角,则该两直线垂直。
例1:过点K作直线KF,使于直线CD正交。
提示:利用第三投影
例2:求下列两题中点A到直线BC的距离。
例3:已知菱形ABCD的对角线BD的投影和另一对角线AC端点A的水平投影a,试完成菱形的投影
提示:利用菱形的对角线互相垂直平分。
