几何体外接球常用结论及方法
立体几何高考专题--外接球的几种常见求法

立体几何高考专题--外接球的几种常见求法高三微专题:外接球在立体几何中,外接球问题是一个重点和难点。
其实质是确定球心O的位置和使用勾股定理求解外接球半径(其中底面外接圆半径r可根据正弦定理求得)。
一、由球的定义确定球心在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心。
简单多面体外接球问题是立体几何中的重点和难点。
二、球体公式球的表面积公式为S=4R²,球体积公式为V=4/3R³。
三、球体几个结论:1)长方体、正方体外接球直径等于体对角线长。
2)侧棱相等,顶点在底面投影为底面外接圆圆心。
3)直径所对的球周角为90°(大圆的圆周角)。
4)正三棱锥对棱互相垂直。
四、外接球几个常见模型1.长方体(正方体)模型例1:长方体的长、宽、高分别为3、2、1,其顶点都在球O的球面上,则球O的表面积为14。
练1:体积为8的正方体的顶点都在同一球面上,则该球的表面积为12。
2.正棱锥(圆锥)模型对于侧棱相等,底面为正多边形的正棱锥,其外接球的球心位置位于顶点与底面外心连线线段(或延长线)上。
半径公式为R²=(h-R)²+r²(其中R为外接球半径,r为底面外接圆半径,h为棱锥的高,r可根据正弦定理a=2rsinA求得)。
例2:已知各顶点都在同一个球面上的正四棱锥高为h,体积为V,则这个球的表面积为____。
正四棱锥的高为h,体积为V,易知底面面积为,底面边长为。
正四棱锥的外接球的球心在它的高上,记为,得,在中。
由勾股定理,所以球的表面积为。
练2:正三棱锥S-ABC中,底面ABC是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于。
解析:ABC外接圆的半径为,三棱锥S-ABC的直径为2R=,外接球半径R=,外接球体积V=4/3R³=。
对于侧棱与底面垂直的直棱柱和圆柱,其外接球的球心位置在上下底面外心连线中点处。
立体几何专题:外接球问题中常见的8种模型(学生版)

立体几何专题:外接球问题中常见的8种模型1.知识梳理一、墙角模型适用范围:3组或3条棱两两垂直;可在长方体中画出该图且各顶点与长方体的顶点重合直接用公式(2R )2=a 2+b 2+c 2,即2R =a 2+b 2+c 2,求出R【补充】图1为阳马,图2和图4为鳖臑二、麻花模型适用范围:对棱相等相等的三棱锥对棱相等指四面体的三组对棱分别对应相等,且这三组对棱构成长方体的三组对面的对角线。
推导过程:三棱锥(即四面体)中,已知三组对棱分别相等,(AB =CD ,AD =BC ,AC =BD )第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为a ,b ,c ,AD =BC =x ,AB =CD =y ,AC =BD =z ,列方程组,a 2+b 2=x 2b 2+c 2=y 2c 2+a 2=z 2⇒(2R )2=a 2+b 2+c 2=x 2+y 2+z 22,补充:V A −BCD =abc −16abc ×4=13abc 第三步:根据墙角模型,2R =a 2+b 2+c 2=x 2+y 2+z 22,R 2=x 2+y 2+z 28,R =x 2+y 2+z 28,求出R .三、垂面模型适用范围:有一条棱垂直于底面的棱锥。
推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r(三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=csin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24四、切瓜模型适用范围:有两个平面互相垂直的棱锥推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线,两条垂线的交点即为球心0,取B C 的中点为E ,连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24五、斗笠模型适用于:顶点的投影在底面的外心上的棱锥推导过程:取底面的外心01,连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h六、矩形模型适用范围:两个直角三角形的斜边为同一边,则该边为球的直径推导过程:图中两个直角三角形ΔPAB 和ΔQAB ,其中∠APB =∠AQB =90°,求外接圆半径取斜边AB 的中点O ,连接OP ,OQ ,则OP =12AB =OA =OB =OQ 所以O 点即为球心,然后在ΔPOQ 中解出半径R 公式:R 2=l22(l 为斜边长度)七、折叠模型适用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,分别过这两个外心做这两个平面的垂线且垂线相交于球心O CH 1=r =BD 2sin ∠BCD,EH 1=h -r ,OH 1=(h -r )tanα2由勾股定理可得:R 2=OC 2=OH 21+CH 21=r 2+(h -r )2tan 2α2.公式:R 2=r 2+(h -r )2tan 2α2八、鳄鱼模型适用范围:所有二面角构成的棱锥,普通三棱锥方法:找两面外接圆圆心到交线的距离m ,n ,找二面角α,找面面交线长度l 推导过程:取二面角两平面的外心分别为O 1,O 2并过两外心作这两个面的垂线,两垂线相交于球心O ,取二面角两平面的交线中点为E ,则O ,O 1,E ,O 2四点共圆,由正弦定理得:OE =2r =O 1O 2sin α①在ΔO 1O 2E 中,由余弦定理得:O 1O 2 2=O 1E 2+O 2E 2-2O 1E O 2E cos α②由勾股定理得:OD 2=O 1O 2+O 1D 2③由①②③整理得:OD2=O 1O 2+O 1D 2=OE 2-O 1E 2+O 1D 2=O 1O 2sin α2-O 1E 2+O 1D 2=O 1E2+O 2E 2-2O 1E O 2E cos αsin 2α-O 1E 2+O 1D 2=O1E2+O2E2-2O1EO2Ecosαsin2α-O1E2+O1B2记O1E=m,O2E=n,AB=l,则R2=m2+n2-2mn cosαsin2α+l22公式:R2=m2+n2-2mn cosαsin2α+l222.常考题型3.题型精析题型一:墙角模型1(2023·高一单元测试)三棱锥A-BCD中,AD⊥平面BCD,DC⊥BD,2AD=BD=DC=2,则该三棱锥的外接球表面积为()A.3π2B.9π2C.9πD.36π1.(2022秋·陕西西安·高一统考期末)在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑A-BCD中,满足AB⊥平面BCD,且AB=BD=5,BC=3,CD=4,则此鳖臑外接球的表面积为()A.25πB.50πC.100πD.200π2.(2023·高一课时练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50πC.100πD.500π33.(2023·广西南宁·统考二模)在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A -BCD 中,AB ⊥平面BCD ,CD ⊥AD ,AB =BD =2,已知动点E 从C 点出发,沿外表面经过棱AD 上一点到点B 的最短距离为10,则该棱锥的外接球的体积为.4.(2023春·辽宁朝阳·高二北票市高级中学校考阶段练习)已知四棱锥P -ABCD 的外接球O 的表面积为64π,PA ⊥平面ABCD ,且底面ABCD 为矩形,PA =4,设点M 在球O 的表面上运动,则四棱锥M -ABCD 体积的最大值为.题型二:麻花模型1(2023春·广东梅州·高二统考期中)已知三棱锥S -ABC 的四个顶点都在球O 的球面上,且SA =BC =2,SB =AC =7,SC =AB =5,则球O 的体积是()A.83π B.3223π C.423π D.823π1.(2022春·江西景德镇·高一景德镇一中校考期中)在△ABC 中,AB =AC =2,cos A =34,将△ABC 绕BC 旋转至△BCD 的位置,使得AD =2,如图所示,则三棱锥D -ABC 外接球的体积为.2.(2023秋·吉林·高一吉林一中校考阶段练习)如图,在△ABC 中,AB =25,BC =210,AC =213,D ,E ,F 分别为三边中点,将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π3.(2023·江西·统考模拟预测)在三棱锥P -ABC 中,已知PA =BC =213,AC =BP =41,CP =AB =61,则三棱锥P -ABC 外接球的表面积为()A.77πB.64πC.108πD.72π4.(2022·全国·高三专题练习)已知四面体ABCD 的棱长满足AB =AC =BD =CD =2,BC =AD =1,现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD 可以在圆锥中任意转动,则圆锥侧面积的最小值为.题型三:垂面模型1(2023·高一单元测试)在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,则三棱锥P -ABC 的外接球半径为()A.3B.23C.32D.61.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且边长为3,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.4πB.8πC.16πD.32π2.(2020春·天津宁河·高一校考期末)在三棱锥P -ABC 中,AP =2,AB =3,PA ⊥面ABC ,且在△ABC 中,C =60°,则该三棱锥外接球的表面积为()A.20π3B.8πC.10πD.12π3.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且其面积为334,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.πB.2πC.4πD.8π4.(2022春·山东聊城·高一山东聊城一中校考阶段练习)在四棱锥P -ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为矩形,BC =2,PC 与平面PAB 所成的角为30o ,则该四棱锥外接球的体积为()A.433π B.43πC.823πD.833π题型四:切瓜模型1(2023·贵州贵阳·校联考模拟预测)在三棱锥A -BCD 中,已知AC ⊥BC ,AC =BC =2,AD =BD =6,且平面ABD ⊥平面ABC ,则三棱锥A -BCD 的外接球表面积为()A.8πB.9πC.10πD.12π1.(2023·四川达州·统考二模)三棱锥A -BCD 的所有顶点都在球O 的表面上,平面ABD ⊥平面BCD ,AB =AD =6,AB ⊥AD ,∠BDC =2∠DBC =60°,则球O 的体积为()A.43πB.32π3C.49π3D.323π2.(2023春·陕西西安·高一长安一中校考期中)在直三棱柱ABC -A 1B 1C 1中,AB ⊥BC ,AB =BC =AA 1=4,点P 为B 1C 1的中点,则四面体PABC 的外接球的体积为()A..41416π B.41413π C.41412π D.4141π3.(2022·高一单元测试)四棱锥P -ABCD 的顶点都在球O 的表面上,△PAD 是等边三角形,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,若AB =2,BC =3,则球O 的表面积为()A.12πB.16πC.20πD.32π4.(2021·高一课时练习)在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,且ABCD 为矩形,∠DPA =π2,AD =23,AB =2,PA =PD ,则四棱锥P -ABCD 的外接球的体积为()A.163π B.323π C.643π D.16π5.(2023春·全国·高一专题练习)在四棱锥P-ABCD中,ABCD是边长为2的正方形,AP=PD=10,平面PAD⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为()A.4πB.8πC.136π9D.68π3题型五:斗笠模型1(2023·全国·高一专题练习)正四面体S-ABC内接于一个半径为R的球,则该正四面体的棱长与这个球的半径的比值为()A.64B.33C.263D.31.(2022·高一专题练习)已知正四棱锥P-ABCD(底面四边形ABCD是正方形,顶点P在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为10,若该正四棱锥的体积为50 3,则此球的体积为()A.18πB.86πC.36πD.323π2.(2022·全国·高一专题练习)某四棱锥的底面为正方形,顶点在底面的射影为正方形中心,该四棱锥内有一个半径为1的球,则该四棱锥的表面积最小值是()A.16B.8C.32D.243.(2022春·安徽·高三校联考阶段练习)在三棱锥P-ABC中,侧棱PA=PB=PC=10,∠BAC=π4,BC=22,则此三棱锥外接球的表面积为.题型六:矩形模型1(2022春·全国·高一期末)已知三棱锥A-BCD中,CD=22,BC=AC=BD=AD=2,则此几何体外接球的表面积为()A.2π3B.2π C.82π3D.8π1.(2022春·广东惠州·高一校考期中)在矩形ABCD中,AB=6,BC=8,现将△ABC沿对角线AC翻折,得到四面体DABC,则该四面体外接球的体积为()A.1963π B.10003π C.4003π D.5003π2.(2022春·河北沧州·高一校考阶段练习)矩形ABCD中,AB=4,BC=3,沿AC将三角形ABC折起,得到的四面体A-BCD的体积的最大时,则此四面体外接球的表面积值为()A.25πB.30πC.36πD.100π3.(2022春·四川成都·高一统考期末)在矩形ABCD 中,AB =6,AD =8,将△ABC 沿对角线AC 折起,则三棱锥B -ACD 的外接球的表面积为()A.36πB.64πC.100πD.与二面角B -AC -D 的大小有关题型七:折叠模型1(2022春·陕西西安·高一长安一中校考期末)已知菱形ABCD 的边长为3,∠ABC =60°,沿对角线AC 折成一个四面体,使平面ACD 垂直平面ABC ,则经过这个四面体所有顶点的球的体积为().A.5152π B.6πC.515πD.12π1.已知等边△ABC 的边长为2,将其沿边AB 旋转到如图所示的位置,且二面角C -AB -C 为60°,则三棱锥C -ABC 外接球的半径为2.(2023·广西南宁·统考二模)蹴鞠,又名“蹴球”“蹴圈”等,“蹴”有用脚蹴、踢的含义,鞠最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的足球,现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足AB =BC =CD =DA =DB =433cm ,AC =23cm ,则该“鞠”的表面积为cm 2.3.(2022秋·福建泉州·高三校考开学考试)在三棱锥S -ABC 中,SA =SB =AC =BC =2,SC =1,二面角S -AB -C 的大小为60°,则三棱锥S -ABC 的外接球的表面积为.4.(2022秋·山东德州·高二统考期中)已知在三棱锥中,S -ABC 中,BA ⊥BC ,BA =BC =2,SA =SC =22,二面角B -AC -S 的大小为5π6,则三棱锥S -ABC 的外接球的表面积为()A.56π3B.58π3C.105π4D.124π9题型八:鳄鱼模型1(2022春·四川成都·高一树德中学校考期末)已知在三棱锥S-ABC中,AB⊥BC,AB=BC=2,SA =SC=22,二面角B-AC-S的大小为2π3,则三棱锥S-ABC的外接球的表面积为()A.124π9B.105π4C.105π9D.104π91.(2023春·全国·高一专题练习)如图,在三棱锥P-ABC,△PAC是以AC为斜边的等腰直角三角形,且CB=22,AB=AC=6,二面角P-AC-B的大小为120°,则三棱锥P-ABC的外接球表面积为()A.5103π B.10π C.9π D.4+23π2.(2023·陕西榆林·统考三模)在三棱锥A-BCD中,AB⊥BC,BC⊥CD,CD=2AB=2BC= 4,二面角A-BC-D为60°,则三棱锥A-BCD外接球的表面积为()A.16πB.24πC.18πD.20π3.(2023春·安徽阜阳·高三阜阳市第二中学校考阶段练习)如图1,四边形ABCD中,AB=AD =2,CB=CD=2,AB⊥AD,将△ABD沿BD翻折至△PBD,使二面角P-BD-C的正切值等于2,如图2,四面体PBCD的四个顶点都在同一个球面上,则该球的表面积为()A.4πB.6πC.8πD.9π4.(2023·江西南昌·校联考模拟预测)在平面四边形ABCD中,AD=CD=3,∠ADC=∠ACB =90°,∠ABC=60°,现将△ADC沿着AC折起,得到三棱锥D-ABC,若二面角D-AC-B的平面角为135°,则三棱锥D-ABC的外接球表面积为.5.(2023春·广东广州·高三统考阶段练习)在三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=2,△PAC为正三角形,且二面角P-AC-B的平面角为π6,则三棱锥P-ABC的外接球表面积为.。
高中数学外接球解题技巧

高中数学外接球解题技巧高中数学外接球解题技巧在高中数学中,外接球是一道常见的几何题,其目的是求出几何体 (如正方体、长方体等) 的外接球半径或直径,进而求解几何体的体积或表面积。
下面将介绍一些外接球解题技巧。
1. 熟悉常见几何体的外接球公式对于正方体、长方体等常见几何体的外接球,可以使用以下公式计算其半径或直径:正方体外接球半径 = √3/3 ×正方体边长长方体外接球半径 = √3/3 ×长方体边长×√2球体外接球半径 = 圆周率×球体直径其中,√表示开根号运算,√2 表示圆周率乘以 2。
2. 利用对称性求解外接球半径在某些情况下,几何体的外接球半径可以通过对称性得到求解。
例如,对于正方体,可以利用其对称性求解外接球半径。
正方体有六个等效面,每个面都是一个等边三角形,这些等效面都是正方体的外接球球面的一部分。
因此,可以利用对称性计算出正方体的外接球半径,进而求解其他几何体外接球半径。
3. 利用三角函数求解外接球半径对于一些较为复杂的几何体,可以利用三角函数求解外接球半径。
例如,对于正八面体,其外接球是一个正十二面体,可以利用正弦定理求解外接球半径。
具体而言,正八面体的每个面都是一个等腰三角形,相邻面的夹角为 30 度,正十二面体的每个面都是一个等边三角形,相邻面的夹角为 60 度。
因此,可以利用正弦定理计算正十二面体的外接球半径。
拓展:除了上述技巧外,还有一些其他的技巧可以用来求解外接球半径,例如用极坐标方程求解、用向量法求解等。
此外,外接球问题也与物理学中的牛顿第二定律、圆周运动等问题密切相关。
因此,对于外接球问题,需要从不同角度进行思考,灵活运用各种技巧和方法,以达到求解的目的。
立体几何求外接球球心(包括万能求法)
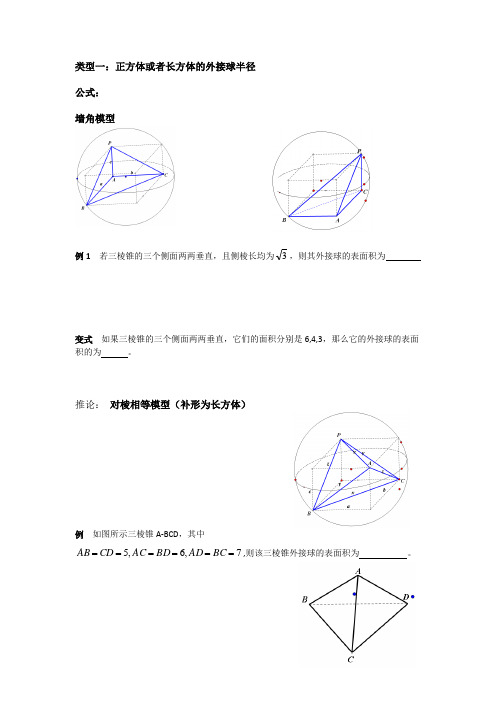
公式:
墙角模型
例1 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积为
变式如果三棱锥的三个侧面两两垂直,它们的面积分别是6,4,3,那么它的外接球的表面积的为。
推论:对棱相等模型(补形为长方体)
例如图所示三棱锥A-BCD,其中
BD
AD
AC
=BC
AB,则该三棱锥外接球的表面积为。
CD
,5=
,6
7
=
=
=
=
222)2(r h R +=公式:
例:直三棱柱111C B A ABC -的各顶点都在同一球面上,若,21===AA AC AB
︒=∠120BAC ,则此球的表面积为
类型三:正棱锥或圆锥
h
l h h r R 222
22=+=公式: 例 正四棱锥ABCD S -的底面边长和各棱长都为2,各顶点都在同一球面上,则此球的体积为
例 一个几何体的三视图如下所示,则该几何体外接球的表面积为( )
.A .π3 .B .π2 .C .
π316 D .以上都不对。
几何体的外接球

几何体的外接球一、球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
二、常见平面几何图形的外接圆外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形也即正三角形,其满足正多边形的基本特征:五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长) (2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,求解过程比较简单,该处不做重点说明。
(3)等腰三角形:结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线即中线上。
由图可得:22)2()(a r h r +-=思考:钝角三角形和锐角三角形外接圆圆心位置的区别。
(4)非特殊三角形:考察较少,若出现除以上三种情况以外的三角形在求解外接圆半径时可以参考使用正弦定理。
2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法类似,等腰梯形的外接圆圆心不在中学考察范围内,不用掌握。
外接圆圆心是在几何图形所在平面的一个到各个顶点距离相同的点;外接球球心则是空间中到几何体各个顶点距离相同的点。
结合上述所讲内容,外接圆圆心与外接球球心有许多相似之处以三角形为例,过三角形的外接圆圆心作三角形所在平面的一条垂线,不难得到:该垂线上的任意一点到该三角形三个顶点的距离恒定相等。
转化到几何体中,如正方体,其外接球球心位于体心位置,其与正方体任一表面正方形的中心连线均垂直于该正方形。
从而我们得出如下结论:几何体的外接球球心与底面外心的连线垂直于底面,也即球心落在过底面外心的垂线上,简单称之为:球心落在底面外心的正上方。
立体几何的外接球问题

立体几何中的外接球问题概 述①长方形的外接圆圆心为对角线的中点,222a b R +=(,a b 为长方形的长、宽)。
长方体的外接球球心为体对角线的中点,222(,,2a b c R a b c ++=为长方体的长、宽、高)。
②三角形的外接圆圆心是底边的中垂线的交点,外接圆半径可由,余弦定理求得2sin a r A=;等边三角形的外心是高的三等分点(靠底边);直角三角形的外心是斜边中点。
③三棱锥或其它几何体,其外接球球心一定在过面的外心且与该面垂直的垂线上。
④过球心的截面截得的圆是大圆。
⑤勾股定理、正弦定理、余弦定理、射影定理、面积法、体积法等平面几何性质灵活应用。
1.圆柱、直棱柱、一侧棱垂直底面的棱锥设底面外接圆半径为r ,高为h ,则外接球半径224h R r =+'Rt OAO ∆。
2、圆锥、各侧棱都相等的棱锥(包括正三棱锥、正四棱锥)设底面外接圆半径为r ,高为H ,则外接球半径222H r R H +=,截面图中1Rt OAO ∆勾股定理解得。
()222222H r R H R r R H+=-+⇒=。
3、等腰四面体补成长、宽、高分别为,,x y z 的长方体,则2222222222222222x y b a b c x z c x y z z y a ⎧+=⎪+++=⇒++=⎨⎪+=⎩外接球半径222222222x y z a b c R ++++==。
注:(1)棱长为a 的正四面体外接球半径2226422a a a aR ++==; (2)从某顶点出发,三棱长为,,a b c 的直角三棱锥外接球半径2222a b c R ++=。
补体法:(1)正四面体;(2)等腰四面体;(3)直角三棱锥或其他。
4、有两个面互相垂直的三棱锥设两垂直面的交线长为l ,两垂直面的外接圆半径分别为12,r r 则外接球半径2222212124l R r d r r =+=+-。
cc b baa r 2O O 2O 1C A5、任意三棱锥已知两面外接圆半径分别为12,r r ,两面外心到交线的距离分别为12,d d ,两面的交线长为l ,已知或可求二面角α,2222111222,44l l O E d r O E d r ==-==-,221212122cos O O d d d d α=+-221212122cos sin sin d d d d O O OE ααα+-==,222222121222cos 4sin 4d d d d l l R OE αα+-=+=+。
简单几何体的外接球半径求解技巧

简单几何体的外接球半径求解技巧外接球是指能够完全包围一个几何体的球,它的半径对于很多几何题目的求解都是十分重要的。
在解决几何问题时,如果涉及到外接球的半径,我们可以通过几何关系和一些数学工具来求解。
下面,我将介绍一些简单几何体的外接球半径求解技巧。
1.球的外接圆半径:对于平面上的一个圆,它的外接圆半径等于原圆半径的根号2倍。
这是由勾股定理和三角形内接圆半径的关系推导而来的。
当给定一个平面上的圆时,可以通过这个公式求解它的外接圆半径。
2.三角形的外接圆半径:对于一个三角形,它的外接圆半径可以通过三角形的边长来求解。
三角形的外接圆半径等于三角形的任意一条边的一半除以三角形的外接圆周角的正弦值。
这个公式可以通过三角形的面积公式、三角形的边长和正弦定理推导而来。
当给定一个三角形时,可以通过这个公式求解它的外接圆半径。
3.四边形的外接圆半径:对于一个四边形,它的外接圆半径可以通过四边形的对角线和角度来求解。
四边形的外接圆半径等于四边形两对对角线的交点之间的距离的一半除以四边形内角的正弦值。
这个公式可以通过四边形的面积公式、四边形的对角线、四边形两对对角线的交点之间的距离和正弦定理推导而来。
当给定一个四边形时,可以通过这个公式求解它的外接圆半径。
4.正多边形的外接圆半径:对于一个正n边形,它的外接圆半径可以通过边长来求解。
正n边形的外接圆半径等于边长的一半乘以正n边形的中心角的余弦值的倒数。
这个公式可以通过正多边形的面积公式、正多边形的边长、正n边形的外接圆的半径和正n边形的中心角的三角函数关系推导而来。
当给定一个正n边形时,可以通过这个公式求解它的外接圆半径。
需要注意的是,这些公式都是在已知几何体的一些参数的前提下求解外接球半径的。
因此,在实际解题时,首先需要明确已知条件,并应用相关的几何定理和公式来求解。
此外,还可以通过数学软件、计算机模拟等工具来求解几何体的外接球半径。
这些工具一般会通过几何关系和数值计算的方法来求解。
几何体外接球常用结论及方法(如何求几何体的外接球半径)

几何体外接球常用结论及方法(如何求几何体的外接球半径)一、在涉及球的问题中,经常用到结论:(1)在三棱锥P ABC -中,PA PB ⊥,PA PC ⊥,PB PC ⊥,则该三棱锥外接球半径2R =(2倍. (3)直角三角形的三角形外接圆的半径等于斜边的一半.(4)一般的三角形ABC 可由正弦定理:2sin sin sin a b c R A B C===(R 为外接圆半径)求得外接圆半径,内切圆的半径通过:12S C r =⋅多边形多边形的周长(r 为内切圆的半径)求得. (5)已知三棱锥P ABC -,PA ⊥面ABC ,若PA a =,ABC △的外接圆半径为r ,则该三棱锥P ABC -的外接球半径为()()22222R r a =+.(6)正方体的外接球、内切球、棱切球的直径分别为正方体的体对角线长2R =、棱长2R a =、面对角线长2R =.(7)在四面体P ABC -,若90APC ∠=︒,90ABC ∠=︒,则四面体P ABC -的外接球的直径是AC .(8)对于正棱锥的外接球的半径计算,也可借用几何法求出.如针对正三棱锥V ABC -,可根据平面几何中射影定理22VA VO VH Rh '=⋅=(h 为正三棱锥的高,VA 为侧棱长,即正棱锥侧棱长的平方等于正棱锥的高与外接球直径的乘积.(9)正四面体的高、外接球的半径与内切球的半径之间关系: ①高:a h 36=;②球心把高分成3:1;③内切球半径:a 126;外接球半径:a 46. (10)有内切球的多面体的内切球的半径计算方法:13V S r =全. (11)三棱锥的两个侧面互相垂直,已知两个相互垂直的面的外接圆半径的长及其公共棱的长度的情形:已知三棱锥A BCD -中,面ABD ⊥面BCD ,且ABD ∆,BCD ∆的外接圆半径分别记为12,r r ,公共棱BD a =,则该三棱锥的外接球半径满足:()()()222212222R r r a =+- 证明:分别在ABD ∆,BCD ∆所在的圆面上调整这两个三角形的开关,如图在ABD ∆的外接圆周上调整A 点的位置到G 点,使GD BD ⊥,在BCD ∆的外接圆周上调整其形状,将B 调整到E ,C 调整到F ,使得EDF ∆是以D 为直角顶点的等腰直角三角形,从而得到新的三棱锥G EDF -,则GD DE ⊥,GD DF ⊥,DE DF ⊥,2214GD r a =-22DE DF r ==,三棱锥G EDF -的外接球与A BCD -的三棱锥外接球是重合的,因此所求得外接球半径满足()()()222212222R r r a =+-. (12)三棱锥给出两个侧面的夹角大小(夹角),及其相应两个侧面的三角形外接圆半径和公共弦长的情形:P ABC -,已知面PAC 与ABC 所形成二面角为()090θθ<≤︒,且已知PAC ∆和ABC ∆的外接圆的半径分别为1r ,2r ,AC a =,则该棱锥P ABC -的外接球半径R 满足: ()()()2222222222212121222cos 22cos 244a a a R R r R r r r r r ⎛⎫⎛⎫+--=+---- ⎪⎪⎝⎭⎝⎭证明:如图,取PAC ∆,ABC ∆的外接圆圆心分别为12,O O ,分别过12,O O 作面PAC ,ABC 垂线,两条垂线必交于一点O ,该O 即为该三棱锥外接球球心.再取公共棱AC 的中点为K ,连接1O K ,2O K ,则四点12,,,O O K O 共圆且12O KO θ∠=,12O OO πθ∠=-在直角三角形1AOO 中,根据勾股定理得:2211OO R r =-,同理可得2222OO R r =-222211124a a O K r r ⎛⎫=-=- ⎪⎝⎭222222224a a O K r r ⎛⎫=-=- ⎪⎝⎭在12O KO ∆和12O OO ∆中,根据12O KO θ∠=,12O OO πθ∠=-,结合余弦定理可得到:12,,,R r r a 之间的等量关系 ()()()2222222222212121222cos 22cos 244a a a R R r R r r r r r ⎛⎫⎛⎫+--=+---- ⎪⎪⎝⎭⎝⎭ (13)计算球的表面积或体积,必须求出球的半径,一般方法有(核心:补体定心)①根据球心到内接多面体各顶点的距离相等确定球心,然后求出半径;(当涉及的多面体较多垂直时,考虑此法,充分利用直角三角形斜边的中点,找出小圆圆心或球心位置,进而求出球的半径.)②考虑补体法,求出多面体的外接球的直径.当三棱锥S ABC -中,三对对棱分别相等时,可构造一个长方体;当三棱锥S ABC -有三条(可不相邻)两两垂直的线段时,也可构造一个长方体,正四面体可将其补成正方体,有侧棱垂直底面棱锥可构造直棱柱.③有时可借用球性质(球心与小圆圆心相连垂直小圆所在的平面),根据几何关系求出球半径.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何体外接球常用结论及方法
几何体的外接球是指能够将该几何体完全包围的球。
在三维空间中,我们常见的几何体有球、正方体、长方体、圆锥体、圆柱体、四面体等。
下面将介绍几何体外接球的常用结论及求解方法:
1.球的外接球:球本身就是一个外接球,其半径即为球的半径。
2.正方体的外接球:正方体的外接球是一个球心位于正方体空间对角线中点处的球。
对角线在空间中的长度可以通过勾股定理求得,即对角线长度等于正方体一条边的平方根乘以根号3、因此,外接球的半径等于对角线长度的一半。
3.长方体的外接球:长方体的外接球是一个球心位于长方体空间对角线中点处的球。
同样,对角线长度可以通过勾股定理求得,即对角线长度等于长方体的长、宽、高的平方和的开方。
因此,外接球的半径等于对角线长度的一半。
4.圆锥体的外接球:圆锥体的外接球是一个球心位于圆锥体顶点与底面圆心连线的中点处的球。
外接球的半径等于该连线的长度。
5.圆柱体的外接球:圆柱体的外接球是一个球心位于圆柱体两个底面圆心连线的中点处的球。
外接球的半径等于该连线的长度。
6.四面体的外接球:四面体的外接球是一个球心位于四面体四个顶点的外接圆圆心的球。
外接球的半径等于外接圆的半径。
以上是几何体外接球的常用结论。
接下来我们介绍一种求解几何体外接球半径的常用方法,即通过计算几何体的顶点坐标来求解。
首先,根据几何体的类型和已知信息,确定几何体的顶点坐标。
对于球、正方体、长方体等简单的几何体,可以通过已知的半径、边长等信息
得到;对于复杂的几何体,可以通过已知的顶点坐标及其它辅助信息求解。
然后,根据顶点坐标计算几何体的外接球的球心坐标。
球心位于几何
体顶点的外接圆的圆心处。
对于球、正方体、长方体等几何体,直接取顶
点坐标的平均值作为球心坐标;对于其它几何体,可以通过求解外接圆的
圆心坐标来得到球心坐标。
最后,根据球心坐标和几何体顶点坐标,计算几何体的外接球半径。
外接球半径就是几何体顶点与球心之间的距离的最大值。
可以使用坐标间
距离的公式计算每个顶点与球心的距离,然后取最大值作为外接球半径。
综上所述,通过计算几何体的顶点坐标来求解外接球的半径是一种常
用的方法。
当然,对于一些特殊的几何体,还可以利用其它的几何性质和
求解方法来得到外接球的半径。
