2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》题型分类练习(附答案)
鲁教版五四制六年级上册习题 3.7 探索与表达规律

探索与表达规律一、基础题1.选择题(1)观察下列数:2,9,28,65,126,…,找出规律是( )A.n(n-1)B.n(n+1)C.n 3+1D.n 2+1(2)有以下两个数串:1 3 5 7 … 1995 1997 1999 和 1 4 7 10 …1993 1996 1999 同时出现在这两个数串中的数的个数共有( )A.333个B. 334个C.335个 D 336个(3)百货大楼进一批花布,出售时要在进价的基础上加一定的利润,其数量x 与售价y 如下表: 数量x(米)1 2 3 4 …售价y (元) 8+0.3 16+0.6 24+0.9 32+1.2 …下列用数量x 表示售价y 的公式中,正确的是 ( )A.y =8x+0.3B.y =8.3xC. y =8+0.3xD.y =8.3+x 二、综合题1.填空题观察下面一组数据,填上适当的数11,-21,31,-41, ,-61… 2.观察下列各式:1+3=22)31(⨯+,1+3+5=23)51(⨯+,1+3+5+7=24)71(⨯+… 则1+3+5+7+…+(2n-1)=3.观察下列等式:12+1=1×2 22+2=2×3 32+3=3×4.……请你将猜想的规律用自然数n (n ≥1)表示是三、综合题1.观察下列两组式子:1=12 1×3=22-1,1+3=12 2×4=32-1,1+3+5=32 3×5=42-1,1+3+5+7=42 4×6=52-1,……(1)试写出1+3+5+7+…+99= ,99× = 2-1;(2)试用字母表示你探索得到的规律.参考答案四、基础题1.选择题(1)C (2)A (3)B五、综合题1.填空题(1)1 5(2)(121)(1)2n n+--(3)n2+n=n(n+1)六、综合题(1)502,101,100(2) 1+3+5+7+……+(2n-1)=n2;n(n-2)=(n+1)2-1。
六年级上册数学鲁教版探索与表达规律2导学案
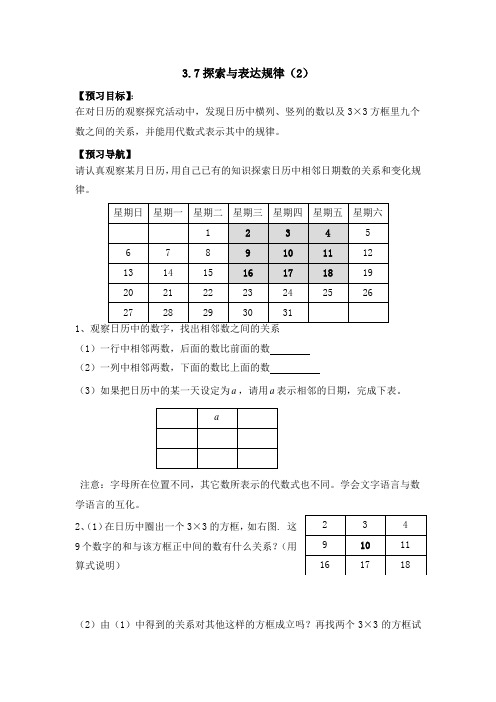
3.7探索与表达规律(2)【预习目标】:在对日历的观察探究活动中,发现日历中横列、竖列的数以及3×3方框里九个数之间的关系,并能用代数式表示其中的规律。
【预习导航】请认真观察某月日历,用自己已有的知识探索日历中相邻日期数的关系和变化规律。
星期日 星期一 星期二 星期三 星期四 星期五 星期六 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27282930311、观察日历中的数字,找出相邻数之间的关系 (1)一行中相邻两数,后面的数比前面的数 (2)一列中相邻两数,下面的数比上面的数(3)如果把日历中的某一天设定为a ,请用a 表示相邻的日期,完成下表。
注意:字母所在位置不同,其它数所表示的代数式也不同。
学会文字语言与数学语言的互化。
2、(1)在日历中圈出一个3×3的方框,如右图. 这9个数字的和与该方框正中间的数有什么关系?(用算式说明)(2)由(1)中得到的关系对其他这样的方框成立吗?再找两个3×3的方框试a2 3 4 9 10 11 161718一试.你能用代数式表示这个关系吗?(3)你认为这个关系对任何一个月的日历都成立a吗?为什么?(提示:如果用a表示中间数请学生按前面找出的关系填出框中另外8个数。
)(4)想一想:这样的方框中的9个数之和能等于100吗?能等于180吗? 270呢?【预习诊断】星期日星期一星期二星期三星期四星期五星期六1 2 3 4 56 7 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 2627 28 29 30 31(1)在十字型框中,5个数字的和等于正中间数的倍(2)在 H 型框中,7个数的和等于正中间数的倍.(3)设中间数为a,用代数式分别表示十字型框和H 型框中所有数字之和。
(4)如果将框上下左右移动,框中的所有数还有这种关系吗?2、小明:“你在心里想好一个两位数,将十位数字乘以2,然后加上3,再把所得新数乘以5,最后把得到的新数加上个位数字,把你的结果告诉我,我就知道你心里想的两位数。
3.7 探索与表达规律 专题探究教学课件-2021-2022学年鲁教版(五四制)六年级数学上册

(2)第n个单项式是(-1)n+1nn, 第n+1个单项式是
(-1)n+2(n+1)n。
等差数列相邻两项相差几就是几n,
你有什么发现?
再让n=1,计算出数看看与第一项相差多少,
就加上或减去该数。
解:由题意知an=
当n=100时,a100=
−
+
×−
×+
2、找到题目中的改变量,并认
=
真观察改变量的变化规律。
3、观察与猜想结合找到变量与
不变量之间的关系。
能力提升:
(2008•湛江)先观察下列等式,然后用你发现的规律解
答下列问题:
=− ,
= − ,
= − ,···
×
×
×
⑴计算
+
×
×
=1− =
⑵
+
+
+ ⋯+
×
×
×
(+)
= − + − + − + ⋯ −
+
= 1=
+ +
⑶
+
+
+ ⋯+
×
×
×
(−)(+)
六年级上册数学鲁教版探索与表达规律1导学案

3.7探索与表达规律(1)【预习目标】:通过摆放桌椅的一个系列活动,展开对其中规律的探索。
【预习导航】下图是按照一定的规律摆放的桌子椅子:……认真观察上图回答:1张桌子的周围摆放6把椅子,2张桌子的周围摆放把椅子,3张桌子的周围摆放把椅子。
想一想:n张桌子的周围能摆放多少把椅子呢?方法一:第一步,观察各个数量的变化规律:当桌子的个数每增加1张时,椅子的个数就增加把。
第二步,猜想归纳规律,完成下表桌子/张 12 3 4 ……n椅子/把 6 10 14 ……变化规律6 6+4 6+4+4 ……归纳表达规律6+4×0 6+4×1 6+4×2 ……第三步,验证规律:当1n=时,有把椅子;当2n=时,有把椅子,结论成立。
得出结论:n张桌子的周围能摆放把椅子。
方法二:第一步,观察上图规律发现:当桌子的个数增加1张时,上下两边椅子的个数;而左右两边椅子个数。
第二步,完成下表:桌子/张 12 3 4 ……n椅子/把 6 10 14 ……变化规律4+2 4+4+2 4+4+4+2 ……归纳表达规律4×1+2 4×2+2 4×3+2 ……第三步,验证规律,得出结论.(请自己动手验证)想一想:你还有其它的解决方法吗?【预习诊断】下图也是按一定的规律摆放的桌子和椅子:……(1)按图示规律填空:桌子/张 1 2 3 4 5 ……椅子/把……(2)按照这样的规律摆放,n张桌子的周围能摆放把椅子。
【预习反思】通过预习,你认为本节课的重点知识是什么,你还有哪些困惑,赶紧写下来吧!【学习目标】1、经历探索数量关系、运用符号表示规律、通过运算验证规律的过程。
2、会用代数式表示简单问题中的数学规律。
【学习过程】一、小组交流,合作解疑。
二、探究活动1、(1)按照预习诊断中的规律每8张拼成1张大桌子,则40张桌子可拼成5张大桌子,桌子的周围共可摆放多少把椅子?(2)如果有8n 张桌子,扔按照上面规律每8张桌子拼成1张,此时桌子的周围共可摆放多少把椅子?2、(1)小明也用上面的8张桌子拼成1张大桌子,但8n 张桌子的周围只能摆放16n 把椅子,你能说出他的桌子是怎么样摆放的吗?(2)若扔用上面的桌子,每8张桌子拼成1张大桌子,你还有其他摆放桌子的方法吗?按照你的摆放方法,8n 张桌子的周围共可摆放多少把椅子?三、随堂练习1、有一列数:12,34,56,78,…,则第n 个数为是2、观察下列各式:①21112+=⨯;②22223+=⨯;③23334+=⨯; ④24445+=⨯;…… 猜测第n 个式子是3、如图所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……则第2012次输出的结果为___________.4、黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:则第n 个图案中有白色地砖______ 块.(用含n 的代数式表示)输入x12x x +3输出x 为偶数x 为奇数5、用火柴棒按下图的规律搭三角形。
最新审定鲁教版数学六年级上册《3.7探索与表达规律》习题(名校资料)

《3.7 探索与表达规律》习题一、基础过关1.一列数a 1,a 2,a 3,…,其中a 1=12 错误!未找到引用源。
,a n =111n a -+ 错误!未找到引用源。
(n 为不小于2的整数),则a 4的值为( ) A.58 错误!未找到引用源。
B.85错误!未找到引用源。
C.138 错误!未找到引用源。
D.错误!未找到引用源。
8132.希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10B.25=9+16C.36=15+21D.49=18+313.如图,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑩个图形中平行四边形的个数是()A.54B.110C.19D.1094.观察下列一组数:23 错误!未找到引用源。
,45 错误!未找到引用源。
,67错误!未找到引用源。
,89错误!未找到引用源。
,1011 错误!未找到引用源。
,…,它们是按一定规律排列的,那么这一组数的第k 个数是 .5.观察下列等式:12错误!未找到引用源。
=1-错误!未找到引用源。
,错误!未找到引用源。
+错误!未找到引用源。
=1-错误!未找到引用源。
, 错误!未找到引用源。
233111112222++=- ,…请根据上面的规律计算:231011112222++++ 错误!未找到引用源。
= . 6.如图是在正方形网格中按规律填成的阴影,根据此规律,第n 个图中的阴影部分小正方形的个数是 .二、综合训练7.如图是用棋子摆成的“T”字图案.从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子.(1)照此规律,摆成第四个图案需要几枚棋子?(2)摆成第n 个图案需要几枚棋子?(3)摆成第2014个图案需要几枚棋子?8.(8分)有规律排列的一列数:2,4,6,8,10,12,…它的每一项可用式子2n(n 是正整数)来表示.有规律排列的一列数:1,-2,3,-4,5,-6,7,-8,…(1)它的每一项你认为可用怎样的式子来表示?(2)它的第100个数是多少?(3)2013是不是这列数中的数?如果是,是其中的第几个数?三、拓展应用9.观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×=×25;②×396=693×.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b且a b≠0)..参考答案一、基础过关1. A.2. C.3. D.4. 221k k + 5.10112-6. n(n+1)+2二、综合训练7. (1)9+5=14(枚).故摆成第四个图案需要14枚棋子.(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n 个图案需5+3×(n-1) =5+3n-3=(3n+2)枚棋子.(3)3×2014+2=6044(枚),即第2014个图案需6044枚棋子.8. (1)它的每一项可以用式子(-1)n+1n(n 是正整数)表示.(2)它的第100个数是(-1)100+1×100=-100.(3)当n=2013时,(-1)2013+1×2013=2013,所以2013是其中的第2013个数.三、拓展应用9. (1)①因为5+2=7,所以左边的三位数是275,右边的三位数是572,所以52×275=572×25.②因为左边的三位数是396,所以左边的两位数是63,右边的两位数是36,63×396=693×36.(2)因为左边两位数的十位数字为a,个位数字为b,所以左边的两位数是10a+b,三位数是100b+10(a+b)+a,右边的两位数是10b+a,三位数是100a+10(a+b)+b,所以一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+ b]×(10b+a).。
鲁教版数学六年级上册3.7《探索与表达规律》说课稿

鲁教版数学六年级上册3.7《探索与表达规律》说课稿一. 教材分析鲁教版数学六年级上册3.7《探索与表达规律》这一节的内容,主要让学生通过观察、分析、归纳等方法,探索数字的变化规律,并能够用字母表示出来。
这一节内容是学生在掌握了基本的数学运算和数学符号的基础上,进一步培养学生的逻辑思维能力和抽象概括能力。
内容具有一定的挑战性,需要学生通过不断的尝试和思考,找出数字之间的规律。
二. 学情分析六年级的学生已经具备了一定的数学基础,对于数字的变化和规律有一定的认识。
但是,对于通过观察和分析找出数字之间的规律,并用字母表示出来,可能还存在一定的困难。
因此,在教学过程中,教师需要引导学生观察和分析,引导学生用自己的语言表达出数字之间的规律,再逐步引导学生用字母表示出来。
三. 说教学目标1.知识与技能目标:学生能够通过观察和分析,找出数字之间的变化规律,并能够用字母表示出来。
2.过程与方法目标:学生通过自主探索和合作交流,培养逻辑思维能力和抽象概括能力。
3.情感态度与价值观目标:学生体验数学探索的乐趣,增强自信心,提高学习数学的兴趣。
四. 说教学重难点1.教学重点:学生能够通过观察和分析,找出数字之间的变化规律,并能够用字母表示出来。
2.教学难点:学生能够用自己的语言准确地表达出数字之间的规律,并能够用字母表示出来。
五. 说教学方法与手段在本节课中,我将采用引导发现法、自主探究法和合作交流法进行教学。
同时,利用多媒体课件和教学辅助工具,帮助学生更好地理解和表达数字之间的规律。
六. 说教学过程1.导入新课:通过一个有趣的数字游戏,引发学生对数字变化规律的兴趣,激发学生的学习动机。
2.自主探究:学生通过观察和分析,找出数字之间的变化规律,并用自己的语言表达出来。
3.引导发现:教师引导学生通过合作交流,总结和归纳数字之间的变化规律,并用字母表示出来。
4.练习巩固:学生通过做一些相关的练习题,加深对数字变化规律的理解和运用。
3.7 探索与表达规律 专题探究 学案-2021-2022学年鲁教版(五四制)六年级数学上册

《探索规律》专题探究最近几年,全国多数地市的中考试题都有找规律的题目,人们开始逐渐重视这一类数学题目。
所谓规律探索题,指的是给出一组具有某种特定关系的数字、式子、图形,或者是给出与图形有关的操作、变化过程,要求通过观察,分析,推理探索其中所蕴含的规律,进而归纳或猜想出一般性的结论。
这类问题在素材的选择、文字的表述、题型的设计等方面都比较新颖灵活,由于这类题目没有固定的形式和方法,要求学生通过阅读、观察、分析、比较、猜想、概括等探索活动来解决问题,它体现了“特殊到一般”的数学思想方法。
研究发现数学规律题的解题思想,不但能够提高学生的考试成绩,而且更有助于创新型人才的培养。
但究竟怎样才能把这种题目做好,是一个值得探究的问题。
下面就解决这类问题作一个初步的探究。
一、常见题型 1.代数中的规律 2.平面图形中的规律 3.空间图形中的规律 二、一般步骤成立三、应用举例:(一)代数中的规律:找数字规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把项数和项放在一起加以比较,就比较容易发现其中的奥秘。
<一>数字中的规律:数字中的规律包括等差数列、等比数列、乘方的数列、循环数列等。
这些是我们在学习猜想规律 察 观察 特 例 表达规律 察验证规律 察 应用规律证重新探索中会经常遇到的。
我们先来看一下等差数列。
1.等差数列:这类数列的规律是每相邻两个数之间的差值是相等的,整个数字序列依次递增或递减。
等差数列中比较简单的是自然数数列,如:0,1,2,3,4,5,·······,n. 奇数数列,如:1,3,5,7,9,·······2 n -1. 偶数数列2,4,6,8,10·······2 n 。
鲁教版小学数学六年级上册《探索与表达规律》同步练习2

《探索与表达规律》同步练习21.如图下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n (2≥n )个棋子,按下图的排列规律推断,第八个图案的棋子数是多少,第n 个图案的棋子数表示出来.2.观察下列各式:4333,3222,2111222⨯=+⨯=+⨯=+…,用n (自然数)把这个规律表示出来.3.下面一组式子211211-=⨯;31213121-=⨯;41314131-=⨯;51415141-=⨯… (1)写出这一组式子所表达的一般规律. (2)利用这一规律,计算.1009919291191901⨯++⨯+⨯4.探索规律225152=可写成25)11(1100++⨯⨯625252=可写成25)12(2100++⨯⨯1225352=可写成25)13(3100++⨯⨯2025452=可写成25)14(4100++⨯⨯…(1)把这个规律用含有n 的式子写出来;(2)计算952.5.观察:41)7131(731⨯-=⨯ 41)151111(1511141)11171(1171⨯-=⨯⨯-=⨯ … 计算:59551151111171731⨯+⨯+⨯+⨯.6.观察下列等式9-1=8,16-4=12,25-9=16,36-16=20,……这些等式反映出自然数间的什么规律呢?设n 表示自然数,请用含有n 的等式表示出来。
参考答案1.).1(4-n〔提示:4=4×(2-1) 8=4×(3-1) 12=4×(4-1) 16=4×(5-1)… 4(n -1)〕2.).1(2+=+n n n n3.(1)111111+-=+⨯n n n n (2)90011001901=- 4.(1)25)1(100)510(2++⨯⨯=+n n n (提示:设十位数字是n ,则任何一个个位是5的两位数都可以写成510+n(2)90255.由上列等式可以得如下规律:.1771441)411()4(1=⨯+-=+n n n n 6.)1(4)2(22+=-+n n n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》题型分类训练(附答案)一.规律型:数字的变化类1.列数81,82,83,84,…,82022,其中个位数字是8的数有()A.672个B.506个C.505个D.252个2.若a≠2,则我们把称为a的“友好数”,如3的“友好数”是,﹣2的“友好数”是,已知a1=3,a2是a1的“友好数”,a3是a2的“友好数”,a4是a3的“友好数”,……,依此类推,则a2021=()A.3 B.﹣2 C.D.3.已知,a1=,a2=,a3=,…,a n=,S n=a1+a2+…+a n,则S2020=.4.观察表一寻找规律,表二,表三分别是从表一中截取的一部分,则a=,b=.5.右边是一个按某种规律排列的数阵:根据规律,自然数2021应该排在从上向下数的第m行,是该行中的从左向右数的第n个数,那么m+n的值是()A.131 B.130 C.129 D.1286.十九世纪的时候,MorizStern(1858)与AchilleBro cot(1860)发明了“一棵树”,称之为有理数树,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,在第层第个数(从左往右数).7.我国宋代数学家杨辉在《详解九章算法》中发现了二项和的乘方规律,如(a+b)0=1,(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2a+b3,试计算(a ﹣b)6的第二项是.8.杨辉三角是二项式系数在三角形中的一种几何排列(在欧洲也称为帕斯卡三角形),它是中国古代数学的杰出研究成果之一,是一种离散型的数形结合.如图,是杨辉三角的一部分,则图中第五行中的所有数字之和为.9.如图被称为“杨辉三角”或“贾宪三角”.其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为a n,则a6+a10的值为()A.76 B.74 C.72 D.7010.一个白色圆生成一个黑色圆,一个黑色圆生成一个白色圆和一个黑色圆,按如图方式排列,依此类推,第十行圆的个数为()A.30个B.34个C.55个D.89个11.斐波那契数列因意大利数学家斐波那契以兔子繁殖为例引入,故又称为“兔子数列”,即:1,1,2,3,5,8,13,21,34…在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列在现代物理及化学等领域也有着广泛的应用.若斐波那契数列中的第n个数记为a n,则1+a3+a5+a7+a9+..+a2021与斐波那契数列中的第个数相同.12.任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数,再将这个新数按上述方式重新排列,再相减,….这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.该“卡普雷卡尔黑洞数”为()A.594 B.459 C.954 D.49513.已知一列数x1,x2,x3…,x2021满足x1+x2+…+x2021=×(1+2+…+2021),且|x1﹣3x2+1|=|x2﹣3x3+2|=…=|x2020﹣3x2021+2020|=|x2021﹣3x1+2021|,则x1﹣2x2﹣3x3=.二.规律型:图形的变化类14.下面是一种利用图形计算正整数乘法的方法,请根据图1~图4四个算图所示的规律,可知图5所表示的算式为.15.如图所示,正方形的边长均是a,以图①、②、③呈现的规律类推,图⑩中阴影部分的面积是.16.妈妈想考一考读七年级的儿子,她让儿子先把面积为1的矩形等分成两个面积为的矩形,再把面积为的矩形等分成两个面积为的矩形,再把面积为的矩形等分成两个面积为的矩形,如此进行下去,试用如图所揭示的规律计算++++++=.17.如图所示,直线AB,CD相交于点O,“阿基米德曲线”从点O开始生成,如果将该曲线与每条射线的交点依次标记为1,﹣2,3,﹣4,5,﹣6….那么标记为“2021”的点在()A.射线OA上B.射线OB上C.射线OC上D.射线OD上18.如图,已知∠PMQ=30°,点A1,A2,A3…在射线MQ上,点B1,B2,B3…均在射线MP上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若MA1=1,则△A2021B2021A2022的边长为.19.如图,将边长都为1的正方形按如图所示摆放,点A1、A2、…A n分别是正方形的中心,则2021个这样的正方形重叠部分的面积和为.20.如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△A1A2A3;再以对角线OA3为边作第四个正方形OA3A4B4,连接A2A4,得到△A2A3A4,…,则△A n A n+1A n+2的面积等于.参考答案一.规律型:数字的变化类1.解:∵81的个位数字是8,82的个位数字是4,83的个位数字是2,84的个位数字是6,85的个位数字是8,86的个位数字是4,…∴这列数的个位数字以8,4,2,6,每4个数循环出现,∵2022÷4=505…2,∴第2021个数的个位数是8,∴个数数字是8的个数为:505+1=506(个).故选:B.2.解:∵a1=3,a2是a1的“友好数”,∴a2==﹣2,∵a3是a2的“友好数”,∴a3==,∵a4是a3的“友好数”,∴a4==,∵a5是a4的“友好数”,∴a5==3,……∴每四个数是一组循环,∵2021÷4=505…1,∴a2021=a1=3,故选:A.3.解:∵a n===2(﹣),∴S n=a1+a2+…+a n=2×()+2×()+2×()+...+2(﹣)=2×(+﹣+...+﹣)=2×()=,∴S2020==,故答案为:.4.解:由图可知,a在第6行第5列,所以,a=6×5=30,∵70在第10行第7列,∴b在第11行第8列,∴b=11×8=88.故答案为:30;88.5.解:∵每行的最后一个数是这个行的行数m的平方,第m行的数字的个数是2m﹣1,∵442=1936,所以2021在第45行,∵452=2025,∴45行最后一个数字是2025,第45行有2×45﹣1=89个数字,从2025往前数4个数据得到2021,从而得出2021是第85个数据,∴m=45,n=85,∴m+n=45+85=130.故选:B.6.解:由图可知,向右发散的都是真分数,规律是→,向左发散的都是假分数,规律是→,∴→→→→→→→→→,∴在第10层,由图知,左边有1个数,的左边有3个数,左边有7个数,左边有15个数,左边有31个数,左边有63个数,左边有126个数,的左边有252个数,∴在第10层从左往右数第253个数,故答案为:10;253.7.解:由题意可知,从第二个式子开始,每个式子的第二项依次是b,2ab,3a2b,......,根据此规律,第n个式子的第二项应为(n﹣1)a n﹣2b,∵(a﹣b)6是第7个式子,∴取n=7,又∵(a﹣b)6=[a+(﹣b)]6,∴(a﹣b)6的第二项为(7﹣1)a7﹣2(﹣b)=﹣6a5b,故答案为﹣6a5b.8.解:由题意得:第五行中的数字分别为:1,4,6,4,1,∴1+4+6+4+1=16.故答案为:16.9.解:由题意可知:a1=1,a2=1+2=3,a3=1+2+3=6,......a6=1+2+3+4+5+6=21,......a10=1+2+3+4+5+6+7+8+9+10=55,∴a6+a10=21+55=76,故选:A.10.解:由题意知前六行圆数为:1,1,2,3,5,8,即从第三行开始圆数为前两行圆数之和,∴第七行为:13,第八行为:21,第九行为:34,第十行为:55,故选:C.11.解:∵斐波那契数列中a1=a2=1,∴1=a2.∴1+a3+a5+a7+a9+•••+a2021=a2+a3+a5+a7+a9+•••+a2021=a4+a5+a7+a9+•••+a2021=a6+a7+a9+•••+a2021=a8+a9+••••+a2021=a10+•••+a2021=•••=a2020+a2021=a2022.故答案为:2022.12.解:若选的数为325,则用532﹣235=297,以下按照上述规则继续计算:972﹣279=693,963﹣369=594,954﹣459=495,954﹣459=495,….故“卡普雷卡尔黑洞数”是495.故选:D.13.解:根据上面的分析,可以得到:x1﹣3x2+1=+M,x2﹣3x3+2=+M,…x2021﹣3x1+2021=+M.上面2021个等式相加(上面n个等式中,可能有部分右边是﹣M),(x1+x2+…+x2021)﹣3(x1+x2+…+x2021)+(1+2+3+…+2021)=p*M.(右边的和是P个M,p≠0),而条件1+2+3+…+2021=2(x1+x2+…+x2021).所以得到0=p×M,而p≠0,只有M=0.∴x1﹣3x2+1=0,x2﹣3x3+2=0.这两个等式相加得到x1﹣2x2﹣3x3=﹣3.答案为:﹣3.二.规律型:图形的变化类14.解:图5中标的数字个位逆时针顺序排列正是结果,左下方的三组交点个数逆时针排列为321,右下方的三组交点个数逆时针排列为123,它们为两个因数,即321×123=39483.故答案为:321×123=39483.15.解:∵图①中阴影部分面积S①=a2﹣π(a)2=a2;图②中阴影部分面积S②=a2﹣4(π•a2)=a2;图③中阴影部分面积S③=a2﹣9(π•a2)=a2;……∴图⑩中阴影部分的面积是a2.故答案为:a2.16.解:原式=1﹣=.故答案为:.17.解:观察图形的变化可知:奇数项:1、3、5、…2n﹣1(n为正整数);偶数项:﹣2、﹣4、﹣6、…﹣2n.∵2021是奇数项,每四条射线为一组,OA为始边,∴标记为“2021”的点在射线OA上.故选:A.18.解:∵△A1B1A2为等边三角形,∴∠B1A1A2=60°,∵∠PMQ=30°,∴∠MB1A1=∠B1A1A2﹣∠PMQ=30°,∴∠MB1A1=∠PMQ,∴A1B1=MA1=1,同理可得:A2B2=MA2=2,A3B3=MA3=4=22,A4B4=MA4=23,...∴△A2021B2021A2022的边长=22020,故答案为:22020.19.解:过点A1作A1D⊥A2D于D、A1E⊥A2E于E,如图所示:∵A1是正方形的中心,∴A1D=A1E,A1D⊥A1E,∵∠BA1D+∠BA1E=∠CA1E+∠BA1E,∴∠BA1D=∠CA1E,在△A1BD和△A1CE中,,∴△A1BD≌△A1CE(ASA),∴2个正方形重叠阴影部分的面积=正方形面积的=×12=,∴2021个这样的正方形重叠部分的面积和=×(2021﹣1)=505,故答案为:505.20.解:设△AA1A2、△A1A2A3、△A2A3A4的面积分别为S1、S2、S3,∵四边形OAA1B1是正方形,∴OA=AA1=A1B1=1,∴S1=,∵∠OAA1=90°,∴OA2=A2A3=2,∴S2=,同理可求:S3=,S4=4…,∴S n=2n﹣2,∴△A n A n+1A n+2的面积S n+1=2n﹣1,故答案为:2n﹣1.。
