切线长定理 课件 1 人教版
合集下载
九年级数学《切线长定理》课件

PB,切点分别是A、B.
求证: AP=BP, ∠OPA=∠OPB
证明:连接OA,OB
A
∵PA,PB与⊙O相切,
点A,B是切点
∴OA⊥PA,OB⊥PB
即 ∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
B
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长 相等,这一点和圆心的连线平分两条切线的夹角
AD、BE、CF C
A D
O
C B
PF
A
E
O B
D
24.4.3 切线长定理
平面内任取一点P,作圆O的切线, 你能作几条?怎么作?
O
概念辨析
切线长:切线上一点与切点之间的线段 长叫做这点到圆的切线长
思考:切线和切线长有何区别和联系?
(1)切线是一条与圆相切的直线,不能度量.
(2)切线长是一条线段的长,它是一个数量,
可以度量.
A
B
已知:从⊙O外的一点P引两条切线PA,
(2)若∠APB=60°,则∠AOB= ,PA= ;
连接AB,则AB=
;
在A、B之间弧上任取
A
一点C,则∠ACB= .
4 30°
2
B
3、如左图,PA、PB、DE是圆O的三条切线,
∆PCD的周长为8,则PA=
.
4、如图,∆ABC的内切圆O与AB、BC、AC相
切于点D、E、F,且AB=5,BC=9,AC=6,求
符号语言:
A
∵PA、PB分别切⊙O于点A、B
∴PA = PB;∠OPA=∠OPB
切线长定理 初中九年级数学教学课件PPT 人教版

3、你还有哪些收获?
P101 第5、6题 P102第11、 12题
三角形外接圆
C
.o A B
三角形内切圆
C
.o
A
B
外接圆圆心:三角形三 边垂直平分线的交点。
外接圆的半径:交点到 三个顶点的距离。
内切圆圆心:三角形三 个内角平分线的交点。
内切圆的半径:交点到 三边的距离。
N
D O
P
AL
C M B
例2:已知:在△ABC中,BC=9cm,AC=14cm, AB=13cm,它的内切圆分别和BC、AC、AB切于点 D、E、F,求AF、BD和CE的长。(学生黑板板书 过程)
数学语言:
A
∵ PA、PB分别切⊙O
于点A、B.
P
O
∴ PA = PB
B
∠OPA=∠OPB
例1.PA、PB是⊙O的两条切线,
A
A、B为切点,直线OP交于⊙O
于点D、E,交AB于C.
E O CD
P
(1)写出图中所有的垂直关系.
解:OA⊥PA,OB ⊥PB,AB ⊥OP .
B
(2)写出图中与∠OAC相等的角. 解: ∠OAC=∠OBC=∠APC=∠BPC.
切线长定义
A
O·
P
B
从圆外一点能够作圆的两条切线,切线 上这一点和切点间的线段长叫做这点到 圆的切线长.
A
O
P
B
1、切线是一条与圆相切的直线,不能度量; 2、切线长是线段的长,这条线段的两个端点分 别是圆外一点和切点,可以度量。
A
1、PA、PB相等吗?为什么?
2、∠OPA、∠OPB相等吗?
P
为什么?
反思:在解决有关圆的
P101 第5、6题 P102第11、 12题
三角形外接圆
C
.o A B
三角形内切圆
C
.o
A
B
外接圆圆心:三角形三 边垂直平分线的交点。
外接圆的半径:交点到 三个顶点的距离。
内切圆圆心:三角形三 个内角平分线的交点。
内切圆的半径:交点到 三边的距离。
N
D O
P
AL
C M B
例2:已知:在△ABC中,BC=9cm,AC=14cm, AB=13cm,它的内切圆分别和BC、AC、AB切于点 D、E、F,求AF、BD和CE的长。(学生黑板板书 过程)
数学语言:
A
∵ PA、PB分别切⊙O
于点A、B.
P
O
∴ PA = PB
B
∠OPA=∠OPB
例1.PA、PB是⊙O的两条切线,
A
A、B为切点,直线OP交于⊙O
于点D、E,交AB于C.
E O CD
P
(1)写出图中所有的垂直关系.
解:OA⊥PA,OB ⊥PB,AB ⊥OP .
B
(2)写出图中与∠OAC相等的角. 解: ∠OAC=∠OBC=∠APC=∠BPC.
切线长定义
A
O·
P
B
从圆外一点能够作圆的两条切线,切线 上这一点和切点间的线段长叫做这点到 圆的切线长.
A
O
P
B
1、切线是一条与圆相切的直线,不能度量; 2、切线长是线段的长,这条线段的两个端点分 别是圆外一点和切点,可以度量。
A
1、PA、PB相等吗?为什么?
2、∠OPA、∠OPB相等吗?
P
为什么?
反思:在解决有关圆的
山东专用人教版九年级数学《切线长定理》课件

2、如图,已知∠AOB=30°,M为OB上一点,
且OM=5cm,以M为圆心,r为半径的圆与 直线OA有怎样的位置关系?为什么?
N
A
①r=2cm;②r=4cm;③r=2.5cm。
相离
相交
相切 O
MB
3、直线L 和⊙O有公共点,则直线L与⊙O( D ).
A、相离;B、相切;C、相交;D、相切或相交。
问题1、经过平面上一个已知点,作已知 圆的切线会有怎样的情形?
C
.o
A
B
外接圆圆心(外心):三 角形三边垂直平分线的交 点。到三角形三个顶点的 距离相等。 外切圆的半径:交点到三 角形任意一个定点的距离。
三角形内切圆
C
.o
A
B
内切圆圆心(内心): 三角形三个内角平分 线的交点。到三角形 三边的距离相等。
内切圆的半径:交点 到三角形任意一边的 垂直距离。
例2 已知:如图, △ABC的内切圆⊙O与 BC 、CA、 AB 分别相交于点D 、 E 、 F ,且AB=9厘米,BC =14厘米,CA = 13厘米,求AF、BD、CE的长。
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的相似三角形 △AOC∽ △BOC∽ △POA∽△POB∽ △PAC∽PBC
(5)写出图中所有的等腰三角形 △ABP △AOB
(6)若PA=4、PD=2,求半径OA
o.
o.
.
三角形外接圆
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL)
试用文字语言 叙述你所发现 的结论
∴ PA = PB ∠OPA=∠OPB
34第三课时切线长定理用课件
22cm
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
切线长定理 初中九年级数学教学课件PPT 人教版

(3)写出图中所有的全等三角形?
△ AOP≌ △ BOP, △ AOC≌ △ BOC,△ ACP≌ △ BCP
(4)写出图中所有的等腰三角形?
△ ABP,△ AOB
练习
1.如图, P 为⊙O 外一点,PA,PB 为⊙O的切线,A和B为切点. (1)若PA=3,则PB= _3__ (2)若PA=2x-1,PB=x+5,则x=_6__
中考链接
如图,PA,PB切⊙O于A,B,MN切
⊙O于C,交PA于M,交PB于N,
PA=7.5cm,则△PMN的周长是( C)
A.7.5cm
B.10cm
C.15cm
D.12.5cm
巩固练习
△ABC中,∠ ABC=50°, ∠ACB=70 °, 点O是⊙O的内心,求∠ BOC的度数.
解:∵点O是⊙O的内心 ∴BO平分∠ABC,CO平分∠ACB ∴∠1=1/2∠ABC=25° ∠3=1/2∠ACB=35° ∴∠BOC=180°-25°-35° =120°
解:连接AO,BO. ∵PA,PB是⊙O的两条切线, ∴OA⊥AP ,OB⊥BP.
又 OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP (HL)
∴ PA=PB, ∠OPA=∠OPB.
切线长定理:
从圆外一点可以引圆的两 条切线,它们的切线长相等, 这一点和圆心的连线平分两 条切线的夹角.
符号语言
24.2.2 直线和圆的位置关系
第3课时 切线长定理
1.理解切线长的概念.理解并掌握切线长 定理.
2.知道三角形内切圆、内心的概念.
3.运用切线长定理和三角形内切圆知识 解题.
复习旧知
1、直线和圆有什么位置关系?
相交、相切、相离
△ AOP≌ △ BOP, △ AOC≌ △ BOC,△ ACP≌ △ BCP
(4)写出图中所有的等腰三角形?
△ ABP,△ AOB
练习
1.如图, P 为⊙O 外一点,PA,PB 为⊙O的切线,A和B为切点. (1)若PA=3,则PB= _3__ (2)若PA=2x-1,PB=x+5,则x=_6__
中考链接
如图,PA,PB切⊙O于A,B,MN切
⊙O于C,交PA于M,交PB于N,
PA=7.5cm,则△PMN的周长是( C)
A.7.5cm
B.10cm
C.15cm
D.12.5cm
巩固练习
△ABC中,∠ ABC=50°, ∠ACB=70 °, 点O是⊙O的内心,求∠ BOC的度数.
解:∵点O是⊙O的内心 ∴BO平分∠ABC,CO平分∠ACB ∴∠1=1/2∠ABC=25° ∠3=1/2∠ACB=35° ∴∠BOC=180°-25°-35° =120°
解:连接AO,BO. ∵PA,PB是⊙O的两条切线, ∴OA⊥AP ,OB⊥BP.
又 OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP (HL)
∴ PA=PB, ∠OPA=∠OPB.
切线长定理:
从圆外一点可以引圆的两 条切线,它们的切线长相等, 这一点和圆心的连线平分两 条切线的夹角.
符号语言
24.2.2 直线和圆的位置关系
第3课时 切线长定理
1.理解切线长的概念.理解并掌握切线长 定理.
2.知道三角形内切圆、内心的概念.
3.运用切线长定理和三角形内切圆知识 解题.
复习旧知
1、直线和圆有什么位置关系?
相交、相切、相离
九年级数学切线长定理课件人教版

B
OP垂直平分AB
O
。
M
P
A 证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB
∵OA=OB
∴OP垂直平分AB
例题讲解: 已知:如图,PA,PB是⊙O 的两条切线,A、B为切点。直线OP交⊙O 于点D、E,交AB于点C。 (1)写出图中所有的垂直关系; B OA⊥PA,OB⊥PB, OP⊥AB
:
.A 1.切线长:在经过 圆外一点的圆的切 F o. . P D 线上,这点和切点 .B 小 之间的线段的长, 结 叫做这点到圆的切 : 线长。 2.切线长定理:从圆外一点引圆的两条切 线,它们的切线长相等,圆心和这一点的 连线平分两条切线的夹角。
达 标 检 测
已知:如图,P为⊙ O外一点,PA、 PB 为⊙ O 的切线,A和B是切点, BC是直径 求证:AC∥OP
(2)写出图中所有的全 E 等三角形;
O
。
C D A
P
△OAP≌△OBP;△OCA≌△OCB △ACP≌△BCP
(3)图中有哪些线段相等(除半径外)、弧相 等? PB=PA;BC=AC 弧BD=弧AD; 弧EB=弧EA
A E P
O C B
D
(5)如果PA=4cm,
PD=2,①求半径OA的长。
②求弦AB的长。
切线长:在经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这 点到圆的切线长。
A P
思考: 切线长 和切线 的区别?
O
B
小结:切线是直线,不可以度量;切线长 是指切线上的一条线段的长,可以度量。
探索!
o.
.BA
B B A B
.P
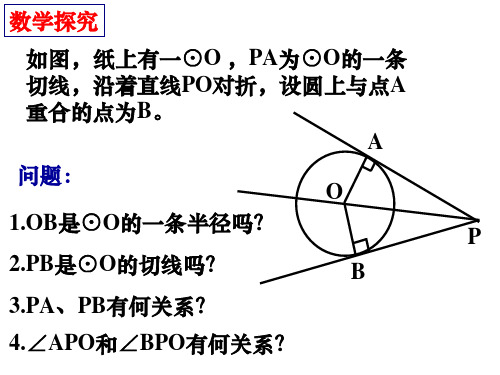
OB是⊙O的一条半径吗?PB是 线段PA与PB, ∠ APO 与∠BPO ⊙O的切线吗? 有什么关系?
OP垂直平分AB
O
。
M
P
A 证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB
∵OA=OB
∴OP垂直平分AB
例题讲解: 已知:如图,PA,PB是⊙O 的两条切线,A、B为切点。直线OP交⊙O 于点D、E,交AB于点C。 (1)写出图中所有的垂直关系; B OA⊥PA,OB⊥PB, OP⊥AB
:
.A 1.切线长:在经过 圆外一点的圆的切 F o. . P D 线上,这点和切点 .B 小 之间的线段的长, 结 叫做这点到圆的切 : 线长。 2.切线长定理:从圆外一点引圆的两条切 线,它们的切线长相等,圆心和这一点的 连线平分两条切线的夹角。
达 标 检 测
已知:如图,P为⊙ O外一点,PA、 PB 为⊙ O 的切线,A和B是切点, BC是直径 求证:AC∥OP
(2)写出图中所有的全 E 等三角形;
O
。
C D A
P
△OAP≌△OBP;△OCA≌△OCB △ACP≌△BCP
(3)图中有哪些线段相等(除半径外)、弧相 等? PB=PA;BC=AC 弧BD=弧AD; 弧EB=弧EA
A E P
O C B
D
(5)如果PA=4cm,
PD=2,①求半径OA的长。
②求弦AB的长。
切线长:在经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这 点到圆的切线长。
A P
思考: 切线长 和切线 的区别?
O
B
小结:切线是直线,不可以度量;切线长 是指切线上的一条线段的长,可以度量。
探索!
o.
.BA
B B A B
.P
OB是⊙O的一条半径吗?PB是 线段PA与PB, ∠ APO 与∠BPO ⊙O的切线吗? 有什么关系?
24.2.2 切线长定理课件 2024-2025学年人教版数学九年级上册
A D
P
C
O
课堂练习
2.如图,在△ABC中,点I是内心, (1)若∠ABC=50°, ∠ACB=70°,∠BIC=12_0_°___.
A
(2)若∠A=80 °,则∠BIC =130 度.
I
(3)若∠BIC=100 °,则∠A =20 度.
B
C
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
课堂练习
(2)
【例1】如图,边长为4的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E
是切点,点F在AD上,BE是⊙O的弦,求△CDF的面积.
D
C
解:设AF=x.
∵四边形ABCD是正方形. ∴∠DAB=90º,即DA⊥AB.
E
∵AB是⊙O的直径. ∴AD是⊙O的切线.
F
∵CF是⊙O的切线,E是切点. ∴EF=AF=x.
能使裁下的圆的面积尽可能大呢?
问题1 如果最大圆存在,它与三角形三边应有怎样的 位置关系?
O
O
最大的圆与三角
形三边都相切
O
O
问题2 如何求作一个圆,使它与三角形的三边都相切? (1) 如果半径为 r 的☉I 与△ABC 的三边都相切,那么
圆心 I 应满足什么条件?
(2) 在△ABC 的内部,如何找到满足条件的圆心 I 呢?
A
2、过点I作ID⊥BC,垂足为D
3、以I为圆心、ID为半径作⊙I
I
⊙I就是所求的圆
N
M
B
D
C
知识要点
1. 与三角形三边都相切的圆叫做三角形的内切圆. 2. 三角形内切圆的圆心叫做这个三角形的内心. 3. 这个三角形叫做这个圆的外切三角形.
人教版九年级数学上册24.2.3切线长定理课件 (共20张PPT)
例、已知:如图,PA、PB是⊙O的切线,切点分别是A、 B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于 E、F点,已知PA=12cm,∠P=70°,求: (1)△PEF的周长 (2)∠EOF的大小。 E Q P F B
A
O
当堂训练
1、如图,PA、PB是O的切线,切点分别是A、B, 如果∠P=60°,PA=5,那么∠AOB=___ 120, AB=___. 5
O E D B
C
(培优)如图,⊙O是△ABC的外接圆, AC是直径,过点O 作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE ⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。 (1)求证:OD=OE; P (2)PF是⊙O的切线。 F A
O E D B
C
y D E
C
M A 2QEA来自B FO G C
当堂训练
5、如图,PA、PB是⊙O的切线,C为圆上一点,
65 ° 若∠ P=50°,则∠C=_____
当堂训练
变式、如图,PA、PB是⊙O的切线,D为圆上一点,
115 ° 若∠ P=50°,则∠D=_____
C
D
当堂训练
6、如图,△ABC中, ∠ B=90°,O是AB上一点, 以O为圆心,OB为半径的圆与AB交于点E,与AC相 切于点D。求证:DE∥OC C
时间:6分钟.
自学效果检测
1、什么是切线长?
·
O
A
·
·
P
经过圆外一点作圆的切线,这点和切点之间的线 段的长叫做切线长。 经过圆外一点可以作圆的几条切线?
自学效果检测(一)
2、如图,纸上有一⊙O ,PA为⊙O的一条切线,沿着 直线PO对折,设圆上与点A重合的点为B。
人教版九年级数学--切线长定理公开课课件
A
·
B
p
切线长定理:
从圆外一点可以引圆的两条切线,切线长相等, 这一点和圆心的连线平分两条切线的夹角。
o
探究:切线长定理的拓展 A
E
O
C
D
P
B 相等线段: AP=BP,AO=BO,AC=BC ⌒ ⌒ ⌒ ⌒ 相等的弧: AD=BD, AE=BE 相等的角: ∠APO=∠BPO,∠AOP=∠BOP, ACP= ∠BCP 垂直关系: ∠ AO ⊥PA,AB ⊥ OP,BO ⊥ BP
6、从圆外一点引圆的两条切线,它们的切线长相等,
圆心和这一点的连线平分两条切线的夹角。
切线长定理:从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线平分两 条切线的夹角。
你还有什么疑惑?
课本P101 第5,6,11,12题
牛刀小试:
1.如图所示,PA、PB分别切⊙O于A、B, 若PA=6cm,∠APB=60 °
A
(1)则PB=
6cm ;
O B
M
P
° (2)则∠APO= 30 , ∠AOB= 120 ; (3)AB= 6cm ; (4)半径OA= 2 3 ;
例1:已知:如图,PA、PB是⊙O的切线,切点 分别是A、B,Q为弧AB上一点,过Q点作⊙O的切线, 交PA、PB于E、F点,已知PA=12cm,∠P=700, (1)求证:EF=AE+BF (2)求△PEF的周长; (3)求∠EOF的度数。
A
△PEF的周长为24cm EOF 550
P
E
O
Q
F B
如图,已知:在△ABC中,∠B=90°,O是 AB上一点,以O为圆心,OB为半径的圆交AB于 点E,交AC于切点D。求证:DE∥OC
·
B
p
切线长定理:
从圆外一点可以引圆的两条切线,切线长相等, 这一点和圆心的连线平分两条切线的夹角。
o
探究:切线长定理的拓展 A
E
O
C
D
P
B 相等线段: AP=BP,AO=BO,AC=BC ⌒ ⌒ ⌒ ⌒ 相等的弧: AD=BD, AE=BE 相等的角: ∠APO=∠BPO,∠AOP=∠BOP, ACP= ∠BCP 垂直关系: ∠ AO ⊥PA,AB ⊥ OP,BO ⊥ BP
6、从圆外一点引圆的两条切线,它们的切线长相等,
圆心和这一点的连线平分两条切线的夹角。
切线长定理:从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线平分两 条切线的夹角。
你还有什么疑惑?
课本P101 第5,6,11,12题
牛刀小试:
1.如图所示,PA、PB分别切⊙O于A、B, 若PA=6cm,∠APB=60 °
A
(1)则PB=
6cm ;
O B
M
P
° (2)则∠APO= 30 , ∠AOB= 120 ; (3)AB= 6cm ; (4)半径OA= 2 3 ;
例1:已知:如图,PA、PB是⊙O的切线,切点 分别是A、B,Q为弧AB上一点,过Q点作⊙O的切线, 交PA、PB于E、F点,已知PA=12cm,∠P=700, (1)求证:EF=AE+BF (2)求△PEF的周长; (3)求∠EOF的度数。
A
△PEF的周长为24cm EOF 550
P
E
O
Q
F B
如图,已知:在△ABC中,∠B=90°,O是 AB上一点,以O为圆心,OB为半径的圆交AB于 点E,交AC于切点D。求证:DE∥OC
人教九年级数学上册《切线长定理课件》课件
A
D
P
·O
E
C B
例题3
、如图,四边形ABCD的边AB、BC、CD、DA和圆 ⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD 证明:由切线长定理得
C N
பைடு நூலகம்
∴AL=AP,LB=学M科B网 ,NC=MCD, DN=DP
M O
P
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
请证明你所发现的结论。 B
PA = PB
∠OPA=∠OPB
O
P
学 科网
A 证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL)
试用文字语言 叙述你所发现 的结论
∴ PA = PB ∠OPA=∠OPB
AL
B
想一想
A
反思:在解决有关圆的
切线长问题时,往往需
。
要我们构建基本图形。 O
P
学 科网
B
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
思考
如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?
I
D
内切圆和内心的定义:
与三角形各边都相切的圆叫做三角形的内切圆.
连结OA、OB、OC、OD、OE、OF, D
F
则OD⊥AB,OE⊥BC,OF⊥AC.
O·
∴S△ABC=S△AOB+S△BOC +S△AOC B
D
P
·O
E
C B
例题3
、如图,四边形ABCD的边AB、BC、CD、DA和圆 ⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD 证明:由切线长定理得
C N
பைடு நூலகம்
∴AL=AP,LB=学M科B网 ,NC=MCD, DN=DP
M O
P
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
请证明你所发现的结论。 B
PA = PB
∠OPA=∠OPB
O
P
学 科网
A 证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL)
试用文字语言 叙述你所发现 的结论
∴ PA = PB ∠OPA=∠OPB
AL
B
想一想
A
反思:在解决有关圆的
切线长问题时,往往需
。
要我们构建基本图形。 O
P
学 科网
B
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
思考
如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?
I
D
内切圆和内心的定义:
与三角形各边都相切的圆叫做三角形的内切圆.
连结OA、OB、OC、OD、OE、OF, D
F
则OD⊥AB,OE⊥BC,OF⊥AC.
O·
∴S△ABC=S△AOB+S△BOC +S△AOC B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
32 、肯承认错误则错已改了一半。
?
33 、快乐不是因为拥有的多而是计较的少。
?
34 、好方法事半功倍,好习惯受益终身。
?
35 、生命可以不轰轰烈烈,但应掷地有声。
?
36 、每临大事,心必静心,静则神明,豁然冰释。
?
37 、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。
?
38 、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。
∠BOC的度数。
解:? 点O是内心 ? ? OBC ? 1 ? ABC ? 250
2 ? OCB ? 1 ? ACB ? 37.50
2 ? ? BOC ? 180 0 ? ? OBC ? ? OCB ? 117.5 0
B
A
O
C
例题:
例2 如图,ABC 的内切圆⊙O与BC、CA、
AB 分别相切于点D、E、F,且
?
巩固:
1、下列说法错误的是( ) A 、过圆上一点可以作一条直线和圆相切 B、过圆外一点可以作两条直线与圆相切 C、从圆外一点引圆的两条切线,它们的长相 等 D、从圆外一点引圆的两条切线,切线长相等
巩2、固如:图,AE 、AD 、BC 分别切⊙O于E、
D、F,若AD=20cm ,则△ABC 的周长 为.
?
8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。
?
9、永远不要逃避问题,因为时间不会给弱者任何回报。
?
10 、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。
?
11 、明天是世上增值最快的一块土地,因它充满了希望。
?
12 、得意时应善待他人,因为你失意时会需要他们。
AB=9cm,BC=14cm ,CA=13cm, 求AF、
BD 、CE的长度。
xA x
F
E
9? x
O
13 ? x
B
C
9 ? x D 13 ? x
5、△ABC 中的内切圆半径为r,△ABC的周
长为l,求△ABC 的面积S。
解:记 ? ABC的内心为 O,连接 OA、OB、OC
? S ? S? AOB ? S? BOC ? S? COA
D
F
I
ID=IE=IF=⊙I的半径 r. B
C
E
思考:
如何作出这个圆?(尺规作图)
?与三角形的各边都相切的
A
圆叫做三角形的内切圆,内
切圆的圆心是三角形三I
B
?三角形的内心到三角形三
C E
边的距离相等。
巩4、固如:图,△ABC 中,
∠ABC=50 0,∠ACB=75 0,点O是内心,求
?
39 、人的价值,在遭受诱惑的一瞬间被决定。
?
40 、事虽微,不为不成;道虽迩,不行不至。
?
41 、好好扮演自己的角色,做自己该做的事。
?
42 、自信人生二百年,会当水击三千里。
?
43 、要纠正别人之前,先反省自己有没有犯错。
1
1
1
? AB ?r ? BC ?r ? CA ?r
2
2
2
? 1 ?AB ? BC ? CA?r
F
2
? 1 lr 2
B
A
E O
C D
6、已知三角形的内切圆半径为3,三角形 的周长为20,则该三角形的面积为 。
A
O
B
C
7、Rt△ABC中,斜边AB=10cm,
AC=6cm ,则内切圆半径为
.
B
面积法
?
13 、人生最大的错误是不断担心会犯错。
?
14 、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
?
15 、不管怎样,仍要坚持,没有梦想,永远到不了远方。
?
16 、心态决定命运,自信走向成功。
?
17 、第一个青春是上帝给的;第二个的青春是靠自己努力的。
?
18 、励志照亮人生,创业改变命运。
D B
O F A
CE
3、如图,四边形ABCD四条边都与圆O相 切,切点分别为E、F、G、H,且AD=8 , BC=18,求四边形ABCD的周长。
B
E A
O H
DG
F C
思考:
如图,是一张三角形的铁皮,如何在它上
面截下一块圆形的用料,并且使圆的面积
尽可能大呢?
A
⊙I与△ABC 的三边相
切于点D、E、F.因此
人教版九年级上册
24.2.2 切线长定理
A
O
长线切
B
如图,P是⊙O外 一点,PA 、PB 是⊙O的两条切
P线,A、B为切点,
我们把线段PA , PB 叫做点P到 ⊙O的切线长.
经过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这 点到圆的切线长。
A
切线和切线长
O
P
B 切线和切线长是两个不同的概念,切线 是直线,不能度量;
A
∵ PA 、PB是⊙O的 两条切线,A 、B 是切 点
∴ PA=PB ,∠1=∠2
切线长定理:
1
O
M 2⌒ P
B
从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切线 的夹角。
A
D
O HC
P
B
已知PA 、PB 是⊙O的两条 切线,A 、B是切点
你想 还一 可想 以? 得根 到据 什图 么形 结? 论
?
25 、世上最累人的事,莫过於虚伪的过日子。
?
26 、事不三思终有悔,人能百忍自无忧。
?
27 、智者,一切求自己;愚者,一切求他人。
?
28 、有时候,生活不免走向低谷,才能迎接你的下一个高点。
?
29 、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。
?
30 、经验是由痛苦中粹取出来的。
?
31 、绳锯木断,水滴石穿。
?
19 、就算生活让你再蛋疼,也要笑着学会忍。
?
20 、当你能飞的时候就不要放弃飞。
?
21 、所有欺骗中,自欺是最为严重的。
?
22 、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。
?
23 、天行健君子以自强不息;地势坤君子以厚德载物。
?
24 、态度决定高度,思路决定出路,细节关乎命运。
O
C
A
?
1 、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。
?
2、从善如登,从恶如崩。
?
3、现在决定未来,知识改变命运。
?
4、当你能梦的时候就不要放弃梦。
?
5、龙吟八洲行壮志,凤舞九天挥鸿图。
?
6、天下大事,必作于细;天下难事,必作于易。
?
7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。
切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
探究:
如图,A是⊙O上一点,PA 为⊙O的切线,沿
直线OP翻折,设圆上与点A重合的点为B,请问:
OB 是⊙O的半径吗?PB 是⊙O的切线吗?利用
图形的对称性,说明图中PA 与PB,∠APO与
∠BPO 有什么关系?
A
O
P
B
数学语言:
