中考数学压轴题动点
中考数学动点压轴题

中考数学专题复习:动点压轴题1.ABC 中,90B ∠=︒,5cm AB =,6cm BC =,点P 从点A 开始沿边AB 向终点B 以1cm /s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2cm /s 的速度移动.如果点P 、Q 分别从点A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动时间为t 秒.(1)填空:BQ =________,PB =________(用含t 的代数式表示);(2)是否存在t 的值,使得PBQ △的面积等于24cm ?若存在,请求出此时t 的值;若不存在,请说明理由.2.如图,在△ABC 中,∠C =90°,AC =16cm ,BC =8cm 动点P 从点C 出发沿着CB 方向以2cm /s 的速度向点B 运动,另一动点Q 从点A 出发沿着AC 方向以4cm /s 的速度向点C 运动,P 、Q 两点同时出发,当点P 到达B 点或点Q 到达C 点即停止运动,设运动时间为t (s ).(1)当t 为多少秒时,以P 、C 、Q 为顶点的三角形和△ABC 相似?(2)当t 为多少秒时,△PCQ 的面积是△ACB 面积的143.如图,在ABC 中,90B ∠=︒,6cm AB =,8cm BC =点P 从A 开始沿边AB 向点B 以1cm/s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向点C 以2cm /s 的速度移动.点P ,Q 同时出发,当点Q 运动到点C 时,两点停止运动,设运动时间为t 秒.(1)填空:BQ =______cm ,PB =______cm ,(用含t 的代数式表示)(2)当t 为几秒时,PBQ △的面积等于25cm ?(3)是否存在某一时刻t ,使四边形APQC 的面积等于ABC 面积的23?如果存在,求出t 的值,如果不存在,请说明理由.4.如图①,在Rt △ABC 中,90C ∠=︒,8BC cm =,6AC cm =,点P 由A 点出发以1cm /s 的速度向终点C 匀速移动,同时点Q 由点C 出发以2cm /s 的速度向终点B 匀速移动,当一个点到达终点时另一个点也随之停止移动.(1)填空:在______秒时,△PCQ 的面积为△ACB 的面积的38;(2)经过几秒,以P ,C ,Q 为顶点的三角形与△ACB 相似?(3)如图②,D 为AB 上一点,且AD AC =,运动时间t 为多少时,CD PQ ⊥?5.如图所示,在平面直角坐标系中,直线3:3(0)4=-+>AB y x b b 与x 轴,y 轴分别交于B 点、A 点,点P 从点B 开始沿BA 边向终点A 以1厘米/秒的速度移动;点Q 从点A开始沿AO 边向终点O 以1厘米/秒的速度移动.若点P ,Q 同时出发,运动时间为t 秒.(1)当5s =t 时,①P 点的坐标__________;(用b 来表示)②当APQ 为直角三角形时,求b 的值;(2)当APQ 的面积为8平方厘米时,求b 与t 的数量关系.6.如图,在直角梯形ABCD 中,AB CD ∥,90BCD ∠=︒,10cm AB AD ==,8cm BC =.点P 从点A 出发,以每秒3cm 的速度沿折线ABC 方向运动,点Q 从点D 出发,以每秒2cm 的速度沿线段DC 方向向点C 运动.已知动点P 、Q 同时发,当点Q 运动到点C 时,P 、Q 运动停止,设运动时间为t .(1)求CD 的长;(2)当四边形PBQD 为平行四边形时,求四边形PBQD 的周长;(3)在点P 、点Q 的运动过程中,是否存在某一时刻,使得BPQ V 的面积为215cm ?若存在,请求出所有满足条件的t 的值;若不存在,请说明理由.7.已知:如图,菱形ABCD 中,5AB =cm ,6AC =cm ,动点P 从点B 出发,沿BA 方向匀速运动;同时,动点Q 从点C 出发,沿CB 方向匀速运动,它们的运动速度均为1cm/s .过点P 做PM BC ∥,过点B 做BM PM ⊥,垂足为M ,连接QP .设运动时间为t (s )()05t <<.解答下列问题:(1)菱形ABCD 的高为______cm ,cos ABC ∠的值为______;(2)在运动过程中,是否存在某一时刻t ,使四边形MPQB 为平行四边形?若存在,求出t 的值;若不存在,请说明理由.(3)是否存在某一时刻t ,使四边形MPQB 的面积是菱形ABCD 面积的225若存在,求出t 的值;若不存在,请说明理由.(4)是否存在某一时刻t ,使点M 在PQB ∠的角平分线上?若存在,求出t 的值;若不存在,请说明理由.8.如图,△ABC 是边长为6cm 的等边三角形,动点P ,Q 同时从A ,B 两点出发,分别沿AB ,BC 匀速移动,它们的速度都是2cm/s ,当点P 到达点B 时,P ,Q 两点都停止运动,设点P 的运动时间为t s ,解答下列问题:(1)求△ABC 的面积;(2)当t 为何值时,△PBQ 是直角三角形?(3)是否存在t ,使四边形APQC 的面积是△ABC 面积的23若存在,求出t 的值;若不存在,请说明理由.9.如图,在矩形ABCD 中,AD =4cm ,AB =8cm ,点P 以1cm/s 的速度沿DA 向终点A 运动;同时点Q 从点B 出发,以2cm/s 的速度沿BA 向终点A 运动;当一个点到达终点时,另一个点同时停止运动.设点P 的运动时间为t ()s ,线段PQ 扫过的面积2(cm )y .(1)AQ =cm (用含t 的代数式表示);(2)求y 与t 之间的函数关系式;(3)当线段PQ 扫过的面积为矩形ABCD 面积的38时,求t 的值.10.如图,以等边△OAB 的边OB 所在直线为x 轴,点O 为坐标原点,使点A 在第一象限建立平面直角坐标系,其中△OAB 边长为6个单位,点P 从O 点出发沿折线OAB 向B 点以3单位/秒的速度向B 点运动.点Q 从O 点出发以2单位/秒的速度沿折线OBA 向A 点运动,两点同时出发.运动时间为t (单位:秒),当两点相遇时运动停止.(1)点A 坐标为;(2)当t =2时,S △OPQ =;当t =3时,S △OPQ =;(3)当t =2时,试求在y 轴上能否找一点M ,使得以M 、P 、Q 为顶点的三角形是等腰三角形,若能找到请直接写出M 点的坐标,若不能找到请简单说明理由.(4)设△OPQ 的面积为S ,直接写出S 关于t 的函数关系式.11.如图所示,在矩形ABCD 中,AB =12cm ,BC =6cm .点P 沿AB 边从点A 开始向点B 以2cm/秒的速度移动,点Q 沿DA 边从点D 开始向点A 以1cm/秒的速度移动,如果P 、Q 同时出发,用t (秒)表示移动的时间(0≤t ≤6),那么:(1)点Q 运动多少秒时,△APQ 的面积为5cm 2;(2)当t 为何值时,△QAP 与△ABC 相似?12.如图,在矩形ABCD 中,6cm AB =,12cm BC =,点P 从点A 出发沿边AB 以1cm/s 的速度向点B 移动;同时,点Q 从点B 出发沿边BC 以2cm/s 的速度向点C 移动,当点P 运动到点B 后,运动停止,设运动时间为x (s ).(1)BP =______cm ,CQ =______cm (用含x 的式子表示);(2)若PQ =时,求x 的值;(3)当x 为何值时,DPQ V 将成为以DP 为斜边的直角三角形.13.如图所示,在△ABC 中,∠C =30°,BC =20,AC =16,E 为BC 中点.动点P 从点B 出发,沿BE 方向匀速运动,速度为每秒1个单位长度;同时,点Q 从点C 出发,沿CE 方向匀速运动,速度为每秒1个单位长度,当一个点停止移动时,另一个点也立即停止移动.过点P 作PD //AC ,交AB 于D ,连接DQ ,设点P 运动的时间为t (s ).(0<t <10)(1)当t =3时,求PD 的长;(2)设△DPQ 面积为y ,求y 关于t 的函数关系式;(3)是否存在某一时刻t ,使S △DPQ :S △ABC =3:25?若存在,请求出t 的值;如果不存在,请说明理由.14.如图,在Rt △ABC 中,90ACB ∠=︒,10AC BC ==cm .点D 从A 出发沿AC 以1cm/s 的速度向点C 移动;同时,点F 从B 出发沿BC 以2cm/s 的速度向点C 移动,移动过程中始终保持DE CB ∥(点E 在AB 上).当其中一点到达终点时,另一点也同时停止移动.设移动时间为t (s )(其中0t ≠).(1)当t 为何值时,四边形DEFC 的面积为182cm ?(2)是否存在某个时刻t ,使得DF BE =,若存在,求出t 的值,若不存在,请说明理由.(3)点E 是否可能在以DF 为直径的圆上?若能,求出此时t 的值,若不能,请说明理由.15.如图,在等腰梯形ABCD 中,AB ∥CD ,AB =8cm ,CD =2cm ,AD =6cm .点P 从A 点出发,以2cm /s 的速度沿AB 向B 点运动(运动到B 点即停止);点Q 从C 点出发,以1cm/s的速度沿CD−DA向A点运动(当点P停止运动时,点Q也即停止),设P、Q同时出发并运动了t秒.(1)求梯形ABCD的高和∠A的度数;(2)当PQ将梯形ABCD分成两个直角梯形时,求t的值;(3)试问是否存在这样的t的值,使四边形PBCQ的面积是梯形ABCD面积的一半,若存在,请求出t的值;若不存在,请说明理由.16.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动,速度为1cm/;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动时间为xs(0<x<2),解答下列问题:(1)如图①,当x为何值时,△APQ与△ACB相似;(2)如图②,连接PC,当x为何值时,PQ=PC;(3)是否存在某时刻x,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x 的值;若不存在,说明理由.17.如图,矩形ABCD中,AB=8cm,BC=12cm,P、Q分别是AB、BC上运动的两点.若点P从点A出发,以1cm/s的速度沿AB方向运动,同时,点Q从点B出发以2cm/s的速度沿BC 方向运动,设点P ,Q 运动的时间为x 秒.(1)当x 为何值时,△PBQ 的面积等于12cm 2;(2)当x 为何值时,以P ,B ,Q 为顶点的三角形与△BDC 相似18.如图,,,,A B C D 为矩形的四个顶点,16cm,6cm AB AD ==,动点,P Q 分别从点,A C 同时出发,点P 以3cm/s 的速度向点B 移动,一直到达B 点为止,点Q 以2m/s 的速度向D 点移动,当点P 到达B 点时点Q 随之停止运动,(1)AP =,BP =,CQ =,DQ =(用含t 的代数式表示);(2)t 为多少时,四边形PBCQ 的面积为233cm ;(3)t 为多少时,点P 和点Q 的距离为10cm .19.如图,在矩形ABCD 中,AB =10cm ,BC =12cm ,点P 从点A 开始沿边AB 向终点B 以2cm /s 的速度移动,点Q 从点B 开始沿边BC 向终点C 以4cm /s 的速度移动.如果点P ,Q 分别从点A ,B 同时出发,当点Q 运动到点C 时,两点都停止运动.设运动时间为t s (t >0).(1)线段BQ =cm ,PB =cm ;(用含t 的代数式表示)(2)当t 为何值时,PQ 的长为cm ?(3)是否存在t ,使得五边形APQCD 的面积等于99cm 2?若存在,请求出此时t 的值;若不存在,请说明理由.20.如图,在矩形ABCD中,AB=6cm,BC=12cm.点M从A点出发沿AB以1cm/s的速度向B点运动;同时点N从B点出发沿BC以2cm/s的速度向C点运动.当其中一点到达终点时,另一点也停止运动.设点M、N的运动时间为t秒.(1)当t为何值时,MN29cm?(2)当t为何值时,MN的长度最短,最短长度是多少?(3)当t为何值时,△DMN为等腰三角形.参考答案:1.(1)2t ,5t-(2)存在,当1t =时,PBQ △的面积等于24cm 2.(1)当点P 、Q 同时运动2秒或165秒后,△PCQ 与△ACB 相似;(2)当t =2s 时△PCQ 的面积为△ABC 面积的14.3.(1)2t ,()6-t ;(2)当1t =时,PBQ △的面积等于25cm ;(3)ABC 面积的23,t 的值为24.(1)3;(2)经过125秒或1811秒,以P ,C ,Q 为顶点的三角形与△ACB 相似;(3)运动时间t 为1.2秒时,PQ ⊥CD5.(1)①(44,3)b -;②当APQ ∆为直角三角形时,b 的值为85或2516或83;(2)当APQ ∆的面积为28cm 时,b 与t 的关系式为25200t bt -+=或15310b t -=.6.(1)16CD =;(2)四边形PBQD 的周长为8+(3)满足条件的t 的值为2512秒或5秒7.(1)245cm ,725(2)存在,当12532t =时,四边形MPQB 为平行四边形,理由见详解;(3)存在,当12536t -=时,四边形MPQB 的面积是菱形ABCD 面积的225,理由见详解;(4)不存在,理由见详解8.(1)2(2)1t =或2t =(3)不存在9.(1)82t-(2)28y t t =-(3)2t =10.(1)(3,2(3)点M的坐标为(0,)或(0,19)或(00,0,﹣(4)S()()2202231835ttt⎧≤≤⎪⎪⎪⎪=+≤⎨⎪⎪⎫+≤⎪⎪⎭⎪⎩<<11.(1)1或5秒(2)3或1.212.(1)(6)x-,(122)x-(2)10.4x=或22x=(3)当x为1.5或6时,DPQV是以DP为斜边的直角三角形13.(1)125(2)()2240105y t t t=-+<<(3)4t=或6t=14.(1)4t=(2)不存在(3)能,103t=15.(1)梯形ABCD的高为,∠A=60°(2)53t=(3)存在t为92s时,使四边形PBCQ的面积是梯形ABCD面积的一半16.(1)当x=107或2513秒时,△APQ与△ACB相似;(2)109x=;(3)存在x使线段PQ恰好把△ABC的面积平分17.(1)2或6;(2)247或218.(1)AP=3t,BP=16-3t,CQ=2t,DQ=16-2t;(2)5;(3)85s或4.8s.19.(1)(10−2t);4t;(2)t=1秒(3)t=32秒或t=72秒20.(1)t=1s或75s;(2)t=65s;(3)t=(8-)s或t=(18)s。
中考数学压轴题----《与动点有关的计算》例题讲解

中考数学压轴题----《与动点有关的计算》例题讲解1.(2021•即墨区校级二模)如图,正方形ABCD的边长为3,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是()A.3B.1.5C.3D.【答案】D【解答】解:如图,在AC上取AD'=AD=3,作D'P⊥AD于P,交AE于Q.∵AE平分∠DAC,∴∠DAQ=∠D'AQ,∴△DAQ≌△D'AQ(SAS),∴DQ=D'Q,∴DQ+PQ=D'Q+PQ≥D'P,∴D'P=AP=AD'=,故选:D.2.(2020•潮南区模拟)如图,在△ABC中,AB=AC,BC=4,面积是14,AC 的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()A.10B.9C.8D.6【答案】B【解答】解:连接AD,AM,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S=BC•AD=×4×AD=14,解得AD=7,△ABC∵EF是线段AC的垂直平分线,∴AM=CM,当点M在AD上时,DM+CM最小,最小值为AD,∴△CDM的周长最短=(CM+MD)+CD=AD+BC=7+×4=7+2=9.故选:B.3.(2021•枣庄)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC =6,BD=6,点P是AC上一动点,点E是AB的中点,则PD+PE的最小值为()A.3B.6C.3D.6【解答】解:如图,连接DE,在△DPE中,DP+PE>DE,∴当点P在DE上时,PD+PE的最小值为DE的长,∵四边形ABCD是菱形,∴AO=CO=3,BO=DO=3,AC⊥BD,AB=AD,∴tan∠ABO==,∴∠ABO=60°,∴△ABD是等边三角形,∵点E是AB的中点,∴DE⊥AB,∵sin∠ABD=,∴=,∴DE=3,故选:A.4.(2022•赤峰)如图,菱形ABCD,点A、B、C、D均在坐标轴上.∠ABC=120°,点A(﹣3,0),点E是CD的中点,点P是OC上的一动点,则PD+PE 的最小值是()A.3B.5C.2D.【解答】解:根据题意得,E点关于x轴的对称点是BC的中点E',连接DE'交AC与点P,此时PD+PE有最小值为DE',∵四边形ABCD是菱形,∠ABC=120°,点A(﹣3,0),∴OA=OC=3,∠DBC=60°,∴△BCD是等边三角形,∴DE'=OC=3,即PD+PE的最小值是3,故选:A.5.(2022•广安)如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE+PF的最小值是()A.2B.C.1.5D.【答案】A【解答】解:如图,取AB的中点T,连接PT,FT.∵四边形ABCD是菱形,∴CD∥AB,CD=AB,∵DF=CF,AT=TB,∴DF=AT,DF∥AT,∴四边形ADFT是平行四边形,∴AD=FT=2,∵四边形ABCD是菱形,AE=DE,AT=TB,∴E,T关于AC对称,∴PE=PT,∴PE+PF=PT+PF,∵PF+PT≥FT=2,∴PE+PF≥2,∴PE+PF的最小值为2.故选:A.6.(2022•泰安)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC 上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为()A.B.C.﹣D.﹣2【答案】D【解答】解:如图,取AD的中点O,连接OB,OM.∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC=4,∴∠BAP+∠DAM=90°,∵∠ADM=∠BAP,∴∠ADM+∠DAM=90°,∴∠AMD=90°,∵AO=OD=2,∴OM=AD=2,∴点M在以O为圆心,2为半径的⊙O上,∵OB===,∴BM≥OB﹣OM=﹣2,∴BM的最小值为﹣2.故选:D.7.(鄂尔多斯)如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA 上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为.【答案】【解答】解:∵AM垂直于直线BP,∴∠BMA=90°,∴点M的路径是以AB的中点N为圆心,AB长的一半为半径的,连接ON,∵直线y=﹣x+4与两坐标轴交A、B两点,∴OA=OB=4,∴ON⊥AB,∴∠ONA=90°,∵AB==4,∴ON=2,∴=•2=.故答案为:π.8.(2022•贺州)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为.【答案】【解答】解:如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.∵四边形ABCD是矩形,∴∠A=∠ADT=90°,∵∠AHT=90°,∴四边形AHTD是矩形,∵AE=DE=AD=3.AF=FB=AB=4,∴AH=DT=3,HF=AF﹣AH=4﹣3=1,HT=AD=6,∴FT===,∵DG平分∠ADC,DE=DT,∴E、T关于DG对称,∴PE=PT,∴PE+PF=PF+PT≥FT=,∵EF===5,∴△EFP的周长的最小值为5+,故答案为:5+.9.(2020•广西)如图,在边长为2的菱形ABCD中,∠C=60°,点E,F 分别是AB,AD上的动点,且AE=DF,DE与BF交于点P.当点E从点A 运动到点B时,则点P的运动路径长为.【答案】π【解答】解:如图,作△CBD的外接圆⊙O,连接OB,OD,∵四边形ABCD是菱形,∴∠A=∠C=60°,AB=BC=CD=AD,∴△ABD,△BCD都是等边三角形,∴BD=AD,∠BDF=∠DAE,∵DF=AE,∴△BDF≌△DAE(SAS),∴∠DBF=∠ADE,∵∠ADE+∠BDE=60°,∴∠DBF+∠BDP=60°,∴∠BPD=120°,∵∠C=60°,∴∠C+∠DPB=180°,∴B,C,D,P四点共圆,由BC=CD=BD=2,可得OB=OD=2,∵∠BOD=2∠C=120°,∴点P的运动的路径的长==π.故答案为π.10.(2021•威海)如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G,连接BG.若AE=BF,则BG的最小值为.【答案】﹣1【解答】解:如图,取AD的中点T,连接BT,GT,∵四边形ABCD是正方形,∴AD=AB=2,∠DAE=∠ABF=90°,在△DAE和△ABF中,,∴△DAE≌△ABF(SAS),∴∠ADE=∠BAF,∵∠BAF+∠DAF=90°,∴∠EDA+∠DAF=90°,∴∠AGD=90°,∵DT=AT,∴GT=AD=1,BT===,∴BG≥BT﹣GT,∴BG≥﹣1,∴BG的最小值为﹣1.故答案为:﹣1.。
中考数学常见题型几何动点问题

中考数学压轴题型研究(一)——动点几何问题例1:在△ABC 中,∠B=60°,BA=24CM,BC=16CM, (1)求△ABC 的面积;(2)现有动点P 从A 点出发,沿射线AB 向点B 方向运动,动点Q 从C 点出发,沿射线CB 也向点B 方向运动。
如果点P 的速度是4CM/秒,点Q 的速度是2CM/秒,它们同时出发,几秒钟后,△PBQ的面积是△ABC 的面积的一半?(3)在第(2)问题前提下,P ,Q 两点之间的距离是多少?例2: ()已知正方形ABCD 的边长是1,E 为CD 边的中点, P 为正方形ABCD 边上的一个动点,动点P 从A 点出发,沿A →B → C →E 运动,到达点E.若点P 经过的路程为自变量x ,△APE 的面积为函数y ,(1)写出y 与x 的关系式 (2)求当y =13时,x 的值等于多少?例3:如图1 ,在直角梯形ABCD 中,∠B=90°,DC ∥AB ,动点P 从B 点出发,沿梯形的边由B →C → D → A 运动,设点P 运动的路程为x ,△ABP 的面积为y , 如果关于x 的函数y 的图象如图2所示 ,那么△ABC 的面积为( )A .32B .18C .16D .10ACB By例4:直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O →B →A 运动.(1)直接写出A B 、两点的坐标;(2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标.例5:已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作AB 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.(1)线段MN 在运动的过程中,t 为何值时,四边形MNQP 恰为矩形?并求出该矩形的面积; (2)线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .求四边形MNQP 的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围.例6:如图(3),在梯形ABCD 中,906DC AB A AD ∠==∥,°,厘米,4DC =厘米,BC 的坡度34i =∶,动点P 从A 出发以2厘米/秒的速度沿AB 方向向点B 运动,动点Q 从点B 出发以3厘米/秒的速度沿B C D →→方向向点D 运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.(1)求边BC 的长;(2)当t 为何值时,PC 与BQ 相互平分;图(3)BC PQBA MN(3)连结PQ ,设PBQ △的面积为y ,探求y 与t 的函数关系式,求t 为何值时,y 有最大值?最大值是多少?二、利用函数与方程的思想和方法将所解决图形的性质(或所求图形面积)直接转化为函数或方程。
中考数学压轴题专题-动点综合问题
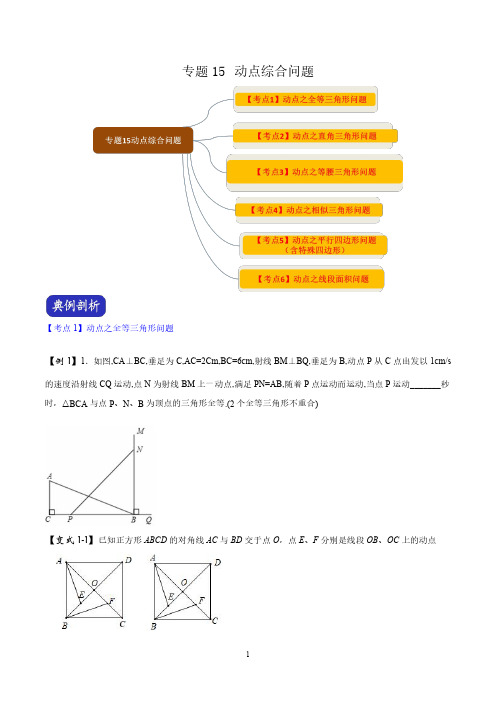
专题15动点综合问题【考点1】动点之全等三角形问题【例1】1.如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【变式1-1】已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是线段OB、OC上的动点(1)如果动点E 、F 满足BE =OF (如图),且AE ⊥BF 时,问点E 在什么位置?并证明你的结论;(2)如果动点E 、F 满足BE =CF (如图),写出所有以点E 或F 为顶点的全等三角形(不得添加辅助线).【变式1-2】如图①,将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ,其中AB =8cm ,BC =6cm ,AC =10cm .现将△ABC 和△EDF 按如图②的方式摆放(点A 与点D 、点B 与点E 分别重合).动点P 从点A 出发,沿AC 以2cm /s 的速度向点C 匀速移动;同时,动点Q 从点E 出发,沿射线ED 以acm /s (0<a <3)的速度匀速移动,连接PQ 、CQ 、FQ ,设移动时间为ts (0≤t ≤5).(1)当t =2时,S △AQF =3S △BQC ,则a =;(2)当以P 、C 、Q 为顶点的三角形与△BQC 全等时,求a 的值;(3)如图③,在动点P 、Q 出发的同时,△ABC 也以3cm /s 的速度沿射线ED 匀速移动,当以A 、P 、Q 为顶点的三角形与△EFQ 全等时,求a 与t 的值.【考点2】动点之直角三角形问题【例2】如图,在四边形纸片ABCD 中,//AB CD ,60A ∠=︒,30B ∠=︒,2CD =,4BC =,点E 是AB 边上的动点,点F 是折线A D C --上的动点,将纸片ABCD 沿直线EF 折叠,使点A 的对应点A '落在AB 边上,连接A C ',若A BC ' 是直角三角形,则AE 的长为________.【变式2-1】(2019·辽宁中考模拟)如图,已知二次函数y =ax 2+bx+4的图象与x 轴交于点A(4,0)和点D(﹣1,0),与y 轴交于点C ,过点C 作BC 平行于x 轴交抛物线于点B ,连接AC(1)求这个二次函数的表达式;(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动;点N 从点B 同时出发,以每秒1个单位长度的速度向点C 运动,其中一个动点到达终点时,另一个动点也随之停动,过点N 作NQ 垂直于BC 交AC 于点Q ,连结MQ.①求△AQM 的面积S 与运动时间t 之间的函数关系式,写出自变量的取值范围;当t 为何值时,S 有最大值,并求出S 的最大值;②是否存在点M ,使得△AQM 为直角三角形?若存在,求出点M 的坐标;若不存在,说明理由.【变式2-2】如图,在矩形OAHC 中,8,12OC OA ==,B 为CH 中点,连接AB .动点M 从点O 出发沿OA 边向点A 运动,动点N 从点A 出发沿AB 边向点B 运动,两个动点同时出发,速度都是每秒1个单位长度,连接,,CM CN MN ,设运动时间为t (秒)(010)t <<.则t =_____时,CMN ∆为直角三角形【考点3】动点之等腰三角形问题【例3】如图,AB 是⊙O 的直径,BC 是弦,10cm AB =,6cm BC =.若点P 是直径AB 上一动点,当PBC 是等腰三角形时,AP =__________cm .【变式3-1】如图①,已知正方形ABCD 边长为2,点P 是AD 边上的一个动点,点A 关于直线BP 的对称点是点Q ,连结PQ 、DQ 、CQ 、BQ .设AP=x.(1)当1x =时,求BP 长;(2)如图②,若PQ 的延长线交CD 边于E ,并且90CQD ∠=o ,求证:CEQ ∆为等腰三角形;(3)若点P 是射线AD 上的一个动点,则当CDQ ∆为等腰三角形时,求x 的值.【变式3-2】(2019·河南中考模拟)如图,抛物线y=ax 2+bx+3交y 轴于点A ,交x 轴于点B (-3,0)和点C (1,0),顶点为点M .(1)求抛物线的解析式;(2)如图,点E 为x 轴上一动点,若△AME 的周长最小,请求出点E 的坐标;(3)点F 为直线AB 上一个动点,点P 为抛物线上一个动点,若△BFP 为等腰直角三角形,请直接写出点P 的坐标.【变式3-3】(2019·广西中考真题)已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -,点O 为坐标原点,点P 为抛物线上的动点,直线y x b =-+与x 轴、y 轴分别交于A B 、两点.(1)求m b 、的值;(2)当PAM ∆是以AM 为底边的等腰三角形时,求点P 的坐标;(3)满足(2)的条件时,求sin BOP ∠的值.【考点4】动点之相似三角形问题【例4】如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC 是相似三角形,求AP的长.【变式4-1】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=3 4AC(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.【变式4-2】如图,正方形ABCD,点P为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.(1)请找出图中一对相似三角形,并证明;(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.【考点5】动点之平行四边形问题(含特殊四边形)【例5】如图,抛物线23y ax bx =++与x 轴交于(3,0),(1,0)A B -两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 是抛物线上的动点,且满足2PAO PCO S S ∆∆=,求出P 点的坐标;(3)连接BC ,点E 是x 轴一动点,点F 是抛物线上一动点,若以B 、C 、E 、F 为顶点的四边形是平行四边形时,请直接写出点F 的坐标.备用图【变式5-1】(2019·江西中考真题)在图1,2,3中,已知,,点为线段上的动点,连接,以为边向上作菱形,且.(1)如图1,当点与点重合时,________°;(2)如图2,连接.①填空:_________(填“>”,“<”,“=”);②求证:点在的平分线上;(3)如图3,连接,,并延长交的延长线于点,当四边形是平行四边形时,求的值.【变式5-2】(2019·湖南中考真题)如图,二次函数213y x bx c =-++的图象过原点,与x 轴的另一个交点为()8,0(1)求该二次函数的解析式;(2)在x轴上方作x轴的平行线1y m=,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;(3)在(2)的条件下,动点P从点A出发沿射线AB以每秒1个单位长度匀速运动,同时动点Q以相同的速度从点A出发沿线段AD匀速运动,到达点D时立即原速返回,当动点Q返回到点A时,P、Q两点同时停止运动,设运动时间为t秒(0t>).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.【变式5-3】.如图,在平面直角坐标系中,AOB∆的顶点O是坐标原点,点A坐标为()1,3,A、B两点关于直线y x=对称,反比例函数()0ky xx=>图象经过点A,点P是直线y x=上一动点.(1)B点的坐标为______;(2)若点C是反比例函数图象上一点,是否存在这样的点C,使得以A、B、C、P四点为顶点的四边形是平行四边形?若存在,求出点C坐标;若不存在,请说明理由;(3)若点Q 是线段OP 上一点(O 不与O 、P 重合),当四边形AOBP 为菱形时,过点Q 分别作直线OA 和直线AP 的垂线,垂足分别为E 、F ,当QE QF QB ++的值最小时,求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图,在平面直角坐标系中,平行四边形如图放置,将此平行四边形绕点O 顺时针旋转90°得到平行四边形.抛物线经过点A 、C 、A′三点.(1)求A 、A′、C 三点的坐标;(2)求平行四边形和平行四边形重叠部分的面积;(3)点M 是第一象限内抛物线上的一动点,问点M 在何处时,的面积最大?最大面积是多少?并写出此时M 的坐标.【变式6-1】(1)发现:如图1,点A 为线段BC 外一动点,且BC =α,AB b =(0)a b >>,当点A 位于时,线段AC 的长取得最大值,最大值为(用含,a b 的式子表示);(2)应用:如图2,点A 为线段BC 外一动点,4BC =,2AC =,以AB 为边作等边ABD ∆,连接CD ,求线段CD 的最大值;(3)拓展:如图3,线段3AB =,点P 为线段AB 外一动点,且2AP =,PM PB =,90BPM ∠=︒,求线段AM 长的最大值及此时PBM ∆的面积.【变式6-2】如图,矩形ABCD 中,3,4AD AB ==,点P 是对角线AC 上一动点(不与A C 、重合),连接PB ,过点P 作PE PB ⊥,交射线DC 于点E ,以线段,PE PB 为邻边作矩形BPEF ,过点P 作GH CD ⊥。
中考数学压轴题(动点)

中考数学压轴题总结(动点)(一) 因动点产生的相似三角形问题例1,已知抛物线的方程C 1:1(2)()y x x m m=-+- (m >0)与x 轴交于点B 、C ,与y 轴交于点E ,且点B 在点C 的左侧.(1)若抛物线C 1过点M (2, 2),求实数m 的值; (2)在(1)的条件下,求△BCE 的面积;(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使得BH +EH 最小,求出点H 的坐标;(4)在第四象限内,抛物线C 1上是否存在点F ,使得以点B 、C 、F 为顶点的三角形与△BCE 相似?若存在,求m 的值;若不存在,请说明理由.图1思路点拨1.第(3)题是典型的“牛喝水”问题,当H 落在线段EC 上时,BH +EH 最小. 2.第(4)题的解题策略是:先分两种情况画直线BF ,作∠CBF =∠EBC =45°,或者作BF //EC .再用含m 的式子表示点F 的坐标.然后根据夹角相等,两边对应成比例列关于m 的方程.满分解答(1)将M (2, 2)代入1(2)()y x x m m =-+-,得124(2)m m=-⨯-.解得m =4.(2)当m =4时,2111(2)(4)2442y x x x x =-+-=-++.所以C (4, 0),E (0, 2).所以S △BCE =1162622BC OE ⋅=⨯⨯=.(3)如图2,抛物线的对称轴是直线x =1,当H 落在线段EC 上时,BH +EH 最小. 设对称轴与x 轴的交点为P ,那么HP EOCP CO=. 因此234HP =.解得32HP =.所以点H 的坐标为3(1,)2. (4)①如图3,过点B 作EC 的平行线交抛物线于F ,过点F 作FF ′⊥x 轴于F ′. 由于∠BCE =∠FBC ,所以当CE BCCB BF=,即2BC CE BF =⋅时,△BCE ∽△FBC . 设点F 的坐标为1(,(2)())x x x m m -+-,由''FF EO BF CO =,得1(2)()22x x m m x m+-=+. 解得x =m +2.所以F ′(m +2, 0).由'CO BF CE BF =4m BF +=.所以BF =. 由2BC CE BF =⋅,得2(2)m +=整理,得0=16.此方程无解.图2 图3 图4②如图4,作∠CBF =45°交抛物线于F ,过点F 作FF ′⊥x 轴于F ′, 由于∠EBC =∠CBF ,所以BE BCBC BF=,即2BC BE BF =⋅时,△BCE ∽△BFC . 在Rt △BFF ′中,由FF ′=BF ′,得1(2)()2x x m x m+-=+. 解得x =2m .所以F ′(2,0)m .所以BF ′=2m +2,2)BF m =+.由2m=±=⋅,得2BC BE BF(2)2)+=+.解得2m m综合①、②,符合题意的m为2+例2,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1思路点拨1.已知抛物线与x轴的两个交点,用待定系数法求解析式时,设交点式比较简便.2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长.3.按照两条直角边对应成比例,分两种情况列方程.4.把△DCA可以分割为共底的两个三角形,高的和等于OA.满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y .(2)设点P 的坐标为))4)(1(21,(---x x x .①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM ,x AM -=4. 如果2==CO AOPM AM ,那么24)4)(1(21=----x x x .解得5=x 不合题意.如果21==COAOPM AM ,那么214)4)(1(21=----x x x .解得2=x . 此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM ,4-=x AM . 解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-.解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4.解方程24)4)(1(21=---x x x ,得3-=x .此时点P 的坐标为)14,3(--.解方程214)4)(1(21=---x x x ,得0=x .此时点P 与点O 重合,不合题意.综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3 图4 (3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y . 设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m m m ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m m DE m m 2212+-=.因此4)221(212⨯+-=∆m m S DAC m m 42+-=4)2(2+--=m .当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).(二) 因动点产生的等腰三角形问题例3,抛物线y =ax 2+bx +c 经过A (-1,0)、B (3, 0)、C (0 ,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标; (3)在直线l 上是否存在点M ,使△MAC 为等腰三角形,若存在,直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.图1 .思路点拨1.第(2)题是典型的“牛喝水”问题,点P在线段BC上时△PAC的周长最小.2.第(3)题分三种情况列方程讨论等腰三角形的存在性.满分解答(1)因为抛物线与x轴交于A(-1,0)、B(3, 0)两点,设y=a(x+1)(x-3),代入点C(0 ,3),得-3a=3.解得a=-1.所以抛物线的函数关系式是y=-(x+1)(x-3)=-x2+2x+3.(2)如图2,抛物线的对称轴是直线x=1.当点P落在线段BC上时,PA+PC最小,△PAC的周长最小.设抛物线的对称轴与x轴的交点为H.由BH PH=,BO=CO,得PH=BH=2.BO CO所以点P的坐标为(1, 2).图2 (3)点M的坐标为(1, 1)、、(1,或(1,0).考点伸展第(3)题的解题过程是这样的:设点M的坐标为(1,m).在△MAC中,AC2=10,MC2=1+(m-3)2,MA2=4+m2.①如图3,当MA=MC时,MA2=MC2.解方程4+m2=1+(m-3)2,得m=1.此时点M的坐标为(1, 1).②如图4,当AM=AC时,AM2=AC2.解方程4+m2=10,得m=.此时点M的坐标为或(1,.③如图5,当CM=CA时,CM2=CA2.解方程1+(m-3)2=10,得m=0或6.当M(1, 6)时,M、A、C三点共线,所以此时符合条件的点M的坐标为(1,0).图3 图4 图5例4,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.图1思路点拨1.用代数法探求等腰三角形分三步:先分类,按腰相等分三种情况;再根据两点间的距离公式列方程;然后解方程并检验.2.本题中等腰三角形的角度特殊,三种情况的点P 重合在一起.满分解答(1)如图2,过点B 作BC ⊥y 轴,垂足为C .在Rt △OBC 中,∠BOC =30°,OB =4,所以BC =2,OC =所以点B 的坐标为(2,--.(2)因为抛物线与x 轴交于O 、A (4, 0),设抛物线的解析式为y =ax (x -4),代入点B (2,--,2(6)a -=-⨯-.解得a =.所以抛物线的解析式为2(4)y x x =-=.(3)抛物线的对称轴是直线x =2,设点P 的坐标为(2, y ). ①当OP =OB =4时,OP2=16.所以4+y 2=16.解得y =± 当P 在时,B 、O 、P 三点共线(如图2).②当BP =BO =4时,BP 2=16.所以224(16y ++=.解得12y y ==- ③当PB =PO 时,PB2=PO 2.所以22224(2y y ++=+.解得y =- 综合①、②、③,点P 的坐标为(2,-,如图2所示.图2 图3考点伸展如图3,在本题中,设抛物线的顶点为D,那么△DOA与△OAB是两个相似的等腰三角形.由2=-=-,得抛物线的顶点为D.(4)2)y x x x因此tan DOA∠=DOA=30°,∠ODA=120°.(三)因动点产生的直角三角形问题例5:在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).(1)当k=-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y随x增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k 的值.思路点拨1.由点A(1,k)或点B(-1,-k)的坐标可以知道,反比例函数的解析式就是k=.题yx目中的k都是一致的.2.由点A (1,k )或点B (-1,-k )的坐标还可以知道,A 、B 关于原点O 对称,以AB 为直径的圆的圆心就是O .3.根据直径所对的圆周角是直角,当Q 落在⊙O 上是,△ABQ 是以AB 为直径的直角三角形.满分解答(1)因为反比例函数的图象过点A (1,k ),所以反比例函数的解析式是ky x=. 当k =-2时,反比例函数的解析式是2y x=-.(2)在反比例函数ky x=中,如果y 随x 增大而增大,那么k <0.当k <0时,抛物线的开口向下,在对称轴左侧,y 随x 增大而增大.抛物线y =k (x 2+x +1)=215()24k x k +-的对称轴是直线12x =-. 图1 所以当k <0且12x <-时,反比例函数与二次函数都是y 随x 增大而增大. (3)抛物线的顶点Q 的坐标是15(,)24k --,A 、B 关于原点O 中心对称,当OQ =OA =OB 时,△ABQ 是以AB 为直径的直角三角形.由OQ 2=OA 2,得222215()()124k k -+-=+.解得1k =2),2k =3).图2 图3考点伸展如图4,已知经过原点O 的两条直线AB 与CD 分别与双曲线ky x=(k >0)交于A 、B 和C 、D ,那么AB 与CD 互相平分,所以四边形ACBD 是平行四边形.问平行四边形ABCD 能否成为矩形?能否成为正方形?如图5,当A 、C 关于直线y =x 对称时,AB 与CD 互相平分且相等,四边形ABCD 是矩形.因为A 、C 可以无限接近坐标系但是不能落在坐标轴上,所以OA 与OC 无法垂直,因此四边形ABCD 不能成为正方形.图4 图5例6,已知抛物线y =x 2+bx +c 与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C (0,-3),对称轴是直线x =1,直线BC 与抛物线的对称轴交于点D .(1)求抛物线的函数表达式; (2)求直线BC 的函数表达式;(3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P 在第三象限.①当线段34PQ AB =时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图1思路点拨1.第(1)、(2)题用待定系数法求解析式,它们的结果直接影响后续的解题. 2.第(3)题的关键是求点E 的坐标,反复用到数形结合,注意y 轴负半轴上的点的纵坐标的符号与线段长的关系.3.根据C 、D 的坐标,可以知道直角三角形CDE 是等腰直角三角形,这样写点E 的坐标就简单了.满分解答(1)设抛物线的函数表达式为2(1)y x n =-+,代入点C (0,-3),得4n =-.所以抛物线的函数表达式为22(1)423y x x x =--=--.(2)由223(1)(3)y x x x x =--=+-,知A (-1,0),B (3,0).设直线BC 的函数表达式为y kx b =+,代入点B (3,0)和点C (0,-3),得30,3.k b b +=⎧⎨=-⎩ 解得1k =,3b =-.所以直线BC 的函数表达式为3y x =-.(3)①因为AB =4,所以334PQ AB ==.因为P 、Q 关于直线x =1对称,所以点P 的横坐标为12-.于是得到点P 的坐标为17,24⎛⎫-- ⎪⎝⎭,点F 的坐标为70,4⎛⎫- ⎪⎝⎭.所以75344FC OC OF =-=-=,522EC FC ==.进而得到51322OE OC EC =-=-=,点E 的坐标为10,2⎛⎫- ⎪⎝⎭. 直线BC:3y x =-与抛物线的对称轴x =1的交点D 的坐标为(1,-2).过点D 作DH ⊥y 轴,垂足为H .在Rt △EDH 中,DH =1,13222EH OH OE =-=-=,所以tan ∠CED 23DH EH ==.②1(12)P -,25(1)2P -.图2 图3 图4考点伸展第(3)题②求点P 的坐标的步骤是:如图3,图4,先分两种情况求出等腰直角三角形CDE 的顶点E 的坐标,再求出CE 的中点F 的坐标,把点F 的纵坐标代入抛物线的解析式,解得的x 的较小的一个值就是点P 的横坐标.(四) 因动点产生的平行四边形问题例7,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (1, 0)、C (3, 0)、D (3, 4).以A 为顶点的抛物线y =ax 2+bx +c 过点C .动点P 从点A 出发,沿线段AB 向点B 运动,同时动点Q 从点C 出发,沿线段CD 向点D 运动.点P 、Q 的运动速度均为每秒1个单位,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E .(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)过点E 作EF ⊥AD 于F ,交抛物线于点G ,当t 为何值时,△ACG 的面积最大?最大值为多少?(3)在动点P 、Q 运动的过程中,当t 为何值时,在矩形ABCD 内(包括边界)存在点H ,使以C 、Q 、E 、H 为顶点的四边形为菱形?请直接写出t 的值.图1思路点拨1.把△ACG 分割成以GE 为公共底边的两个三角形,高的和等于AD . 2.用含有t 的式子把图形中能够表示的线段和点的坐标都表示出来.3.构造以C 、Q 、E 、H 为顶点的平行四边形,再用邻边相等列方程验证菱形是否存在.满分解答(1)A (1, 4).因为抛物线的顶点为A ,设抛物线的解析式为y =a (x -1)2+4, 代入点C (3, 0),可得a =-1.所以抛物线的解析式为y =-(x -1)2+4=-x 2+2x +3. (2)因为PE //BC ,所以2AP AB PE BC ==.因此1122PE AP t ==. 所以点E 的横坐标为112t +.将112x t =+代入抛物线的解析式,y =-(x -1)2+4=2144t -.所以点G 的纵坐标为2144t -.于是得到2211(4)(4)44GE t t t t =---=-+.因此22111()(2)1244ACG AGE CGE S S S GE AF DF t t t ∆∆∆=+=+=-+=--+.所以当t =1时,△ACG 面积的最大值为1. (3)2013t =或20t =- 考点伸展第(3)题的解题思路是这样的:因为FE //QC ,FE =QC ,所以四边形FECQ 是平行四边形.再构造点F 关于PE 轴对称的点H ′,那么四边形EH ′CQ 也是平行四边形.再根据FQ =CQ 列关于t 的方程,检验四边形FECQ 是否为菱形,根据EQ =CQ 列关于t 的方程,检验四边形EH ′CQ 是否为菱形.1(1,4)2E t t +-,1(1,4)2F t +,(3,)Q t ,(3,0)C .如图2,当FQ =CQ 时,FQ 2=CQ 2,因此2221(2)(4)2t t t -+-=.整理,得240800t t -+=.解得120t =-220t =+.如图3,当EQ =CQ 时,EQ 2=CQ 2,因此2221(2)(42)2t t t -+-=.整理,得213728000t t -+=.(1320)(40)0t t --=.所以12013t =,240t =(舍去).图2 图3(五) 因动点产生的梯形问题例8:已知直线y =3x -3分别与x 轴、y 轴交于点A ,B ,抛物线y =ax 2+2x +c 经过点A ,B .(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,点B 关于直线l 的对称点为C ,若点D 在y 轴的正半轴上,且四边形ABCD 为梯形.①求点D 的坐标;②将此抛物线向右平移,平移后抛物线的顶点为P ,其对称轴与直线y =3x -3交于点E ,若73tan =∠DPE ,求四边形BDEP 的面积.图1思路点拨1.这道题的最大障碍是画图,A 、B 、C 、D 四个点必须画准确,其实抛物线不必画出,画出对称轴就可以了.2.抛物线向右平移,不变的是顶点的纵坐标,不变的是D 、P 两点间的垂直距离等于7.3.已知∠DPE 的正切值中的7的几何意义就是D 、P 两点间的垂直距离等于7,那么点P 向右平移到直线x =3时,就停止平移.满分解答(1)直线y =3x -3与x 轴的交点为A (1,0),与y 轴的交点为B (0,-3). 将A (1,0)、B (0,-3)分别代入y =ax 2+2x +c , 得20,3.a c c ++=⎧⎨=-⎩ 解得1,3.a c =⎧⎨=-⎩所以抛物线的表达式为y =x 2+2x -3. 对称轴为直线x =-1,顶点为(-1,-4).(2)①如图2,点B 关于直线l 的对称点C 的坐标为(-2,-3). 因为CD //AB ,设直线CD 的解析式为y =3x +b ,代入点C (-2,-3),可得b =3.所以点D 的坐标为(0,3).②过点P 作PH ⊥y 轴,垂足为H ,那么∠PDH =∠DPE . 由73tan =∠DPE ,得3tan 7PH PDH DH ∠==.而DH =7,所以PH =3. 因此点E 的坐标为(3,6). 所以1()242BDEP S BD EP PH =+⋅=梯形.图2 图3考点伸展第(2)①用几何法求点D 的坐标更简便: 因为CD //AB ,所以∠CDB =∠ABO .因此13BC OA BD OB ==.所以BD =3BC =6,OD =3.因此D (0,3).例9:已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D 的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.图1思路点拨1.用待定系数法求抛物线的解析式,设交点式比较简便.2.过△AOD 的三个顶点分别画对边的平行线与抛物线相交,可以确定存在三个梯形. 3.用抛物线的解析式可以表示点M 的坐标.满分解答(1)因为BC //x 轴,点D 在BC 上,C (0,-2),所以点D 的纵坐标为-2.把y =-2代入x y 32-=,求得x =3.所以点D 的坐标为(3,-2). (2)由于抛物线与x 轴交于点O 、A (4,0),设抛物线的解析式为y =ax (x -4),代入D (3,-2),得23a =.所求的二次函数解析式为2228(4)333y x x x x =-=-. (3) 设点M 的坐标为228,33x x x ⎛⎫- ⎪⎝⎭. ①如图2,当OM //DA 时,作MN ⊥x 轴,DQ ⊥x 轴,垂足分别为N 、Q .由tan ∠MON =tan ∠DAQ ,得228332x xx-=. 因为x =0时点M 与O 重合,因此28233x -=,解得x =7.此时点M 的坐标为(7,14).②如图3,当AM //OD 时,由tan ∠MAN =tan ∠DOQ ,得22823343x x x -=-. 因为x =4时点M 与A 重合,因此2233x -=,解得x =-1.此时点M 的坐标为10(1,)3-.③如图4,当DM //OA 时,点M 与点D 关于抛物线的对称轴对称,此时点M 的坐标为(1,-2).图2 图3 图4(六) 因动点产生的面积问题例10,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值;(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图1思路点拨1.第(1)题由于CP //y 轴,把∠ACP 转化为它的同位角. 2.第(2)题中,PD =PC sin ∠ACP ,第(1)题已经做好了铺垫.3.△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比. 4.两个三角形的面积比为9∶10,要分两种情况讨论.满分解答(1)设直线112y x =+与y 轴交于点E ,那么A (-2,0),B (4,3),E (0,1).在Rt △AEO 中,OA =2,OE =1,所以AE .所以sin AEO ∠=因为PC //EO ,所以∠ACP =∠AEO .因此sin ACP ∠=将A (-2,0)、B (4,3)分别代入y =ax 2+bx -3,得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =,12b =-. (2)由211(,3)22P m m m --,1(,1)2C m m +,得221111(1)(3)42222PC m m m m m =+---=-++.所以221sin 4)1)2PD PC ACP m m m =∠==-++=-+.所以PD . (3)当S △PCD ∶S △PCB =9∶10时,52m =; 当S △PCD ∶S △PCB =10∶9时,329m =.图2考点伸展第(3)题的思路是:△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比.而211cos cos 4)(2)(4)25DN PD PDN PD ACP m m m m =∠=∠=-++=-+-, BM =4-m .①当S △PCD ∶S △PCB =9∶10时,19(2)(4)(4)510m m m -+-=-.解得52m =. ②当S △PCD ∶S △PCB =10∶9时,110(2)(4)(4)59m m m -+-=-.解得329m =.(七)因动点产生的相切问题例11,A (-5,0),B (-3,0),点C 在y 轴的正半轴上,∠CBO =45°,CD //AB ,∠CDA =90°.点P 从点Q (4,0)出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1)求点C 的坐标;(2)当∠BCP =15°时,求t 的值;(3)以点P 为圆心,PC 为半径的⊙P 随点P 的运动而变化,当⊙P 与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.图1答案 (1)点C 的坐标为(0,3).(2)如图2,当P 在B 的右侧,∠BCP =15°时,∠PCO =30°,4t =如图3,当P 在B 的左侧,∠BCP =15°时,∠CPO =30°,4t =+.图2 图3(3)如图4,当⊙P 与直线BC 相切时,t =1;如图5,当⊙P 与直线DC 相切时,t =4;如图6,当⊙P 与直线AD 相切时,t =5.6.图4 图5 图6(八)因动点产生的线段和差问题例12,在平面直角坐标系中,抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,与y 轴交于点C ,点D 是抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.试探究:随着点P的运动,在抛物线上是否存在点Q,使以A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;(3)请在直线AC上找一点M,使△BDM的周长最小,求出点M的坐标.图1思路点拨1.第(2)题探究平行四边形,按照AP为边或者对角线分两种情况讨论.2.第(3)题是典型的“牛喝水”问题,构造点B关于“河流”AC的对称点B′,那么M落在B′D上时,MB+MD最小,△MBD的周长最小.满分解答(1)由y=-x2+2x+3=-(x+1)(x-3)=-(x-1)2+4,得A(-1, 0)、B(3, 0)、C(0, 3)、D(1, 4).直线AC的解析式是y=3x+3.(2, 3),Q2(13-),Q3(13-).(2)Q(3)设点B关于直线AC的对称点为B′,联结BB′交AC于F.联结B′D,B′D与交AC的交点就是要探求的点M.作B′E⊥x轴于E,那么△BB′E∽△BAF∽△CAO.在Rt △BAF中,13AF BF ==AB =4,所以BF = 在Rt △BB ′E中,'13B E BE ==,'2BB BF =12'5B E =,365BE =. 所以3621355OE BE OB =-=-=.所以点B ′的坐标为2112(,)55-. 因为点M 在直线y =3x +3上,设点M 的坐标为(x , 3x +3). 由''''''DD MM B D B M =,得''''yD yB yM yB xD xB xM xB --=--.所以1212433552121155x x -+-=++. 解得935x =.所以点M 的坐标为9132(,)3535.图2 图3考点伸展第(2)题的解题思路是这样的:①如图4,当AP 是平行四边形的边时,CQ //AP ,所以点C 、Q 关于抛物线的对称轴对称,点Q 的坐标为(2, 3).②如图5,当AP 是平行四边形的对角线时,点C 、Q 分居x 轴两侧,C 、Q 到x 轴的距离相等.解方程-x 2+2x +3=-3,得1x =所以点Q 的坐标为(13-)或(13-).。
中考压轴题十大类型之动点问题

念书破万卷下笔如有神第一讲中考压轴题十大种类之动点问题一、解题策略和解法精讲解决动点问题的要点是“动中求静”.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,经过“对称、动点的运动”等研究手段和方法,来研究与发现图形性质及图形变化,在解题过程中浸透空间见解和合情推理。
在动点的运动过程中察看图形的变化情况,理解图形在不同样地址的情况,做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”研究题的基本思路 ,这也是动向几何数学问题中最中心的数学本质。
二、精讲精练1.(2011 吉林)如图,梯形 ABCD 中, AD∥BC,∠ BAD=90°, CE⊥ AD 于点E,AD=8cm,BC=4cm,AB=5cm.从初始时辰开始,动点 P,Q 分别从点 A,B 同时出发,运动速度均为 1cm/s,动点 P 沿 A-B-C-E 方向运动,到点 E 停止;动点 Q 沿 B-C-E- D 方向运动,到点 D 停止,设运动时间为x s,△ PAQ 2的面积为 y cm ,(这里规定:线段是面积为0 的三角形)解答以下问题:(1)当x=2s 时, y=_____ cm2;当x =9 s 时, y=_______ cm2.2(2)当5 ≤x ≤14时,求y 与x 之间的函数关系式.(3)当动点P 在线段BC 上运动时,求出y4S 梯形ABCD时x 的值.15(4)直接写出在整个运动过程中,使 PQ 与四边形 ABCE 的对角线平行的所..有 x 的值.2.(2007 河北)如图,在等腰梯形 ABCD 中, AD∥BC,AB=DC=50,AD=75,BC=135.点 P 从点 B 出发沿折线段 BA-AD-DC 以每秒 5 个单位长的速度向点 C 匀速运动;点 Q 从点 C 出发沿线段 CB 方向以每秒 3 个单位长的速度匀速运动,过点 Q 向上作射线 QK⊥BC,交折线段 CD-DA-AB 于点 E.点 P、Q 同时开始运动,当点 P 与点 C 重合时停止运动,点 Q 也随之停止.设点 P、Q 运动的时间是 t 秒( t>0).(1)当点 P 抵达终点 C 时,求 t 的值,并指出此时BQ 的长;(2)当点 P 运动到 AD 上时, t 为何值能使 PQ∥DC ?(3)设射线 QK 扫过梯形 ABCD 的面积为 S,分别求出点 E 运动到 CD、DA 上时, S 与 t 的关系式;(4)△PQE 可否成为直角三角形?若能,写出 t 的取值范围;若不能够,请说明原因.A DK A DP EBQ CBC备用图3.(2008 河北)如图,在Rt△ABC中,∠ C=90°, AB=50,AC=30,D,E,F 分别是 AC,AB,BC 的中点.点 P 从点D出发沿折线 DE-EF-FC-CD 以每秒7 个单位长的速度匀速运动;点Q从点 B 出发沿BA方向以每秒 4 个单位长的速度匀速运动,过点 Q 作射线 QK AB ,交折线BC-CA于点 G .点 P,Q 同时出发,当点 P 绕行一周回到点D时停止运动,点Q也随之停止.设点P, Q 运动的时间是t秒( t 0 ).(1)D,F两点间的距离是;(2)射线QK可否把四边形CDEF分成面积相等的两部分?若能,求出t 的值.若不能够,说明原因;(3)当点 P 运动到折线EF FC 上,且点P又恰巧落在射线 QK 上时,求t的值;(4)连接PG,当PG∥AB时,请直接写出 t 的值...C K CD F D FP GA EQB A E B备用图4(.2011 山西太原)如图,在平面直角坐标系中,四边形 OABC 是平行四边形.直线 l 经过O、C两点.点A的坐标为( 8,0),点B的坐标为( 11,4),动点P在线段 OA 上从点 O 出发以每秒 1 个单位的速度向点 A 运动,同时动点 Q 从点 A出发以每秒 2 个单位的速度沿A→ B→C 的方向向点 C 运动,过点 P 作 PM 垂直于 x 轴,与折线 O- C- B 订交于点 M.当 P、 Q 两点中有一点抵达终点时,另一点也随之停止运动,设点 P、Q 运动的时间为 t 秒 ( t 0 ) ,△ MPQ 的面积为 S.(1)点 C 的坐标为 ________,直线l的剖析式为 __________.(2)试求点 Q 与点 M 相遇前 S 与 t 的函数关系式,并写出相应的 t 的取值范围.(3)试求题 ( 2) 中当 t 为何值时, S 的值最大,并求出S 的最大值.(4)随着 P、Q 两点的运动,当点 M 在线段 CB 上运动时,设 PM 的延长线与直线 l 订交于点N.试试究:当t为何值时,△QMN为等腰三角形?请直接写出 t 的值.ylC BM Qyl C QBMOP AxylC M Q BO P A x5.( 2011四川重庆)如图,矩形ABCD 中,AB=6,BC=2 3,点 O 是 AB 的中点,点 P 在 AB 的延长线上,且 BP= 3.一动点 E 从 O 点出发,以每秒 1 个单位长度的速度沿OA 匀速运动,抵达A 点后,立刻以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1 个单位长度的速度沿射线PA 匀速运动,点E、F 同时出发,当两点相遇时停止运动.在点 E、F 的运动过程中,以 EF 为边作等边△EFG,使△EFG 和矩形 ABCD 在射线 PA 的同侧,设运动的时间为 t 秒(t≥0).(1)当等边△EFG 的边 FG 恰巧经过点 C 时,求运动时间 t 的值;(2)在整个运动过程中,设等边△ EFG 和矩形 ABCD 重叠部分的面积为 S,请直接写出 S与 t 之间的函数关系式和相应的自变量t 的取值范围;(3)设 EG 与矩形 ABCD 的对角线 AC 的交点为 H,可否存在这样的 t,使△AOH 是等腰三角形?若存在,求出对应的 t 的值;若不存在,请说明原因.D C D CEO B F P A E O B F P备用图 1D CAE O BF P备用图 2三、测试提高1. (2011 山东烟台)如图,在直角坐标系中, 梯形 ABCD 的底边 AB 在 x 轴上, 底边 CD 的端点 D 在 y 轴上.直线 CB 的表达式为 y4 x16,点 A 、D3 3的坐标分别为(- 4,0),(0,4).动点 P 自 A 点出发,在 AB 上匀速运动.动点 Q 自点 B 出发,在折线 BCD 上匀速运动,速度均为每秒 1 个单位.当其中一个动点抵达终点时, 它们同时停止运动. 设点 P 运动 t (秒)时,△OPQ 的面积为 S (不能够组成△ OPQ 的动点除外). (1)求出点 B 、C 的坐标; (2)求 S 随 t 变化的函数关系式;(3)当 t 为何值时 S 有最大值?并求出最大值.备用图。
九年级中考数学动点问题压轴题专题训练(含答案)

九年级中考数学动点问题压轴题专题训练1.如图1, 在平面直角坐标系中, 四边形OABC各顶点的坐标分别为O(0, 0), A(3, 3 ), B(9, 5 ), C(14, 0). 动点P与Q同时从O点出发, 运动时间为t秒, 点P沿OC方向以1单位长度/秒的速度向点C运动, 点Q沿折线OA-AB-BC运动, 在OA, AB, BC上运动的速度分别为3, , (单位长度/秒). 当P, Q中的一点到达C点时, 两点同时停止运动.(1)求AB所在直线的函数表达式.(2)如图2, 当点Q在AB上运动时, 求△CPQ的面积S关于t的函数表达式及S的最大值.(3)在P, Q的运动过程中, 若线段PQ的垂直平分线经过四边形OABC的顶点, 求相应的t值.图1 图22.如图, 抛物线y=-x2+bx+c与x轴交于A, B两点(A在B的左侧), 与y轴交于点N, 过A点的直线l:y=kx+n与y轴交于点C, 与抛物线y=-x2+bx+c的另一个交点为D, 已知A(-1, 0), D(5, -6), P 点为抛物线y=-x2+bx+c上一动点(不与A, D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时, 过P点作PE∥x轴交直线l于点E, 作PF ∥y轴交直线l于点F, 求PE+PF的最大值;(3)设M为直线l上的点, 探究是否存在点M, 使得以点N, C, M, P为顶点的四边形为平行四边形.若存在, 求出点M的坐标;若不存在, 请说明理由.3.如图, 在平面直角坐标系中, 抛物线y=ax2+bx+c经过A(-2, -4 )、O(0, 0)、B(2, 0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点, 求AM+OM的最小值.4.设直线l1: y=k1x+b1与l2: y=k2x+b2, 若l1⊥l2, 垂足为H, 则称直线l1与l2是点H的直角线.(1)已知直线①;②;③;④和点C(0, 2), 则直线_______和_______是点C的直角线(填序号即可);(2)如图, 在平面直角坐标系中, 直角梯形OABC的顶点A(3, 0)、B(2, 7)、C(0, 7), P为线段OC上一点, 设过B、P两点的直线为l1, 过A、P两点的直线为l2, 若l1与l2是点P的直角线, 求直线l1与l2的解析式.5.如图①, 在平面直角坐标系xOy中, 已知抛物线y=ax2-2ax-8a与x轴相交于A, B两点(点A在点B的左侧), 与y轴交于点C(0, -4).(1)点A的坐标为, 点B的坐标为, 线段AC的长为, 抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.如果在x轴上存在点Q, 使得以点B, C, P, Q为顶点的四边形是平行四边形, 求点Q的坐标.①6.如图, 已知抛物线(b是实数且b>2)与x轴的正半轴分别交于点A.B(点A位于点B是左侧), 与y轴的正半轴交于点C.(1)点B的坐标为______, 点C的坐标为__________(用含b的代数式表示);(2)请你探索在第一象限内是否存在点P, 使得四边形PCOB的面积等于2b, 且△PBC是以点P为直角顶点的等腰直角三角形?如果存在, 求出点P的坐标;如果不存在, 请说明理由;(3)请你进一步探索在第一象限内是否存在点Q, 使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在, 求出点Q的坐标;如果不存在, 请说明理由.7.如图, 已知A.B是线段MN上的两点, , , . 以A为中心顺时针旋转点M, 以B为中心逆时针旋转点N, 使M、N两点重合成一点C, 构成△ABC, 设.(1)求x的取值范围;(2)若△ABC为直角三角形, 求x的值;(3)探究: △ABC的最大面积?8.如图, 已知抛物线y=-x2+bx+c经过A(0, 1)、B(4, 3)两点.(1)求抛物线的解析式;(2)求tan∠ABO的值;(3)过点B作BC⊥x轴, 垂足为C, 在对称轴的左侧且平行于y轴的直线交线段AB于点N, 交抛物线于点M, 若四边形MNCB为平行四边形, 求点M的坐标.9.在平面直角坐标系中, 反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).(1)当k=-2时, 求反比例函数的解析式;(2)要使反比例函数与二次函数都是y随x增大而增大, 求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q, 当△ABQ是以AB为斜边的直角三角形时, 求k的值.10.如图, 已知抛物线y=ax2+bx+4(a≠0)的对称轴为直线x=3, 抛物线与x轴相交于A, B两点, 与y轴相交于点C, 已知B点的坐标为(8, 0).(1)求抛物线的解析式;(2)点M为线段BC上方抛物线上的一点, 点N为线段BC上的一点, 若MN∥y 轴, 求MN的最大值;(3)在抛物线的对称轴上是否存在点Q, 使△ACQ为等腰三角形?若存在, 求出符合条件的Q点坐标;若不存在, 请说明理由.11.如图, 直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m, 8), 与x轴交于点B, 平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M, 交AB于点N, 连接BM.(1)求m的值和反比例函数的解析式;(2)观察图象, 直接写出当x>0时不等式2x+6->0的解集;(3)直线y=n沿y轴方向平移, 当n为何值时, △BMN的面积最大?最大值是多少?12.如图, 在平面直角坐标系xOy中, 顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B, AO=BO=2, ∠AOB=120°.(1)求这条抛物线的表达式;(2)连结OM, 求∠AOM的大小;(3)如果点C在x轴上, 且△ABC与△AOM相似, 求点C的坐标.13.在直角梯形OABC中, CB//OA, ∠COA=90°, CB=3, OA=6, BA=. 分别以OA.OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.(1)求点B的坐标;(2)已知D.E分别为线段OC.OB上的点, OD=5, OE=2EB, 直线DE交x轴于点F. 求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点, 在x轴上方的平面内是否存在另一点N, 使以O、D、M、N为顶点的四边形是菱形?若存在, 请求出点N的坐标;若不存在, 请说明理由.14.如图, 已知一次函数y=-x+7与正比例函数的图象交于点A, 且与x轴交于点B. (1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C, 过点B作直线l//y轴. 动点P从点O出发, 以每秒1个单位长的速度, 沿O—C—A的路线向点A运动;同时直线l从点B出发, 以相同速度向左平移, 在平移过程中, 直线l交x轴于点R, 交线段BA或线段AO于点Q. 当点P到达点A时, 点P和直线l都停止运动. 在运动过程中, 设动点P运动的时间为t秒.①当t为何值时, 以A.P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在, 求t的值;若不存在, 请说明理由.15.如图, 二次函数y=a(x2-2mx-3m2)(其中a、m是常数, 且a>0, m>0)的图像与x轴分别交于A.B(点A位于点B的左侧), 与y轴交于点C(0,-3), 点D在二次函数的图像上, CD//AB, 联结AD. 过点A作射线AE交二次函数的图像于点E, AB平分∠DAE.(1)用含m的式子表示a;(2)求证: 为定值;(3)设该二次函数的图像的顶点为F.探索:在x轴的负半轴上是否存在点G, 联结GF, 以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在, 只要找出一个满足要求的点G即可, 并用含m的代数式表示该点的横坐标;如果不存在, 请说明理由.16.如图, 二次函数y=-x2+4x+5的图象的顶点为D, 对称轴是直线l, 一次函数y= x+1的图象与x轴交于点A, 且与直线DA关于l的对称直线交于点B.(1)点D的坐标是.(2)直线l与直线AB交于点C, N是线段DC上一点(不与点D, C重合), 点N的纵坐标为n.过点N作直线与线段DA, DB分别交于点P, Q, 使得△DPQ与△DAB 相似.①当n= 时, 求DP的长;②若对于每一个确定的n的值, 有且只有一个△DPQ与△DAB相似, 请直接写出n的取值范围.17.已知直线y=3x-3分别与x轴、y轴交于点A, B, 抛物线y=ax2+2x+c经过点A, B. (1)求该抛物线的表达式, 并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l, 点B关于直线l的对称点为C, 若点D在y 轴的正半轴上, 且四边形ABCD为梯形.①求点D的坐标;②将此抛物线向右平移, 平移后抛物线的顶点为P, 其对称轴与直线y=3x-3交于点E, 若, 求四边形BDEP的面积.18.如图, 在平面直角坐标系xOy中, 二次函数y=-x2+2x+8的图象与一次函数y=-x+b的图象交于A.B两点, 点A在x轴上, 点B的纵坐标为-7.点P是二次函数图象上A.B两点之间的一个动点(不与点A.B重合), 设点P的横坐标为m, 过点P作x轴的垂线交AB于点C, 作PD ⊥AB于点D.(1)求b及sin∠ACP的值;(2)用含m的代数式表示线段PD的长;(3)连接PB, 线段PC把△PDB分成两个三角形, 是否存在适合的m值, 使这两个三角形的面积之比为1∶2?如果存在, 直接写出m的值;如果不存在, 请说明理由.19.如图, 抛物线与x轴交于A.B两点(点A在点B的左侧), 与y轴交于点C.(1)求点A.B的坐标;(2)设D为已知抛物线的对称轴上的任意一点, 当△ACD的面积等于△ACB 的面积时, 求点D的坐标;(3)若直线l过点E(4, 0), M为直线l上的动点, 当以A、B、M为顶点所作的直角三角形有且只有三个时, 求直线l的解析式.20.已知平面直角坐标系中两定点A(-1, 0)、B(4, 0), 抛物线y=ax2+bx-2(a≠0)过点A.B, 顶点为C, 点P(m, n)(n<0)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时, 求m的取值范围;(3)若m>, 当∠APB为直角时, 将该抛物线向左或向右平移t(0<t<)个单位, 点C、P平移后对应的点分别记为C′、P′, 是否存在t, 使得顺次首尾连接A、B、P′、C′所构成的多边形的周长最短?若存在, 求t的值并说明抛物线平移的方向;若不存在, 请说明理由.2021中考数学压轴专题训练之动点问题-答案一、解答题(本大题共20道小题)1.【答案】【思维教练】(1)设一次函数解析式, 将已知点A、B的坐标值代入求解即可;(2)S △CPQ=·CP·Qy, CP=14-t, 点Q在AB上, Qy即为当x=t时的y值, 代入化简得出S与t的函数关系式, 化为顶点式得出最值;(3)垂直平分线过顶点需以时间为临界点分情况讨论, 当Q在OA上时, 过点C;当Q在AB上时, 过点A;当Q在BC上时, 过点C和点B, 再列方程并求解.解图1解: (1)把A(3, 3 ), B(9, 5 )代入y=kx+b,得, 解得,∴y=33x+23;(3分)(2)在△PQC中, PC=14-t,∵OA==6且Q在OA上速度为3单位长度/s,AB==4 且Q点在AB上的速度为单位长度/s,∴Q在OA上时的横坐标为t, Q在AB上时的横坐标为t,PC边上的高线长为33t+2 3.(6分)所以S=(14-t)( t+2 )=-t2+t+14 (2≤t≤6).当t=5时, S有最大值为.(7分)解图2(3)①当0<t ≤2时, 线段PQ 的中垂线经过点C(如解图1). 可得方程(332t )2+(14-32t )2=(14-t )2.解得t1= , t2=0(舍去), 此时t = .(8分)解图3②当2<t ≤6时, 线段PQ 的中垂线经过点A(如解图2).可得方程(33)2+(t -3)2=[3(t -2)]2.解得t1= , ∵t2= (舍去), 此时t = .③当6<t ≤10时,(1)线段PQ 的中垂线经过点C(如解图3).可得方程14-t =25- t, 解得t = .(10分)解图4(2)线段PQ 的中垂线经过点B(如解图4).可得方程(53)2+(t -9)2=[52(t -6)]2.解得t1= , t2= (舍去).此时t=38+2027.(11分)综上所述, t的值为, , , .(12分)【难点突破】解决本题的关键点在于对PQ的垂直平分线过四边形顶点的情况进行分类讨论, 在不同阶段列方程求解.2.【答案】[分析] (1)将点A, D的坐标分别代入直线表达式、抛物线的表达式, 即可求解;(2)设出P点坐标, 用参数表示PE, PF的长, 利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况, 分别求解即可.解:(1)将点A, D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A, D的坐标代入抛物线表达式,得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1,∴C(0, -1), 则直线l与x轴的夹角为45°, 即∠OAC=45°,∵PE∥x轴, ∴∠PEF=∠OAC=45°.又∵PF∥y轴, ∴∠EPF=90°, ∴∠EFP=45°.则PE=PF.设点P坐标为(x, -x2+3x+4),则点F(x, -x-1),∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18,∵-2<0, ∴当x=2时, PE+PF有最大值, 其最大值为18.(3)由题意知N(0, 4), C(0, -1), ∴NC=5,①当NC是平行四边形的一条边时, 有NC∥PM, NC=PM.设点P坐标为(x, -x2+3x+4), 则点M的坐标为(x, -x-1),∴|yM-yP|=5, 即|-x2+3x+4+x+1|=5,解得x=2±或x=0或x=4(舍去x=0),则点M坐标为(2+ , -3- )或(2- , -3+ )或(4, -5);②当NC是平行四边形的对角线时, 线段NC与PM互相平分.由题意, NC的中点坐标为0, ,设点P坐标为(m, -m2+3m+4),则点M(n', -n'-1),∴0= = ,解得:n'=0或-4(舍去n'=0), 故点M(-4, 3).综上所述, 存在点M, 使得以N, C, M, P为顶点的四边形为平行四边形, 点M的坐标分别为:(2+ , -3- ), (2- , -3+ ), (4, -5), (-4, 3).3.【答案】(1)。
中考数学压轴题专题解析---直角三角形中的动点问题

中考数学压轴题专题解析---直角三角形中的动点问题这节课我们学什么1.动点直角三角形一线三直角问题2.动点直角三角形SAS问题3.动点直角三角形三角比问题4.动点直角三角形勾股定理问题知识点梳理动点直角三角形问题,一般都需要讨论哪个角是可能构成直角,然后根据题型,运用不同的方法.如下为总结的四种方法:1.先讨论哪个角是直角,然后第一类用一线三直角构造相似求解,分别用未知数的式子表示出一线三直角模型的边长;2.用边角边,即两边对应成比例夹角相等,一般是动点构成的直角三角形与已知的直角三角形相似,需要求出已知直角三角形的边长,以及用未知数的式子求出动点直角三角形的边长,通过对应边成比例建立等式;3.利用三角比来求解,实际上这个和上面一种情况类似,但是动点构成的直角三角形中,某个锐角的三角比已知,这样,直接在动点三角形中运用三角比直接可以建立等式;4.第四种方法就比较简单粗暴了,就是把动点直角三角形三边的长度用未知数的式子,或者直接是数字表示出来,用勾股定理建立等式,求解出未知数.典型例题分析1、动点直角三角形一线三直角问题; 例1.已知如图在平面直角坐标系xoy 中,抛物线与轴分别交于点(2,0)A 、点B (点B 在点A 的右侧),与y 轴交于点C ,1tan 2CBA ∠=. (1)求该抛物线的表达式;(2)设该抛物线的顶点为D ,求四边形ABCD 的面积;(3)设抛物线上的点E 在第一象限,BCE ∆是以BC 为一条直角边的直角三角形,请直接写出点E 的坐标.【答案:(1)∵当时,,∴(0,3)C在Rt COB ∆中,∵∴∴∴点(6,0)B把(2,0)A (6,0)B 分别代入,得:得解得:∴该抛物线表达式为(2)∵∴顶点41D -(,) ∴(3)点E 的坐标是108(,)或1635(,)】2、动点直角三角形SAS 问题 例2.已知:如图,抛物线2445y x mx =-++与y 轴交于点C ,与x 轴交于点A 、B ,(点A 在点B 的左侧)且满足4OC OA =.设抛物线的对称轴与x 轴交于点M . (1)求抛物线的解析式及点M 的坐标;(2)联接CM ,点Q 是射线CM 上的一个动点,当QMB ∆与COM ∆相似时,求直线AQ 的解析式.【答案:(1)根据题意:04C (,)∵4OC OA = ∴0A (-1,) 把点A 代入得4045m =--+ 解得∴抛物线的解析式∴(2)根据题意得:3BM =,2tan CMO ∠=,直线CM :4y x =+ (i )当90COM MBQ ∠=∠=︒时,COM QBM ∆∆∽ ∴2BQtan BMQ BM∠== ∴6BQ =即5,6Q -()∴AQ :(ii )当90COM BQM ∠=∠=︒时,COM BQM ∆∆∽ 同理Q () ∴AQ :】例3.如图,在ABC Rt ∆中,︒=∠90C ,5=AB ,43tan =B ,点D 是BC 的中点,点E 是AB 边上的动点,DE DF ⊥交射线AC 于点F . (1)求AC 和BC 的长;(2)当EF BC //时,求BE 的长;(3)联结EF ,当DEF ∆和ABC ∆相似时,求BE 的长.【答案:解:(1)在中,∠C ∵43tan ==BC AC B ,∴设k AC 3=,k BC 4= ∴55==k AB ,∴1=k ∴3=AC ,4=BC(2)过点E 作BC EH ⊥,垂足为H .A C易得EHB ACB ∆∆∽设k CF EH 3==,k BH 4=,k BE 5=∵EF BC //∴FDC EFD ∠=∠∵︒=∠=∠90C FDE ∴EFD FDC ∆∆∽ ∴CDFDFD EF =∴CD EF FD ⋅=2 即)44(2492k k -=+化简,得04892=-+k k 解得91324±-=k (负值舍去)∴92013105-==k BE(3)过点E 作BC EH ⊥,垂足为H .易得EHB ACB ∆∆∽ 设k EH 3=,k BE 5=∵︒=∠+∠90HDE HED ︒=∠+∠90HDE FDC ∴FDC HED ∠=∠∵︒=∠=∠90C EHD ∴EHD DCF ∆∆∽∴DFDECD EH =当DEF ∆和ABC ∆相似时,有两种情况:①43==BC AC DF DE ;∴43=CD EH 即4323=k 解得21=k ∴255==k BE②34==AC BC DF DE ;∴34=CD EH 即3423=k 解得98=k∴9405==k BE综合①、②,当DEF ∆和ABC ∆相似时,BE 的长为25或940.】3、动点直角三角形三角比问题例4.已知:如图,在Rt ABC ∆中,90C ∠=︒,2BC =,4AC =,P 是斜边AB 上的一个动点,PD AB ⊥,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且EPD A ∠=∠.设A 、P 两点的距离为x ,BEP ∆的面积为y . (1)求证:2AE PE =;(2)求y 关于x 的函数解析式,并写出它的定义域; (3)当BEP ∆与ABC ∆相似时,求BEP ∆的面积.【答案:(1)∵90APD C ∠=∠=︒,A A ∠=∠,∴ADP ABC ∆∆∽.∴21==AC BC AP PD . ∵EPD A ∠=∠,PED AEP ∠=∠,∴EPD EAP ∆∆∽. ∴21==AP PD AE PE . ∴2AE PE =.(2)由EPD EAP ∆∆∽,得21==AP PD PE DE ,∴2PE DE =. ∴24AE PE DE ==. 作EHAB ⊥,垂足为点H .∵AP x =,∴x PD 21=.∵PD HE //,∴34==AD AE PD HE .∴x HE 32=. 又∵52=AB ,∴x x y 32)52(21⋅-=,即x x y 352312+-=.定义域是5580<<x .另解:由EPD EAP ∆∆∽,得21==AP PD PE DE ,∴2PE DE =. ∴24AE PE DE ==.ABD E∴x x AE 3522534=⨯=.∴12233ABE S x x ∆⋅⨯==.∴AB BP S S ABE BEP =∆∆,即5252352x xy-=.∴x x y 352312+-=.定义域是5580<<x . (3)由PEH BAC ∆∆∽,得AC AB HE PE =,∴x x PE 352532=⋅=.当BEP ∆与ABC ∆相似时,只有两种情形:90BEP C ∠=∠=︒或90EBP C ∠=∠=︒.(i )当90BEP ∠=︒时,AB BC PB PE =,∴515235=-x x.解得453=x . ∴1625453352516931=⨯+⨯⨯-=y . (ii )当90EBP ∠=︒时,同理可得253=x ,45=y .】PGABCDFPGABCD例5.已知ABC ∆为等边三角形,6AB =,P 是AB 上的一个动点(与A 、B 不重合),过点P 作AB 的垂线与BC 相交于点D ,以点D 为正方形的一个顶点,在ABC ∆内作正方形DEFG ,其中D 、E 在BC 上,F 在AC 上,(1)设BP 的长为x ,正方形DEFG 的边长为y ,写出y 关于x 的函数解析式及定义域;(2)当2BP =时,求CF 的长;(3)GDP ∆是否可能成为直角三角形?若能,求出BP 的长;若不能,请说明理由.【答案:(1)∵ABC ∆为等边三角形, ∴60B C ∠=∠=︒,6AB BC AC ===. ∵DP AB ⊥,BP x =,∴2BD x = 又∵四边形DEFG 是正方形, ∴EF BC ⊥,EF DE y ==, ∴y EC 33=. ∴6332=++y y x , ∴339)33(-+-=x y .(≤<3)(2)当2BP =时,3392)33(-+⨯-=y 33-=.DEFBC23232-==y CF .(3)GDP ∆能成为直角三角形. ①90PGD ∠=︒时,y y x +=-36,61)3)9x x -=⋅+-得到:113630-=x . ②90GPD ∠=︒时,y x x 234+=, ⋅+=234x x ]339)33[(-+-x , 得到:336-=x .∴当GDP ∆为直角三角形时,BP 的长为113630-或者336-=x .】DABCGP EF4. 二动点直角三角形勾股定理问题例6.如图,AOB ∆的顶点A 、B 在二次函数21332y x bx =-++的图像上,又点A 、B 分别在y 轴和x 轴上,tan 1ABO ∠=.(1)求此二次函数的解析式;(2)过点A 作AC BO //交上述函数图像于点C ,点P 在上述函数图像上,当POC ∆与ABO ∆相似时,求点P【答案:(1)∵点A 在二次函数23312++-=bx x y 的图像上,)23,0(A 在Rt AOB ∆中,︒=∠90AOB ∵1tan ==∠BO AO ABO ,∵23==AO BO ,∴)0,23(-B ∵点B 在二次函数23312++-=bx x y 的图像上 ∴02323)23(312=+--⨯-b ∴21=b ∴2321312++-=x x y (2)∵AC BO //交上述函数图像于点C ,∴设)23,(x C ∴232321312=++-x x ,解得23,021==x x ∵)23,23(C ∴23==AO AC ,223=OC 设抛物线2321312++-=x x y 与x 轴的另一交点为D 可得,)0,3(D∴223)230()233(22=-+-=CD ,3=OD ∴222OD CD OC =+,∴︒=∠90OCD易得,Rt OCA Rt ABO ∆∆∽,Rt ODC Rt ABO ∆∆∽ ∴)23,0(P 或)0,3(P 】课后练习练1.如图,在平面直角坐标系中,二次函数2y x bx c =++的图像与x 轴交于A 、B 两点,B 点的坐标为(3,0),与y 轴交于点(0,3)C -,点P 是直线BC 下方抛物线上的任意一点;(1)求这个二次函数2y x bx c =++的解析式;(2)联结PO 、PC ,并将POC ∆沿y 轴对折,得到四边形POP C ',如果四边形POP C '为菱形,求点P 的坐标;(3)如果点P 在运动过程中,能使得以P 、C 、B 为顶点的三角形与AOC ∆相似,请求出此时点P 的坐标.【答案:】练2.如图,直角坐标平面内的梯形OABC ,OA 在x 轴上,OC 在y 轴上,//OA BC ,点E 在对角线OB 上,点D 在OC 上,直线DE 与x 轴交于点F ,已知2OE EB =,3CB =,6OA =,BA =5OD =.(1)求经过点A 、B 、C 三点的抛物线解析式:(2)求证:ODE OBC ∆∆∽:(3)在y 轴上找一点G ,使得OFG ODE ∆∆∽,直接写出点G 的坐标.【答案:(1)2163y x x =-++或者436)23(312+--=x y(2)24E (,),OE =,OB =OE OC OD OB==,DOE BOC ∠=∠ 故得证 (3)05(,)、05-(,)、020(,)、020-(,)】练3.已知:如图,二次函数22416333y x x =--的图像与x 轴交于点A 、B (点A 在点B 的左侧),抛物线的顶点为Q ,直线QB 与y 轴交于点E .(1)求点E 的坐标;(2)在x 轴上方找一点C ,使以点C 、O 、B 为顶点的三角形与BOE ∆相似,请直接写出点C 的坐标.【答案:(1)令0y =,得224160333x x --= 解方程得122,4x x =-=(4,0)B 又22(1)63y x =-- ∴(1,6)Q -设直线BQ :(0)y kx b k =+≠406k b k b +=⎧⎨+=-⎩解得28y x =-(0,8)E ∴-(2)12345616848(0,2),(0,8),(4,2),(4,8),(,),(,)5555C C C C C C 】练4.已知:正方形ABCD 的边长为4,点E 为BC 边的中点,点P 为AB 边上一动点长,沿PE 翻折BPE ∆得到FPE ∆,直线PF 交CD 边于点Q ,交直线AD 于点G .(1)如图,当 1.5BP =时,求CQ 的长;(2)如图,当点G 在射线AD 上时,设BP x =,DG y =,求y 关于x 的函数关系式,并写出x 的取值范围;(3)延长EF 交直线AD 于点H ,若CQE FHG ∆∆∽,求BP 的长.【答案:(1)由题意,得,90,BE EF PFE B BEP FEP =∠=∠=︒∠=∠ ∵点E 为BC 的中点22BE EC EF EC ∴==∴== 又90,EFQ C EQ EQ ∠=∠=︒=∴EFQ ECQ ∆∆≌,90FEQ CEQ BEP CEQ ∴∠=∠∴∠+∠=︒又90BPE BEP BPE CEQ ∠+∠=︒∴∠=∠90B C ∠=∠=︒∴BPE CEQ ∆∆∽ 1.522BP BE EC QC CQ ∴==即83CQ ∴= (2)由(1)知:BPE CEQ ∆∆∽,BP BE EC CQ ∴= 242x CQ CQ x ∴=∴=44DQ x ∴=- ∵QD AP //4,4DG DQ AP x AG y AG AP∴==-=+又 4444y x y x -∴=+-21616(12)4x y x x -∴=<<-(3)由题意知:90C GFH ∠︒∠==①当点G 在线段AD 的延长线上时,由题意知:G CQE ∠∠=∵CQE FQE ∠∠=∴22DQC FQC CQE G ∠∠∠∠===∴90DQG G ∠+∠︒=∴30G ∠︒=∴30BQP CQE G ∠∠∠︒===tan30BP BE ∴=⋅︒=②当点G 在线段DA 的延长线上时,由题意知:G QCE ∠=∠同理可得:30G ∠=︒30BPE G ∴∠=∠=︒cot30BP BE ∴=⋅︒=综上所述,BP 】课后小测验1.如图,二次函数2y x bx c =++图像经过原点和点(2,0)A ,直线AB 与抛物线交于点B ,且45BAO ∠=︒.(1)求二次函数解析式及其顶点C 的坐标;(2)在直线AB 上是否存在点D ,使得BCD ∆为直角三角形.若存在,求出点D 的坐标,若不存在,说明理由.【答案:(1)(2)由可以知道直线AB 的一次项系数为-1,从而可求得直线AB 的解析式为.当时.根据相互垂直的两直线的一次项系数之积等于-1可求得直线CD 的解析式为,将与联立可求得点D 的坐标为;当时.将与联立得求得点B 的坐标为,然后根据待定系数法求得直线BC 的解析式为直线BC 的解析式为,根据相互垂直的两直线的一次项系数之积等于-1可求得直线CD 的解析式为,将与联立可求得点D 的坐标为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考专题——动点问题详细分层解析(一)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式例1如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围). (3)如果△PGH 是等腰三角形,试求出线段PH 的长. 解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段,这条线段是GH=32NH=2132⋅OP=2. (3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x .经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x .经检验,0=x 是原方程的根,但不符合题意. ③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y .(1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式;(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.H M N G PO A B图1 x y例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP. (2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域. (3)当BF=1时,求线段AP 的长.三、应用求图形面积的方法建立函数关系式例3 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时,△AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.A E D CB 图2 A 3(2) A 3(1 A B CO 图8HC A B CDE O l A ′ 中考专题——动点问题(二)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、以动态几何为主线的压轴题(一)点动问题.1.如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F .(1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长;(3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE 的长.[题型背景和区分度测量点] 本题典型的一线三角(三等角)问题,试题在原题的基础上改编出第一小题,当E 点在AB 边上运动时,渗透入圆与圆的位置关系(相切问题)的存在性的研究形成了第二小题,加入直线与圆的位置关系(相切问题)的存在性的研究形成了第三小题.区分度测量点在直线与圆的位置关系和圆与圆的位置关系,从而利用方程思想来求解. [区分度性小题处理手法]1.直线与圆的相切的存在性的处理方法:利用d=r 建立方程.2.圆与圆的位置关系的存在性(相切问题)的处理方法:利用d=R ±r(r R >)建立方程. 3.解题的关键是用含x 的代数式表示出相关的线段. (二)线动问题在矩形ABCD 中,AB =3,点O 在对角线AC 上,直线l 过点O ,且与AC 垂直交AD 于点E.(1)若直线l 过点B ,把△ABE沿直线l 翻折,点A 与矩形ABCD 的对称中心A '重合,求BC 的长; (2)若直线l 与AB 相交于点F ,且AO =41AC ,设AD 的长为x ,五边形BCDEF 的面积为S.①求S 关于x 的函数关系式,并指出x 的取值范围;A B C D E O l F ②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在,请求出x 的值;若不存在,请说明理由.[题型背景和区分度测量点] 本题以矩形为背景,结合轴对称、相似、三角等相关知识编制得到.第一小题考核了学生轴对称、矩形、勾股定理三小块知识内容;当直线l 沿AB 边向上平移时,探求面积函数解析式为区分测量点一、加入直线与圆的位置关系(相切问题)的存在性的研究形成了区分度测量点二. [区分度性小题处理手法]1.找面积关系的函数解析式,规则图形套用公式或用割补法,不规则图形用割补法.2.直线与圆的相切的存在性的处理方法:利用d=r 建立方程.3.解题的关键是用含x 的代数式表示出相关的线段.例1:已知⊙O 的弦AB 的长等于⊙O 的半径,点C 在⊙O 上变化(不与A 、B )重合,求∠ACB 的大小 .分析:点C 的变化是否影响∠ACB 的大小的变化呢?我们不妨将点C 改变一下,如何变化呢?可能在优弧AB 上,也可能在劣弧AB 上变化,显然这两者的结果不一样。
那么,当点C 在优弧AB 上变化时,∠ACB 所对的弧是劣弧AB ,它的大小为劣弧AB 的一半,因此很自然地想到它的圆心角,连结AO 、BO ,则由于AB=OA=OB ,即三角形ABC 为等边三角形,则∠AOB=600,则由同弧所对的圆心角与圆周角的关系得出: ∠ACB= ∠AOB=300, 当点C 在劣弧AB 上变化时,∠ACB 所对的弧是优弧AB ,它的大小为优弧AB 的一半,由∠AOB=600得,优弧AB 的度数为3600-600=3000,则由同弧所对的圆心角与圆周角的关系得出:∠ACB=1500,因此,本题的答案有两个,分别为300或1500.反思:本题通过点C 在圆上运动的不确定性而引起结果的不唯一性。
从而需要分类讨论。
这样由点C 的运动变化性而引起的分类讨论在解题中经常出现。
变式1:已知△ABC 是半径为2的圆内接三角形,若32=AB ,求∠C 的大小.本题与例1的区别只是AB 与圆的半径的关系发生了一些变化,其解题方法与上面一致,在三角形AOB 中, , 则 ,即0120=∠AOB , 从而当点C 在优弧AB 上变化时,∠C 所对的弧是劣弧AB ,它的大小为劣弧AB 的一半,即060=∠C , 当点C 在劣弧AB 上变化时,∠C 所对的弧是优弧AB ,它的大小为优弧AB 的一半,由∠AOB=1200得,优弧AB 的度数为3600-1200=2400,则由同弧所对的圆心角与圆周角的关系得出:21232121sin ==∠OB AB AOB 06021=∠AOB∠C=1200,因此060=∠C 或∠C=1200.变式2: 如图,半经为1的半圆O 上有两个动点A 、B ,若AB=1,判断∠AOB 的大小是否会随点A 、B 的变化而变化,若变化,求出变化范围,若不变化,求出它的值。
四边形ABCD 的面积的最大值。
解:(1)由于AB=OA=OB ,所以三角形AOB 为等边三角形,则∠AOB=600,即∠AOB 的大小不会随点A 、B 的变化而变化。
(2)四边形ABCD 的面积由三个三角形组成,其中三角形AOB 的面积为43,而三角形AOD 与三角形BOC 的面积之和为)(212121BG AF BG OC AF OD +=⨯+⨯,又由梯形的中位线定理得三角形AOD 与三角形BOC 的面积之和EH BG AF =+)(21,要四边形ABCD 的面积最大,只需EH 最大,显然EH ≤OE=23,当AB ∥CD 时,EH=OE ,因此四边形ABCD 的面积最大值为43+23=433. 对于本题同学们还可以继续思考:四边形ABCD 的周长的变化范围.变式3: 如图,有一块半圆形的木板,现要把它截成三角形板块.三角形的两个顶点分别为A 、B ,另一个顶点C 在半圆上,问怎样截取才能使截出的三角形的面积最大?要求说明理由(广州市2000年考题)分析:要使三角形ABC 的面积最大,而三角形ABC 的底边AB 为圆的直径为常量,只需AB 边上的高最大即可。
