中考数学压轴题：最值路径问题分析
2023年中考数学压轴题专题11 二次函数与单线段最值问题【含答案】
专题11二次函数与单线段最值问题【例1】（2022•襄阳）在平面直角坐标系中，直线y＝mx﹣2m与x轴，y轴分别交于A，B两点，顶点为D 的抛物线y＝﹣x2+2mx﹣m2+2与y轴交于点C．（1）如图，当m＝2时，点P是抛物线CD段上的一个动点．①求A，B，C，D四点的坐标；②当△PAB面积最大时，求点P的坐标；（2）在y轴上有一点M（0，m），当点C在线段MB上时，①求m的取值范围；②求线段BC长度的最大值．【例2】（2022•湖州）如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上．抛物线y＝﹣x2+bx+c经过A，C两点，与x轴交于另一个点D．（1）①求点A，B，C的坐标；②求b，c的值．（2）若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P 在BC上运动时，点M也随之运动．设BP＝m，CM＝n，试用含m的代数式表示n，并求出n的最大值．【例3】（2021•青海）如图，在平面直角坐标系中，直线y＝x+2与坐标轴交于A，B两点，点A在x轴上，点B在y轴上，C点的坐标为（1，0），抛物线y＝ax2+bx+c经过点A，B，C．（1）求抛物线的解析式；（2）根据图象写出不等式ax2+（b﹣1）x+c＞2的解集；（3）点P是抛物线上的一动点，过点P作直线AB的垂线段，垂足为Q点．当PQ＝时，求P点的坐标．【例4】（2022•雅安）已知二次函数y＝ax2+bx+c的图象过点A（﹣1，0），B（3，0），且与y轴交于点C （0，﹣3）．（1）求此二次函数的表达式及图象顶点D的坐标；（2）在此抛物线的对称轴上是否存在点E，使△ACE为Rt△，若存在，试求点E的坐标，若不存在，请说明理由；（3）在平面直角坐标系中，存在点P，满足PA⊥PD，求线段PB的最小值．1．（2020•河北模拟）已知抛物线C：y＝ax2+bx+c（a＞0，c＜0）的对称轴为x＝4，C为顶点，且A（2，0），C（4，﹣2）【问题背景】求出抛物线C的解析式．【尝试探索】如图2，作点C关于x轴的对称点C′，连接BC′，作直线x＝k交BC′于点M，交抛物线C于点N．①连接ND，若四边形MNDC′是平行四边形，求出k的值．②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时，请直接写出线段MN的长度的最大值．【拓展延伸】如图4，作矩形HGOE，且E（﹣3，0），H（﹣3，4），现将其沿x轴以1个单位每秒的速度向右平移，设运动时间为t，得到矩形H′G′O′E′，连接AC′，若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分，请求出t的取值范围．2．（2018秋•宁城县期末）已知，如图，抛物线与x轴交点坐标为A（1，0），C（﹣3，0），（1）如图1，已知顶点坐标D为（﹣1，4）或B点（0，3），选择适当方法求抛物线的解析式；（2）如图2，在抛物线的对称轴DH上求作一点M，使△ABM的周长最小，并求出点M的坐标；（3）如图3，将图2中的对称轴向左移动，交x轴于点P（m，0）（﹣3＜m＜﹣1），与抛物线，线段BC的交点分别为点E、F，用含m的代数式表示线段EF的长度，并求出当m为何值时，线段EF最长．3．（2021•桥西区模拟）如图1，抛物线y＝ax2+bx+3与x轴交于A（﹣1，0），B两点，与y轴交于点C，且CO＝BO，连接BC．（1）求抛物线的解析式；（2）如图2，抛物线的顶点为D，其对称轴与线段BC交于点E，求线段DE的长度；（3）如图3，垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，连接CP，CD，抛物线上是否存在点P，使△CDE∽△PCF，如果存在，求出点P的坐标，如果不存在，请说明理由．4．（2022•和平区二模）如图，在平面直角坐标系中，已知抛物线顶点A的坐标为（﹣2，4），且经过坐标原点，与x轴负半轴交于点B．（1）求抛物线的函数表达式并直接写出点B的坐标；（2）过点A作AC⊥x轴于点C，若点D是y轴左侧的抛物线上一个动点（点D与点A不重合），过点D 作DE⊥x轴于点E，连接AO，DO，当以A，O，C为顶点的三角形与以D，O，E为顶点的三角形相似时，求点D的坐标；（3）在（2）的条件下，当点D在第二象限时，在平面内存在一条直线，这条直线与抛物线在第二象限交于点F，在第三象限交于点G，且点A，点B，点D，到直线FG的距离都相等，请直接写出线段FG的长．5．（2022•鹿城区校级二模）如图，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），B（5，0），与y轴交于点C．（1）求抛物线的解析式和顶点D的坐标．（2）连结AD，点E是对称轴与x轴的交点，过E作EF∥AD交抛物线于点F（F在E的右侧），过点F作FG∥x轴交ED于点H，交AD于点G，求HF的长．6．（2021•南岗区模拟）如图，抛物线y＝ax2+bx﹣4交x轴于点A（﹣3，0），B（4，0），交y轴于点C．（1）求抛物线的解析式；（2）点P为第一象限抛物线上一点，过点P作x轴的平行线，与抛物线的另一个交点为点G，连接CG交x轴于点N，设点P的横坐标为t，ON的长为d，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，连接PB，将线段PB绕着点P顺时针旋转90°得到线段PD，点D恰好落在y轴上，点E在线段OB上，连接PE，点Q在EB的延长线上，且EQ＝PE，连接DQ交PE于点F，若PE＝3PF，求QN的长．7．（2021•凉山州模拟）如图1，在平面直角坐标系中，已知B点坐标为（1，0），且OA＝OC＝3OB，抛物线y＝ax2+bx+c（a≠0）图象经过A，B，C三点，其中D点是该抛物线的顶点．（1）求抛物线的解析式；（2）判断△ADC的形状并且求△ADC的面积；（3）如图2，点P是该抛物线第三象限部分上的一个动点，过P点作PE⊥AC于E点，当PE的值最大时，求此时P点的坐标及PE的最大值．8．（2022•无锡二模）已知抛物线y＝mx2﹣2mx+3（m＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB＝3OA．（1）求抛物线的函数表达式；（2）若M、N是第一象限的抛物线上不同的两点，且△BCN的面积总小于△BCM的面积，求点M的坐标；（3）若D为抛物线的顶点，P为第二象限的抛物线上的一点，连接BP、DP，分别交y轴于点E、F，若EF＝OC，求点P的坐标．9．（2021•乳源县三模）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+c与x轴交于A（5，0），B（﹣1，0）两点，与y轴交于点C（0，）．（1）求抛物线的解析式；（2）若点M是抛物线的顶点，连接AM，CM，求△AMC的面积；（3）若点P是抛物线上的一个动点，过点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线，垂足为点F，连接EF，当线段EF的长度最短时，求出点P的坐标．10．（2021•河池）在平面直角坐标系中，抛物线y＝﹣（x﹣1）2+4与x轴交于A，B两点（A在B的右侧），与y轴交于点C．（1）求直线CA的解析式；（2）如图，直线x＝m与抛物线在第一象限交于点D，交CA于点E，交x轴于点F，DG⊥CA于点G，若E为GA的中点，求m的值．（3）直线y＝nx+n与抛物线交于M（x1，y1），N（x2，y2）两点，其中x1＜x2．若x2﹣x1＞3且y2﹣y1＞0，结合函数图象，探究n的取值范围．11．（2021•桂林）如图，已知抛物线y＝a（x﹣3）（x+6）过点A（﹣1，5）和点B（﹣5，m），与x轴的正半轴交于点C．（1）求a，m的值和点C的坐标；（2）若点P是x轴上的点，连接PB，PA，当＝时，求点P的坐标；（3）在抛物线上是否存在点M，使A，B两点到直线MC的距离相等？若存在，求出满足条件的点M的横坐标；若不存在，请说明理由．12．（2021•吉林）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象经过点A（0，﹣），点B（1，）．（1）求此二次函数的解析式；（2）当﹣2≤x≤2时，求二次函数y＝x2+bx+c的最大值和最小值；（3）点P为此函数图象上任意一点，其横坐标为m，过点P作PQ∥x轴，点Q的横坐标为﹣2m+1．已知点P与点Q不重合，且线段PQ的长度随m的增大而减小．①求m的取值范围；②当PQ≤7时，直接写出线段PQ与二次函数y＝x2+bx+c（﹣2≤x＜）的图象交点个数及对应的m的取值范围．13．（2020•武汉模拟）已知：在平面直角坐标系中，抛物线y＝ax2﹣2ax﹣3a交x轴于A、B两点（点A在点B的左边），交y轴负半轴于点C．（1）则点A的坐标为，点B的坐标为．（2）如图1，过点A的直线y＝ax+a交y轴正半轴于点F，交抛物线于点D，过点B作BE∥y轴交AD于E，求证：AF＝DE．（3）如图2，直线DE：y＝kx+b与抛物线只有一个交点D，与对称轴交于点E，对称轴上存在点F，满足DF＝FE．若a＝1，求点F坐标．14．（2020•哈尔滨模拟）如图，抛物线y＝ax2+bx+5经过坐标轴上A、B和C三点，连接AC，tan C＝，5OA＝3OB．（1）求抛物线的解析式；（2）点Q在第四象限的抛物线上且横坐标为t，连接BQ交y轴于点E，连接CQ、CB，△BCQ的面积为S，求S与t的函数解析式；（3）已知点D是抛物线的顶点，连接CQ，DH所在直线是抛物线的对称轴，连接QH，若∠BQC＝45°，HR∥x轴交抛物线于点R，HQ＝HR，求点R的坐标．15．（2019•衡阳）如图，二次函数y＝x2+bx+c的图象与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点N，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接CP，过点P作CP的垂线与y 轴交于点E．（1）求该抛物线的函数关系表达式；（2）当点P在线段OB（点P不与O、B重合）上运动至何处时，线段OE的长有最大值？并求出这个最大值；（3）在第四象限的抛物线上任取一点M，连接MN、MB．请问：△MBN的面积是否存在最大值？若存在，求出此时点M的坐标；若不存在，请说明理由．16．（2020•天津）已知点A（1，0）是抛物线y＝ax2+bx+m（a，b，m为常数，a≠0，m＜0）与x轴的一个交点．（Ⅰ）当a＝1，m＝﹣3时，求该抛物线的顶点坐标；（Ⅱ）若抛物线与x轴的另一个交点为M（m，0），与y轴的交点为C，过点C作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点，EF＝2．①当点E落在抛物线上（不与点C重合），且AE＝EF时，求点F的坐标；②取EF的中点N，当m为何值时，MN的最小值是？17．（2020•凉山州）如图，二次函数y＝ax2+bx+c的图象过O（0，0）、A（1，0）、B（，）三点．（1）求二次函数的解析式；（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ 的长最大时，求点P的坐标．18．（2020•滨州）如图，抛物线的顶点为A（h，﹣1），与y轴交于点B（0，﹣），点F（2，1）为其对称轴上的一个定点．（1）求这条抛物线的函数解析式；（2）已知直线l是过点C（0，﹣3）且垂直于y轴的定直线，若抛物线上的任意一点P（m，n）到直线l 的距离为d，求证：PF＝d；（3）已知坐标平面内的点D（4，3），请在抛物线上找一点Q，使△DFQ的周长最小，并求此时△DFQ周长的最小值及点Q的坐标．19．（2016•巴彦淖尔）如图所示，抛物线y＝ax2﹣x+c经过原点O与点A（6，0）两点，过点A作AC⊥x 轴，交直线y＝2x﹣2于点C，且直线y＝2x﹣2与x轴交于点D．（1）求抛物线的解析式，并求出点C和点D的坐标；（2）求点A关于直线y＝2x﹣2的对称点A′的坐标，并判断点A′是否在抛物线上，并说明理由；（3）点P（x，y）是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点Q，设线段PQ的长为l，求l与x的函数关系式及l的最大值．20．（2018•葫芦岛）如图，抛物线y＝ax2+4x+c（a≠0）经过点A（﹣1，0），点E（4，5），与y轴交于点B，连接AB．（1）求该抛物线的解析式；（2）将△ABO绕点O旋转，点B的对应点为点F．①当点F落在直线AE上时，求点F的坐标和△ABF的面积；②当点F到直线AE的距离为时，过点F作直线AE的平行线与抛物线相交，请直接写出交点的坐标．【例1】（2022•襄阳）在平面直角坐标系中，直线y＝mx﹣2m与x轴，y轴分别交于A，B两点，顶点为D 的抛物线y＝﹣x2+2mx﹣m2+2与y轴交于点C．（1）如图，当m＝2时，点P是抛物线CD段上的一个动点．①求A，B，C，D四点的坐标；②当△PAB面积最大时，求点P的坐标；（2）在y轴上有一点M（0，m），当点C在线段MB上时，①求m的取值范围；②求线段BC长度的最大值．【分析】（1）根据函数上点的坐标特点可分别得出A，B，C，D的坐标；①当m＝2时，代入上述坐标即可得出结论；②过点P作PE∥y轴交直线AB于点E，设点P的横坐标为t，所以P（t，﹣t2+4t﹣2），E（t，2t﹣4）．根据三角形的面积公式可得△PAB的面积，再利用二次函数的性质可得出结论；（2）由（1）可知，B（0，﹣2m），C（0，﹣m2+2），①y轴上有一点M（0，m），点C在线段MB上，需要分两种情况：当点M的坐标大于点B的坐标时；当点M的坐标小于点B的坐标时，分别得出m的取值范围即可；②根据①中的条件可知，分两种情况，分别得出BC的长度，利用二次函数的性质可得出结论．【解答】解：（1）∵直线y＝mx﹣2m与x轴，y轴分别交于A，B两点，∴A（2，0），B（0，﹣2m）；∵y＝﹣（x﹣m）2+2，∴抛物线的顶点为D（m，2），令x＝0，则y＝﹣m2+2，∴C（0，﹣m2+2）．①当m＝2时，﹣2m＝﹣4，﹣m2+2＝﹣2，∴B（0，﹣4），C（0，﹣2），D（2，2）．②由上可知，直线AB的解析式为：y＝2x﹣4，抛物线的解析式为：y＝﹣x2+4x﹣2．如图，过点P作PE∥y轴交直线AB于点E，设点P的横坐标为t，∴P（t，﹣t2+4t﹣2），E（t，2t﹣4）．∴PE＝﹣t2+4t﹣2﹣（2t﹣4）＝﹣t2+2t+2，∴△PAB的面积为：×（2﹣0）×（﹣t2+2t+2）＝﹣（t﹣1）2+3，∵﹣1＜0，∴当t＝1时，△PAB的面积的最大值为3．此时P（1，1）．（2）由（1）可知，B（0，﹣2m），C（0，﹣m2+2），①∵y轴上有一点M（0，m），点C在线段MB上，∴需要分两种情况：当m≥﹣m2+2≥﹣2m时，可得≤m≤1+，当m≤﹣m2+2≤﹣2m时，可得﹣3≤m≤1﹣，∴m的取值范围为：≤m≤1+或﹣3≤m≤1﹣．②当≤m≤1+时，∵BC＝﹣m2+2﹣（﹣2m）＝﹣m2+2m+2＝﹣（m﹣1）2+3，∴当m＝1时，BC的最大值为3；当m≤﹣m2+2≤﹣2m时，即﹣3≤m≤1﹣，∴BC＝﹣2m﹣（﹣m2+2）＝m2﹣2m﹣2＝（m﹣1）2﹣3，当m＝﹣3时，点M与点C重合，BC的最大值为13．∴当m＝1时，BC的最大值为3；当m＝﹣3时，BC的最大值为13．【例2】（2022•湖州）如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上．抛物线y＝﹣x2+bx+c经过A，C两点，与x轴交于另一个点D．（1）①求点A，B，C的坐标；②求b，c的值．（2）若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P 在BC上运动时，点M也随之运动．设BP＝m，CM＝n，试用含m的代数式表示n，并求出n的最大值．【分析】（1）①根据正方形的性质得出点A，B，C的坐标；②利用待定系数法求函数解析式解答；（2）根据两角相等证明△MCP∽△PBA，列比例式可得n与m的关系式，配方后可得结论．【解答】解：（1）①四边形OABC是边长为3的正方形，∴A（3，0），B（3，3），C（0，3）；②把A（3，0），C（0，3）代入抛物线y＝﹣x2+bx+c中得：，解得：；（2）∵AP⊥PM，∴∠APM＝90°，∴∠APB+∠CPM＝90°，∵∠B＝∠APB+∠BAP＝90°，∴∠BAP＝∠CPM，∵∠B＝∠PCM＝90°，∴△MCP∽△PBA，∴＝，即＝，∴3n＝m（3﹣m），∴n＝﹣m2+m＝﹣（m﹣）2+（0≤m≤3），∵﹣＜0，∴当m＝时，n的值最大，最大值是．【例3】（2021•青海）如图，在平面直角坐标系中，直线y＝x+2与坐标轴交于A，B两点，点A在x轴上，点B在y轴上，C点的坐标为（1，0），抛物线y＝ax2+bx+c经过点A，B，C．（1）求抛物线的解析式；（2）根据图象写出不等式ax2+（b﹣1）x+c＞2的解集；（3）点P是抛物线上的一动点，过点P作直线AB的垂线段，垂足为Q点．当PQ＝时，求P点的坐标．【分析】（1）根据题意得出A、B点的坐标，然后利用待定系数法求出二次函数的解析式；（2）根据（1）的解析式由图象判断即可；（3）作PE⊥x轴于点E，交AB于点D，根据函数图象点P的位置分三种情况分别计算出P点的坐标即可．【解答】解：（1）当x＝0，y＝0+2＝2，当y＝0时，x+2＝0，解得x＝﹣2，∴A（﹣2，0），B（0，2），把A（﹣2，0），C（1，0），B（0，2）代入抛物线解析式，得，解得，∴该抛物线的解析式为：y＝﹣x2﹣x+2；（2）方法一：ax2+（b﹣1）x+c＞2，即﹣x2﹣2x+2＞2，当函数y＝﹣x2﹣2x+2＝2时，解得x＝0或x＝﹣2，由图象知，当﹣2＜x＜0时函数值大于2，∴不等式ax2+（b﹣1）x+c＞2的解集为：﹣2＜x＜0；方法二：ax2+（b﹣1）x+c＞2，即﹣x2﹣x+2＞x+2，观察函数图象可知当﹣2＜x＜0时y＝﹣x2﹣x+2的函数值大于y＝x+2的函数值，∴不等式ax2+（b﹣1）x+c＞2的解集为：﹣2＜x＜0；（3）作PE⊥x轴于点E，交AB于点D，作PQ⊥AB于Q，①如图1，当P在AB上方时，在Rt△OAB中，∵OA＝OB＝2，∴∠OAB＝45°，∴∠PDQ＝∠ADE＝45°，在Rt△PDQ中，∠DPQ＝∠PDQ＝45°，∴PQ＝DQ＝，∴PD＝＝1，设点P（x，﹣x2﹣x+2），则点D（x，x+2），∴PD＝﹣x2﹣x+2﹣（x+2）＝﹣x2﹣2x，即﹣x2﹣2x＝1，解得x＝﹣1，∴此时P点的坐标为（﹣1，2），②如图2，当P点在A点左侧时，同理①可得PD＝1，设点P（x，﹣x2﹣x+2），则点D（x，x+2），∴PD＝（x+2）﹣（﹣x2﹣x+2）＝x2+2x，即x2+2x＝1，解得x＝±﹣1，由图象知此时P点在第三象限，∴x＝﹣﹣1，∴此时P点的坐标为（﹣﹣1，﹣），③如图3，当P点在B点右侧时，在Rt△OAB中，∵OA＝OB＝2，∴∠OAB＝45°，∴∠PDQ＝∠DPQ＝45°，在Rt△PDQ中，∠DPQ＝∠PDQ＝45°，∴PQ＝DQ＝，∴PD＝＝1，设点P（x，﹣x2﹣x+2），则点D（x，x+2），∴PD＝（x+2）﹣（﹣x2﹣x+2）＝x2+2x，即x2+2x＝1，解得x＝±﹣1，由图象知此时P点在第一象限，∴x＝﹣1，∴此时P点的坐标为（﹣1，），综上，P点的坐标为（﹣1，2）或（﹣﹣1，﹣）或（﹣1，）．【例4】（2022•雅安）已知二次函数y＝ax2+bx+c的图象过点A（﹣1，0），B（3，0），且与y轴交于点C （0，﹣3）．（1）求此二次函数的表达式及图象顶点D的坐标；（2）在此抛物线的对称轴上是否存在点E，使△ACE为Rt△，若存在，试求点E的坐标，若不存在，请说明理由；（3）在平面直角坐标系中，存在点P，满足PA⊥PD，求线段PB的最小值．【分析】（1）设二次函数的表达式为交点式，将点C坐标代入，进而求得结果；（2）先把AC，CE，AE的平方求出或表示出来，然后分为∠CAE＝90°，∠ACE＝90°及∠AEC＝90°，然后根据勾股定理逆定理列出方程，解方程，进而求得结果；（3）根据∠APD＝90°确定点P在以AD的中点为圆心，为半径的圆上，进一步求得结果．【解答】解：（1）由题意设二次函数表达式为：y＝a（x+1）•（x﹣3），∴a•（﹣3）＝﹣3，∴a＝1，∴y＝（x+1）•（x﹣3）＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴D（1，﹣4）；（2）存在点E，使△ACE是直角三角形，过程如下：设点E（1，m），∵A（﹣1，0），C（0，﹣3），∴AC2＝10，AE2＝4+m2，CE2＝1+（m+3）2，当∠EAC＝90°时，AE2+AC2＝CE2，∴14+m2＝1+（m+3）2，∴m＝，∴E1（1，），当∠ACE＝90°时，AC2+CE2＝AE2，∴11+（m+3）2＝4+m2，∴m＝﹣，∴E2（1，﹣），当∠AEC＝90°时，AE2+CE2＝AC2，∴5+m2+（m+3）2＝10，∴m＝﹣1或﹣2，∴E3（1，﹣1），E4（1，﹣2），综上所述：点E（1，）或（1，﹣）或（1，﹣1）或（1，﹣2）；（3）设AD的中点为I，∵A（﹣1，0），D（1，﹣4），∴AD＝＝2，I（0，﹣2），∴PA⊥PD，∴∠ADP＝90°，∴点P在以AD的中点I为圆心，为半径的圆上，∵BI＝＝，＝﹣．∴PB最小1．（2020•河北模拟）已知抛物线C：y＝ax2+bx+c（a＞0，c＜0）的对称轴为x＝4，C为顶点，且A（2，0），C（4，﹣2）【问题背景】求出抛物线C的解析式．【尝试探索】如图2，作点C关于x轴的对称点C′，连接BC′，作直线x＝k交BC′于点M，交抛物线C于点N．①连接ND，若四边形MNDC′是平行四边形，求出k的值．②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时，请直接写出线段MN的长度的最大值．【拓展延伸】如图4，作矩形HGOE，且E（﹣3，0），H（﹣3，4），现将其沿x轴以1个单位每秒的速度向右平移，设运动时间为t，得到矩形H′G′O′E′，连接AC′，若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分，请求出t的取值范围．【分析】【问题背景】A（2，0），对称轴为x＝4，则点B（6，0），则抛物线的表达式为：y＝a（x﹣2）（x ﹣6），将点C的坐标代入上式即可求解；【尝试探索】①四边形MNDC′是平行四边形，则MN＝DC′＝2，即|k2﹣4k+6﹣（﹣k+6）|＝2，解得：k＝3或3，②MN＝（﹣k+6）﹣（k2﹣4k+6）＝﹣k2+3k，即可求解；【拓展延伸】（Ⅰ）当t＝2时，矩形过点A，此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分；（Ⅱ）当H′E′与对称轴右侧抛物线有交点时，此时y＝H′E′＝4，即x2﹣4x+6＝4，解得：x＝4（舍去4﹣2），即可求解．【解答】解：【问题背景】A（2，0），对称轴为x＝4，则点B（6，0），则抛物线的表达式为：y＝a（x﹣2）（x﹣6），将点C的坐标代入上式得：﹣2＝a（4﹣2）•（4﹣6），解得：a＝，故抛物线的表达式为：…①；【尝试探索】①点C′（4，2），由点B、C′的坐标可得，直线BC′的表达式为：y＝﹣x+6…②，四边形MNDC′是平行四边形，则MN＝DC′＝2，设点N的坐标为：（x，k2﹣4k+6），则点M（k，﹣k+6），即|k2﹣4k+6﹣（﹣k+6）|＝2，解得：k＝3或3，故k的值为：；②联立①②并解得：x＝0或6，故抛物线C与直线BC′围成的封闭图形对应的k值取值范围为：0≤k≤6，MN＝（﹣k+6）﹣（k2﹣4k+6）＝﹣k2+3k，∵0，故MN有最大值，最大值为；【拓展延伸】由点A、C′的坐标得，直线AC′表达式为：y＝x﹣2…③，联立①③并解得：x＝2或8，即封闭区间对应的x取值范围为：2≤x≤8，（Ⅰ）当t＝2时，矩形过点A，此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分，（Ⅱ）当H′E′与对称轴右侧抛物线有交点时，此时y＝H′E′＝4，即x2﹣4x+6＝4，解得：x＝4（舍去4﹣2），即x＝4+2，则t＝3+4+2＝7+2，故t的取值范围为：2≤t≤．2．（2018秋•宁城县期末）已知，如图，抛物线与x轴交点坐标为A（1，0），C（﹣3，0），（1）如图1，已知顶点坐标D为（﹣1，4）或B点（0，3），选择适当方法求抛物线的解析式；（2）如图2，在抛物线的对称轴DH上求作一点M，使△ABM的周长最小，并求出点M的坐标；（3）如图3，将图2中的对称轴向左移动，交x轴于点P（m，0）（﹣3＜m＜﹣1），与抛物线，线段BC的交点分别为点E、F，用含m的代数式表示线段EF的长度，并求出当m为何值时，线段EF最长．【分析】（1）根据顶点D坐标设其顶点式，再将点C（2）连接BC，交DH于点M，使△ABM周长最小，即AM+BM最小，先求出BC直线解析式，再令x＝﹣1，求得M（﹣1，2）；（3）由题意得出E（m，﹣m2﹣2m+3），F（m，m+3），据此可知EF＝EP﹣FP＝﹣m2﹣2m+3﹣（m+3），再根据二次函数的性质可得答案．【解答】解：（1）由抛物线的顶点D的坐标（﹣1，4）可设其解析式为y＝a（x+1）2+4，将点C（﹣3，0）代入，得：4a+4＝0，解得a＝﹣1，则抛物线解析式为y＝﹣（x+1）2+4＝﹣x2﹣2x+3；（2）连接BC，交DH于点M，此时△ABM的周长最小，当y＝0时，﹣（x+1）2+4＝0，解得x＝﹣3或x＝1，则A（1，0），C（﹣3，0），当x＝0时，y＝3，则B（0，3），设直线BC的解析式为y＝kx+b，将B（0，3），C（﹣3，0）代入得，解得：，∴直线BC解析式为y＝x+3，当x＝﹣1时，y＝﹣1+3＝2，所以点M坐标为（﹣1，2）；（3）由题意知E（m，﹣m2﹣2m+3），F（m，m+3），则EF＝EP﹣FP＝﹣m2﹣2m+3﹣（m+3）＝﹣m2﹣3m＝﹣（m+）2+，∴当m＝﹣时，线段EF最长．3．（2021•桥西区模拟）如图1，抛物线y＝ax2+bx+3与x轴交于A（﹣1，0），B两点，与y轴交于点C，且CO＝BO，连接BC．（1）求抛物线的解析式；（2）如图2，抛物线的顶点为D，其对称轴与线段BC交于点E，求线段DE的长度；（3）如图3，垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，连接CP，CD，抛物线上是否存在点P，使△CDE∽△PCF，如果存在，求出点P的坐标，如果不存在，请说明理由．【分析】（1）根据题意可求得点C，B的坐标，将A，B坐标代入抛物线解析式求出a，b的值，即可得到抛物线解析式；（2）设直线BC的解析式为y＝kx+b，将点C，B的坐标代入求得k，b的值，即可求得直线BC的解析式，再求DE即可；（3）根据△CDE∽△PCF，DE∥PF，可得：＝，设点P坐标为（t，﹣t2+2t+3），点F坐标为（t，﹣t+3），建立关于t的方程求解即可．【解答】解：（1）在抛物线y＝ax2+bx+3中，令x＝0，得y＝3，∴C（0，3），∴CO＝3，∵CO＝BO，∴BO＝3，∴B（3，0），∵A（﹣1，0），∴，解得：，∴抛物线的解析式为：y＝﹣x2+2x+3；（2）设直线BC的解析式为y＝kx+b，∵B（3，0），C（0，3），∴，解得：，∴直线BC的解析式为y＝﹣x+3，∵抛物线y＝﹣x2+2x+3的顶点D坐标为（1，4），∴当x＝1时，y＝﹣1+3＝2，∴E（1，2），∴DE＝2；（3）∵PF∥DE，∴∠CED＝∠CFP，当＝时，△PCF∽△CDE，由D（1，4），C（0，3），E（1，2），利用勾股定理，可得CE＝＝，DE＝4﹣2＝2，设点P坐标为（t，﹣t2+2t+3），点F坐标为（t，﹣t+3），∴PF＝﹣t2+2t+3﹣（﹣t+3）＝﹣t2+3t，CF＝＝t，∴＝，∵t≠0，∴t＝2，当t＝2时，﹣t2+2t+3＝﹣22+2×2+3＝3，∴点P坐标为（2，3）．4．（2022•和平区二模）如图，在平面直角坐标系中，已知抛物线顶点A的坐标为（﹣2，4），且经过坐标原点，与x轴负半轴交于点B．（1）求抛物线的函数表达式并直接写出点B的坐标；（2）过点A作AC⊥x轴于点C，若点D是y轴左侧的抛物线上一个动点（点D与点A不重合），过点D 作DE⊥x轴于点E，连接AO，DO，当以A，O，C为顶点的三角形与以D，O，E为顶点的三角形相似时，求点D的坐标；（3）在（2）的条件下，当点D在第二象限时，在平面内存在一条直线，这条直线与抛物线在第二象限交于点F，在第三象限交于点G，且点A，点B，点D，到直线FG的距离都相等，请直接写出线段FG的长．【分析】（1）设该抛物线解析式为y＝a（x+2）2+4（a≠0），把点（0，0）代入，即可求解；（2）根据题意得OC＝2，AC＝4，设点D（x，﹣x2﹣4x），则DE＝|﹣x2﹣4x|，OE＝﹣x，根据∠ACO＝∠DEO＝90°，可得当以A，O，C为顶点的三角形与以D，O，E为顶点的三角形相似时，∠AOC＝∠ODE 或∠AOC＝∠DOE，分两种讨论，即可求解；（3）求出直线BD的解析式y＝x+14，直线BD与y轴交于（0，14），可得过点A平行于BD的直线AM的解析式为y＝x+11，交y轴于（0，11），可得直线FG的的解析式为y＝x+，联立方程组，得到点F．G的坐标，即可求解．【解答】解：（1）∵抛物线顶点的坐标为（﹣2，4），∴设抛物线解析式为y＝a（x+2）2+4（a≠0），把点（0，0）代入得：0＝a（x+2）2+4．解得：a＝﹣1，∴抛物线解析式为y＝﹣（x+2）2+4＝﹣x2﹣4x．令y﹣0，则﹣x2﹣4x＝0，解得：x1＝﹣4，x2＝0，∴点B（﹣4，0），∴抛物线解析式为y＝﹣x2﹣4x．点B（﹣4，0）；（2）∵AC⊥x轴，点A（﹣2，4），∴点C（﹣2，0），∴OC＝2，AC＝4，∵∠ACO＝∠DEO＝90°，∴当以A，O，C为顶点的三角形与以D，O，E为顶点的三角形相似时，∠AOC＝∠ODE或∠AOC＝∠DOE，设D（x，﹣x2﹣4x），①当∠AOC＝∠ODE时，△AOC∽△ODE，如图：∵∠AOC＝∠ODE，∴tan∠AOC＝tan∠ODE，∴＝＝2，∴＝2，∴﹣x＝2（x2+4x）或﹣x＝﹣2（x2+4x），∴x1＝0（舍去），x2＝﹣或x3＝0（舍去），x4＝﹣，∴点D的坐标为（﹣，﹣）或（﹣，）；②当∠AOC＝∠DOE时，△AOC∽△DOE，如图：∵∠AOC＝∠DOE，∴tan∠AOC＝tan∠DOE，∴＝＝2，∴＝2，∴﹣2x＝x2+4x或2x＝x2+4x，∴x1＝0（舍去），x2＝﹣6或x3＝0（舍去），x4＝﹣2（舍去），∴点D的坐标为（﹣6，﹣12）；点D（﹣6，﹣12）；综上所述，当以A，O，C为顶点的三角形与以D，O，E为顶点的三角形相似时，点D的坐标为（﹣6，﹣12）或（﹣，﹣）或（﹣，）；（3）∵在（2）的条件下，点D在第二象限，∴点D的坐标为（﹣，），直线BD的解析式y＝kx+m，∴，解得，∴直线BD的解析式y＝x+14，直线BD与y轴交于（0，14），∴过点A平行于BD的直线AM的解析式为y＝x+11，交y轴于（0，11），∵点A，点B，点D，到直线FG的距离都相等，∴直线FG的的解析式为y＝x+，联立得，解得，，∴F（﹣，），G（﹣5，﹣5），∴FG＝＝．5．（2022•鹿城区校级二模）如图，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），B（5，0），与y轴交于点C．（1）求抛物线的解析式和顶点D的坐标．（2）连结AD，点E是对称轴与x轴的交点，过E作EF∥AD交抛物线于点F（F在E的右侧），过点F作FG∥x轴交ED于点H，交AD于点G，求HF的长．【分析】（1）把点A（﹣1，0），B（5，0）代入抛物线解析式即可求解；（2）延长FG交y轴于点I，根据A，E，D坐标求出AE＝3，DE＝9，在Rt△EAD中，tan∠EAD＝3，再根据四边形AGFE是平行四边形，得出tan∠EFH＝tan∠EAD＝3，设HF＝m，EH＝3m，易证四边形OIHE是矩形，把点F（m+2，﹣3m）代入y＝x2﹣4x﹣5，求出m即可．【解答】解：（1）把点A（﹣1，0），B（5，0）代入抛物线解析式，得：，解得：，∴y＝x2﹣4x﹣5＝（x﹣2）2﹣9，∴抛物线解析式为y＝x2﹣4x﹣5，顶点D坐标为（2，﹣9）；（2）延长FG交y轴于点I，∵A（﹣1，0），E（2，0），D（2，﹣9），∴AE＝3，DE＝9，∴在Rt△EAD中，，∵EF∥AD，FG∥x轴，∴四边形AGFE是平行四边形，∴tan∠EFH＝tan∠EAD＝3，∴在Rt△EHF中，EH＝3HF，设HF＝m，EH＝3m，易证四边形OIHE是矩形，把点F（m+2，﹣3m）代入y＝x2﹣4x﹣5，得，﹣3m＝（m+2）2﹣4（m+2）﹣5，解得：或m＝（舍去），∴．6．（2021•南岗区模拟）如图，抛物线y＝ax2+bx﹣4交x轴于点A（﹣3，0），B（4，0），交y轴于点C．（1）求抛物线的解析式；（2）点P为第一象限抛物线上一点，过点P作x轴的平行线，与抛物线的另一个交点为点G，连接CG交x轴于点N，设点P的横坐标为t，ON的长为d，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，连接PB，将线段PB绕着点P顺时针旋转90°得到线段PD，点D恰好落在y轴上，点E在线段OB上，连接PE，点Q在EB的延长线上，且EQ＝PE，连接DQ交PE于点F，若PE＝3PF，求QN的长．【分析】（1）运用待定系数法即可得出答案；（2）设P（t，t2﹣t﹣4），则G（1﹣t，t2﹣t﹣4），利用tan∠GCH＝＝，求出CN，即可得出答案；（3）过点P作PT⊥x轴于点T，可证得△PDH≌△PBT（AAS），过点F作x轴的垂线，垂足为K，过点D 作KF的垂线，垂足为R，KR与PH交于点M，再证得△DRF≌△QKF（ASA），过点Q作QW∥PD，可证得△DPF≌△QWF（AAS），过点Q作QZ⊥PE于点Z，再证明△EQZ≌△EPT（AAS），再利用HL证明Rt △QWZ≌Rt△PBT，设EB＝m，运用勾股定理建立方程求解即可．【解答】解：（1）∵抛物线y＝ax2+bx﹣4交x轴于点A（﹣3，0），B（4，0），∴，解得：，∴抛物线的解析式为；（2）如图1，设P（t，t2﹣t﹣4），∵抛物线的对称轴为直线，PG∥x轴，∴点G与点P是抛物线上的一对对称点，∴G（1﹣t，t2﹣t﹣4），设PG与y轴交于点H，则H（0，t2﹣t﹣4），在抛物线中，令x＝0，得y＝﹣4，∴C（0，﹣4），∴OC＝4，又CH＝t2﹣t﹣4﹣（﹣4）＝t2﹣t，GH＝t﹣1，∵tan∠GCH＝＝，∴，解得：，∴d与t之间的函数解析式为d＝；（3）如图2，过点P作PT⊥x轴于点T，∵∠DPB＝∠PHO＝∠HOB＝∠PTO＝∠PHD＝90°，∴四边形PHOT为矩形，∴∠HPT＝90°，∴∠DPH＝∠BPT，∵PD＝PB，∴△PDH≌△PBT（AAS），∴DH＝BT，PH＝PT，∴，解得：t1＝6，t2＝﹣2（舍），∴P（6，6），∴T（6，0），∴DH＝BT＝2，ON＝d＝2，过点F作x轴的垂线，垂足为K，过点D作KF的垂线，垂足为R，KR与PH交于点M，∵PE＝3PF，∴EF＝2PF，∵cos∠PFM＝cos∠EFK，∴，∴FK＝2FM，∵∠MPT＝∠PTK＝∠TKM＝90°，∴四边形PMKT为矩形，∴MK＝PT＝6，∴FM＝2，FK＝4，同理四边形DHMR为矩形，∴DH＝RM＝2，RF＝FK＝4，∠R＝∠FKQ＝90°，∵∠DFR＝∠KFQ，∴△DRF≌△QKF（ASA），∴DF＝QF，过点Q作QW∥PD，∴∠DPF＝∠QWF∵∠DFP＝∠WFQ，DF＝FQ，∴△DPF≌△QWF（AAS），∴DP＝QW＝PB，PF＝WF，∴，过点Q作QZ⊥PE于点Z，∴∠EZQ＝∠PTE＝90°，∵∠PET＝∠QEZ，EP＝EQ，∴△EQZ≌△EPT（AAS），∴PT＝QZ，EZ＝ET，∵QW＝PB，∴Rt△QWZ≌Rt△PBT（HL），∴WZ＝BT，∴EW＝EB．设EB＝m，则EW＝WF＝FP＝m，∴EP＝3m，∵BT＝2，∴ET＝m+2，PT＝6，在Rt△EPT中，∵PE2＝ET2+PT2，∴（3m）2＝（m+2）2+62，解得：，m2＝﹣2（舍），∴，∴BQ＝2BE＝5，∵OB＝4，∴OQ＝9，∵ON＝2，∴QN＝OQ+ON＝11．7．（2021•凉山州模拟）如图1，在平面直角坐标系中，已知B点坐标为（1，0），且OA＝OC＝3OB，抛物线y＝ax2+bx+c（a≠0）图象经过A，B，C三点，其中D点是该抛物线的顶点．（1）求抛物线的解析式；（2）判断△ADC的形状并且求△ADC的面积；（3）如图2，点P是该抛物线第三象限部分上的一个动点，过P点作PE⊥AC于E点，当PE的值最大时，求此时P点的坐标及PE的最大值．【分析】（1）根据B点坐标为（1，0），且OA＝OC＝3OB，得出B，C点的坐标，用待定系数法求解析式即可；（2）根据坐标求出三角形各边的长，利用勾股定理判断其为直角三角形，再用三角形面积公式求面积即可；（3）求出直线AC的解析式，过点P作PH∥y轴交AC于H，设出P点和H点坐标，用含x的代数式求出PE的值，根据二次函数性质求最值即可．【解答】解：（1）∵B点坐标为（1，0），∴OB＝1，又∵OA＝OC＝3OB，∴OA＝OC＝3，∴A（﹣3，0），C（0，﹣3），将A，B，C三点代入解析式得，，解得，∴抛物线的解析式为：y＝x2+2x﹣3；（2）由（1）知抛物线的解析式为y＝x2+2x﹣3，∴对称轴为直线x＝﹣＝﹣1，当x＝﹣1时，y＝（﹣1）2+2×（﹣1）﹣3＝﹣4，∴D点的坐标为（﹣1，﹣4），∴|AD|＝＝2，|AC|＝＝3，|CD|＝＝，∵|AD|2＝|AC|2+|CD|2，∴△ACD是直角三角形，S△ABC＝|AC|•|CD|＝×＝3；（3）设直线AC的解析式为y＝sx+t，代入A，C点坐标，得，解得，∴直线AC的解析式为y＝﹣x﹣3，如右图，过点P作y轴的平行线交AC于点H，∵OA＝OC，∴∠OAC＝∠OCA＝45°，∵PH∥y轴，∴∠PHE＝∠OCA＝45°，设点P（x，x2+2x﹣3），则点H（x，﹣x﹣3），∴PH＝﹣x﹣3﹣（x2+2x﹣3）＝﹣x2﹣3x，∴PE＝PH•sin∠PHE＝（﹣x2﹣3x）×＝﹣（x+）2+，∴当x＝﹣时，PE有最大值为，此时P点的坐标为（﹣，﹣）．8．（2022•无锡二模）已知抛物线y＝mx2﹣2mx+3（m＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB＝3OA．（1）求抛物线的函数表达式；（2）若M、N是第一象限的抛物线上不同的两点，且△BCN的面积总小于△BCM的面积，求点M的坐标；（3）若D为抛物线的顶点，P为第二象限的抛物线上的一点，连接BP、DP，分别交y轴于点E、F，若EF＝OC，求点P的坐标．【分析】（1）设A（x1，0），B（x2，0），因为OB＝3OA，所以x2＝﹣3x1，又由于x1，x2是方程mx2﹣2mx+3＝0的两根，所以x1+x2＝2，从而求出x1的值，得到A点坐标，代入到解析式中，求出m，即可解决问题；（2）由题意可得，只要求得第一象限内M点，使△BCM面积最大，过M作y轴平行线交BC于G点，设M（a，﹣a2+2a+3），先求出直线BC的解析式，可以得到G（a，﹣a+3），从而得的MG＝﹣a2+3a，利用S＝S△MGC+S△MGB，得到S△MBC＝，当a＝时，△MBC面积最大，从而求得M点坐△MBC标；。
中考数学教学指导：求解线段最值问题的常用方法
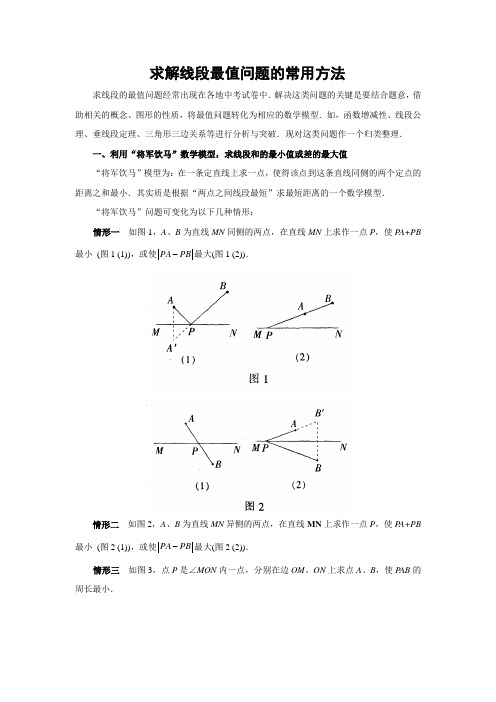
求解线段最值问题的常用方法求线段的最值问题经常出现在各地中考试卷中．解决这类问题的关键是要结合题意，借助相关的概念、图形的性质，将最值问题转化为相应的数学模型．如，函数增减性、线段公理、垂线段定理、三角形三边关系等进行分析与突破．现对这类问题作一个归类整理．一、利用“将军饮马”数学模型，求线段和的最小值或差的最大值“将军饮马”模型为：在一条定直线上求一点，使得该点到这条直线同侧的两个定点的距离之和最小．其实质是根据“两点之间线段最短”求最短距离的一个数学模型．“将军饮马”问题可变化为以下几种情形：情形一如图1，A、B为直线MN同侧的两点，在直线MN上求作一点P，使P A+PB-最大(图1 (2))．最小(图1 (1))，或使PA PB情形二如图2，A、B为直线MN异侧的两点，在直线MN上求作一点P，使P A+PB-最大(图2 (2))．最小(图2 (1))，或使PA PB情形三如图3，点P是∠MON内一点，分别在边OM、ON上求点A、B，使P AB的周长最小．情形四如图4，点P、Q是∠MON内两点，分别在边OM、ON上求点A、B，使四边形P ABQ的周长最小；上述几种情形都利用了轴对称的性质，不妨把情形一、二简称为“两点一线”，情形三为“一点两线”，情形四为“两点两线”．例1如图5，在平面直角坐标系中，Rt△OAB的顶点A在x轴正半轴上．顶点B的坐标为(3，3)，点C的坐标为(12，0．)，点P为斜边OB上的一个动点，则P A+PC的最小值为．例2如图6，已知A (12，y1)，B (2，y2) 为反比例函数y=1x图像上的两点，动点P在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是．例3如图7，在平面直角坐标系中，已知点A (－1，0)，B (4，0)，C (2，－3)，P (3，－2)，当P、C同时向左平移t个单位时得到的对应点分别为P1，C1，则当四边形AB P1C1的周长最小时t的值为．简析例1是“两点一线”(定点A、C和直线OB) 模型，P A+PC的最小值为312．例2延长线段AB交x轴可得P (2．5，0)．例3实际为“两点(点A、B) 一线(过点P平行x轴的直线l ) 一平移(平移距离和方向均为PC)”模型．如图7，过点A作AA1∥PC，AA1=PC，作点A1关于直线l的对称点A2，连结A2B，交直线l于点P1，作P1C1∥PC，P1C1=PC，四边形ABP1C1的周长即为最小，求得t =PP1=0．6．或过点B用类似作法一样可求，此时“一线”应是过点C平行x轴的直线．二、构造三角形求不定线段的最大值若P A、PB是两条定长线段，AB是一条不定的线段，由三角形三边关系PA PB≤AB ≤P A+PB (等号当且仅当P、A、B三点一直线时成立)，求得不定线段AB的最大值或最小值．例4如图8，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB 边上一动点，将△AMN沿MN所在的直线翻折得到△A'MN，连结A'C．则A'C长度的最小值是简析因为A'M=AM，所以A'M、MC为定长线段，当A'、M、C三点共线时，最小值A'C72．例5如图9，△ABC中，∠C=90°，AC=6，BC=3，点A、C分别在x轴、y轴正半轴上．当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，求点B到原点的最大和最小距离．简析取AC中点D，连结BD、OD，则BD、OD为定长线段．当点B在第一象限，且B、O、D三点共线时，最大值BO=3柜+3；当点j5}在第三象限，j!}、D、D三点共线时，最小值BO = 32－3．例6如图10，在△ABC中，AB=3，BC=4，∠ACB=30°，将△ABC绕点B按逆时针方向旋转得到△A1BC1．如图，点E为线段AB中点，点P是线段AC上的动点，在△ABC 绕点B按逆时针方向旋转的过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．简析EB为定长线段，当点P1在A1C1上运动时，BP1的最长距离为BC1= 4，最短距离为垂线段长2．当按E、B、C1顺序并且三点共线时，最长EP1=4 + 1．5 = 5．5；类似地，最短EP1=2－1．5 = 0．5．在上述三个问题中，找到定长的两条线段很重要，需要根据题意，结合图形特征，熟悉图形性质．例如，定圆的半径为定值，斜边一定的直角三角形斜边中线为定值，两平行线间的距离为定值等．要仔细分析，有时需要添加适当的辅助线．三、利用“垂线段最短”求线段的最值“两点之间线段最短”，最短距离为“点点距”，指的是点到点的距离；“垂线段最短”，最短距离为“点线距“，指的是直线外一点到直线的距离．利用“垂线段最短“求线段最值，需要运用动态的观点，结合图形性质，多数情况下要构造直角三角形，利用直角三角形性质 解决问题．例7 如图11，在Rt △AOB 中，OA=OB=32，⊙O 的半径为1，点P 是AB 边上的动点．过点P 作⊙O 的一条切线PQ (点Q 为切点)，则切线PQ 的最小值为 ．简析 由切线性质得PQ =22OP OQ ，OQ 为定值．当OP 最小，即OP 为AB 边上的垂线段时，PQ 最小，最小值PQ =22．例8 如图12，在△ABC 中，AB =10，AC =8，BC =6，经过点C 且与边AB 相切的动圆与CA 、CB 分别相交于点P ，Q ，则线段PQ 长度的最小值是 ．简析 ∠C 是直角，则PQ 为直径．连结CD ，当C D ⊥AB 且CD 成为直径时，最小值PQ=CD =4．8．四、建立函数模型求线段最值一些动态问题的两个变量之间存在着某种函数关系，建立函数关系式，在自变量取值范围内利用函数性质求线段最值．数形结合，把几何问题代数化，以达到快捷解决最值问题的目的．例9 如图13，在△ABC中，AB=AC=10，点D是边BC上一动点(不与B，C重合)，∠ADE=∠B=α，DE交AC于点E，且cos α=45，求CE的最大值．简析先求得BC=16，由△ABD～△DCE，得CEBD=DCAB．设BD=x，CE=(16)10x x，当x=8时，最大值CE=6．4．综上，线段的最值问题需要在动态情形中对图形特殊位置作出深入的探索，既要寻找合适的模型，又要具体问题具体分析，这样才能达到顺利解决问题之目的．。
最全二次函数区间的最值问题(中考数学必考题型)
二次函数的最值问题二次函数的最值问题，是每年中考的必考题，也是考试难点，经常出现在压轴题的位置，解决二次函数的最值问题，特别是含参数的二次函数，一定要考虑二次函数的三个要素：开口方向，对称轴，自变量的取值范围，对于二次函数能够分析出三要素，二次函数的问题就迎刃而解了。
例1.对于二次函数342+-=x x y（1）求它的最小值和最大值.（2）当1≤x ≤4时，求它的最小值和最大值.（3）当-2≤x ≤1时，求它的最小值和最大值.（4）二次函数的最值与哪些因素有关？对于给定的范围，最值可能出现在哪些位置？练习1.二次函数y ＝x 2+2x ﹣5有（ ）A ．最大值﹣5B ．最小值﹣5C ．最大值﹣6D ．最小值﹣6练习2.在二次函数y ＝x 2﹣2x ﹣3中，当0≤x ≤3时，y 的最大值和最小值分别是（ ）A ．0，﹣4B ．0，﹣3C ．﹣3，﹣4D ．0，0练习3若抛物线y ＝﹣x 2+4x +k 的最大值为3，则k ＝ ．练习4（多元消参，利用平方的性质确定自变量的取值范围）若实数a 、b 满足a +b 2＝2，则a 2+5b 2的最小值为 ．练习5如图，P 是抛物线y ＝x 2﹣2x ﹣3在第四象限的一点，过点P 分别向x 轴和y 轴作垂线，垂足分别为A 、B ，求四边形OAPB 周长的最大值及点P 的横坐标练习6．（回归教材）如图，一张正方形纸板的边长为8cm ，将它割去一个正方形，留下四个全等的直角三角形（图中阴影部分）．设AE ＝BF ＝CG ＝DH ＝x （cm ），阴影部分的面积为y （cm 2）．（1）求y 关于x 的函数解析式并写出x 的取值范围；（2）当x 取何值时，阴影部分的面积最大，最大面积是多少．一、对开口方向（二次项前面系数）进行讨论例2.当 41≤≤x 时，二次函数a ax ax y 342+-= 的最大值等于6．求二次项系数a 的值练习1已知二次函数y ＝mx 2+2mx ﹣1（m ＞0）的最小值为﹣5，则m 的值为（ ）A ．﹣4B ．﹣2C ．2D ．4练习2已知二次函数y ＝mx 2+（m 2﹣3）x +1，当x ＝﹣1时，y 取得最大值，则m ＝ ． 练习3已知二次函数y ＝mx 2+2mx +1（m ≠0）在﹣2≤x ≤2时有最小值﹣2，求m 的值二、对二次函数的对称轴的位置进行讨论例3.当 12≤≤x -时，二次函数a ax x y 342+-= 的最小值等于-1．求a 的值．变式1当﹣2≤x ≤1时，二次函数y ＝﹣（x ﹣m ）2+m 2+1有最大值4，求实数m 的值．变式2当﹣1≤x ≤1时，函数y ＝﹣x 2﹣2mx +2n +1的最小值是﹣4，最大值是0，求m 、n 的值．三、对二次函数的x 取值范围进行讨论例4.当 2+≤≤a x a 时，二次函数a x x y 342+-= 的最大值等于-6．求a 的值．练习1.当a ﹣1≤x ≤a 时，函数y ＝x 2﹣2x +1的最小值为1，求a 的值．练习2.若t ≤x ≤t +2时，二次函数y ＝2x 2+4x +1的最大值为31，求t 的值练习3.已知二次函数y ＝﹣x 2+6x ﹣5．当t ≤x ≤t +3时，函数的最大值为m ，最小值为n ，若m ﹣n ＝3，求t 的值．练习4.设a ，b 是任意两个不等实数，我们规定：满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间，表示为[a ，b ]．对于任何一个二次函数，它在给定的闭区间上都有最小值．求函数y ＝x 2﹣4x ﹣4在区间[t ﹣2，t ﹣1]（t 为任意实数）上的最小值y min 的解析式．练习5.若关于x 的函数y ，当t ﹣≤x ≤t +时，函数y 的最大值为M ，最小值为N ，令函数h ＝，我们不妨把函数h 称之为函数y 的“共同体函数”．若函数y ＝﹣x 2+4x +k ，是否存在实数k ，使得函数y 的最大值等于函数y 的“共同体函数“h 的最小值．若存在，求出k 的值；若不存在，请说明理由．拓展：C 2的解析式为：y ＝a （x +2）2﹣3（a ＞0），当a ﹣4≤x ≤a ﹣2时，C 2的最大值与最小值的差为2a ，求a 的值．作业：1.矩形的周长等于40，则此矩形面积的最大值是2.若实数x ，y 满足x +y 2＝3，设s ＝x 2+8y 2，则s 的取值范围是 ．3.已知二次函数y ＝ax 2+4x +a ﹣1的最小值为2，则a 的值为 ．4.已知实数满足x 2+3x ﹣y ﹣3＝0，则x +y 的最小值是 ．5.若二次函数y ＝﹣x 2+mx 在﹣2≤x ≤1时的最大值为5，则m 的值为6.当a ≤x ≤a +1时，函数y ＝x 2﹣2x +1的最小值为1，则a 的值为7.已知二次函数y =122+-ax ax ，当30≤≤x 时，y 的最大值为2，则a 的值为8.如图，在Rt △ABC 中，∠B ＝90°，AB ＝6cm ，BC ＝8cm ，点P 从A 点开始沿AB 边向点B 以1cm /s 的速度移动，点Q 从B 点开始沿BC 边向点C 以2cm /s 的速度移动，则P 、Q 分别从A 、B 同时出发，经过多少秒钟，使△PBQ 的面积最大．9.设a、b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．若二次函数y＝x2﹣x﹣是闭区间[a，b]上的“闭函数”，求实数a，b的值．10．抛物线y＝x2+bx+3的对称轴为直线x＝1．（1）b＝；（2）若关于x的一元二次方程x2+bx+3﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数根，则t的取值范围是．11.已知关于x的二次函数y1＝x2+bx+c（实数b，c为常数）．（1）若二次函数的图象经过点（0，4），对称轴为x＝1，求此二次函数的表达式；（2）若b2﹣c＝0，当b﹣3≤x≤b时，二次函数的最小值为21，求b的值；（3）记关于x的二次函数y2＝2x2+x+m，若在（1）的条件下，当0≤x≤1时，总有y2≥y1，求实数m的最小值．12.已知抛物线y＝﹣2x2+（b﹣2）x+（c﹣2020）（b，c为常数）．（1）若抛物线的顶点坐标为（1，1），求b，c的值；（2）若抛物线上始终存在不重合的两点关于原点对称，求c的取值范围．（3）在（1）的条件下，存在正实数m，n（m＜n），当m≤x≤n时，恰好，求m，n的值．。
中考数学最值问题解题技巧
中考数学最值问题解题技巧
在中考数学中，最值问题是一个常见的难点，通常涉及到几何、代数等多个知识点。
以下是一些常见的解题技巧：
1.特殊位置与极端位置法：考虑特殊位置或极端位置，确定相应
位置时的数值，再进行一般情形下的推证。
2.几何定理法：应用几何中的不等量性质、定理，比如“三边关
系”或“将军饮马”问题。
3.数形结合法：揭示问题中变动元素的代数关系，建立方程或函
数来进行处理。
4.轨迹法：探寻动点轨迹而求最值，往往又会涉及到几何定理法
和数形结合法的运用。
5.找临界的特殊情况：确定最大值和最小值。
6.利用轴对称转化为两点之间的直线段。
7.利用三角形两边之和大于第三边，两边之差小于第三边。
8.利用一点到直线的距离：垂线段最短——将点到直线的折线段
转化为点到直线的垂线段。
9.利用特殊角度（30°，45°，60°）将成倍数的线段转化为首
尾相连的折线段，在转化为两点之间的直线段最短。
中考专题第九讲几何最值及路径长
中考专题第九讲几何最值及路径长第九讲几何最值及路径长预览1.如图，a，b为定点，p为直线l上一点，若点p恰好使ap+bp最短，请画出点p的位置．提示：a① 分析固定点（a，b），移动点（P在直线L上移动）和不变特征lp②以l为对称轴利用轴对称进行转化③ 位置由“两点之间的最短线段”确定2.如图，a，b为定点，mn为直线l上一可以移动的线段，且mn长度固定，若点m恰好使am+mn+bn最短的，请画出M点的位置。
提示：①分析定点（a，b），动点（m，n在l上动，且mn长度固定），不变特征②先平移bn，使平移后的点n与m重合，将其转化为问题1③ 以l为对称轴，用轴对称变换④ 通过“两点之间，最短线段”确定位置3.如图，∠aob=60°，点p在∠aob的平分线上，op=10cm，点e，f分别是∠aob两边oa，ob当△ PEF最小，从点P到EF的距离为① 分析固定点（P）、移动点（e在OA上移动，f在OB上移动）和不变特征② 分别以OA和ob为对称轴，对称通过p得到P1和P2③连接p1p2，由“两点之间，线段最短”确定位置，进而求解p到ef的距离．aPeofbamnlb知识点1.几何极大值问题的处理思路①分析定点、动点，寻找不变特征；② 如果是常见的模型或结构，调用该模型或结构来解决问题；若不属于常见模型，要结合所求目标，根据不变特征转化为基本定理或表达为函数解决问题．转化原则：尽量减少变量，接近固定点、固定线段和固定图形，或者使用相同的变量来表达所需的目标。
基本定理：两点之间，线段最短（已知两个定点）垂线段最短（已知一个定点、一条定直线）三角形三边关系（已知两边的长度是固定的，或和与差是固定的）过圆内一点，最长的弦为直径，最短的弦为垂直于直径的弦常用模型、结构示例：①轴对称最值模型一bapb'lab'pbl求pa+pb的最小值，使点在线异侧b'b求| PA Pb |的最大值，使点位于直线的同一侧a固定长度段Mn在直线L上滑动，以找到am+Mn+BN的最小值。
中考函数压轴--最值问题(19年真题干货)
函数压轴题之最值问题【2019 深圳】如图抛物线经y=ax2+bx+c过点A（-1，0），点C（0，3），且OB=OC ．（1）求抛物线的解析式及其对称轴；（2）点D、E在直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值；（3）点P为抛物线上一点，连接CP，直线CP把四边形APBC面积分为3∶5两部分，求点P的坐标．【2019 陇南】如图，抛物线y=ax2+bx+4交x轴于A（-3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．（1）求此抛物线的表达式；（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？【2019 庆阳】如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．（1）求此抛物线的表达式；（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？【2019 甘肃】如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．（1）求二次函数的解析式；（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．【2019 广州】已知抛物线G ：32y 2--=mx mx 有最低点。
中考数学动点最值问题归纳及解法
中考数学动点最值问题归纳及解法最值问题是初中数学的重要内容，也是一类综合性较强的问题，它贯穿初中数学的始终，是中考的热点问题，它主要考察学生对平时所学的内容综合运用，无论是代数问题还是几何问题都有最值问题，在中考压轴题中出现比较高的主要有利用重要的几何结论（如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等）。
利用一次函数和二次函数的性质求最值。
动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。
）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
“坐标几何题”（动点问题）分析动点个数两个一个两个问题背景特殊菱形两边上移动特殊直角梯形三边上移动抛物线中特殊直角梯形底边上移动考查难点探究相似三角形探究三角形面积函数关系式探究等腰三角形考点①菱形性质②特殊角三角函数③求直线、抛物线解析式④相似三角形⑤不等式①求直线解析式②四边形面积的表示③动三角形面积函数④矩形性质①求抛物线顶点坐标②探究平行四边形③探究动三角形面积是定值④探究等腰三角形存在性特点①菱形是含60°的特殊菱形；△AOB是底角为30°的等腰三角形。
②一个动点速度是参数字母。
③探究相似三角形时，按对应角不同分类讨论；先画图，再探究。
④通过相似三角形过度，转化相似比得出方程。
⑤利用a、t范围，运用不等式求出a、t的值。
①观察图形构造特征适当割补表示面积②动点按到拐点时间分段分类③画出矩形必备条件的图形探究其存在性①直角梯形是特殊的（一底角是45°）②点动带动线动③线动中的特殊性（两个交点D、E是定点；动线段PF长度是定值，PF=OA）④通过相似三角形过度，转化相似比得出方程。
⑤探究等腰三角形时，先画图，再探究（按边相等分类讨论）近几年共同点：①特殊四边形为背景；②点动带线动得出动三角形；③探究动三角形问题（相似、等腰三角形、面积函数关系式）；④求直线、抛物线解析式；⑤探究存在性问题时，先画出图形，再根据图形性质探究答案。
备战2020年中考数学一轮专项复习——动点、最值问题(压轴题)(含详细解答)
备战2020年中考数学一轮专项复习——动点、最值问题（压轴题）1．（2019眉山中考 第26题 11分）如图1，在平面直角坐标系中，抛物线y ＝﹣94x 2+bx+c 经过点A （﹣5，0）和点B （1，0）.（1）求抛物线的解析式及顶点D 的坐标；（2）点P 是抛物线上A 、D 之间的一点，过点P 作PE ⊥x 轴于点E ，PG ⊥y 轴，交抛物线于点G.过点G 作GF ⊥x 轴于点F.当矩形PEFG 的周长最大时，求点P 的横坐标；（3）如图2，连接AD 、BD ，点M 在线段AB 上（不与A 、B 重合），作∠DMN ＝∠DBA , MN 交线段AD 于点N ，是否存在这样点M ，使得△DMN 为等腰三角形？若存在，求出AN 的长；若不存在，请说明理由.x2.（2019绵阳中考第24题）在平面直角坐标系中，将二次函数y=ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA=1，经过点A的一次函数y=kx+b（k≠0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，△ABD的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E在一次函数的图象下方，求△ACE面积的最大值，并求出此时点E的坐标；（3）若点P为x轴上任意一点，在（2）的结论下，求PE+PA的最小值．3.（2019攀枝花中考第24题）在平面直角坐标系xOy中，已知A（0，2），动点P在y=x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．（1）求线段AP长度的取值范围；（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．（3）当△OPQ为等腰三角形时，求点Q的坐标．4.已知抛物线y=-x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C（0，3）．（1）求b，c的值；（2）直线1与x轴相交于点P．①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．5.（2019绵阳中考25题）如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．（1）求证：△DEF是等腰直角三角形；（2）当点H恰好落在线段BC上时，求EH的长；（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．6．（2019资阳中考第24题）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．（1）求此抛物线和直线AB的解析式；（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．7.在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD的内部作正方形EFGH．（1）如图，当AB＝BC＝8时，①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．8.（2019金华中考 第24题 ）如图，在等腰Rt △ABC 中，∠ACB =90°，AB =142点D ，E 分别在边AB ，BC 上，将线段ED 绕点E 按逆时针方向旋转90°得到EF .（1）如图1，若AD=BD ，点E 与点C 重合，AF 与DC 相交于点O ,求证：BD=2DO .（2）已知点G 为AF 的中点.①如图2，若AD=BD ，CE =2，求DG 的长.②若AD =6BD ,是否存在点E ,使得△DEG 是直角三角形？若存在，求CE 的长；若不存在，试说明理由.图1 图2 图3DA(E )BC FFGDAE BCFG DAEBCO9.（2019资阳中考第24题13分）如图，抛物线y＝﹣x2+bx+c过点A（3，2），且与直线y＝﹣x+交于B、C两点，点B的坐标为（4，m）．（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM＝45°？若存在，求点Q的坐标；若不存在，请说明理由．参考答案1．（2019眉山中考 第26题 11分）如图1，在平面直角坐标系中，抛物线y ＝﹣94x 2+bx+c 经过点A （﹣5，0）和点B （1，0）.（1）求抛物线的解析式及顶点D 的坐标；（2）点P 是抛物线上A 、D 之间的一点，过点P 作PE ⊥x 轴于点E ，PG ⊥y 轴，交抛物线于点G.过点G 作GF ⊥x 轴于点F.当矩形PEFG 的周长最大时，求点P 的横坐标；（3）如图2，连接AD 、BD ，点M 在线段AB 上（不与A 、B 重合），作∠DMN ＝∠DBA , MN 交线段AD 于点N ，是否存在这样点M ，使得△DMN 为等腰三角形？若存在，求出AN 的长；若不存在，请说明理由.【解析】（1）抛物线的解析式为：y ＝﹣94(x +5）(x ﹣1) ＝﹣94x 2﹣916x+920 ………………2分 配方得：y ＝﹣94（x+2）2+4 ，∴顶点D 的坐标为（﹣2，4）. ………………………………3分 （2）设点P 的坐标为（a ，﹣94a 2﹣916a+920）, 则PE ＝﹣94a 2﹣916a+920，PG ＝2(﹣2﹣a )＝﹣4﹣2a. ………………………………4分 ∴矩形PEFG 的周长＝2(PE+PG)＝2(﹣94a 2﹣916a+920﹣4﹣2a)＝﹣98a 2﹣968a ﹣932 ＝﹣98(a +417)2+18225 ……………………………6分 ∵﹣98＜0, ∴当a ＝﹣417时，矩形PEFG 的周长最大， 此时，点P 的横坐标为﹣417.…………………… ………7分 （3）存在.∵AD ＝BD ， ∴∠DAB ＝∠DBA.∵∠AMN+∠DMN ＝∠MDB+∠DBA,又∵∠DMN ＝∠DBA, ∴∠AMN ＝∠MDB,∴△AMN ∽△BDM,∴MB AN ＝DBAM ………………………………………………………8分 易求得：AB ＝6，AD ＝DB ＝5. △DMN 为等腰三角形有三种可能：①当MN ＝DM 时，则△AMN ≌△BDM,∴AM ＝BD ＝5, ∴AN ＝MB ＝1; ………………………………………………………9分②当DN ＝MN 时，则∠ADM ＝∠DMN ＝∠DBA,又∵∠DAM ＝∠BAD, ∴△DAM ∽△BAD,∴AD 2＝AM •BA.∴AM ＝625, BM ＝6﹣625＝611, ∵MB AN ＝DBAM , ∴ 611AN ＝5625, ∴AN ＝3655. ………………………………………………………………10分 ③DN ＝DM 不成立.∵∠DNM ＞∠DAB, 而∠DAB ＝∠DMN ，∴∠DNM ＞∠DMN ，∴DN ≠DM.综上所述，存在点M 满足要求，此时AN 的长为1或3655.………………………………………11分2.（2019绵阳中考 第24题）在平面直角坐标系中，将二次函数y =ax 2（a ＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x 轴交于点A 、B （点A 在点B 的左侧），OA =1，经过点A 的一次函数y =kx +b （k ≠0）的图象与y 轴正半轴交于点C ，且与抛物线的另一个交点为D ，△ABD 的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E 在一次函数的图象下方，求△ACE 面积的最大值，并求出此时点E 的坐标； （3）若点P 为x 轴上任意一点，在（2）的结论下，求PE +PA 的最小值．【解析】（1）将二次函数y =ax 2（a ＞0）的图象向右平移1个单位，再向下平移2个单位，得到的抛物线解析式为y =a （x -1）2-2，∵OA =1，∴点A 的坐标为（-1，0），代入抛物线的解析式得，4a -2=0，∴，∴抛物线的解析式为y =，即y =．令y =0，解得x 1=-1，x 2=3，∴B （3，0），∴AB =OA +OB =4，∵△ABD 的面积为5，∴=5，∴y D=，代入抛物线解析式得，，解得x1=-2，x2=4，∴D（4，），设直线AD的解析式为y=kx+b，∴，解得：，∴直线AD的解析式为y=．（2）过点E作EM∥y轴交AD于M，如图，设E（a，），则M（a，），∴=，∴S△ACE=S△AME-S△CME===，=，∴当a=时，△ACE的面积有最大值，最大值是，此时E点坐标为（）．（3）作E关于x轴的对称点F，连接EF交x轴于点G，过点F作FH⊥AE于点H，交轴于点P，∵E（），OA=1，∴AG=1+=，EG=，∴，∵∠AGE=∠AHP=90°∴sin，∴，∵E、F关于x轴对称，∴PE=PF，∴PE+AP=FP+HP=FH，此时FH最小，∵EF=，∠AEG=∠HEF，∴=，∴．∴PE+PA的最小值是3．3.（2019攀枝花中考第24题）在平面直角坐标系xOy中，已知A（0，2），动点P在y=x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．（1）求线段AP长度的取值范围；（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．（3）当△OPQ为等腰三角形时，求点Q的坐标．【解析】（1）由y=x知：∠POQ=30°，当AP⊥OP时，AP取得最小值=OA•sin∠AOP=2sin60°=；（2）过点P作PH⊥x轴于点H、交过点A平行于x轴的直线与点G，∴∠APQ=90°，∴∠AGP+∠APG=90°，∠APG+∠QPH=90°，∴∠QPH=∠PAG，∴△PAG∽△QPH，∴tan∠PAQ====，则∠QAP=30°；（3）设：OQ=m，则AQ2=m2+4=4PQ2，①当OQ=PQ时，即PQ=OQ=m，则m2+4=4m2，解得：m=；②当PO=OQ时，同理可得：m=±（4+4）；③当PQ=OP时，同理可得：m=；故点Q的坐标为（，0）或（-，0）或（4+4，0）或（-4-4，0）或（2，0）或（-2，0）．6.已知抛物线y=-x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C（0，3）．（1）求b，c的值；（2）直线1与x轴相交于点P．①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．【解析】（1）由题意得：，∴b=2，c=3，（2）①如图1，∵点C关于直线x=1的对称点为点D，∴CD∥OA，∴3=-x2+2x+3，解得：x1=0，x2=2，∴D（2，3），∵抛物线的解析式为y=-x2+2x+3，∴令y=0，解得x1=-1，x2=3，∴B（-1，0），A（3，0），设直线AC的解析式为y=kx+b，∴，解得：，∴直线AC的解析式为y=-x+3，设F（a，-a2+2a+3），E（a，-a+3），∴EF=-a2+2a+3+a-3=-a2+3a，四边形CEDF的面积=S△EFC+S△EFD===-a2+3a=，∴当a=时，四边形CEDF的面积有最大值，最大值为．②当△PCQ∽△CAP时，∴∠PCA=∠CPQ，∠PAC=∠PCQ，∴PQ∥AC，∵C（0，3），A（3，0），∴OA=OC，∴∠OCA=∠OAC=∠PCQ=45°，∴∠BCO=∠PCA，如图2，过点P作PM⊥AC交AC于点M，∴，设PM=b，则CM=3b，AM=b，∵，∴，∴，∴，∴，∴，设直线l的解析式为y=-x+n，∴，∴．∴直线l的解析式为y=-x+．5.（2019绵阳中考25题）如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．（1）求证：△DEF是等腰直角三角形；（2）当点H恰好落在线段BC上时，求EH的长；（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．【解析】（1）证明：∵四边形ABCD是正方形，∴∠DAC=∠CAB=45°，∴∠FDE=∠CAB，∠DFE=∠DAC，∴∠FDE=∠DFE=45°，∴∠DEF=90°，∴△DEF是等腰直角三角形；（2）设OE=t，连接OD，∴∠DOE=∠DAF=90°，∵∠OED=∠DFA，∴△DOE∽△DAF，∴，∴t，又∵∠AEF=∠ADG，∠EAF=∠DAG，∴△AEF∽△ADG，∴，∴，又∵AE=OA+OE=2+t，∴，∴EG=AE-AG=，当点H恰好落在线段BC上∠DFH=∠DFE+∠HFE=45°+45°=90°，∴△ADF∽△BFH，∴，∵AF∥CD，∴，∴，∴，解得：t1=，t2=（舍去），∴EG=EH=；（3）过点F作FK⊥AC于点K，由（2）得EG=，∵DE=EF，∠DEF=90°，∴∠DEO=∠EFK，∴△DOE≌△EKF（AAS），∴FK=OE=t，∴S=．6．（2019资阳中考第24题）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b 都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．（1）求此抛物线和直线AB的解析式；（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．【解析】（1）∵抛物线y＝ax2﹣2x+c经过A（0，﹣3）、B（3，0）两点，∴，∴，∴抛物线的解析式为y＝x2﹣2x﹣3，∵直线y＝kx+b经过A（0，﹣3）、B（3，0）两点，∴，解得：，∴直线AB的解析式为y＝x﹣3，（2）∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点C的坐标为（1，﹣4），∵CE∥y轴，∴E（1，﹣2），∴CE＝2，①如图，若点M在x轴下方，四边形CEMN为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a﹣3﹣（a2﹣2a﹣3）＝﹣a2+3a，∴﹣a2+3a＝2，解得：a＝2，a＝1（舍去），∴M（2，﹣1），②如图，若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a2﹣2a﹣3﹣（a﹣3）＝a2﹣3a，∴a2﹣3a＝2，解得：a＝，a＝（舍去），∴M（，），综合可得M点的坐标为（2，﹣1）或（）．（3）如图，作PG∥y轴交直线AB于点G，设P（m，m2﹣2m﹣3），则G（m，m﹣3），∴PG＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，∴S△PAB＝S△PGA+S△PGB＝＝＝﹣，∴当m＝时，△PAB面积的最大值是，此时P点坐标为（）．8.在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD的内部作正方形EFGH．（1）如图，当AB＝BC＝8时，①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．【解答】解：（1）①如图1中，∵四边形EFGH是正方形，AB＝BC，∴BE＝BG，AE＝CG，∠BHE＝∠BGH＝90°，∴∠AEH＝∠CGH＝90°，∵EH＝HG，∴△AEH≌△CGH（SAS），∴AH＝CH．②如图1中，当0＜t≤4时，重叠部分是正方形EFGH，S＝t2．如图2中，当4＜t≤8时，重叠部分是五边形EFGMN，S＝S△ABC﹣S△AEN﹣S△CGM＝×8×8﹣2×（8﹣t）2＝﹣t2+32t﹣32．综上所述，S＝．（2）如图3﹣1中，延长AH交BC于M，当BM＝CM＝4时，直线AH将矩形ABCD的面积分成1：3两部分．∵EH∥BM，∴＝，∴＝，∴t＝．如图3﹣2中，延长AH交CD于M交BC的延长线于K，当CM＝DM＝3时，直线AH将矩形ABCD的面积分成1：3两部分，易证AD＝CK＝8，∵EH∥BK，∴＝，∴＝，∴t＝．如图3﹣3中，当点E在线段AC上时，延长AH交CD于M，交BC的延长线于N．当CM＝DM时，直线AH 将矩形ABCD的面积分成1：3两部分，易证AD＝CN＝8．在Rt △ABC 中，AC ＝＝10，∵EF ∥AB ，∴＝，∴＝，∴EF ＝（16﹣t ），∵EH ∥CN ，∴＝，∴＝，解得t ＝．综上所述，满足条件的t 的值为s 或s 或s ．8.（2019金华中考 第24题 ）如图，在等腰Rt △ABC 中，∠ACB =90°，AB =142点D ，E 分别在边AB ，BC 上，将线段ED 绕点E 按逆时针方向旋转90°得到EF .（1）如图1，若AD=BD ，点E 与点C 重合，AF 与DC 相交于点O ,求证：BD=2DO .（2）已知点G 为AF 的中点.①如图2，若AD=BD ，CE =2，求DG 的长.②若AD =6BD ,是否存在点E ,使得△DEG 是直角三角形？若存在，求CE 的长；若不存在，试说明理由.图1 图2 图3DA(E )BC FFGDA E BCFG DAEBC(第24题)O【解析】（1）由旋转性质得：CD =CF ，∠DCF =90°.∵△ABC 是等腰直角三角形，AD =BD . ∴∠ADO =90°，CD =BD =AD , ∴∠DCF =∠ADC . 在△ADO 和△FCO 中，ADO FCO AOD FOC AD FC =⎧⎪=⎨⎪=⎩∠∠，∠∠，， ∴△ADO ≌△FCO . ∴DO =CO . ∴BD =CD =2OD .（2）①如图1,分别过点D ,F 作DN ⊥BC 于点N ,FM ⊥BC 于点M ,连结BF .∴∠DNE =∠EMF =90°. 又∵∠NDE =∠MEF ,DE =EF ,∴△DNE ≌△EMF , ∴DN =EM . 又∵BD=∠ABC =45°,∴DN =EM =7, ∴BM=BC －ME －EC=5,∴MF=NE= NC －EC=5. ∴BF= ∵点D ,G 分别是AB,AF 的中点, ∴DG =12BF②过点D 作DH ⊥BC 于点H .∵AD =6BD ，AB=BD=ⅰ）当∠DEG =90°时，有如图2，3两种情况，设CE=t .∵∠DEF=90°，∠DEG=90°，G FDCABE N M 图1∴点E 在线段AF 上.∴BH=DH =2,BE =14－t ，HE=BE －BH=12－t.∵△DHE ∽△ECA ，∴=DH HE EC CA ，即212=14tt -，解得6t =±∴6CE =+6CE =-ⅱ） 当DG ∥BC 时，如图4.过点F 作FK ⊥BC 于点K ,延长DG 交AC 于点N ，延长AC 并截取MN=NA .连结 FM .则NC=DH =2,MC =10. 设GN=t,则FM =2t,BK=14－2t.∵△DHE ≌△EKF ， ∴KE=DH =2,KF=HE =14－2t, ∵MC=FK , ∴14－2t=10, 得t =2. ∵GN=EC =2, GN ∥EC ， ∴四边形GECN 是平行四边形. 而∠ACB =90°，∴四边形GECN 是矩形，∴∠EGN =90°.∴当EC =2时，有∠DGE =90°.图2 图3 图4FGD AEB CHFG D AE B CHFGD AE B CHN MKⅲ）当∠EDG =90°时，如图5.过点G ，F 分别作AC 的垂线，交射线AC 于点N , M ，过点E 作EK ⊥FM 于点K ，过点D 作GN 的垂线，交NG 的延长线于点P .则PN =HC =BC -HB =12, 设GN =t ，则FM =2t ，∴PG =PN -GN =12-t . 由△DHE ≌△EKF 可得：FK =2， ∴CE =KM =2t -2，∴HE =HC -CE =12-(2t -2)=14-2t ， ∴EK =HE =14-2t ,AM =AC +CM =AC +EK =14+14-2t =28-2t ，∴MN =12AM =14-t ，NC =MN -CM =t ， ∴PD =t -2，由△GPD ∽△DHE 可得：=PG PD HD HE ，即122=2142t t t---， 解得11014t =-，21014t =+（舍去）.∴CE=2t-2=18214-. 所以，CE 的长为：622-,622+,2或18214-.9．（2019资阳中考 第24题13分）如图，抛物线y ＝﹣x 2+bx +c 过点A （3，2），且与直线y ＝﹣x +交于B 、C 两点，点B 的坐标为（4，m ）．F GD AE B CH NMKP图5（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM＝45°？若存在，求点Q的坐标；若不存在，请说明理由．【解答】解：（1）将点B的坐标为（4，m）代入y＝﹣x+，m＝﹣4+＝﹣，∴B的坐标为（4，﹣），将A（3，2），B（4，﹣）代入y＝﹣x2+bx+c，解得b＝1，c＝，∴抛物线的解析式y＝；（2）设D（m，），则E（m，﹣m+），DE＝（）﹣（﹣m+）＝＝﹣（m﹣2）2+2，∴当m＝2时，DE有最大值为2，此时D（2，），作点A关于对称轴的对称点A'，连接A'D，与对称轴交于点P．PD+PA＝PD+PA'＝A'D，此时PD+PA最小，∵A（3，2），∴A'（﹣1，2），A'D＝＝，即PD+PA的最小值为；（3）作AH⊥y轴于点H，连接AM、AQ、MQ、HA、HQ，∵抛物线的解析式y＝，∴M（1，4），∵A（3，2），∴AH＝MH＝2，H（1，2）∵∠AQM＝45°，∠AHM＝90°，∴∠AQM＝∠AHM，可知△AQM外接圆的圆心为H，∴QH＝HA＝HM＝2设Q（0，t），则＝2，t＝2+或2﹣∴符合题意的点Q的坐标：Q1（0，2﹣）、Q2（0，2）．。
《2020年中考数学保A必刷压轴题(湖南长沙专版)》(二)：最值问题专题(解析版)
《2020年中考数学保A必刷压轴题(湖南长沙专版)》（二）最值问题专题1.（2019•十堰）如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝6．解：作DH⊥AE于H，如图，∵AF＝4，当△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，在Rt△ABF中，BF＝＝3，∵∠EAF＝90°，∴∠BAF+∠BAH＝90°，∵∠DAH+∠BAH＝90°，∴∠DAH＝∠BAF，在△ADH和△ABF中，∴△ADH≌△ABF（AAS），∴DH＝BF＝3，∴S△ADE＝AE•DH＝×3×4＝6．故答案为6．2.（2019•黄冈）如图，AC，BD在AB的同侧，AC＝2，BD＝8，AB＝8，点M为AB的中点，若∠CMD＝120°，则CD的最大值是．解：如图，作点A关于CM的对称点A′，点B关于DM的对称点B′．∵∠CMD＝120°，∴∠AMC+∠DMB＝60°，∴∠CMA′+∠DMB′＝60°，∴∠A′MB′＝60°，∵MA′＝MB′，∴△A′MB′为等边三角形∵CD≤CA′+A′B′+B′D＝CA+AM+BD＝2+4+8＝14，∴CD的最大值为14，故答案为14．3.（2019•南京）在△ABC中，AB＝4，∠C＝60°，∠A＞∠B，则BC的长的取值范围是4＜BC≤．解：作△ABC的外接圆，如图所示：∵∠BAC＞∠ABC，AB＝4，当∠BAC＝90°时，BC是直径最长，∵∠C＝60°，∴∠ABC＝30°，∴BC＝2AC，AB＝AC＝4，∴AC＝，∴BC＝；当∠BAC＝∠ABC时，△ABC是等边三角形，BC＝AC＝AB＝4，∵∠BAC＞∠ABC，∴BC长的取值范围是4＜BC≤；故答案为：4＜BC≤．4.（2019•连云港）如图，在矩形ABCD 中，AB ＝4，AD ＝3，以点C 为圆心作⊙C 与直线BD 相切，点P 是⊙C 上一个动点，连接AP 交BD 于点T ，则的最大值是 3 ．方法1、解：设C 的半径为R ，如图，作BD 的平行线P E '，使P E '切C 于P '，则PE 与BD 的最大距离为2R ，BD 与C 相切，∴点C 到BD 的距离为R ，∴四边形ABCD 是矩形，∴点A 到BD 的距离为R ，∴点A 到PE 的最大距离为3R ，∴AP AT 的最大值为33R R=； 方法2、解：如图，过点A 作AG BD ⊥于G ，BD 是矩形的对角线，90BAD ∴∠=︒，5BD ∴==，1122AB AD BD AG =， 125AG ∴=，BD 是C 的切线，C ∴的半径为125过点P 作PE BD ⊥于E ，AGT PET ∴∠=∠，ATG PTE ∠=∠，AGT PET ∴∆∆∽， ∴AG AT PE PT=， ∴512PT PE AT =⨯ 1AP AT PT PTAT AT AT+==+， 要AP AT最大，则PE 最大， 点P 是C 上的动点，BD 是C 的切线，PE ∴最大为C 的直径，即：245PE =最大， ∴AP AT 最大值为8134+=， 故答案为3．方法3、解：如图，过点P 作//PE BD 交AB 的延长线于E ，AEP ABD ∴∠=∠，APE ATB ∆∆∽， ∴AP AE AT AB=， 4AB =，4AE AB BE BE ∴=+=+， ∴14AP BE AT =+， BE ∴最大时，AP AT最大， 四边形ABCD 是矩形，3BC AD ∴==，4CD AB ==，过点C 作CH BD ⊥于H ，交PE 于M ，并延长交AB 于G ， BD 是C 的切线，90GME ∴∠=︒，在Rt BCD ∆中，5BD ，90BHC BCD ∠=∠=︒，CBH DBC ∠=∠，BHC BCD ∴∆∆∽， ∴BH CH BC BC DC BD==， ∴3345BH CH ==， 95BH ∴=，125CH =， 90BHG BAD ∠=∠=︒，GBH DBA ∠=∠，BHG BAD ∴∆∆∽， ∴HG BG BH AD BD AB==， ∴95354HG BG ==，2720HG ∴=，94BG =， 在Rt GME ∆中，33sin 55GM EG AEP EG EG =∠=⨯=， 而94BE GE BG GE =-=-， GE ∴最大时，BE 最大，GM ∴最大时，BE 最大，2720GM HG HM HM =+=+， 即：HM 最大时，BE 最大，延长MC 交C 于P '，此时，HM 最大2425HP CH '===， 1234GP HP HG ''∴=+=， 过点P '作//P F BD '交AB 的延长线于F ，BE ∴最大时，点E 落在点F 处，即：BE 最大BF =，在Rt △GP F '中，1234143sin sin 45GP GP FG F ABD ''====∠∠， 8BF FG BG ∴=-=， ∴AP AT 最大值为8134+=， 故答案为：3．5.（2019•镇江）已知抛物线y＝ax2+4ax+4a+1（a≠0）过点A（m，3），B（n，3）两点，若线段AB的长不大于4，则代数式a2+a+1的最小值是．解：∵抛物线y＝ax2+4ax+4a+1（a≠0）过点A（m，3），B（n，3）两点，∴＝﹣＝﹣2∵线段AB的长不大于4，∴4a+1≥3∴a≥∴a2+a+1的最小值为：（）2++1＝；故答案为．6.（2019•潍坊）如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△P AB的周长最小时，S△P AB＝．解：，解得，或，∴点A的坐标为（1，2），点B的坐标为（4，5），∴AB＝＝3，作点A关于y轴的对称点A′，连接A′B与y轴的交于P，则此时△P AB的周长最小，点A′的坐标为（﹣1，2），点B的坐标为（4，5），设直线A′B的函数解析式为y＝kx+b，，得，∴直线A′B的函数解析式为y＝x+，当x＝0时，y＝，即点P的坐标为（0，），将x＝0代入直线y＝x+1中，得y＝1，∵直线y＝x+1与y轴的夹角是45°，∴点P到直线AB的距离是：（﹣1）×sin45°＝＝，∴△P AB的面积是：＝，故答案为：．7.（2019•泰安）如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2B．4C．D．解：如图：当点F与点C重合时，点P在P1处，CP1＝DP1，当点F与点E重合时，点P在P2处，EP2＝DP2，∴P1P2∥CE且P1P2＝CE当点F在EC上除点C、E的位置处时，有DP＝FP由中位线定理可知：P1P∥CE且P1P＝CF∴点P的运动轨迹是线段P1P2，∴当BP⊥P1P2时，PB取得最小值∵矩形ABCD中，AB＝4，AD＝2，E为AB的中点，∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝2∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°∴∠DP2P1＝90°∴∠DP1P2＝45°∴∠P2P1B＝90°，即BP1⊥P1P2，∴BP的最小值为BP1的长在等腰直角BCP1中，CP1＝BC＝2∴BP1＝2∴PB的最小值是2故选：D．8.（2019•东营）如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点B出发，沿表面爬到AC的中点D处，则最短路线长为（）A．3B．C．3D．3解：如图将圆锥侧面展开，得到扇形ABB′，则线段BF为所求的最短路程．设∠BAB′＝n°．∵＝4π，∴n＝120即∠BAB′＝120°．∵E为弧BB′中点，∴∠AFB＝90°，∠BAF＝60°，∴BF＝AB•sin∠BAF＝6×＝3，∴最短路线长为3．故选：D．9.（2019•自贡）如图，已知A、B两点的坐标分别为（8，0）、（0，8），点C、F分别是直线x＝﹣5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，tan∠BAD的值是（）A．B．C．D．解：如图，设直线x＝﹣5交x轴于K．由题意KD＝CF＝5，∴点D的运动轨迹是以K为圆心，5为半径的圆，∴当直线AD与⊙K相切时，△ABE的面积最小，∵AD是切线，点D是切点，∴AD⊥KD，∵AK＝13，DK＝5，∴AD＝12，∵tan∠EAO＝＝，∴＝，∴OE＝，∴AE＝＝，作EH ⊥AB 于H ．∵S △ABE ＝•AB •EH ＝S △AOB ﹣S △AOE ，∴EH ＝，∴AH ＝＝，∴tan ∠BAD ＝＝＝，故选：B ．10.（2019•台州）如图，直线l 1∥l 2∥l 3，A ，B ，C 分别为直线l 1，l 2，l 3上的动点，连接AB ，BC ，AC ，线段AC 交直线l 2于点D ．设直线l 1，l 2之间的距离为m ，直线l 2，l 3之间的距离为n ，若∠ABC ＝90°，BD ＝4，且＝，则m +n 的最大值为 ．解：过B 作1BE l ⊥于E ，延长EB 交3l 于F ，过A 作2AN l ⊥于N ，过C 作2CM l ⊥于M ， 设AE x =，CF y =，BN x =，BM y =，4BD =，4DM y ∴=-，4DN x =-，90ABC AEB BFC CMD AND ∠=∠=∠=∠=∠=︒，90EAB ABE ABE CBF ∴∠+∠=∠+∠=︒，EAB CBF ∴∠=∠，ABE BFC∴∆∆∽，∴AE BEBF CF=，即x mn y=，xy mn∴=，ADN CDM∠=∠，CMD AND∴∆∆∽，∴AN DNCM DM=，即4243m xn y-==-，3102y x∴=-+，23mn=，32n m∴=，5()2m n m∴+=最大，∴当m最大时，5()2m n m+=最大，22333(10)10222mn xy x x x x m ==-+=-+=，∴当1010332()2x=-=⨯-时，250332mn m==最大，103m∴=最大，m n∴+的最大值为51025233⨯=．故答案为：253．。
中考压轴题突破：几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)
中考压轴题突破：几何最值问题大全（将军饮马、造桥选址、胡不归、阿波罗尼斯圆等）一、基本图形所有问题的老祖宗只有两个：①[定点到定点]：两点之间，线段最短；②[定点到定线]：点线之间，垂线段最短。
由此派生：③[定点到定点]：三角形两边之和大于第三边；④[定线到定线]：平行线之间，垂线段最短；⑤[定点到定圆]：点圆之间，点心线截距最短（长）；⑥[定线到定圆]：线圆之间，心垂线截距最短；⑦[定圆到定圆]：圆圆之间，连心线截距最短（长）。
余不赘述，下面仅举一例证明：[定点到定圆]：点圆之间，点心线截距最短（长）。
已知⊙O半径为r，AO=d，P是⊙O上一点，求AP的最大值和最小值。
证明：由“两点之间，线段最短”得AP≤AO+PO，AO≤AP+PO，得d-r≤AP≤d+r，AP最小时点P在B处，最大时点P在C处。
即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。
(可用“三角形两边之和大于第三边”，其实质也是由“两点之间，线段最短”推得）。
上面几种是解决相关问题的基本图形，所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式，如圆与线这些图形不是直接给出，而是以符合一定条件的动点的形式确定的；再如过定点的直线与动点所在路径不相交而需要进行变换的。
类型分三种情况：（1）直接包含基本图形；（2）动点路径待确定；（3）动线（定点）位置需变换。
（一）直接包含基本图形例 1.在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是。
（二）动点路径待确定例2.，如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B 重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是。
（三）动线（定点）位置需变换线段变换的方法：（1）等值变换：翻折、平移；（2）比例变换：三角、相似。
中考压轴题突破：几何最值问题(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)
中考压轴题突破：几何最值问题大全（将军饮马、造桥选址、胡不归、阿波罗尼斯圆等）一、基本图形所有问题的老祖宗只有两个：①[定点到定点]：两点之间，线段最短；②[定点到定线]：点线之间，垂线段最短。
由此派生：③[定点到定点]：三角形两边之和大于第三边；④[定线到定线]：平行线之间，垂线段最短；⑤[定点到定圆]：点圆之间，点心线截距最短（长）；⑥[定线到定圆]：线圆之间，心垂线截距最短；⑦[定圆到定圆]：圆圆之间，连心线截距最短（长）。
余不赘述，下面仅举一例证明：[定点到定圆]：点圆之间，点心线截距最短（长）。
已知⊙O半径为r，AO=d，P是⊙O上一点，求AP的最大值和最小值。
证明：由“两点之间，线段最短”得AP≤AO+PO，AO≤AP+PO，得d-r≤AP ≤d+r，AP最小时点P在B处，最大时点P在C处。
即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。
(可用“三角形两边之和大于第三边”，其实质也是由“两点之间，线段最短”推得）。
上面几种是解决相关问题的基本图形，所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式，如圆与线这些图形不是直接给出，而是以符合一定条件的动点的形式确定的；再如过定点的直线与动点所在路径不相交而需要进行变换的。
类型分三种情况：（1）直接包含基本图形；（2）动点路径待确定；（3）动线（定点）位置需变换。
（一）直接包含基本图形例1.在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是。
简析：由∠B=30°知弧AD一定，所以D是定点，C是直线AC上的动点，即为求定点D到定线AC的最短路径，求得当CD⊥AC时最短为3。
（二）动点路径待确定例2.，如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是。
2021年中考数学必刷压轴题专题：抛物线之最值问题(含解析)-个人用心整理
中考数学抛物线压轴题之最值问题1．如图，在平面直角坐标系xOy中，抛物线y＝ax2+x+c与x轴交于A，B两点（点A在点B的左侧），交y轴于点C，经过B，C两点的直线为y＝．（1）求抛物线的函数表达式；（2）点P为抛物线上的动点，过点P作x轴的垂线，交直线BC于点M，连接PC，若△PCM为直角三角形，求点P的坐标；（3）当P满足（2）的条件，且点P在直线BC上方的抛物线上时，如图2，将抛物线沿射线BC方向平移，平移后B，P两点的对应点分别为B′，P′，取AB的中点E，连接EB′，EP′，试探究EB'+EP'是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．2．如图，抛物线y＝ax2+bx+c与x轴相交于A（3，0）、B两点，与y轴交于点C（0，3），点B在x轴的负半轴上，且OA＝3OB．（1）求抛物线的函数关系式；（2）若P是抛物线上且位于直线AC上方的一动点，求△ACP的面积的最大值及此时点P的坐标；（3）在线段OC上是否存在一点M，使BM+CM的值最小？若存在，请求出这个最小值及对应的M点的坐标；若不存在，请说明理由．3．在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A、B，C，已知A（﹣1，0），C（0，3）．（1）求抛物线的解析式；（2）如图1，P为线段BC上一动点，过点P作y轴的平行线，交抛物线于点D，是否存在这样的P点，使线段PD的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；（3）如图2，抛物线的顶点为E，EF⊥x轴于点F，N是直线EF上一动点，M（m，0）是x轴一个动点，请直接写出CN+MN+MB的最小值以及此时点M、N的坐标，直接写出结果不必说明理由．4．如图1，点A在x轴上，OA＝4，将OA绕点O逆时针旋转120°至OB的位置．（1）求经过A、O、B三点的抛物线的函数解析式；（2）在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3 ）如图2，OC＝4，⊙A的半径为2，点M是⊙A上的一个动点，求MC+OM的最小值．5．如图，二次函数y＝﹣x2+x+2的图象与x轴交于点A，B，与y轴交于点C．点P是该函数图象上的动点，且位于第一象限，设点P的横坐标为x．（1）写出线段AC，BC的长度：AC＝，BC＝；（2）记△BCP的面积为S，求S关于x的函数表达式；（3）过点P作PH⊥BC，垂足为H，连结AH，AP，设AP与BC交于点K，探究：是否存在四边形ACPH为平行四边形？若存在，请求出的值；若不存在，请说明理由，并求出的最大值．6．如图，直线y＝x+2与抛物线y＝x2﹣2mx+m2+m交于A、B两点（A在B的左侧），与y轴交于点C，抛物线的顶点为D，抛物线的对称轴与直线AB交于点M．（1）当四边形CODM是菱形时，求点D的坐标；（2）若点P为直线OD上一动点，求△APB的面积；′（3）作点B关于直线MD的对称点B'，以点M为圆心，MD为半径作⊙M，点Q是⊙M上一动点，求QB'+ QB的最小值．7．如图，对称轴x＝﹣1的抛物线y＝ax2+bx+c与x轴交于A（2，0），B两点，与y轴交于点C（0，﹣2），（1）求抛物线的函数表达式；（2）若点P是直线BC下方的抛物线上的动点，求△BPC的面积的最大值；（3）若点P在抛物线对称轴的左侧运动，过点P作PD⊥x轴于点D，交直线BC于点E，且PE＝OD，求点P的坐标；（4）在对称轴上是否存在一点M，使△AMC的周长最小．若存在，请求出M点的坐标和△AMC周长的最小值；若不存在，请说明理由．8．已知抛物线y＝ax2+bx﹣4经过点M（﹣4，6）和点N（2，﹣6）．（1）试确定该抛物线的函数表达式；（2）若该抛物线与x轴交于点A，B（点A在点B的左侧），与y轴交于点C①试判断△ABC的形状，并说明理由；②在该抛物线的对称轴上是否存在点P，使PM+PC的值最小？若存在，求出它的最小值；若不存在，请说明理由．9．如图，抛物线y＝ax2﹣2ax+c的图象经过点C（0，﹣2），顶点D的坐标为（1，﹣），与x轴交于A、B 两点．（1）求抛物线的解析式．（2）连接AC，E为直线AC上一点，当△AOC∽△AEB时，求点E的坐标和的值．（3）点F（0，y）是y轴上一动点，当y为何值时，FC+BF的值最小．并求出这个最小值．（4）点C关于x轴的对称点为H，当FC+BF取最小值时，在抛物线的对称轴上是否存在点Q，使△QHF 是直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．10．在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A、B、C，已知A（﹣1，0），C（0，3）．（1）求抛物线的解析式；（2）如图1，P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△CDP为等腰三角形时，求点P的坐标；（3）如图2，抛物线的顶点为E，EF⊥x轴于点F，N是直线EF上一动点，M（m，0）是x轴一个动点，请直接写出CN+MN+MB的最小值以及此时点M、N的坐标．11．如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（9，0）两点，与y轴交于点C，连接AC，BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B 向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ，过点Q作QD⊥x轴，与抛物线交于点D，连接PD与BC交于点E．设点P的运动时间为t秒（t＞0）（1）求抛物线的表达式；（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）．②在点P，Q运动的过程中，当PQ＝PD时，求t的值；（3）点M为线段BC上一点，在点P，Q运动的过程中，当点E为PD中点时，是否存在点M使得PM+BM 的值最小？若存在，请求出PM+BM的最小值；若不存在，请说明理由．12．已知抛物线y＝ax2+bx+c（a≠0）过点A（1，0），B（3，0）两点，与y轴交于点C，OC＝3．（1）求抛物线的解析式及顶点D的坐标；（2）过点A作AM⊥BC，垂足为M，求证：四边形ADBM为正方形；（3）点P为抛物线在直线BC下方图形上的一动点，当△PBC面积最大时，求点P的坐标；（4）若点Q为线段OC上的一动点，问：AQ+QC是否存在最小值？若存在，求岀这个最小值；若不存在，请说明理由．13．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与直线AB相交，与x轴、y轴交于A（2，0）、B．（1）求点O关于AB的对称点P的坐标；（2）若点P在二次函数y＝ax2+bx+c（a≠0）的图象上，求二次函数y＝ax2+bx+c（a≠0）的关系式．（3）在（2）的条件下，在△ABP内存在点M，使得MA+MB+MP的值最小，则相应点M的坐标为．14．如图（1），二次函数y＝ax2﹣bx（a≠0）的图象与x轴、直线y＝x的交点分别为点A（4，0）、B（5，5）．（1）a＝，b＝，∠AOB＝°；（2）连接AB，点P是抛物线上一点（异于点A），且∠PBO＝∠OBA，求点P的坐标；（3）如图（2），点C、D是线段OB上的动点，且CD＝2．设点C的横坐标为m．①过点C、D分别作x轴的垂线，与抛物线相交于点F、E，连接EF．当CF+DE取得最大值时，求m的值并判断四边形CDEF的形状；②连接AC、AD，求m为何值时，AC+AD取得最小值，并求出这个最小值．15．如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角形叫做“半高三角形”．如图1，对于△ABC，BC边上的高AD等于BC的一半，△ABC就是半高三角形，此时，称△ABC是BC类半高三角形；如图2，对于△EFG，EF边上的高GH等于EF的一半，△EFG就是半高三角形，此时，称△EFG是EF类半高三角形．（1）直接写出下列3个小题的答案．①若一个三角形既是等腰三角形又是半高三角形，则其底角度数的所有可能值为．②若一个三角形既是直角三角形又是半高三角形，则其最小角的正切值为．③如图3，正方形网格中，L，M是已知的两个格点，若格点N使得△LMN为半高三角形，且△LMN为等腰三角形或直角三角形，则这样的格点N共有个．（2）如图，平面直角坐标系内，直线y＝x+2与抛物线y＝x2交于R，S两点，点T坐标为（0，5），点P是抛物线y＝x2上的一个动点，点Q是坐标系内一点，且使得△RSQ为RS类半高三角形．①当点P介于点R与点S之间（包括点R，S），且PQ取得最小值时，求点P的坐标．②当点P介于点R与点O之间（包括点R，O）时，求PQ+QT的最小值．16．如图1，抛物线y＝ax2+（a+2）x+2（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点P（m，0）（0＜m＜4），过点P作x轴的垂线交直线AB于点N，交抛物线于点M．（1）求a的值；（2）若PN：MN＝1：3，求m的值；（3）如图2，在（2）的条件下，设动点P对应的位置是P1，将线段OP1绕点O逆时针旋转得到OP2，旋转角为α（0°＜α＜90°），连接AP2、BP2，求AP2+BP2的最小值．17．如图1，抛物线y＝ax2+bx+c经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC，CD．（1）求抛物线的函数表达式；（2）E是抛物线上的点，求满足∠ECD＝∠ACO的点E的坐标；（3）点M在y轴上且位于点C上方，点N在直线BC上，点P为第一象限内抛物线上一点．若以点C，M，N，P为顶点的四边形是菱形，求菱形的边长．（4）如图2，E为OB的中点，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′B、E′C，求E′B+E′C的最小值，请直接写出答案．18．如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+E′B的最小值．19．在平面直角坐标系中，已知y＝﹣x2+bx+c（b、c为常数）的顶点为P，等腰直角三角形ABC的顶点A 的坐标为（0，﹣1），点C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若抛物线经过A、B两点，求抛物线的解析式．（2）平移（1）中的抛物线，使顶点P在直线AC上并沿AC方向滑动距离为时，试证明：平移后的抛物线与直线AC交于x轴上的同一点．（3）在（2）的情况下，若沿AC方向任意滑动时，设抛物线与直线AC的另一交点为Q，取BC的中点N，试探究NP+BQ是否存在最小值？若存在，求出该最小值；若不存在，请说明理由．20．如图，已知一条直线过点（0，4），且与抛物线y＝x2交于A，B两点，其中点A的横坐标是﹣2．（1）求这条直线的函数关系式及点B的坐标．（2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由．（3）过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？21．如图，抛物线y＝x2﹣4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y＝x+m与对称轴交于点Q．（1）这条抛物线的对称轴是，直线PQ与x轴所夹锐角的度数是；（2）若两个三角形面积满足S△POQ＝S△PAQ，求m的值；（3）当点P在x轴下方的抛物线上时，过点C（2，2）的直线AC与直线PQ交于点D，求：①PD+DQ的最大值；②PD•DQ的最大值．22．如图，已知一次函数y1＝x+b的图象l与二次函数y2＝﹣x2+mx+b的图象C′都经过点B（0，1）和点C，且图象C′过点A（2﹣，0）．（1）求二次函数的最大值；（2）设使y2＞y1成立的x取值的所有整数和为s，若s是关于x的方程＝0的根，求a的值；（3）若点F、G在图象C′上，长度为的线段DE在线段BC上移动，EF与DG始终平行于y轴，当四边形DEFG的面积最大时，在x轴上求点P，使PD+PE最小，求出点P的坐标．23．如图，抛物线y＝（x+1）2+k与x轴交于A、B两点，与y轴交于点C（0，﹣3）；（1）求抛物线的对称轴及k的值；（2）抛物线的对称轴上是否存在一点P，使得|PB﹣PC|的值最大？若存在，求出点P的坐标；（3）如果点M是抛物线在第三象限的一动点；当M点运动到何处时，M点到AC的距离最大？求出此时的最大距离及M的坐标．24．如图（1）抛物线y＝ax2+bx+c（a≠o）的顶点为C（1，4），交x轴于A、B两点，交y轴于点D，其中点B的坐标为（3，0）（1）求抛物线的函数解析式；（2）如图（2）T是抛物线上的一点，过点T作x轴的垂线，垂足为点M，过点M作MN∥BD，交线段AD于点N，连接MD，若△DNM∽△BMD，求点T的坐标；（3）如图（3），过点A的直线与抛物线相交于E，且E点的横坐标为2，与y轴交于点F；直线PQ是抛物线的对称轴，G是直线PQ上的一动点，试探究在x轴上是否存在一点H，使D、G、H、F四点围成的四边形周长最小？若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由．25．如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B 左侧），与y轴交于点C．（1）求抛物线的解析式及点A、B、C的坐标；（2）直线AN交y轴于点F，P是抛物线的对称轴x＝1上动点，H是X轴上一动点，请探索：是否存在这样的P、H，使四边形CFHP的周长最短？若存在，请求出四边形CFHP的最短周长和点P、H的坐标；若不存在，请说明理由；（3）若点Q是∠MDB的角平分线上动点，点R是线段DB上的动点，Q、R在何位置时，BQ+QR的值最小．请直接写出BQ+QR的最小值和Q、R的坐标．26．在平面直角坐标系中，已知抛物线y＝x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；（ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．27．如图，抛物线y＝ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD＝OC．（1）求直线CD的解析式；（2）求抛物线的解析式；（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ∽△CDO；（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．28．已知如图，二次函数y＝ax2+2ax﹣3a（a≠0）图象的顶点为H，与x轴交于A、B两点（B在A点右侧），点H、B关于直线l：对称．（1）求A、B两点坐标，并证明点A在直线l上；（2）求二次函数解析式；（3）设点s是三角形ABH上的一动点，从点A沿着AHB方向以每秒1个单位长度移动，运动时间为t秒，到达点B时停止运动．当t为何值时，以点s为圆心的圆与两坐标轴都相切．（4）过点B作直线BK∥AH交直线l于K点，M、N分别为直线AH和直线l上的两个动点，连接HN、NM、MK，求HN+NM+MK和的最小值．1．【解答】解：（1）y＝，过点B，C，则点B、C的坐标分别为：（3，0）、（0，），则c＝，将点B的坐标代入抛物线表达式并解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+x+；（2）①当∠PCM＝90°时，由点A、B、C的坐标知，△ABC为直角三角形，故AC⊥BC，当△PCM为直角三角形时，点P与点A重合，∴点P（﹣1，0）；②当∠CPM＝90°时，则点C、P关于函数对称轴对称，此时点P（2，），故点P的坐标为（﹣1，0）或（2，）；（3）存在，理由：点P（2，），设图象沿BC方向向左平移3m个单位，则向上平移m个单位，则平移后点B′、P′的坐标分别为：（3﹣3m，m）、（2﹣3m，m+），点E（1，0），分别过点A、E作直线BC的平行线n、m，过点B′作直线m的对称点B″，则EB′＝EB″，当B″、E、P′三点共线时，EB'+EP'＝EB″+EP′＝B″P′最小；点E是AB的中点，则直线m与直线n、直线m与直线AC等距离，则点B″在直线n上，直线BC的倾斜角为30°，则直线B′B″的倾斜角为60°，则设直线B′B″的表达式为：y＝x+b，将点B′的坐标代入上式并解得：直线B′B″表达式为：y＝x+（4m﹣3）…①，设过点A的直线n的表达式为：y＝﹣x+b′，将点A的坐标代入上式并解得：直线n的表达式为：y＝﹣（x+1）…②，联立①②并解得：x＝2﹣3m，故点B″（2﹣3m，m﹣），而P′（2﹣3m，m+），故EB'+EP'的最小值B″P′＝2．2．【解答】解：（1）OA＝3OB＝3，则点B（﹣1，0），抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），即﹣3a＝3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3；（2）过点P作y轴的平行线交CA于点H，由点A、C的坐标得，直线AC的表达式为：y＝﹣x+3△ACP的面积＝PH×OA＝3×（x2﹣2x+3+x﹣3）＝（﹣x2+3x），当x＝时，△ACP的面积的最大，最大值为：，此时点P（，）；（3）过点M作MN⊥AC，则MN＝CM，故当B、M、N三点共线时，BM+CM＝BN最小，直线CA的倾斜角为45°，BN⊥AC，则∠NBA＝45°，即BN＝AB＝2＝AN，则点N（1，2），由点B、N的坐标得，直线BN的表达式为：y＝x+1，故点M（0，1）．3．【解答】解：（1）y＝﹣x2+bx+c经过点C，则c＝3，将点A的坐标代入抛物线表达式：y＝﹣x2+bx+3并解得：b＝2，抛物线的表达式为：y＝﹣x2+2x+3；（2）存在，理由：令y＝0，则x＝﹣1或3，故点B（3，0），将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝﹣x+3，设点D（x，﹣x2+2x+3），则点P（x，﹣x+3），则PD＝（﹣x2+2x+3）﹣（﹣x+3）＝﹣x2+3x，当x＝时，PD最大值为：；（3）过点B作倾斜角为30°的直线BH，过点C作CH⊥BH交于点H，CH交对称轴于点N，交x轴于点M，则点M、N为所求，直线BH表达式中的k值为，则直线CH的表达式为：y＝﹣x+3，当x＝1时，y＝3﹣，当y＝0时，x＝，故点N、M的坐标分别为：（1，3﹣）、（，0），CN+MN+MB的最小值＝CH＝CM+FH＝．4．【解答】解：（1）如图1，过点B作BD⊥x轴于点D，∴∠BDO＝90°，∵OA绕点O逆时针旋转120°至OB，∴OB＝OA＝4，∠AOB＝120°，B在第二象限，∴∠BOD＝60°，∴sin∠BOD＝，cos∠BOD＝，∴BD＝OB＝2，OD＝OB＝2，∴B（﹣2，2），设过点A（4，0），B（﹣2，2），O（0，0）的抛物线解析式为y＝ax2+bx+c，∴，解得：，∴抛物线的函数解析式为y＝x2﹣x；（2）存在△POB为等腰三角形，∵抛物线与x轴交点为A（4，0），O（0，0），∴对称轴为直线x＝2，设点P坐标为（2，p），则OP2＝22+p2＝4+p2，BP2＝（2+2）2+（p﹣2）2＝p2﹣4p+28，①若OP＝OB＝4，则4+p2＝42解得：p1＝2，p2＝﹣2，当p＝﹣2时，∠POA＝60°，即点P、O、B在同一直线上，∴p≠﹣2，∴P（2，2），②若BP＝OB＝4，则p2﹣4p+28＝42解得：p1＝p2＝2，∴P（2，2）；③若OP＝BP，则4+p2＝p2﹣4p+28，解得：p＝2，∴P（2，2）；综上所述，符合条件的点P只有一个，坐标为（2，2）；（3）在OA上取点K，使AK＝1，连接CK交圆与点M，连接OM、CM，此时，MC+OM＝MC+KM＝CK为最小值，理由：∵AK＝1，MA＝2，OA＝4，∴AM2＝AK•OA，而∠MAO＝∠OAM，∴△AKM∽△AMO，∴＝，即：MC+OM＝MC+KM＝CK，CK＝＝5，即：MC+OM的最小值为CK＝5．5．【解答】解：（1）二次函数y＝﹣x2+x+2，当x＝0时，y＝2，∴C（0，2），∴OC＝2，当y＝0时，﹣x2+x+2＝0，解得：x1＝4，x2＝﹣1，∴A（﹣1，0），B（4，0），∴OA＝1，OB＝4，由勾股定理得：AC＝＝，BC＝＝2；故答案为：，2；（4分）（2）∵B（4，0），C（0，2），∴直线BC的解析式为：y＝﹣x+2，如图1，过P作PD∥y轴，交直线BC于D，设P（x，﹣x2+x+2），则D（x，﹣x+2），∴PD＝（﹣x2+x+2）﹣（﹣x+2）＝﹣x2+2x，有S＝PD•OB＝×4（﹣+2x）＝﹣x2+4x（0＜x＜4）；（6分）（3）不存在，如图2，∵AC2+BC2＝＝25＝AB2，∴△ABC为直角三角形，即AC⊥BC，∵PH⊥BC，∴AC∥PH，要使四边形ACPH为平行四边形，只需满足PH＝AC＝，（10分）∴S＝BC•PH＝×2×＝5，∵而S＝﹣x2﹣4x＝﹣（x﹣2）2+4≤4，所以不存在四边形ACPH为平行四边形，∵AC∥PH，∴△AKC∽△PHK，∴＝＝＝S≤；∴的最大值是．（12分）（说明：写出不存在给1分，其他说明过程酌情给分）6．【解答】解：（1）∵D（m，m），OD＝m，四边形CODM为菱形，∴OD＝OC＝2＝m，∴m＝，∴D（）；（2）∵y＝x+2与抛物线y＝x2﹣2mx+m2+m交于A、B两点，∴联立，解得，，∵点A在点B的左侧，∴A（m﹣1，m+1），B（m+2，m+4），∴AB＝＝3，∵直线OC的解析式为y＝x，直线AB的解析式为y＝x+2，∴AB∥OC，两直线AB、OC之间距离h＝2×＝，∴S△APB＝AB•h＝×3×＝3；（3）∵A（m﹣1，m+1），B（m+2，m+4），∴AM＝1×＝，BM＝2×＝2，由M点坐标（m，m+2），D点坐标（m，m）可知以MC为半径的圆的半径为（m+2）﹣m＝2，取MB的中点N，连接QB、QN、QB′，∴MN＝BM＝，∵，∠QMN＝∠BMQ，∴△MNQ∽△MQB，∴，∴，由三角形三边关系，当Q、N、B′三点共线时QB′+QB最小，∵直线AB的解析式为y＝x+2，∴直线AB与对称轴夹角为45°，∵点B、B′关于对称轴对称，∴∠BMB′＝90°，由勾股定理得，QB′+QB最小值为B'N＝＝＝．即QB'+QB的最小值是．7．【解答】解：（1）∵对称轴x＝﹣1的抛物线y＝ax2+bx+c与x轴交于A（2，0），B两点，∴B（﹣4，0）．设抛物线解析式是：y＝a（x+4）（x﹣2）（a≠0）．把C（0，﹣2）代入，得a（0+4）（0﹣2）＝﹣2．解得a＝．故该抛物线解析式是：y＝（x+4）（x﹣2）或y＝x2+x﹣2；（2）设直线BC的解析式为y＝mx+n，把B（﹣4，0），C（0，﹣2）代入得，解得，∴直线BC的解析式为y＝﹣x﹣2；作PQ∥y轴交BC于Q，如图，设P（t，t2+t﹣2），则Q（t，﹣t﹣2），则PQ＝﹣t﹣2﹣（t2+t﹣2）＝﹣t2﹣t，S△PBC＝S△PBQ+S△PCQ＝•PQ•4＝﹣t2﹣2t＝﹣（t+2）2+2，当t＝﹣2时，△PBC面积有最大值，最大值为2，此时P点坐标为（﹣2，﹣2）；（3）设D（m，0），∵DP∥y轴，∴E（m，﹣m﹣2），P（m，m2+m﹣2），∵PE＝OD，∴|﹣m|＝4|﹣m﹣2﹣m2﹣m+2|，∴m2+3m＝0或m2+5m＝0，∴m＝﹣3，m＝0（舍去）或m＝﹣5，m＝0（舍去）∴P（﹣3，﹣）或P（﹣5，）；（4）∵点A、B关于对称轴对称，∴点M为BC与对称轴的交点时，MA+MC的值最小，此时△AMC的周长最小．∵直线BC的解析式为y＝﹣x﹣2．抛物线的对称轴为直线x＝﹣1．∴当x＝﹣1时，y＝﹣．∴抛物线对称轴上存在点M（﹣1，﹣）符合题意，此时△AMC周长的最小值为AC+BC＝2+2．8．【解答】解：（1）将点M、N的坐标代入抛物线表达式得：，解得：，故抛物线的表达式为：y＝x2﹣x﹣4；（2）①y＝x2﹣x﹣4，令y＝0，则x＝﹣2或8，x＝0，则y＝﹣4，故点A、B、C的坐标分别为：（﹣2，0）、（8，0）、（0，﹣4），则函数的对称轴为：x＝3，则AB＝10，BC＝，AC＝，则AB2＝BC2+AC2，故△ABC为直角三角形；②作点M关于函数对称轴的对称点D（10，6），连接CD交函数对称轴于点P，则点P为所求，将点CD的坐标代入一次函数表达式：y＝kx+b并解得：直线CD的表达式为：y＝x﹣4，当x＝3时，y＝﹣1，故点P（3，﹣1），此时PM+PC的值最小为CD＝10．9．【解答】解：（1）由题可列方程组：，解得：∴抛物线解析式为：y＝x2﹣x﹣2；（2）如图1，∠AOC＝90°，AC＝，AB＝4，设直线AC的解析式为：y＝kx+b，则，解得：，∴直线AC的解析式为：y＝﹣2x﹣2；当△AOC∽△AEB时＝（）2＝（）2＝，∵S△AOC＝1，∴S△AEB＝，∴AB×|y E|＝，AB＝4，则y E＝﹣，则点E（﹣，﹣）；由△AOC∽△AEB得：∴；（3）如图2，连接BF，过点F作FG⊥AC于G，则FG＝CFsin∠FCG＝CF，∴CF+BF＝GF+BF≥BE，当折线段BFG与BE重合时，取得最小值，由（2）可知∠ABE＝∠ACO∴BE＝ABcos∠ABE＝ABcos∠ACO＝4×＝，|y|＝OBtan∠ABE＝OBtan∠ACO＝3×＝，∴当y＝﹣时，即点F（0，﹣），CF+BF有最小值为；（4）①当点Q为直角顶点时（如图3）：由（3）易得F（0，﹣），∵C（0，﹣2）∴H（0，2）设Q（1，m），过点Q作QM⊥y轴于点M．则Rt△QHM∽Rt△FQM∴QM2＝HM•FM，∴12＝（2﹣m）（m+），解得：m＝，则点Q（1，）或（1，）当点H为直角顶点时：点H（0，2），则点Q（1，2）；当点F为直角顶点时：同理可得：点Q（1，﹣）；综上，点Q的坐标为：（1，）或（1，）或Q（1，2）或Q（1，﹣）．10．【解答】解：（1）∵抛物线y＝﹣x2+bx+c经过点A、B、C，把A（﹣1，0），C（0，3）代入解析式得，∴，解得b＝2，c＝3．故该抛物线解析式为：y＝﹣x2+2x+3．（2）令﹣x2+2x+3＝0，解得x1＝﹣1，x2＝3，即B（3，0），设直线BC的解析式为y＝kx+b′，则，解得：，故直线BC的解析式为y＝﹣x+3；∴设P（t，3﹣t），∴D（t，﹣t2+2t+3），∴PD＝（﹣t2+2t+3）﹣（3﹣t）＝﹣t2+3t，∵OB＝OC＝3，∴△BOC是等腰直角三角形，∴∠OCB＝45°，当CD＝PC时，则∠CPD＝∠CDP，∵PD∥y轴，∴∠CPD＝∠OCB＝45°，∴∠CDP＝45°，∴∠PCD＝90°，∴直线CD的解析式为y＝x+3，解得或，∴D（1，4），此时P（1，2）；当CD＝PD时，则∠DCP＝∠CPD＝45°，∴∠CDP＝90°，∴CD∥x轴，∴D点的纵坐标为3，代入y＝﹣x2+2x+3得，3＝﹣x2+2x+3，解得x＝0或x＝2，此时P（2，1）；当PC＝PD时，∵PC＝t，∴t＝﹣t2+3t，解得t＝0或t＝3﹣，此时P（3﹣，）；综上，当△CDP为等腰三角形时，点P的坐标为（1，2）或（2，1）或（3﹣，）．（3）CN+MN+MB的最小值为，N坐标为（1，3﹣），M坐标为（，0）．理由如下：如图，取G点坐标为（0，﹣），连接BG，∵B（3，0），∴直线BG解析式为：y＝，∴tan∠GBO＝，∴∠GBO＝30°，过M点作MB′⊥BG，∴，∴CN+MN+MB＝CN+MN+B′M，∴CN+MN+MB取最小值时，C、M、N、B′在同一条直线上，即CB′⊥BG，设直线CB′解析式为，∵C（0，3）故直线CB′解析式为为，∵抛物线的顶点为E坐标为（1，4），EF⊥x轴，N在EF、CB′上，∴N坐标为（1，3﹣），M（m，0）是x轴一个动点，也是CB′与x轴交点，∴M（，0）．∵CG＝3+，∠CGB＝60°，∴CB′＝CGsin∠CGB＝（3+）×＝，综上所述：CN+MN+MB的最小值为，N坐标为（1，3﹣），M坐标为（，0）．11．【解答】解：（1）将A（﹣3，0），B（9，0）代入y＝ax2+bx+3，得：，解得：，∴抛物线的表达式为y＝﹣x2+x+3…①；（2）由题意得：∠ACO＝∠OBC＝30°，∠ACB＝90°，将点B、C（0，3）的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝﹣x+3…②；①点P的坐标为（﹣3+t，t），点Q（9﹣2t，0），将点Q的坐标代入①式并整理得：点D[9﹣2t，（6t﹣t2）]；②当PQ＝PD时，则DQ中点的纵坐标＝点P的纵坐标，即：[（6t﹣t2）]＝t，解得：t＝；（3）点P的坐标为（﹣3+t，t）、点D[9﹣2t，（6t﹣t2）]，点E是PQ的中点，则点E[3﹣t，t+（6t﹣t2）]，将点E的坐标代入②式并整理得：t2﹣6t+9＝0，解得：t＝3，即点P（﹣，）即点P是AC的中点，作点P关于直线BC的对称点P′，过点P′作P′H⊥x轴、BC于点H、M，过点P作PN⊥y轴于点N，则MH＝MB，则此时，PM+BM＝PM+MH＝P′H为最小值，∵∠ACB＝90°，PC＝P′C，∠P′CM＝∠NCP，∠P′MC＝∠PNC＝90°，∴△P′MC≌△PNC（AAS），∴MC＝NC＝OC，OM＝OC＝＝P′H，故PM+BM的最小值为．12．【解答】解：（1）函数的表达式为：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3），即：3a＝3，解得：a＝1，故抛物线的表达式为：y＝x2﹣4x+3，则顶点D（2，﹣1）；（2）∵OB＝OC＝3，∴∠OBC＝∠OCB＝45°，AM＝MB＝ABsin45°＝＝AD＝BD，则四边形ADBM为菱形，而∠AMB＝90°，∴四边形ADBM为正方形；（3）将点B、C的坐标代入一次函数表达式：y＝mx+n并解得：直线BC的表达式为：y＝﹣x+3，过点P作y轴的平行线交BC于点H，设点P（x，x2﹣4x+3），则点H（x，﹣x+3），则S△PBC＝PH×OB＝（﹣x+3﹣x2+4x﹣3）＝（﹣x2+3x），∵﹣＜0，故S△PBC有最大值，此时x＝，故点P（，﹣）；（4）存在，理由：如上图，过点C作与y轴夹角为30°的直线CH，作QH⊥CH，垂足为H，则HQ＝CQ，AQ+QC最小值＝AQ+HQ＝AH，直线HC所在表达式中的k值为，直线HC的表达式为：y＝x+3…①则直线AH所在表达式中的k值为﹣，则直线AH的表达式为：y＝﹣x+s，将点A的坐标代入上式并解得：则直线AH的表达式为：y＝﹣x+…②，联立①②并解得：x＝，故点H（，），而点A（1，0），则AH＝，即：AQ+QC的最小值为．13．【解答】解：（1）连接AB，过点O作OP⊥AB交AB于点G，过点P作PH⊥x轴于点H，∵点O关于AB的对称点P，∴OG＝PG，tan∠BAO＝＝，则∠BAO＝60°，则∠GOA＝∠GPA＝30°，∠GAO＝∠GAP＝∠PAH＝60°，则GA＝OA＝1，∵∠GAP＝∠PAH，∴AH＝AG＝1，则PH＝AHtan60°＝，故点P（3，）；（2）将点A，B，P的坐标代入二次函数表达式得：，解得：，故抛物线的表达式为：y＝x2﹣x+2；（3）连接PB，由题意得：AB＝4，AP＝AO＝2，BP＝BO＝＝2，则△ABP为直角三角形，△ABO、△ABP是两个全等的，均有一个角为30°的直角三角形，即AB＝OB＝2，AB＝4，AP＝OA＝2，∠PBA＝∠BAO＝30°，∠BAO＝∠BAP＝60°，当∠BMA＝∠BMC＝∠AMC＝120°时，MA+MB+MP的值最小（证明见备注），以BP边向上作等边三角形APA′，以AP边为基础向右作等边三角形APB′，连接AA′、BB′交于点M，则点M为所求点，BP＝2，则∠A′BO＝∠OBA+∠PBA+∠PBA′＝30°+30°+60°＝120°，则直线A′B的长度为2，倾斜角为30°，则x A′＝A′Bcos30°＝3，同理y A′＝3，故点A′（3，3），由点AA′的坐标可得，直线AA′的表达式为：y＝3（x﹣2）…①；同理可得：直线BB′的表达式为：y＝x+2…②，联立①②并解得：x＝，故点M（，），故答案为：（，）．备注：已知三角形ABC，在其内部找一点P，使得PA+PB+PC为最小．如图，将三角形ABP逆时针旋转60度至三角形A'BP'，连接PP'，CA'．根据旋转变换，三角形P'BP为等边三角形，所以有PA+PB+PC＝P'A'+PP'+PC．利用两点之间线段最短，当点P，P'在直线CA'上时，所求为最短，于是，转化为下图：则∠BPC＝180°﹣∠BPP′＝180°﹣60°＝120°，∠BPA＝∠BP′A′＝180°﹣∠BP′P＝120°，故∠APC＝120°，故满足P的点，必须使∠APB＝∠BPC＝∠APB＝120°．14．【解答】解：（1）将点A、B的坐标代入二次函数表达式得：，解得：，故二次函数表达式为：y＝x2﹣4x，故：答案为：1，4，45°；（2）设直线BP交y轴于点H，∵∠HOB＝∠AOB＝45°，∠PBO＝∠OBA，BO＝BO，∴△HOB≌△AOB（AAS），∴OA＝OH＝4，即点H（0，4），则直线PB的表达式为：y＝kx+4，将点B坐标代入上式并解得：直线PB的表达式为：y＝x+4，将上式与二次函数表达式联立并解得：x＝5或﹣（舍去正值），则点P（﹣，）；（3）①由题意得：直线OB的表达式为：y＝x，设点C（m，m），CD＝2，直线OB的倾斜角为45度，则点D（m+2，m+2），则点F（m，m2﹣4m），点E[（m+2），（m+2）2﹣4（m+2）]，则CF+DE＝m﹣m2+4m+（m+2）﹣[（m+2）2﹣4（m+2）]＝﹣2m2+6m+6，∵﹣2＜0，故CF+DE有最大值，此时，m＝，则点C、F、D、E的坐标分别为（，）、（，﹣）、（，）、（，﹣），则CF＝DE＝，CF∥ED，故四边形CDEF为平行四边形；②如图所示，过点A作CD的平行线，过点D作AC的平行线，交于点G，则四边形ACDG是平行四边形，。
专题03 选择压轴题之几何最值问题(举一反三)(解析版)
【方法点拨】涉及旋转、对称、折叠的最值问题中, 若无法直接求解,可先找到关键点的运动轨迹,再利用 “垂线段最短”来求解.【例1】（2020•南谯区二模）如图，△ABC 中，∠A ＝30°，∠ACB ＝90°，BC ＝2，D 是AB 上的动点，将线段CD 绕点C 逆时针旋转90°，得到线段CE ，连接BE ，则BE 的最小值是（ ）A ．√3−1B ．√32C ．√3D ．2【分析】如图，过点C 作CK ⊥AB 于K ，将线段CK 绕点C 逆时针旋转90°得到CH ，连接HE ，延长HE 交AB 的延长线于J ．首先证明四边形CKJH 是正方形，推出点E 在直线HJ 上运动，求出BJ ，根据垂线段最短解决问题即可．【解答】解：如图，过点C 作CK ⊥AB 于K ，将线段CK 绕点C 逆时针旋转90°得到CH ，连接HE ，延长HE 交AB 的延长线于J ．∵∠DCE ＝∠KCH ＝90°，∴∠DCK ＝∠ECH ，∵CD ＝CE ，CK ＝CH ，∴△CKD≌△CHE（SAS），∴∠CKD＝∠H＝90°，∵∠CKJ＝∠KCH＝∠H＝90°，∴四边形CKJH是矩形，∵CK＝CH，∴四边形CKJH是正方形，∴点E在直线HJ上运动，当点E与J重合时，BE的值最小，在Rt△CBK中，∵BC＝2，∠ABC＝60°，∴CK＝BC•sin60°=√3，BK＝BC•cos60°＝1，∴KJ＝CK=√3∴BJ＝KJ﹣BK=√3−1，∴BE的最小值为√3−1，补充方法：AC上截取CF＝2，得三角形CFD全等于三角形CBE，DF在DF垂直AB时最小．故选：A．【点睛】本题考查旋转的性质，全等三角形的判定和性质，解直角三角形，正方形的判定和性质，垂线段最短等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题．【变式1-1】（2021•怀宁县模拟）如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，P是△ABC的高CD 上一个动点，以B点为旋转中心把线段BP逆时针旋转45°得到BP′，连接DP′，则DP′的最小值是（）A．2√2−2B．4﹣2√2C．2−√2D．√2−1【分析】在BC上截取BE＝BD，由等腰直角三角形的性质可得BA＝4√2，∠ABC＝∠BAC＝∠BCD＝∠DCA＝45°，BD＝CD＝AD＝2√2=BE，由旋转的性质可得BP＝BP'，∠PBP'＝45°，可证△BDP'≌△BEP，可得PE＝P'D，当PE⊥CD时，PE有最小值，即DP'有最小值，由直角三角形的性质可求DP′的最小值．【解答】解：如图，在BC上截取BE＝BD，连接EP，∵∠ACB＝90°，AC＝BC＝4，CD⊥AB，∴BA＝4√2，∠ABC＝∠BAC＝∠BCD＝∠DCA＝45°，BD＝CD＝AD＝2√2=BE∵旋转∴BP＝BP'，∠PBP'＝45°，∵BE＝BD，∠ABC＝∠PBP'＝45°，BP＝BP'∴△BDP'≌△BEP（SAS）∴PE＝P'D∴当PE⊥CD时，PE有最小值，即DP'有最小值，∵PE⊥CD，∠BCD＝45°，∴CE=√2PE＝BC﹣BE＝4﹣2√2∴PE＝2√2−2故选：A．【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形判定和性质，添加恰当辅助线构造全等三角形是本题的关键．【变式1-2】（2020•南山区校级一模）如图，▱ABCD中，∠DAB＝60°，AB＝6，BC＝2，P为边CD上的一动点，则PB+√32PD的最小值等于（）A．√3B．3C．3√3D．2+2√3【分析】过点P作PE⊥AD，交AD的延长线于点E，有锐角三角函数可得EP=√32PD，即PB+√32PD＝PB+PE，则当点B，点P，点E三点共线且BE⊥AD时，PB+PE有最小值，即最小值为BE．【解答】解：如图，过点P作PE⊥AD，交AD的延长线于点E，∵AB∥CD，∴∠EDP＝∠DAB＝60°，∴sin∠EDP=EPDP=√32，∴EP=√32PD∴PB+√32PD＝PB+PE∴当点B，点P，点E三点共线且BE⊥AD时，PB+PE有最小值，即最小值为BE，∵sin∠A=BEAB=√32，∴BE＝3√3，故选：C．【点睛】本题考查了平行四边形的性质，垂线段最短，解直角三角形等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型．【变式1-3】（2021•太和县一模）在△ABC中，∠ACB＝90°，P为AC上一动点，若BC＝4，AC＝6，则√2BP+AP的最小值为（）A．5B．10C．5√2D．10√2【分析】√2BP+AP=√2（BP+√22AP），求BP+√22AP的最小值属“胡不归”问题，以A为顶点，AC为一边在下方作45°角即可得答案．【解答】解：以A为顶点，AC为一边在下方作∠CAM＝45°，过P作PF⊥AM于F，过B作BD⊥AM 于D，交AC于E，如图：√2BP+AP=√2（BP+√22AP），要使√2BP+AP最小，只需BP+√22AP最小，∵∠CAM＝45°，PF⊥AM，∴△AFP是等腰直角三角形，∴FP=√22AP，∴BP+√22AP最小即是BP+FP最小，此时P与E重合，F与D重合，即BP+√22AP最小值是线段BD的长度，∵∠CAM＝45°，BD⊥AM，∴∠AED＝∠BEC＝45°，∵∠ACB＝90°，∴sin∠BEC＝sin45°=BCBE，tan∠BEC=BCCE，又BC＝4，∴BE＝4√2，CE＝4，∵AC＝6，∴AE＝2，而sin∠CAM＝sin45°=DE AE，∴DE =√2，∴BD ＝BE +DE ＝5√2，∴√2BP +AP 的最小值是√2BD ＝10，故选：B ．【点睛】本题考查线段和的最小值，解题的关键是做45°角，将求BP +√22AP 的最小值转化为求垂线段的长．【方法点拨】“将军饮马”问题是中考的热点问题之一,解决这类问题的方法是找出两定点中任一点关于动 点所在直线的对称点,再将另一点与对称点相连,连线与直线的交点即为所求的点.通常情况下, 求三角形 或四边形的周长的最小值时,往往也是利用轴对称进行解题.【例2】（2021•淮南一模）如图，Rt △ABC 中．∠BAC ＝90°，AB ＝1，AC ＝2√2．点D ，E 分别是边BC ，AC 上的动点，则DA +DE 的最小值为（ ）A ．89B ．169C ．8√29D ．16√29【分析】如图，作A 关于BC 的对称点A '，连接AA '，交BC 于F ，过A '作A 'E ⊥AC 于E ，交BC 于D ，则AD ＝A 'D ，此时AD +DE 的值最小，就是A 'E 的长，根据相似三角形对应边的比可得结论．【解答】解：作A 关于BC 的对称点A '，连接AA '，交BC 于F ，过A '作A 'E ⊥AC 于E ，交BC 于D ，则AD ＝A 'D ，此时AD +DE 的值最小，就是A 'E 的长；Rt △ABC 中，∠BAC ＝90°，AB ＝1，AC ＝2√2，∴BC =√12+(2√2)2=3，S △ABC =12AB •AC =12BC •AF ，∴1×2√2=3AF ，AF =2√23，∴AA '＝2AF =4√23，∵∠A 'FD ＝∠DEC ＝90°，∠A 'DF ＝∠CDE ，∴∠A '＝∠C ，∵∠AEA '＝∠BAC ＝90°，∴△AEA '∽△BAC ，∴AA′A′E=BC AC ， ∴4√23A′E =2√2，∴A 'E =169， 即AD +DE 的最小值是169；故选：B ．【点睛】本题考查轴对称﹣最短问题、三角形相似的性质和判定、两点之间线段最短、垂线段最短等知识，解题的关键是灵活运用轴对称以及垂线段最短解决最短问题，属于中考填空题中的压轴题．【变式2-1】（2020•荆门）在平面直角坐标系中，长为2的线段CD （点D 在点C 右侧）在x 轴上移动，A （0，2），B （0，4），连接AC ，BD ，则AC +BD 的最小值为（ ）A ．2√5B ．2√10C ．6√2D ．3√5【分析】设C （m ，0），则有AC +BD =√m 2+22+√(m +2)2+42，推出要求AC +BD 的最小值，相当于在x 轴上找一点P （m ，0），使得点P 到M （0，2）和N （﹣2，4）的距离和最小，如图1中，作点M关于x轴的对称点Q，连接NQ交x轴于P′，连接MP′，此时P′M+P′N的值最小，求出NQ即可解决问题．【解答】解：设C（m，0），∵CD＝2，∴D（m+2，0），∵A（0，2），B（0，4），∴AC+BD=√m2+22+√(m+2)2+42，∴要求AC+BD的最小值，相当于在x轴上找一点P（m，0），使得点P到M（0，2）和N（﹣2，4）的距离和最小，如图1中，作点M关于x轴的对称点Q，连接NQ交x轴于P′，连接MP′，此时P′M+P′N的值最小，∵N（﹣2，4），Q（0，﹣2）P′M+P′N的最小值＝P′N+P′Q＝NQ=√22+62=2√10，∴AC+BD的最小值为2√10．故选：B．【点睛】本题考查轴对称﹣最短路径问题，坐标与图形的性质，两点间距离公式等知识，解题的关键是学会利用参数解决问题，学会利用数形结合的思想思考问题，学会用转化的思想解决问题，属于中考选择题中的压轴题．【变式2-2】（2020•红桥区一模）如图，在四边形ABCD中，∠A＝∠D＝90°，AB＝5，AD＝4，CD＝3，点P是边AD上的动点，则△PBC周长的最小值为（）A．8B．4√5C．12D．6√5【分析】作点C关于AD的对称点E，连接EB交AD于点P′，连接CP′，则EP′＝CP′，ED＝CD，此时△P′BC周长最小为：P′C+P′B+BC＝PE+P′B+BC＝EB+BC，作BF⊥DC的延长线于点F，在Rt△BCF和Rt△BFE中，根据勾股定理即可得△PBC周长的最小值．【解答】解：作点C关于AD的对称点E，连接EB交AD于点P′，连接CP′，则EP′＝CP′，ED＝CD，此时△P′BC周长最小为：P′C+P′B+BC＝PE+P′B+BC＝EB+BC，作BF⊥DC的延长线于点F，∠A＝∠ADC＝90°，∴四边形ABFD是矩形，∴BF＝AD＝4，DF＝AB＝5，∴CF＝DF﹣CD＝5﹣3＝2，EF＝DF+ED＝5+3＝8，∴在Rt△BCF和Rt△BFE中，根据勾股定理，得BC=√CF2+BF2=2√5，BE=√BF2+EF2=4√5，∴BC+BE＝6√5．所以△PBC周长的最小值为6√5．故选：D．【点睛】本题考查了轴对称﹣最短路线问题、勾股定理，解决本题的关键是掌握轴对称性质．【变式2-3】（2020•市南区二模）如图，在矩形ABCD中，AD＝12，AE⊥BD，垂足为E，ED＝3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）A．4√2B．2√2C．6√3D．4√3【分析】在Rt△ABE中，利用三角形相似可求得AE、DE的长，设A点关于BD的对称点A′，连接A′D，可证明△ADA′为等边三角形，当PQ⊥AD时，则PQ最小，所以当A′Q⊥AD时AP+PQ最小，从而可求得AP+PQ的最小值等于DE的长，可得出答案．【解答】解：设BE＝x，则DE＝3x，∵四边形ABCD为矩形，且AE⊥BD，∴△ABE∽△DAE，∴AE2＝BE•DE，即AE2＝3x2，∴AE=√3x，在Rt△ADE中，由勾股定理可得AD2＝AE2+DE2，即122＝（√3x）2+（3x）2，解得x＝2√3，∴AE＝6，DE＝6√3，如图，设A点关于BD的对称点为A′，连接A′D，P A′，则A′A＝2AE＝12＝AD，AD＝A′D＝12，∴△AA′D是等边三角形，∵P A＝P A′，∴当A′、P、Q三点在一条线上时，A′P+PQ最小，又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，∴AP+PQ＝A′P+PQ＝A′Q＝DE＝6√3．故选：C．【点睛】本题主要考查轴对称的应用，利用最小值的常规解法确定出A的对称点，从而确定出AP+PQ 的最小值的位置是解题的关键，利用条件证明△A′DA是等边三角形，借助几何图形的性质可以减少复杂的计算．【方法点拨】利用“到定点的距离等于定长的点位于同一个圆上”或“90°的圆周角所对的弦是直径”等可以确定某些动点的运动轨迹是圆(或圆弧).当圆外一定点与圆上一动点位于圆心同侧,且三点共线时,该动点到圆外定点的距离最短;当圆外一定点与圆上一动点位于圆心异侧,且三点共线时,该动点到圆外定点的距离最长.【例3】（2020•百色模拟）如图，在长方形纸片ABCD中，AB＝4，AD＝6．点E是AB的中点，点F是AD边上的一个动点．将△AEF沿EF所在直线翻折，得到△GEF．则GC长的最小值是（）A．2√10−2B．2√10−1C．2√13D．2√10【分析】以点E为圆心，AE长度为半径作圆，连接CE，当点G在线段CE上时，GC的长取最小值，根据折叠的性质可知GE＝2，在Rt△BCE中利用勾股定理可求出CE的长度，用CE﹣GE即可求出结论．【解答】解：以点E为圆心，AE长度为半径作圆，连接CE，当点G在线段CE上时，GC的长取最小值，如图所示根据折叠可知：GE＝AE=12AB＝2．在Rt△BCE中，BE=12AB＝2，BC＝6，∠B＝90°，∴CE=√BE2+BC2=2√10，∴GC的最小值＝CE﹣GE＝2√10−2．故选：A．【点睛】本题考查了翻折变换、矩形的性质以及勾股定理，利用作圆，找出GC取最小值时点A′的位置是解题的关键．【变式3-1】（2020•河北模拟）数学兴趣小组在“中学生学习报”中了解到“直角三角形斜边上的中线等于斜边的一半”，用含30°角的直角三角板做实验，如图，∠ACB＝90°，BC＝6cm，M，N分别是AB，BC的中点，标记点N的位置后，将三角板绕点C逆时针旋转，点M旋转到点M′，在旋转过程中，线段NM′的最大值是（）A．7cm B．8 cm C．9cm D．10cm【分析】根据直角三角形的性质得到AB＝2BC＝12，CM＝6，CN＝3，在旋转过程中，点M′始终在以C为圆心，CM为半径的圆上，当M′旋转当与B，C在一条直线上时，即到D的位置时，线段NM′的值最大，于是得到结论．【解答】解：∵∠ACB＝90°，BC＝6cm，∠A＝30°，∴AB＝2BC＝12，∵M，N分别是AB，BC的中点，∴CM＝6，CN＝3，∵将三角板绕点C逆时针旋转，点M旋转到点M′，在旋转过程中，点M′始终在以C为圆心，CM为半径的圆上，∴当M′旋转当与B，C在一条直线上时，即到D的位置时，线段NM′的值最大，即NM′的最大值＝DN＝6+3＝9，故选：C．【点睛】本题考查了旋转的性质，含30°角的直角三角形的性质，直角三角形斜边上的中线，熟练掌握直角三角形的性质是解题的关键．【变式3-2】（2020•芜湖二模）如图，已知正方形ABCD的边长为8，点E是正方形内部一点，连接BE，CE，且∠ABE＝∠BCE，点P是AB边上一动点，连接PD，PE，则PD+PE长度的最小值为（）A．8√2B．4√10C．8√5−4D．4√13−4【分析】根据正方形的性质得到∠ABC＝90°，推出∠BEC＝90°，得到点E在以BC为直径的半圆上移动，如图，设BC的中点为O，作正方形ABCD关于直线AB对称的正方形AFGB，则点D的对应点是F，连接FO交AB于P，交⊙O于E，则线段EF的长即为PD+PE的长度最小值，根据勾股定理即可得到结论．【解答】解：∵四边形ABCD是正方形，∴∠ABC＝90°，∴∠ABE+∠CBE＝90°，∵∠ABE＝∠BCE，∴∠BCE+∠CBE＝90°，∴∠BEC＝90°，∴点E在以BC为直径的半圆上移动，如图，设BC的中点为O，作正方形ABCD关于直线AB对称的正方形AFGB，则点D的对应点是F，连接FO交AB于P，交半圆O于E，则线段EF的长即为PD+PE的长度最小值，OE＝4，∵∠G＝90°，FG＝BG＝AB＝8，∴OG＝12，∴OF=√FG2+OG2=4√13，∴EF＝4√13−4，∴PD+PE的长度最小值为4√13−4，故选：D．【点睛】本题考查了轴对称﹣最短路线问题，正方形的性质，勾股定理的综合运用．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．【变式3-3】（2021•海安市模拟）如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝60°，BC＝2√3，Q为AC上的动点，P为Rt△ABC内一动点，且满足∠APB＝120°，若D为BC的中点，则PQ+DQ的最小值是（）A．√43−4B．√43C．4D．√43+4【分析】如图以AB为边，向左边作等边△ABE，作△ABE的外接圆⊙O，连接OB，则点P在⊙O上．作点D关于AC的对称点D′，连接OD′，OP，PD′，PD′交AC于Q，则PQ+QD＝PQ+QD′＝PD′，根据PD′≥OD′﹣OP，求出OP，OD′即可解决问题．【解答】解：如图以AB为边，向左边作等边△ABE，作△ABE的外接圆⊙O，连接OB，则点P在⊙O 上．在Rt△ABC中，∵∠ACB＝90°，∠ABC＝60°，BC＝2√3，∴AB＝4√3，则易知OB＝4，OB⊥BC，作点D关于AC的对称点D′，连接OD′，OP，PD′，PD′交AC于Q，则PQ+QD＝PQ+QD′≥PD′，∵PD′≥OD′﹣OP，OP＝OB＝4，OD′=√42+(3√3)2=√43，∴PD′≥√43−4，∴PQ+DQ的最小值为√43−4，故选：A．【点睛】本题考查轴对称﹣最短问题，解直角三角形等知识，解题的关键是学会利用轴对称解决最短问题，属于中考选择题中的压轴题．【方法点拨】几何图形面积最值问题的解题通法:1.观察几何图形,若能直接判断出当动点在何位置时,几何图形的面积取得最值,则直接计算即可.2.若根据动点的位置,无法直接判断几何图形面积的最值,则可设出未知数,用含未知数的代数式表示出该几何图形的面积,利用函数的性质求解.【例4】（2020•立山区二模）如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB＝45°，则四边形MANB面积的最大值是（）A．2√2B．4C．4√2D．8√2【分析】过点O作OC⊥AB于C，交⊙O于D、E两点，连接OA、OB、DA、DB、EA、EB，根据圆周角定理推出△OAB为等腰直角三角形，求得AB=√2OA＝2√2，根据已知条件即可得到结论．【解答】解：过点O作OC⊥AB于C，交⊙O于D、E两点，连接OA、OB、DA、DB、EA、EB，如图，∵∠AMB＝45°，∴∠AOB＝2∠AMB＝90°，∴△OAB为等腰直角三角形，∴AB=√2OA＝2√2，∵S四边形MANB＝S△MAB+S△NAB，∴当M点到AB的距离最大，△MAB的面积最大；当N点到AB的距离最大时，△NAB的面积最大，即M点运动到D点，N点运动到E点，此时四边形MANB面积的最大值＝S四边形DAEB＝S△DAB+S△EAB=12AB•CD+12AB•CE=12AB（CD+CE）=12AB•DE=12×2√2×4＝4√2．故选：C．【点睛】本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了圆周角定理，正确的作出辅助线是解题的关键．【变式4-1】（2020•岐山县二模）如图，正方形BEFG的顶点E在正方形ABCD的边AD上，CD、EF交于点H，AD＝16，连接EC，FC，则△CEF的面积的最小值为（）．A．16√2B．48C．96D．256【分析】由于S △CEF ＝S △CHF +S △CHE =12CH •EM ，根据全等三角形的性质得到EM ＝AB ＝16，求得S △CEF ＝8CH ，根据相似三角形的性质得到DE AB =DH AE ，设AE 为x ，于是得到DH =116（﹣x 2+16x ）=−116（x ﹣8）2+4≤4，即可得到结论．【解答】解：过F 作FG ⊥DC 于点G ，FM ⊥AD ，交AD 的延长线于M ，连接CF ，∵S △CEF ＝S △CHF +S △CHE =12CH •EM ，∵△EMF ≌△BAE ，∴EM ＝AB ＝16，∴S △CEF ＝8CH ，∵△EDH ∽△BAE ，∴DE AB =DH AE ，设AE 为x ，则DH =116（﹣x 2+16x ）=−116（x ﹣8）2+4≤4， ∴DH ≤4，∴CH ≥12，CH 最小值是12，∴△CEF 面积的最小值是96．故选：C ．【点睛】本题考查了正方形的性质，解题的关键是找出线段DN 的最大值，根据三角形的面积公式找出其去最值的条件，再结合二次函数的性质去解决最值问题．【变式4-2】（2020•昆山市二模）如图，在△ABC 中，AB ＝10，AC ＝2√5，∠ACB ＝45°，D 为AB 边上一动点（不与点B 重合），以CD 为边长作正方形CDEF ，连接BE ，则△BDE 的面积的最大值等于（ ）.A．9√2B．18C．36D．20√5【分析】如图，过点E作EM⊥BA于M，过点C作CN⊥BA交BA的延长线于N，过点A作AH⊥BC于H．解直角三角形求出BN的长，设BD＝x，则DN＝12﹣x，再利用全等三角形的性质证明EM＝DN＝12﹣x，利用三角形的面积公式构建二次函数，利用二次函数的性质即可解决问题．【解答】解：如图，过点E作EM⊥BA于M，过点C作CN⊥BA交BA的延长线于N，过点A作AH⊥BC于H．在Rt△ACH中，∵∠AHC＝90°，∠ACH＝45°，AC＝2√5，∴AH＝CH＝AC•cos45°=√10，在Rt△ABH中，∵∠AHB＝90°，AB＝10，AH=√10，∴BH=√AB2−AH2=√102−(√10)2=3√10，∴BC＝BH+CH＝4√10，∵S△ACB=12•BC•AH=12•AB•CN，∴CN＝4，在Rt△ACN中，AN=√AC2−CN2=√(2√5)2−42=2，∴BN＝BA+AN＝12，设BD＝x，则DN＝12﹣x，∵四边形EFCD是正方形，∴DE＝DC，∠EDC＝∠EMD＝∠DNC＝90°，∴∠EDM+∠ADC＝90°，∠ADC+∠DCN＝90°，∴∠EDM＝∠DCN，∴△EMD≌△DNC（AAS），∴EM＝DN＝12﹣x，∴S△DBE=12•BD•EM=12•x•（12﹣x）=−12x2+6x=−12（x﹣6）2+18，∵−12＜0，∴当x ＝6时，△BDE 的面积的最大，最大值为18．故选：B ．【点睛】本题考查正方形的性质，解直角三角形，二次函数的性质等知识，解题的关键是学会利用参数构建二次函数，利用二次函数的性质解决问题．16．（2021•石家庄模拟）如图，在平面直角坐标系xOy 中，半径为2的⊙O 与x 轴的正半轴交于点A ，点B 是⊙O 上一动点，点C 为弦AB 的中点，直线y =34x ﹣3与x 轴、y 轴分别交于点D 、E ，则△CDE 面积的最小值与最大值分别为（ ）．A ．2；7B ．3；6C ．4；9D ．5；16【分析】连接OC ，由垂径定理得OC ⊥AB ，再由圆周角定理得点C 在以OA 为直径的圆上（点O 、A 除外），以OA 为直角作⊙P ，过P 点作直线PH ⊥DE 于H ，交⊙P 于M 、N ，利用一次函数解析式确定D （0，﹣3），D （4，0），则AB ＝5，然后证△DPH ∽△DEO ，利用相似比求出PH 的长，得MP 、NH 的长，当C 点与M 点重合时，S 最大；C 点与N 点重合时，S 最小，然后计算出S △NED 和S △MED 得到S 的范围，即可求解．【解答】解：连接OC ，如图，∵点C 为弦AB 的中点，∴OC ⊥AB ，∴∠ACO ＝90°，∴点C 在以OA 为直径的圆上（点O 、A 除外），以OA 为直角作⊙P ，过P 点作直线PH ⊥DE 于H ，交⊙P 于M 、N ，当x ＝0时，y =34x ﹣3＝﹣3，则D （0，﹣3），当y ＝0时，34x ﹣3＝0，解得x＝4，则D（4，0），∴OD＝4，∴AB=√32+42=5，∵A（2，0），∴P（1，0），∴OP＝1，∴PD＝OD﹣OP＝3，∵∠PDH＝∠EDO，∠PHD＝∠EOD，∴△DPH∽△DEO，∴PH：OE＝DP：DE，即PH：3＝3：5，解得PH=9 5，∴MP＝PH+1=145，NH＝PH﹣1=45，∴S△NED=12×5×45=2，S△MED=12×5×145=7，设△CDE面积为S，当C点与M点重合时，S最大；C点与N点重合时，S最小，∴S的范围为2≤S≤7，∴△CDE面积的最小值为2，△CDE面积的最大值为7，故选：A．【点睛】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了圆周角定理、相似三角形的判定与性质和一次函数的性质．。
中考数学压轴题之几何最值及路径长(作业及答案)
1几何最值及路径长（作业）例1：如图，在矩形ABCD 中，AB=12，AD=3，E，F 分别为AB，CD 上的两个动点，则AF+FE+EC 的最小值为．【思路分析】所求目标是AF+FE+EC 的最小值，属于最值问题．分析定点、动点，寻找不变特征．A，C 为定点，E，F 为动点，且点E 在定线段AB 上动，点F 在定线段CD 上动．由定点、动点的特征判断为轴对称最值模型．作定点A 关于定直线CD 的对称点A′，作定点C 关于定直线AB 的对称点C′．根据对称可知，A′F=AF，C′E=CE，所求问题转化为求A′F+FE+C′E 的最小值，根据定理“两点之间，线段最短”，连接A′C′，线段A′C′的长度即为最小值．判断所求最值为线段A′C′的长，设计方案求解．根据勾股定理，A′C′=15，即最小值为15．例2：如图，已知AB=10，点C，D 在线段AB 上，且AC=BD=2．P 是线段CD 上的一动点，分别以AP，PB 为边在线段AB 的同侧作等边三角形AEP 和等边三角形PFB，连接EF，设EF 的中点为G．当点P 从点C 运动到点D 时，点G 移动的路径长为．23【思路分析】分析不变特征．在点P 运动的过程中，两个等边三角形始终不变、点G 为EF 的中点不变、线段AB 的长度不变．猜测运动路径．分别选择点P 在起点C、终点D 时的对应图，结合已知图中点G 的位置，猜测路径为线段，如图1，图2．图1 图2验证运动路径．猜测运动路径是线段，且平行于AB，只需证明点G 到线段AB 的距离为定值即可，故分别过点E，F，G 作AB 的垂线，如图3，可证GH 为梯形EMNF 的中位线，GH =1(EM +FN )；2因为△APE 和△BPF 均为等边三角形，故EM +FN =3(PM +PN ) =动路径为线段．3AB ，因此GH 为定值，可确定点G 的运2图3 图4设计方案计算路径长．补全，得图形4，可知QECF 为平行四边形，则G1 为QC 中点，同理可知G2 为QD 中点，故G1G2=1CD =1(10 - 2 - 2) =3 ．2 2123422.如图，当四边形PABN 的周长最小时，a 的值为．3.如图，在菱形ABCD 中，∠A=60°，AB=3，⊙A，⊙B 的半径分别为2 和1，P，E，F 分别是边CD，⊙A 和⊙B 上的动点，则PE+PF 的最小值是．4.如图，在Rt△AOB 中，OA=OB= 3 ，⊙O 的半径为1，点P是AB 边上的动点，过点P 作⊙O 的一条切线PQ（点Q 为切点），则PQ 长度的最小值为．5.如图，折叠矩形纸片ABCD，使点B 落在边AD 上，折痕EF的两端分别在AB，BC 上（含端点），且AB=6cm，BC=10cm，则折痕EF 的最大值是．第3 题图第4 题图第2 题图第1 题图D．2 6）C．2 3B．3 2A．31. 如图，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P，使PD+PE的和最小，则这个最小值为（6.动手操作：在矩形纸片ABCD 中，AB=5，AD=13．如图所示，折叠纸片，使点A 落在BC 边上的A′处，折痕为PQ，当点A′ 在BC 边上移动时，折痕的端点P，Q 也随之移动．若限定点P，Q 分别在AB，AD 边上移动，则点A′在BC 边上可移动的最大距离为．7.如图，在△ABC 中，∠ACB=90°，AC=6，BC=2，点A，C 分别在x 轴、y 轴上．当点A 在x 轴上运动时，点C 随之在y 轴上运动，则在运动过程中，点B 到原点的最大距离为．第7 题图第8 题图8.如图，正方形ABCD 的边长是2，M 是AD 的中点，点E 从点A 出发，沿AB 运动到点B 停止．连接EM，过M 作EM 的垂线交射线BC 于点F，连接EF．若P 是MF 的中点，则在点E 运动的过程中，点P 运动的路径长为．9.如图，正方形ABCD 的边长为2，将长为2 的线段EF 的两端放在正方形的相邻两边上同时滑动．如果点E 从点A 出发，按A→B→C→D→A 的方向滑动到点A 为止，同时点F 从点B 出发，按B→C→D→A→B 的方向滑动到点B 为止，则在这个过程中，线段EF 的中点M 经过的路径所围成的图形面积为．10.如图，以G(0，1)为圆心，2 为半径的圆与x 轴交于A，B 两点，与y 轴交于C，D 两点，点E 为⊙G 上一动点，CF⊥AE 于点F．当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为．11.如图，在Rt△ABC 中，∠C=90°，AC=6，BC=8，动点P 从点A 开始沿边AC 向点C 以每秒1 个单位长度的速度运动，动点Q 从点C 开始沿边CB 向点B 以每秒2 个单位长度的速度运动，过点P 作PD∥BC，交AB 于点D，连接PQ．点P，Q 分别从点A，C 同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t 秒（t≥0）．求在整个运动过程中线段PQ 的中点M 所经过的路径长．【参考答案】1. C2. 7 43. 34. 25. 10 1036. 47. 3+ 138. 29. 4 - π 10. 311. 22 3π5。
中考数学题型三 选择压轴题之几何最值问题
类型 2 利用“轴对称”求最值
高分技法
“将军饮马”问题是中考的热点问题之一,解决这类问题的方法 是找出两定点中任一点关于动点所在直线的对称点,再将另一点 与对称点相连,连线与直线的交点即为所求的点.通常情况下,求 三角形或四边形的周长的最小值时,往往也是利用轴对称进行解 题(详细讲解见“高分突破·微专项 利用对称解决与线段长有 关的最值问题”).
类型 3 利用“隐形圆”求最值
高分技法
利用“到定点的距离等于定长的点位于同一个圆上”或“90°的 圆周角所对的弦是直径”等可以确定某些动点的运动轨迹是圆 (或圆弧).当圆外一定点与圆上一动点位于圆心同侧,且三点共线 时,该动点到圆外定点的距离最短; 当圆外一定点与圆上一动点 位于圆心异侧,且三点共线时,该动点到圆外定点的距离最长.
题型帮
题型三 选择压轴题之几何最值问题
目录
考法帮
• 类型1 利用“垂线段最短”求最值 • 类型2 利用“轴对称”求最值 • 类型3 利用“隐形圆”求最值 • 类型4 利用“旋转”求最值 • 类型5 利用二次函数的性质求最值
考法帮
类型 1 利用“垂线段最短”求最值
例1 如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB
类型 4 利用“旋转”求最值 例4 [2021山东淄博中考改编]两张宽为3的纸条交叉重叠成四边形 ABCD,如图所示.若α=30°,则对角线BD上的动点P到A,B,C三点距 离之和的最小值是 ( )B
A.3 B.6 2C.2 5D.5
类型 5 利用二次函数的性质求最值
例5 如图,在△ABC中,AB=AC=5,BC=4 5,D为边AB上一动点(不与B 点重合),以CD为一边作正方形CDEF,连接BE,则△BDE的面积的最大 值为 8 .
压轴题中路径最值问题
1路径最值问题1、如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。
（1）求该抛物线的解析式；（2）动点P 在轴上移动，当△PAE 是直角三角形时，求点P 的坐标P 。
（3）在抛物线的对称轴上找一点M ，使||AM MC -的值最大，求出点M 的坐标。
2、如图，已知抛物线y＝ax2＋bx＋c与y轴交于点A(0，3)，与x轴分别交于B(1，0)、C(5，0)两点．（1）求此抛物线的解析式；（2）若一个动点P自OA的中点M出发，先到达x轴上的某点（设为点E），再到达抛物线的对称轴上某点（设为点F），最后运动到点A．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．23、已知,如图11,二次函数223y ax ax a=+-(0)a≠图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y对称.（1）求A、B两点坐标,并证明点A在直线l上;（2）求二次函数解析式;（3）过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN NM MK++和的最小值.1,4），交x轴于A、B，交y轴于D，其中B点的坐标F，其中E点的横坐标为2，若直线PQ为抛物线的D、G、F、H四点围成的四边形周长最小.若存在，M，过点M作直线MN∥BD，交线段AD于点.34路径最值问题1、如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。
（1）求该抛物线的解析式；（2）动点P 在轴上移动，当△PAE 是直角三角形时，求点P 的坐标P 。
（3）在抛物线的对称轴上找一点M ，使||AM MC -的值最大，求出点M 的坐标。
中考最值问题和路径问题精选
最值问题和路径问题精选1．（2019•锡山区一模）在平面直角坐标系中，已知平行四边形ABCD的点A（0，﹣2）、点B（3m，4m+1）（m≠﹣1），点C（6，2），则对角线BD的最小值是（）A．3B．2C．5 D．62．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E为⊙G上一动点，CF⊥AE于F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（）A．B．C．D．3．（2018•江阴市模拟）如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE＝2，BF＝EG，DG＞AE，则DI的最小值等于（）A．+3 B．2﹣2 C．2﹣D．2+3 4．（2018•惠山区校级二模）如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为（）A．3+2B．4+3C．2+2D．10 5．（2017•江阴市校级模拟）直线y＝x+4分别与x轴、y轴相交于点M，N，边长为2的正方形OABC一个顶点O在坐标系的原点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点（0，2）长度的最小值是（）A．2﹣2 B．3﹣2C．D．1 6．（2017•南长区一模）如图，已知△ABC在平面直角坐标系中，其中点A、B、C三点的坐标分别为（1，2），（﹣1，0），（3，0），点D为BC中点，P是AC上的一个动点（P 与点A、C不重合），连接PB、PD，则△PBD周长的最小值是（）A．2+2 B．3+2 C．4D．2+3 7．（2014•徐州二模）如图，在△ABC中，∠C＝90°，AC＝4，BC＝2，点A、C分别在x 轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是（）A．6 B．C．D．8．（2018•连云港模拟）如图，P为正方形ABCD对角线BD上一动点，若AB＝2，则AP+BP+CP 的最小值为（）A．+B．+C．4 D．3 9．（2012•台州）如图，菱形ABCD中，AB＝2，∠A＝120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（）A．1 B．C．2 D．+1 10．（2016•张家界模拟）如图，OP平分∠MON，P A⊥ON于点A，点Q是射线OM上一个动点，若P A＝3，则PQ的最小值为（）A．B．2 C．3 D．211．如图，已知▱OABC的顶点A、C分别在直线x＝1和x＝4上，O是坐标原点，则对角线OB长的最小值为．12．（2018•苏州模拟）如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE＝1，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段，垂足为点H，在点P从点F（0，）运动到原点O的过程中，点H的运动路径长为．13．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点F在边AC上，并且CF＝2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB 距离的最小值是．14．（2016•滨湖区模拟）在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标为（，0）、（3，0）、（0，5），点D在第一象限，且∠ADB＝60°，则线段CD的长的最小值为．15．（2017•江阴市校级一模）如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC＝2，P是△ABC所在平面内一点，且满足P A⊥PB，则PC的取值范围为．16．（2015•台州）如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为．17．（2015•无锡模拟）如图，⊙O的半径为1，点P（a，a﹣4）为⊙O外一点，过点P作⊙O的两条切线，切点分别为点A和点B，则四边形PBOA面积的最小值是．18．（2015•惠山区二模）如图，菱形ABCD的对角线AC上有一动点P，BC＝6，∠ABC＝150°，则线段AP+BP+PD的最小值为．19．（2015•滨湖区二模）已知线段AB＝10，C．D是AB上两点，且AC＝DB＝2，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF 的中点，点P由点C移动到点D时，G点移动的路径长度为．20．（2018•陕西模拟）如图，正方形ABCD中，AB＝2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP 的最小值为．21．（2018•大荔县三模）如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是．22．（2018春•凤翔县月考）如图，在正方形ABCD中，AB＝4，E是BC边的中点，F是CD 边上的一点，且DF＝1，若M、N分别是线段AD、AE上的动点，则MN+MF的最小值为．23．（2018秋•兰州期中）如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线BD上有一点P，使PC+PE的和最小，则这个最小值为．24．（2018春•九台区期末）如图，正方形ABCD的边长为8，点M在边DC上，且DM＝2，N为对角线AC上任意一点，则DN+MN的最小值为．25．（2017•吉州区模拟）如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为．26．（2019•锡山区一模）在平面直角坐标系中，已知A（2，4）、P（1，0），B为y轴上的动点，以AB为边构造△ABC，使点C在x轴上，∠BAC＝90°．M为BC的中点，则PM的最小值为．27．（2019•锡山区一模）如图，△ABC中，∠BAC＝90°，AC＝12，AB＝10，D是AC上一个动点，以AD为直径的⊙O交BD于E，则线段CE的最小值是．28．（2019•宜兴市一模）如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点F在边AC 上，并且CF＝1，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．29．（2019•常州模拟）如图，⊙O的半径为1，P是⊙O外一点，OP＝2，Q是⊙O上的动点，线段PQ的中点为M，连接OP、OM，则线段OM的最小值是．30．（2018•无锡模拟）如图，⊙O的直径AB＝8，C为的中点，P为⊙O上一动点，连接AP、CP，过C作CD⊥CP交AP于点D，点P从B运动到C时，则点D运动的路径长为．31．（2018•滨湖区二模）如图，在四边形ABCD中，AB∥CD，AB＝BC＝BD＝2，AD＝1，则AC＝．32．（2017•无锡一模）如图，正方形ABCD的边长为1，点P为BC上任意一点（可以与B 点或C重合），分别过B，C，D作射线AP的垂线，垂足分别是B'，C'，D'，则BB'+CC'+DD'的最大值与最小值的和为．33．如图，△ABC∽△ADE，∠BAC＝∠DAE＝90°，AB＝6，AC＝8，F为DE中点，若点D在直线BC上运动，连接CF，则在点D运动过程中，线段CF的最小值是．34．如图，线段AB为⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，点P是⊙O 上一动点，连接CP，以CP为斜边在PC的上方作Rt△PCD，且使∠DCP＝60°，连接OD，则OD长的最大值为．35．（2017•江阴市一模）如图，在平行四边形ABCD中，∠BCD＝30°，BC＝6，CD＝，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．36．（2017•南长区一模）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB ∥x轴．直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么AD的长为．37．（2017•惠山区模拟）已知，在平面直角坐标系中，点A（4，0），点B（m，m），点C为线段OA上一点（点O为原点），则AB+BC的最小值为．38．（2016•宜兴市校级一模）在菱形ABCD中，AB＝10cm，对角线BD＝16cm，M、N分别是BD、BC上的动点，则CM+MN的最值为cm．39．如图，矩形ABCD中，AB＝6，AD＝8，点E在边AD上，且AE：ED＝1：3．动点P 从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交射线BC于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为．参考答案与试题解析1．（2019•锡山区一模）在平面直角坐标系中，已知平行四边形ABCD的点A（0，﹣2）、点B（3m，4m+1）（m≠﹣1），点C（6，2），则对角线BD的最小值是（）A．3B．2C．5 D．6【分析】方法1：先根据B（3m，4m+1），可知B在直线y＝x+1上，所以当BD⊥直线y＝x+1时，BD最小，找一等量关系列关于m的方程，作辅助线：过B作BH⊥x轴于H，则BH＝4m+1，利用三角形相似得BH2＝EH•FH，列等式求m的值，得BD的长即可．方法2：先根据B（3m，4m+1），可知B在直线y＝x+1上，所以当BD⊥直线y＝x+1时，BD最小，因为平行四边形对角线交于一点，且AC的中点一定在x轴上，可得F是AC的中点，F（3，0），设直线BF的解析式为y＝﹣x+b，根据待定系数法可求BF的解析式，进一步得到B点坐标，根据两点间的距离公式可求BF，进一步得到对角线BD 的最小值．【解答】解：方法1：如图，∵点B（3m，4m+1），∴令，∴y＝x+1，∴B在直线y＝x+1上，∴当BD⊥直线y＝x+1时，BD最小，过B作BH⊥x轴于H，则BH＝4m+1，∵BE在直线y＝x+1上，且点E在x轴上，∴E（﹣，0），G（0，1），∵平行四边形对角线交于一点，且AC的中点一定在x轴上，∴F是AC的中点，∵A（0，﹣2），点C（6，2），∴F（3，0）．在Rt△BEF中，∵BH2＝EH•FH，∴（4m+1）2＝（3m+）（3﹣3m），解得：m1＝﹣（舍），m2＝，∴B（，），∴BD＝2BF＝2×＝6，则对角线BD的最小值是6；方法2：如图，∵点B（3m，4m+1），∴令，∴y＝x+1，∴B在直线y＝x+1上，∴当BD⊥直线y＝x+1时，BD最小，∵平行四边形对角线交于一点，且AC的中点一定在x轴上，∴F是AC的中点，∵A（0，﹣2），点C（6，2），∴F（3，0）．设直线BF的解析式为y＝﹣x+b，则﹣×3+b＝0，解得b＝，则直线BF的解析式为y＝﹣x+，∴4m+1＝﹣×3m+，解得m＝，∴B（，），∴BF＝＝3，∴BD＝2BF＝6，则对角线BD的最小值是6．故选：D．【点评】本题考查了平行四边形的性质、利用待定系数法求一次函数的解析式、射影定理或三角形相似的判定、图形与坐标特点、勾股定理，本题利用B的坐标确定点B所在的直线的解析式是关键．2．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E为⊙G上一动点，CF⊥AE于F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（）A．B．C．D．【分析】连接AC，AG，由OG垂直于AB，利用垂径定理得到O为AB的中点，由G的坐标确定出OG的长，在直角三角形AOG中，由AG与OG的长，利用勾股定理求出AO 的长，进而确定出AB的长，由CG+GO求出OC的长，在直角三角形AOC中，利用勾股定理求出AC的长，由CF垂直于AE，得到三角形ACF始终为直角三角形，点F的运动轨迹为以AC为直径的半径，如图中红线所示，当E位于点B时，CO⊥AE，此时F 与O重合；当E位于D时，CA⊥AE，此时F与A重合，可得出当点E从点B出发顺时针运动到点D时，点F所经过的路径长，在直角三角形ACO中，利用锐角三角函数定义求出∠ACO的度数，进而确定出所对圆心角的度数，再由AC的长求出半径，利用弧长公式即可求出的长．【解答】解：连接AC，AG，∵GO⊥AB，∴O为AB的中点，即AO＝BO＝AB，∵G（0，1），即OG＝1，∴在Rt△AOG中，根据勾股定理得：AO＝＝，∴AB＝2AO＝2，又CO＝CG+GO＝2+1＝3，∴在Rt△AOC中，根据勾股定理得：AC＝＝2，∵CF⊥AE，∴△ACF始终是直角三角形，点F的运动轨迹为以AC为直径的半圆，当E位于点B时，CO⊥AE，此时F与O重合；当E位于D时，CA⊥AE，此时F与A 重合，∴当点E从点B出发顺时针运动到点D时，点F所经过的路径长，在Rt△ACO中，tan∠ACO＝＝，∴∠ACO＝30°，∴度数为60°，∵直径AC＝2，∴的长为＝π，则当点E从点B出发顺时针运动到点D时，点F所经过的路径长π．故选：B．【点评】此题属于圆综合题，涉及的知识有：坐标与图形性质，勾股定理，锐角三角函数定义，弧长公式，以及圆周角定理，其中根据题意得到点E从点B出发顺时针运动到点D时，点F所经过的路径长是解本题的关键．3．（2018•江阴市模拟）如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE＝2，BF＝EG，DG＞AE，则DI的最小值等于（）A．+3 B．2﹣2 C．2﹣D．2+3【分析】过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，根据HL证明Rt △BAF≌Rt△EMG，可得∠ABF＝∠MEG，所以再证明∠EPF＝90°，由直角三角形斜边上的中线等于斜边的一半可得OI＝BE，由OD﹣OI≤DI，当O、D、I共线时，DI 有最小值，即可求DI的最小值．【解答】解：如图，过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，∵四边形ABCD是正方形，∴AB＝AD，∠A＝∠D＝∠DME＝90°，AB∥CD，∴四边形ADME是矩形，∴EM＝AD＝AB，∵BF＝EG，∴Rt△BAF≌Rt△EMG（HL），∴∠ABF＝∠MEG，∠AFB＝∠EGM，∵AB∥CD∴∠MGE＝∠BEG＝∠AFB∵∠ABF+∠AFB＝90°∴∠ABF+∠BEG＝90°∴∠EIF＝90°，∴BF⊥EG；∵△EIB是直角三角形，∴OI＝BE，∵AB＝6，AE＝2，∴BE＝6﹣2＝4，OB＝OE＝2，∵OD﹣OI≤DI，∴当O、D、I共线时，DI有最小值，∵IO＝BE＝2，∴OD＝＝2，∴ID＝2﹣2，即DI的最小值为2﹣2，故选：B．【点评】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，三角形的三边关系，熟记性质并作辅助线构造出全等三角形是解题的关键，也是本题的难点，在几何证明中常利用三角形的三边关系解决线段的最值问题．4．（2018•惠山区校级二模）如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为（）A．3+2B．4+3C．2+2D．10【分析】将△AMD绕点A逆时针旋转60°得到△AM’D’，MD＝M’D’，易得到△ADD’和△AMM’均为等边三角形，推出AM＝MM’可得MA+MD+ME＝D’M+MM’+ME，共线时最短；由于点E也为动点，可得当D’E⊥BC时最短，此时易求得D’E＝DG+GE 的值；【解答】解：将△AMD绕点A逆时针旋转60°得到△AM’D’，MD＝M’D’，易得到△ADD’和△AMM’均为等边三角形，∴AM＝MM’，∴MA+MD+ME＝D’M+MM’+ME，∴D′M、MM′、ME共线时最短，由于点E也为动点，∴当D’E⊥BC时最短，此时易求得D’E＝DG+GE＝4+3，∴MA+MD+ME的最小值为4+3．故选：B．【点评】本题考查轴对称、旋转变换、矩形的性质等知识，解题的关键是学会添加常用辅助线，构造等边三角形解决问题，学会用转化的思想思考问题，属于中考选择题中的压轴题．5．（2017•江阴市校级模拟）直线y＝x+4分别与x轴、y轴相交于点M，N，边长为2的正方形OABC一个顶点O在坐标系的原点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点（0，2）长度的最小值是（）A．2﹣2 B．3﹣2C．D．1【分析】首先证明△MOC≌△NOA，推出∠MPN＝90°，推出P在以MN为直径的圆上，所以当圆心G，点P，C（0，2）三点共线时，P到C（0，2）的最小值．求出此时的PC 即可．【解答】解：在△MOC和△NOA中，，∴△MOC≌△NOA，∴∠CMO＝∠ANO，∵∠CMO+∠MCO＝90°，∠MCO＝∠NCP，∴∠NCP+∠CNP＝90°，∴∠MPN＝90°∴MP⊥NP，在正方形旋转的过程中，同理可证，∴∠CMO＝∠ANO，可得∠MPN＝90°，MP⊥NP，∴P在以MN为直径的圆上，∵M（﹣4，0），N（0，4），∴圆心G为（﹣2，2），半径为2，∵PG﹣GC≤PC，∴当圆心G，点P，C（0，2）三点共线时，PC最小，∵GN＝GM，CN＝CO＝2，∴GC＝OM＝2，这个最小值为GP﹣GC＝2﹣2．故选：A．【点评】本题考查一次函数与几何变换、正方形的性质、圆的有关知识，解题的关键是发现点P在以MN为直径的圆上，确定点P的位置是解题的关键，属于中考常考题型．6．（2017•南长区一模）如图，已知△ABC在平面直角坐标系中，其中点A、B、C三点的坐标分别为（1，2），（﹣1，0），（3，0），点D为BC中点，P是AC上的一个动点（P 与点A、C不重合），连接PB、PD，则△PBD周长的最小值是（）A．2+2 B．3+2 C．4D．2+3【分析】首先根据给出的点的坐标判定三角形ABC是等边三角形，作点B关于AC的对称点E，连接EP、EB、ED、EC，则PB+PD＝PE+PD，因此ED的长就是PB+PD的最小值，即当点P运动到ED与AC的交点G时，△PBD的周长最小．【解答】解：如图，作点B关于AC的对称点E，连接EP、EB、ED、EC，则PB+PD＝PE+PD，因此ED的长就是PB+PD的最小值，即当点P运动到ED与AC的交点G时，△PBD的周长最小．∵A、B、C三点的坐标分别为（1，2），（﹣1，0），（3，0），点D为BC中点，∴AB＝＝4，BC＝4，AC＝＝4，∴△ABC是等边三角形，从点D作DF⊥BE，垂足为F，因为BC＝4，所以BD＝2，BE＝2＝4，因为∠DBF＝30°，所以DF＝BD＝1，BF＝，EF＝BE﹣BF＝4﹣＝3，DE＝＝2，所以△PBD的周长的最小值是2+2，故选：A．【点评】本题考查了等边三角形的判定和性质以及勾股定理的灵活运用，解本题的关键是作出恰当的图形，并且根据勾股定理求各边长．7．（2014•徐州二模）如图，在△ABC中，∠C＝90°，AC＝4，BC＝2，点A、C分别在x 轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是（）A．6 B．C．D．【分析】点A，C分别在x轴、y轴上，当点A在x轴运动时，点C随之在y轴上运动，在运动过程中，点O在到AC的中点的距离不变．本题可通过设出AC的中点坐标，根据B、D、O在一条直线上时，点B到原点O的最大可得出答案．【解答】解：作AC的中点D，连接OD、DB，∵OB≤OD+BD，∴当O、D、B三点共线时OB取得最大值，∵D是AC中点，∴OD＝AC＝2，∵BD＝＝2，OD＝AC＝2，∴点B到原点O的最大距离为2+2，故选：D．【点评】此题主要考查了两点间的距离，以及勾股定理的应用，本题的难度较大，理解D到O的距离不变是解决本题的关键．8．（2018•连云港模拟）如图，P为正方形ABCD对角线BD上一动点，若AB＝2，则AP+BP+CP 的最小值为（）A．+B．+C．4 D．3【分析】如图将△ABP绕点A顺时针旋转60°得到△AEF，当E、F、P、C共线时，P A+PB+PC 最小，作EM⊥DA交DA的延长线于M，ME的延长线交CB的延长线于N，在RT△ECN 中理由勾股定理即可解决问题．【解答】解：如图将△ABP绕点A顺时针旋转60°得到△AEF，当E、F、P、C共线时，P A+PB+PC最小．理由：∵AP＝AF，∠P AF＝60°，∴△P AF是等边三角形，∴P A＝PF＝AF，EF＝PB，∴P A+PB+PC＝EF+PF+PC，∴当E、F、P、C共线时，P A+PB+PC最小，作EM⊥DA交DA的延长线于M，ME的延长线交CB的延长线于N，则四边形ABNM 是矩形，在RT△AME中，∵∠M＝90°，∠MAE＝30°，AE＝2，∴ME＝1，AM＝BN＝，MN＝AB＝2，EN＝1，∴EC＝＝＝＝＝＝+．∴P A+PB+PC的最小值为+．故选：B．【点评】本题考查正方形的性质、轴对称﹣最短问题、旋转变换等知识，解题的关键是利用旋转添加辅助线，构造全等三角形，属于中考常考题型．9．（2012•台州）如图，菱形ABCD中，AB＝2，∠A＝120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（）A．1 B．C．2 D．+1【分析】先根据四边形ABCD是菱形可知，AD∥BC，由∠A＝120°可知∠B＝60°，作点P关于直线BD的对称点P′，连接P′Q，PC，则P′Q的长即为PK+QK的最小值，由图可知，当点Q与点C重合，CP′⊥AB时PK+QK的值最小，再在Rt△BCP′中利用锐角三角函数的定义求出P′C的长即可．【解答】解：∵四边形ABCD是菱形，∴AD∥BC，∵∠A＝120°，∴∠B＝180°﹣∠A＝180°﹣120°＝60°，作点P关于直线BD的对称点P′，连接P′Q，P′C，则P′Q的长即为PK+QK的最小值，由图可知，当点Q与点C重合，CP′⊥AB时PK+QK的值最小，在Rt△BCP′中，∵BC＝AB＝2，∠B＝60°，∴P′Q＝CP′＝BC•sin B＝2×＝．故选：B．【点评】本题考查的是轴对称﹣最短路线问题及菱形的性质，根据题意作出辅助线，构造出直角三角形是解答此题的关键．10．（2016•张家界模拟）如图，OP平分∠MON，P A⊥ON于点A，点Q是射线OM上一个动点，若P A＝3，则PQ的最小值为（）A．B．2 C．3 D．2【分析】首先过点P作PB⊥OM于B，由OP平分∠MON，P A⊥ON，P A＝3，根据角平分线的性质，即可求得PB的值，又由垂线段最短，可求得PQ的最小值．【解答】解：过点P作PB⊥OM于B，∵OP平分∠MON，P A⊥ON，P A＝3，∴PB＝P A＝3，∴PQ的最小值为3．故选：C．【点评】此题考查了角平分线的性质与垂线段最短的知识．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．11．如图，已知▱OABC的顶点A、C分别在直线x＝1和x＝4上，O是坐标原点，则对角线OB长的最小值为5．【分析】过点B作BD⊥直线x＝4，交直线x＝4于点D，过点B作BE⊥x轴，交x轴于点E．则OB＝．由于四边形OABC是平行四边形，所以OA＝BC，又由平行四边形的性质可推得∠OAF＝∠BCD，则可证明△OAF≌△BCD，所以OE的长固定不变，当BE最小时，OB取得最小值，从而可求．【解答】解：过点B作BD⊥直线x＝4，交直线x＝4于点D，过点B作BE⊥x轴，交x 轴于点E，直线x＝1与OC交于点M，与x轴交于点F，直线x＝4与AB交于点N，如图：∵四边形OABC是平行四边形，∴∠OAB＝∠BCO，OC∥AB，OA＝BC，∵直线x＝1与直线x＝4均垂直于x轴，∴AM∥CN，∴四边形ANCM是平行四边形，∴∠MAN＝∠NCM，∴∠OAF＝∠BCD，∵∠OF A＝∠BDC＝90°，∴∠FOA＝∠DBC，在△OAF和△BCD中，，∴△OAF≌△BCD．∴BD＝OF＝1，∴OE＝4+1＝5，∴OB＝．由于OE的长不变，所以当BE最小时（即B点在x轴上），OB取得最小值，最小值为OB＝OE＝5．故答案为：5．【点评】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．12．（2018•苏州模拟）如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE＝1，已知点P为y轴上一动点，连接EP，过点O 作直线EP的垂线段，垂足为点H，在点P从点F（0，）运动到原点O的过程中，点H的运动路径长为π．【分析】H经过的路径是以OE为直径的弧，连接OE，首先求得△OPE的面积，然后利用三角形面积公式求得OH的长，然后在直角△OEH中，利用三角函数求得∠OEH的度数，然后利用长公式即可求解．【解答】解：连接OE．当点P与点F重合时，S△OPE＝××7＝，在直角△OEA中，OE＝＝＝＝5，PE＝＝，∵S△OPE＝PE•OH，即×OH＝，∴OH＝5，∴在直角△OEH中，sin∠OEH＝＝＝，∴∠OEH＝45°，点H的运动路径长是：＝π．故答案是：π．【点评】本题考查了点的运动轨迹以及弧长公式，理解H运动的路径，求得对应的圆心角是关键．13．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点F在边AC上，并且CF＝2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB 距离的最小值是 1.2．【分析】如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小，利用△AFM ∽△ABC，得到＝求出FM即可解决问题．【解答】解：如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．（点P 在以F为圆心CF为半径的圆上，当FP⊥AB时，点P到AB的距离最小）∵∠A＝∠A，∠AMF＝∠C＝90°，∴△AFM∽△ABC，∴＝，∵CF＝2，AC＝6，BC＝8，∴AF＝4，AB＝＝10，∴＝，∴FM＝3.2，∵PF＝CF＝2，∴PM＝1.2∴点P到边AB距离的最小值是1.2．故答案为1.2．【点评】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理．垂线段最短等知识，解题的关键是正确找到点P位置，属于中考常考题型．14．（2016•滨湖区模拟）在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标为（，0）、（3，0）、（0，5），点D在第一象限，且∠ADB＝60°，则线段CD的长的最小值为2﹣2．【分析】作圆，求出半径和PC的长度，判出点D只有在CP上时CD最短，CD＝CP﹣DP求解．【解答】解：作圆，使∠ADB＝60°，设圆心为P，连结P A、PB、PC，PE⊥AB于E，如图所示：∵A（，0）、B（3，0），∴E（2，0）又∠ADB＝60°，∴∠APB＝120°，∴PE＝1，P A＝2PE＝2，∴P（2，1），∵C（0，5），∴PC＝＝2，又∵PD＝P A＝2，∴只有点D在线段PC上时，CD最短（点D在别的位置时构成△CDP）∴CD最小值为：2﹣2．故答案为：2﹣2．【点评】本题主要考查坐标与图形的性质，圆周角定理及勾股定理，解决本题的关键是判出点D只有在CP上时CD最短．15．（2017•江阴市校级一模）如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC＝2，P是△ABC所在平面内一点，且满足P A⊥PB，则PC的取值范围为﹣1≤PC≤+1．【分析】据条件可知线段AB是定值且AB所对的张角∠APB是定值，根据直径所对圆周角为直角可知，动点P的运动轨迹在过点A、B、P三点的圆周上（不与A、B重合），连结CO并延长交圆O分别为P1、P2，PC的在P1C最小，P2C最大，据此求解可得．【解答】解：∵P A⊥PB，即∠APB＝90°，AB＝BC＝2，∴点P在以AB为直径、AB的中点O为圆心的⊙O上，如图，连接CO交⊙O于点P1，并延长CO交⊙O于点P2，∵BO＝AB＝1、BC＝2，∠ABC＝90°，∴CO＝＝＝，当点P位于点P1时，PC的长度最小，此时PC＝OC﹣OP＝﹣1；当点P位于点P2时，PC的长度最大．此时PC＝OC+OP＝+1；∴﹣1≤PC≤+1，故答案为：﹣1≤PC≤+1．【点评】本题主要考查圆周角定理、勾股定理、点与圆的位置关系，根据AB是定值且AB所对的张角∠APB＝90°得出点P的运动轨迹是解题的关键．16．（2015•台州）如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为．【分析】当正六边形EFGHIJ的边长最大时，要使AE最小，六边形对角线EH与正方形的边长相等就可解决问题．【解答】解：当正六边形EFGHIJ的边长最大时，要使AE最小，六边形对角线EH与正方形的边长相等，AE的最小值为＝．故答案为．【点评】本题考查了正多边形的性质与运动的轨迹问题，解决本题的关键是首先找到正六边形的边长最大时正六边形在正方形内的位置，再旋转正六边形使得AE最小．17．（2015•无锡模拟）如图，⊙O的半径为1，点P（a，a﹣4）为⊙O外一点，过点P作⊙O的两条切线，切点分别为点A和点B，则四边形PBOA面积的最小值是．【分析】由点P的坐标为（a，a﹣4），得到OP＝＝，由于P A，PB是⊙O的两条切线，得到P A＝PB，∠OAP＝∠OBP，由于△OP A≌△OBP，在Rt△OAP中，根据勾股定理得到P A的长度，于是得到四边形PBOA面积＝2×△OP A的面积＝2×OA•P A＝＝，即可得到结果．【解答】解：∵点P的坐标为（a，a﹣4），∴OP＝＝，∵P A，PB是⊙O的两条切线，∴P A＝PB，∠OAP＝∠OBP，在△OP A与△OBP中，，∴△OP A≌△OBP，在Rt△OAP中，P A＝＝＝，∴四边形PBOA面积＝2×△OP A的面积＝2×OA•P A＝＝，∵2＞0∴当a＝4时，四边形PBOA面积最小，最小值为，解法二：几何法，点p在直线y＝x﹣4上，因此只要点O到直线的距离最小即可，可得面积的最小值为．故答案为．【点评】本题考查了切线的性质，全等三角形的判定与性质，最值问题，能求得四边形PBOA面积＝是解题的关键．18．（2015•惠山区二模）如图，菱形ABCD的对角线AC上有一动点P，BC＝6，∠ABC＝150°，则线段AP+BP+PD的最小值为6．【分析】将△ADC逆时针旋转60°，得到△AD′C′，连接BD′交AC于P，交AC′于E，连接PD，求出BD′，证明P A＝PE，PD＝ED′，根据两点之间线段最短得到答案．【解答】解：将△ADC逆时针旋转60°，得到△AD′C′，连接BD′交AC于P，交AC′于E，连接PD，∵∠BAD＝30°，∠DAD′＝60°，∴∠BAD′＝90°，又AB＝AD＝AD′，∴BD′＝＝6，∠ABP＝45°，又∠BAP＝15°，∴∠APE＝∠P AE＝60°，∴△EAP为等边三角形，∴P A＝PE，又∵△APD≌△AED′，∴PD＝ED′，根据两点之间线段最短，∴AP+BP+PD的最小值＝PB+PE+ED′＝6，故答案为：6．【点评】本题考查的是菱形的性质、轴对称变换和两点之间线段最短的知识，正确找出辅助线是解题的关键，注意轴对称变换的性质的正确运用．19．（2015•滨湖区二模）已知线段AB＝10，C．D是AB上两点，且AC＝DB＝2，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF 的中点，点P由点C移动到点D时，G点移动的路径长度为3．【分析】分别延长AE、BF交于点M，易证四边形PEMF为平行四边形，得出G为PM 中点，则G的运行轨迹△MCD的中位线，运用中位线的性质求出HI的长度即可．【解答】解：如图，分别延长AE、BF交于点M，∵∠A＝∠DPF＝60°，∴AM∥PF，∵∠B＝∠EP A＝60°，∴BM∥PE，∴四边形PEMF为平行四边形，∴EF与MP互相平分．∵G为EF的中点，∴G正好为PM的中点，即在P的运动过程中，G始终为PM的中点，∴G的运行轨迹为△MCD的中位线HI，∵HI＝CD＝×（10﹣2﹣2）＝3，∴G点移动的路径长度为3．故答案为：3．【点评】本题考查了三角形中位线定理及等边三角形的性质，解答本题的关键是作出辅助线，找到点G移动的规律，判断出其运动路径，综合性较强．20．（2018•陕西模拟）如图，正方形ABCD中，AB＝2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP 的最小值为．【分析】首先作出点D关于BC的对称点D′从而可知当点P、M、D′在一条直线上时，路径最短，当点E与点D重合，点F与点C重合时，PG和GD′均最短，即PD′最短，然后由正方形的性质和轴对称图形的性质可知：PG＝1，GD′＝3，最后由勾股定理即可求得PD′的长，从而可求得MD+MP的最小值．【解答】解：如图作点D关于BC的对称点D′，连接PD′，由轴对称的性质可知：MD＝D′M，CD＝CD′＝2∴PM+DM＝PM+MD′＝PD′过点P作PE垂直DC，垂足为G，易证AF⊥BE，故可知P的轨迹为以AB为直径的四分之一圆弧上，当点E与点D重合，点F与点C重合时，PG和GD′均最短，∴此时，PD′最短．∵四边形ABCD为正方形，∴PG＝，GC＝．∴GD′＝3．在Rt△PGD′中，由勾股定理得：PD′＝＝．故答案为：．【点评】本题主要考查的是最短路径问题，由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键．21．（2018•大荔县三模）如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是2．【分析】过D作AE的垂线交AE于F，交AC于D′，再过D′作AP′⊥AD，由角平分线的性质可得出D′是D关于AE的对称点，进而可知D′P′即为DQ+PQ的最小值．【解答】解：作D关于AE的对称点D′，再过D′作D′P′⊥AD于P′，∵DD′⊥AE，∴∠AFD＝∠AFD′，∵AF＝AF，∠DAE＝∠CAE，∴△DAF≌△D′AF，∴D′是D关于AE的对称点，AD′＝AD＝4，∴D′P′即为DQ+PQ的最小值，∵四边形ABCD是正方形，。