凸轮轮基本尺寸的设计
凸轮机构基本尺寸的确定

s
0
0
1
4
9
4
10
1
2
3 t
4
5
6
没有刚性冲击
但在δ =0、δt /2、δt 处,a发生有限值突
变,有柔性冲击。
适用于中速、轻载场合
(2)n = 5 五次多项式运动
s v
C0 ds
C1 C2 2 C3 / dt C1 2C2
3 C4 4 3C3
5、偏置平底直动从动件盘形凸轮
s
8 9 10
7 5 3 1
11 12
13 14
1 3 5 7 8 9 11 13 15
120º 60º 90º 90º
取长度比例尺l绘图
13 12 11
10
9
8 7
14 1 2
3 4 5 6
6、尖底摆动从动件盘形凸轮
已②知等凸分轮位的移基曲圆线半及径
◆组合运动规律
说明:凸轮一般为等速运动,有 t, 推杆运动规律常表
示为推杆运动参数随凸轮转角δ变化的规律。
1、多项式运动规律
s C0 C1 C2 2 Cn n s
(1)n = 1
h
等速运动
运动线图→
t
始、末位置:a
lim
v0 t
v
t 0
t
s
推程
远休止
h
回程
从动件位移线图
tD
s
近休止
二、从动件常用运动规律 ◆多项式运动规律
重点: 掌握各种运动规律的
运动特性
★一次多项式运动规律——等速运动 ★二次多项式运动规律——等加速等减速运动 ★五次多项式运动规律
凸轮机构基本尺寸
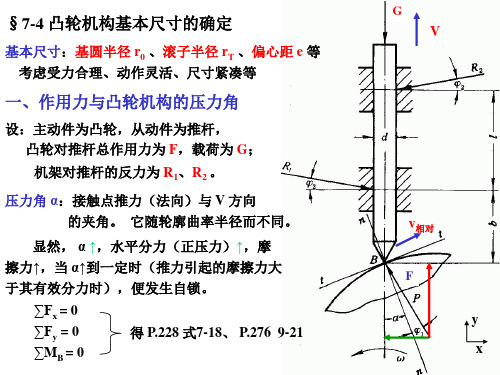
注意:对于平底推杆 凸轮机构,也会产生失 真现象,见图。 增大 r0可避免
平底推杆凸轮机构,当平底推杆的运动规律使位移变化 太快时产生失真现象。图
增大 r0可避免
凸轮机构基本的确定要考虑因素较多:受力、效率及自 锁、运动失真、结构等,要综合考虑。可进行结构优化。
tgα = CP / (( r02 - e2 )1/ 2 + s) = (ds / dδ – e) / (( r02 - e2 )1/ 2 + s)
结论: ① s = F( δ ) 一定时,某一时刻 v 一定:
r0↓ → α↑
② 不同时刻 δ , α 不同,有一个αman 。
∴据 αman = [α] ---- 极限情况 确定 r0min 。
§7-4 凸轮机构基本尺寸的确定
基本尺寸:基圆半径 r0 、滚子半径 rT 、偏心距 e 等 考虑受力合理、动作灵活、尺寸紧凑等
Hale Waihona Puke 一、作用力与凸轮机构的压力角
设:主动件为凸轮,从动件为推杆, 凸轮对推杆总作用力为 F,载荷为 G; 机架对推杆的反力为 R1、R2 。
压力角 α:接触点推力(法向)与 V 方向 的夹角。 它随轮廓曲率半径而不同。
显然, α ↑,水平分力(正压力)↑,摩 擦力↑,当 α↑到一定时(推力引起的摩擦力大 于其有效分力时),便发生自锁。
∑Fx = 0 ∑Fy = 0 ∑MB = 0
得 P.228 式7-18、 P.276 9-21
G
V
v相对
F
y x
G = F [ cos (α+ φ1 ) – (1 +2b / l )sin (α+ φ1 ) tgφ2 ]
基本尺寸的确定
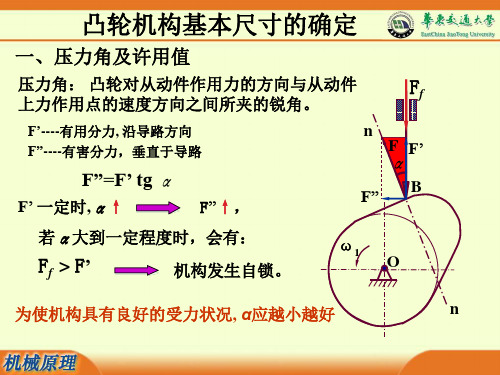
lCP = (s2+s0 )tanα
s2
rb
s0
rb e
2
2
2
C
O
P
n
ds2 e d 1 s 2 tan
e ds2/dφ 1
e2
为使机构的结构更紧凑, α应越大越好
凸轮机构基本尺寸的确定
为了保证凸轮机构能顺利工作,要求: α ≤ [α] [α]= 30˚ ----直动从动件; [α]= 35°~45°----摆动从动件; [α]= 70°~80°----回程。
tan ds2 / d1 e s2 rb 2 e 2
ω1
v2 B
s2
v2 P s0
n
ds2/dφ1
凸轮机构基本尺寸的确定
同理,当导路位于中心左侧时,有: n s2 B ω1 Dα r
min
lOP =lCP- lOC
tan
lCP = ds2/dφ 1 + e
ds2 / d1 e
凸轮机构基本尺寸的确定
一、压力角及许用值
压力角: 凸轮对从动件作用力的方向与从动件 上力作用点的速度方向之间所夹的锐角。
F’----有用分力, 沿导路方向 F”----有害分力,垂直于导路
Ff
n F F’
F”=F’ tg α
F’ 一定时,α↑
F”↑, ω1 若α大到一定程度时,会有:
α
F”
B
Ff > F’
a rT
凸轮机构基本尺寸的确定
四、滚子半径的选择
2、外凸的凸轮轮廓: a rT
a min min rT a
凸轮机构的压力角和基本尺寸

2.凸轮理论轮廓的外凸部分
amin min rT
min rT
amin =min-rT
min>rT amin =min-rT>0
min rT
´
´
min<rT amin =min-rT<0
´
为避免运动失真,
min=rT
amin =min-rT=0
rT<
min
凸轮机构的压力角和基本尺寸
一、凸轮机构的压力角
二、凸轮基圆半径的确定 三、滚子从动件滚子半径的选择
第四节 凸轮机构的压力角和基本尺寸
一、凸轮机构的压力角
1. 压力角 :
在不计摩擦力、重力、惯性力的条件下,机 构中驱使从动件运动的力的方向线与从动 件上受力点的速度方向线所夹的锐角。
Q n
F F2 v2
回程时:[]=70º ~80º
3、压力角与凸轮机构尺寸之间的关系 P点为速度瞬心, 于是有: v=lOPω → lOP =v / ω = ds/dφ = lOC + lCP lOC = e lCP = ds/dφ - e lCP = (S+S0 )tg α S0= r20 -e2 ds/dφ - e tgα = S + r20 - e2 r 0↑ →α ↓
F1 A
2. 压力角与凸轮机构受力情况的关系 Q—作用在从动件上的载荷
F—凸轮对从动件的作用力
F1 F cos F2 F sin
o
推动从动件运动的有效分力 阻碍从动件运动的有害分力
越小,受力越好。
n
F1 F cos F2 F sin
推动从动件运动的有效分力
阻碍从动件运动的有害分力
凸轮机构基本尺寸的确定

5
h/r0 等加等减速运动
10
85 5 80 10
作者:潘存云教授
h/r0 余弦加速度运动
85
80
15 20
α 最大压力角 max
75 70
25
65
30
60
35 40
45
50
55
15 20
最大压力角αmax
75 70
25
65
30
60
35 40
45
50
55
应用实例:一对心直动滚子推杆盘形凸轮机构, δ0=45º,h=13 mm, 推杆以正弦加速度运动, 要求:αmax ≦30º,试确定凸轮的基圆半径r0 。 作图得:h/r0=0.26 r0 ≧ 50 mm
n
∴ tgα = ds/dδ + e
s + r20 - e2
e ↑ α↑
e ds/dδ
此时,当偏距e增大时,压力角反而增大。
对于直动推杆凸轮机构存在一个正确偏置的问题!
综合考虑两种情况有: tgα = ds/dδ ± e
s + r20 - e2 “+” 用于导路和瞬心位于凸轮回转中心的两侧; “-” 用于导路和瞬心位于凸轮回转中心的同侧; 显然,导路和瞬心位于中心同侧时,压力角将减小。
对于外凸轮廓,要保证正常工作,应使: ρmin> rT
曲线之曲率半径: ρ=( x2+y2)3/2/( xy-yx ) 式中:x=dx/dδ,y=dy/dδ, x=d2x/dδ2, y=d2y/dδ2
可用求极值的方法求得ρmin ,常采用上机编程求得ρmin
工程上要求ρa ≥1~5
若不满足此条件时:
= [ds/dt] / [dδ/dt]
平面盘形凸轮机构系统的设计与基本尺寸的分析

1 凸轮机构系统的设计思路
1 . 1 系统 开发 的功 能要 求和 总体规 划
凸轮 C A D系统 的开 发是 目前对 凸轮机构 进行 研究 的方 向之 一 。本系 统采 用 了基 于参 数 化 的设计 , 不仅
可以使设计人员从 大量繁琐 的绘 图工作中解脱 出来 , 而且还可以提高设计效率。本系统的基本 的功能为 : 当 选择某种类型的凸轮, 从设计管理界面输入构成凸轮所需的基本结构参数 , 并通过计算机绘制 出位移 、 速度 、 加 速度 曲线 图 , 计 算 出 凸轮 的理论轮 廓线 、 实 际轮廓 线 、 保存 或调 用 已生成 合格 的 凸轮参数 等 。
。。
s i n ( 0 + )
】 , ∈ [ 一 号 , 予 ]
J …
c ,
c 2
( 3 )
。 =
端
对上 式求 导 , 并令( 。 )
0, 可得 :
”
s i n ( 2 a一 ) : [ 1 一( 1 + ) c o s ( 2  ̄一 ) 】
关键词 : 凸轮 ; 系统 ; 设计 ; 基 本 尺 寸
中图分类号 : T H1 2 2
文献标 志码 : A
文章编号 : 1 0 0 9—3 9 0 7 ( 2 0 1 4) 0 2— 0 1 6 4— 0 4
平面盘形凸轮作为一种常见 的机构 , 在实际的生活中有着广泛 的运用。一般来说 , 凸轮轮廓 的设计主要 有 图解 法 和解析法 两 种 , 图解法 因其 精度 差 、 效率低 , 难 于 满 足 实 际精 度 的要 求 , 更 多 的 是 运用 在 理 论 教 学 上 。因此 , 可 以说凸轮机构 C A D是顺应 C A D技术发展趋势的必然产物¨ ] 。凸轮机构 C A D系统的研究主要 的内容是 : 凸轮机构类型运动规律的选择 、 机构 的基本尺寸 的确定 、 绘制所生成的轮廓 、 生成速度、 加速度及 位移曲线图等等。当确定凸轮机构的类型以后 , 从动件的运动规律、 凸轮机构的基本尺寸及其轮廓设计就成 为设计 的 主要 问题 J 。
第4.4节(凸轮机构基本尺寸的设计)

第四节 凸轮机构基本尺寸设计无论是作图法还是解析法,在设计凸轮廓线前,除了需要根据工作要求选定从动件的运动规律外,还需要确定凸轮机构的一些基本参数,如基圆半径b r 、偏距e 、滚子半径r r 等。
一般来讲,这些参数的选择除了应保证从动件能够准确地实现预期的运动规律外,还应当使机构具有良好的受力状况和紧凑的结构。
本节讨论凸轮机构基本尺寸设计的原则和方法。
一、移动滚子从动件盘形凸轮机构1. 压力角同连杆机构一样,压力角也是衡量凸轮机构传力特性好坏的一个重要参数。
所谓凸轮机构的压力角,是指在不计摩擦的情况下,凸轮对从动件作用力的方向线与从动件上力作用点的速度方向之间所夹的锐角。
对于图4-22所示的移动滚子从动件盘形凸轮机构来说,过滚子中心所作理论廓线的法线nn 与从动件运动方向之间的夹角α就是压力角。
(1)压力角与作用力的关系 由图4-22可以看出,凸轮对从动件的作用力F 可以分解成两个分力,即沿着从动件运动方向的分力F '和垂直于运动方向的分力F ''。
只有前者是推动从动件克服载荷的有效分力,而后者将增大从动件与导路间的摩擦,它是一种有害分力。
压力角α越大,有害分力越大。
当压力角α增大到某一数值时,有害分力所引起的摩擦阻力将大于有效分力F ',这时无论凸轮给从动件的作用力有多大,都不能推动从动件运动,即机构将发生自锁。
因此为减小侧向推力,避免自锁,压力角α应越小越好。
图4-22 凸轮机构的压力角(2)压力角与机构尺寸的关系 设计凸轮时,除了应使机构具有良好的受力状况外,还希望机构结构紧凑。
而凸轮尺寸的大小取决于凸轮基圆半径的大小。
在实现相同运动规律的情况下,基圆半径越大,凸轮的尺寸也越大。
因此,要获得轻便紧凑的凸轮机构,就应当使基圆半径尽可能地小。
但是基圆半径的大小又和凸轮机构的压力角有直接的关系。
下面以图4-22为例来说明这种关系。
图中,过滚子中心B 所作理论廓线的法线nn 与过凸轮轴心0A 所作从动件导路的垂线交于P 点,由瞬心定义可知,该点即为凸轮与从动件在此位置时的瞬心,且ϕωd ds v P A ==0。
凸轮设计方法

平面凸轮机构基本尺寸的确定
凸轮基圆半径的确定 一、基圆半径对压力角的影响
ds/d e PD OP e tan s0 s BD r02 e 2 s
增大基圆半径,可使凸轮机构的压力角减小; 增大基圆半径会使凸轮机构的整体尺寸增大 在压力角不超过许用值的原则下,应尽可能采用 较小的基圆半径。
从动件尖底的运 动轨迹就是凸轮 的廓线
偏置直动尖顶从动件
s
e
120° 90 ° 90 ° 60 °
偏置直动尖顶从动件
s
e 120 ° 90 ° 90 ° 60 °
偏置直动尖顶从动件
s
1
2 3
4 5
6
7
8 9
e
1 2 3 9 8
4
6
7
5
偏置直动尖顶从动件
s
120 ° 90 ° 90 ° ° 60
• 偏置直动尖顶从动件盘形凸轮 • 偏置直动滚子从动件盘形凸轮 • 对心直动平底从动件
摆动从动件盘形凸轮
凸轮廓线设计的基本原理——反转法 为了便于绘出凸轮轮廓 曲线, 应使工作中转动着的 凸轮与不动的图纸间保持相 对静止。 如果给整个凸轮机构加 上一个与凸轮转动角度ω数 值相等、 方向相反的“-ω” 角速度, 则凸轮处于相对静 止状态。
从动件的基本运动规律
从动件位移s对凸轮转角的函数
s
关系s( )称为从动件运动规律
ds s d
d 2s s d 2
s
s
s( ) — 类速度 s( ) — 类加速度
0
ds ds d v s dt d dt d 2 s d 2 s d 2 2 a 2 ( ) s 2 dt d dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节 凸轮机构基本尺寸的设计在设计凸轮的轮廓曲线时,不仅要保证从动件能够按给定要求实现预期的运动规律,还应该保证凸轮机构具有合理的结构尺寸和良好的运动、力学性能。
对于基圆半径、偏距和滚子半径等基本尺寸,在进行凸轮轮廓曲线的设计之前都是事先给定的。
如果这些基本参数选择不当,就会存在凸轮机构的结构是否合理、运动是否失真以及受力状况是否良好等问题。
因此,本节主要讨论有关凸轮机构基本尺寸的设计问题,为正确、合理选择这些基本参数提供一定的理论依据。
一、凸轮机构的压力角凸轮机构的压力角是指不计摩擦时,凸轮与从动件在某瞬时接触点处的公法线方向与从动件运动方向之间所夹的锐角,常用α表示。
压力角是衡量凸轮机构受力情况好坏的一个重要参数,是凸轮机构设计的重要依据。
1.直动从动件凸轮机构的压力角如图6—29所示为直动从动件盘形凸轮机构的压力角示意图。
其中,图6—29a 为尖底从动件的压力角示意图,图6—29b 为平底从动件的压力角示意图。
现以滚子从动件凸轮机构为例,来说明直动从动件盘形凸轮机构压力角的计算方法。
根据图6—30中的几何关系,可得压力角的表达为图6—29直动从动件的压力角图 6—30偏置直动从动件的压力角(6—34)由三心定理,P 点为瞬心,ωOP v v P ==,ϕωd d s vOP ==(由从动件速度公式ϕωd d s v =) 式中,“ ”号与从动件的偏置方向有关。
图6—30所示应该取“-”号,反之,如果从动件导路位于凸轮回转中心O 的左侧,则应该取“+”号。
显然,这种情况属于从动件的偏置方向选择不合理,因为增大了凸轮机构的压力角,降低了机械效率,甚至可能会导致凸轮机构发生自锁。
因此,正确选择从动件的偏置方向有利于减小机构的压力角。
此外,压力角还与凸轮的基圆半径和偏距等有关。
(当v 、ω、s 一定时,若凸轮基圆半径增大,则压力角α将减小,但机构尺寸随之增大;若凸轮基圆半径减小,压力角α将增大,机构的受力情况变差。
)当偏距e =0时,代入式(6—34),即可得到对心直动从动件盘形凸轮机构的压力角计算公式:)(d d d d tan 00220s r v s r ss e r s +=+=+-=ωϕϕα (6—35) 对于直动平底从动件盘形凸轮机构(图6—29所示),根据图中的几何关系,其压力角为α=90°-γ式中,γ为从动件的平底与导路中心线的夹角,其值为一常数。
显然,平底直动从动件凸轮机构的压力角为常数,机构的受力方向不变,运转平稳性好。
如果从动件的平底与导路中心轴线之间的夹角γ=90°,则压力角α=0°。
2.摆动从动件凸轮机构的压力角图6—31所示为摆动从动件盘形凸轮机构的压力角示意图。
其中,图6—31a 为滚子从动件的压力角示意图,图6—31b 为平底从动件的压力角示意图。
(a ) (b ) 图6—31 摆动从动件盘形凸轮机构的压力角对于摆动滚子从动件凸轮机构(图6—31a),设摆杆的长度AB =l ,机架的长度OA =a 。
过瞬心P (三心定理)作摆杆AB 的垂线,交AB 的延长线于D 点,则根据图中的几何关系,有(6-36)(BD =AD -AB =AD -l )(ω1d t =d ψ,ω2d t =d φ)根据瞬心的性质可得,所以,将上式代入式(6-36)并整理,即可得到摆动滚子从动件凸轮机构压力角的计算公式:(6—37)对于摆动平底从动件盘形凸轮机构,如图6—31b 所示,凸轮与从动件的接触点B 的速度方向垂直于AB ,而B 点的受力方向垂直于平底。
因此,其压力角计算公式为ABe=αsin (6—38) 式中,长度AB 按照式(6—28)的方法计算。
显然,如果e=0,则其压力角也为零。
由式(6—37)、式(6—38)可知,对于摆动从动件盘形凸轮机构,其压力角受从动件的运动规律、摆杆长度、机架长度等因素的影响,在设计时要加以注意。
3.凸轮机构的许用压力角凸轮机构的压力角与基圆半径、偏距和滚子半径等基本尺寸有直接的关系,而且这些参数之间往往是互相制约的。
以直动滚子从动件凸轮机构为例,在其他参数不变的情况下,增大凸轮的基圆半径可以获得较小的压力角,从而可以改善机构的受力状况,但缺点是凸轮尺寸增大。
反之,减小凸轮的基圆半径虽然可以获得较为紧凑的结构,但同时又使凸轮机构的压力角增大。
压力角过大会导致凸轮机构发生自锁而无法运转,而且当压力角增大到接近某一极限值时,即使机构尚未发生自锁,也会导致驱动力急剧增大,发生轮廓严重磨损和效率迅速降低的情况。
因此为了使凸轮机构能够正常工作并具有较高的传动效率,设计时必须对凸轮机构的最大压力角加以限制,使其小于许用压力角,即αmax <[α]。
凸轮机构的许用压力角如表6—2所示。
二、凸轮机构基本尺寸的设计1.基圆半径的设计对于直动滚子从动件盘形凸轮,可根据式(6—34)求解出凸轮的基圆半径:(6—39)显然,压力角α越大,基圆半径越小,机构就越容易获得紧凑的尺寸。
在其他参数不变的情况下,当α=[α],并且选择正确的从动件偏置方向后,可以得到最小的基圆半径r 0min ,从而可以使设计出的凸轮机构在满足压力角条件的同时,获得紧凑的结构尺寸。
此时,最小基圆半径为(6—40)(对心尖顶推杆盘形凸轮机构 s v r b -=αωtan 12)(e =0)对于直动平底从动件盘形凸轮,可按照“凸轮廓线全部外凸”的条件来设计凸轮的基圆半径。
也就是说,凸轮廓线上各点的曲率半径ρ>0。
由高等数学的知识可知,曲率半径的计算公式为")'1(2/32y y +=ρ (6-41)式中,ϕϕd dx d dy dxdy y ==',代人式(6—41)并整理得 (6-42)选择所允许的最小曲率半径ρmin ,与平底从动件盘形凸轮的廓线方程联立求解,可得22min b ϕρd sd s r --> (6—43)经验公式r b ≈2r H (r H 为凸轮轴孔的半径)s =9.4α=25°33'46"s =9.446°28'1"2.滚子半径的设计在滚子从动件盘形凸轮机构中,凸轮的实际廓线是其理论廓线上滚子圆族的包络线,因此其形状必然与滚子的半径大小有关。
在设计滚子尺寸时,必须保证滚子同时满足运动特性要求和强度要求。
从运动特性要求考虑,凸轮机构不能发生运动的失真现象。
图6—32所示为凸轮的外凸廓线中的滚子圆族的包络情况。
设理论廓线上某点的曲率半径为ρ,实际廓线在对应点的曲率半径为ρa ,滚子半径为r r ,根据图中的几何关系有ρa =ρ—r r 。
图6—32外凸廓线的包络线如果r r ≥ρmin ,则该点处将发生实际廓线的曲率半径为零或负值的情况。
实际廓线曲率半径为零,表明在该位置出现尖点,运动过程中容易磨损;而实际廓线曲率半径为负值,说明在包络加工过程中,图中交叉的阴影部分将被切掉,从而导致机构的运动发生失真。
因此,为了避免发生这种现象,要对滚子的半径加以限制。
ρ实际廓线正常尖顶失真理论廓线r r>ρTr r =ρTρTρ实际廓线理论廓线r rρTr r <ρT通常情况下,应保证r r ≤0.8ρmin对于内凹凸轮廓线中滚子圆族的包络情况,同样可按照上述方法进行分析,这里不再详述。
从强度要求考虑,滚子半径应满足以下条件:r r≥(0.1~0.5)r0(基圆半径)3.平底长度的设计如图6—33所示,在平底从动件盘形凸轮机构运动过程中,应能保证从动件的平底在任意时刻均与凸轮接触,因此平底的长度l应满足以下条件:式中,△l为附加长度,由具体的结构而定,一般取△l=5~7 mm。
4.偏距的设计从动件的偏置方向可直接影响凸轮机构压力角的大小,因此在选择从动件的偏置方向时需要遵循的原则是:尽可能域小凸轮机构在推程阶段的压力角,其偏置的距离(即偏距e)可按下式计算:图6—33平底从动件的长度(6-4)一般情况下,从动件运动速度的最大值发生在凸轮机构压力角最大的位置,则式(6—44)可改写为(6-45) 由于压力角为锐角,故有v max-eω≥0。
由式(6—45)可知,增大偏距,有利于减小凸轮机构的压力角,但偏距的增加也有限度,其最大值应满足以下条件:设计偏置式凸轮机构时,其从动件偏置方向的确定原则是:从动件应置于使该凸轮机构的压力角减小的位置。
综上所述,在进行凸轮机构基本尺寸的设计时,由于各参数之间是互相制约的,设计时应该综合考虑各种因素,使其综合性能指标满足设计要求。
补例1一对心尖底推杆盘形凸轮机构,凸轮为一偏心圆盘。
已知圆盘半径为r,偏心距O1O等于e。
试确定该凸轮机构的基本参数和压力角最大值。
解由图可见,当凸轮顺时针转动,凸轮上的A、B两点与推杆接触时,推杆位于推程的起点和终点,故行程h=(r+e)-(r-e)=2e推程运动角与回程运动角相等,φ=φ’=180°,故无休止阶段,φs=φs’=0。
基圆半径r b=r-eOK与导路的夹角为压力角α。
当O1O垂直于导路时,ON=e,压力角为最大值αmax。
补例2 求图示凸轮机构的推程H、推程角φ、远休止角φs、基圆半径r b和最大压力角αmax。
图中尺寸单位为mm。
解行程h=12×2/sin60°=27.7mm推程运动角φ= 180°;远休止角φs=近休止角φ’s=0基圆半径r b=20-12=8mm;压力角α恒等于30°。
