人教版八年级上册 数学几何习题集含答案
1、如图：在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线，DE⊥AB垂足为E，DF⊥AC，垂足为点F，且BD=CD 求证：BE＝CF3、如图，点B和点C分别为∠MAN两边上的点，AB=AC。
（1）按下列语句画出图形：①AD⊥BC，垂足为D；②∠BCN的平分线CE与AD的延长线交于点E；③连结BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：____≌____，____≌____；（3）并选择其中的一对全等三角形予以证明。
已知：AB=AC，AD⊥BC，CE平分∠BCN，求证：△ADB≌△ADC；△BDE≌△CDE。
AB D CM NE4、如图，PB、PC分别是△ABC的外角平分线且相交于点P.求证：点P在∠A的平分线上AB CP5、如图，△ABC中，p是角平分线AD，BE的交点. 求证：点p在∠C的平分线上6、下列说法中，错误的是（）A．三角形任意两个角的平分线的交点在三角形的内部B．三角形两个角的平分线的交点到三边的距离相等C．三角形两个角的平分线的交点在第三个角的平分线上D．三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图，AP、CP分别是△ABC外角∠MAC与∠NCA的平分线，它们相交于点P，PD⊥BM于点D，PF⊥BN于点F．求证：BP为∠MBN的平分线。
9、如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．求证：点C在∠AOB 的平分线上．10、如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.（1）若连接AM，则AM是否平分∠BAD？请你证明你的结论；（2）线段DM与AM有怎样的位置关系？请说明理由．11、八（1）班同学上数学活动课，利用角尺平分一个角（如图所示）．设计了如下方案：（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由；（2）在方案（Ⅰ）PM=PN的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB．此方案是否可行？请说明理由．12、如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE=AF。
求证：（1）PE=PF；（2）点P在∠BAC的角平分线上。
13、如图，点D、B分别在∠A的两边上，C是∠A内一点，AB=AD，BC=CD，CE⊥AD于E，CF⊥AF于F。
求证：CE=CF14、若三角形的两边长分别是2和7，则第三边长C的取值范围是___；当周长为奇数时，第三条边为__ ____；当周长是5的倍数时，第三边长为_______。
15、一个等腰三角形的两边分别为8cm和6cm，则它的周长为_______cm。
16、已知三角形三边长为a，b，c，且丨a+b+c丨+丨a-b-c丨=10，求b的值。
17、一个两边相等的三角形的周长为28cm，有一边的长为8cm。
求这个三角形各边边长。
18、△ABC中，a=6，b=8，则周长C的取值范围是______.19、已知等腰三角形ABC中，AB=AC=10cm，D为Ac边上一点，且BD=AD，三角形ＢＣＤ的周长为１５ｃｍ，则底边ＢＣ长为。
20、若等腰三角形的腰长为6，则它的底边长a的取值范围是；若等腰三角形的底边长为4，则它的腰长b的取值范围是。
21、a+1，a+2，a+3，这三条线段是否能组成三角形？22、若三角形三边分别为2，x-1，3，求x的范围？23、若三角形两边长为7和10,求最长边x的范围？24、如图，∠BAD=∠CAD,AD⊥BC，垂足为点D，BD=CD可知哪些线段是哪个三角形的角平分线、中线、高？25、如图所示，在△ABC中，已知AC=8，BC=6，AD⊥BC于D,AD=5，BE⊥AC于E，求BE的长26、如图，AD是△ABC的角平分线，DE∥AB，DF∥AC，EF交AD于点O．请问：DO是△DEF的角平分线吗？请说明理由。
（2）若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件交换，所得命题正确吗？27、如图，△ABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件，求∠BIC的度数．（1）若∠ABC=70°，∠ACB=50°，则∠BIC= °（2）若∠ABC+∠ACB=120°，则∠BIC= °（3）若∠A=90°，则∠BIC= °；（4）若∠A=n°则∠BIC= °（5）从上述计算中，我们能发现∠BIC与∠A的关系吗？AIB C28、如图,求证∠A+∠B+∠C+∠D+∠E=180°29、如图，不规则的五角星图案，求证：∠A+∠B+∠C+∠D+∠E=180°30、D为△ABC的边AB上一点,且∠ADC=∠ACD.求证：∠ACB＞∠B31、如图，D是BC延长线上的一点，∠ABC.∠ACD的平分线交于点E，求证：∠E=1/2∠A32、如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线。
（1）试求∠F与∠B,∠D的关系;（2）若∠B:∠D：∠F=2：4：x 求X的值33、如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC= 度。
实验班错题答案1、因为∠1=∠B所以∠DEA=2∠B=∠C因为AD是△ABC的角平分线所以∠CAD=∠EAD因为AD=AD所以△ADC全等于△ADE所以AC=AE CD=DE因为∠1=∠B所以△EDB为等腰三角形所以EB=DE因为AB=AE+EB AC=AE CD=DE EB=DE所以AB=AC+CD2、因为ad是∠bac的角平分线，,DE⊥AB，DF⊥AC, 所以DE=DF三角形DEB和三角形DFC均为直角三角形，又因为BD=CD 所以BE=CF3、4、作PF⊥AD，PH⊥BC，PG⊥AE∵PB平分∠DBC，PC平分∠ECB，PF⊥AD，PH⊥BC，PG⊥AE∴PF=PH，PG=PH（角平分线上的点到这个角的两边的距离相等）∴PF=PG∵PF⊥AD，PG⊥AE，PF=PG∴PA平分∠BAC（在一个角的内部，且到角的两边距离相等的点，在这个角的平分线上）5、作PG⊥BC,PH⊥AC,PQ⊥AB,垂足分别为G、H、Q,AD为∠A的平分线，PH=PQ;BE为∠B的平分线，PQ=PG;所以PG=PH,又CP为RT△CGP和RT△CEP的公共斜边，所以△CGP≌△CHP,所以∠GCP=∠ECP,CP为∠的平分线，P点在∠C的平分线上6、A7、∵BM=MC，∴∠MBC=∠MCB，∵∠ABM=∠ACM，∴∠ABM+∠MBC=∠ACM+∠MCB，即∠ABC=∠ACB，∴AB=AC，在ΔAMB与ΔAMC中，AB=AC，∠ABM=∠ACM，MB=MC，∴ΔAMB≌ΔAMC(SAS)，∴∠MAB=∠MAC，即AM平分∠BAC。
8、过点P作PE⊥AC于E∵AP平分∠MAC，PD⊥BM，PE⊥AC∴RT△PDA≌RT△PEA（角角边）∴PE＝PD∵CP平分∠NCA，PF⊥BN，PE⊥AC∴RT△PFC≌RT△PEC（角角边）∴PE＝PF∴PD＝PF∴RT△PDB≌RT△PFB （角角边）∴∠PBD=∠PBF∴BP平分∠MBN9、证明：∵OM=ON，OE=OD，∠MOE=∠NOD，∴△MOE≌△NOD，∴∠OME=∠OND，又DM= EN，∠DCM=∠ECN，∴△MDC≌△NEC，∴MC= NC，易得△OMC≌△ONC( SSS)，∴∠MOC=∠NOC，∴点C在∠AOB的平分线上．10、⑴延长DM交AB的延长线于N，∵∠C=∠B=90°，∴AB∥CD，∴∠2=∠N，∠C=∠MBN=90°，∵MC=MB，∴ΔMCD≌ΔMBN，∴MD=MN，∵∠1=∠N，∴AN=AD，∴∠3=∠4(等腰三角形三线合一)，即AM平分∠BAD。
⑵∵AN=AD，MD=MN，∴AM⊥DN(等腰三角形三线合一)。
：（1）作MN⊥AD交AD于N∵∠1=∠2，DM为公共边∴Rt△DCM≌Rt△DNM∴MN=MC=MB 又：AM为公共边∴Rt△ABM≌Rt△ANM ∴∠3=∠4 ∴AM平分∠BAD （2）DM⊥AM，理由如下：∵∠B=∠C=90°∴DC//AB ∴∠BAD=∠CDA=180°∵∠1=∠2,∠3=∠4 ∴∠1+∠3=90°∴△ADM是直角三角形∴∠DMA=90°∴DM⊥AM11、分析：（1）方案（Ⅰ）中判定PM=PN并不能判断P就是∠AOB的角平分线，关键是缺少△OPM≌△OPN的条件，只有“边边”的条件；方案（Ⅱ）中△OPM和△OPN是全等三角形（三边相等），则∠MOP=∠NOP，所以OP为∠AOB的角平分线；（2）可行．此时△OPM和△OPN都是直角三角形，可以利用HL证明它们全等，然后利用全等三角形的性质即可证明OP为∠AOB的角平分线．解答：解：（1）方案（Ⅰ）不可行．缺少证明三角形全等的条件，∵只有OP=OP，PM=PN不能判断△OPM≌△OPN；∴就不能判定OP就是∠AOB的平分线；方案（Ⅱ）可行．证明：在△OPM和△OPN中$\left\{\begin{array}{l}OM=ON\\PM=PN\\OP=OP\end{array}\right.$∴△OPM≌△OPN（SSS），∴∠AOP=∠BOP（全等三角形对应角相等）（5分）；∴OP就是∠AOB的平分线．（2）当∠AOB是直角时，方案（Ⅰ）可行．∵四边形内角和为360°，又若PM⊥OA，PN⊥OB，∠OMP=∠ONP=90°，∠MPN=90°，∴∠AOB=90°，∵若PM⊥OA，PN⊥OB，且PM=PN，∴OP为∠AOB的平分线（到角两边距离相等的点在这个角的角平分线上）；当∠AOB为直角时，此方案可行．12、证明：（1）如图，连结AP，∴∠AEP=∠AFP=90°，又AE=AF，AP=AP，∴Rt△AEP≌Rt△AFP，∴PE=PF；（2）∵Rt△AEP≌Rt△AFP，∴∠EAP=∠FAP，∴AP是∠BAC的角平分线，故点P在∠BAC的角平分线上。
八年级上册几何题及答案
八年级上册几何题及答案【篇一：八年级数学上几何典型试题及答案】class=txt>一．选择题（共10小题）1．（2013?铁岭）如图，在△abc和△dec中，已知ab=de，还需添加两个条件才能使△abc≌△dec，不能添加的一组条件是（）2．（2011?恩施州）如图，ad是△abc的角平分线，df⊥ab，垂足为f，de=dg，△adg和△aed的面积分别为50和39，则△edf的面积为（）ac=8cm，f是高ad和be的交点，则bf的长是（）4．（2010?海南）如图，a、b、c分别表示△abc的三边长，则下面与△abc一定全等的三角形是（）6．（2013?十堰）如图，将△abc沿直线de折叠后，使得点b与点a重合．已知ac=5cm，△adc的周长为17cm，则bc的长为（）二．填空题（共10小题）12．（2013?黔西南州）如图，已知△abc是等边三角形，点b、c、d、e在同一直线上，且cg=cd，df=de，则∠e= _________ 度．13．（2013?枣庄）若14．（2013?内江）若m﹣n=6，且m﹣n=2，则m+n=．15．（2013?菏泽）分解因式：3a﹣12ab+12b=16．（2013?盐城）使分式17．（2013?南京）使式子1+18．（2012?茂名）若分式19．在下列几个均不为零的式子，x﹣4，x﹣2x，x﹣4x+4，x+2x，x+4x+4中任选两个都可以组成分式，请你选择一个不是最简分式的分式进行化简： _________ ．20．不改变分式的值，把分式分子分母中的各项系数化为整数且为最简分式是 222222222，，则a+b的值为．的值为零的条件是x=有意义的x的取值范围是的值为0，则a的值是 _________ ．三．解答题（共8小题）21．（2013?遵义）已知实数a满足a+2a﹣15=0，求．23．（2007?资阳）设a1=3﹣1，a2=5﹣3，…，an=（2n+1）﹣（2n﹣1）（n为大于0的自然数）．（1）探究an是否为8的倍数，并用文字语言表述你所获得的结论；（2）若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”．试找出a1，a2，…，an，…这一列数中从小到大排列的前4个完全平方数，并指出当n满足什么条件时，an为完全平方数（不必说明理由）．那么在△abc中，仍然有条件“ad是∠bac的角平分线，点e和点f，分别在ab和ac上”，请探究以下两个问题：22222225．（2012?遵义）如图，△abc是边长为6的等边三角形，p是ac边上一动点，由a向c运动（与a、c不重合），q是cb延长线上一点，与点p同时以相同的速度由b向cb延长线方向运动（q不与b重合），过p作pe⊥ab于e，连接pq交ab于d．（2）当运动过程中线段ed的长是否发生变化？如果不变，求出线段ed的长；如果变化请说明理由．26．（2005?江西）将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下图的形式，使点b、f、c、d在同一条直线上．（1）求证：ab⊥ed；（1）当cm与ab垂直时，求点m运动的时间；（2）当点a′落在△abc的一边上时，求点m运动的时间．28．已知点c为线段ab上一点，分别以ac、bc为边在线段ab同侧作△acd和△bce，且ca=cd，cb=ce，∠acd=∠bce，直线ae与bd交于点f，【篇二：初二数学----几何证明初步经典练习题(含答案)】编辑整理：临朐王老师1 作cm∥ab，则∠a= ，∠b= ，∵∠acb +∠1+∠2=180（，∴∠a+∠b+∠acb=180．○2 作mn∥bc，则∠2=，∠3= ，∵∠1+∠2+∠3=180，∴∠bac+∠b+∠c=180．○6.求证:两条直线相交有且只有一个交点.7.如图，在平面内，ab是l的斜线，cd是l的垂线。
八年级上册几何证明题专项练习 (附答案)
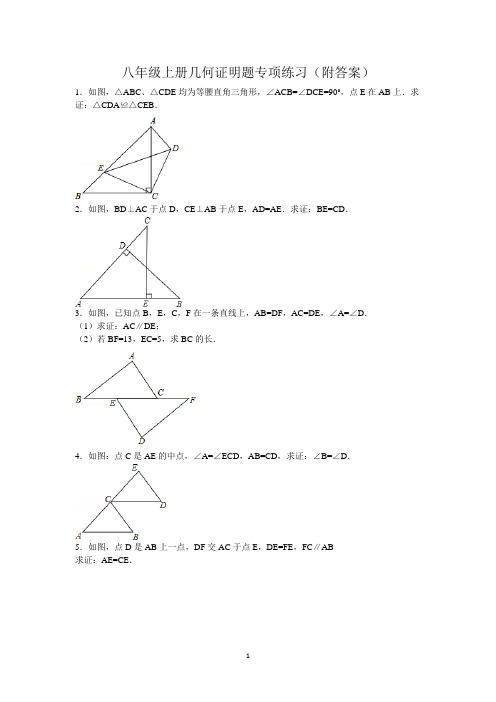
八年级上册几何证明题专项练习（附答案）1．如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB．2．如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．3．如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．（1）求证：AC∥DE；（2）若BF=13，EC=5，求BC的长．4．如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D．5．如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB求证：AE=CE．6．如图，BE⊥AC，CD⊥AB，垂足分别为E，D，BE=CD．求证：AB=AC．7．如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB．8．如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：DE=DF．9．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．10．如图，已知∠CAB=∠DBA，∠CBD=∠DAC．求证：BC=AD．11．如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE．12．如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF．13．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．（1）求证：BD=CE；（2）求证：∠M=∠N．14．如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：△ACD≌△CBE．15．如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．16．如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．①求证：△ABE≌△CBD；②若∠CAE=30°，求∠BDC的度数．17．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：（1）FC=AD；（2）AB=BC+AD．18．如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN=70°，求∠MCN的度数．19．已知△ABC中，AD是∠BAC的平分线，AD的垂直平分线交BC的延长线于F．求证：∠BAF=∠ACF．20．如图所示，在Rt△ABC中，∠ACB=90°，AC=BC，D为BC边上的中点，CE⊥AD于点E，BF∥AC交CE的延长线于点F，求证：AB垂直平分DF．21．如图：在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；说明：（1）CF=EB．（2）AB=AF+2EB．22．如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．求证：（1）∠ECD=∠EDC；（2）OC=OD；（3）OE是线段CD的垂直平分线．23．如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．求证：（1）AM⊥DM；（2）M为BC的中点．24．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．25．如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．26．如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O（1）求证：OB=OC；（2）若∠ABC=50°，求∠BOC的度数．27．如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE．（1）求证：△DEF是等腰三角形；（2）当∠A=40°时，求∠DEF的度数．28．如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．（1）求∠F的度数；（2）若CD=2，求DF的长．29．图1、图2中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．（1）如图1，线段AN与线段BM是否相等？证明你的结论；（2）如图2，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．30．如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．（1）图中有几个等腰三角形？猜想：EF与BE、CF之间有怎样的关系，并说明理由．（2）如图②，若AB≠AC，其他条件不变，图中还有等腰三角形吗？如果有，分别指出它们．在第（1）问中EF与BE、CF间的关系还存在吗？（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由．参考答案1．证明：,ACB DCEACB ACE DCE ACE BCE ACD ABC BC AC EC DC BC DC BCE ACD EC AC CDA CEB ∠=∠∴∠-∠=∠-∠∠=∠∴===⎧⎪∠=∠⎨⎪=⎩∴≅Q QV V V V V 即为等腰直角三角形同理在BCE 与ACD 中,得证.2．证明：9090,.BD AC ADB AEC ADB AECADB AECAD AE A A SDB AEC AB ACAB AE AC AD BE CD ⊥∴∠=︒∠=︒∴∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=∴-=-=Q V V V V 同理,在ADB 与AEC 中即得证 3．（1）证明：,.AB DF A D AC DE ABC DFE AC DE =⎧⎪∠=∠⎨⎪=⎩∴≅∴V V V V 在ABC 与DFE 中∥得证（2）解(1)21351329ABC DFE BC EFBC EC EF EC BE CFBC BF ECBF ECBF ≅∴=∴-=-=∴=--=--=-=V V 由知,即4．证明：.C AE AC CE AB CD A ECD AC CE ABC CDE B D ∴==⎧⎪∠=∠⎨⎪=⎩∴≅∴∠=∠Q V V V V 点是的中点在ABC 与CDE 中,得证5．证明：.AD FC ADF CEF CFE ADF DFC DE EFAED CEF ADE CFE AE CE ∴∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=Q V V V V ∥在ADE 与中,得证 6．证明：t .BE CD BC BCBDC CEB ABC ACB AB AC =⎧⎨=⎩∴≅∴∠=∠∴=V V V V 在Rt BDC 与R CEB 中,得证7．证明：.CE DF ACE BDF AC FD ACE BDF EC BD ACE BDF AE FB ∴∠=∠=⎧⎪∠=∠⎨⎪=⎩∴=∴=Q V V V V ∥在ACE 与BDF 中,得证 8．证明：.,90451,2,1.2,90,45.90CD ABC AC BC C ABC A D AB CD Rt ABC AD AB CD AB DCF ACB CD AD CDA DCF A DCF DE DF EDF ADC EDFADC CDE EDF CDE A =∠=︒∴∴∠=︒∴∠∴⊥∠=∠=∠=︒∠=︒∴∠=∠⊥∴∠=︒∴∠=∠∴∠-∠=∠-∠∠QV V Q V Q 连接中是等腰直角三角形点是的中点是等腰中的中线,且是AB 边上的高，且是ACB 的角平分线.CD=即即.DE CDF A DCF AD CDADE CDF ADE CDF DE DF =∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=V V V V 在ADE 与CDF 中,得证9．证明：.AC BDAC DC BD DC AD BD A B AD BDADE BCF AED BFC DE CF =∴+=+=∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=Q V V V V 即在AED 与BFC 中,得证10．证明：.CBA DAB AB ABDBA CAB ABC BAD BC AD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=V V V V 在ABC 与BAD 中,得证 11．证明：.BE CFBE EC CF EC BC EF AB DE BC EF AC DF ABC DEF ABC DEF AB DE =∴+=+==⎧⎪=⎨⎪=⎩∴≅∴∠=∠∴Q V V V V 即在ABC 与DEF 中,∥得证12．证明：.AB CD ABE BED AFB DFE ABE BED EF BFAFB DFE AFB DFE AF DF ∴∠=∠∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=Q Q V V V V ∥又在AFB 与DFE 中,得证13．（1）证明：12.AB AC AD AE ABD ACE BD CE =⎧⎪∠=∠⎨⎪=⎩∴≅∴=V V V V 在ABD 与ACE 中,得证 （2）证明：.B C AB ACBAN CAM ABN ACM M N ≅∴∠∠∠∴∠∠∠∠∠∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴∠=∠V V Q V V V V 由(1)知,ABD ACE B=C 11+MAN=2+MAN 即BAN=CAM 在ABN 与ACM 中,得证14．证明：909090.ACB BCE ACE BE CE CEB Rt CEB E ADC A ACE BC AC BCE CAD ∠=︒∴∠+∠=︒⊥∴∠=︒∴∠∠︒∴∠∠⊥∴∠︒∴∠∠∠=∠⎧⎪∠=∠⎨⎪=⎩∴≅Q Q V Q V V V V 在中,BCE+B=90B=ACE AD CE ADC=90E=ADC 在BCE 与CAD 中,得证15．证明：36090180180.EAB BAE BCE B AEC AEC CED B CED AB DE B CED BC DE ABC DEC ︒∠∠∠∠=︒∠=∠=︒∴∠+∠=︒∠+∠=︒∴∠=∠=⎧⎪∠=∠⎨⎪=⎩∴≅Q Q Q V V V V 四边形ABCE 的内角和为360即B+BCE+CEA+又在ABC 与DEC 中,得证16．①证明：36090180180.EAB BAE BCE B AEC AEC CED B CED AB DE B CED BC DE ABC DEC ︒∠∠∠∠=︒∠=∠=︒∴∠+∠=︒∠+∠=︒∴∠=∠=⎧⎪∠=∠⎨⎪=⎩∴≅Q Q Q V V V V 四边形ABCE 的内角和为360即B+BCE+CEA+又在ABC 与DEC 中,得证②,;90.45453015180()180(1590)75,75ABC AB CD ABC ABC BAC ABE BAC EAC AEB BAE ABC ABE CBD BDC AEB =∠=︒∴∴∠=︒∴∠=∠-∠=︒-︒=︒∴∠=︒-∠+∠=︒-︒+︒=︒≅∴∠=∠=︒QV V V V 中是等腰直角三角形由①知 17．证明：（1）.AD BC D ECF E CD DE EC AED CEF D ECF DE EC AED F ADE FCE FC AD ∴∠=∠∴=∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=Q Q Q V V V V ∥点为的中点又在ADE 与FCE 中,得证（2）1,901,.ADE FCE AE FEBE AEBEA BEF BE BE BEA BEF AE FE BEA BEF AB BF CF AD AB BC AD ≅∴=⊥∴∠=∠=︒=⎧⎪∠=∠⎨⎪=⎩∴≅∴==∴=+V V Q V V V V 由（）知在BEA 与BEF 中,即AB=BC+CF 由（）知得证18．解：（1）,15DM AC AM MC BN NCAB AM MN NC MC MN NC C CMN cm∴==∴=++=++==Q V 垂直平分同理（2）90,90360360()180110:,,.2.,1102218070,4DM AC CDM CEN DCE DCE F DCM x MCN y BCN z CMN x CNM y x y z x y z x y z ∴∠=︒∠=︒︒∠∠∠∠=︒∴∠=︒-∠∠∠=︒-∠=︒∠=∠=∠=∠=∠=++=︒⎧⎨++=︒⎩+=︒-=Q Q 垂直平分同理四边形CDFE 的内角和为360即CDM+F+CEF+CDM+F+CEF 设则依题意得①②由②-①得,③由①③得040MCN ︒∴∠=︒19．证明：111222.EF AD AEF DEF EAF EDF EDF B EAF B AD BAC EAF B EAF CAF B CAFACF B BAC CAF BAC ACF BAF ∴≅∴∠=∠∠=∠+∠∴∠=∠+∠∠∴∠=∠∴∠=∠+∠∠=∠+∠∴∠=∠∴∠=∠+∠=∠+∠∠=∠Q V V Q Q Q 垂直平分平分即得证20．证明：.,90,90DF AB N CE AD Rt AEC CAE ACE Rt AADC CAE EDC CAE DCE BF AC CBF ACD CAE DCE AC CBACD CBF ADC CFB CD BF D BC BD CD BD BF AC BC CAB CBA BF AC CAB FBA C ⊥∴∠+∠=︒∠+∠=︒∴∠=∠=∴∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=∴=∴==∴∠=∠∴∠=∠∴∠Q V Q V Q V V V V Q Q Q 连接交于点中中在ADC 与CFB 中,点为的中点∥,90.BA FBA BD BF CBA FBA BN BN BND BNF BND BNF DN FND N F BND BNF AB DF DN FN AD DF =∠=⎧⎪∠=∠⎨⎪=⎩∴≅∴∠=∠=∴∠=∠=︒⊥=∴V V V V Q Q 在BND 与BNF 中,点、、共线即垂直平分得证21．证明：（1）.AD BAC CD EDEDF CD ED DF DBRt CDF Rt DEF CF EB ∠∴==⎧⎨=⎩∴≅∴=Q V V V V 平分在Rt CDF 与Rt 中,得证（2）(1),2.AD BAC Rt ACD Rt AED AC AE AB AE EB AC EBAC AF FCAB AF FC EB FC EBAB AF EB EB AF EB ∠∴≅∴=∴=+=+=+∴=++=∴=++=+Q V V Q 平分由知得证22．证明：（1）.,..OE DC F OE BOA Rt ODE Rt OCE DE EC OED OEC DE EC OED OEC EF EF DEF CEF ECD EDC ∠∴≅∴=∠=∠=⎧⎪∠=∠⎨⎪=⎩∴≅∴∠=∠Q V V V V V V 标记交于点平分在DEF 与CEF 中,得证（2）(1),.OED OECOD OC ≅∴=V V 由知得证（3）(1),,.90.DEF CEF DF CF DFE CFE D DFE CFE OE CD DF CF OE CD ≅∴=∠=∠∴∠=∠=︒⊥=∴V V Q Q 由知点、F 、C 共线即垂直平分得证23．证明：,.M MN AD N ⊥过点作垂足于点（1）1802,22218090180()1809090.AB CDBAD ADC AM BAD BAD MAD ADC ADMMAD ADM MAD ADM AMD MAD ADM AM DM ∴∠+∠=︒∠∴∠=∠∠=∠∴∠+∠=︒∠+∠=︒∠=︒-∠+∠=︒-︒=︒∴⊥Q Q Q ∥平分同理即得证（2）1809090,,.,.AB CD C B BC CD B BC CD AM BAD BM AB MN AD BM MN CM MN BM CM M BC ∴∠=︒-∠=︒∴⊥∠=︒∴⊥∠⊥⊥∴==∴=Q Q Q ∥平分同理即点为的中点得证24．证明：.,..90.90AD BE F ABC AB AC ABC AD AD BC BAC AD BC BDF DAC DAB BE AC AEF AEF BDF AEF BFDDB =∴∴∠∴⊥∠=︒∠=∠⊥∴∠=︒∠=∠∠=∠∠︒∠∠∠∠︒∠∠∴∠∠∠∠∴∠QV V Q Q Q Q Q 标记交于点中是等腰三角形是BC 边上的中线是边上的高线;且是的平分线，即；即又EAF=180-(AEF+AFE)DBF=180-(BDF+BFD)EAF=DBF DAC=DAB .F DABCBE BAD =∠∠=∠即得证25．证明：22.AD BC DBC D AD AB ADB DABC ABD DBCD AB AC C ABC C D ∴∠=∠=∴∠=∠∴∠=∠+∠=∠=∴∠=∠∠=∠Q Q Q ∥即得证26．（1）证明：90.BD CE ADB AEC ADB AEC A A AB AC ABD ACE BD CEBEC BD CE BC BCRt BEC Rt CDB OCB OBC OB OC ∴∠=∠=︒∠=∠⎧⎪∠=∠⎨⎪=⎩∴≅∴==⎧⎨=⎩∴≅∴∠=∠∴=Q V V V V V V V V 、是高线在ABD 与ACE 中,在Rt 与Rt CDB 中,得证（2）解,180()180(9050)40(1),40,180()180(4040)100Rt BEC OCB BEC ABC OB OCOBC OCB BOC BOC OBC OCB ∠=︒-∠+∠=︒-︒+︒=︒=∴∠=∠=︒∠=︒-∠+∠=︒-︒+︒=︒V V 在中有知中27．（1）证明：AB AC C B BD EC B C BE CF BED CFE DE EFDEF =∴∠=∠=⎧⎪∠=∠⎨⎪=⎩∴≅∴=∴Q V V V V 在BED 与CFE 中,是等腰三角形（2）解：(1),.180218040270,18018070110180()18011070C B AB BDE BED DEB B DEF BED CEF ∠=∠︒-∠∴∠=︒-︒==︒∴∠+∠=︒-∠=︒-︒=︒∴∠=︒-∠+∠=︒-︒=︒V 由知中28．解：（1）6090180()180(6090)30ABC B DE DE EF DEF F EDC DEF ∴∠=︒∴∠∠︒⊥∴∠=︒∴∠=︒-∠+∠=︒-︒+︒=︒QV Q Q 是正三角形∥ABEDC=B=60（2）601,60.180()180(6060)602909060301,60.2224ABC ACB EDC DEC ACB DEC CDE EC DC DEF CEF DEF DEC F CAF F CF ECCF EC DC DF DC CF ∴∠=︒∠=︒∴∠=︒-∠+∠=︒-︒+︒=︒∴∴==∠=︒∴∠=∠-∠=︒-︒=︒∠=︒∴∠=∠∴=∴===∴=+=+=QV V Q 是正三角形由（）知是正三角形由（）知29．（1）.,,60.,,60..AN BM AMC AC MC ACM CN CB NCB ACM NCBACM MCN MCN NCB ACN MCB AC MC ACN MCB CN CB ACN MCB AN BM =∴=∠=︒=∠=︒∴∠=∠∴∠+∠=∠+∠∠=∠=⎧⎪∠=∠⎨⎪=⎩∴≅∴=QV V V V V 证明如下是正三角形同理即在ACN 与MCB 中,得证（2）,1,.,60.,60.180()180(6060)60CEF ACN MCB NAC BMC AMC AC MC ACM MCB A C B ECF ACM MCB ACM ECF NAC BMC AC MCACM ECF AEC MFC EC FCC ≅∴∠=∠∴=∠=︒∠=︒∴∠=︒-∠+∠=︒-︒+︒=︒∴∠=∠∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=∴V V V QV Q V V V V V 是等边三角形.证明如下由（）知是等边三角形同理点、、共线在AEC 与MFC 中,EF CEF ∠︒∴Q V 是等腰三角形ECF=60是等边三角形30．（1）5.①图中有个等腰三角形12,12,.,.,.EF BE FC ABCOBC ABO ABCOCB ACO ACBABC ACBOBC ABO OCB ACO OBC OCB BOC EF BC EOB OBC FOC OCB EBO OBC FCO OCB EBO EOB FCO FOC BEO CFO =+∠∴∠=∠=∠∠=∠=∠∠=∠∴∠=∠=∠=∠∠=∠∴∴∠=∠∠=∠∠=∠∠=∠∴∠=∠∠=∠∴Q Q Q V Q Q V V V ②证明如下,BO 平分同理是等腰三角形∥、是等腰三角形在BEO .EBO FCO BO COEOB FOC BEO CFO BE FCBE ED FO FC EF EO FO BE FC AB ACAB BE AC FC AE AFAEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴≅∴=∴===∴=+=+=∴-=-=∴V V V Q V V V V V V 与CFO 中,②得证即是等腰三角形综上，图中的等腰三角形有:AEF 、ABC 、BED 、CFD 、BOC 五个.②得证.（2）.1.,,,.,.,..BED CFO EF BE CF BO EBC BEO OBC FCO OCB EF BC EOB OBC FOC OCB EBO OBC FCO FOC BE EO FC FO EF EO FO BE CF =+∠∴∠=∠∠=∠∴∠=∠∠=∠∴∠=∠∠=∠∴==∴=+=+V V Q Q ①、是等腰三角形②（）中命题依然成立证明如下平分同理∥得证（3）,..BEO CFO EO BC EOB OBC EBC EOB BE EO FC FO EF EO FO EF BE CF ∠∴∠∠∴∠=∠∴∠=∠∴===-∴=-V V Q Q Q ①、是等腰三角形.②EF=BE-CF.证明如下,BC 平分ABC EBO=OBC ∥同理得证。
八年级数学上册 尺规作图(习题及答案)(人教版)
八年级数学上册尺规作图(习题及答
案)(人教版)
尺规作图是一种古老的几何学方法，可以使用尺子和圆规来进行几何图形的构造。
在练中，我们需要注意作图语言的描述是否正确，例如延长线段、作平分线、作弧等。
同时，我们还需要掌握一些基本的作图方法，如已知边长作等边三角形、作角平分线等。
在完成题目时，要保留作图痕迹，并根据题目要求进行精确的构造。
尺规作图起源于古希腊的数学课题，其目的是使用圆规和直尺有限次来解决平面几何作图问题。
XXX是最早提出作图要有次数限制的人，但由于政治原因被囚禁并判处死刑。
在狱中，他用一根绳子画圆、用破木棍作直尺来思考改圆成方等问题，因此尺规作图也被称为“安那萨哥拉斯问题”。
尺规作图的三大难题包括：化圆为方问题、三等分角问题和倍立方问题。
其中，化圆为方问题要求求出一个正方形的边长，使其面积与一已知圆的面积相等；三等分角问题要求求出一角，使其角度是一已知角度的三分之一；倍立方问题要求求出一立方体的棱长，使其体积是一已知立方体的二倍。
以化圆为方问题为例，其解法为：（1）作线段AB使AB=a；（2）分别以点A、点B为圆心，a长为半径作弧，两弧交于点C；（3）连接AC、BC。
则△XXX即为所求。
人教版八年级数学上册几何证明习题集
C八年级上册几何证明题题集1、 已知：在⊿ABC 中，AB=AC ，延长AB 到D ，使AB=BD ，E 是AB 的中点。
求证：CD=2CE 。
2、 已知：在⊿ABC 中，作∠FBC=∠ECB=21∠A 。
求证：BE=CF 。
B3、 已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。
CB4、 已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。
ABB DCA B C DE P 图 ⑴5、如图甲，Rt ∆ABC 中，AB=AC ，点D 、E 是线段AC 上两动点，且AD=EC ，AM ⊥BD ，垂足为M ，AM 的延长线交BC 于点N ，直线BD 与直线NE 相交于点F 。
（1）试判断∆DEF 的形状，并加以证明。
（2）如图乙，若点D 、E 是直线AC 上两动点，其他条件不变，试判断∆DEF 的形状，并加以证明。
6、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。
7、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．①②③图88、△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论．9、在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。
八上几何习题集及答案.doc
八上几何习题集1、如图：在左ABC中,ZC=2ZB,AD是左ABC的角平分线,21 =匕B,试说明AB=AC+CD2、如图,AD是ZBAC的角平分线，DE1AB垂足为E, DF1AC,垂足为点F,且BD=CD求证：BE=CF3、如图，点B和点C分别为匕MAN两边上的点，AB=ACo（1）按下列语句画出图形：①ADJLBC,垂足为D；②ZBCN的平分线CE与AD的延长线交于点E；③连结BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ ABD^AACD外的两对全等三角形: —丝—，—#—;（3）并选择其中的一对全等三角形予以证明。
己知：AB=AC, AD1BC, CE 平分匕BCN,求证：AADB^AADC； ABDE^ACDEo4、如图，PB、PC分别是AABC的外角平分线且相交于点P.求证：点P在NA的平分线上A5、如图，AABC中，p是角平分线AD, BE的交点.求证：点p在NC的平分线上6、下列说法中，错误的是（）A.三伯形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的距离相等C.三角形两个角的平分线的交点在笫三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三的形ABC中BM=MC ZABM= ZACM求证AM平分匕BAC8、如图，AP、CP分别是AABC外角ZMAC与ZNCA的平分线，它们相交于点P, PD±BM于点D, PF±BN于点F.求证：BP为ZMBN的平分线。
9、如图，在ZAOB的两边OA, 0B ±分别取OM=ON, OD=OE, DN和EM相交于点C.求证：点C在ZAOB 的平分线上.1()、如图,ZB=ZC=90° , M 是BC 的中点，DM 平分ZADC.(1)若连接AM,则AM是否平分ZBAD?清你证明你的结论;(2)线段DM与AM有怎样的位置关系？请说明理由.11、八(1)班同学上数学活动课，利用角尺平分一个角(如图所示).设计了如下方案：(I ) ZAOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN,过角尺顶点P的射线OP就是ZAOB的平分线.(II) ZAOB是一个任意角，在边OA、0B±分别取0M=ON,将角尺的直角顶点P介于射线OA、0B之间，移动们尺使角尺两边相同的刻度与M、N重合，即PM=PN,过怕尺顶点P的射线OP就是ZAOB的平分线.(1)方案(I)、方案(1【)是否可行？若可行，请证明；若不可行，请说明理由；(2)在方,案(I ) PM=PN的情况卜《继续移动角尺，同时使PM_LOA, PN±OB.此方案是否可行？清说明理由.12、如图，P是ZBAC内的一点，PE1AB, PF1AC,垂足分别为点E, F, AE=AF。
人教版八年级数学上册专题集训(二)几何与图形(含答案解析)
人教版八年级数学上册专题集训(二)几何与图形(时间:90分钟总分:100分)题号一二三总分得分一、选择题(每小题3分，共30分)1.下列线段能构成三角形的是( )A.2,2,4B.3,4,5C.1,2,3D.2,3, 62.用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是( )3.如图，为估计池塘岸边A 、B两点的距离，小方在池塘的一侧选取一点O，测得OA ＝8米，OB＝6米，A、B间的距离不可能是( )A.12米B.10米C. 15米D.8米4.下列事例应用了三角形稳定性的有( )①人们通常会在栅栏门上斜着钉上一根木条;②新植的树木，常用一些粗木与之成角度的支撑起来防止倒斜;③四边形模具.A.1个B.2个C.3个D.0个，5.一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是( )A. 3B.4C.6D.126.如图，在△ABC中，∠A＝45°，点D、E分别在AB、AC上，则∠1+∠2的大小为( )A.225°B.135°C.180°D.315°7.如图，若△OAD≌△OBC，∠0＝65°，∠C＝20°，则∠OAD＝( )A.65°B.75°C.85°D.95°8.在以下节水、回收、节能、绿色食品四个标志中，是轴对称图形的是( )9.如图，在△ABC中，AB＝AC＝20cm，DE垂直平分AB，垂足为E且交AC于点の，若△DBC的周长为35cm，则BC的长为( )A.5cmB.10cmC.15cmD.17.5cm10.如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD＝DE，连接BE交CD 于点O，连接AO，下列结论不正确的是( )A.△AOB≌△BOCB.△BOC≌△EODC.△AOD≌△EODD.△AOD≌△BOC二、填空题(每小题3分，共24分)11.直角三角形两个锐角度数比是1:2，则两个锐角的度数分别是___________、_____________.12.在△ABC中，∠B的外角平分线与∠C的外角平分线相交于点P，且∠BPC＝80°，则∠BAP的度数为_____________.13.一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M如果∠ADF＝100°，那么∠BMD为_____________.14.等腰三角形的一边长为3，另一边长为6，则该三角形的周长是_____________.15.如图，△ABC≌△DEF，请根图中提供的信息，写出x＝_____________.16.如图，将三个相同的等边三角形(三个内角都是609)的一个顶点重合放置，若∠BAE＝10,∠HAF＝35°，则∠CAD_____________.17.如图，在△ABC中，∠ABC＝90°，AB＝3，AC＝5，点E在BC上，将△ABC沿AE 折叠，使点B落在AC边上的点B处，则BE的长为_____________.18.如图，在平面直角坐标系中，已知点A(2、3)，点B(-2，1)，在x轴上存在一点P到A，B两点的距离之和最小，则P点的坐标是_____________. 二、解答题(46分)19.(6分)如图，已知DF⊥AB于点F，且∠A＝45°，∠D＝30°，求∠ACB 的度数.20.(6分)一个三角形的两边长分别为2和9，第三边为奇数，求此三角形的周长.21.(6分)如图，点F是△ABC的边BC延长线上一点，DF⊥AB，∠A＝30°，∠F=40°，求∠ACF的度数.22.(9分)如图，在△ABC中，AB＝CB，∠AB C＝909，D为AB延长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC.①求证:△ABE≌△CBD;②若∠CAE＝30°，求∠BDC的度数.23.(9分)如图，在平面直角坐标系中，A(-1，5)，B(-1, 0)，C(-4, 3)(1)求出△ABC的面积;(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;(3)写出点A1，B1，C1的坐标.24.(10分)如图，在四边形ABCD中，AB＝DC，延长线段CB到E，使BE＝AD，连接AE、AC，且AE＝AC，求证:(1)△ABE≌△CDA;(2)AD∥EC.参考答案几何与图形1.B2.A3.C4.B5.B6.A7.D8.D9.C 10.A 11.30°60°12.10°13.85°14.15 15.20 16.15°17. 18.(-1,0)19.解:∵DF⊥AB于点F，∴∠EFA＝90°，∵∠A＝45°∴∠AEF＝45,∴∠CED＝∠AEF＝45°，又∵∠D＝30°∴∠ACB＝∠CED+∠D＝45+30°＝75°20.解:设第三边长为x，根据三角形三边关系，∴9-2＜x＜2+9，即7＜x＜1，∵x为奇数，∴x＝9∴三角形的周长为2+9+9＝2021.解:在△DFB中，∵DF⊥AB，∴∠FDB＝90°∵∠F＝40°，∠FDB+∠F+∠B＝180°，∴∠B＝50.在△ABC中，∵∠A＝30°，∠B＝50，∴∠ACF＝30°+50°＝8022.①证明:在△ABE和△CBD中AB=CB∠ABC＝∠CBD=90°，∴△ABE≌△CBD(SAS);BE=BD ②解:∵在△ABC中，AB＝CB，∠ABC＝90°∴∠BAC＝∠ACB＝45°，由①得:△ABE≌△CBD∴∠AEB＝∠BDC，∵∠AEB为△AEC的外角，∴∠AEB＝∠ACB+∠CAE＝30°+45°＝75°，则∠BDC＝75°23.(1)图略，△ABC的面积为3×5×21=215 (2)图略. (3)A1(1,5),B1(1,0),C1(4,3)24.解:(1)在△ABE和△CDA中AE=ACAB＝DC，∴△ABE≌△CDA(SSS)BE=AD(2)∵△ABE≌△CDA，∴∠E＝∠CAD∵AE＝AC，∴∠E＝∠ACE.∴∠ACE＝∠CAD，∴AD∥EC.。
人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)
人教版八年级数学上册期末专题复习：几何压轴题强化训练试题1、如图，AB＞AC，∠BAC的平分线与BC边的中垂线GD相交于点D，过点D作DE⊥AB于点E，DF⊥AC于点F，求证：BE=CF．2、如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α．（0°＜α＜90°）得到△A1B1C1，连接BB1．设CB1交AB于D，A1B1分别交AB、AC于E、F．（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以说明（△ABC与△A1B1C1全等除外）；（2）当△BB1D是等腰三角形时，求α．3、如图，在△ABC中，∠BAC=120°，AD，BE分别为△ABC的角平分线，连结DE．（1）求证：点E到DA，DC的距离相等；（2）求∠DEB的度数．4、在△ABC中，∠ACB=90°，AC=BC，直线，MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．（1）当直线MN绕点C旋转到如图1的位置时，求证：DE=AD+BE；（2）当直线MN绕点C旋转到如图2的位置时，求证：DE=AD﹣BE；（3）当直线MN绕点C旋转到如图3的位置时，线段DE、AD、BE之间又有什么样的数量关系？请你直接写出这个数量关系，不要证明．5、概念学习：规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．理解概念（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，请写出图中两对“等角三角形”．概念应用（2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．求证：CD为△ABC的等角分割线．（3）在△ABC中，∠A＝42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．6、如图,∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点。
(word完整版)人教版八年级上册数学几何练习题
人教版八年级上册数学几何练习题1、已知：在⊿ABC中，∠A=90，AB=AC，在BC上任取一点P，作PQ∥AB交AC于Q，作PR∥CA交BA于R，D是BC的中点，求证：⊿RDQ是等腰直角三角形。
2、已知：在⊿ABC中，∠A=90，AB=AC，D是AC的中点，AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。
B3、已知：在⊿ABC中BD、CE是高，在BD、CE或其延长线上分别截取BM=AC、CN=AB，求证：MA⊥NA。
C4、已知：如图，在△ABC中，BP、CP分别平分∠ABC 和∠ACB，DE过点P交AB于D，交AC于E，且DE∥BC．求证：DE－DB=EC． APE DBC图⑴5、在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。
写出点O到△ABC的三个顶点A、B、C的距离的大小关系；如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。
A M B6、如图，△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，连结EC、ED，求证：CE=DE7、如图，等腰三角形ABC中，AB＝AC，∠A＝90°，BD平分∠ABC，DE⊥BC且BC＝10，求△DCE的周长。
几何证明习题答案1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度, 又由平行关系得,四边形RPQA为矩形,所以AQ=RP, △BRP也是等腰直角三角行,即BR=PR,所以AQ=BR由边角边,△BRD全等于△AQD,所以∠BDR=∠ADQ,DR=DQ, ∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度, 所以△RDQ是等腰RT△。
2. 作AG平分∠BAC交BD于G ∵∠BAC=90° ∴∠CAG= ∠BAG=45° ∵∠BAC=90° AC=AB ∴∠C=∠ABC=45°∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90°∵∠CAF+∠BAE=90° ∴∠CAF=∠ABE ∵ AC=AB ∴△ACF ≌△BAG ∴CF=AG ∵∠C=∠DAG =45°CD=AD ∴△CDF ≌△ADG ∴∠CDF=∠ADB3. 易证△ABM≌△NAC．∠NAM＝∠NAE＋∠BAM＝∠NAE＋ANE＝90°4. 略5.因为直角三角形的斜边中点是三角形的外心，所以O到△ABC的三个顶点A、B、C距离相等；△OMN是等腰直角三角形。
(完整版)八年级数学几何经典题【含答案】
F八年级数学几何经典题【含答案】1、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．2、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．3、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．.4、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．B5、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．6、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．7如图，△ABC 中，∠C 为直角，∠A=30°，分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ，DE 与AB 交于F 。
求证：EF=FD 。
8如图，正方形ABCD 中，E 、F 分别为AB 、BC 的中点，EC 和DF 相交于G ，连接AG ，求证：AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA，九年级数学【答案】1.如下图连接AC 并取其中点Q ，连接QN 和QM ，所以可得∠QMF=∠F ，∠QNM=∠DEN 和∠QMN=∠QNM ，从而得出∠DEN ＝∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ，CI ，FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ，可得EG=AI ，由△BFH ≌△CBI ，可得FH=BI 。
人教版八年级上册几何压轴题专项训练 含答案
人教版八年级上册几何压轴题专项训练1．已知，如图，△ABC为等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥AD于Q．（1）求证：BE＝AD；（2）求∠BPQ的度数；（3）若PQ＝3，PE＝1，求AD的长．2．如图，已知在△ABC中，∠BAC为直角，AB＝AC，D为AC上一点，CE⊥BD于E，交BA的延长线于F．（1）求证：△ABD≌△ACF；（2）若BD平分∠ABC，求证：CE＝BD；（3）若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，直接写出它的度数．3．如图1，△ABE是等腰三角形，AB＝AE，∠BAE＝45°，过点B作BC⊥AE于点C，在BC上截取CD＝CE，连接AD、DE，并延长AD交BE于点P；（1）求证：AD＝BE；（2）试说明AD⊥BE；（3）如图2，将△CDE绕着点C旋转一定的角度，那么AD与BE的位置关系是否发生变化，说明理由．4．如图，已知△ABC中，AB＝AC＝10厘米，∠ABC＝∠ACB，BC＝8厘米，点D为AB 的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，设点P运动的时间为t．（1）用含有t的代数式表示线段PC的长度；（2）若点Q的运动速度与点P的运动速度相等，经过1秒后△BPD与△CQP是否全等，请说明理由；（3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？5．以点A为顶点作等腰Rt△ABC，等腰Rt△ADE，其中∠BAC＝∠DAE＝90°，如图1所示放置，使得一直角边重合，连接BD、CE．（1）试判断BD、CE的数量关系，并说明理由；（2）延长BD交CE于点F，试求∠BFC的度数；（3）把两个等腰直角三角形按如图2放置，（1）、（2）中的结论是否仍成立？请说明理由．6．如图1，在△ABC中，AB＝AC，点D是BC边上一点（不与点B，C重合），以AD为边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE．设∠BAC＝α，∠BCE ＝β．（1）求证：△CAE≌△BAD；（2）探究：当点D在BC边上移动时，α、β之间有怎样的数量关系？请说明理由；（3）如图2，若∠BAC＝90°，CE与BA的延长线交于点F．求证：EF＝DC．7．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠F AE的度数；（3）求证：CD＝2BF+DE．8．如图，在平面直角坐标系中，OA＝OB，AC＝CD，已知两点A（4，0），C（0，7），点D在第一象限内，∠DCA＝90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N．（1）点B的坐标为：；（2）求点D的坐标；（3）求证：CM＝CN．9．已知：如图1所示，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，直线MN经过点A，BD⊥MN于点D，CE⊥MN于点E．（1）求证：△BAD≌△ACE；（2）试判断线段DE，BD，CE之间的数量关系，并说明理由；（3）当直线MN运动到如图2所示位置时，其余条件不变，判断线段DE，BD，CE之间的数量关系．10．如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．（1）请说出AD＝BE的理由；（2）试说出△BCH≌△ACG的理由；（3）试猜想：△CGH是什么特殊的三角形，并加以说明．11．（1）如图1，△ABC和△DCE都是等边三角形，且B，C，D三点在一条直线上，连接AD，BE相交于点P，求证：BE＝AD．（2）如图2，在△BCD中，若∠BCD＜120°，分别以BC，CD和BD为边在△BCD外部作等边△ABC，等边△CDE，等边△BDF，连接AD、BE、CF恰交于点P．①求证：AD＝BE＝CF；②如图2，在（2）的条件下，试猜想PB，PC，PD与BE存在怎样的数量关系，并说明理由．12．已知：在等边△ABC中，点D、E、F分别为边AB、BC、AC的中点，点G为直线BC 上一动点，当点G在CB延长线上时，有结论“在直线EF上存在一点H，使得△DGH 是等边三角形”成立（如图①），且当点G与点B、E、C重合时，该结论也一定成立．问题：当点G在直线BC的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．13．如图，在△ABC中，AB＝BC＝AC＝20cm．动点P，Q分别从A，B两点同时出发，沿三角形的边匀速运动．已知点P，点Q的速度都是2cm/s，当点P第一次到达B点时，P，Q两点同时停止运动．设点P的运动时间为t（s）．（1）∠A＝度；（2）当0＜t＜10，且△APQ为直角三角形时，求t的值；（3）当△APQ为等边三角形时，直接写出t的值．14．如图，在三角形ABC中，AB＝8，BC＝16，AC＝12．点P从点A出发以2个单位长度/秒的速度沿A→＞B→C→A的方向运动，点Q从点B沿B→C→A的方向与点P同时出发；当点P第一次回到A点时，点P，Q同时停止运动；用t（秒）表示运动时间．（1）当t＝秒时，P是AB的中点．（2）若点Q的运动速度是个单位长度/秒，是否存在t的值，使得BP＝2BQ．（3）若点Q的运动速度是a个单位长度/秒，当点P，Q是AC边上的三等分点时，求a的值．15．如图，等边△ABC的边长为15cm，现有两点M，N分别从点A，点B同时出发，沿三角形的边顺时针运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M，N同时停止运动（1）点M、N运动几秒后，M，N两点重合？（2）点M、N运动几秒后，△AMN为等边三角形？（3）当点M，N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M，N运动的时间．16．如图，已知△ABC中，AB＝AC＝10cm，BC＝8cm，点D为AB的中点．（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA 上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？参考答案1．（1）证明：∵△ABC为等边三角形，∴AB＝CA，∠BAE＝∠C＝60°，在△AEB与△CDA中，，∴△AEB≌△CDA（SAS），∴BE＝AD；（2）解：由（1）知，△AEB≌△CDA，则∠ABE＝∠CAD，∴∠BAD+∠ABD＝∠BAD+∠CAD＝∠BAC＝60°，∴∠BPQ＝∠BAD+∠ABD＝60°；（3）解：如图，由（2）知∠BPQ＝60°．∵BQ⊥AD，∴∠PBQ＝30°，∴PQ＝BP＝3，∴BP＝6∴BE＝BP+PE＝7，即AD＝7．2．解：（1）∵∠BAC是直角，CE⊥BD，∴∠BAC＝∠CAF＝∠BEC＝90°，∴∠CDE+∠DCE＝90°，∠ABD+∠ADB＝90°，∵∠ADB＝∠CDE，∴∠ABD＝∠ACF，在△ABD和△ACF中，，∴△ABD≌△ACF（ASA）；（2）由（1）知，△ABD≌ACF，∴BD＝CF，∵BD⊥CE，BD平分∠ABC，∴BC＝BF，∵BD⊥CE，∴CE＝EF，∴CE＝CF＝BD；（3）∠AED不变化理由：如图，过点A作AG⊥⊥CF于G，作AH⊥BD于H，由（1）证得△BAD≌△CAF（ASA），∴S△BAD＝S△CAF，BD＝CF，∴BD•AH＝CF•AG，而BD＝CF，∴AH＝AG，∵AH⊥EB，AG⊥EG，∴EA平分∠BEF，∴∠BEA＝∠BEG＝45°，即：∠AED不变化．3．解：（1）∵BC⊥AE，∠BAE＝45°，∴∠CBA＝∠CAB，∴BC＝CA，在△BCE和△ACD中，，∴△BCE≌△ACD（SAS），∴AD＝BE．（2）∵△BCE≌△ACD，∴∠EBC＝∠DAC，∵∠BDP＝∠ADC，∴∠BPD＝∠DCA＝90°，∴AD⊥BE．（3）AD⊥BE不发生变化．理由：如图（2），∵△BCE≌△ACD，∴∠EBC＝∠DAC，∵∠BFP＝∠AFC，∴∠BPF＝∠ACF＝90°，∴AD⊥BE．4．解：（1）由运动知，BP＝3t，∵BC＝8，∴PC＝BC﹣BP＝8﹣3t；（2）全等，理由：当t＝1时，BP＝3，CP＝5，CQ＝3，∴BP＝CQ，∵点D是AB的中点，∴BD＝AB＝5，∴CP＝BD，在△BPD和△CQP中，，∴△BPD≌△CQP（SAS）；（3）∵BP＝3t，CP＝8﹣3t，设点Q的运动速度为xcm/s，∴CQ＝xt，当△BPD≌△CQP时，∴BP＝CQ，∴3t＝xt，∴x＝3（不符合题意），当△BPD≌△CPQ时，∴BP＝CP，BD＝CQ，∴3t＝8﹣3t，5＝xt，∴t＝，x＝，∴点Q的运动速度为cm/s时，能够使△BPD与△CQP全等．5．解：（1）CE＝BD，理由如下：∵等腰Rt△ABC，等腰Rt△ADE，∴AE＝AD，AC＝AB，在△EAC与△DAB中，，∴△EAC≌△DAB（SAS），∴CE＝BD；（2）∵△EAC≌△DAB，∴∠ECA＝∠DBA，∴∠ECA+∠CBF＝∠DBA+∠CBF＝45°，∴∠ECA+∠CBF+∠DCB＝45°+45°＝90°，∴∠BFC＝180°﹣90°＝90°；（3）成立，∵等腰Rt△ABC，等腰Rt△ADE，∴AE＝AD，AC＝AB，在△EAC与△DAB中，，∴△EAC≌△DAB（SAS），∴CE＝BD；∵△EAC≌△DAB，∴∠ECA＝∠DBA，∴∠ECA+∠CBF＝∠DBA+∠CBF＝45°，∴∠ECA+∠CBF+∠DCB＝45°+45°＝90°，∴∠BFC＝180°﹣90°＝90°．6．（1）证明：∵∠DAE＝∠BAC，∴∠DAE﹣∠DAC＝∠BAC﹣∠DAC，∴∠CAE＝∠BAD．∵AD＝AE，AC＝AB，∴△CAE≌△BAD（SAS）．（2）解：α+β＝180°，理由如下：由△CAE≌△BAD，∴∠ACE＝∠B．∵AB＝AC，∴∠B＝∠ACB．∴∠ACE＝∠B＝∠ACB．∴∠BCE＝β＝2∠B，在△ABC中，∠BAC＝α＝180°﹣2∠B．∴α+β＝180°．（3）证明：由（1）知，△CAE≌△BAD，∴CE＝BD．∵∠BAC＝90°，AB＝AC，∴∠B＝∠ACB＝45°，由（2）得，∠BCF+∠BAC＝180°．∴∠BCF＝90°．∴∠F＝∠B＝45°，∴CF＝CB．∴CF﹣CE＝CB﹣BD．∴EF＝DC．7．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CF A＝90°，∴∠CAF＝45°，∴∠F AE＝∠F AC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．8．解：（1）∵A（4，0），∴OA＝OB＝4，∴B（0，4），故答案为：（0，4）．（2）∵C（0，7），∴OC＝7，过点D作DE⊥y轴，垂足为E，∴∠DEC＝∠AOC＝90°，∵∠DCA＝90°，∴∠ECD+∠BCA＝∠ECD+∠EDC＝90°∴∠BCA＝∠EDC，∴△DEC≌△COA（AAS），∴DE＝OC＝7，EC＝OA＝4，∴OE＝OC+EC＝11，∴D（7，11）；（3）证明：∵BE＝OE﹣OB＝11﹣4＝7∴BE＝DE，∴△DBE是等腰直角三角形，∴∠DBE＝45°，∵OA＝OB，∴∠OBA＝45°，∴∠DBA＝90°，∴∠BAN+∠ANB＝90°，∵∠DCA＝90°，∴∠CDN+∠DNC＝90°，∵∠DNC＝∠ANB，∴∠CDN＝∠BAN，∵∠DCA＝90°，∴∠ACM＝∠DCN＝90°，∴△DCN≌△ACM（ASA），∴CM＝CN．9．（1）证明：∵BD⊥MN，CE⊥MN，∴∠BDA＝∠AEC＝90°，∴∠BAD+∠ABD＝90°，又∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∴∠ABD＝∠CAE，在△BAD和△ACE中，，∴△BAD≌△ACE（AAS），（2）解：DE＝BD+CE．理由如下：由（1）得：△BAD≌△ACE，∴BD＝AE，AD＝CE，又DE＝AE+AD，∴DE＝BD+CE，（3）DE＝CE﹣BD，同（1）可得：△BAD≌△ACE，故BD＝AE，AD＝CE，又DE＝AD﹣AE，∴DE＝CE﹣BD．10．解：（1）∵△ABC和△CDE均为等边三角形∴AC＝BC，EC＝DC∠ACB＝∠ECD＝60°∴∠ACD＝∠ECB∴△ACD≌△BCE∴AD＝BE；（2）∵△ACD≌△BCE∴∠CBH＝∠CAG∵∠ACB＝∠ECD＝60°，点B、C、D在同一条直线上∴∠ACB＝∠ECD＝∠ACG＝60°又∵AC＝BC∴△ACG≌△BCH；（3）△CGH是等边三角形，理由如下：∵△ACG≌△BCH∴CG＝CH（全等三角形的对应边相等）又∵∠ACG＝60°∴△CGH是等边三角形（有一内角为60度的等腰三角形为等边三角形）；11．（1）证明：∵△ABC和△DCE都是等边三角形，∴BC＝AC，CE＝CD，∠ACB＝∠DCE＝60°，∴∠ABC+∠ACE＝∠DCE+∠ACE，即∠BCE＝∠ACD，∴∠BCE≌△ACD（SAS），∴BE＝AD；（2）①证明：∵△ABC和△CDE是等边三角形，∴AB＝BC，CD＝BE，∠ACB＝∠DCE＝60°，∴∠ACB+∠BCD＝∠DCE+∠BCD，即∠ACD＝∠BCE，∴△ACD≌△BCE（SAS），∴AD＝BE，同理：△ABD≌△CBF（SAS），即AD＝BE＝CF；②解：结论：PB+PC+PD＝BE，理由：如图2，AD与BC的交点记作点Q，则∠AQC＝∠BQP，由①知，△ACD≌△BCE，∴∠CAD＝∠CBE，在△ACQ中，∠CAD+∠AQC＝180°﹣∠ACB＝120°，∴∠CBE+∠BQP＝120°，在△BPQ中，∠APB＝180°﹣（∠CBE+∠BQP）＝60°，∴∠DPE＝60°，同理：∠APC＝60°，∴∠CPD＝120°，在PE上取一点M，使PM＝PC，∴△CPM是等边三角形，∴CP＝CM，∠PCM＝∠CMP＝60°，∴∠CME＝120°＝∠CPD，∵△CDE是等边三角形，∴CD＝CE，∠DCE＝60°＝∠PCM，∴∠PCD＝∠MCE，∴△PCD≌△MCE（SAS），∴BE＝PB+PM+ME＝PB+PC+PD．12．证明：连接DE、EF、DF．（1）当点G在线段BE上时，如图①，在EF上截取EH使EH＝BG．∵D、E、F是等边△ABC三边中点，∴△DEF、△DBE也是等边三角形且DE＝AB＝BD．在△DBG和△DEH中，，∴△DBG≌△DEH（SAS），∴DG＝DH．∴∠BDG＝∠EDH．∵∠BDE＝∠GDE+∠BDG＝60°，∴∠GDH＝∠GDE+∠EDH＝60°∴在直线EF上存在点H使得△DGH是等边三角形．（2）当点G在射线EC上时，如图②，在EF上截取EH使EH＝BG．由（1）可证△DBG≌△DEH．∴DG＝DH，∠BDG＝∠EDH．∵∠BDE＝∠BDG﹣∠EDG＝60°，∴∠GDH＝∠EDH﹣∠EDG＝60°．∴在直线EF上存在点H使得△DGH是等边三角形．（3）当点G在BC延长线上时，如图③，与（2）同理可证，结论成立．综上所述，点G在直线BC上的任意位置时，该结论成立．13．解：（1）∵AB＝BC＝AC，∴△ABC为等边三角形，∴∠A＝60°，故答案为：60．（2）∵∠A＝60°，当∠APQ＝90°时，∠AQP＝90°﹣60°＝30°．∴QA＝2P A．即20﹣2t＝2t×2．解得．当∠AQP＝90°时，∠APQ＝90°﹣60°＝30°．∴P A＝2QA．即2（20﹣2t）＝2t．解得．∴当0＜t＜10，且△APQ为直角三角形时，t的值为．（3）①由题意得：AP＝2t，AQ＝20﹣2t，∵∠A＝60°，∴当AQ＝AP时，△APQ为等边三角形，∴2t＝20﹣2t，解得t＝5，②当P于B重合，Q与C重合，则所用时间为：4÷2＝20，综上，当△APQ为等边三角形时，t＝5或20．14．解：（1）∵AB＝8，点P的运动速度为2个单位长度/秒，∴当P为AB中点时，即4÷2＝2（秒）；故答案为：2．（2）由题意可得：当BP＝2BQ时，P，Q分别在AB，BC上，∵点Q的运动速度为个单位长度/秒，∴点Q只能在BC上运动，当点P在AB上，∴BP＝8﹣2t，BQ＝t，则8﹣2t＝2×t，解得t＝，当点P在BC上时，BP＝2t﹣8，BQ＝，∴2t﹣8＝2×t，解得t＝12．当点P运动到AC上时，不存在BP＝2BQ；故t＝12或，使得BP＝2BQ．（3）当点P为靠近点A的三等分点时，如图1，AB+BC+CP＝8+16+8＝32，此时t＝32÷2＝16，∵BC+CQ＝16+4＝20，∴a＝20÷16＝，当点P为靠近点C的三等分点时，如图2，AB+BC+CP＝8+16+4＝28，此时t＝28÷2＝14，∵BC+CQ＝16+8＝24，∴a＝24÷14＝．综上可得：a的值为或．15．解：（1）设运动t秒，M、N两点重合，根据题意得：2t﹣t＝15，∴t＝15，答：点M，N运动15秒后，M、N两点重合；（2）如图1，设点M、N运动x秒后，△AMN为等边三角形，∴AN＝AM，由运动知，AN＝15﹣2x，AM＝x，∴15﹣2x＝x，解得：x＝5，∴点M、N运动5秒后，△AMN是等边三角形；（3）假设存在，如图2，设M、N运动y秒后，得到以MN为底边的等腰三角形AMN，∴AM＝AN，∴∠AMN＝∠ANM，∵△ABC是等边三角形，∴AB＝AC，∠C＝∠B＝60°，∴△ACN≌△ABM（AAS），∴CN＝BM，∴CM＝BN，由运动知，CM＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以MN为底边的等腰三角形AMN，此时M，N运动的时间为20秒．16．解：（1）①∵t＝1s，∴BP＝CQ＝3×1＝3cm，∵AB＝10cm，点D为AB的中点，∴BD＝5cm．又∵PC＝BC﹣BP，BC＝8cm，∴PC＝8﹣3＝5cm，∴PC＝BD．又∵AB＝AC，∴∠B＝∠C，在△BPD和△CQP中，∴△BPD≌△CQP（SAS）．②∵v P≠v Q，∴BP≠CQ，若△BPD≌△CPQ，∠B＝∠C，则BP＝PC＝4cm，CQ＝BD＝5cm，∴点P，点Q运动的时间s，∴cm/s；（2）设经过x秒后点P与点Q第一次相遇，由题意，得x＝3x+2×10，解得．∴点P共运动了×3＝80cm．△ABC周长为：10+10+8＝28cm，若是运动了三圈即为：28×3＝84cm，∵84﹣80＝4cm＜AB的长度，∴点P、点Q在AB边上相遇，∴经过s点P与点Q第一次在边AB上相遇．。