夫兰克-赫兹实验思考题(DOC)
夫兰克-赫兹实验思考题

弗兰克赫兹实验1、简要解释伏安特性曲线的奇特性?玻尔的原子理论指出:①原子只能处于一些不连续的能量状态E1、E2……,处在这些状态的原子是稳定的,称为定态。
原子的能量不论通过什么方式发生改变,只能是使原子从一个定态跃迁到另一个定态;②原子从一个定态跃迁到另一个定态时,它将发射或吸收辐射的频率是一定的。
如果用Em和En分别代表原子的两个定态的能量,则发射或吸收辐射的频率由以下关系决定:hv=|Em-En|h为普朗克常量。
原子从低能级向高能级跃迁,也可以通过具有一定能量的电子与原子相碰撞进行能量交换来实现。
本实验即让电子在真空中与氩蒸气原子相碰撞。
设氩原子的基态能量为E1,第一激发态的能量为E2,从基态跃迁到第一激发态所需的能量就是E2-E1。
初速度为零的电子在电位差为U的加速电场作用下具有能量eU,若eU小于E2-E1这份能量,则电子与氩原子只能发生弹性碰撞,二者之间几乎没有能量转移。
当电子的能量eU≥E2-E1时,电子与氩原子就会发生非弹性碰撞,氩原子将从电子的能量中吸收相当于E2-E1的那一份,使自己从基态跃迁到第一激发态,而多余的部分仍留给电子。
设使电子具有E2-E1能量所需加速电场的电位差为U0,则eU0=E2-E1U0为氩原子的第一激发电位(或中肯电位)在充氩的F—H管中,电子由热阴极发出,阴极K和第二栅极G2之间的加速电压UG2K 使电子加速。
第一栅极对电子加速起缓冲作用,避免加速电压过高时将阴极损伤。
在板极P和G2间加反向拒斥电压UpG2 。
当电子通过KG2空间,如果具有较大的能量(≥eUpG2 )就能冲过反向拒斥电场而达到板极形成板流,被微电流计pA检测出来。
如果电子在KG2空间因与氩原子碰撞,部分能量给了氩原子,使其激发,本身所剩能量太小,以致通过栅极后不足以克服拒斥电场而折回,通过电流计pA的电流就将显著减小。
当UG2K 逐渐增加时,电子在加速过程中能量也逐渐增大,但电压在初升阶段,大部分电子达不到激发氩原子的动能,与氩原子只是发生弹性碰撞,基本上不损失能量,于是穿过栅极到达板极,形成的板流Ip随UG2K 的增加而增大。
弗兰克赫兹含思考题

西安交通大学实验报告成绩第 1 页(共 9 页)课程:_______近代物理实验_______ 实验日期:年月日专业班号___ ___组别_______ 交报告日期:年月日姓名__Bigger __学号_ _ 报告退发:(订正、重做)同组者__ ________ 教师审批签字:实验名称:弗兰克-赫兹实验一、实验目的1)通过测氩原子第一激发电位,了解Franck和Hertz在研究原子内部能量量子化方面所采用的实验方法。
2)了解电子和原子碰撞和能量交换过程的微观图像。
二、实验仪器FH—1A、Franck-Hertz实验仪、示波器等。
三、实验原理图1是充氩四极Franck-Hertz实验原理图。
图1 Franck-Hertz实验原理图电子与原子的碰撞过程可以用一下方程描述:22221111''2222e e m v MV m v MV E +=++∆(2.1)式中:m e ——原子质量; M ——电子质量; v ——电子碰撞前的速度; v ’——电子碰撞后的速度; V ——原子碰撞前的速度; V ’——原子碰撞后的速度; ΔE ——原子碰撞后内能的变化量。
按照波尔原子能级理论,ΔE = 0 弹性碰撞; ΔE = E 1 - E 0 非弹性碰撞;式中:E 0——原子基态能量; E 1——原子第一激发态能量。
电子碰撞前的动能1/2m e v 2 < E 1 - E 0时,电子与原子的碰撞为完全弹性碰撞,ΔE = 0,原子仍然停留在基态。
电子只有在加速电场的作用下碰撞前获得的动能1/2m e v 2 ≥ E 1 - E 0,才能在电子产生非弹性碰撞,使得电子获得某一值(E 1 - E 0)的内能从基态跃迁到第一激发态,调整加速电场的强度,电子与原子由弹性碰撞到非弹性碰撞的变化过程将在电流上显现出来。
Franck-Hertz 管即是为此目的而专门设计的。
在充入氩气的F-H 管中(如图2所示),阴极K 被灯丝加热发射电子,第一栅极(G1)与阴K 之间的电压V G1K 约为1.5V ,其作用是消除空间电荷对阴极K 的影响。
弗兰克赫兹实验思考题2

弗兰克赫兹实验思考题2弗兰克赫兹实验思考题一、解释伏安特性曲线的奇特性。
1(玻尔提出的量子理论指出:原子只能较长久地停留在一些稳定状态(简称定态),原子在这些状态时,不发射或吸收能量;各定态有一定的能量,其数值是彼此分立的,这些能量值称为能级,最低能级所对应的状态称为基态,其他高能级所对应的态称为激发态。
原子的能量不论通过什么方式发生改变,它只能使原子由一个定态跃迁到另一个定态。
原子从一个定态跃迁到另一个定态而发射或吸收辐射时,辐射频率是一定的。
如果用Em和En代表有关两定态的能量,辐射的频率ν确定于普朗克公式: h??Em?En (8-1)式(8-1)中的h为普朗克常数,其值为6.6260×10-34J?s。
为了使原子从低能级向高能级跃迁,可以通过具有一定频率ν的光子来实现,也可以通过具有一定能量的电子与原子碰撞(非弹性碰撞)进行能量交换的方法来实现。
后者为本实验采用的方法。
设初速度为零的电子在电势差为V的加速电场作用下,获得eV的能量。
在充氩气的夫兰克—赫兹管中,具有一定能量的电子将与氩原子发生碰撞。
如果以E0代表氩原子的基态能量,E1代表氩原子的第一激发态的能量,当电子与氩原子相碰撞时传递给氩原子的能量恰好是eV0=E1-E0 (8-2)则氩原子就会从基态跃迁到第一激发态,而相应的电势差V0称为氩原子的第一激发电位。
其他元素气体原子的第一激发电位也可以按此法测量得到。
1914年,夫兰克和赫兹首次用慢电子轰击汞蒸气中汞原子的实验方法,测定了汞原子的第一激发电位。
2(夫兰克—赫兹实验的物理过程本仪器采用的充氩四极夫兰克—赫兹管,实验原理如图8-1所示。
图8 -1 夫兰克—赫兹实验原理图管内有发射电子的阴极K,它由VF通电加热管中的灯丝K而产生热电子发射。
管中还有用于消除空间电荷对阴极电子发射的影响同时提高电子发射效率的第一栅极G1、用于加速电子的第二栅极G2和收集电子的板极P。
图8-2 F—H管空间电位分布在充氩气的管中,电子由热阴极K发出,阴极K和栅极G2之间的可调加速电压VG2使电子加速。
实验二十三 夫兰克—赫兹实验

2.测量 U GK - IA 曲线,计算氩原子的第一激发电位 U0。 【实验步骤】 见附录。 【数据记录与处理】 1. 测试条件 灯丝电压(V) : 第一阳极电压(V) : 反向拒斥电压(V) : 环境温度(℃) : 2. “程控”状态下,计算机数据自动记录与绘图 3. “键控”方式下,记录数据并手工作图 4 2.5 7.5
IA (nA)
aCO源自b d U1 U2 U3 U4 U5 U6 U7
U GK (V)
图 23-3 夫兰克-赫兹管 IA~ U G 2 K 曲线 系曲线。该曲线反映了氩原子在 KG 空间与电子进行能量交换的情况。当 KG 空间电压逐渐 增加时,电子在 KG 空间被加速而取得越来越大的能量。在起始阶段由于电压较低,电子的 能量较小(eU <E1 - E0) ,即使运动过程中电子与原子只能发生弹性碰撞,由于电子质量远 小于氩原子质量,电子的能量几乎不会减少,穿过栅极电子形成的板极电流 IA 将随栅极电 压 U GK 的增加而增大,即图中 Oa 段。 当 KG 间的电压达到 U0 时,电子能量达到 eU0<E1 - E0, 电子在栅极 G 附近与氩原子 之间将发生非弹性碰撞, 将自己从加速电场中获得的能量交给氩原子, 并使氩原子从基态被 激发到第一激发态。 而电子本身由于把能量给了氩原子, 即使穿过栅极也不能克服反向拒斥 电场而被折回栅极,板极电流 IA 将显著减小,如图中 ab 段。随着栅极电压 U GK 的增加,电 子的能量也随之增加,在与氩原子相碰撞后,一部分能量(E1 - E0)交换给氩原子,还留下 一部分能量足够克服反向拒斥电场而达到板极 A,这时板极电流 IA 又开始上升,即曲线中 的 bc 段,直到 KG 间的电压是 2U0 时,电子在 KG 空间会因与氩原子发生两次非弹性碰撞 而失去 2eU0 的能量,又造成了第二次板极电流的下降,即图中的 cd 段。同理,凡是在
近代物理实验内容及思考题

近代物理实验内容及思考题第一轮实验项目:一、 夫兰克—赫兹实验实验内容:1、 仪器的安装调试。
2、 逐点手动测量激发电位:在同一张坐标纸上作出I p ~V G2曲线,由曲线确定出各极值电位值。
求出氩原子第一激发态电位和测量误差。
3、 自动测量激发电位:在示波器上调出I p ~V G2曲线,直接读出氩原子第一激发态电位值。
4、 示波器观察分别改变减速电压V p 和灯丝电压V f 曲线I p -V G2应有何变化。
课后思考题:1、 解释曲线I p -V G2形成的原因。
2、 实验中,取不同的减速电压V p 时,曲线I p -V G2应有何变化?为什么?3、 实验中,取不同的灯丝电压V f 时,曲线I p -V G2应有何变化?为什么?二、塞曼效应实验内容:1、调整光路,从测量望远镜中可观察到清晰明亮的一组同心干涉圆环。
2、接通电磁铁稳流电源,缓慢地增大磁场B ,从测量望远镜中可观察到细锐的干涉圆环逐渐变粗,然后发生分裂。
旋转偏振片为00、450、900各不同位置时,观察偏振性质不同的π成分和σ成分。
3、选定干涉级K 和K-1的位置,测量干涉圆环直径,用特斯拉计测出磁场B ,根据下式求出电子的比荷(e/m )值。
(标准值m e /=1.76⨯1011C/kg ) dB c D D D D m e K K a b π422122⋅--=-(式中d=5mm ) 4、观察沿磁场方向的塞曼分裂,将电磁铁旋转900,并抽出铁芯,放上1/4波片与偏振片,以区分左旋和右旋偏振光。
课后思考题:1、什么叫塞曼效应,磁场为何可使谱线分裂?2、叙述各光学器件在实验中各起什么作用?3、如何判断F-P 标准具已调好?4、实验中如何观察和鉴别塞曼分裂谱线中的π成分和σ成分?如何观察和分辨σ成分中的左旋和右旋偏振光? 三、核磁共振实验内容:1、 观察氢核1H 的NMR 现象(1)分别改变不同实验条件(射频场强度、扫场电压、样品在磁极间的位置)观察吸收信号的变化;(2)比较掺入顺磁物质浓度不同的水样品,观察吸收信号的差别。
弗兰克赫兹含思考题

西安交通大学实验报告第 1 页〔共 9 页〕课程:_______近代物理实验_______ 实 验 日 期 : 年 月 日 专业班号___ ___组别_______ 交报告日期: 年 月 日 姓 名__Bigger __学号_ _ 报 告 退 发 : 〔订正、重做〕 同 组 者__ ________ 教师审批签字:实验名称:弗兰克-赫兹实验一、 实验目的1) 通过测氩原子第一激发电位,了解Franck 和Hertz 在研究原子内部能量量子化方面所采用的实验方法。
2) 了解电子和原子碰撞和能量交换过程的微观图像。
二、 实验仪器FH—1A 、Franck-Hertz 实验仪、示波器等。
三、 实验原理图1是充氩四极Franck-Hertz 实验原理图。
图1 Franck-Hertz 实验原理图电子与原子的碰撞过程可以用一下方程描述:22221111''2222e e m v MV m v MV E +=++∆ (2.1) 式中:m e ——原子质量; M ——电子质量; v ——电子碰撞前的速度; v ’——电子碰撞后的速度; V ——原子碰撞前的速度; V ’——原子碰撞后的速度; ΔE ——原子碰撞后内能的变化量。
按照波尔原子能级理论,ΔE = 0 弹性碰撞; ΔE = E 1 - E 0 非弹性碰撞;式中:E 0——原子基态能量; E 1——原子第一激发态能量。
电子碰撞前的动能1/2m e v 2 < E 1 - E 0时,电子与原子的碰撞为完全弹性碰撞,ΔE = 0,原子仍然停留在基态。
电子只有在加速电场的作用下碰撞前获得的动能1/2m e v 2 ≥ E 1 - E 0,才能在电子产生非弹性碰撞,使得电子获得某一值〔E 1 - E 0〕的内能从基态跃迁到第一激发态,调整加速电场的强度,电子与原子由弹性碰撞到非弹性碰撞的变化过程将在电流上显现出来。
Franck-Hertz 管即是为此目的而专门设计的。
弗兰克—赫兹实验

弗兰克—赫兹实验弗兰克-赫兹实验是1914年由德国物理学家弗兰克和赫兹设计完成的。
该实验研究电子与原子碰撞前后能量的变化,能观测到汞原子的激发电势和电离电势,可以证明原子能级的存在,为波尔的原子结构理论假说提供有力的实验证据。
该实验的方法至今仍是探索原子结构的重要手段之一。
1913年丹麦物理学家玻尔(N?Bohr)提出了原子能级的概念并建立了原子模型理论。
该理论指出,原子处于稳定状态时不辐射能量,当原子从高能态(能量Em)向低能态(能量En)跃迁时才辐射。
辐射能量满足?E = Em?En (1)对于外界提供的能量,只有满足原子跃迁到高能级的能级差,原子才吸收并跃迁,否则不吸收。
【实验目的】1、了解弗兰克-赫兹实验仪的结构、原理,学会它的调节和使用方法。
2、了解电子与原子之间的弹性碰撞和非弹性碰撞。
3、测量氩原子的第一激发电位;4、证实原子能级的存在,加深对原子结构的了解;【实验器材】智能型弗兰克-赫兹实验仪,计算机,示波器灯丝电压【实验原理】一、第二栅极。
UGK-G1-G2加正向电压,为电子提供能量。
1K图1弗兰克-赫兹实验原理图夫兰克一赫兹实验原理如图1所示,在真空管中充待测氩气,阴极K,阳极A,G1 、G2分别为第的作用主要是消除空间电荷对阴极电子发射的影响,提高发射效率。
G2-A加反向电压,形成拒斥电场。
电子从K发出,在K-G2区间获得能量,在G2-A区间损失能量。
如果电子进入G2-A区域时动能大于或等于eUG2A,就能到达阳极形成阳极电流I.电子在不同区间的情况:1. K-G1区间电子迅速被电场加速而获得能量。
12. G1-G2区间电子与氩原子碰撞。
当其能量小于氩原子第一激发态与基态的能级差?E=E2?E1 时,氩原子基本不吸收电子的能量,碰撞属于弹性碰撞。
当电子的能量达到?E,则可能在碰撞中被氩原子吸收这部分能量,这时的碰撞属于非弹性碰撞。
?E称为临界能量。
3. G2-A区间电子受阻,被拒斥电场吸收能量。
弗兰克赫兹实验思考题-(1)
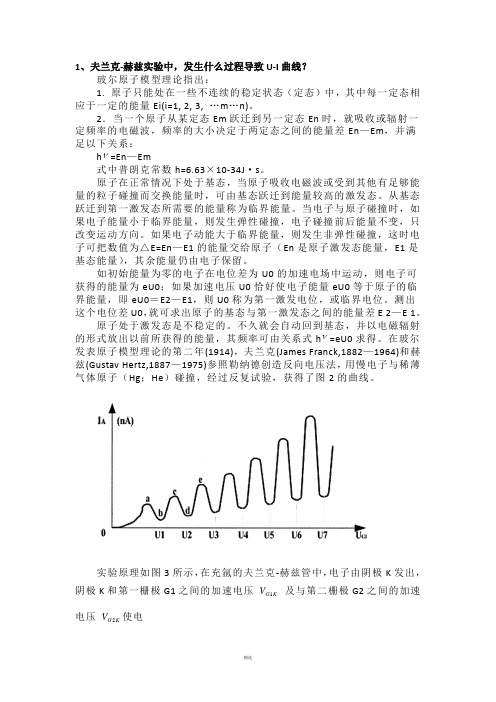
1、夫兰克-赫兹实验中,发生什么过程导致U-I 曲线?玻尔原子模型理论指出:1. 原子只能处在一些不连续的稳定状态(定态)中,其中每一定态相应于一定的能量Ei(i=1, 2, 3, …m …n)。
2.当一个原子从某定态Em 跃迁到另一定态En 时,就吸收或辐射一定频率的电磁波,频率的大小决定于两定态之间的能量差En —Em ,并满足以下关系:h ν=En —Em式中普朗克常数h=6.63×10-34J ·s 。
原子在正常情况下处于基态,当原子吸收电磁波或受到其他有足够能量的粒子碰撞而交换能量时,可由基态跃迁到能量较高的激发态。
从基态跃迁到第一激发态所需要的能量称为临界能量。
当电子与原子碰撞时,如果电子能量小于临界能量,则发生弹性碰撞,电子碰撞前后能量不变,只改变运动方向。
如果电子动能大于临界能量,则发生非弹性碰撞,这时电子可把数值为△E=En —E1的能量交给原子(En 是原子激发态能量,E1是基态能量),其余能量仍由电子保留。
如初始能量为零的电子在电位差为U0的加速电场中运动,则电子可获得的能量为eU0;如果加速电压U0恰好使电子能量eU0等于原子的临界能量,即eU0=E2—E1,则U0称为第一激发电位,或临界电位。
测出这个电位差U0,就可求出原子的基态与第一激发态之间的能量差E 2—E 1。
原子处于激发态是不稳定的。
不久就会自动回到基态,并以电磁辐射的形式放出以前所获得的能量,其频率可由关系式h ν=eU0求得。
在玻尔发表原子模型理论的第二年(1914),夫兰克(James Franck,1882—1964)和赫兹(Gustav Hertz,1887—1975)参照勒纳德创造反向电压法,用慢电子与稀薄气体原子(Hg ;He )碰撞,经过反复试验,获得了图2的曲线。
实验原理如图3所示,在充氩的夫兰克-赫兹管中,电子由阴极K 发出,阴极K 和第一栅极G1之间的加速电压K G V 1 及与第二栅极G2之间的加速电压K G V 2使电图3 夫兰克-赫兹原理图子加速。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、夫兰克-赫兹管的伏安特性曲线的奇异性的来源玻尔原子模型理论指出:1. 原子只能处在一些不连续的稳定状态(定态)中,其中每一定态对应于一定的能量(1,2,3,)i E i =。
2.当一个原子从某定态m E 跃迁到另一定态n E 时,就吸收或辐射一定频率的电磁波,频率的大小决定于两定态之间的能量差m n E E -,并满足以下关系:m n hv E E =-式中普朗克常数346.62610h J s -=⨯⋅。
原子在正常情况下处于基态,当原子吸收电磁波或受到其他有足够能量的粒子碰撞而交换能量时,可由基态跃迁到能量较高的激发态。
从基态跃迁到第一激发态所需要的能量称为临界能量。
当电子与原子碰撞时,如果电子能量小于临界能量,则发生弹性碰撞,电子碰撞前后能量不变,只改变运动方向。
如果电子能量大于临界能量,则发生非弹性碰撞,这时电子可把数值为21E E E ∆=-的能量传递给原子(2E 是原子第一激发态能量,1E 是基态能量),其余能量仍由电子保留。
在充氩的夫兰克-赫兹管中,电子由阴极K 发出,阴极K 和第一栅极1G 之间的加速电压1G K V 及与第二栅极2G 之间的加速电压2G K V 使电子加速。
在板极A 和第二栅极2G 之间可设置拒斥电压2G A V ,管内空间电压分布如图2所示。
当灯丝加热时,阴极的外层即发射电子,电子在1G 和2G 间的电场图 1 夫兰克-赫兹实验原理图 作用下被加速而取得越来越大的能量。
但在起始阶段,由于电压2G K V 较低,电子的能量较小,即使在运动过程中,它与原子相碰撞(弹性碰撞)也只有微小的能量交换。
这样,穿过图 2 夫兰克-赫兹管内空间电位分布原理图 第二栅极的电子所形成的电流A I 随第二栅极电压2G K V 的增加而增大(图 3 oa 段)。
当2G K V 达到氩原子的第一激发电位时,电子在第二栅极附近与氩原子相碰撞(非弹性碰撞)。
电子把从加图 3 夫兰克-赫兹管的伏安特性曲线 速电场中获得的全部能量传递给氩原子,使氩原子从基态激发到第一激发态,而电子本身由于把全部能量传递给了氩原子,即使它穿过第二栅极,也不能克服拒斥电压2G A V 从而被折回第二栅极,所以板极电流A I 将显著减小(图3 ab 段)。
氩原子在第一激发态不稳定,会跃迁回基态,同时以光量子形式向外辐射能量。
以后随着第二栅极电压2G K V 的增加,电子的能量也随之增加,与氩原子相碰撞后还留下足够的能量,这样就可以克服拒斥电压2G A V 的作用力而到达板极A ,这时电流又开始上升(图3 bc 段)。
直到2G K V 是2倍氩原子的第一激发电位时,电子在2G 与K 间又会因第二次弹性碰撞失去能量,因而造成了第二次板极电流A I 的下降(图3 cd 段)。
这种能量转移随着加速电压的增加而呈周期性的变化。
若以2G K V 为横坐标,以板10 50 100 2G (V)极电流A I 值为纵坐标就可以得到谱峰曲线,两相邻峰尖(或谷点)间的加速电压差值,即为氩原子的第一激发电位。
这个实验就说明了夫兰克-赫兹管内的电子缓慢地与氩原子碰撞,能使氩原子从低能级被激发到高能级。
通过测量氩原子的第一激发电位,说明了玻尔原子能级的存在。
二、第一激发电位及其物理含义原子只能存在于不连续的稳定状态即定态,各定态的能量值彼此分离。
原子从一个定态跃迁到另一定态时伴随着电磁波的发射或吸收,如果用m E 和n E 代表两个定态能量,h 为普朗克常数,则从m E 到n E 辐射的频率v 满足m n hv E E =-。
设1E 为原子的基态能量,2E 为原子的第一激发态能量,电子被加速而获得能量eV ,若21eV E E <-,则电子与氩原子发生弹性碰撞;增大V 至g V ,使21g eV E E ≥-,则电子与原子发生非弹性碰撞,把能量全部传递给原子,使原子从基态跃迁到第一激发态,并释放频率为21()g v hv eV E E ==-的光子,则g V 就是被测原子的第一激发电位。
类似的,设1E 为原子的基态能量,3E 为原子的第二激发态能量,电子被加速而获得能量eV ,若31eV E E <-,则电子与氩原子发生弹性碰撞,或非弹性碰撞使原子从基态跃迁到第一激发态;增大V 至s V ,使31s eV E E ≥-,则电子与原子发生非弹性碰撞,把能量全部传递给原子,使原子从基态跃迁到第二激发态,并释放频率为31()s v hv eV E E ==-的光子,则s V 就是被测原子的第二激发电位。
在测量氩的第二激发电位等较高激发电位时,我们把1G K V 作为加速电压;而在测量第一激发电位时,它只是引出阴极电子的“引出”电压。
这里把12G G V 作为等势区(加补偿电压),作为电子与氩原子的碰撞区;而在测量第一激发电位时,我们把12G G V 作为电子加速区,使电子边加速边和氩原子碰撞。
把1G K V 作为加速电压,使电子在1KG 间进行加速,是因为1KG 距离很近,小于电子在氩中的平均自由程,与氩原子碰撞的机会少,在1KG 间可以把能量加高,然后在较大的12G G 区域进行碰撞,以至可以观察到在测第一激发电位时所观察不到的能级。
把12G G 区域作为等势区域,是使电子和氩原子在这里以较大的几率和相同的能量进行碰撞,可以提高实验的分辨能力。
通过测量不同1G K V 下的板极电流A I 值,用作图法拟合出1A G K I V 曲线,分析曲线上不同峰尖处对应的1G K V 值,结合先前得到的氩原子的第一激发电位g V ,便可得到氩原子的第二激发电位s V 。
三、夫兰克-赫兹实验的历史夫兰克原在柏林大学的瓦尔堡指导下从事电晕放电方面的研究,后来鉴于那种工作不容易得出有价值的结果,改为研究在简单条件下的电子、离子的运动, 用卢瑟福的方法测量离子的迁移率。
1911年他获得大学授课资格。
当时赫兹刚刚获得博士学位,接替夫克兰当了助教。
于是他们两人进行了合作,从事关于各种元素(原子和分子)的电离电势的研究。
1914 年5月他们发表了有关电离电势的第一篇论文。
夫兰克-赫兹实验是从1911年开始进行的。
该实验基本上采用了勒纳德的方法,但是作了适当的改进。
例如原来的栅极离灯丝只有5毫米,现在离灯丝4厘米,而集电极离栅极只有1毫米或2毫米(原来是2.5厘米)。
他们在文章的开头追述了他们以前工作中发现的下述事实:1. 在气体分子和电子碰撞时,若电子的动能比分子的电离能小,一般说来, 电子被弹回。
气体的电子亲合势越小,电子损失的能量越少。
2. 电子和气体分子的碰撞引起电离时,电子失去其全部动能。
3. 如果电子的动能等于或大于电离能,引起电离的碰撞几率小于1。
他们这篇论文的结论如下:“ 1. 文中证明,汞蒸气中的电子将和分子进行弹性碰撞,直到电子获得了一个临界速度为止。
2. 描述了一种测量这一临界速度达到0.1伏特精确度的方法。
这个速度和电子通过4.9伏特的电势差以后所得到的速度相等效。
3. 文中证明,一个4.9伏特的能量等于汞谱线253.6uu 的能量子。
4. 给出了理由,表明4.9伏特射线在其中损失能量的那些碰撞,有一部分会导致电离,因此4.9伏特可能代表汞蒸气的电离电势。
另外一部分碰撞似乎是激发了光的发射,而且我们假设它是和谱线253.6uu 的发射联系着的。
”夫兰克和赫兹相信他们测量的精确度已达到0.1伏特,测得的汞的电离电势为4.9伏特,而当时的理论(不是玻尔理论)所预言的值为4.84伏特,与测量值极为一致。
他们写道:“伍德曾发现汞蒸气有一显著的固有频率,所谓共振线,波长为253.6uu 。
如果对于这个频率计算乘积hv ,得到的能量是电子通过4.84伏特电势差应具有的能量,这和我们测得的数值相当符合,很难相信这是偶然的巧合。
”于是他们想,可能存在这种情况:电子损失的能量,不是使汞原子电离,而是激发了辐射。
他们不能在同一仪器上验证这个新看法,改用石英作了一个能透紫外线的新管。
结果很出乎意料。
当加速电势差小于4.9伏特时,汞蒸气没有任何辐射现象,可是当大于4.9伏特时,汞辐射了,且仅仅辐射253.6uu 的谱线。
于是他们于同年发表了第二篇论文,其结论如下:“ 1. 只要电子的动能还低于hv 这个数量,此处v 是共振谱线的频率,电子就会被汞原子所反射而并不损失能量。
2. 电子的动能一达到hv 这个值,这个量子就会在随后的某一次碰撞中被传递给原子内部的频率为v 的光谱。
3. 被传递的能量部分地用于电离,部分地作为频率为γ的光而被发射。
4. 由这些实验算得的恒量h 是276.5910-⨯尔格·秒, 可能的误差是2%。
” 玻尔在发表他的“三部曲”时,夫兰克和赫兹的论文还没有发表,但是他却在自己的文章中预见了碰撞实验应有的结果。
他写道:“这些计算很强烈地暗示着,一个高速电子在通过一个原子并和柬缚电子相碰撞时,将按照确定的有限的量子形式而损失能量。
正如可以立即看到的,假如碰撞结果是由通常的力学定律来支配的,这种情况就和我们所可预料的情况很不相同了。
经典力学在这种问题中的失效,也可以根据自由电子或原子中的束缚电子之间不存在任何类似于动能均分的现象而事先料到。
……但是,当考虑一个自由电子和一个束缚电子的碰撞时,那就可以推知,束缚电子通过碰撞而得到的能量是不可能小于和相邻定态相对应的能量差,而且由此可知,和它碰撞的那个自由电子也不能损失那么小的能量。
”按照这种看法,4.9伏特并不可能对应于汞的电离电势。
事实上,玻尔预料的电离电势当然比激发电势大得多。
后来当夫兰克-赫兹实验结果发表以后,玻尔进一步地分析了这个问题,并撰写了新的文章。
他在1915年的《论辐射的量子论和原子的结构》一文中写道:“夫兰克和赫兹认为 4.9伏特对应于从汞原子中取走一个电子时所需的能量,但是看来他们的实验结果或许和下述假设相一致:这一电压只对应于从中性原子的正常态到某一另外定态的跃迁。
按照现在这种理论,我们应该预期从汞原子中取走一个电子所需的能量可以根据帕邢的单谱线系……的极限来算出。
……这样算出的电离电势是10.5伏特而不是4.9伏特。
如果以上的考虑是正确的,那么就可以看到,夫兰克和赫兹的测量对本论文中所考虑的理论给予了有力的支持。
另一方面,假若汞的电离电势竟然被证实为夫兰克和赫兹所假设的那样低,那么它就会给以上关于里德伯恒量的考虑造成一种严重的困难,至少在汞光谱的情况中是如此,因为这一光谱含有频率比谱线2536的频率更高的一些谱线。
”这种看法当时还不是一下子就被夫兰克他们所接受,双方还进行过一定的辩论。
玻尔在1958年11月的《卢瑟福纪念演讲》中追述了这段历史。
他说:“至于原子结构的问题,在1914年发表的夫兰克和赫兹用电子碰撞来激发原子的那些著名实验,也给这种问题带来了新的冲击。
