对数函数的图象和性质PPT教学课件
合集下载
第4_4_2对数函数的图象和性质优质教学课件PPT

令t=x2-2x-8,则y=ln t(t>0).
∵要求f(x)的单调递增区间,且y=ln t是增函数,
∴根据复合函数的单调性可知,只需求出t=x2-2x-8在定义域内的单调递增区间即
可.
∵x∈(4,+∞)时,t=x2-2x-8为增函数,
∴函数f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞),故选D.
(2)含有绝对值的函数的图象一般是经过对称变换得到的.
第1讲 描述运第动四的章基本指概数念函数与对数函数
已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是 ( B )
第1讲 描述运第动四的章基本指概数念函数与对数函数
思路点拨 可利用函数的性质识别图象,注意底数a对图象的影响,也可根据图象的位置结合单 调性来判断. 解析 解法一:首先,曲线y=ax只可能在x轴上方,y=loga(-x)的图象只可能在y轴左侧, 从而排除A,C, 然后,y=ax与y=loga(-x)的增减性正好相反,又可排除D.故选B. 解法二:若0<a<1,则函数y=ax在其定义域上单调递减且图象过点(0,1),而函数y=loga (-x)在其定义域上单调递增且图象过点(-1,0),所有选项均不符合这些条件; 若a>1,则函数y=ax在其定义域上单调递增且图象过点(0,1),而函数y=loga(-x)在其定 义域上单调递减且图象过点(-1,0),只有B满足条件.
x∈(0,1)时,y∈(0,+∞); x∈[1,+∞)时,y∈(-∞,0]
函数y=logax与y= log1x的图象关于③ x轴 对称
a
第1讲 描述运第动四的章基本指概数念函数与对数函数
反函数 一般地,指数函数y=ax(a>0,且a≠1)与对数函数④ y=logax(a>0,a≠1) 互为反 函数.它们的定义域与值域正好互换. 互为反函数的两个函数的单调性相同,但单调区间不一定相同. 互为反函数的两个函数的图象关于直线y=x对称.
对数函数的图像与性质(公开课》省公开课获奖课件说课比赛一等奖课件
比较两个同底对数值旳大小时:
1.观察底数是不小于1还是不不小于1( a>1时为增函
小数
2.比较真数值旳大小;
结
0<a<1时为减函数)
3.根据单调性得出成果。
练习3
变一变还能口答吗?
lg 6 < lg 8 log10 m< log10 n 则 m < n
log0.5 6 < log0.5 4 log0.5 m> log0.5 n 则 m < n
提醒:分别将 y=2x 和y=log2x
y=0.5x 和y= log0.5x 旳图象画在一种坐标内 ,观察图象旳特点!
(书面作业)
•P82--- 5
例3 比较下列各组中两个值旳大小: ⑴.log 67 , log 7 6 ; ⑵.log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
(一)对数函数旳定义
★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量,定义域是(0,+∞)
对数函数解析式有哪些构造特征? ①底数:不小于0且不等于1旳常数 ②真数: 单个自变量x
③系数: log a x 旳系数为1
想一想?
练习1
下列函数中,哪些是对数函数?
① y loga x2; ② y log2 x 1; ③ y 2 log8 x;
解2:考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间(0,+∞)上是减函数; ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
• 例2:比较下列各组中,两个值旳大小: • (1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7
对数函数图像与性质ppt课件
型的频率 80% 10% 10% 0%
配子的 A(
) A( )1a0(% ) a( )
比率
A( 90%)
a( )
子一代基 AA
Aa
aa
因型频率 ( 81%)
( 18% ) ( 1% )
子一代基 因频率
A ( 90% )
a (10% )
(p+q)2 = p2 + 2pq + q2 =1
(A% + a%) 2 = (AA% + Aa% + aa%)
0<b<a<1 0<b<a<1
11
五、回顾小结:
本节课学习了以下内容:
1.对数函数定义、图象、性质;
2.比较两个对数大小,其方法是:
①若底数为同一常数,则可由对数函数的单调性 直接进行判断;
②若底数为同一字母,则按对数函数的单调性对底 数进行分类讨论 ;
③若底数、真数都不相同,则常借助与1、0、-1等 中间量进行比较. ④若底数不同、真数相同,则可用换底公式化为 同底再进行比较.
种群中普遍存在的 可遗传变异 是自然 选择的前提,也是生物进化的前提。
基因在传递给后代时如何分配?
25
种群基因频率的平衡和变化
1、种群:生活在一定区域的同种生物的全部个体。
2、一个种群全部等位基因总和称为什么? 基因库
3、基因频率:种群中,某一等位基因的数目占这个基因 可能出现的所有等位基因总数比例。
aa占16%。 (3)子代种群的基因频率:A占60%;a占40%。
31
三、遗传平衡定律(哈代-温伯格定律):
在一个大的随机交配的种群里,基因频率和基因 型频率在没有迁移、突变、选择的情况下,世代相传 不发生变化,并且基因型频率由基因频率所决定。
《对数函数的概念》《对数函数的图象和性质》指数函数与对数函数PPT

-1
2
2
1
化简可得 ≤x2≤2.
2
再由 x>0 可得 2≤x≤
2
2
答案:(1)A (2)
, 2
2
2
2
2
1
,
2,故函数 f(x)的定义域为
2
,
2
2 .
课堂篇
探究学习
探究一
探究二
探究三
探究四
探究五
思想方法
随堂演练
反思感悟 定义域问题注意事项
(1)要遵循以前已学习过的求定义域的方法,如分式分母不为零,
偶次根式被开方式大于或等于零等.
a>1
0<a<1
图象
性
质
定义域
值域
过定点
单调性
奇偶性
(0,+∞)
R
(1,0),即当 x=1 时,y=0
在(0,+∞)
在(0,+∞)
上是增函数
上是减函数
非奇非偶函数
课前篇
自主预习
一
二
三
3.做一做
(1)若函数y=logax的图象如图所示,则a的值可能是 (
)
A.0.5 B.2
C.e D.π
(2)下列函数中,在区间(0,+∞)内
.
2 -2-8 = 0,
解析:(1)由题意可知 + 1 > 0, 解得 a=4.
+ 1 ≠ 1,
(2)设对数函数为f(x)=logax(a>0,且a≠1).
则由题意可得f(8)=-3,即loga8=-3,
所以
a-3=8,即
1
3
-
第1课时 对数函数的概念、图象及性质 课件(40张)

⑥也不是对数函数;只有③④符合对数函数的定义.故选B.
数学
2
即时训练 1-1:(1)若函数 f(x)=log(a+1)x+(a -2a-8)是对数函数,则 a=
(2)已知对数函数 f(x)的图象过点 M(8,3),则 f( )=
.
.
-- = ,
解析:(1)由题意可知 + > 0, 解得 a=4.
+ > ,
所以函数的定义域是{x|-3<x<3}.
+ > 0,
(2)由题意有
解得 x>- 且 x≠0,
+ ≠ ,
则函数的定义域为(- ,0)∪(0,+∞).
数学
[变式训练2-1] 把本例(1)中的函数改为y=loga(x-3)+loga(x+3)呢?
解:由 - > 0, 得 x>3.
为(
)
解析:法一
函数 y=-lg |x+1|的定义域为{x|x≠-1},可排除 A,C;当 x=1
时,y=-lg 2<0,显然只有 D 符合题意.故选 D.
法二
y=-lg |x+1|=
-( + ), > -,
-(--), < -,
又 x∈(-1,+∞)时,y=-lg(x+1)是减函数,因此选 D.
数学
即时训练5-1:(2020·海南高一期中)如图,若C1,C2分别为函数y=logax和
y=logbx的图象,则(
)
(A)0<a<b<1
(B)0<b<a<1
数学
2
即时训练 1-1:(1)若函数 f(x)=log(a+1)x+(a -2a-8)是对数函数,则 a=
(2)已知对数函数 f(x)的图象过点 M(8,3),则 f( )=
.
.
-- = ,
解析:(1)由题意可知 + > 0, 解得 a=4.
+ > ,
所以函数的定义域是{x|-3<x<3}.
+ > 0,
(2)由题意有
解得 x>- 且 x≠0,
+ ≠ ,
则函数的定义域为(- ,0)∪(0,+∞).
数学
[变式训练2-1] 把本例(1)中的函数改为y=loga(x-3)+loga(x+3)呢?
解:由 - > 0, 得 x>3.
为(
)
解析:法一
函数 y=-lg |x+1|的定义域为{x|x≠-1},可排除 A,C;当 x=1
时,y=-lg 2<0,显然只有 D 符合题意.故选 D.
法二
y=-lg |x+1|=
-( + ), > -,
-(--), < -,
又 x∈(-1,+∞)时,y=-lg(x+1)是减函数,因此选 D.
数学
即时训练5-1:(2020·海南高一期中)如图,若C1,C2分别为函数y=logax和
y=logbx的图象,则(
)
(A)0<a<b<1
(B)0<b<a<1
人教版高中数学必修1《对数函数的图像与性质》PPT课件

液的酸性就越强.
新知运用
例 3 溶 液 酸 碱 度 是 通 过 pH 计 量 的 .pH 的 计 算 式
pH=− + ,其中 + 表示溶液中氢离子的浓度,单位是
摩尔/升.
(2)已知纯净水中氢离子的浓度为 + = − 摩尔/升,
计算纯净水的 pH 值;
【解析】 = −− = ,所以纯净水的 pH 值
反思总结
1.思想方法:
(1)数形结合:由解析式到图象(由数到形,以形读数),
由图象到性质(由形到数,以数观形);
(2)分类整合:底数的两个范围对单调性的影响.
2.知识联系:指、对不分家!指数函数与对数函数不仅在概念、
图象与性质上有联系,在解决问题的类型上也有联系,所以
要将两者作为一个整体学习与应用.
所以. < − + < . ,即−. < + < −. ,
所以−. < + < −. ,
所以−. < + < −. ,
所以这种饮用水中氢离子的浓度范围是−. < + <
−. (单位:摩尔/升).
x 0.5 1
log2x −
2
(2)描点画图.
3
1.6
4
5
6
7
2.3 2.6 2.8
8
新知探求
2.画函数 = 的图象.
由换底公式得 = Байду номын сангаас =
= − ,所以
函数 = 的图象与 = 的图象关于
新知运用
例 3 溶 液 酸 碱 度 是 通 过 pH 计 量 的 .pH 的 计 算 式
pH=− + ,其中 + 表示溶液中氢离子的浓度,单位是
摩尔/升.
(2)已知纯净水中氢离子的浓度为 + = − 摩尔/升,
计算纯净水的 pH 值;
【解析】 = −− = ,所以纯净水的 pH 值
反思总结
1.思想方法:
(1)数形结合:由解析式到图象(由数到形,以形读数),
由图象到性质(由形到数,以数观形);
(2)分类整合:底数的两个范围对单调性的影响.
2.知识联系:指、对不分家!指数函数与对数函数不仅在概念、
图象与性质上有联系,在解决问题的类型上也有联系,所以
要将两者作为一个整体学习与应用.
所以. < − + < . ,即−. < + < −. ,
所以−. < + < −. ,
所以−. < + < −. ,
所以这种饮用水中氢离子的浓度范围是−. < + <
−. (单位:摩尔/升).
x 0.5 1
log2x −
2
(2)描点画图.
3
1.6
4
5
6
7
2.3 2.6 2.8
8
新知探求
2.画函数 = 的图象.
由换底公式得 = Байду номын сангаас =
= − ,所以
函数 = 的图象与 = 的图象关于
对数函数的图像和性质课件人教A版高中数学必修第一册(共32张PPT)
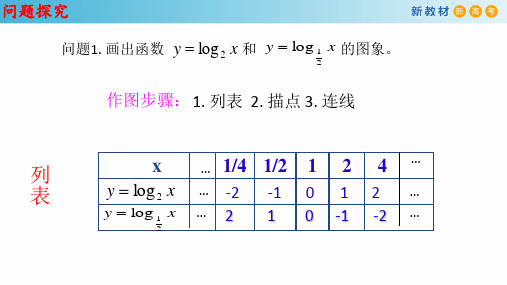
对数函数y=log a x (a>0, a≠1)
y o1
y=logax (a>1)
x
y=logax (0<a<1) (1)定义域: (0,+∞) (2)值域:R
(3)过点(1,0), 即x=1 时, y=0
(4) a>1时, x<0,0<y<1; x>0,y>1 (4) a>1时,0<x<1,y<0; x>1,y>0
⑴定义域:
性 ⑵值域:
(0,+∞) R
质 ⑶过特殊点: 过点(1,0),即x=1时y=0 ⑷单调性 : 在(0,+∞)上是增函数 ⑷单调性:在(0,+∞)上是减函数
记忆口诀
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数; 底数只能大于0, 等于1来也不行; 底数若是大于1, 图象从下往上增; 底数0到1之间, 图象从上往下减; 无论函数增和减, 图象都过(1,0)点.
解(2):考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间(0,+∞)上是减函数; ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
例题解析
例1:比较下列各组中,两个值的大小:
(3) log a 5.1与 log a 5.9 (a>0,且a≠1)
解(3):考察函数log a 5.1与 log a 5.9 可看作函数y=log a x的 两个函值 , 对数函数的单调性取决于底数a是大于1还是小于1, 因此需要对底数a进行讨论
线
-2
y=log1/2x
关于x轴对称
问题探究
人教版数学必修一.2对数函数图像及其性质PPT课件

人教版数学必修一.2对数函数图像及 其性质P PT课件
2.(71页)探究:
画出对数函数 y log 3 x和y log 1 x的图象。
y
1.函数图象分布在哪些 象限? 一、四
2
2.函数图象有哪些
1 11
特殊点? (1,0)
42
0 1 23 4
3
y log 2 x y log 3 x
x
3.函数图象的单调性 -1 与底数a的关系? -2
注:例2是利用对数函数的增减性比较两个对数 的大小的,对底数与1的大小关系未明确指出时,要分 情况对底数进行讨论来比较两个对数的大小.
人教版数学必修一.2对数函数图像及 其性质P PT课件
例3 比较下列各组中两个值的大小:
⑴.log 67 , log 7 6 ; ⑵.log 32 , log 2 0.8 .
x
定义域
奇偶性 值域
定点
单调性 函数值 符号
(0,+∞)
非奇非偶函数
非奇非偶函数
R ( 1 , 0 ) 即 x = 1 时,y = 0 在 ( 0 , + ∞ ) 上是增函数 在 ( 0 , + ∞ ) 上是减函数
当 x>1 时,y>0
当 x>1 时,y<0
当 0<x <1 时, y<0 当 0<x<1 时,y>0
x…
列 表
y log 2
y log 1
x
x
… …
2
y
描
2
点
1 11
42
0 12
连
-1
线
-2
1/4 1/2 1
-2 -1 0 2 10
y=log2x
34
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当a>1时,函数y=log ax在(0,+∞)上是增函数,于是 log a5.1<log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是 log a5.1>log a5.9
注:例1是利用对数函数的增减性比较两个对数的大小的, 对底数与1的大小关系未明确指出时,
要分情况对底数进行讨论来比较两个对数的大小.
0 (1,0) x 0
x
象
y=logax
(0<a<1)
定义域 : ( 0 ,+∞)
性 值域: R
过点 ( 1 , 0 ) , 即当 x =1时, y=0
质 在 ( 0 ,+∞)上 在 ( 0 ,+∞)上
是增函数
是减函数
㈠ 若底数为同一常数,则可由对数函数 的单调性直接进行判断. ㈡ 若底数为同一字母,则按对数函数的 单调性对底数进行分类讨论. ㈢ 若底数、真数都不相同,则常借助1、 0、-1等中间量进行比较
y=log2x
5 4
3
3
2
2
1
1
y=x x
-3 -2 -1 0 1 2 3 4 5 6 7 8 x
-1 -2 -3
-3 -2 -1 0 1 2 3 4 5 6 7 8
-1
y= log 1x
-2
2
-3
y
㈠ y = log2x
01
x
㈡ y = log 1x
2
图象特征
函数性质
图像都在 y 轴右侧
定义域是( 0,+∞)
在 R 上是增函数 在 R 上是减函数
指数式和对数式的互化:将 ab= N化成对数式,会得到
logaN = b
问题:求指数函数 y = ax ( a > 0 ,且 a ≠ 1 )的反函数
解: 从 y = ax 可以解得:x = logay 因此指数函数 y = ax 的反函数是
y=logax ( a > 0 ,且 a ≠ 1 )
再见
两直线的位置关系
直线与直线的位置关系:
( 1 ) 有 斜 率 的 两 直 线 l1:y=k1x+b1;l2:
y=k2x+b2
① l1∥l2 k1=k2且b1≠b2; ②l1⊥l2 k1·k2= -1
对数函数和指数函数 互为反函数
问题:作出函数 y = log 2 x 和函数 y =log 1x的图像.
2
【分析:互为反函数的两个函数图像关于直线 y=x 对称】
y=log2x 的反函数为
y
y= 2x
y=
2x
y
y= log 1 =1 x 2
2
x
的反函数为 y
y
= 1x
2
8 7
y=x
8 7
6
6
5 4
练习: 比较下列各题中两个值的大小: ⑴ log106 < log108 ⑵ log0.56 < log0.54 ⑶ log0.10.5 > log0.10.6 ⑷ log1.51.6 > log1.51.4
例2 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; 提示 : log aa=1
⑵ log 3π , log 2 0.8 . 提示: log a1=0
解: ⑴ ∵ log67>log66=1
log76<log77=1
∴
log67>log76
⑵ ∵ log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8
注:例2是利用对数函数的增减性比较两个对数的大小. 当不能直接进行比较时,可在两个对数中间插入一 个已知数(如1或0等),间接比较上述两个对数的大小
⑵考察对数函数 y = log 0.3 x,因为它的底数为0.3, 即0<0.3<1,所以它在(0,+∞)上是减函数,于是 log 0.31.8>log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 ) 对数函数的增减性决定于对数的底数是大于1还是小于1.
而已知条件中并未指出底数a与1哪个大, 因此需要对底数a进行讨论:
对数函数的定义 : 对数函数的图象和性质 比较两个对数值的大小
作业
Ⅰ 熟记对数函数 的图象和性质
Ⅱ 习题2.8 3
函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.其中 x是自变量,
函数的定义域是( 0 , +∞)
a>1
0 <a <1
图
y x=1y=logax (a>1)
y
(1,0)
又因为 y = ax 的值域为(0,+∞)
所以 y=logax ( a > 0 ,且 a ≠ 1 )
的定义域为(0,+∞)
结论:
函数 y = logax (a>0,且a≠1)是指数函数 y = ax的反函数
函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)
y=logax在(0,+∞)是减函数
a>1
0 <a <1
图
y x=1y=logax (a>1)
y
(1,0)
0 (1,0)
象
x0
x y=logax (0<a<1)
定义域 : ( 0 ,+∞)
性 值域: R
过点 ( 1 , 0 ) , 即当 x =1时, y=0
质 在 ( 0 ,+∞)上 在 ( 0 ,+∞)上
是增函数
是减函数
例1 比较下列各组数中两个值的大小: ⑴ log 23.4 , log 2⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解 ⑴考察对数函数 y = log 2x,因为它的底数2>1, 所以它在(0,+∞)上是增函数,于是 log 23.4<log 28.5
课题:2.8 对数函数
复习:一般的,函数 y = ax ( a > 0, 且 a ≠ 1 ) 叫做指数函数,
其中x是自变量.函数的定义域是 R.
a>1
0<a<1
y y=ax
y=ax
y
图
(a>1)
(0<a<1)
y=1
y=1
(0,1)
(0,1)
象
0
x
0
x
性
定义域:R 值 域:(0,+ )
质 过 点 ( 0 , 1 ) ,即 x = 0 时, y = 1 .
图像都经过 (1,0) 点
1 的对数是 0
图像㈠在(1,0)点右边的 纵坐标都大于0,在(1,0)点 左 图边像㈡的纵则正坐好标相都反小于0; 自左向右看,
图像㈠逐渐上升 图像㈡逐渐下降
当当当底底a>数数1a0时><,1a时<1时00<<xx>>xx<<11 ,,11则则,,则 则lloolgglooaaggxxaa><xx><0000 y当=0l<ogaa<x在1时(0,,+∞)是增函数
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是 log a5.1>log a5.9
注:例1是利用对数函数的增减性比较两个对数的大小的, 对底数与1的大小关系未明确指出时,
要分情况对底数进行讨论来比较两个对数的大小.
0 (1,0) x 0
x
象
y=logax
(0<a<1)
定义域 : ( 0 ,+∞)
性 值域: R
过点 ( 1 , 0 ) , 即当 x =1时, y=0
质 在 ( 0 ,+∞)上 在 ( 0 ,+∞)上
是增函数
是减函数
㈠ 若底数为同一常数,则可由对数函数 的单调性直接进行判断. ㈡ 若底数为同一字母,则按对数函数的 单调性对底数进行分类讨论. ㈢ 若底数、真数都不相同,则常借助1、 0、-1等中间量进行比较
y=log2x
5 4
3
3
2
2
1
1
y=x x
-3 -2 -1 0 1 2 3 4 5 6 7 8 x
-1 -2 -3
-3 -2 -1 0 1 2 3 4 5 6 7 8
-1
y= log 1x
-2
2
-3
y
㈠ y = log2x
01
x
㈡ y = log 1x
2
图象特征
函数性质
图像都在 y 轴右侧
定义域是( 0,+∞)
在 R 上是增函数 在 R 上是减函数
指数式和对数式的互化:将 ab= N化成对数式,会得到
logaN = b
问题:求指数函数 y = ax ( a > 0 ,且 a ≠ 1 )的反函数
解: 从 y = ax 可以解得:x = logay 因此指数函数 y = ax 的反函数是
y=logax ( a > 0 ,且 a ≠ 1 )
再见
两直线的位置关系
直线与直线的位置关系:
( 1 ) 有 斜 率 的 两 直 线 l1:y=k1x+b1;l2:
y=k2x+b2
① l1∥l2 k1=k2且b1≠b2; ②l1⊥l2 k1·k2= -1
对数函数和指数函数 互为反函数
问题:作出函数 y = log 2 x 和函数 y =log 1x的图像.
2
【分析:互为反函数的两个函数图像关于直线 y=x 对称】
y=log2x 的反函数为
y
y= 2x
y=
2x
y
y= log 1 =1 x 2
2
x
的反函数为 y
y
= 1x
2
8 7
y=x
8 7
6
6
5 4
练习: 比较下列各题中两个值的大小: ⑴ log106 < log108 ⑵ log0.56 < log0.54 ⑶ log0.10.5 > log0.10.6 ⑷ log1.51.6 > log1.51.4
例2 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; 提示 : log aa=1
⑵ log 3π , log 2 0.8 . 提示: log a1=0
解: ⑴ ∵ log67>log66=1
log76<log77=1
∴
log67>log76
⑵ ∵ log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8
注:例2是利用对数函数的增减性比较两个对数的大小. 当不能直接进行比较时,可在两个对数中间插入一 个已知数(如1或0等),间接比较上述两个对数的大小
⑵考察对数函数 y = log 0.3 x,因为它的底数为0.3, 即0<0.3<1,所以它在(0,+∞)上是减函数,于是 log 0.31.8>log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 ) 对数函数的增减性决定于对数的底数是大于1还是小于1.
而已知条件中并未指出底数a与1哪个大, 因此需要对底数a进行讨论:
对数函数的定义 : 对数函数的图象和性质 比较两个对数值的大小
作业
Ⅰ 熟记对数函数 的图象和性质
Ⅱ 习题2.8 3
函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.其中 x是自变量,
函数的定义域是( 0 , +∞)
a>1
0 <a <1
图
y x=1y=logax (a>1)
y
(1,0)
又因为 y = ax 的值域为(0,+∞)
所以 y=logax ( a > 0 ,且 a ≠ 1 )
的定义域为(0,+∞)
结论:
函数 y = logax (a>0,且a≠1)是指数函数 y = ax的反函数
函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)
y=logax在(0,+∞)是减函数
a>1
0 <a <1
图
y x=1y=logax (a>1)
y
(1,0)
0 (1,0)
象
x0
x y=logax (0<a<1)
定义域 : ( 0 ,+∞)
性 值域: R
过点 ( 1 , 0 ) , 即当 x =1时, y=0
质 在 ( 0 ,+∞)上 在 ( 0 ,+∞)上
是增函数
是减函数
例1 比较下列各组数中两个值的大小: ⑴ log 23.4 , log 2⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解 ⑴考察对数函数 y = log 2x,因为它的底数2>1, 所以它在(0,+∞)上是增函数,于是 log 23.4<log 28.5
课题:2.8 对数函数
复习:一般的,函数 y = ax ( a > 0, 且 a ≠ 1 ) 叫做指数函数,
其中x是自变量.函数的定义域是 R.
a>1
0<a<1
y y=ax
y=ax
y
图
(a>1)
(0<a<1)
y=1
y=1
(0,1)
(0,1)
象
0
x
0
x
性
定义域:R 值 域:(0,+ )
质 过 点 ( 0 , 1 ) ,即 x = 0 时, y = 1 .
图像都经过 (1,0) 点
1 的对数是 0
图像㈠在(1,0)点右边的 纵坐标都大于0,在(1,0)点 左 图边像㈡的纵则正坐好标相都反小于0; 自左向右看,
图像㈠逐渐上升 图像㈡逐渐下降
当当当底底a>数数1a0时><,1a时<1时00<<xx>>xx<<11 ,,11则则,,则 则lloolgglooaaggxxaa><xx><0000 y当=0l<ogaa<x在1时(0,,+∞)是增函数
