习题课一第12章
有机化学课后习题答案12第十二章醛和酮核磁共振谱(第5轮)答案

1. 2-丁烯醛
CH3CH=CHCHO
2,4-戊二酮
4-氯-4-甲基-2-戊烯醛
14. CH3COCH2CH2OH 15. (CH3)2 CHCH2CHO
4-羟基-2-丁醇
4-甲基丁醛
2. 二苯甲酮
C O
3. 2,2-二甲基环戊酮
O
C
CH3
CH3
4. 3-(间羟基苯基)丙醛
5. 甲醛苯腙
6. 丙酮缩氨脲
)。
A.糠醛
B.甲醛
C.乙醛
D.苯甲醛
9. 醛.酮与锌汞齐(Zn-Hg)和浓盐酸一起加热,羰基即被( C )。
A.氧化为羧基 B.转变成卤代醇 C.还原为亚甲基 D.还原为醇羟基
10. C6H5COCH2CH2C6H5 的系统命名法名称应该是:(B )
A.1,3-二苯基-3-丙酮
B.1,3-二苯基-1-丙酮
8.
CHCHO
CH3
2-环己基丙醛
9.
O CH3
CH3 C CHCH2CHO
3-甲基-4-氧代戊醛
10. CH3CHCH2COCH2CH3
CH2CH3
11. CH3COCH2COCH3
Cl
12.
(CH3)2CCH CHCHO
5-甲基-3-庚酮
13.
CH3 CH3C N OH
丙酮肟
二.写出下列化合物结构式
R CH R' OH
R CH2 R'
NH2NH2 , NaOH (HOCH2CH2)2O
R
CH2
R'
还原能力较强,还能还原碳碳不饱和键。 还原能力较弱,仅能将羰基还原成羟基。 还原能力比四氢硼钠稍强,能还原羧基。 Clemmensen 还原法 黄鸣龙还原法
大学物理第12章课后习题

第十二章 静电场中的导体和电介质12-1将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将如何变化.答:电场中通常以无穷远处的电势为零电势参考点。
导体B 离A 很远时,其电势为零。
A 带正电,所以其电场中各点的电势均为正值。
因此B 靠近A 后,处于带电体A 的电场中时,B 的电势为正,因而B 处的电势升高。
12-2 如附图所示,一导体球半径为R 1,外罩一半径为R 2的同心薄球壳,外球壳所带总电荷为Q ,而内球的电势为U 0,求此系统的电势和电场分布。
解:根据静电平衡时电荷的分布,可知电场分布呈球对称.设内球壳带电量为q 取同心球面为高斯面,由高斯定理()()∑⎰⋅=⋅=⋅02/π4d εq r E r r E S E ,根据不同半径的高斯面内的电荷分布,解得各区域内的电场分布为r <R 1时, ()01=r E R 1<r <R 2 时,()202π4rεq r E =r >R 2 时, ()202π4rεq Q r E +=由电场强度与电势的积分关系,可得各相应区域内的电势分布. r <R 1时,20103211π4π4d d d d 2211R Q R q U R R R R rrεε+=⋅+⋅+⋅=⋅=⎰⎰⎰⎰∞∞l E l E l E l ER 1<r <R 2 时,200322π4π4d d d 22R Q rq U R R rrεε+=⋅+⋅=⋅=⎰⎰⎰∞∞l E l E l Er >R 2 时,rQ q U r03π4d ε+=⋅=⎰∞l E 3由题意得201001π4π4R Q R q U U εε+==代入电场、电势的分布得 r <R 1时,01=E ;01U U =R 1<r <R 2 时,22012012π4rR Q R rU R E ε-=;rR Q R r rU R U 201012π4)(ε--=r >R 2 时,220122013π4)(rR Q R R rU R E ε--=;rR Q R R rU R U 2012013π4)(ε--=12-3证明:对于两个无限大的平行平面带电导体板来说,(1) 相向的两面上,电荷的面密度总是大小相等而符号相反;(2) 相背的两面上,电荷的面密度总是大小相等且符号相同。
03 电磁学:第12、13章 习题课及部分习题解答-修订补充版
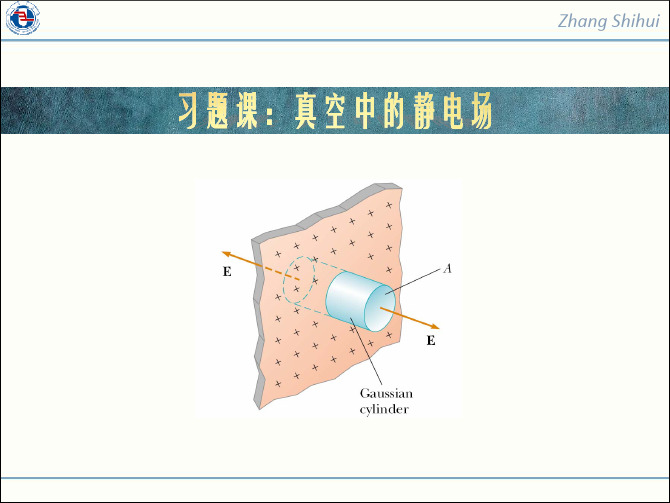
R
∫
S
E ⋅ dS ⇒2πrlE =
R
q
ε0
r l
q=∫
0
2 Ar ⋅ 2πrldr = πAlR 3 3
3
AR E= 3ε 0 r
(r > R)
目录·电势的计算
作业册·第十三章 电势·第8题
Zhang Shihui
③ 内外电势分布 内部电势 U =
∫
L
r R
Edr Ar AR dr + ∫ dr R 3ε r 3ε 0 0
dl = Rdθ
λ dl cos θ dEx = dE cos θ = 2 4πε 0 a
q q cos θ dθ = cos θ ⋅ adθ = 2 4πε 0 a θ 0 a 4πε 0 a 2θ 0 1
θ0
2
θ
−
θ0
2
θ0
2
dE
x
q 2 沿x正 E = ∫ θ0 dEx = (sin + sin ) = − 4πε 0 a 2θ 0 2 2 2πε 0 a 2θ 0 方向 2
均匀带电细棒垂面上场强
2.电势的计算
Zhang Shihui
① 叠加原理,取微 U = 元,直接求电势 ② 先利用高斯定理 求场强,再求电势
∑ 4πε r
0
qi
i
,U =∫
b a
dq 4πε 0 r
作业册 第13章电势 第1题 第8题 第2题
V
∫
S
E ⋅ dS =
Q
ε0
, U a = ∫ E ⋅ dl
ΔS
O
ΔS
x
ρd = 2ε 0
−x
截面放大后
机械课后习题答案第12章习题及解答

(2) 由表 14.8 查得 fT=0.95,载荷负荷平稳,由表 14.9 查得 fF=1.0,对球轴承取=3, 对
滚子轴承=10/3。将以上有关数据代入下式
Lh
106 60n
fT C fPF
对球轴承
Lh
106 0.95 22800 3 60 1000 5880
833.1
h,
不满足要求,
再选 6408 (Cr=50200, C0r=37800),得
T 9.55106 P 9.55106 2.6 64661.4 N·mm
n
384
Ft 2T1 129322.8 2917.5 N d1 44.326
Fr 1107.5 N
Fa 864.2 N
(2) 计算轴向力
R2V=457.98 R1V=649.5 R1H= R2H =1458.75
由机械零件设计手册得 30307 圆锥滚子轴承的 Cr=71200 N, C0r=50200 N , Y = 1.9, e=0.31 表 14.12 可知圆锥滚子轴承轴承的内部轴向力 SA、SB 为
S1= R1/2Y=584/(2×1.9)=153.6 N S2= R2/2Y=1776/(2×1.9)=467.4 N
h
所选轴承型号为 N410 合适。
12.15一齿轮轴由一对 30206 轴承支承,支点间的跨距为 200 mm,齿轮位于两支点的中央。
已知齿轮模数 mn=2.5 mm,齿数 z1=17,螺旋角=16.5,传递功率 P=2.6 kW,齿轮轴
的转速 n=384r/min。试求轴承的额定寿命。
解: (1) 计算齿轮的作用力
每个轴承的径向载荷 R=5880 N,载荷平稳,工作温度 t=125C,预期寿命 Lh=5000 h,
管理学_高教版_周三多主编_第二版__第12章习题

第十二章激励一、填充题1.无论是激励还是动机,都包含三个关键要素:_____,_____和_____.激励是由动机推动的一种______.2._________是产生激励的起点,进而导致某种行为.3.要通过激励促成组织中人的行为的产生,取决于某一行动的______和______.4.马斯洛认为,每个人其实都有五个层次的需要:_____,______,_____,_____,_____.5.双因素理论的研究重点,是_______.6.根据赫兹伯格的理论,______和_____,其中,______是那些与人们的不满情绪有关的因素,_____是指那些与人们的满意情绪有关的因素.7.根据道格拉斯•麦格雷戈的理论,管理者对人性的假设有两种对立的基本观点:一是______;另一种是_____.8.公平理论中,员工选择的与自己进行比较的参照类型有三种,分别是_____,_____,和______.9.期望理论的核心是______,_______,______.10.期望理论的假说是__________.11.期望理论的关键是,正确识别个人目标和判断三种关系,即______,_______,______.12.根据强化的________和_______,强化可以分为两大类型:正强化和负强化。
13.常用的主要有四种激励方式:_______,________,______以及______.14.绩效工资实际上是激励的_____和______的逻辑结果。
15.德鲁克的目标管理理论和卢克的目标设定理论都有一个共同基础:____,_____.16.当目标_______并具有______时,能更有效地激励个体或团队行动。
17.目标管理理论将目标的______,______,______,______作为目标激励的四个组成部分。
18.根据目标管理理论,绩效目标要根据_______来设定。
19.激励计划的一个最明显的优势是企业增强了对熟练员工的______,最终有效降低了对这种员工的______和_______.20.公平理论认为人们将通过两个方面的比较来判断其所获报酬的公平性,即_____比较和______比较。
城规划原理课后习题和答案与解析(第四版)1_12章

城市规划原理(第四版)课后习题解答第一章1.城市由哪些基本要素构成?产业构成、人口数量、职能。
(当然,还有一些非基本要素:市政和公共设施、人造和自然景观、建筑数量等)2.工业前城市与工业城市各自的特征是什么?工业前城市:①城市规模小②依赖风力和水力天然能源③以马车为主要交通工具工业城市:①城市圈层式向外扩张②出现城市仓储用地③出现商务贸易活动区④火车、轮船成为城市对外运输的主要工具,汽车成为城市运输的主要工具⑤城市类型增加3.中国城市化面临的主要挑战是什么?依你的推测,2030年中国城市化的水平将达到多少?①城市化进程分为三个阶段:起步、加速和稳定三个阶段,我国正处于加速发展阶段。
②中国幅员辽阔,不同地区经济社会发展和和环境条件存在巨大差异,以统一的标准衡量中国城镇化发展,并以此制定政策,不能满足需求。
③城镇化是一种现象,不是人类社会的发展目标,实现城市及区域的永续和谐发展是重点。
60%以上,官方预测为70%(8月27日发布的《2013中国人类发展报告》预测,到2030年,中国将新增3.1亿城市居民,城镇化水平将达到70%。
届时,中国城市人口总数将超过10亿。
),进入城市化的稳定阶段。
4.城市化有哪些基本规律?城市化发展与全球气候变化有哪些关系?①城市人口占总人口的比重不断上升。
②产业结构由第一产业向第二三产业转变。
③农业人口剩余推动城市化发展。
①城市用地增加,农业用地、森林、湿地等非城市用地减少。
②城市化耗费大量煤、石油等非天然能源,造成环境污染。
③城市化同时促进科技发展,产生电池、塑料、建筑垃圾等人造污染物。
第二章1.中国古代的城市格局反映了哪些重要的城市规划思想?①整体观念和长远发展(《管子》提出功能分区)、(《商君书》提出从城乡关系、区域经济、交通布局考虑)②人工环境和自然环境和谐【道家】(战国时代,吴国国都阖闾城建设,伍子胥提出“相土尝水,象天法地”)、(秦统一中国,规划时,也提出“象天法地”,强调方位)、(三国时期,吴国国都选址金陵,“以石头山、长江险要为界,依托玄武湖防御”)③严格有序的城市等级制度:中轴对称,道路分等级等【儒家】(周礼考工记,周王城建造,按封建等级)、(曹邺魏城、隋唐长安城、元大都皆是依据周王城而建)2.你认为哪些古代经典城市的规划案例,对未来的城市发展仍然有重要意义?①曹魏邺城,采用功能分区布局。
有机化学第二版高占先课后习题第12章答案
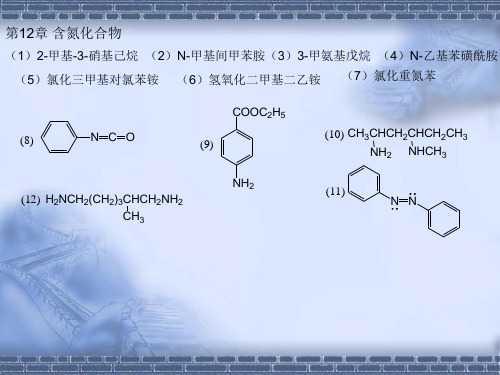
H N
O NH2 H N
NH2
OHH N
H2/Pd
12-12 根据下列反应,试确定A的构造式。
(1)CH3I过量 A(C8H15N) (2湿)Ag2O, △ 答案 A N H
(1)CH3I过量 (2湿)Ag2O, △
12-13 (1)利用RX和NH3合成伯胺的过程有什么副反应? (2)如何避免或减少这些副反应? (3)在这一合成中哪一种卤代烷不合适? (1)可发生二烷基化、三烷基化反应,生成R2NH和R3N; (2)使NH3大量过量,以增加 RX和NH3的碰撞机会生成RNH2; (3)叔卤代烃将发生消除反应,芳卤ArX也不易发生该反应。
CH3 (4)
2HNO3 2 H2SO4
CH3 NO2
Cl2 hv
CH2Cl NO2
(1) NaCN
CH2COOH NO2
Fe/HCl
CH2COOH NH2
(2) H3O,△
NO2
NO2
NO2
NH2
(5)
2HNO3 2 H2SO 4
NO2
((NH4)2S
NO2
NO2
NaNO 2-HCl 0~5¡ æ
pH=8~10
NH2 NaNO2-HCl
0~5℃
N N OH
(3)
参考(1)合成
OH COCH3 CH2CH3
HNO3 H2SO4
CH2CH3
Sn/HCl
CH2CH3
CH3COCl AlCl3
Zn-Hg HCl
CH2CH3
NaNO2-HCl 0~5℃ pH=8~10
OH H3CH2C
NO2
HO
NH2
NaNO2 / HCl
大学物理课后习题答案(上下册全)武汉大学出版社 第12章 习题解答

第12章 习题与答案12-1 在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的光程为[ ]A. 1.5λ.B. 1.5λ/n .C. 1.5n .D. 3λ. [答案:A ]12-2 平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为[ ]A. 2πn 2e / ( n 1λ1).B. 4πn 1e / ( n 2λ1)] +π.C. 4πn 2e / ( n 1λ1) ]+π.D. 4πn 2e / ( n 1λ1).[答案: C ]12-3 两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的[ ]A. 间隔变小,并向棱边方向平移.B. 间隔变大,并向远离棱边方向平移.C. 间隔不变,向棱边方向平移.D.间隔变小,并向远离棱边方向平移. [答案: A ]12-4 用劈尖干涉法可检测工件表面缺陷,当波长为λ的单色平行光垂直入射时,若观察到的干涉条纹如题12-4图所示,每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切,则工件表面与条纹弯曲处对应的部分[ ]A. 凸起,且高度为4λ.B. 凸起,且高度为2λ.C. 凹陷,且深度为2λ.D. 凹陷,且深度为4λ.[答案: C ]12-5 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中,则干涉条纹[ ]A .中心暗斑变成亮斑. B. 间距变大. C. 间距变小. D. 间距不变. [答案: C ]题12-4图12-6 在光栅光谱中,假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,因而实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为[ ] A. =3a b . B. =2a b . C. =a b . D. =0.5a b [答案: C ]12-7 对某一定波长的垂直入射光 衍射光栅的屏幕上只能出现零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该[ ]A. 换一个光栅常数较小的光栅.B. 换一个光栅常数较大的光栅.C. 将光栅向靠近屏幕的方向移动.D. 将光栅向远离屏幕的方向移动.[答案: B ]12-8如果两个偏振片堆叠在一起,且偏振化方向之间夹角为60°,光强为I 0的自然光垂直入射在偏振片上,则出射光强为[ ]A. I 0 / 8.B. I 0 / 4.C. 3 I 0 / 8.D. 3 I 0 / 4.[答案: A ]12-9一束自然光自空气射向一块平板玻璃(如题12-9图),设入射角等于布儒斯特角i 0,则在上表面的出射光2是[ ]A. 自然光.B. 线偏振光且光矢量的振动方向平行于入射面.C. 线偏振光且光矢量的振动方向垂直于入射面.D. 部分偏振光.[答案: C ]12-10相干光的必要条件为________________________,________________________,________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案:真值分别为 0, 1, 0, 0
3. 设 A 与 B 均为含 n 个命题变项的公式,判断下列 命题是否为真? (1) AB 当且仅当 A 与 B 有相同的主析取范式 (2) 若 A 为重言式,则 A 的主合取范式为 0 (3) 若 A 为矛盾式,则 A 的主析取范式为 1 (4) 任何公式都能等值地化成{, }中的公式 (5) 任何公式都能等值地化成{, , }中的公式
4.通过求主范式判公式类型 (1)(pq)(qp) ( 2 ) (p q )q (3)(pq)p 5.已知命题公式 A 中含 3 个命题变项 p, q, r, 并知道它的成真 赋值为 001, 010, 111, 求 A 的主析取范式和主合取范式,及 A 对应的真值函数.
例如,若命题公式 A 中含有 3 个命题变项,且 A 的主析取范 式中含有 4 个极小项 m0 , m1 , m5 , m7 ,即, A m0 m1 m5 m7 (0,1,5,7) , 则 A 的主析取范式中含有的极小项个数为 23-4=4,且分别为 m2 , m3 , m4 , m6 ,即, A m2 m3 m4 m6 (2,3,4,6) , 于是,A 的主合取范式为: A M 2 M 3 M 4 M 6 (2,3,4,6) 由此可见, 只要我们熟练地掌握了求命题公式 A 的主析取范式 的方法,就可以很快写出 A 的主合取范式,反之亦然。另外,主合 取范式的用途与主析取范式的用途相同(见前面分析) 。 要掌握用公式 A 的真值表求 A 的主范式 若已知公式 A 的真值表, 则可从中找出所有使公式 A 成真 (成 假)的赋值及其对应的公式 A 的主析取范式(主合取范式)中所含 有的全部极小项(极大项) ,从而可立即写出公式 A * 为 p∧q,于是由( 1)可得:(p∨q) p∧q,
[注]:如果证明了一个等值公式,则其对偶式的等值式同时也成立。这样,
补充知识二: 由主析取范式求解主合取范式 6. 最后说明两点:
要掌握由公式 A 的主析取范式确定它的主合取范式,反之亦然 . 设命题公式 A 中含有 n 个命题变项, 且设 A 的主析取范式中含 有 k 个极小项, 记为 mi1 mi2 , mik , 即 A mi1 mi2 mik , 则A 的主析取范式中必含有 2n-k 个极小项 (注意,这 2n-k 个极小项实际 上是含有 n 个命题变项构成的所有极小项中除去 A 的主析取范式中 含 有 的 k 个 极 小 项 mi1 mi2 , mik 后 剩 余 的 其 他 极 小 项 ) ,记为
由表 1-7 可知,001、 011、 101、110、111 是原公式的成真赋值, m3 、 m5 、 m1 、 因而, 对应的原公式的主析取范式中所含的全部极小项为:
m6 、 m7 ,则 pq r m1 m3 m5 m6 m7 (1,3,5,6,7)
(请大家自己考虑主合取范式的分析)
3)A:((p∨q)∧0)∧(1∧ (r∨p)),A*: ((p∧q)∨ 1)∨(0∨ (r∧p))
2. 定理 1.5.1: 设 A 和 A*互为对偶式,p 1,p2,…,pn 是出现在 A 和 A*中的 全部命题变项,将 A 和 A*写成 n 元函数形式,则, (1) A(p1,p 2,…,pn) A* ( p1, p 2,…, pn) (2) A( p1, p2,…, pn) A* (p1,p2,…,pn) 类似地,由( 2)可得:p∨q (p∧q),这就是 De Morgan 律。 3. 定理 1.5.2(对偶原理) : 设 A,B 为两个命题公式,若 A B ,则 A* B*. 通过对偶原理,可以由有限个等值公式推出更多个其它的等值公式,起到 事半功倍的效果。 例如:由已知的等值公式: (p∧q)∨(p ∨(p∨q)) p∨q , 我们可以得到一个新的等值公式:(p ∨q)∧(p∧(p ∧q)) p ∧q.
二、 练习题 1.将下列命题符号化 (1) 豆沙包是由面粉和红小豆做成的. (2) 苹果树和梨树都是落叶乔木. (3) 王小红或李大明是物理组成员. (4) 王小红或李大明中的一人是物理组成员. (5) 由于交通阻塞,他迟到了. (6) 如果交通不阻塞,他就不会迟到. (7) 他没迟到,所以交通没阻塞. (8) 除非交通阻塞,否则他不会迟到. (9) 他迟到当且仅当交通阻塞.
6.在以下各联结词集中各求一个公式与 A = (pq)r 等值. ( 1 ) { , , } ( 2 ) { , } ( 3 ) { , } ( 4 ) { , } ( 5 ) { } ( 6 ) { }
7. 一公安人员审查一件盗窃案,已知的事实如下: (1) 甲或乙盗窃了录音机; (2) 若甲盗窃了录音机,则作案时间不能发生在午夜前; (3) 若乙的证词正确,则午夜时屋里的灯光未灭; (4) 若乙的证词不正确,则作案时间发生在午夜之前; (5) 午夜时屋里的灯光灭了. 试用主析取范式法(或主合取范式法)分析盗窃录音机的人是 甲还是乙? 解此类问题的步骤应为:
(1 )
(pq)(pq)(pq)(pq)
结论: (1)为重言式
(2 )
(pq)q ① ② ③ ④
(pq)q pqq 0 M0 M1 M2 M3 问:由②如何得③? ③为主析取范式,④为主合取范式 结论: (2)为矛盾式. (3 ) (pq)p m0 m1 M2 M3 请自己等值演算得①与② 结论: (3)为可满足式 请用真值表再解此题
练习题1. 提示与答案 练习题1.提示:
分清复合命题与简单命题 分清相容或与排斥或 分清必要与充分条件及必要充分条件 答案: (1)是简单命题 (2)是合取式 (3)是析取式(相容或) (4)是析取式(排斥或) 请分别写出(1)—(4)的符号化形式 设 p: 交通阻塞,q: 他迟到 (5) pq, (7)qp 或 pq, (9)pq 或pq 可见(5)与(7) , (6)与(8)相同(等值) (6)pq 或 qp (8)qp 或pq
m j1 m j2 , m j2n k ,即 A m j1 m j2 m j2n k 。于是,利用极小项
mi 与极大项 Mi 之间的关系:mi Mi, Mi m i,可得: A A ( m j1 m j2 m j2n k ) m j1 m j2 m j2n k M j1 M j2 M j2n k 这就是 A 的主合取范式。
3.内容二 等值式与等值演算 基本的等值式(16 组,24 个公式) 联结词全功能集(完备集) 主析取范式与主合取范式 4.内容二学习要求 深刻理解等值式的概念; 牢记基本等值式的名称及它们的内容; 了解简单析取式、简单合取式、析取范式、合取范式的概念; 深刻理解极小项、极大项的概念、名称及下角标与成真、成假赋值 的关系,并理解简单析取式与极小项的关系; 熟练掌握求主范式的方法(等值演算、真值表等) ; 会用公式的主范式求公式的成真、成假赋值及判断公式的类型、简 单应用; 会将任何公式化成任何联结词全功能集(完备集)中的公式。
补充知识一: 对偶式与对偶原理
一、 对偶式和对偶原理 1. 定义 1.5.1: 在仅含有联结词 , ∧,∨的命题公式 A 中, 将∨换成∧ , ∧ 换成∨,若 A 中含有 0 或 1,就将 0 换成 1,1 换成 0,所得命题公式称为 A 的对偶式,记为 A*. [注 ]:从定义不难看出,(A*)* 还原成 A,即对偶是相互的。 例 1.5.1:试写出下列命题公式的对偶式 1)A:(p∧q)∨r, 2)A:(p∧q)∨(p∧ (q∨s)), A*: (p∨q)∧r A*: (p∨q) ∧ (p∨ (q∧s))
1 将简单命题符号化 ○ 2 写出各复合命题 ○ 3 写出由②中复合命题组成的合取式 ○ 4 将③中公式化成析取式(最好是主析取范式) ○
8. 用不同的方法验证下面推理是否正确 . 对于正确的 推理还要在 P 系统中给出证明. (1) 前提:pq, 结论:p (2) 前提:qr, 结论:qp 9. 在 P 系统中构造下面推理的证明: 如果今天是周六,我们就到颐和园或圆明园玩 . 如 果颐和园游人太多,就不去颐和园 . 今天是周六,并且 颐和园游人太多. 所以我们去圆明园或动物园玩. pr q
① ②
练习题5. 提示与答案
5.已知命题公式 A 中含 3 个命题变项 p, q, r,并知道它 的成真赋值为 001, 010, 111, 求 A 的主析取范式和主 合取范式,及 A 对应的真值函数. 答案
A 的主析取范式为 m1 m2 m7 A 的主合取范式为 M0 M3 M4 M5 M6 设 A 对应的真值函数为 F,则 F(001)=F(010)=F(111)=1 F(000)=F(011)=F(100)=F(101)=F(110)=0 试说明以上得出答案的理由
例 1.5.7 试由 pq r 的真值表求它的主析取范式(主合取范式) 解:写出 pqr 的真值表如下表 1-7:
表 1-7:pqr 的真值表
p 0 0 0 0 1 1 1 1
q 0 0 1 1 0 0 1 1
r 0 1 0 1 0 1 0 1
pq 0 0 0 0 0 0 1 1
pqr 0 1 0 1 0 1 1 1
5.内容三 推理的形式结构的不同形式 判断推理是否正确的不同方法 ①真值表法 ②等值演算法 ③主析取范式法 ④构造证明法 … 在自然推理系统 P 中构造证明 6.内容三学习要求 理解并记住推理形式结构的如下形式: ① (A1A2…Ak)B ② 前提:A1, A2, … , Ak 结论:B 熟练掌握判断推理是否正确的不同方法 (如真值表法、 等值演算法、 主析取范式法等) 牢记 P 系统中各条推理规则(内容与名称) 会用附加前提证明法及归谬法
2. 设 p : 2 是素数 q : 北京比天津人口多 r : 美国的首都是旧金山 求下面命题的真值 (1) (pq)r (2) (qr)(pr) (3) (qr)(pr) (4) (qp)((pr)(rq))
