第三讲晶面和晶向
合集下载
晶面和晶向
加一方括号,即为所求的晶面面及晶向的原子密度
所谓某晶面的原子密度指其单位面积中的 原子数,而晶向原子密度则指其单位长度 上的原子数。在各种晶格中,不同晶面和 晶向上的原子密度都是不同的。例如,在 体心立方晶格中的各主要晶面和晶向的原 子密度见表1-2
1.2.3 金属的同素异构转变
实际金属中的缺陷对材料力学性能 的影响如下:
点缺陷的存在,提高了材料的硬度和强度, 降低了材料的塑性和韧性,增加位错密度 可提高金属强度,但塑性随之降低
面缺陷能提高金属材料的强度和塑性 细化晶粒是改善金属力学性能的有效手段
某些金属在不同温度和压力下呈不同的晶体结构,同一 种固态的纯金属(或其他单相物质),在加热或冷却时 发生由一种稳定状态转变成另一种晶体结构不同的稳定 状态的转变,称为同素异构转变。此时除体积变化和热 效应外还会发生其他性质改变。例如Fe、Co、Sn、Mn 等元素都具有同素异构特性。
铁在结晶后继续冷却至室温的过程中,将发生两次晶格 转变,其转变过程如图1.2-14所示。铁在1394℃以上时具 有体心立方晶格,称为δ-Fe;冷却至1394~912℃之间, 转变为面心立方晶格称为γ-Fe;继续冷却至912℃以下又 转变为体心立方晶格,称为α-Fe。
2)确定晶面指数的步骤如下:
(1)设晶格中某一原子为原点,通过该点平行于 晶胞的三棱边作OX、OY、OZ三个坐标轴,以晶 格常数a、b、c分别作为相应的三个坐标轴上的量 度单位,求出所需确定的晶面在三坐标轴上的截 距(见图1.2-6)。
(2)将所得三截距之值变为倒数; (3)再将这三个倒数按比例化为最小整数,并加
3. 晶格的晶面和晶向
(1)晶面指数及晶向指数 (2)晶面及晶向的原子密度
1)晶面指数及晶向指数
所谓某晶面的原子密度指其单位面积中的 原子数,而晶向原子密度则指其单位长度 上的原子数。在各种晶格中,不同晶面和 晶向上的原子密度都是不同的。例如,在 体心立方晶格中的各主要晶面和晶向的原 子密度见表1-2
1.2.3 金属的同素异构转变
实际金属中的缺陷对材料力学性能 的影响如下:
点缺陷的存在,提高了材料的硬度和强度, 降低了材料的塑性和韧性,增加位错密度 可提高金属强度,但塑性随之降低
面缺陷能提高金属材料的强度和塑性 细化晶粒是改善金属力学性能的有效手段
某些金属在不同温度和压力下呈不同的晶体结构,同一 种固态的纯金属(或其他单相物质),在加热或冷却时 发生由一种稳定状态转变成另一种晶体结构不同的稳定 状态的转变,称为同素异构转变。此时除体积变化和热 效应外还会发生其他性质改变。例如Fe、Co、Sn、Mn 等元素都具有同素异构特性。
铁在结晶后继续冷却至室温的过程中,将发生两次晶格 转变,其转变过程如图1.2-14所示。铁在1394℃以上时具 有体心立方晶格,称为δ-Fe;冷却至1394~912℃之间, 转变为面心立方晶格称为γ-Fe;继续冷却至912℃以下又 转变为体心立方晶格,称为α-Fe。
2)确定晶面指数的步骤如下:
(1)设晶格中某一原子为原点,通过该点平行于 晶胞的三棱边作OX、OY、OZ三个坐标轴,以晶 格常数a、b、c分别作为相应的三个坐标轴上的量 度单位,求出所需确定的晶面在三坐标轴上的截 距(见图1.2-6)。
(2)将所得三截距之值变为倒数; (3)再将这三个倒数按比例化为最小整数,并加
3. 晶格的晶面和晶向
(1)晶面指数及晶向指数 (2)晶面及晶向的原子密度
1)晶面指数及晶向指数
晶体生长原理与技术第三讲_晶面和晶向

r a1cos a1 ,n d
A3
Nn
s a2cos a2 ,n d
t a3cos a3 ,n d a 3 d a 2
A2
取a1,a2,a3为天然长度单位,则得: O a 1
A1
111
ca o 1 ,n s : ca o 2 ,n s : ca o 3 ,n s :: rst
向是该晶面的法线方向,它的大小则为该晶面族面间距倒数的
2倍。
1.4.2 倒格与正格的关系
1. ai bj 2πij 2π (ij)
0 ij
a1b1a12πa2a3 Ω
2π
a1b2a12πa3a1 0 Ω
2. Rl Kh 2π (为整数)
解: OB i , OEijk,
BE OE O Bjk
晶列BE的晶列指数为:[011]
c
b
Oa
C
D B
求AD的晶列指数。
E
OA k , OD i 1 j,
A
2
AD O D O Ai1jk c
2
b
AD的晶列指数为: [ 21 2 ] 注意:
Oa
C
D B
(1)晶列指数一定是一组互质的整数; 晶列(11-1)
任一晶面在坐标轴上的截距r,s,t必是一组有理数。
可以证明h1,h2,h3一定是互质的,称它们为该晶面族的 面指数,记为(h1h2h3 ) 。
综上所述,晶面指数(h1h2h3 )表示的意义是;
(1)基矢a1,a2,a3 被平行的晶面等间距的分割成h1、h2、h3 等份;
(2)以 a1,a2,a3为各轴的长度单位所求得的晶面在坐标轴
晶向与晶面

已知铜具有面心立方结构,其点阵常数为 0.3615nm,计算铜晶体(111),(112)晶 面间距。
(2)晶面夹角
两晶向[u1v1w1]与[u2v2w2]间夹角:
cos
u1u2 v1v2 w1w2
u12 v12 w12 u2 2 v2 2 w2 2
晶面(hkl)与晶向[uvw]间夹角:
<111>晶向族如右图。
(2)晶面指数-------(hkl)
例3:
(1)截距r、s、t分别为3,3,5
z
(2)1/r : 1/s : 1/t = 1/3 : 1/3 : 1/5
(3)最小公倍数15,
(4)于是,1/r,1/s,1/t分别
c
乘15得到5,5,3,
ab
y
因此,晶面指标为(553)。
三、晶体的对称性 crystalline symmetry symmetrization of crystals
对称性——晶体的基本性质
对称元素(symmetry elements)
回转对称轴(n)1,2,3,4,6
宏观对称性 元素 对称面(m)
对称中心(i) 回转 — 反演轴 1,2,3,4,6
负号记在上方 [uv w] 。
1、红线代表的晶向由两个结点的坐标之差确定
2、晶向指数同乘、除一个数,晶向不改变。 如[012]---[0 ½ 1]
▪ 如图为立方晶系: X轴、Y轴、
Z轴;长度单位a=b=c=1。
▪例: OD为[101];
▪ Om为:坐标1/2、1、1/2;化
简后[121];
▪EF为:[111]
例如:a1轴的指标可以是[1000],也可以是 [2110].
解决方法:加限制条件:前三个指标之和为0 例如:晶向指标为[u v t w],则u+v+t=0,故a1轴的指
(2)晶面夹角
两晶向[u1v1w1]与[u2v2w2]间夹角:
cos
u1u2 v1v2 w1w2
u12 v12 w12 u2 2 v2 2 w2 2
晶面(hkl)与晶向[uvw]间夹角:
<111>晶向族如右图。
(2)晶面指数-------(hkl)
例3:
(1)截距r、s、t分别为3,3,5
z
(2)1/r : 1/s : 1/t = 1/3 : 1/3 : 1/5
(3)最小公倍数15,
(4)于是,1/r,1/s,1/t分别
c
乘15得到5,5,3,
ab
y
因此,晶面指标为(553)。
三、晶体的对称性 crystalline symmetry symmetrization of crystals
对称性——晶体的基本性质
对称元素(symmetry elements)
回转对称轴(n)1,2,3,4,6
宏观对称性 元素 对称面(m)
对称中心(i) 回转 — 反演轴 1,2,3,4,6
负号记在上方 [uv w] 。
1、红线代表的晶向由两个结点的坐标之差确定
2、晶向指数同乘、除一个数,晶向不改变。 如[012]---[0 ½ 1]
▪ 如图为立方晶系: X轴、Y轴、
Z轴;长度单位a=b=c=1。
▪例: OD为[101];
▪ Om为:坐标1/2、1、1/2;化
简后[121];
▪EF为:[111]
例如:a1轴的指标可以是[1000],也可以是 [2110].
解决方法:加限制条件:前三个指标之和为0 例如:晶向指标为[u v t w],则u+v+t=0,故a1轴的指
晶向、晶面和它们的标志

[001]
[010]
[100]
[010] [001]
[100]
向为等效晶向,写成<100>。
1.3.2 晶面及密勒指数
1.晶面
在晶格中,通过任意三个不在同一直线上的格点作一平面, 称为晶面,描写晶面方位的一组数称为晶面指数。 /
(1)平行的晶面组成晶面族,晶面族包含所有格点;
O a1 cosa1 , n : cosa2 , n : cosa3 , n h1 : h2 : h3
晶面的法线与三个基矢的夹角余弦之比等于三个整数之比。
1 1 1 又 cos a1 , n : cos a2 , n : cos a3 , n : : r s t
(1)晶列指数一定是一组互质的整数; 晶列(11-1) (2)晶列指数用方括号表示[ ]; 晶列[11-1] 晶列(111) 晶列[111] /
(3)遇到负数在该数上方加一横线。
(4)等效晶向。
在立方体中有,沿立方边的 晶列一共有6个不同的晶向,由于 晶格的对称性,这6个晶向并没有 什么区别,晶体在这些方向上的 性质是完全相同的,统称这些方
(hkl)
AEG 的密勒指数是(111); OEFG的密勒指数是(001); DIHG的密勒指数是(120)。
C B I
G
a
O
E
H
F
/
例3:
在立方晶系中画出(210)、 (121) 晶面。
晶面在三个坐标轴上的截距分别为:
a
(210)
1 2
1
b1Leabharlann c 1CE
B D A
a
c
G
O a E H DIHG 2 1
F
材料物理基础第二章固体结构-(3)晶面与晶向-201209

{123} = (123) + (123) + (123) + (123) + (132) + (132) + (132) + (132) + (231) + (231) + (231) + (23 1) + (213) + (213) + (2 13) + (213) + (312) + (312) + (3 12) + (312) + (321) + (321) + (321) + (32 1)
⎛ k1l1 ⎞ ⎛ l1h1 ⎞ ⎛ h1k1 ⎞ u :v:w = ⎜ ⎟:⎜ ⎟:⎜ ⎟ ⎝ k 2 l2 ⎠ ⎝ l 2 h2 ⎠ ⎝ h 2 k2 ⎠
27
u = k1l2 − k2l1 , v = l1h2 − l2 h1 ,
w = h1k2 − h2 k1
固体结构 — 晶面与晶向
课堂练习: (1)求(112)和(123)晶面的晶带轴。 (2)判断空间两个晶向或两个晶面是否相互垂直。
材料物理基础
Fundamentals of Materials Sciences
第二章 固体结构 (3)晶面与晶向
2012年9月
1
固体结构 — 晶面与晶向
晶面指数和晶向指数标定
y三轴坐标系 y四轴坐标系
术语,符号 概念,定义
重要概念
y晶面,晶向,晶面族,晶向族, y晶带,晶带轴,晶带面 y球面投影,极射投影
(110), (112), (111), (021)
(3)判断某一晶向是否在某一晶面上(或平行于该晶面)。 (4)已知晶带轴,判断哪些晶面属于该晶带。 [hkl] [uvw] (hkl)
晶向与晶面

同一晶带轴中的所有晶面的共同特点 :所有晶面的法线都与晶带轴垂直。
晶带轴[u v w]与该晶带的晶面(h k l)之间存在以下 关系
hu + kv + lw=0 ————晶带定律 凡满足此关系的晶面都属于以[u v w]为晶带轴的晶带
如果(h1k1l1)(h2k2l2)(h3k3l3)属于同一 晶带,则(nh1+mh2+jh3 nk1+mk2+jk3 nl1+ml2+jl3)仍属于上述晶带.
(012)和(123)晶面的确定
例6:立方晶系晶面指数的标注
几点说明:
1.hkl分别对应xyz上的截距,不可互换; 2.若晶面与对应坐标平行,则截距为∞,在该坐标上
的指数为0. 晶面指数规律: (1)某一晶面指数代表了一组相互平行且无限大的
晶面。 (2) 若晶面指数相同,但正负符号相反,则两晶面
(1)晶向指数----[uvw]
求法1(平移法) 1) 确定坐标系 2) 过坐标原点,作直线 (OP)与待求晶向平行; 3) 在该直线上取点(距原 点最近),并确定该点P的 坐标(x,y,z) 4)该值乘最小公倍数化成 最小整数u,v,w并加以方 括号[u v w]即是。
设坐标,求坐标,化整数,列括号
求法2(两点法)
1. 以晶胞的某一阵点为原点,以晶 轴为坐标轴X、Y、Z,以晶胞的边 长为三坐标轴的长度单位。
2. 确定晶向上任两点的坐标 (x1,y1,z1) (x2,y2,z2)。
3. 计算x2-x1 : y2-y1 : z2-z1 ; 4. 化成最小、整数比u:v:w ; 5. 放在方括号[uvw]中,不加逗号,
例如:a1轴的指标可以是[1000],也可以是 [2110].
解决方法:加限制条件:前三个指标之和为0 例如:晶向指标为[u v t w],则u+v+t=0,故a1轴的指
晶带轴[u v w]与该晶带的晶面(h k l)之间存在以下 关系
hu + kv + lw=0 ————晶带定律 凡满足此关系的晶面都属于以[u v w]为晶带轴的晶带
如果(h1k1l1)(h2k2l2)(h3k3l3)属于同一 晶带,则(nh1+mh2+jh3 nk1+mk2+jk3 nl1+ml2+jl3)仍属于上述晶带.
(012)和(123)晶面的确定
例6:立方晶系晶面指数的标注
几点说明:
1.hkl分别对应xyz上的截距,不可互换; 2.若晶面与对应坐标平行,则截距为∞,在该坐标上
的指数为0. 晶面指数规律: (1)某一晶面指数代表了一组相互平行且无限大的
晶面。 (2) 若晶面指数相同,但正负符号相反,则两晶面
(1)晶向指数----[uvw]
求法1(平移法) 1) 确定坐标系 2) 过坐标原点,作直线 (OP)与待求晶向平行; 3) 在该直线上取点(距原 点最近),并确定该点P的 坐标(x,y,z) 4)该值乘最小公倍数化成 最小整数u,v,w并加以方 括号[u v w]即是。
设坐标,求坐标,化整数,列括号
求法2(两点法)
1. 以晶胞的某一阵点为原点,以晶 轴为坐标轴X、Y、Z,以晶胞的边 长为三坐标轴的长度单位。
2. 确定晶向上任两点的坐标 (x1,y1,z1) (x2,y2,z2)。
3. 计算x2-x1 : y2-y1 : z2-z1 ; 4. 化成最小、整数比u:v:w ; 5. 放在方括号[uvw]中,不加逗号,
例如:a1轴的指标可以是[1000],也可以是 [2110].
解决方法:加限制条件:前三个指标之和为0 例如:晶向指标为[u v t w],则u+v+t=0,故a1轴的指
第3章 晶体学基础 - 晶体结构、晶向、晶面(完整版)

2020/2/13
此处添加公司信息
4
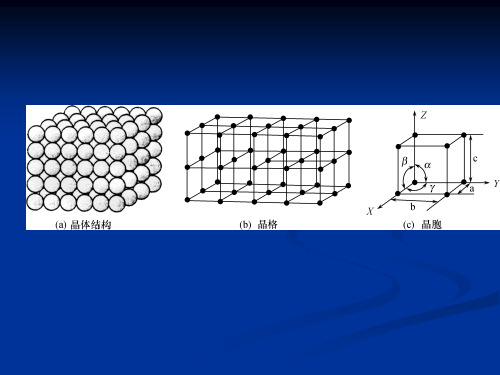
3.1.2 晶体结构和空间点阵
LOGO
晶体结构:晶体中的组成粒子在三维空间作有规则 的周期性重复排列,这种规则排列的方式即称晶体 结构。
2020/2/13
此处添加公司信息
5
3.1.2 晶体结构和空间点阵
LOGO
➢晶格:为了便于表明晶体内部原子排列的规律, 有必要把原子抽象化,把每个原子看成一个点,这 个点代表原子的振动中心。把这些点用直线连接起 来 ,便形成一个空间格子,叫做晶格。 ➢晶胞:能代表晶格原子排列规律的最小几何单元. ➢原子半径:晶胞中原子密度最大方向上相邻原子 间距的一半。 ➢晶胞原子数:一个晶胞内所包含的原子数目。 ➢配位数:晶格中与某一原子距离最近且距离相等 的原子数目。 ➢致密度:晶胞中原子本身所占的体积百分数。
2020/2/13
此处添加公司信息
16
3.3.1晶向指数的标定 LOGO 17
若原点不在待标晶向上,还可以这样操作:
LOGO
(1)找出该晶向上两点的坐标(x1,y1,z1)和(x2,y2,z2); (2)将(x1-x2),(y1-y2),(zl-z2)化成互质整数u,v,w; (3)满足u:v:w=(x1一x2):(y1一y2) :(zl—z2)。
2020/2/13
此处添加公司信息
10
2)面心立方晶胞 FCC
晶格常数:a(a=b=c)
原子半径: r 2 a 4
原子个数:4 配位数: 12 致密度:0.74 常见金属:-Fe、Ni、 Al、 Cu、Pb等
2020/2/13
此处添加公司信息
LOGO
11
3.2.3 常见的三种晶体结构
1.3晶面和晶向解析

O a1 cosa1 , n : cosa2 , n : cosa3 , n h1 : h2 : h3
晶面的法线与三个基矢的夹角余弦之比等于三个整数之比。
1 1 1 又 cos a1 , n : cos a2 , n : cos a3 , n : : r s t
AD的晶列指数为: [212] 注意:
1 OD i j , 2
C D
a
O
B
(1)晶列指数一定是一组互质的整数; 晶列(11-1) (2)晶列指数用方括号表示[ ]; 晶列[11-1] 晶列(111) 晶列[111]
(3)遇到负数在该数上方加一横线。
(4)等效晶向。
在立方体中有,沿立方边的 晶列一共有6个不同的晶向,由于 晶格的对称性,这6个晶向并没有 什么区别,晶体在这些方向上的 性质是完全相同的,统称这些方
如图取一格点为顶点,原胞的三 个基矢 a1 , a 2 , a 3 为坐标系的三个轴, A3
设某一晶面与三个坐标轴分别交于
A1,A2,A3,设晶面的法线ON交晶面 A1A2A3于N,ON长度为d,d为该晶 面族相邻晶面间的距离,为整数, 该晶面法线方向的单位矢量用 示,则晶面A1A2A3的方程为:
l1 1, l2 2, l3 1
[ l1 , l2 , l3]晶列上格点的周期= ?
(2)以布拉维原胞基矢表示
如果从晶列上一个格点沿晶向到任一格点的位矢为
R m a nb p c
a , b , c 为布拉维原胞基矢
E
其中 m , n , p 为有理数,将 m , n , p化为互质的整数 m,n,p, 记为[mnp],[mnp]即为该晶列的晶列指数.
h1 : h2 : h3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
称为晶面,描写晶面方位的一组数称为晶面指数。
(1)平行的晶面组成晶面族,晶面族包含所有格点; (2)晶面上格点分布具有周期性; (3)同一晶面族中的每一晶面上,格点分布(情况)相同; (4)同一晶面族中相邻晶面间距相等。
同一个格子,两组不同的晶面族
2.晶面指数
晶面方位
晶面的法线方向(法线方向与三个坐标轴夹角) 晶面在三个坐标轴上的截距
C EB
cD
b aF GA
密勒指数是(210) 的晶面是ABCD面;
密勒指数是 (121) 的晶面是EFG面;
§1.4 倒格子 —— 晶格具有周期性,一些物理量具有周期性 势能函数 势能函数是以
为周期的三维周期函数
1.4.1倒格与傅里叶变换
在任意两个原胞的相对应点上,晶体的物理性质相同。
r Rl r
可以证明:r,s,t必是一组有理数---阿羽依的有理数定理。
设a1,a2 ,a3的末端上的格点分别在离原点距离h1d、h2d、
h3d的晶面上,这里 h1、h2、h3为整数 。
(1)所有格点都包容在一族晶面上;因此给定晶面族中必
有一个晶面通过坐标系的原点;在基矢 a1,a2,a3 末端上的格点 也一定落在该晶面族的晶面上;
倒格 倒格基矢 b1,b2 ,b3 倒格(点位)矢:
Rn n1a1 n2 a2 n3 a3
K n h1b1 h2b2 h3b3
1.4.1 倒格定义
倒格基矢定义为:
b1 2π a2 a3 Ω
b2 2π a3 a1 Ω 2π b3 a1 a2
Ω
其中 a1 , a2 , a3 是正格基矢,
(1)基矢a1,a2,a3 被平行的晶面等间距的分割成h1、h2、h3
等份;
(2)以 a1 ,a2 ,a3为各轴的长度单位所求得的晶面在坐标轴
上的截距倒数的互质比;
(3)晶面的法线与基矢夹角的方向余弦的比值。
设
末端上的格点分别落在离原点的距离
的晶面上
—— 整数 —— 晶面间距
—— 最靠近原点的晶面 在坐标轴上的截距
§1.3 晶向、晶面和它们的标志
1.3.1 晶向及晶向指数
1.晶向 通过晶格中任意两个格点 连一条直线称为晶列,晶列的 取向称为晶向,描写晶向的一 组数称为晶向指数(或晶列指数 )。 过一格点可以有无数晶列。
(1)平行晶列组成晶列族,晶列 族包含所有的格点;
(2)晶列上格点分布是周期性的; (3)晶列族中的每一晶列上, 格点分布都是相同的;
取a1 ,a2 ,a3为天然长度单位得:
O a1
A1
cosa1 , n : cosa2 , n : cosa3 , n h1 : h2 : h3
晶面的法线与三个基矢的夹角余弦之比等于三个整数之比。
又
cosa1 , n :
cosa2 , n :
cosa3 , n
1 r
:
1 s
:
1 t
h1
: h2
: h3
记为[ l1l2l3], [l1l2l3 ]即为该晶列的晶列指数。
如遇到负数,将该数的上面加一横线。
如[121]表示 l1 1, l2 2, l3 1
(2)以布拉维原胞基矢表示
如果从晶列上一个格点沿晶向到任一格点的位矢为
R ma nb p c a ,b ,c 为布拉维原胞基矢
其中 m,n, p 为有理数,将 m,n, p化为互质的整数 m,n,p,
1 r
:
1 s
:1 t
h1
: h2
: h3
1 : 1 :1 r st
因为h1、h2、h3为整数,所以r、s、t必为有理数。
任一晶面在坐标轴上的截距r,s,t必是一组有理数。
可以证明h1,h2,h3一定是互质的,称它们为该晶面族的 面指数,记为(h1h2h3 ) 。
综上所述,晶面指数(h1h2h3 )表示的意义是;
晶列一共有6个不同的晶向,由于
晶格的对称性,这6个晶向并没有[100]
什么区别,晶体在这些方向上的
[001] [010] [100]
性质是完全相同的,统称这些方 向为等效晶向,写成<100>。
[010] [001]
1.3.2 晶面及密勒指数
1.晶面
在晶格中,通过任意三个不在同一直线上的格点作一平面,
Ωa1
Ω*
2π 3
a2
a3
Ω
Ω
a1
2π3
Ω
4.倒格矢 K h h1b1 h2 b2 h3 b3 与正格中晶面族(h1h2h3)
正交,且其长度为 2π 。
d h1h2h3
(1)证明 K h h1b1 h2 b2 h3 b3 与晶面族(h1h2h3)正交。
设ABC为晶面族(h1h2h3)中离原点最近的晶面,
(2)同一晶面族中的晶面平行且相邻晶面间距相等,故在原
点与基矢的末端间一定只有整数个晶面。
a1 n h1d a2 n h2d
a1 cos a1,n h1d a2 cos a2,n h2d
X n d
A3
Nn
a3 n h3d
a3 cos a3,n h3d a 3 d
a2
A2
—— 同族中其它晶面的截距是
的整数倍
的倒数是晶面族中最靠近原点的晶面的截距
晶面指数 —— 标记这个晶面系
以布拉维原胞基矢 a, b,c 为坐
标轴来表示的晶面指数称为密勒
指数,用(hkl)表示。
立方晶格的几种主要晶面标记
例2:如图所示 abc ,I和H
分别为BC,EF之中点,试求晶面
AEG,ABCD,OEFG,DIHG的密
(4)在同一平面内,相邻晶列间的 距离相等。
晶列的特点
2.晶向指数
(1) 用固体物理学原胞基矢表示
如果从晶列上一个格点沿晶向到任一格点的位矢为
R l1a1 l2 a2 l3 a3 a1,a 2 ,a 3 为固体物理学原胞基矢
其中
l1,
l
2
,
l
3
为整数,将
l1,
l
2
,
l
3
化为互质的整数
l1 , l2 , l3 ,
记为[mnp],[mnp]即为该晶列的晶列指数.
例1:如图在立方体中,a i,b j,c k
E
D是BC的中点,求BE,AD的晶列指数。 A
解: OB i , OE i j k,
BE OE OB j k
晶列BE的晶列指数为:[011]
c
b
Oa
C
D B
求AD的晶列指数。
E
OA k , OD i 1 j , 2
2π
a1 b2 a1 2π a3 a1 Ω
0
2. Rl K h 2π (为整数)
其中Rl和K h分别为正格点位矢和倒格点位矢。
Rl l1 a1 l2 a 2 l3 a 3 K h h1 b1 h2 b2 h3 b3
Rl K h (l1 a1 l2 a 2 l3 a 3 ) (h1 b1 h2 b2 h3 b3 ) 2π( l1h1 l2h2 l3h3 )
a2
a1
b1
a2 a3 2π
2π
Ω
d1
b2 2π d2
b1
2π b3
d3
一个倒格基矢是和正格原胞中一组晶面相对应的,它的方
向是该晶面的法线方向,它的大小则为该晶面族面间距倒数的
2倍。
1.4.2 倒格与正格的关系
1. ai b j 2π ij 2π ( i j )
0 i j
a1 b1 a1 2π a 2 a 3 Ω
1 1:1: 1 21 (120)
AEG 的密勒指数是(111); OEFG的密勒指数是(001); DIHG的密勒指数是(120)。
D
C
A
BI
c bG
Oa
F
EH
例3: 在立方晶系中画出(210)、 Nhomakorabea121) 晶面。
晶面在三个坐标轴上的截距分别为:
a (210) 1
2
bc 1
(121) 1
1
1
2
Rl 是正格矢。
上式两边分别按傅里叶级数展开:
r (K h) eiKhr
h
r Rl
K ei K h rRl h
h
K h Rl 2π
K h 一定是倒格矢。
§1.4 倒格
晶体结构=晶格+基元
一个晶体结构有两个格子,一个是正格,另一个为倒格。
正格 正格基矢 a1 , a 2 , a 3 正格(点位)矢:
Ω a1 a2 a3
是固体物理学原胞体积
与 K n h1b1 h2b2 h3b3 (h1, h2, h3为整数)所联系的各点
的列阵即为倒格。
倒格基矢的方向和长度如何呢?
b1 2π a2 a3 Ω
b2 2π a3 a1 Ω
b3 2π a1 a2 Ω
b3 ab3 2
ABC在基矢
a1,a2,a3上的 截距分别为
a1 , a2 , a3 。
h1 h2 h3
a3
由图可知: CA OA OC a1 a3 h1 h3
C
Kh
CB OB OC a2 a3
h2 h3 O
a2 B
A a1
K
h
CA
(h1b1
h2 b2
h3 b3 )
a1 h1
a2 h2
0
Kh
倒格 基矢
倒格
b1 2π a2 a3 Ω
b2 2π a3 a1 Ω
b3 2π a1 a2 Ω
a1 ,a2 ,a3 b1 ,b2 ,b3
2π ( i j )
