R语言实验
RStudioR语言与统计分析实验报告

RStudioR语言与统计分析实验报告1. 实验目的本实验旨在介绍RStudio软件和R语言在统计分析中的应用。
通过本实验,可以了解RStudio的基本功能和操作,掌握R语言的基本语法和常用函数,并在实际数据分析中应用所学知识。
2. 实验环境与工具本实验使用RStudio软件进行实验操作。
RStudio是一个集成开发环境(IDE),专门用于R语言编程和统计分析。
它提供了代码编辑器、调试器、数据可视化工具等一系列功能,便于用户进行数据处理和分析。
3. 实验步骤本实验分为以下几个步骤:3.1 安装R和RStudio在开始实验之前,需要先安装R语言和RStudio软件。
R语言是一种统计分析和数据挖掘的编程语言,而RStudio是R语言的集成开发环境。
3.2 RStudio界面介绍在打开RStudio后,可以看到主要分为四个区域:代码编辑器、控制台、环境和帮助。
代码编辑器用于编写R语言代码,控制台用于执行和查看代码运行结果,环境用于查看和管理数据对象,帮助用于查阅R语言文档和函数说明。
3.3 R语言基础研究R语言的基本语法和常用函数是使用RStudio进行统计分析的基础。
实验中将介绍R语言的数据类型、赋值操作、条件语句、循环语句等基本概念,并演示常用函数的使用方法。
3.4 实际数据分析应用通过实际数据分析案例,将R语言和RStudio运用到实际问题中。
根据给定的数据,使用R语言进行数据处理、探索性分析和统计模型建立,并通过可视化工具展示分析结果。
4. 实验总结通过完成本实验,我们了解了RStudio软件和R语言在统计分析中的应用。
掌握了RStudio的基本功能和操作,熟悉了R语言的基本语法和常用函数。
通过实际数据分析案例的应用,提高了数据处理和统计分析能力。
5. 参考资料。
R语言实验报告
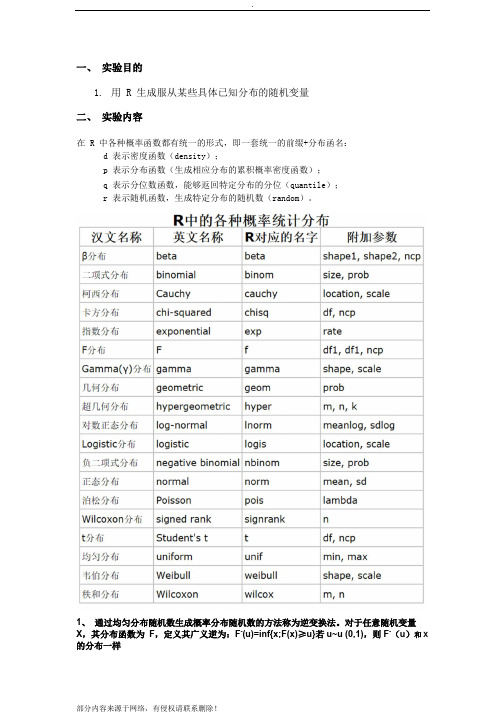
一、实验目的1.用 R 生成服从某些具体已知分布的随机变量二、实验内容在 R 中各种概率函数都有统一的形式,即一套统一的前缀+分布函名:d 表示密度函数(density);p 表示分布函数(生成相应分布的累积概率密度函数);q 表示分位数函数,能够返回特定分布的分位(quantile);r 表示随机函数,生成特定分布的随机数(random)。
1、通过均匀分布随机数生成概率分布随机数的方法称为逆变换法。
对于任意随机变量X,其分布函数为F,定义其广义逆为:F-(u)=inf{x;F(x)≥u}若u~u (0,1),则F-(u)和X 的分布一样Example 1 如果X~Exp(1)(服从参数为 1 的指数分布),F(x)=1-e-x。
若u=1-e-x并且u~u(0,1),则X=-logU~Exp(1)则可以解出x=-log(1-u)通过随机数生成产生的分布与本身的指数分布结果相一致R 代码如下:nsim = 10^4U = runif(nsim)X = -log(U)Y = rexp(nsim)X11(h=3.5)Xpar(mfrow=c(1,2),mar=c(2,2,2,2))hist(X,freq=F,main="Exp from Uniform",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)hist(Y,freq=F,main="Exp from R",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)2、某些随机变量可由指数分布生成。
R语言实验

精心整理实验8假设检验(二)一、实验目的:1.掌握若干重要的非参数检验方法( 2检验——列联表独立性检验,Mcnemar检验——对一个样本两种研究方法是否有差异的检验,符号检验,Wilcoxon 符号秩检验,Wilcoxon秩和检验);2.掌握另外两个相关检验:Spearman秩相关检验,Kendall秩相关检验。
二、实验内容:练习:要求:①完成练习并粘贴运行截图到文档相应位置(截图方法见下),并将所有自己输入文字的字体颜色设为红色(包括后面的思考及小结),②回答思考题,③简要书写实验小结。
④修改本文档名为“本人完整学号姓名1”,其中1表示第1次实验,以后更改为2,3,...。
如文件名为“09张立1”,表示学号为09的张立同学的第1次实验,注意文件名中没有空格及任何其它字符。
最后连同数据文件、源程序文件等(如果有的话,本次实验没有),一起压缩打包发给课代表,压缩包的文件名同上。
截图方法:法1:调整需要截图的窗口至合适的大小,并使该窗口为当前激活窗口(即该窗口在屏幕最前方),按住键盘Alt键(空格键两侧各有一个)不放,再按键盘右上角的截图键(通常印有“印屏幕”或“PrScrn”等字符),即完成截图。
再粘贴到word文档的相应位置即可。
法2:利用QQ输入法的截屏工具。
点击QQ输入法工具条最右边的“扳手”图标,选择其中的“截屏”工具。
)1.自行完成教材第五章的例题。
2.(习题5.11)为研究分娩过程中使用胎儿电子监测仪对剖腹产率有无影响,对5824例分娩的经产妇进行回顾性调查,结果如下表所示,试进行分析。
5824例经产妇回顾性调查结果HHP=9.552e-10<0.05,拒绝原假设,分娩过程中使用胎儿电子监测仪对剖腹产率有影响3.(习题5.12)在高中一年级男生中抽取300名考察其两个属性:B是1500米长跑,C是每天平均锻炼时间,得到4×3列联表,如下表所示。
试对 =0.05,检验B 与C是否独立。
R语言实验一之R基础

18GDPU 课程管理统计学学院专业信息管理与信息系统姓名学号日期2020.03.05实验项目实验一实验1 R基础(一)一、实验目的:1.熟悉实验报告书的书写要求;2.熟悉R的界面及基本操作。
二、实验内容:1.熟悉R官方网站及下载安装方法;2.熟悉R的界面及菜单功能;3.掌握R的简单操作;4.利用R 软件进行一些简单的数学运算。
练习:要求:①完成练习,将所有自己输入文字的颜色设为红色(包括后面的思考及实验小结),将运行结果的截图粘贴到题目相应位置;②回答思考题;③简要书写实验小结。
④修改本文档名为“本人完整学号姓名1”,其中1表示第1次实验,以后更改为2,3,...。
如文件名为“1305543109张立1”,表示学号为1305543109的张立同学的第1次实验,注意文件名中没有空格及任何其它无关字符。
完成后发给课代表,课代表汇总全班同学作业后压缩打包发给我。
两种简单方便的截图方法:法1:利用QQ输入法的截屏工具。
点击QQ输入法工具条最右边的“扳手”图标,选择其中的“截屏”工具。
)法2:在“开始”菜单中的搜索栏中输入“截图”,打开Windows系统自带的“截图工具”。
1.访问R的官方网站,了解网站基本框架和内容:/。
2.在镜像网站CRAN下载最新版R安装程序。
选择离自己最近的国内的镜像网站,点击进入其中一个镜像网站后,下载最新版的Windows下的安装程序。
3.安装R程序(如果实验电脑已经安装,则可跳过此步骤)。
双击R-3.6.2-win.exe(目前最新版)开始安装。
一直点击下一步,各选项默认。
4.在R中进行简单的计算。
实验基本原理与方法:(1)R 的基本界面是一个交互式命令窗口,命令提示符是一个大于号“>”,命令的结果马上显示在命令下面。
(2)R 命令主要有两种形式:表达式或赋值运算(用“<-”表示)。
在命令提示符后键入一个表达式表示计算此表达式并显示结果。
赋值运算把赋值号右边的值计算出来赋给左边的变量。
r语言编程实验报告总结

r语言编程实验报告总结
本次实验主要是对R语言编程的学习和掌握进行实践操作,通过实验了解R语言的基本语法和数据结构,掌握R语言的编程方法和数据分析技巧。
在实验中,我们学习了R语言的基础知识,如基本数据类型、变量、运算符、数据结构等。
同时,我们也学习了R语言的控制结构,如条件语句、循环语句等,这些控制结构可以帮助我们更好地控制程序的执行。
除此之外,我们还学习了R语言的函数和包的使用,在实验中我们使用了一些常用的包,如ggplot2包和dplyr包,这些包可以帮助我们更加方便地进行数据分析和绘图。
同时,我们也学习了如何自己编写函数,并且熟练掌握了函数的调用和参数传递。
通过实验,我们还学习了如何进行数据处理和数据分析,包括数据的读取和写入、数据的清洗和转换、数据的统计分析和可视化等等。
我们使用R语言对一些真实数据进行了处理和分析,这些数据包括房价、气温、人口等等。
在实验中,我们遇到了一些问题,如代码错误、数据异常等等,但是通过对问题的分析和解决,我们不断提升了自己的编程能力和数据分析技能。
综上所述,通过本次实验,我们深入了解了R语言的编程方法和数据分析技巧,掌握了一些常用的包和函数,并且在实践中熟悉了数据处理和分析的整个过程,这对我们今后的学习和工作都具有重要的
意义。
R语言实验报告.

一、试验目的R是用于统计分析、绘图的语言和操作环境。
R是属于GNU系统的一个自由、免费、源代码开放的软件,它是一个用于统计计算和统计制图的优秀工具。
本次试验要求掌握了解R语言的各项功能和函数,能够通过完成试验内容对R语言有一定的了解,会运用软件对数据进行分析。
二、试验环境Windows系统,RGui(32-bit)三、试验内容模拟产生电商专业学生名单(学号区分),记录高数、英语、网站开发三科成绩,然后进行统计分析。
假设有的100 名学生,起始学号为210222001,各科成绩取整,高数成绩为均匀分布随机数,都在75分以上。
英语成绩为正态分布,平均成绩80,标准差为7。
网站开发成绩为正态分布,平均成绩83,标准差为18。
把正态分布中超过100分的成绩变成100分。
1 把上述信息组合成数据框,并写到文本文件中;2计算各种指标:平均分,每个人的总分,最高分,最低分,(使用apply 函数)3求总分最高的同学的学号4绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图(要求指定颜色和缺口)5画星相图,解释其含义6画脸谱图,解释其含义,7画茎叶图、qq图四、试验实现(一)按要求随机生成学号,和对于的高数、英语、网站开发三科成绩。
A、生成学号B、生成高数成绩高数成绩要求:高数成绩为均匀分布随机数,都在75分以上均匀分布函数:runif(n,min=0,max=1)其中,n 为产生随机值个数(长度),min为最小值,max为最大值。
C、生成英语成绩英语成绩要求:正态分布,平均成绩80,标准差为7正态分布函数:rnorm(n, mean = 0, sd = 1)其中,n 为产生随机值个数(长度),mean 是平均数,sd 是标准差。
D、生成网站开发成绩网站开发成绩要求:网站开发成绩为正态分布,平均成绩83,标准差为18。
其中大于100的都记为100。
(二)把上述信息组合成数据框,并写到文本文件中; 计算各种指标:平均分,每个人的总分,最高分,最低分,(使用apply 函数)A、生成文本文件B、打开数据框C、在数据框中命名变量D、计算各种指标:平均分,每个人的总分,最高分,最低分平均分(x4):总分(x5):最低分(x6):最高分(x7):(三)将生成成绩写入文本文件中(四)求总分最高的同学的学号(五)绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图(要求指定颜色和缺口)直方图散点图柱状图饼图箱尾图(要求指定颜色和缺口)(六)画星相图,解释其含义(七)画脸谱图,解释其含义(八)画茎叶图(九)qq图五、试验总结这次试验是我第一次接触R语言,刚开始遇到了很多困难,对于R语言一窍不通,后来经过老师的悉心指导,以及自己积极的去查找资料,对R语言有了进一步的了解。
R语言实验报告范文

R语言实验报告范文实验报告:基于R语言的数据分析摘要:本实验基于R语言进行数据分析,主要从数据类型、数据预处理、数据可视化以及数据分析四个方面进行了详细的探索和实践。
实验结果表明,R语言作为一种强大的数据分析工具,在数据处理和可视化方面具有较高的效率和灵活性。
一、引言数据分析在现代科学研究和商业决策中扮演着重要角色。
随着大数据时代的到来,数据分析的方法和工具也得到了极大发展。
R语言作为一种开源的数据分析工具,被广泛应用于数据科学领域。
本实验旨在通过使用R语言进行数据分析,展示R语言在数据处理和可视化方面的应用能力。
二、材料与方法1.数据集:本实验使用了一个包含学生身高、体重、年龄和成绩的数据集。
2.R语言版本:R语言版本为3.6.1三、结果与讨论1.数据类型处理在数据分析中,需要对数据进行适当的处理和转换。
R语言提供了丰富的数据类型和操作函数。
在本实验中,我们使用了R语言中的函数将数据从字符型转换为数值型,并进行了缺失值处理。
同时,我们还进行了数据类型的检查和转换。
2.数据预处理数据预处理是数据分析中的重要一步。
在本实验中,我们使用R语言中的函数处理了异常值、重复值和离群值。
通过计算均值、中位数和四分位数,我们对数据进行了描述性统计,并进行了异常值和离群值的检测和处理。
3.数据可视化数据可视化是数据分析的重要手段之一、R语言提供了丰富的绘图函数和包,可以用于生成各种类型的图表。
在本实验中,我们使用了ggplot2包绘制了散点图、直方图和箱线图等图表。
这些图表直观地展示了数据的分布情况和特点。
4.数据分析数据分析是数据分析的核心环节。
在本实验中,我们使用R语言中的函数进行了相关性分析和回归分析。
通过计算相关系数和回归系数,我们探索了数据之间的关系,并对学生成绩进行了预测。
四、结论本实验通过使用R语言进行数据分析,展示了R语言在数据处理和可视化方面的强大能力。
通过将数据从字符型转换为数值型、处理异常值和离群值,我们获取了可靠的数据集。
r语言实验报告

r语言实验报告R语言实验报告引言R语言是一种广泛应用于数据分析和统计建模的开源编程语言,具有丰富的包和函数库,适用于各种数据处理和可视化任务。
本实验旨在探讨R语言在数据处理和可视化方面的应用,通过实际案例展示其强大的功能和灵活性。
数据导入与处理我们需要导入数据集,并进行初步的处理。
在R语言中,可以使用read.csv()函数导入csv格式的数据文件,然后通过head()函数查看数据的前几行,以了解数据结构和内容。
接下来,可以使用subset()函数筛选出需要的数据列,并使用na.omit()函数删除缺失值,确保数据的完整性和准确性。
数据可视化数据可视化是数据分析的重要环节,可以帮助我们更直观地理解数据的分布和关系。
在R语言中,可以使用ggplot2包来绘制各种类型的图表,如散点图、折线图和直方图等。
通过设置不同的参数和颜色,可以定制化图表的样式,使其更具有美感和可读性。
统计分析除了数据可视化,R语言还提供了丰富的统计分析函数,可以帮助我们进行各种统计推断和建模分析。
例如,可以使用lm()函数进行线性回归分析,通过summary()函数查看回归模型的拟合效果和显著性检验结果。
此外,还可以使用t.test()函数进行假设检验,判断样本均值之间是否存在显著差异。
结果解释与总结我们需要对分析结果进行解释和总结。
在解释结果时,应该清晰地说明分析方法和推断过程,避免歧义和误导。
在总结部分,可以简要概括分析的主要发现和结论,指出数据分析对问题的解决和决策的重要性和价值。
结论通过本实验,我们深入探讨了R语言在数据处理和可视化方面的应用,展示了其强大的功能和灵活性。
R语言不仅可以帮助我们高效地处理和分析数据,还可以帮助我们更好地理解数据的特征和规律。
希望本实验可以帮助读者更好地掌握R语言的应用技巧,提升数据分析和统计建模的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验8 假设检验(二)一、实验目的:1.掌握若干重要的非参数检验方法( 2检验——列联表独立性检验,Mcnemar检验——对一个样本两种研究方法是否有差异的检验,符号检验,Wilcoxon符号秩检验,Wilcoxon秩和检验);2.掌握另外两个相关检验:Spearman秩相关检验,Kendall秩相关检验。
二、实验内容:练习:要求:①完成练习并粘贴运行截图到文档相应位置(截图方法见下),并将所有自己输入文字的字体颜色设为红色(包括后面的思考及小结),②回答思考题,③简要书写实验小结。
④修改本文档名为“本人完整学号姓名1”,其中1表示第1次实验,以后更改为2,3,...。
如文件名为“1305543109张立1”,表示学号为1305543109的张立同学的第1次实验,注意文件名中没有空格及任何其它字符。
最后连同数据文件、源程序文件等(如果有的话,本次实验没有),一起压缩打包发给课代表,压缩包的文件名同上。
截图方法:法1:调整需要截图的窗口至合适的大小,并使该窗口为当前激活窗口(即该窗口在屏幕最前方),按住键盘Alt键(空格键两侧各有一个)不放,再按键盘右上角的截图键(通常印有“印屏幕”或“Pr Scrn”等字符),即完成截图。
再粘贴到word文档的相应位置即可。
法2:利用QQ输入法的截屏工具。
点击QQ输入法工具条最右边的“扳手”图标,选择其中的“截屏”工具。
)1.自行完成教材第五章的例题。
2.(习题5.11)为研究分娩过程中使用胎儿电子监测仪对剖腹产率有无影响,对5824例分娩的经产妇进行回顾性调查,结果如下表所示,试进行分析。
剖腹产胎儿电子监测仪合计使用未使用是358 229 587否2492 2745 5237合计2850 2974 5824解:提出假设:H0:分娩过程中使用胎儿电子监测仪对剖腹产率无影响H1:分娩过程中使用胎儿电子监测仪对剖腹产率有影响源代码及运行结果:(复制到此处,不需要截图)> x<-c(358,2492,229,2745)> dim(x)<-c(2,2)> chisq.test(x)Pearson's Chi-squared test with Yates' continuity correctiondata: xX-squared = 37.414, df = 1, p-value = 9.552e-10结论:P= 9.552e-10<0.05,拒绝原假设,分娩过程中使用胎儿电子监测仪对剖腹产率有影响3.(习题5.12)在高中一年级男生中抽取300名考察其两个属性:B是1500米长跑,C是每天平均锻炼时间,得到4 ×3列联表,如下表所示。
试对 = 0.05,检验B与C 是否独立。
解:提出假设:H0:B与C独立。
H1:B与C不独立。
源代码及运行结果:(复制到此处,不需要截图)> x<-c(45,46,28,11,12,20,23,12,10,28,30,35)> dim(x)<-c(4,3)> chisq.test(x)Pearson's Chi-squared testdata: xX-squared = 40.401, df = 6, p-value = 3.799e-07结论:P=3.799e-07<0.05,拒绝原假设,B与C不独立,有关系。
4.(习题5.13)为比较两种工艺对产品的质量是否有影响,对其产品进行抽样检查,其结果如下表所示。
试进行分析。
两种工艺下产品质量的抽查结果解:提出假设:H0:两种工艺对产品的质量没影响H1:两种工艺对产品的质量有影响源代码及运行结果:(复制到此处,不需要截图)> x<-c(3,6,4,4)> dim(x)<-c(2,2)> fisher.test(x)Fisher's Exact Test for Count Datadata: xp-value = 0.6372alternative hypothesis: true odds ratio is not equal to 195 percent confidence interval:0.04624382 5.13272210sample estimates:odds ratio0.521271结论:P=0.6372>0.05,接受原假设,两种工艺对产品的质量没影响5.(习题5.14)应用核素法和对比法检测147例冠心病患者心脏收缩运动的符合情况,其结果如下表所示。
试分析这两种方法测定结果是否相同。
两法检查室壁收缩运动的符合情况解:提出假设:H0:这两种方法测定结果不相同H1:这两种方法测定结果相同源代码及运行结果:(复制到此处,不需要截图)> x<-c(58,1,8,2,42,9,3,7,17)> dim(x)<-c(3,3)> mcnemar.test(x)McNemar's Chi-squared testdata: xMcNemar's chi-squared = 2.8561, df = 3, p-value = 0.4144结论:P=0.4144>0.05,因此,不能认为这两种方法测定结果不相同6.(习题5.15)在某养鱼塘中,根据过去经验,鱼的长度的中位数为14.6cm,现对鱼塘中鱼的长度进行一次估测,随机地从鱼塘中取出10条鱼长度如下:13.32 13.06 14.02 11.86 13.58 13.77 13.51 14.42 14.44 15.43将它们作为一个样本进行检验。
试分析,该鱼塘中鱼的长度是在中位数之上,还是在中位数之下。
(1)用符号检验分析;(2)用Wilcoxon符号秩检验分析。
解:(1)用符号检验分析提出假设:H0:M>=14.6H1:M<14.6源代码及运行结果:(复制到此处,不需要截图)> x<-c(13.32 , 13.06 , 14.02 , 11.86 , 13.58 , 13.77 , 13.51 , 14.42 , 14.44 , 15.43)> binom.test(sum(x>14.6),length(x),al="l")Exact binomial testdata: sum(x > 14.6) and length(x)number of successes = 1, number of trials = 10, p-value = 0.01074alternative hypothesis: true probability of success is less than 0.595 percent confidence interval:0.0000000 0.3941633sample estimates:probability of success0.1(2)用Wilcoxon符号秩检验分析提出假设:H0:M>=14.6H1:M<14.6源代码及运行结果:(复制到此处,不需要截图)x<-c(13.32 , 13.06 , 14.02 , 11.86 , 13.58 , 13.77 , 13.51 , 14.42 , 14.44 , 15.43)> wilcox.test(x,mu=14.6,al="l",exact=F)Wilcoxon signed rank test with continuity correctiondata: xV = 4.5, p-value = 0.01087alternative hypothesis: true location is less than 14.6结论:两种方法的P都是小于0.05,拒绝原假设,中位数小于14.67.(习题5.16)用两种不同的测定方法,测定同一种中草药的有效成分,共重复20次,得到实验结果如下表所示。
(2)试用Wilcoxon符号秩检验法检验两测定有无显著差异;(3)试用Wilcoxon秩和检验法检验两测定有无显著差异;(4)对数据作正态性和方差齐性检验,该数据是否能作t检验,如果能,请作t检验;(5)分析各种的检验方法,试说明哪种检验法效果最好。
解:(1)符号检验法提出假设:H0:两测定无显著差异H1:两测定有显著差异源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,20.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> binom.test(sum(x>y),length(x))Exact binomial testdata: sum(x > y) and length(x)number of successes = 14, number of trials = 20, p-value = 0.1153alternative hypothesis: true probability of success is not equal to 0.595 percent confidence interval:0.4572108 0.8810684sample estimates:probability of success0.7结论:P=0.1153>0.05,接受原假设,两测定无显著差异(2)Wilcoxon符号秩检验法提出假设:H0:两测定无显著差异H1:两测定有显著差异源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,2 0.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> wilcox.test(x,y,paired=T,exact=F)Wilcoxon signed rank test with continuity correctiondata: x and yV = 136, p-value = 0.005191alternative hypothesis: true location shift is not equal to 0结论:P= 0.005191<0.05,拒绝原假设,两测定有显著差异(3)Wilcoxon秩和检验法提出假设:H0:两测定无显著差异H1:两测定有显著差异源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,2 0.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> wilcox.test(x,y,exact=F)Wilcoxon rank sum test with continuity correctiondata: x and yW = 274.5, p-value = 0.04524alternative hypothesis: true location shift is not equal to 0结论:P=0.04524<0.05,拒绝原假设,两测定有显著差异(4)两独立样本t检验,要求判断独立性、正态性和方差齐性①正态性检验提出假设:H0:两组数据服从正态分布H1:两组数据不服从正态分布源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,2 0.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> ks.test(x,pnorm,mean(x),sd(x))One-sample Kolmogorov-Smirnov testdata: xD = 0.14067, p-value = 0.8235alternative hypothesis: two-sidedWarning message:In ks.test(x, pnorm, mean(x), sd(x)) :Kolmogorov - Smirnov检验里不应该有连结> ks.test(y,pnorm,mean(y),sd(y))One-sample Kolmogorov-Smirnov testdata: yD = 0.10142, p-value = 0.973alternative hypothesis: two-sided结论:两组数据P值都大于0.05,接受原假设,两组数据服从正态分布②方差齐性检验提出假设:H0:两组数据方差相同H1:两组数据方差不相同源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,2 0.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> var.test(x,y)F test to compare two variancesdata: x and yF = 1.1406, num df = 19, denom df = 19, p-value = 0.7772alternative hypothesis: true ratio of variances is not equal to 195 percent confidence interval:0.4514788 2.8817689sample estimates:ratio of variances1.140639结论:P=0.7772>0.05,接受原假设,两组数据方差相同③能否作t检验?如果能,请按照前面各题的格式、内容写出作t检验的过程综上,能作t检验提出假设:H0:两测定无显著差异H1:两测定有显著差异源代码及运行结果:(复制到此处,不需要截图)>x<-c(48.0,33.0,37.5,48.0,42.5,40.0,42.0,36.0,11.3,22.0,36.0,27.3,14.2,32.1,52.0,38.0,17.3,20.0,21.0,46.1)>y<-c(37.0,41.0,23.4,17.0,31.5,40.0,31.0,36.0,5.7,11.5,21.0,6.1,26.5,21.3,44.5,28.0,22.6,20.0 ,11.0,22.3)> t.test(x,y,var.equal=T)Two Sample t-testdata: x and yt = 2.2428, df = 38, p-value = 0.03082alternative hypothesis: true difference in means is not equal to 095 percent confidence interval:0.8125529 15.8774471sample estimates:mean of x mean of y33.215 24.870结论:P=0.03082<0.05,拒绝原假设,两测定有显著差异(5)分析各种的检验方法,试说明哪种检验法效果最好。
