灰色关联分析法
(整理)灰色关联度分析法
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。
作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。
因此, 进行科学全面的供应商评价就显得十分必要。
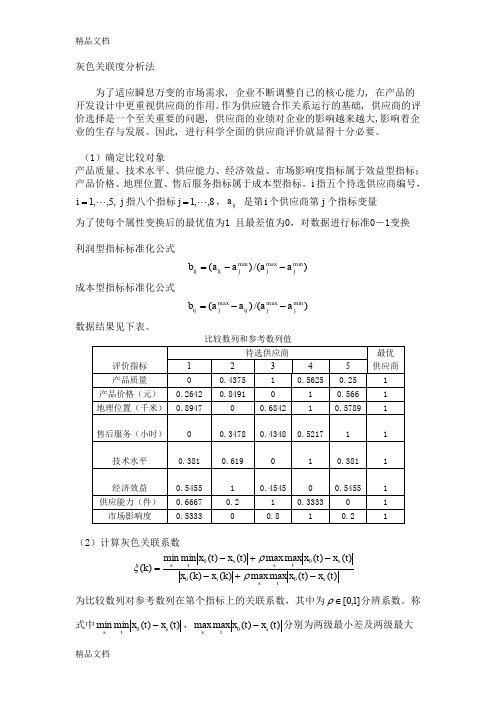
(1)确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标;产品价格、地理位置、售后服务指标属于成本型指标。
i 指五个待选供应商编号,,5,,1 =i j 指八个指标8,,1j =,ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0,对数据进行标准0-1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。
(2)计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数,其中为]1,0[∈ρ分辨系数。
称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。
一般来讲,分辨系数ρ越大,分辨率越大;ρ越小,分辨率越小。
在这里ρ取0.5。
(3)计算灰色加权关联度 灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。
关联系数和关联度值(4)评价分析根据灰色加权关联度的大小,对各评价对象进行排序,可建立评价对象的关联序,关联度越大其评价结果越好。
灰色关联分析法与TOPSIS评价法

与
maxmax x0 (k ) xi (k )
i 1 k 1
n
m
6.计算关联系数 由(12-5)式,分别计算每个比较序列 与参考序列对应元素的关联系数.
i (k )
min min x 0 (k ) xi (k ) max max x0 ( k ) xi ( k )
灰色关联度综合评价法
利用灰色关联分析进行综合评价的步骤 是: 1.根据评价目的确定评价指标体系,收 集评价数据。
2.确定参考数据列 参考数据列应该是一个理想的比较标准, 可以以各指标的最优值 (或最劣值)构 成参考数据列,也可根据评价目的选择 其它参照值.记作
x0 (1) , x0 2 , , x0 m X0
0i (k ) x0 (k ) xi (k )
i 0,1, , n; k 1, 2, ,N
(6.6)
绝对差值阵中最大数和最小数即为最大差和最小 差:
1i n 1 k N
max 0i (k )
1i n 1 k N
(max)
(6.7)
min 0i (k )
同样可计算出表6-4中其余关联系数.
表6-4
年份t 2000 2001 2002 2003 2004 2005
01 (t )
0.4191 0.3796 0.5808 0.7055 0.3696 0.2881
02 (t )
0.6067 0.5178 0.4903 0.8761 0.6141 0.3510
r0i称为序列x0和xi(i=1,2,3)的灰色关联度.由于 r03 r02 r01, 因而第三产业产值与GDP的关 联度最大,其次是第二产业、第一产业. 可以看出,灰色关联分析需要经过以下几个步骤: 1.确定分析序列
灰色关联度分析

1.灰色关联理论
1982年,华中理工大学邓聚龙教 授首先提出灰色系统的概念,并建立了 灰色系统理论。 灰色系统理论认为,人们对客观 事物的认识具有广泛的灰色性,就是信 息的不完全性和不确定性,因而有客观 事物所形成的是一种灰色系统,即部分 信息已知、部分信息未知的系统。例如: 社会系统、经济系统、生态系统等都可 以看作是灰色系统。
\\
(min) (max) 0i (k ) 0i (k ) (max)
最后分别对各产业与GDP的关联系数求 平均可得: r01= (0.4191+0.3796+0.5808+0.7055+0.3696 +0.2881)/6 =0.4571 同样求出: r02=0.5760, r03=0.7209 r0i称为序列x0和xi(i=1,2,3)的灰 色关联。由于r03˃r02˃ r01,因而第三 产业产值与GDP的关联度最大,其次是 第二产业,第一次去农业。
5.用GRA进行综合评价
灰色关联分析的目的是揭示因素间 关系的强弱,其操作对象是因素的时间 序列,最终的结果表现为通过关联度对 各比较序列做出排列。综合评价的对象 也可以看作是时间序列(每个被评价事 物对应的各项指标值),并且往往需要 对这些时间序列做出排序,因而也可以 借助灰色关联分心来进行。
01 (1) 02 (1) ... 0 n (1) (2) (2) ... (2) 01 02 0n ... ... ... 01 ( N ) 02 ( N ) ... 0 n ( N ) N n 其中 0i (k ) x0 (k ) xi (k ) (05式) i 1,2,...n; k 1,2,..., N 绝对差矩阵中最大数和 最小数就是最大差和最 小差: max 0i (k ) (max)( 式) 06
灰色关联分析

灰色关联分析灰色关联分析(Grey Relational Analysis, GRA)什么是灰色关联分析灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度[1]。
灰色系统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory),其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度,来判断因素之间关联程度的方法。
此方法通过对动态过程发展态势的量化分析,完成对系统内时间序列有关统计数据几何关系的比较,求出参考数列与各比较数列之间的灰色关联度。
与参考数列关联度越大的比较数列,其发展方向和速率与参考数列越接近,与参考数列的关系越紧密。
灰色关联分析方法要求样本容量可以少到4个,对数据无规律同样适用,不会出现量化结果与定性分析结果不符的情况。
其基本思想是将评价指标原始观测数进行无量纲化处理,计算关联系数、关联度以及根据关联度的大小对待评指标进行排序。
灰色关联度的应用涉及社会科学和自然科学的各个领域,尤其在社会经济领域,如国民经济各部门投资收益、区域经济优势分析、产业结构调整等方面,都取得较好的应用效果。
[2]关联度有绝对关联度和相对关联度之分,绝对关联度采用初始点零化法进行初值化处理,当分析的因素差异较大时,由于变量间的量纲不一致,往往影响分析,难以得出合理的结果。
而相对关联度用相对量进行分析,计算结果仅与序列相对于初始点的变化速率有关,与各观测数据大小无关,这在一定程度上弥补了绝对关联度的缺陷。
[2]灰色关联分析的步骤[2]灰色关联分析的具体计算步骤如下:第一步:确定分析数列。
确定反映系统行为特征的参考数列和影响系统行为的比较数列。
反映系统行为特征的数据序列,称为参考数列。
影响系统行为的因素组成的数据序列,称比较数列。
设参考数列(又称母序列)为Y={Y(k) | k = 1,2,Λ,n};比较数列(又称子序列)X i={X i(k)| k = 1,2,Λ,n},i = 1,2,Λ,m。
灰色关联分析详解+结果解读

灰色关联分析1、作用对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
因此,灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度。
2、输入输出描述输入:特征序列为至少两项或以上的定量变量,母序列(关联对象)为 1 项定量变量。
输出:反应考核指标与母序列的关联程度。
3、案例示例案例:分析 09-18 年内,影院数量,观影人数,票价、电影上线数量这些因素对全年电影票房的影响。
其中电影票房是母序列,影院数量,观影人数,票价、电影上线数量是特征序列。
4、案例数据灰色关联分析案例数据5、案例操作Step1:新建分析;Step2:上传数据;Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;step4:选择【灰色关联分析】;step5:查看对应的数据数据格式,【灰色关联分析】要求特征序列为定量变量,且至少有一项;要求母序列为定量变量,且只有一项。
step6:设置量纲处理方式(包括初值化、均值化、无处理)、分辨系数(ρ越小,分辨力越大,一般ρ的取值区间为 ( 0 ,1 ),具体取值可视情况而定。
当ρ≤ 0.5463 时,分辨力最好,通常取ρ = 0.5 )step7:点击【开始分析】,完成全部操作。
6、输出结果分析输出结果 1:灰色关联系数图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值(数字越大,代表关联性越强)。
输出结果 2:关联系数图分析:输出结果 1 和输出结果 2 是一样的,输出结果 1 用了表格形式来呈现关联系数,输出结果 2 用了图表形式来呈现关联系数。
图表很直观地展现了,大多数年份的银幕数量和电影上线数量对票房影响更大。
两因素三水平用灰色关联法

灰色关联分析法是一种用于比较多个因素之间关联程度的分析方法,其基本思想是通过比较各因素之间的相似程度来评估它们之间的关联程度。
在两因素三水平的情境下,可以使用灰色关联分析法来比较三个水平之间的关联程度。
具体步骤如下:1.确定参考序列和比较序列。
参考序列是用于比较的基准序列,通常选择一个固定值或者已知的最佳水平作为参考序列。
比较序列是待比较的各个因素在不同水平下的观测值序列。
2.数据预处理。
对参考序列和比较序列进行数据预处理,包括数据清洗、缺失值处理、异常值处理等。
3.计算灰色关联度。
根据灰色关联分析法的原理,计算参考序列与各个比较序列之间的灰色关联度。
灰色关联度的计算公式为:(\gamma(x_0, x_i) = \frac{\min_i |x_0(k) - x_i(k)| + \rho \max_i |x_0(k) -x_i(k)|}{|x_0(k) - x_i(k)| + \rho \max_i |x_0(k) - x_i(k)|})其中,(x_0(k))表示参考序列在时刻k的值,(x_i(k))表示第i个比较序列在时刻k 的值,(\min_i |x_0(k) - x_i(k)|)和(\max_i |x_0(k) - x_i(k)|)分别表示第k时刻所有比较序列与参考序列的差的绝对值的最小值和最大值,(\rho)是一个分辨系数,通常取0.5。
4. 判断关联程度。
根据计算出的灰色关联度,判断各个比较序列与参考序列的关联程度。
灰色关联度越接近于1,表示关联程度越高。
通过以上步骤,可以得出各个水平之间的关联程度,从而为决策提供依据。
需要注意的是,灰色关联分析法只是一种定性的分析方法,其结果具有一定的主观性,因此在具体应用时需要根据实际情况进行合理的解释和判断。
灰色关联分析法原理及解题步骤

灰色关联分析法原理及解题步骤---------------研究两个因素或两个系统的关联度(即两因素变化大小,方向与速度的相对性)关联程度——曲线间几何形状的差别程度灰色关联分析是通过灰色关联度来分析和确定系统因素间的影响程度或因素对系统主行为的贡献测度的一种方法。
灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密1> 曲线越接近,相应序列之间的关联度就越大,反之就越小 2> 灰色关联度越大,两因素变化态势越一致分析法优点它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。
灰色系统关联分析的具体计算步骤如下 1》参考数列和比较数列的确定参考数列——反映系统行为特征的数据序列比较数列——影响系统行为的因素组成的数据序列2》无量纲化处理参考数列和比较数列(1) 初值化——矩阵中的每个数均除以第一个数得到的新矩阵(2) 均值化——矩阵中的每个数均除以用矩阵所有元素的平均值得到的新矩阵(3) 区间相对值化3》求参考数列与比较数列的灰色关联系数ξ(Xi) 参考数列X0比较数列X1、X2、X3……………比较数列相对于参考数列在曲线各点的关联系数ξ(i)称为关联系数,其中ρ称为分辨系数,ρ?(0,1),常取0.5.实数第二级最小差,记为Δmin。
两级最大差,记为Δmax。
为各比较数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值。
记为Δoi(k)。
所以关联系数ξ(Xi)也可简化如下列公式:4》求关联度ri关联系数——比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而信息过于分散不便于进行整体性比较。
因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度ri公式如下:5》排关联序因素间的关联程度,主要是用关联度的大小次序描述,而不仅是关联度的大小。
灰色关联分析法讲解

“非唯一性”
目标非唯一 灰靶思想
目标可约束
目标可接近 信息可扩充 方案可改善 关系可协调 思维可多向 认识可深化 途径可优化
灰色系统理论研究灰元、灰数、灰关系 灰数——指信息不完全的数。
灰关联分析法
(一)什么是灰色系统
灰色系统理论是1982年由邓聚龙创立的一门边缘性学科 (interdisciplinary)
灰色系统用颜色深浅反映信息量的多少。说一个系统是黑色的, 就是说这个系统是黑洞洞的,信息量太少;说一个系统是白色的, 就是说这个系统是清楚的,信息量充足。
这种处于黑白之间的系统,就是灰色系统,或说信息不完全的系 统,成为灰色系统或简称会系统(grey system)。
如“这个人的年龄18岁左右” “今天的气温10 - 15度之间” 灰元——指信息不完全的元素。如“货币”是灰元。
货币的两种功能:流通手段和价值尺度 灰关系——指信息不完全的关系。例:多种经济成份并存、一国两制
换轨思维
例1:小司马光灵机一动,换个角度处置眼前的危急场面。其实, 他砸碎的不完全是一口现实生活中看得见摸得着的缸,同时也打破 了一种旧的思维模式。当我们打破旧思维,再将我们的思路重新组 装的时候,结果一定是一幅好风光。 爱迪生是美国的大发明家。他的一切发明都是和他的思维活跃分不 开的。
例2:一天,爱迪生在实验室里工作,急需知道一个灯泡容量的数 据。由于手头忙不开,他便递给助手一个没有上灯口的玻璃灯泡, 吩咐助手把灯泡的容量数据量出来。过了很久,爱迪生手头的活早 已干完,助手仍未将数据送来。爱迪生只好亲自去找助手,一进门, 就看到助手正忙于计算,桌上演算纸已经推了一大迭。爱迪生忙问: “还需多长时间?”助手说:“一半还没完呢。”爱迪生明白了。 原来,他的助手用软尺测量灯泡的周长、斜度,正在用复杂的公式 计算呢!小伙子还把程序说给爱迪生听,证明自己的思路没错。爱 迪生不等他说完,便拍拍他的肩膀说:“别白忙了,小伙子,瞧我 这么干。”说着,他往灯泡里面注满了水,交给助手:“把这里的 水倒在量杯里,马上告诉我它的容量。”助手听到后,脸马上就红 了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色关联分析法
灰色关联分析法是一种用于研究多个指标之间相关性的统计方法。
它通过计算不同指标之间的关联度来确定它们之间的关系强度。
本文将介绍灰色关联分析法的原理、应用领域以及优点和局限性。
灰色关联分析法最早由中国科学家陈进才于1981年提出,并广泛应用于工程和管理学科领域。
它的核心思想是通过将不同的指标序列转化为灰色级数形式,然后计算各指标之间的关联系数,以揭示它们之间的关系。
灰色关联分析法的基本步骤包括:首先,将各指标序列归一化,使得数据位于相同的量纲范围内;其次,构建灰色级数模型,将指标序列转化为灰色级数;然后,计算各指标之间的关联系数,确定关联度;最后,利用关联度进行综合评价,得出最终的结论。
灰色关联分析法在许多领域具有广泛的应用。
在经济管理领域,它可以用于评估企业绩效、判断市场趋势、研究产业发展等。
在工程领域,它可以用于分析工艺参数对产品质量的影响、评估设备可靠性等。
在环境科学领域,它可以用于评估生态环境质量、分析污染物传输和扩散等。
灰色关联分析法具有一些优点。
首先,它可以对多指标间的关联进行定量分析,较为客观地反映指标之间的关系。
其次,它适用于小样本数据的分析,不依赖于大样本假设。
此外,它对序列变化的敏感性较高,能够较好地发现序列间的规律性或趋势。
然而,灰色关联分析法也存在一些局限性。
首先,它对数据的要求较高,需要有较为完整的时间序列数据。
其次,它假设指标之间的关系是线性的,对非线性关系的分析有一定局限性。
此外,灰色关联分析法对指标权重的确定也有一定的主观性,可能引入一定的误差。
综上所述,灰色关联分析法作为一种多指标关联分析方法,在多个领域得到了广泛应用。
它通过计算不同指标之间的关联程度,为决策提供了科学的依据。
然而,使用灰色关联分析法时需要充分考虑相
关因素,避免误导决策。
未来,随着数据技术的不断发展,灰色关联分析方法也将继续完善和应用于更多的领域中。
