沪教版 九年级数学 暑假同步讲义 第9讲 相似三角形的章节复习(解析版)
沪科九年级数学上相似三角形的判定PPT学习教案

k2 .当且仅当这两个三角形全等时,才有 k=1 =k12.
因此,三角形全等是三角形相似的特例.
第5页/共24页
三.类比猜想
1.两个三角形全等的判定有哪几种方法? 2.是不是需要所有的对应边和对应角都相等? 3.猜想:两个三角形相似是不是也有简便的方法? 简析:1.两个三角形全等的判定方法有:SAS、ASA、SSS、AAS,直角三角形还有HL.
的过程中,培养学生有条理的分析和推理
能力.
第18页/共24页
内容分析
相似三角形的判定是本章的重点内容之 一.本节课是相似三角形的判定的第一课 时, 首先讲述了相似三角形的有关概念,然后 通过探究得出三角形一边的平行线的判定 定理. 三角形一边的平行线的判定定理不仅 可以直接用来证明有关的三角形相似的问 题,而且还是证明其他三个判定定理的主 要依据,所以有时也把它叫做相似三角形 判定定理的预备定理.熟练掌握这一定理对 后面三个定理的证第明19页/至共24页关重要.
沪科九年级数学上相似三角形的判定
会计学
1
一.复习回顾
前面我们学习了相似多边形及相似比的有关概念, 下面请同学们思考以下几个问题:
1.什么样的两个多边形是相似多边形? 2.辨析
(1)四个角分别相等的两个四边形一定相似吗? (2)四组对应边的比分别相等的两个四边形一定相似吗? 3.什么是相似比(相似系数)? 简答:1.两个边数相同的多边形,如果它们的对应角相等,对应边长度
AB BC CA . AB BC CA
第3页/共24页
相似三角形的相似比
将△ABC∽△A′B′C′的相似比记为
△A′B′C′∽△ABC的相似比记为 , 练习 3.已知△ABC∽△DEF,AB=2,DE=3则△ABC与△ DEF的 相似比 和△DEF与△ABC的相似比 是否相等?如果不相等, 和 满足什么关系?如果AB=2,DE=2呢?
最新沪科版九年级相似三角形知识点汇总讲义

相似三角形·基本知识讲义知识点一:放缩与相似1.图形的放大或缩小,称为图形的放缩运动。
2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。
注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。
⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。
⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的.⑷若两个图形形状与大小都相同,这时是相似图形的一种特例——全等形.3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。
注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1. 知识点二:比例线段有关概念及性质(1)有关概念1.比:选用同一长度单位量得两条线段。
a 、b 的长度分别是m 、n ,那么就说这两条线段的比是a :b =m :n (或nm b a =) 2.比的前项,比的后项:两条线段的比a :b 中。
a 叫做比的前项,b 叫做比的后项。
说明:求两条线段的比时,对这两条线段要用同一单位长度。
3.比例:两个比相等的式子叫做比例,如d c b a = 4.比例外项:在比例dc b a =(或a :b =c :d )中a 、d 叫做比例外项。
5.比例内项:在比例dc b a =(或a :b =c :d )中b 、c 叫做比例内项。
6.第四比例项:在比例dc b a =(或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。
7.比例中项:如果比例中两个比例内项相等,即比例为ab b a =(或a:b =b:c 时,我们把b 叫做a 和d 的比例中项。
8.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dc b a =(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)(2)比例性质1.基本性质:bc ad d c b a =⇔= (两外项的积等于两内项积) 2.反比性质: cd a b d c b a =⇒= (把比的前项、后项交换) 3.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d ba dbc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项4.合比性质:d d c b b a d c b a ±=±⇒=(分子加(减)分母,分母不变). 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.5.等比性质:(分子分母分别相加,比值不变.) 如果)0(≠++++====n f d b nm f e d c b a ,那么b a n f d b m e c a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种方法.(2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.知识点三:黄金分割1)定义:在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果AC BC AB AC =即AC 2=AB ×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比。
沪科版九上数学相似三角形知识点总结 (2)

沪科版九上数学图形的相似 知识点总结知识点一1.相似图形:把具有相同形状的图形称为相似图形。
2.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边成比例。
知识点二:比例线段1.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dc b a =(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)2.比例性质的基本性质: bc ad d c b a =⇔= (两外项的积等于两内项积)3.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d b ad b c a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项4.合比性质:dd c b b a d c b a ±=±⇒=(分子加(减)分母,分母不变) 5.等比性质:(分子分母分别相加,比值不变.) 如果)0(≠++++====n f d b n m fe d c b a ,那么ba n f db m ec a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法.(2)应用等比性质时,要考虑到分母是否为零.知识点三:黄金分割1. 定义:在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果AC BC AB AC =,即AC 2=AB×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比。
其中AB AC 215-=≈0.618AB 。
知识点四:相似三角形1.相似三角形:两个三角形中,如果三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。
如△ABC 与△DEF 相似,记作△ABC ∽△DEF 。
专题04 相似三角形的判定(基础)-2020-2021学年九年级数学暑假班精讲专题(沪教版)

专题04 相似三角形的判定(基础)【目标导向】1、了解相似三角形的概念,掌握相似三角形的表示方法及判定方法;2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.【知识点梳理】要点一、相似三角形在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.要点诠释:(1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.要点二、相似三角形的判定定理1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似. 2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.要点诠释:此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点三、相似三角形的常见图形及其变换:【精讲例题】类型一、相似三角形1. 下列能够相似的一组三角形为( ).A.所有的直角三角形B.所有的等腰三角形C.所有的等腰直角三角形D.所有的一边和这边上的高相等的三角形【答案】C【解析】A中只有一组直角相等,其他的角是否对应相等不可知;B中什么条件都不满足;D中只有一条对应边的比相等;C中所有三角形都是由90°、45°、45°角组成的三角形,且对应边的比也相等.答案选C.【总结升华】根据相似三角形的概念,判定三角形是否相似,一定要满足三个角对应相等,三条对应边的比相等.举一反三:【变式】给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有(填序号).【答案】①②④⑤.类型二、相似三角形的判定2. 如图所示,已知中,E为AB延长线上的一点,AB=3BE,DE与BC相交于F,请找出图中各对相似三角形,并求出相应的相似比.【思路点拨】充分利用平行寻找等角,以确定相似三角形的个数.【答案与解析】∵四边形ABCD是平行四边形,∴ AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED.∴△BEF∽△CDF∽△AED.∴当△BEF∽△CDF时,相似比;当△BEF∽△AED时,相似比;当△CDF∽△AED时,相似比.【总结升华】此题考查了相似三角形的判定(有两角对应相等的两三角形相似)与性质(相似三角形的对应边成比例).解题的关键是要仔细识图,灵活应用数形结合思想.举一反三:【变式】如图,AD、CE是△ABC的高,AD和CE相交于点F,求证:AF·FD=CF·FE.【答案】∵ AD、CE是△ABC的高,∴∠AEF=∠CDF=90°, 又∵∠AFE=∠CFE,∴△AEF∽△CDF.∴AF EFCF FD, 即AF·FD=CF·FE.3.(福州)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;(2)求∠ABD的度数.【思路点拨】(1)先求得AD、CD的长,然后再计算出AD2与AC•CD的值,从而可得到AD2与AC•CD的关系;(2)由(1)可得到BD2=AC•CD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.【答案与解析】解:(1)∵AD=BC=1,BC=,∴AD=,DC=1﹣=.∴AD2==,AC•CD=1×=.∴AD2=AC•CD.(2)∵AD=BC,AD2=AC•CD,∴BC2=AC•CD,即.又∵∠C=∠C,∴△BCD∽△ACB.∴,∠DBC=∠A.∴DB=CB=AD.∴∠A=∠ABD,∠C=∠BDC.设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.解得:x=36°.∴∠ABD=36°.【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.4. 已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.【思路点拨】从求证可以判断是运用相似,再根据BP2=PE·PF,可以判定所给的线段不能组成相似三角形,这就需要考虑线段的等量转移了.【答案与解析】连接,,,是的中垂线,,,,.,.又,∽,,.【总结升华】根据求证确定相似三角形,是解决此类题型的捷径. 举一反三:【变式】如图,F 是△ABC 的AC 边上一点,D 为CB 延长线一点,且AF=BD,连接DF,交AB 于E. 求证:DE ACEF BC=.【答案】过点F 作FG ∥BC,交AB 于G.则△DBE ∽△FGE △AGF ∽△ABC∵DE DBEF GF=, 又∵AF=BD,∴.DE AFEF GF= ∵△AGF ∽△ABC∴AF ACGF BC =, 即DE ACEF BC=.【精练巩固】一、选择题1. 下列判断中正确的是( ).A.全等三角形不一定是相似三角形B.不全等的三角形一定不是相似三角形C.不相似的三角形一定不全等D.相似三角形一定不是全等三角形 2.已知△ABC 的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC 与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ).A. B. C. D.3.(大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.4. (盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有()A.0个B.1个C.2个D.3个5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有().A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF 6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ).A. B.8 C.10 D.16二、填空题7.(上海闵行一模)如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.三.解答题13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.15.如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G 点,(1)求证:AC2=CE•CF;(2)若∠B=38°,求∠CFD的度数.【精练答案与解析】一.选择题1.【答案】C.2.【答案】A.【解析】根据三边对应成比例,可以确定3==226第三边,所以第三边是3.【答案】B.【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、只有选项B的各边为1、、与它的各边对应成比例.故选B.4.【答案】C.【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AB∥DC,∴△AEF∽△CBF,△AEF∽△DEC,∴与△AEF相似的三角形有2个.5.【答案】C.【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°,即∠1=∠3,∴△ADE∽△ECF.6.【答案】C.【解析】∵ EF∥AB,∴,∵,∴,,∴ CD=10,故选C.二. 填空题7.【答案】AB∥DE.【解析】∵∠A=∠D,∴当∠B=∠DEF时,△ABC∽△DEF,∵AB∥DE时,∠B=∠DEF,∴添加AB∥DE时,使△ABC∽△DEF.8.【答案】 3 .【解析】∵∠C=∠E,∠CAB=∠EAD,∴△ACB∽△AED,∴,BC=4,在Rt△ABC中,.9.【答案】;.10.【答案】4.【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,∴∠BCA=∠E,∴△ABC∽△CDE.∵C是线段BD的中点,ED=1,BD=4∴BC=CD=2∴AB CDCD DE,即AB=4.11.【答案】△OAB,△OCD.12.【答案】3.【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.三综合题13.【解析】∵DE∥BC,∴△ADE∽△ABC,∵,,∴,∴AC=,∴EC=AC-AE=.14.【解析】∵AD∥BC,∴∠ADB=∠DBC,又∵,∴△ABD∽△DCB,∴∠A=∠BDC,∵∠A=90°,∴∠BDC=90°,∴BD⊥CD .15.【解析】解:(1)∵AD⊥BC,∴∠CFA=90°,∵∠BAC=90°,∴∠CFA=∠BAC,∵∠ACF=∠FCA,∴△CAF∽△CEA,∴=,∴CA2=CE•CF;(2)∵∠CAB=∠CDA,∠ACD=∠BCA,∴△CAD∽△CBA,∴=,∴CA2=CB×CD,同理可得:CA2=CF×CE,∴CD•BC=CF•CE,∴=,∵∠DCF=∠ECB,∴△CDF∽△CEB,∴∠CFD=∠B,∵∠B=38°,∴∠CFD=38°.。
沪教版(上海)初中数学九年级第一学期 本章小结 相似三角形的复习 教案

相似三角形复习(2)教学内容:相似三角形复习课第二节(相似三角形判定定理)教学目标: 1、进一步理解和掌握相似三角形的判定定理、灵活应用这些定理去探索问题和解决问题。
2、培养在基本图形中运用知识的能力。
体会在发现中学习,在学习中发现。
发展学生的数学思维能力。
渗透图形运动、类比、分类讨论等数学思想。
3、提倡学生主动学习、积极参与教学,用所学的知识解决问题,提高学数学的热情。
在师生互动过程中,培养团结协作的精神。
教学重点:相似三角形判定定理的应用。
教学难点:能在复杂图形背景下、识别和判定三角形的相似,并正确推理论证,关注数学的严密性。
设计思想:本节课是在学习了相似三角形判定定理后的一节复习课。
一方面,抓住基本图形的特征,将基本图形通过平移、旋转、翻折、分解、组合成各种图形。
鼓励学生联想,培养学生创新意识。
另一方面,让学生进一步形成学习的主体意识、探究意识和合作意识。
教学过程:教师活动 学生活动 教学设计意图 我们已经认识了相似三角形,学习了相似三角形的判定,这节课我们要巩固我们所学的知识,并把所学的有关判定定理应用到实际的例题中,去探索和解决一些问题。
一;相似三角形基本图形以及判定定理的回顾。
问1: 若DE//BC ,则可以判定哪两个个三角形形相似?用哪条判定定理? 预备定理:如果一条直线平行于三角形的一条边,且这条直线与原三角形的两边(或其延长线)分别相交,那么所构成的三角形与原三角形相似。
这类基本图形我们称为平行线型生:△ADE ∽△ABC ,用预备定理生:△ADC ∽△ACB通过回忆使学生掌握相似三角形的所有的判定方法.1A BCD E 1AECBD三边对应成比例,两三角形相似。
这类网格型的题目还可以用那种判定方法。
通常网格类的相似,还可以用哪个判定定理? 最后,我们来回顾一下直角三角形相似的判定方法:问5:若BDACBE AB =,∠C=∠D=90°则可 以判定哪两个三角形形相似?用哪条判定定理 直角三角形相似的判定定理: 斜边和一条直角边对应成比例,则这两个直角三角形相似 上面我们回顾了相似三角形判定定理及重要 的基本图形,下面我们要应用这些定理来 解决一些几何问题。
沪教版九年级数学-三角形相似的总复习-带答案
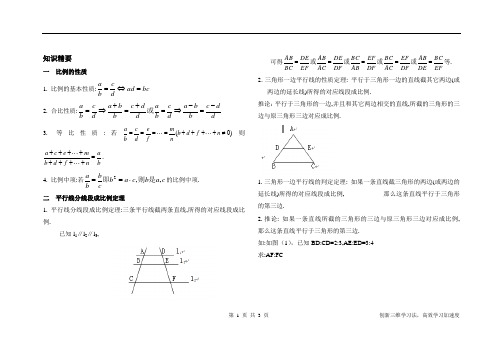
第 1 页 共 3 页 创新三维学习法,高效学习加速度知识精要一 比例的性质1. 比例的基本性质:bc ad dcb a =⇔=2. 合比性质:ddc b b ad c b a d d c b b a d c b a -=-⇒=+=+⇒=或 3.等比性质:若)0(≠+⋅⋅⋅+++=⋅⋅⋅===n f d b nmf e d c b a 则ban f d b m e c a =+⋅⋅⋅++++⋅⋅⋅+++.4. 比例中项:若c a b c a b cbb a ,,2是则即⋅==的比例中项.二 平行线分线段成比例定理1. 平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知l 1∥l 2∥l 3,可得EFBCDE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或等. 2.三角形一边平行线的性质定理: 平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.推论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.1. 三角形一边平行线的判定定理: 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例, 那么这条直线平行于三角形的第三边.2. 推论: 如果一条直线所截的三角形的三边与原三角形三边对应成比例, 那么这条直线平行于三角形的第三边.如:如图(1),已知BD:CD=2:3,AE:ED=3:4 求:AF:FC辅助线当然是添加平行线. 但如图(2), 如果过D作DG∥BF,则在FC中插入了G点,不利求结论AF:FC;如图(3)如果过F做FG∥AD交CD于G时,在CD上插入G,条件BD:DC=2:3就不好用了。
因此应过D做DG∥AC 交BF于G,此辅助线做法既不破坏BD:DC,又不破坏AE:ED,还不破坏AE:FC.解: 过D做DG∥AC交BF于G∵BD:DC=2:3 ∴BD:BC=2:5 则DG:CF=2:5 设DG=2x CF=5 xAE:ED=3:4 AF:DG=3:4 AF:2x=3:4 AF=1.5x AF:FC=1.5x:5x=3:10 三相似三角形的判定及性质1. 相似三角形的判定①两角对应相等的两个三角形相似(此定理用的最多);②两边对应成比例且夹角相等的两个三角形相似;③三边对应成比例的两个三角形相似;④直角边和斜边对应成比例的两个直角三角形相似.2. 直角三角形斜边的高分直角三角形所成的两个直角三角形与原直角三角形相似.3. 相似三角形的性质①相似三角形对应角相等、对应边成比例.②相似三角形对应高、对应角平分线、对应中线、周长的比都等于相似比(对应边的比)第 1 页共3 页创新三维学习法,高效学习加速度第 1 页 共 3 页 创新三维学习法,高效学习加速度一、选择题(本大题共6题,每题4分,满分24分)1.下列图形一定是相似图形的是…………………………( B ) (A )两个矩形; (B )两个正方形; (C )两个直角三角形; (D )两个等腰三角形. 2.小明身高1.5米,在操场的影长为2米,同时测得教学大楼在操场的影长为60米,则教学大楼的高度应为( A ) A .45米B .40米C .90米D . 80米3.下列各组线段中,成比例线段的一组是…………………( B ) (A )1,2,3,4;(B )2,3,4,6;(C )1,3,5,7;(D )2,4,6,8;4.如图,下列条件中不能..判定ABC ACD △∽△的是( C ) A .B ACD ∠=∠; B .ADC ACB ∠=∠; C .AC ABCD BC=; D .AB AD AC •=2.5.如图,已知D 是△ABC 中的边BC 上的一点,∠BAD =∠C ,∠ABC 的平分线交边AC 于E ,交AD 于F ,那么下列结论中错误的是 ( C )(A )△BAC ∽△BDA ; (B )△BF A ∽△BEC ; (C )△BDF ∽△BEC ; (D )△BDF ∽△BAE .B6.下列四个三角形中,与右图中△ABC 相似的是( B )二、填空题(本大题共12题,每题4分,满分48分) 7.如果23x y =,那么x y y+= __ 5/3 __. 8.在比例尺为1:10000的地图上,相距4厘米的两地A 、B 的实际距离为 400 米9.已知在△A BC 中,AD 是中线,G 是重心,如果GD =3cm ,那么AG =6cm .A C ED F第5题BAD CDCBA第4题第 1 页 共 3 页 创新三维学习法,高效学习加速度10.在ABC ∆和111C B A ∆中,已知,5001=∠=∠A A 070=∠B ,要使ABC ∆和111C B A ∆相似,只要._________1=∠B 70或者6011.在△ABC 中,点D 、E 分别在边AB 、AC 上 ,DE ∥BC ,AD =1,AB =3, 则ABC ADE S S ∆∆:= 1:9 .12.如图:M 为平行四边形ABCD 的BC 边的中点,AM 交BD 于点P ,若PM =4,则AP =____8_________.13.已知点D 是线段AB 的黄金分割点(AD >BD ),如果AB=2,那么AD 的长为 √5−1 .14.如图,在∆Rt ABC 中,∠ACB = 90,CD ⊥AB ,垂足是D ,53=AC AD ,⊿ABC 的周长是25,那么⊿ACD 的周长是 15 .15.如图,请在方格图中画出一个与 ABC 相似且相似比不为1的三角形(它的顶点必须在方格图的交叉点).略16、如图,在ABC ∆中,6=BC ,G 是ABC ∆的重心,过G 作边BC 的平行线交AC 于点H ,则GH 的长为___2__.H CBGAPMDCBA第12题第 1 页 共 3 页 创新三维学习法,高效学习加速度17.如图,直线l 1∥l 2∥l 3,已知AG =0.6cm ,BG =1.2cm ,CD =1.5cm ,CH =___05___cm18.已知三角形纸片(△ABC )中,AB =AC =5,BC =8,将三角形按照如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .若以点B ′,F ,C 为顶点的三角形与△ABC 相似,那么BF 的长度是 40/13 .三、(本大题共7题,满分78分)19、如图,在ABC ∆中有一个内接矩形EFGD ,边FG 在AB 上,顶点E 、D 分别在边CA 、CB 上,AB CQ ⊥于点Q ,CQ 交ED 于H ,10=AB ,6=CQ ,ED 的长比EF 多2,求ED 的长。
沪教版初三上册396660《相似三角形》全章复习与巩固(基础) 知识讲解

沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习《相似三角形》全章复习与巩固(基础)知识讲解【学习目标】(1)了解比例的基本性质,了解线段的比、成比例线段的概念;(2)通过具体实例认识图形的相似,探索相似图形的性质,知道相似多边形的对应角相等,对应边成比例,周长的比等于对应边的比,面积的比等于对应边比的平方;(3)了解两个三角形相似的概念,探索两个三角形相似的条件;(4)通过典型实例观察和认识现实生活中物体的相似,利用图形的相似解决一些实际问题( 如利用相似测量旗杆的高度);(5)理解实数与向量相乘的定义及向量数乘的运算律.【知识网络】【要点梳理】要点一、比例线段及比例的性质1.比例线段:(1)线段的比:如果选用同一长度单位量得两条线段a,b的长度分别是m,n,那么就说这两条线段的比是a:b=m:n,或写成,其中a叫做比的前项;b叫做比的后项.(2)成比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(3)比例的项:已知四条线段a,b,c,d,如果,那么a,b,c,d,叫做组成比例的项,线段a,d叫做比例外项,线段b,c叫做比例内项,线段d还叫做a,b,c的第四比例项.(4)比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c或,那么线段b叫做线段a和c的比例中项.要点诠释:通常四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b的单位一致,c,d的单位一致也可以.2.比例的性质(1)比例的基本性质:(2)反比性质:(3)更比性质:或(4)合比性质:(5)等比性质:且3.平行线分线段成比例定理(1)三角形一边的平行线性质定理: 平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.(2)三角形一边的平行线性质定理推论:平行于三角形一边并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边的对应成比例.(3)三角形一边的平行线判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.(4)三角形一边的平行线判定定理推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.(5)平行线分线段成比例定理:两条直线被三条平行的直线所截,截得的对应线段成比例.(6)平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.这几个定理主要提出由平行线可得到比例式;反之,有比例可得到平行线.首先要弄清三个基本图形:这三个基本图形的用途是:1.由平行线产生比例式基本图形(1): 若l1//l2//l3,则或或或基本图形(2): 若DE//BC,则或或或基本图形(3): 若AC//BD,则或或或在这里必须注意正确找出对应线段,不要弄错位置.2.由比例式产生平行线段基本图形(2):若, , , , ,之一成立,则DE//BC.基本图形(3):若, , , , ,之一成立,则AC//DB.要点诠释:(1)平行线等分线段定理是平行线分线段成比例定理的特例;(2)平行线分线段成比例没有逆定理;(3)由于平行线分线段成比例定理中,平行线本身没有参与作比例,因此,有关平行线段的计算问题通常转化到“A”、“X”型中.A型 X型常用的比例式:.(4)判断平行线的条件中,只能是被截的两条直线的对应线段成比例(被判断的平行线本身不能参与作比例).4.三角形的重心三角形三条中线的交点叫做三角形的重心.要点诠释:(1)重心的性质:三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍;(2)重心的画法:两条中线的交点.要点二、黄金分割1.黄金分割是指把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项(AC2=AB·BC),C点为黄金分割点.2.黄金分割的求法①代数求法:已知:线段AB ,求作:线段AB的黄金分割点C.分析:设C点为所求作的黄金分割点,则AC2=AB·CB,设AB=,AC=x,那么CB=-x,由AC2=AB·CB,得:x2=·(-x)整理后,得:x2+x-=0,根据求根公式,得:x=∴ (不合题意,舍去)即AC=AB≈0.618AB,则C点可作.②黄金分割的几何求法(尺规法):已知:线段AB,求作:线段AB的黄金分割点C.作法:如图:(1)过B点作BD⊥AB,使BD=AB.(2)连结AD,在AD上截取DE=DB.(3)在AB上截取AC=AE.则点C就是所求的黄金分割点.证明:∵AC=AE=AD-AB而AD=∴AC=∴C点是线段AB的黄金分割点.要点诠释:①一条线段有两个黄金分割点.②这种分割之所以被人们称为黄金分割,是因为黄金分割存在美学规律和具有实用价值.德国著名天文学家开普勒 (Kepler,1571—1630)把这种分割称为“神圣的比例”,说它是几何中的瑰宝,大家也可以看一下课外的阅读材料,体会一下黄金分割中所蕴含的美学.要点三、相似三角形1.相似多边形(1)相似多边形的特征:相似多边形的对应角相等,对应边的比相等.(2)相似多边形的识别:如果两个多边形的对应角相等,对应边的比相等,那么这两个多边形相似.(3)相似比:我们把相似多边形对应边的比称为相似比.(4)相似多边形的性质①相似多边形的对应角相等,对应边的比相等.②相似多边形的周长比等于相似比.③相似多边形的面积比等于相似比的平方.2.相似三角形(1)相似三角形的定义:形状相同的三角形是相似三角形.(2)相似三角形的表示方法:用“∽”表示,读作相似于.如:△ABC和△DEF相似,可以写成△ABC∽△DEF,也可以写成△DEF ∽△ABC,读作△ABC相似于△DEF.(3)相似三角形的性质:①相似三角形的对应角相等,对应边的比相等.②相似三角形对应边上的高的比相等,对应边上的中线的比相等,对应角的角平分线的比相等,都等于相似比.③相似三角形的周长的比等于相似比,面积的比等于相似比的平方.要点诠释:相似三角形的性质是通过比例线段的性质推证出来的.(4)相似三角形的判定:①平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似;②如果两个三角形的三组对应边的比相等,那么这两个三角形相似;③如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;④如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.⑤如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边的比对应相等,那么这两个直角三角形相似.(5)相似三角形应用举例相似三角形的知识在实际生产和生活中有着广泛的应用,可以解决一些不能直接测量的物体的长度问题,加深学生对相似三角形的理解和认识.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点四、实数与向量相乘1.实数与向量相乘的意义一般的,设为正整数,为向量,我们用表示个相加;用表示个相加.又当为正整数时,表示与同向且长度为的向量.要点诠释:设P为一个正数,P就是将的长度进行放缩,而方向保持不变;—P也就是将的长度进行放缩,但方向相反.2.向量数乘的定义一般地,实数与向量的相乘所得的积是一个向量,记作,它的长度与方向规定如下:(1)如果时,则:①的长度:;②的方向:当时,与同方向;当时,与反方向;(2)如果时,则:,的方向任意.实数与向量相乘,叫做向量的数乘.要点诠释:(1)向量数乘结果是一个与已知向量平行(或共线)的向量;(2)实数与向量不能进行加减运算;(3)表示向量的数乘运算,书写时应把实数写在向量前面且省略乘号,注意不要将表示向量的箭头写在数字上面;(4)向量的数乘体现几何图形中的位置关系和数量关系.3.实数与向量相乘的运算律设为实数,则:(1)(结合律);(2)(向量的数乘对于实数加法的分配律);(3)(向量的数乘对于向量加法的分配律)4.平行向量定理(1)单位向量:长度为1的向量叫做单位向量.要点诠释:任意非零向量与它同方向的单位向量的关系:,.(2)平行向量定理:如果向量与非零向量平行,那么存在唯一的实数,使.要点诠释:(1)定理中,,的符号由与同向还是反向来确定.(2)定理中的“”不能去掉,因为若,必有,此时可以取任意实数,使得成立.(3)向量平行的判定定理:是一个非零向量,若存在一个实数,使,则向量与非零向量平行.(4)向量平行的性质定理:若向量与非零向量平行,则存在一个实数,使.(5)A、B、C三点的共线若存在实数λ,使.要点五、向量的线性运算1.向量的线性运算定义向量的加法、减法、实数与向量相乘以及它们的混合运算叫做向量的线性运算.要点诠释:(1)如果没有括号,那么运算的顺序是先将实数与向量相乘,再进行向量的加减.(2)如果有括号,则先做括号内的运算,按小括号、中括号、大括号依次进行.2.向量的分解平面向量基本定理:如果是同一平面内两个不共线(或不平行)的向量,那么对于这一平面内的任一向量,有且只有一对实数,使得.要点诠释:(1)同一平面内两个不共线(或不平行)向量叫做这一平面内所有向量的一组基底.一组基底中,必不含有零向量.(2) 一个平面向量用一组基底表示为形式,叫做向量的分解,当相互垂直时,就称为向量的正分解.(3) 以平面内任意两个不共线的向量为一组基底,该平面内的任意一个向量都可表示成这组基底的线性组合,基底不同,表示也不同.3.用向量方法解决平面几何问题(1)利用已知向量表示未知向量用已知向量来表示另外一些向量,除利用向量的加、减、数乘运算外,还应充分利用平面几何的一些定理,因此在求向量时要尽可能转化到平行四边形或三角形中,利用三角形中位线、相似三角形对应边成比例等平面几何的性质,把未知向量转化为与已知向量有直接关系的向量来求解.(2)用向量方法研究平面几何的问题的“三步曲”:①建立平面几何与向量的联系,将平面几何问题转化为向量问题.②通过向量运算,研究几何元素的关系.③把运算结果“翻译”成几何关系.【典型例题】类型一、比例线段1.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.(1)求a、b、c的值;(2)若线段x是线段a、b的比例中项,求x的值.【答案与解析】解:(1)∵a:b:c=3:2:6,∴设a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12;(2)∵x是a、b的比例中项,∴x2=ab,∴x2=4×6,∴x=2或x=﹣2(舍去),即x的值为.【总结升华】题目中已知三个量a,b,c的比例关系和有关a,b,c的等式,我们可以利用这个等量关系,通过设参数k, 转化成关于k的一元方程,求出k后,问题得解.举一反三:【变式】已知:,求的值.【答案】根据等比性质:由得.2.如图,在□ABCD中,E为AB中点, ,EF,AC相交于G,求.【答案与解析】分别延长FE,CB相交于H,(构造出了基本图形)在□ABCD中,ADBC,∵E为AB中点,∴AE=BE,∵AD//BC,∴∠AFE=∠H.在△AEF和△BEH中:∴△AEF≌△BEH(AAS)∴AF=BH,∵,设AF=k, 则FD=3k,AD=4k,BH=AF=k,BC=AD=4K,CH=5K,∵AD//BC,即AF//HC.∴∴【总结升华】欲求,就需要有平行线,并使已知条件得以利用,虽然题目中有平行线,但无基本图形,不能使已知条件发挥作用,需通过添加辅助线来寻找解题途径,构造基本图形.此题还有其他辅助线的作法,例如分别延长EF,CD相交于M.或取AC中点N,连结EN.请同学们思考,这两种方法构造了哪些基本图形,如何求出.举一反三:【变式】如图,在是两条中线,则()A.1∶2 B.2∶3C.1∶3 D.1∶4【答案】由题意可知,为的中位线,则△CED∽△CAB,∴,故选D.类型二、相似三角形3.(2016•南平)如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.【思路点拨】根据相似三角形的判定与性质,可得答案.【答案与解析】解:∵DE⊥AB,∴∠BED=90°,又∠C=90°,∴∠BED=∠C.又∠B=∠B,∴△BED∽△BCA,∴=,∴DE===4【总结升华】本题考查了相似三角形的判定与性质,利用相似三角形的性质得出=是解题关键.举一反三:【变式】如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FC与△DG 的面积之比为()A.9:4B.3:2C.4:3D.16:9【答案】D.设CF=x,则BF=3-x,由折叠得F=BF=3-x,在Rt△FC中,由由勾股定理得CF2+C2=F2,x2+12=(3-x)2,解得x=,由已知可证Rt△FC∽Rt△DG,所以S△FC与S△DG的面积比为(:1)2=.类型三、实数与向量相乘4.已知下列命题:①;②;③;④其中正确命题序号是___________.【答案】②、④.【解析】掌握平面向量数量积的含义,平面数量积的运算律不同于实数的运算律.【总结升华】应用向量的运算性质.类型四、向量的线性运算5.如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.(1)求证:FG∥AB;(2)设=,=,请用向量、表示.【答案与解析】(1)证明:∵AD=DE=EB,∴==,∵DF∥BC,EG∥AC,∴==,,∴,∴FG∥AB;(2)解:∵DF∥BC,FG∥AB,∴,,∴FG=AB,∵与同向,∴=,∵=,=,∴=﹣,∴=.【总结升华】此题考查了平面向量的知识以及平行线分线段成比例定理.解题时注意掌握数形结合思想的应用.类型五、相似与其它知识综合问题6.如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.【答案与解析】(1)∵D、C、F分别是△ABC三边中点,∴DE∥AB,DF∥AC,又∵△BDG与四边形ACDG周长相等,即BD+DG+BG=AC+CD+DG+AG.∴BG=AC+AG,∵BG=AB-AG,∴BG==,(2)证明:BG=,FG=BG-BF=-,∴FG=DF,∴∠FDG=∠FGD,又∵DE∥AB,∴∠EDG=∠FGD,∠FDG=∠EDG,∴DG平分∠EDF ,(3)在△DFG中,∠FDG=∠FGD, △DFG是等腰三角形,∵△BDG与△DFG相似,∴△BDG是等腰三角形,∴∠B=∠BGD,∴BD=DG,则CD= BD=DG,∴B、CG、三点共圆,∴∠BGC=90°,∴BG⊥CG.【总结升华】这是一道几何综合题,在计算证明时,根据题中已知条件,结合图形性质来完成.后面的问题可以结合前面问题来做.已知三角形三边中点连线,利用三角形中位线性质计算证明.(1)已知△ABC的边长,由三角形中位线性质知,根据△BDG与四边形ACDG周长相等,可得.(2)由(1)的结论,利用等腰三角形性质和平行线性质可证. (3)利用两个三角形相似,对应角相等,从而等角对等边,BD=DG=CD,即可证明.举一反三:【变式】如图,在口ABCD中,的平分线分别与、交于点、.(1)求证:;(2)当时,求的值.【答案】(1)如图,在口ABCD中,,∴.∵是的平分线,∴.∴.∴.(2)∴△∽△,∴,∴.。
沪科版九年级数学上册 相似三角形 知识点大总结

沪科版九年级数学上册 相似三角形 知识点大总结知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段的长度分别为,那么就说这两条线段的比是,或写b a ,n m ,nmb a =成.注:在求线段比时,线段单位要统一。
n m b a ::=(2)在四条线段中,如果的比等于的比,那么这四条线段叫做成比例线段,d c b a ,,,b a 和d c 和d c b a ,,,简称比例线段.注:①比例线段是有顺序的,如果说是的第四比例项,那么应得比例式为:a d cb ,,.②a 、d 叫比例外项,b 、c 叫比例内项, a 、c 叫比例前项,a d cb =()ac a b cd b d==在比例式::中,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 那么b 叫做a 、d 的比例中项, 此时有a b b d =::。
2b ad =(3)黄金分割:把线段分成两条线段,且使是的比例中项,即AB )(,BC AC BC AC >AC BC AB 和,叫做把线段黄金分割,点叫做线段的黄金分割点,其中2AC AB BC =⋅AB C AB ≈0.618.即简记为:AB AC 215-=AB AC BC AB AC ==长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0)(1) 基本性质:①;②.bc ad d c b a =⇔=::2::a b b c b a c =⇔=⋅注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如,除bc ad =了可化为,还可化为,d c b a ::=d b c a ::=,,,,,.b a dc ::=c ad b ::=c d a b ::=b d a c ::=a b c d ::=a c b d ::=(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)反比性质(把比的前项、后项交换):.a cb d b da c=⇔=(4)合、分比性质:.a c a b c d b d b d±±=⇔=注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:等等.⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a(5)等比性质:如果,那么.)0(≠++++====n f d b n m f e d c b a ba n f db m ec a =++++++++ 注:①此性质的证明运用了“设法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例k 计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:;其中.baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322032≠+-f d b 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD∥BE∥CF,可得等. AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形是初中数学九年级上学期第一章的内容,在本章中,我们学习了比例线段的相关性质,相似三角形的概念、判定及性质和平面向量的线性运算.重点是灵活运用相似三角形的判定定理和性质定理,难点是利用辅助线解决相似三角形问题以及相似三角形与动点问题相结合的类型。
比例线段运算法则比例的性质向量的分解平行向量定理运算律实数与向量相乘向量的线性组合向量的线性运算相似三角形的概念相似三角形的预备定理 相似三角形的判定定理相似三角形的性质定理三角形一边的平行线性质定理及推论三角形一边的平行线判定定理及推论平行线分线段成比例定理相 似 形相似三角形 单元练习:相似三角形内容分析知识结构步同级年九2 / 17A B CDO【练习1】 下列图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形.其中一定相似的有() A .2组B .3组C .4组D .5组【答案】A【解析】判定相似有2个条件:对应角相等,且对应边成比例,两个矩形对应角相等,但长和宽的不一定成比例,两个(等腰三角形)菱形对应边成比例,但对应角又不一定相等,只有③⑥一定相似.【总结】考查学生对相似几何图形性质的理解,对应角相等和对应边成比例两个条件缺一不可.【练习2】 若a cb d=,下列各式中正确的个数有() ①a c d b =;②::d c b a =;③22a a b b =;④55a c b d +=+;⑤a a c b a d +=+;⑥c ma d mb=.A .1个B .2个C .3个D .4个【答案】A【解析】考查比和比例的基本性质,以“内项积等于外项积”检验①不成立,②是对的;比的基本性质是前项和后项同时乘以(或除以)同一个不为零的数,比值不变,③是不成立的;比例线段的等比性质及合并性质也需要学生理解到位;其中⑥不正确的原因是0m ≠.【总结】考查比和比例的基本性质.【练习3】 已知AB //CD ,AD 、BC 相交于点O ,下列比例式中正确的是()A .AB OA CD AD = B .OA OBOD BC= C .AB OB CD OC= D .BC OBAD OD= 【答案】C【解析】∵AB CD ,∴AB AO BODC DO CO ==,对应关系要弄清楚. 【总结】考查“平行型”的A 字模型.【练习4】 下列条件中能判定ABC ∆∽DEF ∆的有( )①45A ∠=︒,12AB =,15AC =,45D ∠=︒,16DE =,40DF =; ②12AB =,15BC =,24AC =,20DE =,25EF =,40DF =;选择题DA BCPA B C DE 1 2③47A ∠=︒,15AB =,20AC =,47E ∠=︒,28DE =,21EF =. A .0个B .1个C .2个D .3个【答案】C【解析】对应角相等,但对应边不成比例,①不成立;三边对应成比例,可以判定②成立;两边对应成比例及夹角相等判定③成立. 【总结】考查相似三角形的判定定理.【练习5】 如图,已知12∠=∠,那么添加一个条件后,仍无法判定ABC ∆∽ADE ∆的是( )A .AB AC AD AE =B .AB BCAD DE=C .BD ∠=∠D .C AED ∠=∠【答案】B【解析】已知一组对应角相等,再添加任意一组对应角相等都可以判定相似,添加对应边成比例需要对应角的夹边成比例. 【总结】考查相似三角形判定定理.【练习6】 如图,已知,电灯P 在横杆AB 的正上方,AB 在灯光下的影子为CD ,AB //CD ,AB = 2m ,CD = 5m ,点P 到CD 的距离是3m ,则P 到AB 的距离是()A .56mB .67mC .65mD .103m【答案】C【解析】相似比等于对应高之比,设P 到AB 的距离为xcm ,列等量关系253x =,解得65x =.【总结】考查相似三角形的性质,相似比等于对应高之比.【练习7】 如图,厨房角柜的台面是三角形,如果把各边中点的连线所围成的三角形铺成黑色的大理石(图中阴影部分),其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石的面积之比是()A .14B .41C .13D【答案】CABCOAB CD E 【解析】相似三角形面积之比是相似比的平方,联结三角形三边中点,将原三角形的面积四等分,所以黑色面积与白色面积之比是13.【总结】考查相似三角形的性质.【练习8】如图,在O中,向量OB,OC,AO是()A.有相同起点的向量B.单位向量C.长度相等的向量D.相等的向量【答案】C【解析】同圆的半径相等,所以OB,OC,AO的长度是相等的.【总结】考查向量的方向、长度及相等向量的概念.【练习9】若a是任一非零向量,b是单位向量,下列各式中,正确的是()①a b>;②a//b;③0a>;④1b=±.A.①④B.③C.①②③D.②③【答案】B【解析】单位向量的长度是单位1,方向是任意的,b是单位向量,但并没有讲是向量a方向上的单位向量,所以②是不对的.【总结】考查单位向量的概念.【练习10】如图,在ABC∆中,DE//BC,BC = 6cm,:1:4ADE ABCS S∆∆=,那么DE的长为()A.1.5cm B.2cm C.2.5cm D.3cm【答案】D【解析】∵:1:4ADE ABCS S∆∆=,∴12DEBC=,∵BC=6cm,∴DE=3cm.【总结】考查相似三角形性质的应用.a x cb A .B .a xc b C .axc b D .axc bAB CP【练习11】 已知线段a ,b ,c ,求作线段x ,使bx = ac ,以下方法中不正确的是()【答案】B【解析】利用平行线分线段成比例,可以验证A 、C 、D 都成立,B 选项不成立的原因是从作图的角度看,不能保证延长线段a 与线段c 相交成的线段长度一定为所求作x . 【总结】考查利用比例线段求作第四条线段的作图方法.【练习12】 如图,若P 为ABC ∆的边AB 上一点(AB >AC ),则下列条件不一定能保证ACP ∆∽ABC ∆的有( )A .ACPB ∠=∠B .APC ACB ∠=∠C .AC AP AB AC =D .PC AC BC AB=【答案】D【解析】如图,两个三角形已经有一组公共角,添加角度条件一定可以判定相似,若是添加对应边成比例不能使用到公共角的对边,所以D 选项不能判定ACP ∆∽ABC ∆. 【总结】考查相似三角形的判定定理.【练习13】 过三角形一边上一点画直线,使直线与另一边相交,且截得的三角形与原三角形相似,那么最多可画这样的直线的条数是( ) A .1条B .2条C .3条D .4条【答案】D【解析】过三角形一边上一点画直线与另一边相交,截得的三角形与 原三角形相似,这样的直线最多可画4条,每条边上两条,其中 包括“平行型”和“斜交型”,如图所示.(当这个点是直角三角形斜边上一点时,最多可以画三条符合题意的直线)【总结】考查相似基本图形.【练习14】 已知P 为线段AB 的黄金分割点,且AP <PB ,则()A .2AP AB PB = B .2AB AP PB =C .2PB AP AB =D .222AP BP AB +=【答案】C【解析】线段的黄金分割点有两个,是对称的,其中三条线段之间存在一个黄金比例关系,=较短较长较长全长,即AP BPBP AB =,即2BP AP AB =. 【总结】考查线段的黄金分割.AB CDEOOB DC C 'A【练习15】 如图,在ABC ∆中,高BD 、CE 交于点O ,下列结论错误的是()A .CO CE CD CA =B .AD AC AE AB = C .OE OC OD OB =D .CO DO BO EO =【答案】D【解析】基本图形“双垂型”,图中有4个三角形两两相似,都可以用“AA”来判定,ABD ACE OBE OCD ∆∆∆∆,对应边成比例换成等积式,其中D 选项比例关系不对. 【总结】考查相似模型之“双垂型”.【练习16】 如图,AD 是ABC ∆的中线,45ADC ∠=︒,把ADC ∆沿AD 对折,点C 落在'C 的位置,则'BC BC 的值为()A .14B .13 CD .1 【答案】C【解析】联结'CC ,因为翻折,所以'CC AD ⊥,设交点为O ,因为∠ADC =45°,所以∠OCD =45°,又因为',DB DC DC ==根据三角形内角和可以证明'90BC C ∠=,所以'BC C ∆为等腰直角三角形,即'BC BC =. 【总结】考查翻折的性质及等腰直角三角形的性质.【练习17】 把平面上所有单位向量归结到共同的始点,那么这些向量的终点所构成的图形是( ) A .一条线段B .一个圆面C .圆上的一群孤点D .一个圆【答案】D【解析】单位向量的长度是一样的,方向是任意的,将同一平面内的单位向量的起点归为同一点,它们的终点汇聚成了一个单位圆,到定点的距离等于定长的点的轨迹是圆. 【总结】考查单位向量的性质及圆的定义.【练习18】 下面几个命题中,真命题的个数是()(1)若a b =,则a b =;(2)两个向量a 、b 相等,则a b =,a //b ; (3)若AB DC =,则四边形ABCD 是平行四边形; (4)若四边形ABCD 是平行四边形,则AB DC =; (5)若a b =,b c =,则a c =; (6)若a //b ,b //c ,则a //c . A .4个B .3个C .2个D .1个【答案】B【解析】长度相等的向量,方向不一定相同,所以(1)不正确;若AB DC =,则四边形ABCD 是平行四边形,这句话也是有漏洞的,当A 、B 、C 、D 四点共线时,构不成平行四边形,不过它的逆命题是正确的;其它选项都是正确的. 【总结】考查平面向量的有关概念与性质.AB CP【练习19】 A 、B 两地的实际距离是200千米,地图上的比例尺为1 : 1000000,则A 、B两地在地图上的距离是______厘米. 【答案】20厘米.【解析】厘米和千米的进率为:1100000km cm =,设图上距离为x 厘米,由题意,得1:1000000:20000000x =,解得20x =.【总结】考查比例尺的运用.【练习20】 2、3、5再配上一个比它们都大的数组成比例式,这个数是______.【答案】152.【解析】设这个数为x ,若其它三个比例项分别为,,a b c ,且abx c=,要使x 最大,则ab 取最大值,c 取最小值,所以351522x ⨯==,若x 的取值没有要求,这样的x (与2、3、5组成比例式)有三个. 【总结】考查比例的基本性质.【练习21】 若x : y : z = 2 : 7 : 5,且x - 2y + 3z = 6,则x =____,y =____,z =____. 【答案】41410x y z ===,,.【解析】∵::2:7:5x y z =,设275x k y k z k ===,,,则227356k k k -⨯+⨯=,解得2k =,∴4,14,10x y z ===. 【总结】考查学生对设“k ”法的理解应用.【练习22】 已知线段a = 8厘米,b = 9厘米,则线段a 和b 的比例中项是______. 【答案】62cm .【解析】a b ,的比例中项c ab =±,当a b ,为线段长时,c 取正值. 【总结】考查比例中项的定义.【练习23】 如图,已知ACP B ∠=∠,AC = 4,AP = 2,则AB = ______. 【答案】AB =8.【解析】∵ACP B ∠=∠,且A A ∠=∠,∴ACP ABC ∆∆填空题8米4米0.8米hABD 则AC APAB AC=,∵42AC AP==,,∴8AB=.【总结】考查相似三角形的判定与性质.【练习24】如图,小智在打网球时,击球点距离球网的距离是8米,已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击球的高度h为______米.【答案】2.4米.【解析】根据平行线分线段成比例,得0.8412h=,解得 2.4h=.【总结】考查平行线分线段成比例的应用,也可以用相似三角形的性质求解h.【练习25】如图,AB是斜靠在墙角的长梯,梯脚B距墙80厘米,梯上点D距墙70厘米,BD长55厘米,则梯子长为______.【答案】440厘米.【解析】设,AB x=根据平行线分线段成比例,得70,80ADAB=即5578xx-=,解得440x=,所以梯子的长为440厘米.【总结】考查平行线分线段成比例的应用.【练习26】若两个相似三角形的面积比为2 : 9,则这两个三角形的对应中线的比是______.3..【总结】考查相似三角形的性质:面积比是相似比的平方比,相似比也是对应中线之比.【练习27】 在边长为1的正方形ABCD 中,设AB a =,BC b =,AC c =,则a b c ++=______;a c b +-=______;c a b --=______.【答案】20;.【解析】(1)2a b c AB BC AC AC ++=++=,因为正方形边长为1,所以AC =即a b c ++=(2)2a c b AB AC BC AB AC CB AB +-=+-=++=,即2a c b +-=; (3)0c a b AC AB BC BC BC --=--=-=,即0c a b --=. 【总结】考查平面向量的线性运算.【练习28】 计算:()()325232a b a b +--=______. 【答案】19b .【解析】()()325232a b a b +--=6156419a b a b b +-+=. 【总结】考查实数与向量相乘及平面向量的加减运算.【练习29】 若()()::a b x y x y =+-,则:x y =______. 【答案】a ba b+-. 【解析】设()()a b k x y a b k x y +=+-=-,,解得22a b x k a b y k +⎧=⎪⎪⎨-⎪=⎪⎩,所以:a b x y a b +=-.【总结】考查设“k ”法的理解应用.【练习30】 点P 是线段AB 的黄金分割点,且AP =2,则AB =______.31+.【解析】(1)当AP为较长的线段时,AP AB =1AB ; (2)当AP为较短的线段时,AP BP =解得1BP =,123AB =+=.【总结】考查线段的黄金分割,等量关系=短长长全,一条线段的黄金分割点有两个,需要学生具有分类讨论的思想.【练习31】 过直角三角形的斜边上一点画直线,使直线与另一边相交,且截得的三角形与原三角形相似,那么最多可画______条这样的直线;过直角三角形的直角边上一点画直线,使直线与另一边相交,且截得的三角形与原三角形相似,那么最多可画______条这样的直线. 【答案】3条;4条.【解析】当这个点在直角边上时,可以画4条这样的直线使得截得的三角形与原三角形相似;当这个点在斜边上时,可以画3条(有2条重合在一起)这样的直线使得截得的三角形与原三角形相似,如图所示.【总结】考查相似基本图形,结论是“直4斜3”.ABCD EF KH【练习32】 如图,AD = DE = EC ,且AB // DF // EH ,AH 交DF 于K ,则EHKF=______. 【答案】23EH KF =. 【解析】∵DK EH ,∴AD DKAE EH =, ∵EH DF ,∴CE EHCD DF=, ∵AD DE EC ==, ∴1122DK EH EH DF ==,, 设DK k =,则24EH k DF k ==,, ∴23EH KF =. 【总结】考查平行线分线段成比例的性质运用.【练习33】 在等边三角形ABC 中,点D 、E 分别在AB 、AC 上,且DE // BC ,如果BC = 8厘米,AD : AB = 1 : 4,那么ADE ∆的周长为_________. 【答案】6厘米.【解析】∵DE BC ,∴ADE ABC ∆∆,∵:1:4AD AB =,∴:1:4ADE ABC C C ∆∆=,因为8BC =,所以24ABC C ∆=,12464ADE C ∆=⨯=.【总结】考查相似三角形的性质运用.【练习34】 如果直角三角形的斜边长为18,那么这个直角三角形的重心到直角顶点的距离为______. 【答案】6.【解析】直角三角形的斜边长为18,则斜边上的中线为9,根据三角形重心的性质,重心到直角顶点的距离是斜边中线的23.【总结】考查直角三角形重心的性质运用.AB CD【练习35】如图,在平行四边形ABCD中,AB a=,CB b=,则向量AO为______.(结果用a和b表示)【答案】1122a b-.【解析】∵平行四边形对角线互相平分,∴11()22AO AC AB BC==+,∵AB a CB b==,,∴1122AO a b=-.【总结】考查平面向量的线性分解及运算,结合平行四边形的性质.【练习36】如图,将①BAD C∠=∠;②ADB CAB∠=∠;③2AB BD BC=;④CA ABAD DB=;⑤BC ACBA DA=;⑥BC DABA AC=中的一个作为条件,另一个作为结论,组成一个真命题,则条件是______,结论是______.(只填序号)【答案】答案不唯一,比如条件是①,结论是③.【解析】这是一个典型的相似基本图形“母子型”,其中可以作为条件的选择不唯一,结论自然也不一,情况如下:(1)当条件为①时,结论可以是②③④⑤;(2)当条件为②时,结论可以是①③④⑤;(3)当条件为③时,结论可以是①②④⑤.【总结】考查相似三角形的判定和性质运用以及对基本图形“母子型”的理解运用.A BCDOAB CD【练习1】已知23a c eb d f ===,18ac e =--,0bd f ++≠,求b d f ++的值. 【答案】27b d f ++=. 【解析】∵203a c e b d f b d f ===++≠,,∴23a c eb d f ++=++,又∵18ac e ++=, ∴27bd f ++=. 【总结】考查等比性质的运用.【练习2】已知b c c a a bx a b c+++===,求x 的值. 【答案】21x =-或.【解析】(1)当0a b c ++=时,b c a c a b a b c +=-+=-+=-,,,∴1ax a-==-; (2)当0a b c ++≠时,b c c a a bx a b c+++===,根据等比性质, 2()2b c c a a b a b c x a b c a b c+++++++===++++;综上,12x =-或.【总结】考查等比性质的运用,需要学生理解等比性质成立的条件,以及有分类的思想.【练习3】如图,已知点D 在ABC ∆的边AB 上,且ACD B ∠=∠,:1:3ACD DBC S S ∆∆=.求ACAB的值. 【答案】12AC AB =.【解析】∵,ACD B A A ∠=∠∠=∠,∴ACD ABC∆∆ ∵:1:3ACD BCD S S ∆∆=,∴:1:4ACD ABC S S ∆∆=,∴12AC AB =. 【总结】考查相似三角形的判定与性质,需要理解相似三角形的相似比与面积比的关系.【练习4】如图,已知点E 、F 分别在矩形ABCD 的边BC 和CD 上,EF AE ⊥,BE = 3cm ,AB = 6cm ,矩形ABCD 的周长为28cm ,求CF 的长.解答题AB CDEFAB CDE FOPAB CDEF【答案】52CF cm=.【解析】∵矩形ABCD,628AB C==,周长,∴8BC=,∵AE EF⊥,AB BC DC BC⊥⊥,,可证ABE ECF∆∆,∴AB BEEC EC=,∵63835AB BE EC===-=,,,∴52CF cm=.【总结】本题在矩形背景下考查“一线三直角”模型.【练习5】如图,已知ABC∆中,AB = AC,CD是边AB上的高,且CD = 2,AD = 1,四边形BDEF是正方形.CEF∆和BDC∆相似吗?试证明你的结论.【答案】CEF BDC∆∆,证明略.【解析】1290AD CD ADC AC==∠=∴=,,,1AB AC AB BD=∴==,,1ABCD BD DE EF∴===正方形,,∴21)3CE=-=∴BDEC==CDEF=,即BD CDEC EF=,又∵90BDC CEF∠=∠=,∴BDC CEF∆∆.【总结】本题结合直角三角形的性质考查相似三角形的判定,同时需要学生扎实的运算功底.【练习6】如图,D、E、F分别是ABC∆的边BC、AB、AC的中点,AD与EF相交于点O,线段CO的延长线交AB于点P.求证:AB = 3AP.【答案】证明略.【解析】∵E F AB AC、分别是、的中点,∴12EF BC EF BC=,,ABCEF∴12AE EO AB BD ==,∵D 是BC 的中点,∴14EO BC =, ∵EO BC ,∴14PE EO PB BC ==,设PE k =,则4PB k =,3BE k =,∴26AB EB k ==,2AP AB PB k =-=,∴:6:23AB AP k k ==,即3AB AP =. 【总结】考查平行线分线段成比例的综合运用.【练习7】如图,在Rt ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,BE CD ⊥,垂足为点F ,BE 交AC 于点E ,CE = 1cm ,AE = 3cm . (1)求证:ECB ∆∽BCA ∆; (2)求斜边AB 的长.【答案】(1)证明略;(2)AB =【解析】(1)∵90,ACB ∠=D AB 为的中点,∴DA DC =,∴A ECF ∠=∠,∵BE CD ⊥,∴90FCB CFB ∠+∠=,∵90FCE ECF ∠+∠=,∴ECF CBF ∠=∠, ∴A CBE ∠=∠,∵ECB BCA ∠=∠,∴ECB BCA ∆∆;(2)∵ECB BCA ∆∆,∴EC CBBC CA=,∵14EC AC AE EC ==+=,,∴2BC =, ∵90ACB ∠=,∴AB = 【总结】考查相似三角形的判定和性质的综合运用.。
