统计学计算题(54学时)
统计学计算题例题(含答案)
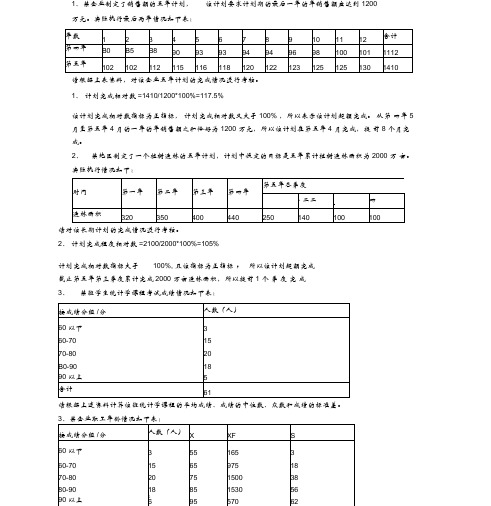
1、某企业制定了销售额的五年计划, 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标, 计划完成相对数又大于 100% ,所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元,所以该计划在第五年 4 月完成,提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 , 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积,所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表:X 二三于=4740/62=76.45 (分)Me=70+ (62/2-18) *10/20=76.5 (分)Mo=70+(20 J5)70/[(2CM5)+(2CM8)]=77 」4 (分)G-7(55-76.45f *3 +⋯⋯+ (95^76.45f *6/62=10.45 (分)4、某学校有5000 名学生,现从中按重复抽样方法抽取250 名同学,调查其每周观看电视的小时数的情况,获得资料如下表:请根据上述资料,以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀(好予f/(工f—1 )二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F (t) =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间,概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验,发现有45 件是不合格的,设定允许的极限误差为1.32% 。
武汉大学2005-2006线性代数试题(工科54学时)

武汉大学数学与统计学院2005-2006学年第一学期《线性代数》A 卷(供工科54学时用)学院 专业 学号 姓名注 所有答题均须有详细过程,内容必须写在答题纸上,凡写在其它地方一律无效。
一、计算题(每题5分,6题共30分):1.设111111111-⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭A ,当 1 n 是不小于的整数时,计算nA .2.设二阶方阵A 满足方程O I A A =+-232,求A 所有可能的特征值. 3.求二次型213232221321)()()(),,(x x x x x x x x x f ++-++=的秩.4.已知阶矩阵(2)n ≥,且非奇异,求**()A .5.设A 是三阶实对称矩阵,其对应的二次型的正负惯性指数均为1,且满足0+==E A E A -,计算A I 323+.6. 设n 阶向量Tx x )00(,,,, =α,矩阵T n I A αα-=,且T n x I A αα+=-1,求实数x .二、解答题(3题共45分,每题15分)1.设10102016A a ⎛⎫ ⎪= ⎪ ⎪⎝⎭,且()2R A =,满足,求a 和.2.已知222254245λλλ--⎛⎫ ⎪=-- ⎪ ⎪---⎝⎭A ,121λ⎛⎫ ⎪= ⎪ ⎪--⎝⎭b ,就方程组=AX b 无解、有唯一解、有无穷多解诸情形,对λ值进行讨论,并在有无穷多解时,求出其通解.3、设二次型222123123122331(,,)222=++---f x x x x x x x x x x x x ,(1).求出二次型f 的矩阵A 的全部特征值; (2).求可逆矩阵P ,使AP P 1-成为对角阵;(3).计算mA (m 是正整数).三、证明题和讨论题(2题共25分):1.(10分)设是阶实方阵,(1).当为奇数且I AA T=及时, 证明:0=-A I .(2).当 m 为给定任意正整数且O I A m =+)(时, 证明:A 可逆.2.(15分)对线性空间3R 中的向量组A :123,,ααα和B :123,,βββ,讨论下面的问题:(1).向量组B 是否能成为3R 中的基?能否用A 线性表示B ?如果可以,试求出由123,,ααα到123,,βββ的过渡矩阵P ,其中1100α⎛⎫ ⎪= ⎪ ⎪⎝⎭ 2110α⎛⎫ ⎪= ⎪ ⎪⎝⎭ 3111α⎛⎫ ⎪= ⎪ ⎪⎝⎭;111β⎛⎫ ⎪= ⎪ ⎪⎝⎭a 2112β⎛⎫ ⎪= ⎪ ⎪-⎝⎭a 3110β-⎛⎫ ⎪= ⎪⎪⎝⎭,且a 为实数.(2).若112321233123(22), (22), (22), βαααβαααβααα=+-=-+=--k k k k 是非零实数,(a )给出向量组123,,βββ线性无关的一个充要条件,并证明之;(b )给出矩阵123(),,βββ为正交阵的一个充要条件,并证明之.(2005-2006上工科54学时)线性代数A 卷参考解答一、计算题:1、11113111111()n --⎛⎫⎪--- ⎪⎪--⎝⎭;2、1212λλ=,=;3、 2 ;4、2n AA -; 5、-10 ; 6、-1 . 二、解答题:1、解:由初等变换求得a =1,(记E I =,下同),由0≠-EA ,因此 可逆 ,且2、解:经计算, 因此方程组有唯一解。
统计学

7 [4000] [4000] 5 4.2
9.5 [4200] [4000]
价格总水平
货物进出口总额(亿美元)
基本稳定
6800 14221
1.4
24.6
研究与试验发展经费支出占国内生产总值比重 (%)
高等教育毛入学率(%)
0.9
11.5
1.5
15
1.3
21
高中阶段教育毛入学率(%)
初中毛入学率(%) 全国总人口(万人)
分组步骤
1.对数据进行排序(升序)
107 108 108 110 112 112 113 114 115 117 117 117 118 118 118 119 120 120 121 122 122 122 122 123 123 123 123 124 124 124 125 125 126 126 127 127 127 128 128 129 130 131 133 133 134 134 135 137 139 139
上世纪末,受宏观经济波动的影响,由于市场需 求渐趋减少,我国粮食播种面积逐年下降,粮食产量 随之逐年减少。粮食产量由1998年的51230万吨逐步 下降到了2003年的43070万吨,下降幅度高达16%。
统计学的主要思想
随机性(偶然性) 如:掷硬币、出生婴儿性别
规律性 如:掷硬币100次,差不多50次正面朝 上,50次反面朝上 婴儿出生性别比107:100 规律也表现出某种随机性: 偏差 例:小儿麻痹症
经济管理(国家宏观经济统计、企业决策、 质量控制、市场开发) 医学、农学、法律… 几个图表
“十五”计划主要指标实现情况
指 标 2000年 “十五” 计划目标 2005年 “十五” 年均增长( %)
统计学相关与回归分析试题

相关与回归分析试题一、单项选择题1、自然界和人类社会中的诸多关系基本上可归纳为两种类型,这就是( )A.函数关系和相关关系B.因果关系和非因果关系C.随机关系和非随机关系D.简单关系和复杂关系 2、相关关系是指变量间的( )A.严格的函数关系B.简单关系和复杂关系C.严格的依存关系D.不严格的依存关系3.具有相关关系的两个变量的关系是()A.一个变量的取值不能由另一个变量唯一确定B.一个变量的取值由另一个变量唯一决定C.变量之间的一种确定性的数量关系D.变量之间存在的一种函数关系 4.当变量x 的值增加时,变量y 的值也随之增加,那么变量x 和变量y 之间存在着()。
A.正相关系 B.负相关系C.不确定关系D.非线性相关关系 5.下列相关系数的取值不正确的是()A. 0B. -0.96C.0.87D.1.066.两个变量之间的线性相关关系越不密切,相关系数r 值就越接近() A.-1 B.+1D.0 D.大于-1或小于+1 7.相关系数的值越接近-1,表明两个变量间()A.正线性相关关系越弱B.负线性相关关系越强C.负线性相关关系越弱D.正线性相关关系越强 8.回归分析中,被解释的变量称为()A.自变量B.因变量C.随机变量D.非随机变量 9.根据最小二乘法配合线性回归方程是使()A.最小)(=∑2y ˆ-y B.最小)(=∑y ˆ-yC.最小)(=∑2y -y D.最小)(=∑y -y10.回归方程 1.5x 123yˆ+=中回归系数的意思是,当自变量每增加一个单位时,因变量()A.增加1.5个单位B.平均增加1.5个单位C.增加123个单位D.平均增加123个单位11.若回归系数b 大于0,表明回归直线是上升的,此时相关系数r 的值() A.一定大于0 B.一定小于0 C.等于0 D.无法判断 12.在回归分析中,F 检验主要用来检验()A.相关系数的显著性B.回归系数的显著性C.线性关系的显著性D.估计标准误差的显著性13.在多元线性回归方程k k 22110x b x b x b b yˆ++++= 中,回归系数i b 表示() A.自变量i x 每变动一个单位因变量y 的平均变动量 B.自变量i x 每变动一个单位因变量y 的变动总量C.在其他条件不变的情况下,自变量i x 每变动一个单位因变量y 的平均变动量D.在其他条件不变的情况下,自变量i x 每变动一个单位因变量y 的变动总量 14.在多元线性回归分析中,t 检验用来检验()A.总体线性关系的显著性B.各回归系数的显著性C.样本线性关系的显著性D.各相关系数的显著性15.在多元线性回归分析中,如果F 检验表明线性关系显著,则意味着() A.至少有一个自变量与因变量之间的线性关系是显著的 B.所有自变量与因变量之间的线性关系都是显著的C.至少有一个自变量与因变量之间的线性关系是不显著的D.所有自变量与因变量之间的线性关系都是不显著的16.在多元线性回归分析中,若自变量i x 对因变量y 的影响很小,则回归系数i b () A.可能接近0 B.可能接近1 C.可能小于0 D.可能大于1 二、多项选择题1.下列关系中属于相关关系的是()A.家庭收入与消费支出的关系B.商品价格与商品需求量的关系C.速度不变,路程与时间的关系D.肥胖程度和死亡率的关系E.利率变动与居民储蓄存款额的关系2.判断变量之间相关关系形态及密切程度的方法有() A.回归方程 B.散点图 C.相关系数 D.回归系数3.回归方程可用于()A.根据自变量预测因变量B.根据给定因变量推算自变量C.确定两个变量之间的相关程度D.解释自变量与因变量的数量依存关系 4.在回归分析中要建立有意义的线性回归方程,应该满足的条件是() A.现象间存在着显著性的线性相关关系 B.相关系数必须等于1C.在两个变量中须确定自变量和因变量D.相关数列的项数应足够多 5.对于简单线性回归方程的回归系数b ,下列说法中正确的是()A.b 是回归直线的斜率B.b 的绝对值介于0~1之间C.b 接近0表明自变量对因变量的影响不大D.b 与r 有相同的符号三、计算题1、为探讨某产品的耗电量x (单位:度)与日产量y (单位:件)的相关关系,随机抽选了10个企业,经计算得到:,,,,要求:①计算相关系数;②建立直线回归方程,解释回归系数的经济意义。
商务与经济统计

Unit 2 第二单元 Estimation:Population Mean, Proportion and Variance总体均值,总体比例和总体方差的参数
估计----学时4
8.1 Interval Estimationof a Population Mean:Large-Sample Case总体均值的区间估计:大样本--2学时练习8.1 8.2 Interval Estimationof a Population Mean:Small-Sample Case总体均值的区间估计:小样本练习8.2 8.3 Determining the Sample Size样本数量的确定---2学时练习8.3 8.4 Interval Estimationof a Population Proportion总体比例的 区间估计练习8.4
Unit 4 第四单元 Analysis of Variance 方差分析---学时4
10.4 Introduction to Analysis of Variance 方差分析介绍----2学时 10.5 Analysis of Variance: Testing for the Equality of k Population Means---2学时 方差分析:k个总体均值相等的检验 练习10.4-10.5
Descriptive Statitics 1---Tabular and Graphical Methods 描述性统计学1 —表格和图形方法----3学时 2.1 Summarizing Qualitative Data定性数据汇 总 2.2 Summarizing Quantitative Data定量数据 汇总 2.4 Crosstablations列联表 and Scatter Diagrams散点图
统计学试题库计算题部分
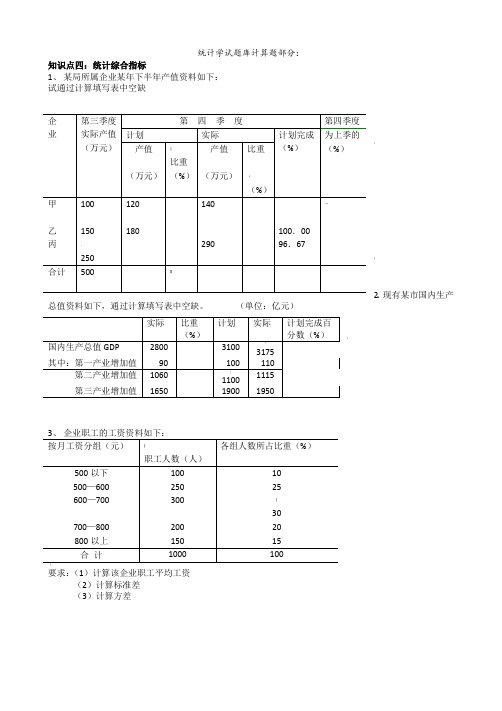
统计学试题库计算题部分:知识点四:统计综合指标1、 某局所属企业某年下半年产值资料如下: 试通过计算填写表中空缺:;2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元):要求:(1)计算该企业职工平均工资(2)计算标准差 (3)计算方差(2)比较哪个企业职工平均年龄更具代表性'、(7、甲、乙两企业工人有关资料如下:~要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性?10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:试比较甲、乙两企业该月上旬钢材供货的均衡性【11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:…要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强\求平均利润率。
问哪一个公司招员考试的成绩比较整齐(用标准差)!知识点五:时间数列及动态分析:试计算该市“九五”时期国民生产总值的年均递增率|(2)预测2004年存款余额将达到多少4、1997—2002年某企业职工人数和非生产人数资料如下:人员占全部职工人数的平均比重|要求:根据上述资料计算该企业这种产品第一季度单位产品成本(2)计算上半年平均计划完成程度,(2)计算四年平均工业增加值占国内生产总值的比重^^(2)用最小平方法配合直线趋势方程)年的销售额。
|知识点六:统计指数'(2)编制产量总指数、计算由于产量变动而增减的产值(3)编制出厂价格总指数,计算由于价格变动而增减的产值(2)计算销售量总指数(3)对总销售额的变动进行因素分析—(2)三种商品价格及销售量的综合变动指数(3)由于价格提高和销售量的增加各使销售额增加多少[(2)物价总指数(3)由于物价变动所引起的总产值的增加或减少额5、&(2)销售量总指数以及由于销售量变动对销售额的影响(8、[.8、某商店出售三种商品,资料如下:试计算价格总指数Array@~'11、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资料如下: 试计算:(1)以单位成本为同度量因素的产量总指数;(2)单位成本总指数;(3)对总成本进行两因素分析。
统计学考试计算题答案统计学试题及答案

统计学考试计算题答案统计学试题及答案一、填空题(每空1分,共10分)1.从标志与统计指标的对应关系来看,标志通常与( )相同。
2.某连续变量数列,其首组为开口组,上限为80,又知其邻组的组中值为95,则首组的组中值为( )。
3.国民收入中消费额和积累额的比例为1:0.4,这是( )相对指标。
4.在+A的公式中,A称为( )。
5.峰度是指次数分布曲线项峰的( ),是次数分布的一个重要特征。
6.用水平法求平均发展速度本质上是求( )平均数。
7.按习惯做法,采用加权调和平均形式编制的物量指标指数,其计算公式实际上是( )综合指数公式的变形。
8.对一个确定的总体,抽选的样本可能个数与( )和( )有关。
9.用来反映回归直线代表性大小和因变量估计值准确程度的指标称( )。
二、是非题(每小题1分,共10分)1.统计史上,将国势学派和图表学派统称为社会经济统计学派。
2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。
3.学生按身高分组,适宜采用等距分组。
4.根据组距数列计算求得的算术平均数是一个近似值。
5.基尼系数的基本公式可转化为2(S1+S2+S3)。
6.对连续时点数列求序时平均数,应采用加权算术平均方法。
7.分段平均法的数学依据是Σ(Y-YC)2=最小值。
8.平均数、指数都有静态与动态之分。
9.在不重复抽样下,从总体N中抽取容量为n的样本,则所有可能的样本个数为Nn个10.根据每对____和y的等级计算结果ΣD2=0,说明____与y之间存在完全正相关。
三、单项选择题(每小题2分,共10分)1.在综合统计指标分析^p 的基础上,对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计分组法C.综合指标法D.模型推断法2.对同一总体选择两个或两个以上的标志分别进行简单分组,形成A.复合分组B.层叠分组C.平行分组体系D.复合分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列,那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中,各个指数的A.同度量因素是变动的B.基期是变动的C.指数化因数是变动的D.时期是变动的四、多项选择题(每小题2分,共10分)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计指标体系B.专题统计指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计指标体系2.典型调查A.是一次性调查B.是专门组织的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.可用采访法取得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口净增加数4.重复抽样的特点是A.各次抽选互不影响B.各次抽选相互影响C.每次抽选时,总体单位数逐渐减少D.每次抽选时,总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.下列关系中,相关系数小于0的现象有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分,共60分)要求:(1)写出必要的计算公式和计算过程,否则,酌情扣分。
统计学计算题(54学时)

统计学习题集第三章数据分布特征的描述五、计算题1。
某企业两个车间的工人生产定额完成情况如下表:技术水平A车间B车间工人数完成定额工时人均完成工时工人数完成工时定额人均完成工时高50 14000 280 20 6000 300中30 7500 250 40 10400 260低20 4000 200 40 8200 205合计100 25500 255 100 24600 246从表中看,各个技术级别的工人劳动生产率(人均完成工时定额)都是A车间低于B车间,试问:为什么A车间的平均劳动生产率又会高于B车间呢?3。
根据某城市500户居民家计调查结果,将居民户按其食品开支占全部消费开支的比重(即恩格尔系数)分组后,得到如下的频数分布资料:恩格尔系数(%) 居民户数20以下620~30 3830~40 10740~50 13750~60 11460~70 7470以上24合计500要求:(1)据资料估计该城市恩格尔系数的中位数和众数,并说明这两个平均数的具体分析意义。
(2)利用上表资料,按居民户数加权计算该城市恩格尔系数的算术平均数.(3)试考虑,上面计算的算术平均数能否说明该城市恩格尔系数的一般水平?为什么?恩格尔系数(%)居民户数(户)f 组中值x 向上累积频数20以下 6 15 620~30 38 25 4430~40 107 35 15140~50 137 45 28850~60 114 55 40260~70 74 65 47670以上24 75 500合计500 --答:(1)Me=47。
226%,指处于中间位置的居民家庭恩格尔系数水平;Mo=45。
661%,指居民家庭中出现最多的恩格尔系数水平;(2)均值=47。
660%;4. 某学院二年级两个班的学生英语统考成绩如下表。
要求:(1)分别计算两个班的平均成绩;(2)试比较说明,哪个班的平均成绩更有代表性?哪个班的学生英语水平差距更大?你是用什么指标来说明这些问题的;为什么?英语统考成绩学生人数A班B班60以下4 660~70 12 1370~80 24 2880~90 6 890以上4 5合计50 605. 利用上题资料,试计算A班成绩分布的极差与平均差,并与标准差的计算结果进行比较,看看三者之间是何种数量关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学习题集第三章数据分布特征的描述五、计算题1. 某企业两个车间的工人生产定额完成情况如下表:技术水平A车间B车间工人数完成定额工时人均完成工时工人数完成工时定额人均完成工时高50 14000 280 20 6000 300中30 7500 250 40 10400 260低20 4000 200 40 8200 205合计100 25500 255 100 24600 246从表中看,各个技术级别的工人劳动生产率(人均完成工时定额)都是A车间低于B车间,试问:为什么A车间的平均劳动生产率又会高于B车间呢3. 根据某城市500户居民家计调查结果,将居民户按其食品开支占全部消费开支的比重(即恩格尔系数)分组后,得到如下的频数分布资料:恩格尔系数(%) 居民户数20以下620~30 3830~40 10740~50 13750~60 11460~70 7470以上24合计500要求:(1)据资料估计该城市恩格尔系数的中位数和众数,并说明这两个平均数的具体分析意义。
(2)利用上表资料,按居民户数加权计算该城市恩格尔系数的算术平均数。
(3)试考虑,上面计算的算术平均数能否说明该城市恩格尔系数的一般水平?为什么?答:(1)Me=47.226%,指处于中间位置的居民家庭恩格尔系数水平;Mo=45.661%,指居民家庭中出现最多的恩格尔系数水平;(2)均值=47.660%;4. 某学院二年级两个班的学生英语统考成绩如下表。
要求:(1)分别计算两个班的平均成绩;(2)试比较说明,哪个班的平均成绩更有代表性?哪个班的学生英语水平差距更大?你是用什么指标来说明这些问题的;为什么英语统考成绩学生人数A班B班60以下4 660~70 12 1370~80 24 2880~90 6 890以上4 5合计50 605. 利用上题资料,试计算A班成绩分布的极差与平均差,并与标准差的计算结果进行比较,看看三者之间是何种数量关系。
7. 给出两个企业的员工工资资料如下表:A企业B企业月工资(元) 员工数(人) 月工资(元) 员工数(人)500以下15 800以下16500~700 30 800~1000 33700~900 65 1000~1200 64900~1100 96 1200~1400 981100~1300 44 1400~1600 431300~1500 33 1600~1800 341500以上17 1800以上18合计300 合计306要求:(1)分别计算两个企业的平均工资和工资标准差。
(2)试比较说明,哪个企业的员工工资水平差距更大?为什么10. 甲、乙两个企业生产三种产品的单位成本和总成本资料如下:产品名称单位成本(元) 总成本(元)甲企业乙企业A 15 2100 3255B 20 3000 1500C 30 1500 1500试比较哪个企业的总平均成本高并分析其原因。
11. 一项关于大学生体重状况的研究发现,男生的平均体重为60kg,标准差为5kg;女生的平均体重为50kg,标准差为5kg,请回答下面的问题:(1)男生的体重差异大还是女生的体重差异大?为什么(2)以磅为单位(1磅=2. 2kg)求体重的平均数和标准差。
13. 2004年某月份某企业按工人劳动生产率高低分组的生产班组数和产量资料如下:按工人劳动生产率分组(件/人) 生产班组生产工人数50~60 10 15060~70 7 10070~80 5 7080~90 2 3090以上1 16合计25 336试计算该企业工人平均劳动生产率。
17. 某百货公司6月份各天的销售数据如下(单位:万元):257 276 297 252 238 310 240 236 265 278271 292 261 281 301 274 267 280 291 258272 284 268 303 273 263 322 249 269 295(1)计算该百货公司日销售额的均值和中位数;(2)计算日销售额的标准差。
18. 已知某地区农民家庭按年人均收入分组的资料如下:按人均收入分组(元) 家庭户数占总户数比重(%)1000以下2.31000~2000 13.72000~3000 19.73000~4000 15.24000~5000 15.15000~6000 20.06000以上14.0合计100.0要求:计算该地区平均每户人均收入的中位数、均值及标准差。
19.对10名成年人和10名幼儿的身高(单位:厘米)进行抽样调查,结果如下:成年组166 169 172 177 180 170 172 174 168 173幼儿组68 69 68 70 71 73 72 73 74 75要求:(1)要比较成年组和幼儿组的身高差异应采用什么样的指标测度值?为什么(2)比较分析哪一组的身高差异大。
21. 某企业有两个生产车间,甲车间20名工人,人均日加工产品数为78件,标准差为8件;乙车间有30名工人,人均日加工产品数为72件,标准差为10件。
计算两个车间日加工产品的平均值及标准差。
22. 已知某地区农民家庭按年人均收入分组的资料如表所示。
按人均收入分组(元)家庭户数占总户数比重(%)100以下2.3100~200 13.7200~300 19.7300~400 15.2400~500 15.1500~600 20.0600以上14.0合计100计算该地区平均每户人均收入的中位数、均值及标准差。
第八章时间序列五、计算题1. 某国对外承包工程营业额历年资料:年份1999 2000 2001 2002 2003 2004 2005营业额(百万美元) 189 316 494 663 819 1114 1253要求:(1)列表计算各年的增减量、发展速度和增减速度。
(2)逐期增减量与累计增减量有何联系(3)定基发展速度与环比发展速度有何联系(4)定基增减速度与环比增减速度如何换算(5)发展速度与增减速度的关系如何(6)结合本例验证(2)(3)(4)(5)。
(7)计算平均增减量、平均发展速度和平均增减速度。
4. 某商场1995年销售额950万元,如果以后每年平均增长15%,试计算多少年后销售额能达到1500万元?5. 某制糖厂1995年生产糖5万吨,如果平均每年增长16%,问多少年后糖的总产量可以达到40 万吨?6. 某地外贸总额1991年至1994年年均增长2.9%,1995年较1994年增长4.5%,1998年较1995年增长20%,试计算该地对外贸易额1991-1998年的平均增长速度。
7.2000年甲地区工业总产值为4.65亿元,乙地区工业总产值为7.52亿元,第十个五年计划期间,乙地区五年的总发展速度为213.68%,试问甲地区要在2005年赶上乙地区,其平均每年增长速度应该是多少?8. 某商店上半年每月末的商品储存额资料如下月份1 2 3 4 5 6月末储存额(万元) 26 30 28 32 31 34已知去年末的储存额为24万元。
试计算上半年平均商品储存额。
9. 某企业2004年职工人数资料如下:日期1月1日3月31日5月1日11月1日12月31日人数(人) 3020 3160 2950 3200 3270试计算全年职工平均人数。
10. 某地区2003年的工业总产值为1500万元,2004年的工业总产值比2003年增长10%,2003年又比2002年增长10%,如果该地区从2003~2010年工业的发展速度每递增7.2%,那么到2010年该地区工业总产值可能达到多少万元?12. 某地区GDP1989-1992年4年间平均每年递增15%,1993年-1995年三年间平均每年递增12% ,1996年-1999年4年间平均每年递增9%,计算:(1)该地区11年来GDP共增长了多少(2)年平均增长速度是多少?13. (1)已知我国1980年年末总人口为9.8705亿人,若要求在20世纪末将人口控制在13亿人以内,在20年内人口自然增长率应控制在什么水平上(2)又知我国1980年的粮食总产量为3205.6亿公斤,若要求20世纪末人均用粮应达到400公斤,在20年间我国粮食产量每年应平均增长百分之几才能达到这一目标(3)仍按上述条件,如果人口自然增长率控制在10‰,粮食产量每年递增3%,到1998年全国每人年平均用粮可达到什么水平?14. 某企业2004年各季度计划产值和产值计划完成程度的资料如下:季度计划产值(万元) 产值计划完成(%)一860 130二887 135三875 138四898 125试计算该企业年度计划平均完成百分比。
15. 某地区2004年下半年各月的社会劳动者人数和国内生产总值资料如下:月份7 8 9 10 11 12国内生产总值(亿元) 300 310 315 325 340 360月初社会劳动者人数(万人) 1680 1800 1760 1860 1920 2060又知2004年末社会劳动者人数为2100万人。
要求:计算该地区2004年下半年以国内生产总值计算的月平均劳动生产率。
16. 某零售商场2004年下半年的零售额,库存额和流通费用额资料:月份7 8 9 10 11 12零售总额(万元) 32 34 33 41 30 46月初库存额(万元) 14 15 12 16 10 13流通费用额(万元) 2.9 3.1 2.7 3.4 3.2 3.0已知2005年1月初库存额55万元。
试计算第三季、第四季和下半年的平均月商品流转次数和商品流通费用率。
(提示:商品流转次数=零售总额÷平均库存额;商品流通费用率=流通费用额÷零售总额)17. 某地商品零售额资料如下:年份第一年第二年第三年第四年第五年第六年第七年商品零售额(百万元) 58 66 74 80 89 94 109要求:(1)配合线性趋势方程。
(2)预测第八年商品零售额。
(3)解释系数a与b的含义。
18. 某公司2002-2005年各月毛线销售量如下:单位:公斤销售量年份2002 2003 2004 20051 8000 15000 24000 280002 6000 9000 15000 140003 2000 4000 6000 80004 1000 2500 4000 30005 600 1000 2000 12006 400 800 1100 9007 800 1200 3200 37008 1200 2000 4000 48009 2000 3500 7000 830010 5000 8500 15000 1400011 21000 34000 42000 4700012 25000 35000 48000 51000要求:(1)按月平均法计算季节比率。
