人教版初中数学圆的经典测试题含答案解析
初中数学圆的经典测试题及解析
解：如图所示，正六边形的边长为2cm，OG⊥BC，
∵六边形ABCDEF是正六边形，
∴∠BOC=360°÷6=60°，
∵OB=OC，OG⊥BC，
∴∠BOG=∠COG= ∠BOC =30°，
∵OG⊥BC，OB=OC，BC=2cm，
∴BG= BC= ×2=1cm，
∴OB= =2cm，
∴OG= ，
∴圆形纸片的半径为 cm，
【详解】
解：如图所示，
∵等腰三角形的底边和高线长均为10cm，
∴等腰三角形的斜边长＝ ＝5 ，即圆锥的母线长为5 cm，圆锥底面圆半径为5，
A． B． C． D．
【答案】C
【解析】
【分析】
连接 ，如图，利用切线的性质得 ，在 中利用勾股定理得 ，利用面积法求得 ，然后利用圆锥的侧面展开图为扇形和扇形的面积公式计算圆锥形纸帽的表面．
【详解】
解：连接 ，作 于 ，如图，
圆锥的母线 与 相切于点 ，
，
在 中， ， ，
，
，
，
圆锥形纸帽的底面圆的半径为 ，母线长为12，
【详解】
设P（x，y），
∵PA2＝（x+1）2+y2，PB2＝（x﹣1）2+y2，
∴PA2+PB2＝2x2+2y2+2＝2（x2+y2）+2，
∵OP2＝x2+y2，
∴PA2+PB2＝2OP2+2，
当点P处于OC与圆的交点上时，OP取得最值，
∴OP的最小值为CO﹣CP＝3﹣1＝2，
∴PA2+PB2最小值为2×22+2＝10．
A． B． C． D．
【答案】A
人教版九年级数学上册《圆》真题精选(含答案解析)
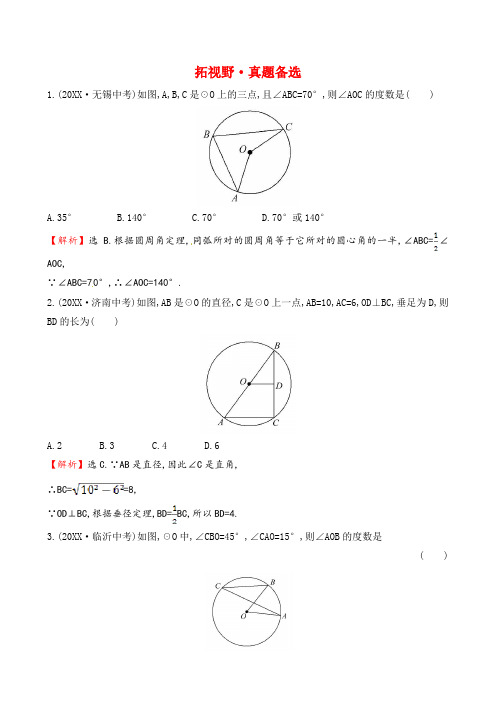
拓视野·真题备选1.(20XX·无锡中考)如图,A,B,C是☉O上的三点,且∠ABC=70°,则∠AOC的度数是( )A.35°B.140°C.70°D.70°或140°【解析】选 B.根据圆周角定理,同弧所对的圆周角等于它所对的圆心角的一半,∠ABC=∠AOC,∵∠ABC=70°,∴∠AOC=140°.2.(20XX·济南中考)如图,AB是☉O的直径,C是☉O上一点,AB=10,AC=6,OD⊥BC,垂足为D,则BD的长为( )A.2B.3C.4D.6【解析】选C.∵AB是直径,因此∠C是直角,∴BC==8,∵OD⊥BC,根据垂径定理,BD=BC,所以BD=4.3.(20XX·临沂中考)如图,☉O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是( )A.75°B.60°C.45°D.30°【解析】选B.连接OC,延长AO与☉O交于点D,∴△BOC为等腰三角形,∴∠BOC=180°-2∠CBO=180°-2×45°=90°,∵∠CAO=15°,∴∠COD=30°,∴∠AOB=60°.4.(20XX·乐山中考)如图,圆心在y轴的负半轴上,半径为5的☉B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与☉B相交于C,D两点,则弦CD的长所有可能的整数值有( )A.1个B.2个C.3个D.4个【解析】选C.半径为5的☉B与y轴的正半轴交于点A(0,1),可知OB=4,所以点B(0,-4).因为P(0,-7),BP=3.当弦CD⊥AB时,弦CD最短.连接BC,由勾股定理得CP===4,由垂径定理可知CD=2CP=8;当弦CD是☉B的直径时,CD=10.所以8≤CD≤10,所以CD的整数值为:8,9,10共三个.5.(20XX·枣庄中考)如图,已知线段OA交☉O于点B,且OB=AB,点P是☉O上的一个动点,那么∠OAP的最大值是( )A.30°B.45°C.60°D.90°【解析】选A.根据题意知,当∠OAP 取最大值时,OP ⊥AP;在Rt △AOP 中,∵OP=OB,OB=AB, ∴OA=2OP,∴∠OAP=30°.6.(20XX ·舟山中考)如图,某厂生产横截面直径为7cm 的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面,为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )A.cmB.cm C.cm D.7πcm【解析】选B.∵字样在罐头侧面所形成的弧的度数为90°,∴此弧所对的圆心角为90°,由题意可得,r=cm,则“蘑菇罐头”字样的长==cm.7.(20XX ·泰安中考)如图,AB,CD 是☉O 的两条互相垂直的直径,点O 1,O 2,O 3,O 4分别是OA,OB,OC,OD 的中点,若☉O 的半径是2,则阴影部分的面积为( )A.8B.4C.4π+4D.4π-4【解析】选A.连接AD,DB,BC,CA,S 阴影面积=S 四边形ADBC =42÷2=8.8.(20XX ·恩施中考)如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD 沿x 轴的正方向无滑动地在x 轴上滚动,当点A 离开原点后第一次落在x 轴上时,点A 运动的路径线与x 轴围成图形的面积为( )A.+B.+1C.π+1D.π+【解析】选C.根据条件看出:点A 到A 1,是以点B 为圆心、AB 为半径所得;点A 1到A 2,是以点C 1为圆心、A 1C 1为半径所得;点A 2到A 3,是以点D 2为圆心、A 2D 2为半径所得.即由2个半径为1、圆心角为90°的扇形和半径为、圆心角为90°的扇形以及2个直角边长为1的等腰直角三角形组成的图形,其面积为π+1.9.(20XX ·赤峰中考)如图,ABCD 是平行四边形,AB 是☉O 的直径,点D 在☉O 上,AD = OA =1,则图中阴影部分的面积为( )A. B.+C.-D.【解析】选A.DC 交☉O 于E,连接OE,过D 作DF ⊥AB 于F,∵OA=OD=AD=1,∴△ADO 是等边三角形.∴AF=,在Rt △ADF 中,根据勾股定理得DF==.在平行四边形ABCD 中,AB∥CD.∴∠EDO=60°.∵OD=OE,∴△ODE 是等边三角形. ∴∠EOB=∠DEO=60°.∵S ▱ABCD =AB ×DF=2×=,S △AOD =S △DOE =×1×=,S 扇形OEB =S 扇形ODE ==.∴阴影部分的面积=S ▱ABCD -S △AOD - S △DOE -S 扇形OEB +S 扇形ODE -S △DOE =-×2-+-=.10.(20XX ·邵阳中考)如图所示,弦AB,CD 相交于点O,连接AD,BC.在不添加辅助线的情况下,请在图中找出一对相等的角,它们是 .【解析】对顶角有:∠AOC=∠BOD,和∠AOD=∠BOC. 同弧所对的圆周角有:∠A=∠C,∠B=∠D.故填∠A=∠C(或∠B=∠D 或∠AOC=∠BOD,或∠AOD=∠BOC).答案:答案不唯一,∠A=∠C,或∠B=∠D,或∠AOC=∠BOD,或∠AOD=∠BOC11.(20XX ·兰州中考)如图,量角器的直径与直角三角板ABC 的斜边AB 重合,其中量角器0刻度线的端点N 与点A 重合,射线CP 从CA 处出发沿顺时针方向以每秒3度的速度旋转,CP 与量角器的半圆弧交于点E,第24秒时,点E 在量角器上对应的度数是 度.【解析】连接OE,∵∠ACB=90°,∴点C在以AB为直径的圆上,即点C在☉O上,∴∠EOA=2∠ECA,∵∠ECA=3°×24=72°,∴∠AOE=2∠ECA=2×72°=144°.答案:14412.(20XX·烟台中考)如图,正方形ABCD的边长为4,点E在BC边上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连接AF,CF,则图中阴影部分的面积为.【解析】设正方形EFGB的边长为a,则阴影部分的面积=+a2+-=4π.答案:4π13.(20XX·衢州中考)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角(∠AOB)为120XXOC的长为2cm,则三角板和量角器重叠部分的面积为.【解析】∵∠AOB=120XX ∴∠BOC=60°,在Rt △BOC 中,OC=2,∴OB=4,BC=2,∴S重叠部分=+×2×2=π+2.答案:π+2cm 214.(20XX ·六盘水中考)把边长为1的正方形纸片OABC 放在直线m 上,OA 边在直线m 上,然后将正方形纸片绕着顶点A 按顺时针方向旋转90°,此时,点O 运动到了点O 1处(即点B 处),点C 运动到了C 1处,点B 运动到了点B 1处,又将正方形纸片AO 1C 1B 1绕B 1点按顺时针方向旋转90°……,按上述方法经过4次旋转后,顶点O 经过的总路程为 .经过61次旋转后,顶点O 经过的总路程为 .【解析】根据图形的旋转性质可知,正方形第一次旋转顶点O 经过的路线长为l 1=×π×1;第二次旋转顶点O 经过的路线长为l 2=×π×;第三次旋转顶点O 经过的路线长为l 3=×π×1;第四次旋转顶点O 经过的路线长为0,所以经过4次旋转后,顶点O 经过的总路程为l 1+l 2+l 3+0=×π×1+×π×+×π×1+0=π.由于61=4×15+1,所以经过61次旋转后,顶点O 经过的总路程为π×15+=π.答案:ππ15.(20XX ·巴中中考)底面半径为1,母线长为2的圆锥的侧面积等于 .【解析】因为圆锥的侧面积就等于母线长乘底面周长的一半,所以圆锥的侧面积=2×2π÷2=2π. 答案:2π16.(20XX·大连中考)用一个圆心角为90°,半径为32cm的扇形作为一个圆锥的侧面(接缝处不重叠),则这个圆锥的底面圆的半径为cm.【解析】扇形的弧长l==16π,16π÷2π=8.答案:817.(20XX·黄石中考)如图,AB是☉O的直径,AM和BN是☉O的两条切线,E是☉O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN.(1)求证:DE是☉O的切线.(2)求证:OF=CD.【证明】(1)连接OE,AM是☉O的切线,OA是☉O的半径,∴∠DAO=90°,∵OD∥BE,∴∠AOD=∠OBE,∠DOE=∠OEB,∵OB=OE,∴∠OEB=∠OBE.∴∠A O D=∠DOE.在△AOD和△DOE中∴△AOD≌△EOD,∴∠DAO=∠DEO=90°,∴DE与☉O相切.(2)∵AM和BN是☉O的两切线,∴MA⊥AB,NB⊥AB,∴AD∥BC,∵O是AB的中点,OF∥BN,∴OF∥AD且OF=(AD+BC).∵DE切☉O于点E,∴DA=DE,CB=CE,∴DC=AD+CB,∴OF=CD.。
初三数学圆试题答案及解析
初三数学圆试题答案及解析1.如图，AB是⊙O的直径，点C，D是半圆O的三等分点，过点C作⊙O的切线交AD的延长线于点E，过点D作DF⊥AB于点F，交⊙O于点H，连接DC，AC．（1）求证：∠AEC=90°；（2）试判断以点A，O，C，D为顶点的四边形的形状，并说明理由；（3）若DC=2，求DH的长．【答案】（1）证明见解析；（2）四边形AOCD为菱形；（3）DH=2．【解析】（1）连接OC，根据EC与⊙O切点C，则∠OCE=90°，由题意得，∠DAC=∠CAB，即可证明AE∥OC，则∠AEC+∠OCE=180°，从而得出∠AEC=90°；（2）四边形AOCD为菱形．由（1）得，则∠DCA=∠CAB可证明四边形AOCD是平行四边形，再由OA=OC，即可证明平行四边形AOCD是菱形（一组邻边相等的平行四边形是菱形）；（3）连接OD．根据四边形AOCD为菱形，得△OAD是等边三角形，则∠AOD=60°，再由DH⊥AB于点F，AB为直径，在Rt△OFD中，根据sin∠AOD=，求得DH的长．试题解析：（1）连接OC，∵EC与⊙O切点C，∴OC⊥EC，∴∠OCE=90°，∵点CD是半圆O的三等分点，∴，∴∠DAC=∠CAB，∵OA=OC，∴∠CAB=∠OCA，∴∠DAC=∠OCA，∴AE∥OC（内错角相等，两直线平行）∴∠AEC+∠OCE=180°，∴∠AEC=90°；（2）四边形AOCD为菱形．理由是：∵，∴∠DCA=∠CAB，∴CD∥OA，又∵AE∥OC，∴四边形AOCD是平行四边形，∵OA=OC，∴平行四边形AOCD是菱形（一组邻边相等的平行四边形是菱形）；（3）连接OD．∵四边形AOCD为菱形，∴OA=AD=DC=2，∵OA=OD，∴OA=OD=AD=2，∴△OAD是等边三角形，∴∠AOD=60°，∵DH⊥AB于点F，AB为直径，∴DH=2DF，在Rt△OFD中，sin∠AOD=，∴DF=ODsin∠AOD=2sin60°=，∴DH=2DF=2．【考点】1.切线的性质2.等边三角形的判定与性质3.菱形的判定与性质4.解直角三角形．2.如图，AB是⊙O的直径，点C是圆上一点，,则 °．【答案】20.【解析】∵AB是⊙O的直径，∴.∵OA=OC，，∴.∴.【考点】1.圆周角定理；2.等腰三角形的性质.3.已知一个圆锥的底面半径为3 cm，母线长为10 cm，则这个圆锥的侧面积为 ()A．15π cm2B．30π cm2C．60π cm2D．3cm2【答案】B【解析】圆锥的侧面积＝π×3×10＝30π cm2.故选B.4.如图，⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长是A．4cm B．6cm C．8cm D．10cm【答案】C.【解析】连接OB；∵CD=10cm，∴OC=5cm；∵OM：OC=3：5，∴OM=3cm；Rt△OCP中，OC=OA=5cm，OM=3cm；由勾股定理，得：所以AB=2AM=8cm，故选C．考点: 1.垂径定理；2.勾股定理．5.如图，点A是半圆上一个三等分点，点B是的中点，点P是直径MN上一动点，若⊙O的半径为1，则AP＋BP的最小值是．【答案】.【解析】本题是要在MN上找一点P，使PA+PB的值最小，设A′是A关于MN的对称点，连接A′B，与MN的交点即为点P．此时PA+PB=A′B是最小值，可证△OA′B是等腰直角三角形，从而得出结果．试题解析：作点A关于MN的对称点A′，连接A′B，交MN于点P，则PA+PB最小，连接OA′，AA′．∵点A与A′关于MN对称，点A是半圆上的一个三等分点，∴∠A′ON=∠AON=60°，PA=PA′，∵点B是弧AN^的中点，∴∠BON=30°，∴∠A′OB=∠A′ON+∠BON=90°，又∵OA=OA′=1，∴A′B=．∴PA+PB=PA′+PB=A′B=．考点: 1.垂径定理；2.勾股定理；3.圆心角、弧、弦的关系；4.轴对称-最短路线问题．6.如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°．若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(秒)(0≤t＜3),连结EF,当t值为________秒时,△BEF是直角三角形．【答案】t=1或或．【解析】∵AB是⊙O的直径,∴∠C=90°．∵∠ABC=60°,∴∠A=30°．又BC=3cm,∴AB=6cm．则当0≤t＜3时,即点E从A到B再到O（此时和O不重合）．若△BEF是直角三角形,则当∠BFE=90°时,根据垂径定理,知点E与点O重合,即t=1;当∠BEF=90°时,则BE=BF=,此时点E走过的路程是或,则运动时间是s或s．故答案是t=1或或．【考点】圆周角定理．7.如图，边长为1的小正方形构成的网格中，⊙O的半径为1，则图中阴影部分两个小扇形的面积之和为（结果保留π）【答案】.【解析】如图,根据正方形和圆的对称性,上方的小扇形与下方的红色小扇形面积相等,所以图中阴影部分两个小扇形的面积之和为四分之一半径为1的圆的面积,即.【考点】1.网格问题;2. 正方形和圆的对称性;3. 扇形的面积;4.转换思想的应用.8.如图，从A地到B地有两条路可走，一条路是大半圆，另一条路是4个小半圆.有一天，一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走，它不敢与猫同行（怕被猫吃掉），就沿着4个小半圆行走.假设猫和老鼠行走的速度相同，那么下列结论正确的是A．猫先到达B地；B．老鼠先到达B地；C．猫和老鼠同时到达B地；D．无法确定.【答案】C．【解析】以AB为直径的半圆的长是：•AB；设四个小半圆的直径分别是a，b，c，d，则a+b+c+d=AB．则老鼠行走的路径长是：a+b+c+d=（a+b+c+d）=•AB．故猫和老鼠行走的路径长相同．故选C．【考点】弧长公式．9.如图，已知在⊙O中，弦AB的长为8cm，半径为5 ㎝，过O作OC AB求点O与AB的距离．【答案】3cm.【解析】连接OA．根据垂径定理求得AC的长，再进一步根据勾股定理即可求得OC的长．试题解析:连接OA．如图：∵OC⊥AB，弦AB长为8cm，∴AC=4（cm）．根据勾股定理，得OC=考点: 1.垂径定理；2.勾股定理．10.如图所示，内接于,，，则______.【答案】．【解析】由圆周角定理知：,由于，得到,所以：．故答案是．【考点】圆周角定理．11.如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径,点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D.（1）求证：CD为⊙O的切线；（2）若DC+DA=6，⊙O的直径为10，求AB的长度.【答案】（1）详见解析；（2）6【解析】（1）连接OC，根据题意可证得∠CAD+∠DCA=90°，再根据角平分线的性质，得∠DCO=90°，则CD为⊙O的切线；（2）过O作OF⊥AB，则∠OCD=∠CDA=∠OFD=90°，得四边形OCDF为矩形，设AD=x，在Rt△AOF中，由勾股定理得（5-x）2+（6-x）2=25，从而求得x的值，由勾股定理得出AB的长．试题解析：（1）连接OC，∵OA=OC，∴∠OCA=∠OAC，∵AC平分∠PAE，∴∠DAC=∠CAO，∴∠DAC=∠OCA，∴PB∥OC，∵CD⊥PA，∴CD⊥OC，CO为⊙O半径，∴CD为⊙O的切线；（2）过O作OF⊥AB，垂足为F，∴∠OCD=∠CDA=∠OFD=90°，∴四边形DCOF为矩形，∴OC=FD，OF=CD．∵DC+DA=6，设AD=x，则OF=CD=6-x，∵⊙O的直径为10，∴DF=OC=5，∴AF=5-x，在Rt△AOF中，由勾股定理得AF2+OF2=OA2．即（5-x）2+（6-x）2=25，化简得x2-11x+18=0，解得x1=2，x2=9．∵CD=6-x大于0，故x=9舍去，∴x=2，从而AD=2，AF=5-2=3，∵OF⊥AB，由垂径定理知，F为AB的中点，∴AB=2AF=6．【考点】1.切线的判定和性质；2.勾股定理；3.矩形的判定和性质4.垂径定理12.如图MN＝10是⊙Ｏ的直径，AE⊥MN于E，CF⊥MN于F，AE＝4，CF＝3，（1）在MN上找一点P，使PA＋PC最短；（2）求出PA＋PC最短的距离。
人教中考数学圆的综合综合练习题含答案解析
一、圆的综合 真题与模拟题分类汇编（难题易错题）1．（1）如图1，在矩形ABCD 中，点O 在边AB 上，∠AOC =∠BOD ，求证：AO =OB ； （2）如图2，AB 是⊙O 的直径，PA 与⊙O 相切于点A ，OP 与⊙O 相交于点C ，连接CB ，∠OPA =40°，求∠ABC 的度数．【答案】（1）证明见解析；（2）25°.【解析】试题分析： （1）根据等量代换可求得∠AOD=∠BOC ，根据矩形的对边相等，每个角都是直角，可知∠A=∠B=90°，AD=BC ，根据三角形全等的判定AAS 证得△AOD ≌△BOC ，从而得证结论．（2）利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数，然后利用圆周角定理来求∠ABC 的度数．试题解析：（1）∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°，AD=BC∴AOD BOC ∆≅∆∴AO=OB（2）解：∵AB 是O 的直径，PA 与O 相切于点A ， ∴PA ⊥AB ，∴∠A=90°.又∵∠OPA=40°，∴∠AOP=50°，∵OB=OC ，∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB ， ∴1252B OCB AOP ∠=∠=∠=︒.2．定义：有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形．（1）如图1，四边形ABCD 内接于⊙O ，∠DCB ﹣∠ADC=∠A ，求证：四边形ABCD 为圆内接倍角四边形；（2）在（1）的条件下，⊙O 半径为5．①若AD为直径，且sinA=45，求BC的长；②若四边形ABCD中有一个角为60°，且BC=CD，则四边形ABCD的面积是；（3）在（1）的条件下，记AB=a，BC=b，CD=c，AD=d，求证：d2﹣b2=ab+cd．【答案】（1）见解析；（2）①BC＝6，②753或754；（3）见解析【解析】【分析】（1）先判断出∠ADC=180°﹣2∠A．进而判断出∠ABC=2∠A，即可得出结论；（2）①先用锐角三角函数求出BD，进而得出AB，由（1）得出∠ADB=∠BDC，即可得出结论；②分两种情况：利用面积和差即可得出结论；（3）先得出BE=BC=b，DE=DA=b，进而得出CE=d﹣c，再判断出△EBC∽△EDA，即可得出结论．【详解】（1）设∠A=α，则∠DCB=180°﹣α．∵∠DCB﹣∠ADC=∠A，∴∠ADC=∠DCB﹣∠A=180°﹣α﹣α=180°﹣2α，∴∠ABC=180°﹣∠ADC=2α=2∠A，∴四边形ABCD是⊙O内接倍角四边形；（2）①连接BD．∵AD是⊙O的直径，∴∠ABD=90°．在Rt△ABD中，AD=2×5=10，sin∠A=45，∴BD=8，根据勾股定理得：AB=6，设∠A=α，∴∠ADB=90°﹣α．由（1）知，∠ADC=180°﹣2α，∴∠BDC=90°﹣α，∴∠ADB=∠BDC，∴BC=AB=6；②若∠ADC=60°时．∵四边形ABCD是圆内接倍角四边形，∴∠BCD=120°或∠BAD=30°．Ⅰ、当∠BCD=120°时，如图3，连接OA，OB，OC，OD．∵BC =CD ，∴∠BOC =∠COD ，∴∠OCD =∠OCB =12∠BCD =60°，∴∠CDO =60°，∴AD 是⊙O 的直径，（为了说明AD 是直径，点O 没有画在AD 上）∴∠ADC +∠BCD =180°，∴BC ∥AD ，∴AB =CD ． ∵BC =CD ，∴AB =BC =CD ，∴△OAB ，△BOC ，△COD 是全等的等边三角形，∴S 四边形ABCD =3S △AOB =3×34×52=7534． Ⅱ、当∠BAD =30°时，如图4，连接OA ，OB ，OC ，OD ．∵四边形ABCD 是圆内接四边形，∴∠BCD =180°﹣∠BAD =150°．∵BC =CD ，∴∠BOC =∠COD ，∴∠BCO =∠DCO =12∠BCD =75°，∴∠BOC =∠DOC =30°，∴∠OBA =45°，∴∠AOB =90°．连接AC ，∴∠DAC =12∠BAD =15°． ∵∠ADO =∠OAB ﹣∠BAD =15°，∴∠DAC =∠ADO ，∴OD ∥AC ，∴S △OAD =S △OCD ． 过点C 作CH ⊥OB 于H ．在Rt △OCH 中，CH =12OC =52，∴S 四边形ABCD =S △COD +S △BOC +S △AOB ﹣S △AOD =S △BOC +S △AOB =1522⨯×5+12×5×5=754． 故答案为：753或754；（3）延长DC ，AB 交于点E ．∵四边形ABCD 是⊙O 的内接四边形，∴∠BCE =∠A =12∠ABC ． ∵∠ABC =∠BCE +∠A ，∴∠E =∠BCE =∠A ，∴BE =BC =b ，DE =DA =b ，∴CE =d ﹣c ． ∵∠BCE =∠A ，∠E =∠E ，∴△EBC ∽△EDA ，∴CE BC AE AD =，∴d c b a b d-=+，∴d 2﹣b 2=ab +cd ．【点睛】本题是圆的综合题，主要考查了圆的内接四边形的性质，新定义，相似三角形的判定和性质，等边三角形的判定和性质，正确作出辅助线是解答本题的关键．3．如图,四边形ABCD是⊙O的内接四边形,AB=CD．(1)如图(1),求证:AD∥BC；(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF；(3)在(2)的条件下,若DG平分∠ADC,GE=53,tan∠ADF=43,求⊙O的半径。
九年级数学上册《圆》练习题及答案解析
九年级数学上册《圆》练习题及答案解析学校:___________姓名：___________班级：___________一、单选题1．下列说法正确的是（）A．直径是弦，弦是直径B．过圆心的线段是直径C．圆中最长的弦是直径D．直径只有二条2．下列语句不正确的有（）个．①直径是弦；①优弧一定大于劣弧；①长度相等的弧是等弧；①半圆是弧．A．1B．2C．3D．43．如图，在①O中，点B,O,C和点A,O,D分别在同一条直线上，则图中有（）条弦.A．2B．3C．4D．54．下列说法正确的是（）A．劣弧一定比优弧短B．面积相等的圆是等圆C．长度相等的弧是等弧D．如果两个圆心角相等，那么它们所对的弧也相等5．下列由实线组成的图形中，为半圆的是（）A．B．C．D．6．下列说法正确的是（）A．平分弦的直径垂直于弦B ．半圆（或直径）所对的圆周角是直角C ．相等的圆心角所对的弧相等D ．若一条直线与一个圆有公共点，则二者相交二、填空题7．如图，已知在Rt△ABC 中，①ACB ＝90°，分别以AC ，BC ，AB 为直径作半圆，面积分别记为S 1，S 2，S 3，若S 3＝9π，则S 1+S 2等于_____．8．如图，Rt ABC 中，90ACB ∠=︒，以点C 为圆心，BC 为半径的圆交AB 于D ，交AC 于点E ，40BCD ∠=︒，则A ∠=______．9．如图，圆中扇子对应的圆心角α（180α）与剩余圆心角β的比值为黄金比时，扇子会显得更加美观，若黄金比取0.6，则βα-的度数是__________．10．数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”，如图所示，它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，若直角三角形较短直角边长为6，大正方形的边长为10，则小正方形的边长为________．11．如图，在O 中，AB 为直径，8AB =，BD 为弦，过点A 的切线与BD 的延长线交于点C ，E 为线段BD 上一点（不与点B 重合），且OE DE =．（1）若35B ∠=︒，则AD 的长为______（结果保留π）；（2）若6AC =，则DE BE=______．三、解答题12．如图，在Rt ABC 中，90ACB ∠=︒，以AC 为直径作O ，交AB 于点D ，E 为BC 的中点，连接DE 并延长交AC 的延长线于点E ．(1)求证：DF 是O 的切线；(2)若2CF =，4DF =，求O 的半径．13．如图，点A ，B 分别在①DPE 两边上，且PA PB =，点C 在①DPE 平分线上．(1)连接AC ，BC ，求证：AC BC =；(2)连接AB 交PC 于点O ，若60APB ∠=︒，6PA =，求PO 的长；(3)若PO OC ，且点O 是PAB △的外心，请直接写出四边形P ACB 的形状．参考答案与解析：1．C【详解】解：A 、直径是弦，但弦不一定是直径，不符合题意；B 、过圆心的弦是直径，但线段不一定是直径，不符合题意；C 、圆中最长的弦是直径，符合题意；D 、直径有无数条，不符合题意，故选C ．2．B【分析】根据圆的概念、等弧的概念、垂径定理、弧、弦直径的关系定理判断即可．【详解】解：①直径是弦，①正确；①在同圆或等圆中，优弧大于劣弧，①错误；①在同圆或等圆中，长度相等的弧是等弧，①错误；①半圆是弧，①正确；故不正确的有2个．故选：B ．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．3．B【详解】根据弦的概念，AB 、BC 、EC 为圆的弦，共有3条弦.故选B.4．B【分析】根据圆的相关概念、圆周角定理及其推论进行逐一分析判断即可．【详解】解：A.在同圆或等圆中，劣弧一定比优弧短，故本选项说法错误，不符合题意；B.面积相等的圆是等圆，故本选项说法正确，符合题意；C.能完全重合的弧才是等弧，故本选项说法错误，不符合题意；D.必须在同圆或等圆中，相等的圆心角所对的弧相等，故本选项说法错误，不符合题意．故选：B ．【点睛】本题主要考查了圆周角定理及其推论、等弧、等圆、以及优弧和劣弧等知识，解题关键是理解各定义的前提条件是在同圆或等圆中．5．B【分析】根据半圆的定义即可判断．【详解】半圆是直径所对的弧，但是不含直径，故选B ．【点睛】此题主要考查圆的基本性质，解题的根据熟知半圆的定义．6．B【分析】利用圆与圆的位置关系、垂径定理、圆周角定理等有关圆的知识进行判断即可【详解】A 、平分弦（不是直径）的直径垂直于弦，故本选项错误；B 、半圆或直径所对的圆周角是直角，故本选项正确；C 、同圆或等圆中，相等的圆心角所对的弧相等，故本选项错误；D 、若一条直线与一个圆有公共点，则二者相交或相切，故本选项错误，故选B ．【点睛】本题考查直线与圆的位置关系，垂径定理，圆心角、弧、弦的关系，圆周角定理.能清楚的知道每个定理的条件和它对应的结论是解题的关键.7．9π．【分析】根据勾股定理和圆的面积公式，可以得到S 1+S 2的值，从而可以解答本题．【详解】解：①①ACB ＝90°，①AC 2+BC 2＝AB 2，①S 1＝π（2AC ）2×12，S 2＝π（2BC ）2×12，S 3＝π（2AB ）2×12， ①S 1+S 2＝π（2AC ）2×12+π（2BC ）2×12＝π（2AB ）2×12＝S 3， ①S 3＝9π，①S 1+S 2＝9π，故答案为：9π．【点睛】本题考查勾股定理，解答本题的关键是利用数形结合的思想解答．8．20°．【分析】由半径相等得CB=CD，则①B=①CDB，在根据三角形内角和计算出①B=12（180°-①BCD）=70°，然后利用互余计算①A的度数．【详解】解：①CB=CD，①①B=①CDB，①①B+①CDB+①BCD=180°，①①B=12（180°-①BCD）=12（180°-40°）=70°，①①ACB=90°，①①A=90°-①B=20°．故答案为20°．【点睛】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了三角形内角和定理．9．90°##90度【分析】根据题意得出α=0.6β，结合图形得出β=225°，然后求解即可．【详解】解：由题意可得：α：β=0.6，即α=0.6β，①α+β=360°，①0.6β+β=360°，解得：β=225°，①α=360°-225°=135°，①β-α=90°，故答案为：90°．【点睛】题目主要考查圆心角的计算及一元一次方程的应用，理解题意，得出两个角度的关系是解题关键．10．2【分析】在Rt①ABC中，根据勾股定理求出AC，即可求出CD．【详解】解：如图，①若直角三角形较短直角边长为6，大正方形的边长为10，①AB ＝10，BC ＝AD ＝6，在Rt ①ABC 中，AC 8，①CD ＝AC ﹣AD ＝8﹣6＝2．故答案为：2．【点睛】本题主要考查了勾股定理，熟练掌握勾股定理是解决问题的关键．11． 149π 2539 【分析】（1）根据圆周角定理求出①AOD =70°，再利用弧长公式求解；（2）解直角三角形求出BC ，AD ，BD ，再利用相似三角形的性质求出DE ，BE ，可得结论．【详解】解：（1）①270AOD ABD ∠=∠=︒，①AD 的长704141809ππ⋅⋅==； 故答案为：149π； （2）连接AD ，①AC 是切线，AB 是直径，①AB AC ⊥，①10BC ，①AB 是直径，①90ADB ∠=︒，①AD CB ⊥，①1122AB AC BC AD ⋅⋅=⋅⋅，①245 AD=，①325 BD==，①OB OD=，EO ED=，①EDO EOD OBD ∠=∠=∠，①DOE DBO△∽△，①DO DE DB DO=，①43245DE=，①52 DE=，①325395210 BE BD DE=-=-=，①5252393910DEBE==．故答案为：25 39．【点睛】本题主要考查圆的相关知识，相似三角形的判定和性质，解直角三角形等知识，熟练掌握各性质及判定定理，正确寻找相似三角形解决问题是解题的关键．12．(1)见解析(2)3【分析】（1）连接OD、CD，由AC为①O的直径知①BCD是直角三角形，结合E为BC的中点知①CDE=①DCE，由①ODC=①OCD且①OCD+①DCE=90°可得答案；（2）设①O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．（1）解：如图，连接OD、CD．①AC为①O的直径，①①ADC=90°，①①CDB=90°，即①BCD是直角三角形，①E为BC的中点，①BE=CE=DE，①①CDE=①DCE，①OD=OC，①①ODC=①OCD，①①ACB=90°，①①OCD+①DCE=90°，①①ODC+①CDE=90°，即OD①DE，①DE是①O的切线；（2）解：设①O的半径为r，①①ODF=90°，①OD2+DF2=OF2，即r2+42=（r+2）2，解得：r=3，①①O的半径为3．【点睛】本题主要考查了圆切线的判定与性质，等腰三角形的性质与判定，直角三角形斜边上的中线，勾股定理等等，熟知圆切线的性质与判定是解题的关键．13．(1)证明见解析(2)(3)正方形，理由见解析【分析】（1）证明①P AC①①PBC即可得到结论；（2）根据已知条件得到①APC=①BPC=30°，OP①AB于O，求得AO=3，再利用勾股定理即可得到结论；P A B C在以O为圆心，OP为半径的圆上，再证明①APB=①PBC=①BCA=①CAP=90°，可得（3）先证明,,,OBP BPC POB根据正方形的判定定理即可得到结论．四边形APBC为矩形，再证明45,90,（1）证明：①点C在①DPE平分线上，① APC BPC ∠=∠ ，又①P A =PB ，PC =PC ，①①P AC ①①PBC （SAS ）；.AC BC（2）解：①,,60,PA PB APOBPO APB ①①APC =①BPC =30°，OP ①AB 于O ；①P A =6，①AO =3， 22633 3.OP（3） 解：如图，①点O 是①P AB 的外心，①OA =OB =OP ，而OP =OC ， ,,,P A B C 在以O 为圆心，OP 为半径的圆上，,AB PC 为圆的直径，①①APB =①PBC =①BCA =①CAP =90°，①四边形APBC 为矩形，PC 平分,APB ∠45,APC BPC,OP OB 45,90,OBP BPC POB①四边形APBC 为正方形．【点睛】本题考查了圆的综合题，全等三角形的判定和性质，正方形的判定，圆的确定，圆周角定理，正确的识别图形是解题的关键．。
人教版九年级数学上册《圆的有关性质》能力测试题及参考答案
人教版九年级数学上册《圆的有关性质》能力测试题及参考答案一、选择题1.如图是一个半径为5cm的圆柱形输油管的横截面,若油面宽AB=8cm,则油面的深度为（）A.2cmB.2.5cmC.3cmD.3.5cm第1题第2题第3题第4题2.如图,AB是⊙O的直径,点C,D是⊙O上的两点,连接AC,OD,CD,且AC//OD,若AB=6,∠ACD=15°,则AC的长为（）A.2√2B.4C.3√2D.3√33.如图,点A,B,C,D都在⊙O上,BD为⊙O的直径,若∠A=65°,则∠DBC的值是（）A.15°B.25°C.35°D.65°4.如图,AB为⊙O的直径,点C,D都在⊙O上,若BD=BC,∠ABC=65°,则∠BOD 的度数（）A.65°B.60°C.50°D.25°5.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD,∠BAC=28°,则∠D的度数是（）A.56°B.58°C.60°D.62°第5题第6题第7题第8题6.如图,四边形ABCD内接于⊙O,∠BOD=84°,则∠C的度数为（）A.88°B.92°C.106°D.138°7.如图,在⊙O中,弦AB,CD相交于点P,∠A=45°,∠APD=80°,则∠B的大小是（）.A.35°B.45°C.60°D.70°8.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF等于（）A.12.5°B.15°C.20°D.22.5°̂的中点,连接9.如图,在⊙O中,弦AB⊥CD,垂足为E,F为CBDAF,BF,AC,AF交CD于点M,过点F作FH⊥AC,垂足为G,交⊙O于点H.̂=DF̂②HC = BF③MF = FC④DF̂+AĤ= BF̂+AF̂.其中现有以下结论:①CF成立的有（）A.1个B.2个C.3个D.4个10.如图,点P在⊙O的直径AB上,作正方形PCDE和正方形PFGH,其中点D,G在直径所在的直线上,点C,E,F,H 都在⊙O 上.若两个正方形的面积之和为16,OP=√2,则DG 的长是（ ） A.6√2 B.2√14 C.7 D.4√3第10题 第11题 第12题 第13题11.如图,⊙O 经过菱形ABCD 的顶点A,B,C,顶点D 在⊙O 内,延长AD,CD 与⊙O 分别交于点E,F,连接 BE,BF.下列结论:①BE=BF ②AB ̂=AF ̂=EF ̂③∠ABC=90°+ 12∠EBF,其中正确的结论是（ ） A.①② B. ①③ C. ②③ D.①②③12.如图,△ABC 内接于⊙O,∠BAC=45°,AD ⊥BC,垂足为D,BD=6,DC=4,则AB 的长（ ）A.6√2B.10C.12D.6√513.如图,在半径为√13的⊙O 中,弦AB 与CD 交于点E,∠DEB=75°,AB=6,AE=1,则CD 的长（ ）A.2√6B.2√10C.2√11D.4√314.过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为（ ）A.(4,176) B .(4,3) C.(5,176) D .(5,3) 15.如图,△ABC 为等边三角形,AB=3.若P 为△ABC 内一动点,且满足∠PAB=∠ACP,则线段PB 长度的最小值为（ ）A.1.5B.√3C.√3D.216.如图,AB 为⊙O 的直径,C 为⊙O 上的一点,AB=4,∠AOC=120°,P 为⊙O 上的一动点,Q 为AP 的中点,连接CQ,则线段CQ 的最大值为（ ）A.3B.1+√6C.1+3√2D.1+√7二、填空题17.如图,在⊙O 的内接五边形ABCDE 中,∠CAD=35°,则∠B+∠E 的度数_______.18.如图,AB,CD 是⊙O 的直径,弦BE 与CD 交于点F,F 为BE 中点,AF//ED,若AF 的长为 2√3,则BC 的长为___.第17题 第18题 第19题19.如图,CD 为⊙O 的直径,弦AB ⊥CD,垂足为E,AB̂=BF ̂,CE =1,AB=6,则弦AF 的长度为___. 20.如图,⊙E 与y 轴相交于A,B 两点(点A 在点B 的上方),与x 轴的正半轴相交于点C,且圆心E 的坐标为(m,0),半径为5;直线l 的函数表达式为y=34x+n,且经过点A 并与x 轴相交于点D(-/2,0).若以C为顶点的抛物线过点B,则该抛物线的函数表达式为___.第20题第21题第22题21.如图,AB是⊙O的弦,AB= 6√3,∠AOB=120°,C为⊙O上的一动点,D,E分别是AC,OB的中点,连接DE,则线段DE的取值范围是____.22.如图,等边△ABC的边长为3,F为BC上的动点,DF⊥AB于点D,EF⊥AC于点E,则DE长的最小值为____.三、解答题̂的中点,连结CD,CA,AD.23.如图 1,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为ABD(1)求证:OC平分∠ACD.(2)如图 2,延长AC,DB相交于点E.①求证:OC//BE.②若CE = 4√5,BD =6,求⊙O的半径.24.如图,⊙O为Rt△ABC的外接圆,∠ACB=90°,BC=4√3,AC=4,点D是⊙O上的动点,且点C,D 分别位于AB的两侧.(1)求⊙O的半径;(2)当CD=4√2时,求∠ACD的度数;(3)设AD的中点为M,在点D的运动过程中,线段CM是否存在最大值?若存在,求出CM的最大值;若不存在,请说明理由.25.如图,在△ACE 中,AC=CE,⊙O 经过点A,C 且与边AE,CE 分别交于点D,F,点B 是AĈ上一点,且DF̂=BC ̂,连接AB,BC,CD. (1)求证:△CDE ≌△ABC;(2)若AC 为⊙O 的直径,填空:①当∠E =______时,四边形ABCD 为正方形;②当∠E =____时,四边形OCFD 为菱形.26.已知⊙O 中,弦AB=AC,点P 是∠BAC 所对弧上一动点,连接PA,PB.(1)如图①,把△ABP 绕点A 逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;(2)如图②,若∠BAC=60°,试探究PA,PB,PC 之间的关系.参考答案一、选择题1-5 ADBCD 6-10 DABCB 11-15 BDCAB 16 D二、填空题17. 215° 18.2√619.485 20.y=−116(x −8)221.3√3-3≤DE ≤3√3+322.94 三、解答题23.(1)提示：圆心角定理，垂径定理.(2)①略②半径长5.24(1)半径长4.(2)15°(3)2√ 3+225.(1)略(2)①45°②60°26.(1)略(2)①PA=PB+PC。
人教版初中数学圆的基础测试题附答案解析
人教版初中数学圆的基础测试题附答案解析一、选择题1.如图，有一个边长为2cm的正六边形纸片，若在该纸片上沿虚线剪一个最大圆形纸根据题意画出图形，再根据正多边形圆心角的求法求出/ AOB的度数，最后根据等腰三角形及直角三角形的性质解答即可.【详解】解：如图所示，正六边形的边长为2cm, OGi± BC,•••六边形ABCDE跳正六边形，BOC=360 + 6=60；•. OB=OC, OGi± BC,/ BOG=/ COG=- / BOC =30 , 2•. OGXBC, OB=OC, BC=2cm,BG=— BC=~ X 2=1cm2 2OB=-BG o =2cm,sin30•・OG=J O B2 BG2&2 12石,•♦・圆形纸片的半径为J3cm, 故选：A.2.3cm D. 4cm 片，则这个圆形纸片的半径是（【答案】A【点睛】本题考查的是正多边形和圆，根据题意画出图形，利用直角三角形的性质及正六边形的性 质解答是解答此题的关键.2.如图，在 ABC 中， ABC 90 , AB 6,点P 是AB 边上的一个动点，以 直径的圆交CP 于点Q,若线段AQ 长度的最小值是3,则 ABC 的面积为（）A. 18B. 27C. 36D. 54【答案】B【解析】【分析】 如图，取BC 的中点T,连接AT, QT.首先证明A, Q, T 共线时，区BC 的面积最大, QT=TB=X 利用勾股定理构建方程即可解决问题.【详解】解：如图，取BC 的中点T,连接AT, QT.•••PB 是。
的直径，/ PQB=Z CQB=90 ,，QT=1B C 关值，AT 是定值， 2•.AQSAT -TQ・•・当A, Q, T 共线时，AQ 的值最小，设 BT=TQ=x 在 RtAABT 中，则有（3+x ） 2=x2+62,解得x=—,2BC=2x=9,G 1 1S ZABC =- ?AB?BC=- X 6x 9=27 22 故选：B.BP 为【点睛】本题考查了圆周角定理，勾股定理，两点之间线段最短等知识，解题的关键是学会添加常 用辅助线，则有中考选择题中的压轴题.P 是以C (- J 2 , 此为圆心，i 为半径的o C 上的 一个动点，已知 A ( - 1, 0) , B (1, 0),连接PA 设点P (x, y),表示出PA 2+P3的值，从而转化为求OP 的最值，代入求解即可.【详解】 设 P (x, y),••• PA 2= (x+1) 2+y 2, PB2= (x — 1)，y 2,1- PA 2+PB^= 2x 2+2y 2+2=2 (x 2+y 2) +2,•.OP 2=x 2+y 2,.-.PA 2+pB^=2OP 2+2,当点P 处于OC 与圆的交点上时，OP 取得最值,・•.OP 的最小值为 CO- CP= 3-1 = 2, ，PA 2+P 田最小值为2X2+2=10.故选：G【点睛】本题考查了圆的综合，解答本题的关键是设出点 P 坐标，将所求代数式的值转化为求解OP的最小值，难度较大.4.如图，AB 是。
人教九上：专题十--圆相关概念及必考题型过关(含解析)
专题十 圆相关概念及必考题型过关一、单选题1．在正方形ABCD 中，以点A 为圆心，AB 长为半径作⊙A ，下列说法错误的是（ ）．A ．点D 在圆上B ．点C 在圆外C ．点B 在圆上D ．点A 在圆上2．如图，若⊙O 的半径为4，圆心O 到某条直线的距离为3，则这条直线可能是（ ）A ．l 1B ．l 2C ．l 3D ．l 43．已知一个圆心角为240°，半径为3的扇形工件，没搬动前如图所示（A ，B 两点触地放置），向右滚动工件至点B 再次触地时停止，则圆心O 所经过的路线长是（ ）A ．6B ．3πC ．6πD ．12π4．在平面中，已知⊙O 的半径OP 等于5，点P 在直线l 上，则圆心O 到直线l 的距离（ ）A ．等于5B ．最小值为5C ．最大值为5D ．不等于55．如图，⊙O 的直径AB ＝10，弦CD ⊥AB 于点P ，若OP ＝3，则CD 的长为（ ）A ．3B ．4C ．6D ．86．Rt △△ABC 中，∠C =90°，AB =5，AC =3，点E 在中线AD 上，以E 为圆心的⊙E 分别与AB 、BC 相切，则⊙E 的半径为（ ）A ．12B ．35C ．67D ．237．已知⊙O 的半径是6.5cm ，点P 是直线l 上一点，且OP =6cm ．那么直线l 与⊙O 的公共点的个数是（）A．0B．1C．2D．无法确定8．平面内，⊙O的半径为5，若直线l与⊙O相离，则圆心O到直线l的距离可能是（）A．6B．5C．4D．39．如图，AB与⊙O相切于点C，OA=OB，且⊙O的直径为8cm，AB=8cm，则阴影部分的面积为（）A．4π−8B．8π−20C．16−4πD．8−π10．如图，△ABC内接于⊙O，过A点作直线DE，当∠BAE=（）时，直线DE与⊙O相切．A．∠B B．∠BAC C．∠C D．∠DAC11．如图，在△ABC中，∠BAC=30°，圆心O在AB上，⊙O与BC相切，C为切点．则∠B的（）．A．20°B．25°C．30°D．35°12．⊙O的直径是4，圆心O到直线l的距离是2，则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．相离或相交13．我国古代数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．如图，⊙O的半径是2，运用“割圆术”，以圆内接正十二边形面积近似估计⊙O的面积，可得π的估计值是（）A．3.1B．3C．1+3D．2214．如图，A、D是⊙O上的两个点，BC是直径，若∠D=32°，则∠OAC等于（ ）A．64°B．58°C．68°D．55°15．已知⊙O的半径为3，点P到圆心O的距离为4，则点P与⊙O的位置关系是（ ）A．点P在⊙O外B．点P在⊙O上C．点P在⊙O内D．无法确定16．圆的直径是14，若圆心与直线上某一点的距离是7，则该直线和圆的位置关系是（）A．相离B．相切C．相交D．相交或相切17．如图所示，△ABC的三个顶点的坐标分别为A(−1,3)、B(−2,−2)、C(4,−2)，则△ABC外接圆半径的长为（）.A．32B．23C．10D．1318．如图，已知⊙O的半径为5，直线AB经过⊙O上一点P，下列条件不能判定直线AB与⊙O相切的是（）A．OP=5B．∠APO=∠BPO C．点O到直线AB的距离是5D．OP⊥AB19．如图，AD是⊙O的直径，AB=CD，若∠AOB=40°，则圆周角∠BPC的度数是（ ）A．40°B．50°C．60°D．70°202122232425A．32°B．52°C．64°D．72°26．某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为2m ，高为23m ，则改建后门洞的圆弧长是（ ）A ．5π3mB ．8π3mC ．10π3m D +2m27．已知⊙O 的半径等于5，圆心O 到直线l 的距离为4，那么直线l 与⊙O 的公共点的个数是（ ）A ．0B ．1C ．2D ．无法确定28．已知⊙O 的半径等于5，圆心O 到直线l 的距离为6，那么直线l 与⊙O 的公共点的个数是（ ）A ．0B ．1C ．2D ．无法确定29．若一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角为 （ ）A ．120°B ．180°C ．240°D ．300°30．已知⊙O 的半径为3，点O 到直线m 的距离为d ，若直线m 与⊙O 公共点的个数为2个，则d 可取（ ）A ．0B ．3C ．3.5D ．431．在平面直角坐标系中，以M(2,2)为圆心，半径为2作⊙M ，判断原点O 与⊙M 的位置关系为（ ）A ．点O 在⊙M 外B ．点O 在⊙M 上C ．点O 在⊙M 内D ．以上都有可能二、填空题32．如图，从一块圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，若围成圆锥的底面半径为1，则该圆形铁皮⊙O 的直径是．33．如图，用圆心角为120°，半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽，则这个纸帽的高是 cm ．34．四边形ABCD是⊙O的外切四边形，若∠AOB=78°，则∠COD的度数是．35363738．如图，在⊙O中，直径AB与弦CD相交于点P，连接AC，AD，BD．若∠C=18°，∠BPC=70°，则∠ADC的度数为．39．在半径为2的⊙O中，弦AB=2，弦CD=22，且AB∥CD，则AB与CD之间的距离为．40．如图，从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形，再将剪下的扇形围成一个圆锥，则圆锥的底面半径为m．41．如图，PM,PN分别与⊙O相切于A,B两点，C是⊙O上异于A,B的点，连接AC,BC．若∠P=50°，则∠ACB的大小是．42．⊙O的半径为1，弦AB=2,点C是圆上异于A、B的一动点，则∠ACB= ．43．如图，⊙O是△ABC的内切圆，∠C=40°，则∠AOB的大小是．44．一圆锥的底面半径为2，母线长为3，则这个圆锥的侧面积为．45．如图，直线EF与⊙O相切于点C，直线EO与⊙O相交于点D，连接CD．若∠DEF=3∠D，则∠DCF=．46．如图，在扇形OAB中，OA=6，∠AOB=110°，将扇形OAB沿过点B的直线折叠，点O恰好落在AB上的点D处，折痕交OA于点C，则弧AD的长为．47．如图，A，B，C是⊙O上的三个点，∠ABC=25°，则∠OAC的度数是．48496 cm50∠BPC=．51．如图，PM，PN分别与⊙O相切于A，B两点，C为⊙O上异于A，B的一点，连接AC，BC．若∠P＝58°，则∠ACB的大小是．52．如图，是一个圆盘及其内接正六边形，随机往圆盘内投飞镖，则飞镖落在正六边形内的概率是．53．如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F，则∠BAF= ．参考答案则AB=a=AD，AC=∵AB<AC，∴点C在⊙A外，点D在圆上，点故选：D．2．B【详解】解：∵⊙O的半径为4，圆心O到某条直线的距离为3，∴3<4，即圆心到直线的距离小于半径，∴该直线与圆相交，由图知，l2与⊙O相交；故选：B．3．C【分析】本题考查了动点经过的路径；确定点O的路径是关键；点O的路径是两个半径为3且圆心角为60°的弧，而平移的距离是一条线段，其长度是扇形工件的弧长，利用弧长公式可求得圆心O所经过的路线长．【详解】解：∵∠AOB=360°−240°=120°，∴∠ABO=12(180°−120°)=30°，当BO旋转到与地面垂直时，旋转角度为90°−30°=60°，此时点O的路径是半径为3且圆心角为60°的弧；扇形工件继续旋转时，点O的路径是一条线段，直至OA垂直地面，其长度是扇形工件的弧长；扇形工件继续绕A旋转，直到点A落地，此时点O的路径是半径为3且圆心角为60°的弧；∴圆心O所经过的路线长为：2×60π×3180+240π×3180=6π；故选：C．4．C【分析】此题考查了直线与圆的位置关系，根据题意可判断直线l与⊙O相切，熟记直线与圆的位置关系是解题的关键．【详解】解：∵⊙O的半径OP等于5，点P在直线l上，∴直线l与⊙O相切或相交，∴圆心O到直线l的距离最大值为5，故选：C．5．D【分析】连接OC，则OC=12AB=5，OP=3，利用勾股定理即可求得PC，最后由CD=2PC完成解答.【详解】解：连接OC，则OC=12AB=5，OP=3，由勾股定理得：PC=OC2−OP2=52−32=4所以CD=2PC=8故答案为D.【点睛】本题考查的是垂径定理，根据题意作出辅助线、构造出直角三角形、运用勾股定理求得PC是解答本题的关键.6．C【分析】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了勾股定理、相似三角形的判定与性质．作EH⊥AC于H，EF⊥BC于F，EG⊥AB于G，连接EB，EC，设⊙E的半径为R，先根据勾股定理计算出BC=4，则DC=2，由以E为圆心的⊙E分别与AB、BC相切，根据切线的性质得EG=EF=R，则HC=R，AH=3−R，再证明△AEH∽△ADC，利用相似比可得到EH和R的关系式，∵∴而∴∵∴∴∵∴∵∴∴R=6．7故选：C．7．C【分析】本题考查直线与圆的位置关系．根据题意先判断直线与圆的位置关系为相交，即可得到本题答案．【详解】解：∵⊙O的半径是6.5cm，点P是直线l上一点，且OP=6cm，∵6<6.5，∴直线l 与⊙O 位置关系为相交，∴直线l 与⊙O 的公共点的个数是2个，故选：C ．8．A【分析】本题考查直线与圆相离的判定，根据相离的判定逐项验证即可得到答案，熟记直线l 与⊙O 相离，得到圆心O 到直线l 的距离大于⊙O 半径是解决问题关键．【详解】解：∵ ⊙O 的半径为5，若直线l 与⊙O 相离，∴由相离定义可知圆心O 到直线l 的距离大于半径5，∴根据四个选项中的距离可知，只有6符合要求，故选：A ．9．C【分析】本题考查求不规则图形面积，涉及切线性质、等腰直角三角形的判定与性质、直角三角形面积和扇形面积公式等知识，根据题意，阴影部分面积可间接表示为△AOB 面积与扇形面积的差，求出线段长代入面积公式求解即可得到答案，熟练掌握不规则图形面积求法及切线性质是解决问题关键．【详解】解：连接OC ，如图所示：∵ AB 与⊙O 相切于点C ，∴OC ⊥AB ，∵ ⊙O 的直径为8cm ，AB =8cm ，∴OC =CA =CB =4cm ，∴△AOC 、△BOC 均为等腰直角三角形，∴∠AOB =∠AOC +∠BOC =45°+45°=90°，∴S △AOC =12AB ⋅OC =12×8×82=16，S 扇形=90360×π×OC 2=4π，∴阴影部分的面积为(16−4π)cm 2，故选：C ．10．C【分析】首先过点O作直径AF，连接BF，根据同弧所对的圆周角相等可得∠C＝∠AFB，进而可得到∠BAE＝∠F，再根据直径所对的圆周角是90°，可证出∠AFB+∠BAF＝90°，再利用等量代换可得∠BAE+∠BAF＝90°，进而得到直线DE与⊙O相切．【详解】解：当∠BAE=∠C时，直线DE与⊙O相切．理由如下：作AF交圆O于F点，连接BF．∵∠F，∠C是同弧AB所对的角，∴∠C＝∠F，∵∠BAE＝∠C，∴∠BAE＝∠F，∵AF为直径，∴∠ABF＝90°，∴在三角形ABF中，∠F+∠BAF＝90°，∵∠F＝∠BAE，∴∠BAE+∠BAF＝90°，∴FA⊥DE，∴直线DE与⊙O相切．故选：C．【点睛】此题主要考查了切线的判定，关键是正确作出辅助线，证明∠BAE+∠BAF＝90°．11．C【分析】本题主要考查了切线的性质、圆周角定理等知识点，掌握圆的切线的性质是解题的关键．如图：连接OC，由圆周角定理可得∠BOC=60°，再根据切线的性质可得∠OCB=90°，最后根据直角三角形两锐角互余即可解答．【详解】解：如图：连接OC，则OA=OC，∴∠BAC=∠ACO=30°，∴∠BOC=2∠BAC=60°，∵⊙O与BC相切，C为切点，∴∠OCB=90°,∴∠B=90°−∠BOC=30°．故选C．12．B【分析】本题主要考查了直线和圆的位置关系，判断直线l与⊙O的位置关系，求出圆心与直线的距离是关键．根据圆心与直线的距离直接判断位置即可．【详解】解：∵⊙O的直径为4，∴半径r=2，∵圆心O到直线l的距离为2，即d=2，∴d=r∴直线l与⊙O的位置关系是相切．故选：B．13．B【分析】过A作AM⊥OB于M，求得∠AOB的度数，根据直角三角形的性质得到AM，求出三角形的面积，于是得到正十二边形的面积，根据圆的面积公式即可得到结论．本题考查了正多边形与圆，三角形的面积的计算，正确地作出辅助线是解题的关键．【详解】如图，AB是正十二边形的一条边，点O是正十二边形的中心，过A作AM⊥OB于M，在正十二边形中，∠AOB=360°÷12=30°，∴AM=12OA=12∴S△AOB=12OB⋅AM=12×1×12=14∴正十二边形的面积为12×14=3,∴3=12×π，∴π=3,∴π的近似值为3，故选：B．14．B【分析】先根据圆周角定理求出∠B及∠BAC的度数，再由等腰三角形的性质求出∠OAB的度数，进而可得出结论．【详解】解：∵∠D=32°，∴∠B=∠D=32°，∵BC是直径，∴∠BAC=90°，∵OA=OB，∴∠BAO=∠B=32°，∴∠OAC=∠BAC−∠BAO=90°−32°=58°．故选：B．【点睛】本题主要考查了圆周角定理、等腰三角形的性质等知识，熟练掌握相关知识是解题关键．15．A【分析】根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系．【详解】解：∵⊙O的半径分别是3，点P到圆心O的距离为4，∴d>r，∴点P与⊙O的位置关系是：点在圆外．故选：A．【点睛】本题考查了点与圆的位置关系．注意若半径为r，点到圆心的距离为d，则有：当d>r时，点在圆外；当d=r时，点在圆上，当d<r时，点在圆内．16．D【分析】比较圆心到直线距离与圆半径的大小关系，进行判断即可．【详解】解：圆的直径是14，故半径为7．圆心与直线上某一点的距离是7，那么圆心到直线的距离可能等于7也可能小于7，因此直线与圆相切或相交．故选D．【点睛】本题主要考查直线与圆的位置关系，解题的关键是掌握：圆心与直线上某一点的距离是a时，圆心到直线的距离可能等于a也可能小于a．17．D【分析】三角形的外心是三边垂直平分线的交点，设△ABC的外心为M，由B，C的坐标可知M必在直线x=1上，由图可知线段AC的垂直平分线经过点(1,0)，由此可得M(1,0)，过点M作MD⊥BC于点D，连接MB，由勾股定理求出MB的长即可．【详解】解：设△ABC的外心为M，∵B(−2,−2)、C(4,−2)，=1上，∴M必在直线x=−2+42由图可知，线段AC的垂直平分线经过点(1,0)，∴M(1,0)，如图，过点M作MD⊥BC于点D，连接MB，Rt△MBD中，MD=2，BD=3，由勾股定理得：MB=MD2+BD2=22+32=13，即△ABC外接圆半径的长为13．故选D．【点睛】本题考查求三角形外接圆的半径，能够根据网格和三角形顶点坐标判断出△ABC外心的位置是解题的关键．18．A【分析】依据切线的判定定理“经过半径的外端且垂直于这条半径的直线”或“圆心到直线的距离等于半径”进行判断即可．【详解】解：A、OP=5，不能判定直线AB与⊙O相切，符合题意；B、由∠APO=∠BPO，得到OP⊥AB，且点P在⊙O上，能判定直线AB与⊙O相切，不符合题意；C、点O到直线AB的距离是5，等于半径，能判定直线AB与⊙O相切，不符合题意；D、OP⊥AB且点P在⊙O上，能判定直线AB与⊙O相切，不符合题意；故选：A．【点睛】本题考查了切线的判定；熟练掌握切线的判定是解题的关键．19∴∵∴∴20点21．A【分析】本题考查了点与圆的位置关系的应用，注意：已知⊙O的半径为r，点P到圆心O的距离是d，①当r>d时，点P在⊙O内，②当r=d时，点P在⊙O上，③当r<d时，点P在⊙O外．根据以上内容判断即可．【详解】解：∵⊙O的半径为4，PO=3，∵3<4，∴点P与⊙O的位置关系是点P在⊙O内部，故选：A．22．C【分析】本题考查了直线与圆的位置关系、坐标与图形性质．直线与圆相离，直线到圆心的距离大于半径；直线与圆相交，直线到圆心的距离小于半径；直线与圆相切，直线到圆心的距离等于半径．将该点的横纵坐标绝对值分别与半径对比，若横坐标绝对值大于半径时，则y轴与该圆相离；若横坐标绝对值小于半径时，则y轴与该圆相交；若横坐标绝对值等于半径时，则y与该圆相切；若纵坐标绝对值大于半径时，则x轴与该圆相离；若纵坐标绝对值小于半径时，则x轴与该圆相交；若纵坐标绝对值等于半径时，则x与该圆相切．【详解】解：∵点(4,3)为圆心，4为半径的圆，则有4=4，3<4，∴这个圆与y轴相切，与x轴相交．故选：C．23．C【分析】根据直角三角形的性质可求出CE=1，再根据垂径定理可求出CD．【详解】解：∵⊙O的直径AB垂直于弦CD，CD∴CE=DE=12∵∠A=30°，AC=2，∴CE=1∴CD=2．故选：C．【点睛】本题考查了直角三角形的性质，垂径定理等知识点，能求出CE=DE是解此题的关键．24．C【分析】设正六边形的中心是O，一边是AB，过O作OG⊥AB于G，在直角△OAG中，根据三角函数即可求得边长AB，从而求出周长．【详解】解：如图，在∴25∴∴∵则26【详解】如图，连接AD，BC，交于O点，∵∠BDC=90°，∴BC是直径，∴BC=CD2+BD2=22+(23)2=4，∵四边形ABDC是矩形，∴OC=OD=12BC=2，∵CD=2，∴OC=OD=CD，∴ΔCOD是等边三角形，∴∠COD=60°，∴门洞的圆弧所对的圆心角为360°−60°=300°，∴改建后门洞的圆弧长是300°π×12 BC180°=300°π×12×4180°=103π(m)，故选：C【点睛】本题考查了弧长公式，矩形的性质以及勾股定理的应用，从实际问题转化为数学模型是解题的关键．27．C【分析】利用直线与圆的位置关系的判断方法得到直线l与⊙O相交，然后根据相离的定义对各选项进行判断．【详解】∵⊙O的的半径为5，圆心O到直线l的距离为4，∴圆心O到直线l的距离小于半径，∴直线l与⊙O相交，∴直线l与⊙O有2个公共点．故选：C．【点睛】本题考查了直线与圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d，则当直线l 与⊙O相交⇔d<r；当直线l与⊙O相切⇔d=r；当直线l与⊙O相离⇔d>r；熟练掌握直线与圆的位置关系是解本题的关键．28．A【分析】圆的半径为r,圆心到直线的距离为d,当d＞r时，圆与直线相离，直线与圆没有交点，当d=r 时，圆与直线相切，直线与圆有一个交点，d＜r时，圆与直线相交，直线与圆有两个交点，根据原理可得答案．【详解】解：∵⊙O的半径等于r为8，圆心O到直线l的距离为d为6，∴d＞r，∴直线l与⊙O相离，∴直线l与⊙O的公共点的个数为0，故选A．【点睛】本题考查的是圆与直线的位置关系，圆与直线的位置关系有相离，相交，相切，熟悉三种位置关系对应的公共点的个数是解本题的关键．29．B【详解】试题分析：设母线长为R，底面半径为r，∴∵∴∴∴30当∴∴031∴MO=22+22=22．∵⊙M的半径为2，且22>2，∴点O在⊙M外．故选：A．32．42【分析】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．连接BC，根据扇形圆心角为90°，得到B,O,C三点共线，BC为⊙O的直径，首先求得扇形的弧长，再求出圆锥的母线长，然后利用勾股定理求出BC即可．【详解】解：如图，连接BC，∵∠BAC=90°，∴B,O,C三点共线，BC为⊙O的直径，∵围成圆锥的底面半径为1，∴BC=1×2π=2π，=2π，∵90×2π⋅AB360∴AB=4，∵AC=AB=4，∴BC=AB2+AC2=42，∴该圆形铁皮⊙O的直径是42，故答案为：42．33．42【分析】先求出扇形弧长，再求出圆锥的底面半径，再根据勾股定理即可出圆锥的高．=4πcm【详解】圆心角为120°，半径为6cm的扇形的弧长为120×6π180∴圆锥的底面半径为4π÷2π=2，故圆锥的高为62−22=42cm故答案为：42【点睛】此题主要考查圆的弧长及圆锥的底面半径，解题的关键是熟知圆的相关公式．34．102°/102度【分析】本题主要考查了切线长定理，解题的关键是熟练掌握切线长定理及其推论．令四边形ABCD 与⊙O分别相切于点E、F、G、H，连接OE,OF,OG,OH，通过证明∠1=∠2，∠3=∠4,∠5=∠6,∠7=∠8即可求解．【详解】解：令四边形ABCD与⊙O分别相切于点E、F、G、H，连接OE,OF,OG,OH，∵ABCD是⊙O的外切四边形，∴AE=AF，∵OE=OF,OA=OA，∴△OAE≌△OAF，∴∵∴∴∴352π∴n=144，∴圆锥的侧面展开图的圆心角的度数为144°，故答案为：144°．36．30°/30度【分析】本题考查了圆周角定理，根据在同圆或等圆中，同弧或等弧所对的圆周角相等可得结论．【详解】解：∵AD所对的圆周角是∠C,∠B，∴∠B =∠C =30°故答案为：30°．37．24【分析】根据圆周角定理得BC 为⊙O 的直径，即BC =2，所以AB =2 ，设该圆锥的底面圆的半径为rm ，根据弧长公式得到2πr ＝90×π×2180，然后解方程即可．【详解】解：∵∠BAC =90°，∴BC 为⊙O 的直径，即BC =2m ，∵AB =AC ，∴AB =2 ，设该圆锥的底面圆的半径为r ，根据题意得2πr ＝90×π×2180，解得r =24 ，即该圆锥的底面圆的半径为24m ．故答案为24．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．解题的关键是弄清扇形弧长和底面圆的周长的关系．38．38°/38度【分析】此题主要考查了圆周角定理，三角形外角和定理等知识，解题关键是熟知圆周角定理的相关知识．先根据圆周角定理得出∠B =∠C =18°，再由三角形外角和定理可知∠BDP =∠BPC−∠B =70°−18°=52°，再根据直径所对的圆周角是直角，即∠ADB =90°，然后利用∠ADB =∠ADC +∠BDP 进而可求出∠ADC ．【详解】解：∵∠C =18°，AD =AD ，∴∠B =∠C =18°，∵∠BPC =70°，∴∠BDP =∠BPC−∠B =70°−18°=52°，又∵AB 为直径，即∠ADB =90°，∴∠ADC =∠ADB−∠BDP =90°−52°=38°，故答案为：38°．39．3±2【分析】本题考查了勾股定理和垂径定理，解答此题时要注意进行分类讨论，不要漏解．由于弦AB 与CD 的具体位置不能确定，故应分两种情况进行讨论：①弦AB 与CD 在圆心同侧；②弦AB 与CD 在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可．【详解】解：①当弦AB 与CD 在圆心同侧时，如图，∵∴∵∴∵∴∴②EF 40．28/182【分析】本题主要考查了求圆锥底面圆半径，90度的圆周角所对的弦是直径．连接BC ，如图，根据圆周角定理得BC 为⊙O 的直径，即BC =2，所以AB =2，设该圆锥的底面圆的半径为r ，根据弧长公式得到方程即可求得．【详解】解：连接BC ，如图，∵∠BAC =90°，∴BC 为⊙O 的直径，即BC =1m ，∴AB =AC =22BC =22m ，设该圆锥的底面圆的半径为r m ，∴2πr =90π×22180，解得r =28，即该圆锥的底面圆的半径为28m ．故答案为：28．41．65°或115°【分析】本题考查的是切线的性质定理，圆周角定理的应用，圆的内接四边形的性质．如图，连接OA ，OB ，利用切线的性质结合四边形的内角和定理求解∠AOB =130°，再分两种情况讨论，结合圆周角定理与圆的内接四边形的性质可得答案．【详解】解：如图，连接OA ，OB ，C 1，C 2（即C ）分别在优弧与劣弧上，∵ PM ，PN 分别与⊙O 相切于A ，B 两点，∴∠PAO =∠PBO =90°，∵∠P =50°，∴∠AOB =360°−90°−90°−50°=130°，∴∠AC 1B =12∠AOB =65°，∠AC 2B =180°−65°=115°．故答案为：65°或115°．42．45°或135°【分析】根据题意画出图形,先判断出∠AOB=90o ,再分两种情况用同弧所对的圆心角和圆周角的关系确定和圆的内接四边形的性质即可.【详解】∵OA=OB=1，AB=2，∴OA2+OB2=AB2，△AOB是直角三角形，∴∠AOB=90°，当点C在优弧AB上时，∠AOB=45°，∠ACB=12∠∴∴43∴∴∴故答案为：110°．【点睛】本题考查了三角形的内切圆和内心，正确证明∠BAO+∠ABO=1（∠BAC+∠ABC）是关键．244．6π【分析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式求解．×2π×2×3＝6π．【详解】解：该圆锥的侧面积＝12故答案为6π．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．45．72°【分析】连接OC，如图，先利用切线的性质得到∠OCE=90°，则根据三角形内角和得到∠E+∠EOC=90°，再根据圆周角定理得到∠EOC=2∠D，加上∠E=3∠D，所以3∠D+2∠D=90°，从而可求出∠D的度数，然后利用三角形外角性质可计算出∠DCF的度数．本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．【详解】解：连接OC，如图，∵直线EF与⊙O相切于点C，∴OC⊥EF，∴∠OCE=90°，∴∠E+∠EOC=90°，∵∠EOC=2∠D，∠E=3∠D，∴3∠D+2∠D=90°，解得∠D=18°，∴∠E=54°，∴∠DCF=∠D+∠E=18°+54°=72°．故答案为：72°．π46．53【分析】本题考查了弧长的计算，翻折变换(折叠问题)，由折叠的性质推知△ODB是等边三角形是解答此题的关键.如图，连接OD.根据折叠的性质、圆的性质推知△ODB是等边三角形，则易求∠AOD=110°−∠DOB=50°，然后由弧长公式弧长的公式l=nπr来求弧AD的长.180【详解】解：如图, 连接OD.根据折叠的性质知，OB=DB.又∵OD=OB,∴OD=OB=DB, 即△ODB是等边三角形，∴∵∴∴47∴∵∴48∠BOD＝69°，∴∠A＝12∴∠BCD＝180°﹣∠A＝111°，∴∠DCE＝180°﹣∠BCD＝69°．故答案为：69°．【点睛】此题考查了圆周角定理与圆的内接四边形的性质．此题比较简单，解题的关键是注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆内接四边形的对角互补定理的应用．49．253/813【分析】设圆的半径为r cm ，连接OB 、OA ，过点A 作AD ⊥OB ，垂足为D ，利用勾股定理，在Rt △AOD 中，得到r 2＝（r −6）2＋82，求出r 即可．【详解】解：连接OB 、OA ，过点A 作AD ⊥OB ，垂足为D ，如图所示：∵CB 与⊙O 相切于点B ，∴OB ⊥CB ，∴∠CBD =∠BDA =∠ACB =90°，∴四边形ACBD 为矩形，∴AD =CB =8，BD =AC =6，设圆的半径为r cm ，在Rt △AOD 中，根据勾股定理可得：OA 2=OD 2+AD 2，即r 2＝（r −6）2＋82，解得：r =253，即⊙O 的半径为253cm ．故答案为：253．【点睛】本题主要考查了切线的性质，矩形的判定和性质，勾股定理，作出辅助线，构造直角三角形，利用勾股定理列出关于半径r 的方程，是解题的关键．50．80°/80度【分析】首先连接OB ，OC ，由PB ，PC 是⊙O 的切线，利用切线的性质，即可求得∠PBO =∠PCO =90∘，又由圆周角定理可得：∠BOC =2∠BAC ，继而求得∠BPC 的度数．【详解】解：连接OB ，OC ，∵PB ，PC 是⊙O 的切线，∴OB ⊥PB ，OC ⊥PC ，∴∠PBO =∠PCO =90°，∵∠BOC =2∠BAC =2×50°=100°，∴∠BPC=360°−∠PBO−∠BOC−∠PCO=360°−90°−100°−90°=80°故答案为：80°．51∵∴∵∴∴和定理的应用，求解∠AOB=122°是解本题的关键.52．332π【分析】设圆的半径为r，先分别求出圆的面积和正六边形的面积，再利用概率公式即可得．【详解】解：如图，设圆的圆心为点O，半径为r，过点O作OC⊥AB于点C，连接OA,OB，则圆的面积为πr 2，OA =OB =r ，∵图中的六边形是正六边形，∴∠AOB =360°6=60°，∴△AOB 是等边三角形，∴AB =OA =r,AC =12AB =12r,OC =OA 2−AC 2=32r ，∴正六边形的面积为6S △AOB =6×12AB ⋅OC =6×12r ⋅32r =332r 2，则飞镖落在正六边形内的概率是332r 2πr 2=332π，故答案为：332π．【点睛】本题考查了求概率、圆与正六边形等知识点，熟练掌握概率的求法是解题关键．53．15°【分析】根据平行四边形的性质和圆的半径相等得到△AOB 为等边三角形，根据等腰三角形的三线合一得到∠BOF ＝∠AOF ＝30°，根据圆周角定理计算即可．【详解】解答：连接OB ，∵四边形ABCO 是平行四边形，∴OC =AB ，又OA =OB =OC ，∴OA =OB =AB ，∴△AOB 为等边三角形.∵OF ⊥OC ,OC ∥AB ，∴OF ⊥AB ，∴∠BOF =∠AOF =30°.由圆周角定理得∠BAF =12∠BOF =15∘ ，故答案为15°.。
人教版初中数学圆的经典测试题
人教版初中数学圆的经典测试题一、选择题1．如图，ABC ∆是一块绿化带，将阴影部分修建为花圃.已知15AB =，9AC =，12BC =，阴影部分是ABC ∆的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）.A ．16 B ．6π C ．8π D ．5π 【答案】B【解析】【分析】由AB=5，BC=4，AC=3，得到AB 2=BC 2+AC 2，根据勾股定理的逆定理得到△ABC 为直角三角形，于是得到△ABC 的内切圆半径=4+3-52=1，求得直角三角形的面积和圆的面积，即可得到结论．【详解】解：∵AB=5，BC=4，AC=3，∴AB 2=BC 2+AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径=4+3-52=1， ∴S △ABC =12AC•BC=12×4×3=6， S 圆=π，∴小鸟落在花圃上的概率=6π ， 故选B ．【点睛】本题考查几何概率，直角三角形内切圆的半径等于两直角边的和与斜边差的一半及勾股定理的逆定理，解题关键是熟练掌握公式.2．如图，在矩形ABCD 中，6,4AB BC ==，以A 为圆心，AD 长为半径画弧交AB 于点E ，以C 为圆心，CD 长为半径画弧交CB 的延长线于点F ，则图中阴影部分的面积是（ ）A ．13πB ．1324π+C ．1324π-D ．524π+【答案】C【解析】【分析】 先分别求出扇形FCD 和扇形EAD 的面积以及矩形ABCD 的面积，再根据阴影面积＝扇形FCD 的面积﹣（矩形ABCD 的面积﹣扇形EAD 的面积）即可得解．【详解】解：∵S 扇形FCD 29036096ππ==⨯⨯，S 扇形EAD 24036094ππ==⨯⨯，S 矩形ABCD 6424=⨯=， ∴S 阴影＝S 扇形FCD ﹣（S 矩形ABCD ﹣S 扇形EAD ）＝9π﹣（24﹣4π）＝9π﹣24+4π＝13π﹣24故选：C ．【点睛】本题考查扇形面积的计算，根据阴影面积＝扇形FCD 的面积﹣（矩形ABCD 的面积﹣扇形EAD 的面积）是解答本题的关键．3．下列命题中，是假命题的是( )A ．任意多边形的外角和为360oB ．在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C VC ．在一个三角形中，任意两边之差小于第三边D ．同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析．【详解】解：A. 任意多边形的外角和为360o ,是真命题；B. 在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V≌'''A B C V ，根据HL ，是真命题；C. 在一个三角形中，任意两边之差小于第三边，是真命题；D. 同弧所对的圆周角等于圆心角的一半，本选项是假命题.故选D ．【点睛】本题考核知识点：判断命题的真假. 解题关键点：熟记相关性质或定义．4．如图，AB 是⊙O 的直径，EF ，EB 是⊙O 的弦，且EF=EB ，EF 与AB 交于点C ，连接OF ，若∠AOF=40°，则∠F 的度数是（ ）A ．20°B ．35°C ．40°D ．55°【答案】B【解析】【分析】 连接FB ，由邻补角定义可得∠FOB=140°，由圆周角定理求得∠FEB=70°，根据等腰三角形的性质分别求出∠OFB 、∠EFB 的度数，继而根据∠EFO ＝∠EBF-∠OFB 即可求得答案.【详解】连接FB ，则∠FOB=180°-∠AOF=180°-40°=140°，∴∠FEB ＝12∠FOB=70°， ∵FO ＝BO ， ∴∠OFB ＝∠OBF=(180°-∠FOB)÷2=20°，∵EF ＝EB ，∴∠EFB ＝∠EBF=(180°-∠FEB)÷2=55°，∴∠EFO ＝∠EBF-∠OFB=55°-20°=35°，故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.5．如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A．4.5 B．4 C．3 D．2【答案】B【解析】【分析】连接AI、BI，因为三角形的内心是角平分线的交点，所以AI是∠CAB的平分线，由平行的性质和等角对等边可得：AD=DI，同理BE=EI，所以图中阴影部分的周长就是边AB 的长．【详解】连接AI、BI，∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI=∠BAI，由平移得：AC∥DI，∴∠CAI=∠AID，∴∠BAI=∠AID，∴AD=DI，同理可得：BE=EI，∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4，即图中阴影部分的周长为4，故选B．【点睛】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识，熟练掌握三角形的内心是角平分线的交点是关键．6．如图，在⊙O，点A、B、C在⊙O上，若∠OAB＝54°，则∠C()A ．54°B ．27°C ．36°D ．46°【答案】C【解析】【分析】 先利用等腰三角形的性质和三角形内角和计算出∠AOB 的度数，然后利用圆周角解答即可.【详解】解：∵OA ＝OB ，∴∠OBA ＝∠OAB ＝54°，∴∠AOB ＝180°﹣54°﹣54°＝72°，∴∠ACB ＝12∠AOB ＝36°． 故答案为C ．【点睛】 本题考查了三角形内角和和圆周角定理,其中发现并正确利用圆周角定理是解题的关键.7．如图，O e 的外切正六边形ABCDEF 的边长为2，则图中阴影部分的面积为( )A 32πB 332πC ．23π-D 33π【答案】A【解析】【分析】【详解】 解：∵六边形ABCDEF 是正六边形，∴∠AOB =60°，∴△OAB 是等边三角形，OA =OB =AB =2，设点G 为AB 与⊙O 的切点，连接OG ，则OG ⊥AB ，∴OG =OA •sin 60°=2×32=3， ∴S 阴影=S △OAB ﹣S 扇形OMN =12×2×3﹣260(3)360π⨯=32π-．故选A ．8．如图，弧 AB 等于弧CD ，OE AB ⊥于点E ，OF CD ⊥于点F ，下列结论中错误．．的是（ ）A ．OE=OFB ．AB=CDC ．∠AOB =∠COD D ．OE ＞OF【答案】D【解析】【分析】 根据圆心角、弧、弦的关系可得B 、C 正确，根据垂径定理和勾股定理可得A 正确，D 错误．【详解】解：∵»»AB CD =，∴AB ＝CD ，∠AOB ＝∠COD ，∵OE AB ⊥，OF CD ⊥，∴BE ＝12AB ，DF ＝12CD ， ∴BE ＝DF ，又∵OB ＝OD ， ∴由勾股定理可知OE ＝OF ，即A 、B 、C 正确，D 错误，故选：D ．【点睛】本题考查了圆心角、弧、弦的关系，垂径定理，勾股定理，熟练掌握基本性质定理是解题的关键．9．用一个直径为10cm 的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具，不倒翁轴截面如图所示，圆锥的母线AB 与O e 相切于点B ，不倒翁的顶点A 到桌面L 的最大距离是18cm .若将圆锥形纸帽表面全涂上颜色，则涂色部分的面积为（ ）A ．260cm πB ．260013cm πC ．272013cm πD ．272cm π【答案】C【解析】【分析】 连接OB ，如图，利用切线的性质得OB AB ⊥，在Rt AOB ∆中利用勾股定理得12AB =，利用面积法求得6013BH =，然后利用圆锥的侧面展开图为扇形和扇形的面积公式计算圆锥形纸帽的表面．【详解】 解：连接OB ，作BH OA ⊥于H ，如图，Q 圆锥的母线AB 与O e 相切于点B ，OB AB ∴⊥，在Rt AOB ∆中，18513OA =-=，5OB =，2213512AB ∴=-=，Q 1122OA BH OB AB =g g ， 512601313BH ⨯∴==， Q 圆锥形纸帽的底面圆的半径为6013BH =，母线长为12， ∴形纸帽的表面2160720212()21313cm ππ=⨯⨯⨯=． 故选：C ．【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆锥的计算．10．中国科学技术馆有“圆与非圆”展品，涉及了“等宽曲线”的知识．因为圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了例以外，还有一些几何图形也是“等宽曲线”，如勒洛只角形(图1)，它是分别以等边三角形的征个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧．三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆．下列说法中错误的是( )A ．勒洛三角形是轴对称图形B ．图1中，点A 到¶BC上任意一点的距离都相等 C ．图2中，勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都相等 D ．图2中，勒洛三角形的周长与圆的周长相等【答案】C【解析】【分析】根据轴对称形的定义，可以找到一条直线是的图像左右对着完全重合，则为轴对称图形.鲁列斯曲边三角形有三条对称轴. 鲁列斯曲边三角形可以看成是3个圆心角为60°，半径为DE 的扇形的重叠，根据其特点可以进行判断选项的正误.【详解】鲁列斯曲边三角形有三条对称轴，就是等边三角形的各边中线所在的直线，故正确；点A 到¶BC上任意一点的距离都是DE ，故正确; 勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都不相等，1O 到顶点的距离是到边的中点的距离的2倍，故错误；鲁列斯曲边三角形的周长=3×60180DE DE ππ⨯=⨯ ,圆的周长=22DE DE ππ⨯=⨯ ,故说法正确.故选C.【点睛】主要考察轴对称图形，弧长的求法即对于新概念的理解．11．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（ ）A ．13B ．12C ．34D ．1【答案】B【解析】【分析】根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长．【详解】圆锥的底面周长是：π；设圆锥的底面半径是r ，则2πr=π．解得：r=12． 故选B ．【点睛】本题考查了圆锥的计算，正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．12．已知线段AB 如图，(1)以线段AB 为直径作半圆弧»AB ，点O 为圆心；(2)过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、，交»AB 于点E F 、；(3)连接,OE OF ．根据以上作图过程及所作图形，下列结论中错误的是( )A ．CE DF =B ．»»AE BF =C ．60EOF ∠=︒D ． =2CE CO【答案】D【解析】【分析】 根据作图可知AC CO OD DB ===,据此对每个选项逐一判断即可.【详解】根据HL 可判定ECO FDO ≅V V ,得CE DF =，A 正确；∵过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、，连接AE ，CE 为OA 的中垂线，AE OE =在半圆中，OA OE =∴OA OE AE ==,AEO △为等边三角形，60EOF =o ∠AOE=∠FOD=∠, C 正确；∴圆心角相等，所对应的弧长度也相等，»»AE BF=，B 正确 ∵60,90EOC =o o ∠AOE=∠, ∴=3CE CO ，D 错误【点睛】 本题考查了全等三角形的判定和性质，勾股定理等知识点，解题的关键在于证明60o ∠AOE=.13．一个圆锥的底面半径是5，高为12，则这个圆锥的全面积是（ ）A ．60πB ．65πC ．85πD ．90π【答案】D【解析】【分析】根据勾股定理求出圆锥侧面母线长，再根据圆锥的全面积=底面积+侧面积求出答案.【详解】∵圆锥的底面半径是5，高为12，∴侧面母线长为2251213+=，∵圆锥的侧面积=51365ππ⨯⨯=，圆锥的底面积=2525ππ⨯=，∴圆锥的全面积=652590πππ+=，故选：D.【点睛】此题考查圆锥的全面积，圆锥侧面母线长与底面圆的半径、圆锥的高的关系，熟记计算公式是解题的关键.14．如图，已知圆O 的半径为10，AB ⊥CD ，垂足为P ，且AB ＝CD ＝16，则OP 的长为( )A ．6B ．6C ．8D ．8 【答案】B【解析】【分析】作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，首先利用勾股定理求得OM的长，然后判定四边形OMPN是正方形，求得正方形的对角线的长即可求得OP的长．【详解】作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，∵AB=CD=16，∴BM=DN=8，∴OM=ON==6，∵AB⊥CD，∴∠DPB=90°，∵OM⊥AB于M，ON⊥CD于N，∴∠OMP=∠ONP=90°∴四边形MONP是矩形，∵OM=ON，∴四边形MONP是正方形，∴OP=．故选B．【点睛】本题考查的是垂径定理，正方形的判定与性质及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．15．若正六边形的半径长为4，则它的边长等于（）A．4 B．2 C．23D．43【答案】A【解析】试题分析：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4．故选A．考点：正多边形和圆．16．如图在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，⊙O是△ABC的内切圆，连接AO，BO，则图中阴影部分的面积之和为（）A．10﹣32πB．14﹣52πC．12 D．14【答案】B【解析】【分析】根据勾股定理求出AB，求出△ABC的内切圆的半径，根据扇形面积公式、三角形的面积公式计算，得到答案．【详解】解：设⊙O与△ABC的三边AC、BC、AB的切点分别为D、E、F，连接OD、OE、OF，在Rt△ABC中，AB＝22AC BC+＝10，∴△ABC的内切圆的半径＝68102+-＝2，∵⊙O是△ABC的内切圆，∴∠OAB＝12∠CAB，∠OBA＝12∠CBA，∴∠AOB＝180°﹣（∠OAB+∠OBA）＝180°﹣12（∠CAB+∠CBA）＝135°，则图中阴影部分的面积之和＝222902113525 21021436023602πππ⨯⨯-+⨯⨯-=-，故选B．【点睛】本题考查的是三角形的内切圆与内心、扇形面积计算、勾股定理，掌握扇形面积公式是解题的关键．17．如图，在⊙O中，OC⊥AB，∠ADC＝26°，则∠COB的度数是（）A．52°B．64°C．48°D．42°【答案】A【解析】【分析】由OC⊥AB，利用垂径定理可得出，再结合圆周角定理及同弧对应的圆心角等于圆周角的2倍，即可求出∠COB的度数．【详解】解：∵OC⊥AB，∴，∴∠COB＝2∠ADC＝52°．故选：A．【点睛】考查了圆周角定理、垂径定理以及圆心角、弧、弦的关系，利用垂径定理找出是解题的关键．18．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为（）A．23B．13C．4 D．32【答案】B【解析】【分析】如下图，作AD⊥BC，设半径为r，则在Rt△OBD中，OD=3－1，OB=r，BD=3，利用勾股定理可求得r.【详解】如图，过A作AD⊥BC，由题意可知AD必过点O，连接OB；∵△BAC是等腰直角三角形，AD⊥BC，∴BD=CD=AD=3；∴OD=AD-OA=2；Rt△OBD中，根据勾股定理，得：22+BD OD13故答案为：B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用，解题关键是利用等腰直角三角形ABC判定点O在AD上.19．如图，⊙O 的直径CD ＝10cm ，AB 是⊙O 的弦，AB ⊥CD ，垂足为M ，OM ：OC ＝3：5，则AB 的长为（ ）A ．91cmB ．8cmC ．6cmD ．4cm【答案】B【解析】【分析】 由于⊙O 的直径CD ＝10cm ，则⊙O 的半径为5cm ，又已知OM ：OC ＝3：5，则可以求出OM ＝3，OC ＝5，连接OA ，根据勾股定理和垂径定理可求得AB ．【详解】解：如图所示，连接OA ．⊙O 的直径CD ＝10cm ，则⊙O 的半径为5cm ，即OA ＝OC ＝5，又∵OM ：OC ＝3：5，所以OM ＝3，∵AB ⊥CD ，垂足为M ，OC 过圆心∴AM ＝BM ，在Rt △AOM 中，22AM=5-3=4，∴AB ＝2AM ＝2×4＝8．故选：B ．【点睛】本题考查了垂径定理和勾股定理的应用，构造以半径、弦心距和弦长的一半为三边的直角三角形，是解题的关键.20．在平面直角坐标系内，以原点O 为圆心，1为半径作圆，点P 在直线323y x =+上运动，过点P 作该圆的一条切线，切点为A ，则PA 的最小值为( )A ．3B ．2C 3D 2【答案】D【解析】【分析】先根据题意，画出图形，令直线y= 3x+ 23与x轴交于点C，与y轴交于点D，作OH ⊥CD于H，作OH⊥CD于H；然后根据坐标轴上点的坐标特点，由一次函数解析式，求得C、D两点的坐标值；再在Rt△POC中，利用勾股定理可计算出CD的长，并利用面积法可计算出OH的值；最后连接OA，利用切线的性质得OA⊥PA，在Rt△POH中，利用勾股定理，得到21PA OP=-，并利用垂线段最短求得PA的最小值即可.【详解】如图，令直线3x+23x轴交于点C，与y轴交于点D，作OH⊥CD于H，当x=0时，y=3D（0，3当y=033，解得x=-2，则C（-2，0），∴222(23)4CD=+=，∵12OH•CD=12OC•OD，∴2233⨯=连接OA，如图，∵PA为⊙O的切线，∴OA⊥PA，∴2221 PA OP OA OP=-=-当OP的值最小时，PA的值最小，而OP的最小值为OH的长，∴PA22(3)12-=故选D.【点睛】本题考查了切线的性质，解题关键是熟记切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．。
人教版初中数学圆的专项训练及解析答案
人教版初中数学圆的专项训练及解析答案一、选择题1．如图，已知ABC ∆和ABD ∆都O 是的内接三角形，AC 和BD 相交于点E ，则与ADE ∆的相似的三角形是（ ）A ．BCE ∆B ．ABC ∆ C ．ABD ∆ D ．ABE ∆【答案】A【解析】【分析】 根据同弧和等弧所对的圆周角相等， 则AB 弧所对的圆周角BCE BDA ∠=∠，CEB ∠和DEA ∠是对顶角，所以ADE BCE ∆∆∽．【详解】解：BCE BDA ∠=∠，CEB DEA ∠=∠ADE BCE ∴∆∆∽，故选：A ．【点睛】 考查相似三角形的判定定理： 两角对应相等的两个三角形相似，关键就是牢记同弧所对的圆周角相等．2．如图，在矩形ABCD 中，6,4AB BC ==，以A 为圆心，AD 长为半径画弧交AB 于点E ，以C 为圆心，CD 长为半径画弧交CB 的延长线于点F ，则图中阴影部分的面积是（ ）A ．13πB ．1324π+C ．1324π-D ．524π+【答案】C【解析】【分析】先分别求出扇形FCD 和扇形EAD 的面积以及矩形ABCD 的面积，再根据阴影面积＝扇形FCD 的面积﹣（矩形ABCD 的面积﹣扇形EAD 的面积）即可得解．【详解】解：∵S 扇形FCD 29036096ππ==⨯⨯，S 扇形EAD 24036094ππ==⨯⨯，S 矩形ABCD 6424=⨯=， ∴S 阴影＝S 扇形FCD ﹣（S 矩形ABCD ﹣S 扇形EAD ）＝9π﹣（24﹣4π）＝9π﹣24+4π＝13π﹣24故选：C ．【点睛】本题考查扇形面积的计算，根据阴影面积＝扇形FCD 的面积﹣（矩形ABCD 的面积﹣扇形EAD 的面积）是解答本题的关键．3．下列命题中，是假命题的是( )A ．任意多边形的外角和为360B ．在ABC 和'''A B C 中，若''AB A B =，''BC B C =，'90C C ∠=∠=，则ABC ≌'''A B CC ．在一个三角形中，任意两边之差小于第三边D ．同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析．【详解】解：A. 任意多边形的外角和为360,是真命题；B. 在ABC 和'''A B C 中，若''AB A B =，''BC B C =，'90C C ∠=∠=，则ABC ≌'''A B C ，根据HL ，是真命题；C. 在一个三角形中，任意两边之差小于第三边，是真命题；D. 同弧所对的圆周角等于圆心角的一半，本选项是假命题.故选D ．【点睛】本题考核知识点：判断命题的真假. 解题关键点：熟记相关性质或定义．4．如图，四边形ABCD 为⊙O 的内接四边形．延长AB 与DC 相交于点G ，AO ⊥CD ，垂足为E ，连接BD ，∠GBC=50°，则∠DBC 的度数为（ ）A ．50°B ．60°C ．80°D ．90°【答案】C【解析】【分析】 根据圆内接四边形的性质得：∠GBC =∠ADC =50°，由垂径定理得：CM DM =，则∠DBC =2∠EAD =80°．【详解】如图，∵四边形ABCD 为⊙O 的内接四边形，∴∠GBC =∠ADC =50°．∵AE ⊥CD ，∴∠AED =90°，∴∠EAD =90°﹣50°=40°，延长AE 交⊙O 于点M ．∵AO ⊥CD ，∴CM DM =，∴∠DBC =2∠EAD =80°．故选C ．【点睛】本题考查了圆内接四边形的性质：圆内接四边形的任意一个外角等于它的内对角，还考查了垂径定理的应用，属于基础题．5．如图，ABC 中，90ACB ∠=︒，O 为AB 中点，且4AB =，CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，则OD 的最小值为（ ）．A ．1B ．22C ．21-D ．222-【答案】D【解析】【分析】 根据三角形角平分线的交点是三角形的内心，得到DO 最小时，DO 为三角形ABC 内切圆的半径，结合切线长定理得到三角形为等腰直角三角形，从而得到答案．【详解】解： CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，D ∴为ABC ∆的内心，OD ∴最小时，OD 为ABC ∆的内切圆的半径，,DO AB ∴⊥过D 作,,DE AC DF BC ⊥⊥ 垂足分别为,,E F,DE DF DO ∴==∴ 四边形DFCE 为正方形，O 为AB 的中点，4,AB =2,AO BO ∴==由切线长定理得：2,2,,AO AE BO BF CE CF r ======sin 4522,AC BC AB ∴==•︒=222,CE AC AE ∴=-=-四边形DFCE 为正方形，,CE DE ∴=222,OD CE ∴==-故选D ．【点睛】本题考查的动态问题中的线段的最小值，三角形的内心的性质，等腰直角三角形的性质，锐角三角函数的计算，掌握相关知识点是解题关键．6．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，点D 在BA 的延长线上，CD 与⊙O 交于另一点E ，DE=OB=2，∠D=20°，则弧BC 的长度为（ ）A．23πB．13πC．43πD．49π【答案】A【解析】【分析】连接OE、OC，如图，根据等腰三角形的性质得到∠D=∠EOD=20°，根据外角的性质得到∠CEO=∠D+∠EOD=40°，根据等腰三角形的性质得到∠C=∠CEO=40°，根据外角的性质得到∠BOC=∠C+∠D=60°，根据求弧长的公式得到结论.【详解】解：连接OE、OC，如图，∵DE=OB=OE，∴∠D=∠EOD=20°，∴∠CEO=∠D+∠EOD=40°，∵OE=OC，∴∠C=∠CEO=40°，∴∠BOC=∠C+∠D=60°，∴BC的长度=260?2360π⨯=23π，故选A.【点睛】本题考查了弧长公式：l=••180n Rπ（弧长为l，圆心角度数为n，圆的半径为R），还考查了圆的认识及等腰三角形的性质及三角形外角的性质，熟练掌握等腰三角形的性质和三角形外角性质是关键．7．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（）A．25cm B．45 cm C．25cm或45cm D．23cm或43cm【答案】C【解析】连接AC，AO，∵O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=12AB=12×8=4cm,OD=OC=5cm,当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴OM=222254OA AM-=-=3cm，∴CM=OC+OM=5+3=8cm，∴AC=22224845AM CM+=+=cm；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5−3=2cm，在Rt△AMC中,AC=22224225AM CM+=+=cm.故选C.8．如图，7×5的网格中的小正方形的边长都为1，小正方形的顶点叫格点，△ABC的三个顶点都在格点上，过点C作△ABC外接圆的切线，则该切线经过的格点个数是（）A．1 B．2 C．3 D．4【答案】C【解析】【分析】作△ABC的外接圆，作出过点C的切线，两条图象法即可解决问题.【详解】如图⊙O即为所求，观察图象可知，过点C作△ABC外接圆的切线，则该切线经过的格点个数是3个，选：C．【点睛】考查三角形的外接圆与外心，切线的判定和性质等知识，解题的关键是理解题意.9．如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O，三角尺的直角顶点C落在直尺的10cm处，铁片与直尺的唯一公共点A落在直尺的14cm 处，铁片与三角尺的唯一公共点为B，下列说法错误的是（）A．圆形铁片的半径是4cm B．四边形AOBC为正方形C．弧AB的长度为4πcm D．扇形OAB的面积是4πcm2【答案】C【解析】【分析】【详解】解：由题意得：BC，AC分别是⊙O的切线，B，A为切点，∴OA⊥CA，OB⊥BC，又∵∠C=90°，OA=OB，∴四边形AOBC是正方形，∴OA=AC=4，故A，B正确；∴AB的长度为：904180π⨯=2π，故C错误；S扇形OAB=2904360π⨯=4π，故D正确．故选C．【点睛】本题考查切线的性质；正方形的判定与性质；弧长的计算；扇形面积的计算．10．如图，△ABC内接于⊙O，∠BAC=120°，AB=AC=4，BD为⊙O的直径，则BD等于（）A．4 B．6 C．8 D．12【答案】C【解析】【分析】根据三角形内角和定理求得∠C=∠ABC=30°，再根据圆周角定理及直角三角形的性质即可求得BD的长.【详解】∵∠BAC=120°，AB=AC=4，∴∠C=∠ABC=30°∴∠D=30°∵BD是直径∴∠BAD=90°∴BD=2AB=8.故选C.11．如图在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，⊙O是△ABC的内切圆，连接AO，BO，则图中阴影部分的面积之和为（）A．10﹣32B．14﹣52πC．12 D．14【答案】B【解析】【分析】根据勾股定理求出AB，求出△ABC的内切圆的半径，根据扇形面积公式、三角形的面积公式计算，得到答案．【详解】解：设⊙O 与△ABC 的三边AC 、BC 、AB 的切点分别为D 、E 、F ，连接OD 、OE 、OF ， 在Rt △ABC 中，AB ＝22AC BC +＝10， ∴△ABC 的内切圆的半径＝68102+-＝2， ∵⊙O 是△ABC 的内切圆，∴∠OAB ＝12∠CAB ，∠OBA ＝12∠CBA ， ∴∠AOB ＝180°﹣（∠OAB+∠OBA ）＝180°﹣12（∠CAB+∠CBA ）＝135°， 则图中阴影部分的面积之和＝22290211352521021436023602πππ⨯⨯-+⨯⨯-=-， 故选B ．【点睛】本题考查的是三角形的内切圆与内心、扇形面积计算、勾股定理，掌握扇形面积公式是解题的关键．12．如图，点,,A B S 在圆上，若弦AB 的长度等于圆半径的2倍，则ASB ∠的度数是( )．A ．22.5°B ．30°C ．45°D ．60°【答案】C【解析】【分析】 设圆心为O ，连接OA OB 、，如图，先证明OAB 为等腰直角三角形得到90AOB ∠=︒，然后根据圆周角定理确定ASB ∠的度数．【详解】解：设圆心为O ，连接OA OB 、，如图，∵弦AB 2倍，即2AB OA =，∴222OA OB AB +=，∴OAB 为等腰直角三角形，90AOB ∠=︒ ，∴1452ASB AOB ∠=∠=°． 故选：C ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．13．如图，在矩形ABCD 中，6AB =，对角线10AC =，O 内切于ABC ∆，则图中阴影部分的面积是（ ）A ．24π-B ．242π-C ．243π-D ．244π-【答案】D【解析】【分析】 先根据勾股定理求出BC ，连接OA 、OB 、OC 、过点O 作OH ⊥AB ，OE ⊥BC ，OF ⊥AC ，设O 的半径为r ，利用面积法求出r=2，再利用三角形ABC 的面积减去圆O 的面积得到阴影的面积．【详解】∵四边形ABCD 是矩形，∴∠B=90°，∵6AB =，10AC =，∴BC=8，连接OA 、OB 、OC 、过点O 作OH ⊥AB ，OE ⊥BC ，OF ⊥AC ，设O 的半径为r ， ∵O 内切于ABC ∆，∴OH=OE=OF=r ， ∵11()22ABC SAB BC AB AC BC r =⋅=++⋅， ∴1168(6108)22r ⨯⨯=++⋅， 解得r=2，∴O 的半径为2，∴2168-2224-4ABC O S SS ππ=-=⨯⨯⨯=阴影， 故选：D ．【点睛】此题考查矩形的性质，勾股定理，三角形内切圆的定义，阴影面积的求法，添加合适的辅助线是解题的关键．14．如图，将边长为2cm 的正方形ABCD 沿直线l 向右翻动（不滑动），当正方形连续翻动8次后，正方形的中心O 经过的路线长是（ ）cm ．A ．2B ．8C ．3πD ．4π【答案】D【解析】【分析】 由题意可得翻转一次中心O 经过的路线长就是1个半径为1，圆心角是90°的弧长，然后进行计算即可解答．【详解】解：∵正方形ABCD 2cm ，∴对角线的一半＝1cm ，则连续翻动8次后，正方形的中心O 经过的路线长＝8×901180π⨯＝4π． 故选：D ．【点睛】本题考查了弧长的计算，审清题意、确定点O 的路线和长度是解答本题的关键．15．下列命题中哪一个是假命题（ ）A ．8的立方根是2B ．在函数y ＝3x 的图象中，y 随x 增大而增大C ．菱形的对角线相等且平分D ．在同圆中，相等的圆心角所对的弧相等【答案】C【解析】【分析】利用立方根的定义、一次函数的性质、菱形的性质及圆周角定理分别判断后即可确定正确的选项．【详解】A 、8的立方根是2，正确，是真命题；B 、在函数3y x =的图象中，y 随x 增大而增大，正确，是真命题；C 、菱形的对角线垂直且平分，故错误，是假命题；D 、在同圆中，相等的圆心角所对的弧相等，正确，是真命题，故选C ．【点睛】考查了命题与定理的知识，能够了解立方根的定义、一次函数的性质、菱形的性质及圆周角定理等知识是解题关键．16．如图，点A 、B 、C 、D 、E 、F 等分⊙O ，分别以点B 、D 、F 为圆心，AF 的长为半径画弧，形成美丽的“三叶轮”图案．已知⊙O 的半径为1，那么“三叶轮”图案的面积为（ ）A ．π+332B ．π-332C ．332π+ D ．332π-【答案】B【解析】【分析】连接OA 、OB 、AB ，作OH ⊥AB 于H ，根据正多边形的中心角的求法求出∠AOB ，根据扇形面积公式计算．【详解】连接OA 、OB 、AB ，作OH ⊥AB 于H ，∵点A 、B 、C 、D 、E 、F 是⊙O 的等分点，∴∠AOB=60°，又OA=OB ，∴△AOB 是等边三角形，∴AB=OB=1，∠ABO=60°，∴OH=2211()2-=32， ∴“三叶轮”图案的面积=（2601360π⨯⨯-12×1×32）×6=π-332， 故选B ．【点睛】本题考查的是正多边形和圆、扇形面积的计算，掌握正多边形的中心角的求法、扇形面积公式是解题的关键．17．如图，已知⊙O 的半径是4，点A,B,C 在⊙O 上，若四边形OABC 为菱形，则图中阴影部分面积为（ ）A ．8833π-B ．16833π-C ．16433π-D ．8433π- 【答案】B【解析】【分析】 连接OB 和AC 交于点D ，根据菱形及直角三角形的性质先求出AC 的长及∠AOC 的度数，然后求出菱形ABCO 及扇形AOC 的面积，则由S 扇形AOC -S 菱形ABCO 可得答案．【详解】连接OB 和AC 交于点D ，如图所示：∵圆的半径为4，OB=OA=OC=4，又四边形OABC 是菱形，∴OB ⊥AC ，OD=12OB=2， 在Rt △COD 中利用勾股定理可知：CD=224223,243AC CD -===,∵sin ∠COD=3,2CD OC = ∴∠COD=60°，∠AOC=2∠COD=120°，∴S 菱形ABCO =114438322OB AC ⨯=⨯⨯=, ∴S 扇形=21204163603ππ⨯⨯=, 则图中阴影部分面积为S 扇形AOC -S 菱形ABCO =16833π-. 故选B.【点睛】考查扇形面积的计算及菱形的性质，解题关键是熟练掌握菱形的面积=12a•b （a 、b 是两条对角线的长度）；扇形的面积=2360n r π.18．如图，有一圆锥形粮堆，其侧面展开图是半径为6m 的半圆，粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食，此时，小猫正在B 处，它要沿圆锥侧面到达P 处捕捉老鼠，则小猫所经过的最短路程长为（ ）A ．3mB ．33C ．35D ．4m【答案】C【解析】【分析】【详解】 如图，由题意得：AP =3，AB =6，90.BAP ∠=∴在圆锥侧面展开图中223635.BP m =+=故小猫经过的最短距离是35.m故选C.19．如图，在圆O中，直径AB平分弦CD于点E，且CD=43，连接AC，OD,若∠A与∠DOB互余，则EB的长是（）A．3B．4 C3D．2【答案】D【解析】【分析】连接CO，由直径AB平分弦CD及垂径定理知∠COB=∠DOB，则∠A与∠COB互余，由圆周角定理知∠A=30°，∠COE=60°，则∠OCE=30°，设OE=x,则CO=2x,利用勾股定理即可求出x，再求出BE即可.【详解】连接CO，∵AB平分CD，∴∠COB=∠DOB，AB⊥CD，3∵∠A与∠DOB互余，∴∠A+∠COB=90°，又∠COB=2∠A，∴∠A=30°，∠COE=60°，∴∠OCE=30°，设OE=x,则CO=2x,∴CO2=OE2+CE2即(2x)2=x23)2解得x=2，∴BO=CO=4，∴BE=CO-OE=2.故选D.【点睛】此题主要考查圆内的综合问题，解题的关键是熟知垂径定理、圆周角定理及勾股定理.20．如图，ABC ∆是一块绿化带，将阴影部分修建为花圃.已知15AB =，9AC =，12BC =，阴影部分是ABC ∆的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）.A ．16 B ．6π C ．8π D ．5π 【答案】B【解析】【分析】由AB=5，BC=4，AC=3，得到AB 2=BC 2+AC 2，根据勾股定理的逆定理得到△ABC 为直角三角形，于是得到△ABC 的内切圆半径=4+3-52=1，求得直角三角形的面积和圆的面积，即可得到结论．【详解】解：∵AB=5，BC=4，AC=3，∴AB 2=BC 2+AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径=4+3-52=1， ∴S △ABC =12AC•BC=12×4×3=6， S 圆=π，∴小鸟落在花圃上的概率=6， 故选B ．【点睛】 本题考查几何概率，直角三角形内切圆的半径等于两直角边的和与斜边差的一半及勾股定理的逆定理，解题关键是熟练掌握公式.。
(常考题)人教版初中数学九年级数学上册第四单元《圆》测试(有答案解析)
一、选择题1．如图，在平面直角坐标系中，P 是直线y ＝2上的一个动点，⊙P 的半径为1，直线OQ 切⊙P 于点Q ，则线段OQ 的最小值为（ ）A ．1B ．2C ．3D ．52．下列说法不正确的是（ ）A ．不在同一直线上的三点确定一个圆B ．90°的圆周角所对的弦是直径C ．平分弦的直径垂直于这条弦D ．等弧所对的圆周角相等 3．如图，A 是B 上任意一点，点C 在B 外，已知2AB =，4BC =，ACD △是等边三角形，则BCD △的面积的最大值为（ ）A ．434+B ．43C ．438+D ．634．如图，AB 、AC 是⊙O 的切线，B 、C 为切点，∠A ＝50°，点P 是圆上异于B 、C 的点，则∠BPC 的度数是（ ）A ．65°B ．115°C ．115°或65°D ．130°或65° 5．如图，AB 为O 的直径，C 为O 上一点，其中6AB =，120AOC ∠=︒，P 为O 上的动点，连AP ，取AP 中点Q ，连CQ ，则线段CQ 的最大值为（ ）A ．37B ．3272+C ．237+D ．337226．已知⊙O ，如图，（1）作⊙O 的直径AB ；（2）以点A 为圆心，AO 长为半径画弧，交⊙O 于C ，D 两点；（3）连接CD 交AB 于点E ，连接AC ，BC ．根据以上作图过程及所作图形，有下面三个推断：①CE DE =；②3BE AE =；③2BC CE =．其中正确的推断的个数是（ ）A ．0个B ．1个C ．2个D ．3个7．下列事件属于确定事件的为（ ）A ．氧化物中一定含有氧元素B ．弦相等，则所对的圆周角也相等C ．戴了口罩一定不会感染新冠肺炎D ．物体不受任何力的时候保持静止状态 8．如图，PA 切O 于点,A PB 切O 于点B PO ，交O 于点C ，下列结论中不一定成立的是（ ）A ．PA PB =B ．PO 平分APB ∠C ．AB OP ⊥D ．2PAB APO ∠=∠ 9．如图，AB 是⊙的直径，DB 、DE 分别切⊙O 于点B 、C ，若∠ACE ＝35°，则∠D 的度数是（ ）A ．65°B ．55°C ．60°D ．70°10．如图，大半圆中有n 个小半圆，若大半圆弧长为1L ，n 个小半圆弧长的和为2L ，大半圆的弦AB ，BC ，CD 的长度和为3L ．则（ ）A ．123L L L =>B ．123L L L =<C ．无法比较1L 、2L 、3L 间的大小关系D ．132L L L >>11．已知圆锥的底面半径为3cm ，母线长为6cm ，则圆锥的侧面积是（ ）A ．18cm 2B ．218cm πC ．27cm 2D ．227cm π 12．如图，△ABC 内接于☉O ，若☉O 的半径为6，∠A=60°，则BC 的长为（ ）A ．2πB ．4πC ．6πD ．8π二、填空题13．一排水管截面如图所示，截面半径13dm OA =，水面宽10dm AB =，则圆心O 到水面的距离OC =______dm ．14．如图，在平面直角坐标系中，点()3,4A ，()3,0B ，以A 为圆心，2为半径作A ，点P 为A 上一动点，M 为OP 的中点，连接BM ，设BM 的最大值为m ，最小值为n ，则m n -的值为_________．15．在直径为10cm的⊙O中，弦AB=5cm，则∠AOB的度数为_______．16．如图，正六边形ABCDEF的边长为2，分别以点A，D为圆心，以AB，DC为半径作扇形ABF，扇形DCE．则图中阴影部分的面积是______．17．如图，半径为10的扇形AOB中，∠AOB=90°，C为AB上一点，CD⊥OA，CE⊥OB，垂足分别为D、E．若∠CDE=36°，则图中阴影部分的面积为____．18．如图，在平面直角坐标系xOy中，A（8，0），⊙O半径为3，B为⊙O上任意一点，P 是AB的中点，则OP的最小值是____．19．在平面直角坐标系xOy中，A（5，6），B（5，2），C（3，0），△ABC的外接圆的圆心坐标为____．20．如图，半径为3的⊙O与边长为8的等边三角形ABC的两边AB、BC都相切，连接OC，则OC＝_____．三、解答题21．如图，在Rt△ABC中，∠ACB＝90°，D为AB边上的一点，以AD为直径的⊙O交BC 于点E，过点C作CG⊥AB交AB于点G，交AE于点F，过点E作EP⊥AB交AB于点P，∠EAD＝∠DEB．（1）求证：BC是⊙O的切线；（2）求证：CE＝EP；（3）若CG＝12，AC＝15，求四边形CFPE的面积．22．如图，在等腰直角ABC中，=90ACB∠，12AB=,P是AB上一个动点，连结CP，以CP为斜边构造等腰直角CPQ(C、Q、P按逆时针方向），射线PQ与CA交于点D.（1）证明：2=CP CD CA⋅.（2）若12QDDP=,求CP的长.（3）连接AQ，记Q关于直线AC的对称点为Q'，若APC△的外接圆经过Q'，则APQ的面积为________（直接写出答案).23．已知△ABC ，请按以下要求完成本题：（1）请作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹）；（2）若在△ABC 中，∠ABC =70°，∠ACB =40°，⊙O 的直径AD 交CB 于E ，则∠DEC = ．24．已知点A 、B 在半径为2的⊙O 上，直线AC 与⊙O 相切，OC OB ，连接AB 交OC 于点D ．（1）如图①，若60ACO ︒∠=，求B ：（2）如图②，OC 与⊙O 交于点E ，若//BE OA ，求AB 的长．25．对于平面上两点,A B ，给出如下定义：以点A 或B 为圆心，AB 长为半径的圆称为点,A B 的“共径圆”．点,A B 的“共径圆”的示意图如图所示．（1）已知点A 的坐标为(0,0)，点B 的坐标为(3,4)，则点,A B 的“共径圆”的面积为_______________；（2）已知点A 在以坐标原点为圆心，以1为半径的圆上，点B 在直线4y x =-+上，求点,A B 的“共径圆”的半径最小值；（3）已知点A 的坐标为(0,0)，点B 是x 轴及x 轴上方的点，如果直线y x b =+上存在两个点B ，使得点,A B 的“共径圆”的面积为4π，直接写出满足条件的b 的取值范围．26．图①、图②均为 4×4 的正方形网格，线段 AB 、BC 的端点均在格点上，按要求在图①、图②中作图并计算其面积．（1）在图①中画一个四边形 ABCD ，点D 在格点上，使四边形 ABCD 有一组对角相等，并求=四边形ABCD S ．（2）在图②中画一个四边形 ABCE ，点E 在格点上，使四边形 ABCE 有一组对角互补，并求ABCE S =四边形 ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】连接PQ 、OP ，如图，根据切线的性质得：PQ ⊥OQ ，再利用勾股定理得出OQ ，利用垂线段最短，当OP 最小时，OQ 最小，即可求解．【详解】连接PQ 、OP ，如图，∵直线OQ 切⊙P 于点Q ，∴PQ ⊥OQ ，在直角OPQ △中，2221OQ OP PQ OP =-=-，当OP 最小时，OQ 最小，当OP ⊥直线y ＝2时，OP 有最小值2，∴OQ 的最小值为2213-=，故选：C ．【点睛】 本题考查了切线的性质：圆的切线垂直于经过切点的半径，也考查了勾股定理，熟练掌握切线的性质以及勾股定理是解答本题的关键．2．C解析：C【分析】根据确定圆的条件对A 进行判断；根据垂径定理的推论对C 进行判断；根据圆周角定理及其推论对B 、D 进行判断．【详解】解：A.不在同一直线上的三点确定一个圆，说法正确；B. 90°的圆周角所对的弦是直径，说法正确；C. 平分弦（非直径）的直径垂直于弦，所以B 选项错误；D. 等弧所对的圆周角相等，说法正确；故选：C 【点睛】此题主要考查了圆的相关知识的掌握．解答此题的关键是要熟悉课本中的性质定理． 3．A解析：A【分析】以BC 为边作等边BCM ，连接DM ，则DCM CAB ≅△△，根据全等三角形的性质得到DM=AB=2为定值，即点D 在以M 为圆心，半径为2的圆上运动，当点D 运动至BC 为中垂线与圆的交点时，BC 边上的高取最大值为232，根据三角形的面积即可得到结论．【详解】解：以BC 为边作等边BCM ，连接DM ，∵60DCA MCB ==∠∠，∴DCM ACB =∠∠，∵DC=AC ，MC=BC ，∴DCM CAB ≅△△（SAS ），∴DM=AB=2为定值，即点D 在以M 为圆心，半径为2的圆上运动，当点D 运动至BC 为中垂线与圆的交点时，BC 边上的高取最大值为232+，此时面积为：434+故选：A【点睛】本题考查了等边三角形的性质，三角形面积的计算，找出点D 的位置是解题的关键． 4．C解析：C【分析】根据切线的性质得到OB ⊥AB ，OC ⊥AC ，求出∠BOC ，分点P 在优弧BC 上、点P 在劣弧BC 上两种情况，根据圆周角定理、圆内接四边形的性质计算即可．【详解】解：∵AB 、AC 是⊙O 的切线，∴OB ⊥AB ，OC ⊥AC ，∴∠OBA ＝90°，∠OCA ＝90°∵∠A ＝50°，∴∠BOC ＝360°﹣90°﹣90°﹣50°＝130°，如图，当点P 在优弧BPC 上时，∠BPC ＝12∠BOC ＝65°， 当点P ′在劣弧BC 上时，∠BP ′C ＝180°﹣65°＝115°，故选：C ．【点睛】本题考查的是切线的性质、圆周角定理、圆内接四边形的性质，掌握圆的切线垂直于经过切点的半径及圆周角定理是解题的关键．5．D解析：D【分析】如图，连接OQ ，作CH ⊥AB 于H ．首先证明点Q 的运动轨迹为以AO 为直径的⊙K ，连接CK ，当点Q 在CK 的延长线上时，CQ 的值最大，利用勾股定理求出CK 即可解决问题；【详解】如图，连接OQ ，作CH ⊥AB 于H ．∵AQ ＝QP ，∴OQ ⊥PA ，∴∠AQO ＝90°，∴点Q 的运动轨迹为以AO 为直径的⊙K ，连接CK ，当点Q 在CK 的延长线上时，CQ 的值最大,∵120AOC ∠=︒∴∠COH ＝60°在Rt △OCH 中，∵∠COH ＝60°，OC=12AB=3， ∴OH ＝12OC ＝32，CH 22332OC OH +=， 在Rt △CKH 中，CK 223332⎛⎫+= ⎪ ⎪⎝⎭372 ∴CQ 的最大值为33722 故选：D ．【点睛】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识，解题的关键是正确寻找点Q 的运动轨迹，学会构造辅助圆解决问题，属于中考填空题中的压轴题． 6．D解析：D【分析】①根据作图过程可得AC AD =，根据垂径定理可判断；②连接OC，根据作图过程可证得△AOC为等边三角形，由等边三角形的性质即可判断；③根据直角三角形中30°角所对的直角边等于斜边的一半即可判断．【详解】解：①∵以点A为圆心，AO长为半径画弧，交⊙O于C，D两点，∴AC AD，根据垂径定理可知，AB⊥CE，CE=DE，∴①正确；②连接OC，∵AC=OA=OC，∴△AOC为直角三角形，∵AB⊥CE，∴AE=OE，∴BE=BO+OE=3AE，∴②正确；③∵AB为直径，∴∠ACB=90°，∵∠CAB=60°，∴∠ABC=30°，∴BC=2CE，∴③正确，故选：D．【点睛】本题考查了垂径定理、圆周角定理、等边三角形的判定与性质、含30°角的直角三角形的性质，理解基本作图知识，熟练掌握各基本性质和综合运用是解答的关键．7．A解析：A【分析】根据确定事件的概念，可知需找出必然事件或不可能事件即可.【详解】A、氧化物是含有两种元素其中一种是氧元素的化合物，必然事件；B、在同圆或等圆中，弦相等所对的圆周角相等或互补，不确定事件；C、戴了口罩一定不会感染新冠肺炎，不确定事件；D、物体不受任何力的时候保持静止状态或匀速运动，不确定事件.故选A.【点睛】本题考查事件的划分，必然事件和不可能事件统称为确定事件，确定事件中，必然出现的事情称为必然事件；不可能出现的事情称为不可能事件.8．D解析：D【分析】利用切线长定理证明△PAG≌△PBG即可得出．【详解】解：连接OA，OB，AB，AB交PO于点G，由切线长定理可得：∠APO＝∠BPO，PA＝PB，又∵PG=PG，∴△PAG≌△PBG，从而AB⊥OP．因此A．B．C都正确．无法得出AB＝PA＝PB，可知：D是错误的．综上可知：只有D是错误的．故选：D．【点睛】本题考查了切线长定理、全等三角形的判定和性质，关键是利用切线长定理解答．9．D解析：D【分析】连结BC，则由已知可以求得∠BCD与∠CBD的度数，最后由三角形的内角和定理可以得到∠D的度数．【详解】解：如图，连结BC，则由弦切角定理可知：∠ABC=∠ACE=35°，∵DB与⊙O相切，∴∠CBD=90°-∠ABC=90°-35°=55°，∵AB 是⊙的直径，∴∠ACB=90°，∴∠BCD=180°-∠ACE-∠90°=55°，∴∠D=180°-∠BCD-∠CBD=70°，故选D ．【点睛】本题考查圆的应用，灵活运用直线与圆相切的性质求解是解题关键．10．A解析：A【分析】利用圆周长公式计算1L 和2L 的长．根据圆周长公式分别写出1L 和2L 的表达式进行比较，再根据“两点之间线段最短的性质”得出13L L >，即可选出答案．【详解】解：设n 个小半圆半径依次为1r ，2r ，⋯，n r ．则大圆半径为()12n r r r ++⋯+()112n L r r r π∴=++⋯+，212n L r r r πππ=++⋯+()12n r r r π=++⋯+，12L L ∴=；根据“两点之间线段最短的性质”可得：13L L >，123L L L ∴=>．．故选A ．【点睛】本题考查了半圆弧长的计算，两点之间线段最短的性质，是基础题，难度不大． 11．B解析：B【分析】已知底面半径即可求得底面周长，即展开图中，扇形的弧长，然后根据扇形的面积公式即可求解．【详解】解：底面周长是2×3π=6π， 则圆锥的侧面积是：12×6π×6=18π（cm 2）．故选：B ．【点睛】本题考查了圆锥的计算，利用了圆的周长公式和扇形面积公式求解．12．B解析：B【分析】连接OB ，OC ，根据圆周角定理求出∠BOC 度数，再由弧长公式即可得出结论．【详解】解：连接OB ，OC ，∵∠A=60°，∴∠BOC=2∠A=120°，∴BC =208161π⨯=4π． 故选：B ．【点睛】 本题考查了三角形的外接圆与外心，根据题意作出辅助线，利用圆周角定理及弧长公式求解是解题的关键．二、填空题13．12【分析】根据垂径定理求出AC=5dm 再根据勾股定理求出OC 即可【详解】∵OC ⊥AB ∴AC=5dm 在Rt △AOC 中∴OC==12dm 故答案为：12【点睛】此题考查垂径定理勾股定理熟记垂径定理是解题解析：12【分析】根据垂径定理求出AC=5dm ，再根据勾股定理求出OC 即可．【详解】∵OC ⊥AB ，10dm AB =，∴AC=5dm ，在Rt △AOC 中，13dm OA =，∴2222135OA AC -=-，故答案为：12【点睛】此题考查垂径定理，勾股定理，熟记垂径定理是解题的关键．14．2【分析】方法一：在轴上取一点连接可求由可得由点在上运动可知共线时可以取得最大值或最小值最大值最小值由最大值与最小值求出即可；方法二：连接取中点连接利用三角形三边关系有可得作差计算即可【详解】解：方 解析：2【分析】方法一：在x 轴上取一点()6,0E ，连接PE ，可求3OB BE ==，22345AE =+=，由OM PM =，OB BE =，可得12BM PE =，由点P 在A 上运动，可知P 、A 、B 共线时，可以取得最大值或最小值，最大值'527EP ==+=，最小值''523EP =-=，由最大值与最小值求出72m =，32n =即可；方法二：连接PA 、OA ，取OA 中点N ，连接MN 、BN ，利用三角形三边关系有BN MN BM BN MN -≤≤+，可得m BN MN =+，n BN MN =-，作差计算22m n MN PA -===即可．【详解】解：方法一：在x 轴上取一点()6,0E ，连接PE ，∵()3,0B ，()3,4A ，∴3OB BE ==，22345AE =+=，∵OM PM =，OB BE =，∴12BM PE =， ∵点P 在A 上运动， ∴P 、A 、B 共线时，可以取得最大值或最小值，最大值'527EP ==+=，最小值''523EP =-=，∴72m =，32n =， ∴2m n -=，故答案为2．方法二：连接PA 、OA ，取OA 中点N ，连接MN 、BN ，BN MN BM BN MN -≤≤+，m BN MN=+，n BN MN=-，22m n MN PA-===．故答案为：2．【点睛】本题考查三角形的中位线，勾股定理，三角形三边关系，线段和差，掌握三角形的中位线，勾股定理，三角形三边关系，线段和差，引辅助线构造准确图形是解题关键．15．60°【分析】如图连接OAOB根据等边三角形的性质求出∠AOB的度数【详解】解：如图在⊙O中直径为10cm弦AB=5cm∴OA=OB=5cm∴OA=OB=AB∴△OAB是等边三角形∴∠AOB=60°解析：60°【分析】如图，连接OA、OB，根据等边三角形的性质，求出∠AOB的度数.【详解】解：如图，在⊙O中，直径为10cm，弦AB=5cm，∴OA=OB=5cm，，∴OA=OB=AB∴△OAB是等边三角形，∴∠AOB=60°，故答案为：60°．【点睛】考查了圆的性质以及等边三角形的性质，熟练掌握运算性质定理是解题的关键.16．﹣【分析】根据题意和图形可知阴影部分的面积是正六边形的面积减去两个扇形的面积从而可以解答本题【详解】解：∵正六边形ABCDEF的边长为2∴正六边形ABCDEF的面积是：6××22＝∠FAB＝∠EDC解析：38 3π【分析】根据题意和图形可知阴影部分的面积是正六边形的面积减去两个扇形的面积，从而可以解答本题．【详解】解：∵正六边形ABCDEF 的边长为2，∴正六边形ABCDEF 的面积是：6×3×22＝63，∠FAB ＝∠EDC ＝120°， ∴图中阴影部分的面积是：63﹣2×21202360π⋅⋅＝63﹣83π， 故答案为：63﹣83π． 【点睛】本题考查正多边形和圆、扇形面积的计算，解答本题的关键是明确题意，利用数形结合的思想解答． 17．10π【分析】连接OC 易得△ODE ≌△ECO 所以扇形OBC 的面积就是图中阴影部分的面积因此求得扇形OBC 的面积即可【详解】解：如下图连接OC ∵∠AOB=90°CD ⊥OACE ⊥OB ∴四边形ODCE 为矩解析：10π【分析】连接OC ，易得△ODE ≌△ECO ，所以扇形OBC 的面积就是图中阴影部分的面积，因此求得扇形OBC 的面积即可．【详解】解：如下图连接OC ，∵∠AOB=90°、CD ⊥OA 、CE ⊥OB∴四边形ODCE 为矩形∴OD=CE ，OE 为公共边∴△ODE ≌△ECO∴△ODE 的面积=△ECO 的面积∴图中阴影部分的面积=2236361010360360O BC SOB πππ-==⨯=． 故答案为：10π．【点睛】本题考查扇形面积的计算和矩形的性质．其关键是用矩形性质对阴影部分进行等积变换，发现△ODE 的面积=△ECO 的面积．18．【分析】作点A 关于y 轴的对称点C 连接BC 由题意可得若OP 取最小值则BC 也为最小因此可根据圆外的点到圆上的距离为最小只需过圆心即可求解【详解】解：作点A 关于y 轴的对称点C 连接BC 如图所示：∴点O 为AC 解析：52【分析】作点A 关于y 轴的对称点C ，连接BC ，由题意可得12OP BC =，若OP 取最小值，则BC 也为最小，因此可根据圆外的点到圆上的距离为最小只需过圆心即可求解．【详解】解：作点A 关于y 轴的对称点C ，连接BC ，如图所示：∴点O 为AC 的中点，∵点P 为AB 的中点，∴12OP BC =，//OP BC ， 当OP 取最小值，则BC 也取最小值，∵()8,0A ，OB=3，∴OA=OC=8，当点C 、O 、B 三点共线时，BC 的长为最小，即为：835BC =-=，∴52OP =，即OP 的最小值为52； 故答案为52． 【点睛】本题主要考查圆的最值问题，关键是根据三角形的中位线得到线段的最值问题，然后根据点与圆的位置关系进行求解即可．19．(14)【分析】如图作AB 和BC 的垂直平分线它们的交点为△ABC 的外接圆的圆心然后直接读出△ABC 的外接圆的圆心坐标【详解】解：如图所示：点P 即为所求；所以点P 的坐标为（14）故答案为（14）【点睛解析：(1，4)【分析】如图，作AB和BC的垂直平分线，它们的交点为△ABC的外接圆的圆心，然后直接读出△ABC的外接圆的圆心坐标．【详解】解：如图所示：点P即为所求；所以点P的坐标为（1,4）．故答案为（1,4）．【点睛】本题主要考查了三角形的外接圆与外心，掌握三角形外接圆的圆心是三角形三条边垂直平分线的交点是解答本题的关键．20．【分析】连接OB作OD⊥BC于D由等边三角形的性质得∠ABC＝60°BC＝8由⊙O与等边三角形ABC的两边ABBC都相切得出OD是⊙O的半径∠OBC＝∠OBA＝30°应用三角函数求出BD＝3CD＝B解析：7【分析】连接OB，作OD⊥BC于D，由等边三角形的性质得∠ABC＝60°，BC＝8，由⊙O与等边三角形ABC的两边AB、BC都相切，得出OD是⊙O的半径，∠OBC＝∠OBA＝30°，应用三角函数求出BD＝3，CD＝BC−BD＝5，由勾股定理得出OC，即可得出答案．【详解】连接OB，作OD⊥BC于D，∵△ABC是边长为8的等边三角形，∴∠ABC＝60°，BC＝8，∵⊙O与等边三角形ABC的两边AB、BC都相切，∠ABC＝30°，∴OD是⊙O的半径，∠OBC＝∠OBA＝12∵tan∠OBC＝OD，BD∴BD＝ODtan30＝33＝3，∴CD＝BC−BD＝8−3＝5，OC＝22OD+CD＝()223+5＝27，故填：27．【点睛】本题考查了切线的性质、等边三角形的性质、勾股定理、三角函数等知识；熟练掌握切线的性质是解题的关键．三、解答题21．（1）见解析；（2）见解析；（3）面积是45【分析】（1）由等腰三角形的性质和直径定理可得∠AED=90°，∠OED=∠ADE，由余角的性质可得∠DEB+∠OED=90°，进而可得∠BEO=90°，可得结论；（2）由平行线的性质和等腰三角形的性质可证AE为∠CAB的角平分线，由角平分线的性质可得CE=EP；（3）连接PF，先证四边形CFPE是菱形，可得CF=EP=CE=PF，由“AAS”可证△ACE≌△APE，可得AP=AC=15，由勾股定理可求CF的长，即可求解．【详解】证明：（1）连接OE，∵OE＝OD，∴∠OED＝∠ADE，∵AD是直径，∴∠AED＝90°，∴∠EAD+∠ADE＝90°，又∵∠DEB＝∠EAD，∴∠DEB+∠OED＝90°，∴∠BEO＝90°，∴OE⊥BC，∴BC是⊙O的切线．（2）∵∠BEO＝∠ACB＝90°，∴AC∥OE，∴∠CAE＝∠OEA，∵OA＝OE，∴∠EAO＝∠AEO，∴∠CAE＝∠EAO，∴AE为∠CAB的角平分线，又∵EP⊥AB，∠ACB＝90°，∴CE＝EP；（3）连接PF，∵CG＝12，AC＝15，∴AG22-9，AC CG-225144∵∠CAE＝∠EAP，∴∠AEC＝∠AFG＝∠CFE，∴CF＝CE，∵CE＝EP，∴CF＝PE，∵CG⊥AB，EP⊥AB，∴CF∥EP，∴四边形CFPE是平行四边形，又∵CE＝PE，∴四边形CFPE是菱形，∴CF＝EP＝CE＝PF，∵∠CAE＝∠EAP，∠EPA＝∠ACE＝90°，CE＝EP，∴△ACE≌△APE（AAS），∴AP＝AC＝15，∴PG＝AP﹣AG＝15﹣9＝6，∵PF2＝FG2+GP2，∴CF2＝（12﹣CF）2+36，∴CF＝152，∴四边形CFPE的面积＝CF×GP＝152×6＝45．【点睛】本题考查了圆的综合题，切线的判定和性质，全等三角形的判定和性质，勾股定理，菱形的判定和性质，垂径定理，正确的作出辅助线是解题的关键．22．（1）ACP PCD∆∆；（2）CP=3）6【分析】（1）根据已知条件证明△ACP∽△PCD即可求解；（2）根据等腰直角△ABC求出，设QD=x，得到DP=2x,QP=3x=CQ，利用勾股定理求出PC，CD，代入2=CP CD CA⋅求出x即可求解；（3）根据题意可知△APC的外接圆是以点Q为圆心，PQ为半径的圆，求出△AQQ’、△CQQ’均为等边三角形，再分别求出APQ的底和高，即可求解．【详解】（1）∵ABC和CPQ是等腰直角三角形∴∠A=∠CPQ=45°又∠ACP=∠PCD∴△ACP∽△PCD∴CP CDCA CP=∴2=CP CD CA⋅；（2）∵在等腰直角△ABC中，∠ACB=90°，AB=12∴AB2=AC2+BC2=2AC2∴设QD=x∵12 QD DP=∴DP=2x,QP=3x=CQ∴=，=∵2=CP CD CA⋅∴()21032=62x x⋅解得x=25∴CP=2532210⨯=；（3）∵∠CAB=45°，△PCQ是等腰直角三角形∴△APC的外接圆是以点Q为圆心，PQ为半径的圆∵Q关于直线AC的对称点为Q'，∴QC=QQ’=QP=QA=Q’A=CQ’∴△AQQ’、△CQQ’均为等边三角形，故△AQC为等腰三角形，设AC,QQ’交于H点，AQ’，PQ交于G点根据对称性可知QQ’⊥AC,AQ’⊥PQ，AH=12AC=32，∵∠QAC=12（180°-120°）=30°∴QH=12AQ，∴AQ2=QH2+AH2=14AQ2+AH2解得AQ=26∴PQ=AQ=26=AQ’∵AG=12AQ’=6∴APQ的面积为12QP×AG=12×26×6=6．故答案为：6．【点睛】此题主要考查圆的综合问题，解题的关键是熟知圆周角定理、相似三角形的判定与性质、等腰直角三角形的性质．23．（1）见解析；（2）60°【分析】（1）分别作出AB 与AC 的垂直平分线，进而得出圆心的位置，再利用圆心到三角形顶点的距离为半径得出圆O 即可；（2）连接BD ．根据圆周角定理求出∠ABD=90°，∠D=∠ACB=40°，则∠DBC=∠ABD-∠ABC=20°，再利用三角形外角的性质即可求出∠DEC ．【详解】解：（1）如图所示：（2）连接BD ．∵AD 是直径，∴∠ABD=90°，∴∠DBC=∠ABD-∠ABC=90°-70°=20°，又∵∠D=∠ACB=40°，∴∠DEC =∠D+∠DBC=40°+20°=60°．【点睛】本题主要考查了三角形外接圆的作法，圆周角定理，三角形外角的性质，熟练掌握相关的定理是解题关键．24．（1）30°；（2）222+【分析】（1）由切线的性质可知∠OAC=90°，由三角形的内角和定理可知∠AOC=30°，由∠AOB=∠AOC+∠BOC 可得出∠AOB 的度数，结合OA=OB 可得出∠B=30°；（2）过B 作BH AO ⊥交AO 的延长线于H ，由BE ∥OA 可得出ABE OAB ∠=∠，结合等腰直角三角形的性质可得出45OBE ︒∠=，根据勾股定理得出2OH BH ==再结合勾股定理即可得出结论．【详解】解：（1））∵AC 与⊙O 相切，∴∠OAC=90°∵∠OCA=60°∴∠AOC=30°∵OC ⊥OB ，∴∠AOB=∠AOC+∠BOC=120°∵OA=OB ，∴180120302B ︒︒︒-∴∠==； （2）过B 作BH AO ⊥交AO 的延长线于H//BE OAABE OAB ∴∠=∠,90OB OE BOE ︒=∠=45OBE ︒∴∠=45HO B OAB OBA ABE OBA OBE ︒∴∠=∠+∠=∠+∠=∠=2OA OB ==2OH BH ∴==2222(22)(2)AB AH BH ∴=+=++842222=+=+【点睛】本题考查了切线的性质，勾股定理，等腰三角形的性质，熟练掌握切线的性质是解本题的关键．25．（1） 25π；（2）221；（3）222b ≤<【分析】（1）由点A 、B 的坐标知，22345,=+=AB 由圆的面积公式得：“共径圆”的面积πr 2=25π；（2）如下图，当O 、A 、B 三点共线，且OB ⊥直线l 时，共径圆”的半径最小，即可求解； （3）设点B 的坐标为（x ，x+b ），设AB 之间的距离为r ，则πr 2=4π，解得r=2（负值已舍去），则AB=x 2+（x+b ）2=22=4，满足条件的B 点有2个，故△=（2b ）2-2×4（b 2-4）＞0，进而求解．【详解】解：（1）A 的坐标为(0,0)，点B 的坐标为(3,4)，∴22345,=+=AB由圆的面积公式得：“共径圆”的面积πr 2=25π，故答案为25π；（2）作OB ⊥直线l 于B 交圆O 于点A ，此时点,A B 的“共径圆”的半径最小值；设直线4y x =-+与,x y 轴交于点,M N ．()4,00,4()M N ∴，），则ON=OM=4，∴ MON △等腰直角三角形， ∴224244=+=MN∴О点到直线MN 的距离为22A 点在O 上，B 点在直线4y x =-+上,A B ∴间的最短距离是221-即,A B 的“共径圆”的最小半径是221-（3）设点B 的坐标为（x ，x+b ），设AB 之间的距离为r ，则πr 2=4π，解得r=2（负值已舍去），则AB=x 2+（x+b ）2=22=4，化简得：2x 2+2bx+b 2-4=0，∵满足条件的B 点有2个，故△=（2b ）2-2×4（b 2-4）＞0，解得：22,-<<b∵点B 是x 轴及x 轴上方的点，故b ＞0，而当b=2时，点B 在x 轴上，∴222b ≤<【点睛】本题为圆的综合题，涉及到一次函数的性质、根的判别式等，这种新定义类的题目，通常按照题设的顺序逐次求解，一般比较容易解答．26．（1）图见详解，6 ；（2）图见详解，4.5【分析】（1）过C 画AB 的平行线，过A 画BC 的平行线，两线交于一点D ，根据平行四边形的判定定理可得四边形ABCD 是平行四边形，由平行四边形的性质可知∠CBA=∠CDA ，然后用用割补法求出面积即可；（2）根据图中正方形网格和∠B 的特点，作出∠E 与∠B 互补，然后用割补法求面积即可．【详解】解：（1）如图，S四边形ABCD=3×4-122⨯×2-222⨯-112⨯=6；（2）如图，S四边形ABCE=3×3-122⨯×2-222⨯-112⨯=92．【点睛】此题主要考查了应用设计作图，首先要理解题意，弄清问题中对所作图形的要求，然后利用割补法求面积．。
人教版初三圆测试题及答案
人教版初三圆测试题及答案一、选择题（每题2分，共10分）1. 半径为2的圆的面积是多少？A. 4πB. 6πC. 8πD. 12π2. 圆的周长公式是：A. C = πrB. C = 2πrC. C = 4πrD. C = 8πr3. 若圆的半径是3，圆心角为60°，那么这个弧长是多少？A. πB. 3πC. 6πD. 9π4. 点P到圆心O的距离是5，圆的半径是3，那么点P与圆的位置关系是：A. 在圆上B. 在圆内C. 在圆外D. 无法确定5. 圆的切线与半径垂直，且切点到圆心的距离等于：A. 半径B. 直径C. 周长的一半D. 面积的平方根二、填空题（每题2分，共10分）6. 半径为4的圆的面积是_________。
7. 若圆的周长为12π，那么圆的半径是_________。
8. 圆心角为120°的弧所对的圆心角是_________。
9. 点P到圆心O的距离是2，圆的半径是4，点P与圆的位置关系是_________。
10. 圆的切线与半径垂直，切点到圆心的距离是_________。
三、计算题（每题5分，共20分）11. 已知圆的半径为5，求圆的周长和面积。
12. 已知圆的周长为16π，求圆的半径。
13. 若圆的半径为7，圆心角为45°，求该弧长。
14. 已知点P到圆心O的距离为10，圆的半径为8，求点P与圆的位置关系。
四、解答题（每题10分，共20分）15. 某圆的半径为6，圆心角为30°，求该弧所对的圆心角和弧长。
16. 已知圆的切线在点M处与圆相切，OM=6，半径为4，求切线PM的长度。
五、综合题（15分）17. 某工厂需要在一块半径为10米的圆形场地上安装一个直径为4米的圆形水池，水池的中心与场地的中心重合。
求水池的半径占场地半径的比例，以及水池的面积占整个场地面积的比例。
六、结束语本测试题覆盖了圆的基本概念、公式和计算方法，旨在帮助学生巩固和检验对圆的相关知识的掌握。
初中数学圆的经典测试题含答案解析
初中数学圆的经典测试题含答案解析一、选择题1．如图，AB是⊙O的直径，AC是⊙O的切线，OC交⊙O于点D，若∠ABD＝24°，则∠C 的度数是（）A．48°B．42°C．34°D．24°【答案】B【解析】【分析】根据切线的性质求出∠OAC，结合∠C＝42°求出∠AOC，根据等腰三角形性质求出∠B＝∠BDO，根据三角形外角性质求出即可．【详解】解：∵∠ABD＝24°，∴∠AOC＝48°，∵AC是⊙O的切线，∴∠OAC＝90°，∴∠AOC+∠C＝90°，∴∠C＝90°﹣48°＝42°，故选：B．【点睛】考查了切线的性质，圆周角定理，三角形内角和定理，解此题的关键是求出∠AOC的度数，题目比较好，难度适中．2．如图，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC=3，AC=4，则sin∠ABD的值是（）A．43B．34C．35D．45【答案】D【解析】【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC，再根据勾股定理求得AB=5，即可求sin∠ABD 的值．【详解】∵AB是⊙O的直径，CD⊥AB，∴弧AC=弧AD，∴∠ABD=∠ABC．根据勾股定理求得AB=5，∴sin∠ABD=sin∠ABC=45．故选D．【点睛】此题综合考查了垂径定理以及圆周角定理的推论，熟悉锐角三角函数的概念．3．如图，正方形ABCD内接于⊙O，AB=22，则»AB的长是（）A．πB．32πC．2πD．12π【答案】A【解析】【分析】连接OA、OB，求出∠AOB=90°，根据勾股定理求出AO，根据弧长公式求出即可．【详解】连接OA、OB，∵正方形ABCD内接于⊙O，∴AB=BC=DC=AD，∴»»»»AB BC CD DA===，∴∠AOB=14×360°=90°，在Rt△AOB中，由勾股定理得：2AO2=（2）2，解得：AO=2，∴»AB的长为902 180´=π，故选A．【点睛】本题考查了弧长公式和正方形的性质，求出∠AOB的度数和OA的长是解此题的关键．4．将直尺、有60°角的直角三角板和光盘如图摆放，A为60°角与直尺的交点，B为光盘与直尺的交点，AB=4，则光盘表示的圆的直径是()A．4 B．83C．6 D．43【答案】B【解析】【分析】设三角板与圆的切点为C，连接OA、OB，根据切线长定理可得AB=AC=3，∠OAB=60°，然后根据三角函数，即可得出答案.【详解】设三角板与圆的切点为C，连接OA、OB，由切线长定理知，AB=AC=3，AO平分∠BAC，∴∠OAB=60°，在Rt△ABO中，OB=AB tan∠OAB3∴光盘的直径为3故选：B．【点睛】本题主要考查了切线的性质，解题的关键是熟练应用切线长定理和锐角三角函数.5．已知下列命题：①若a＞b，则ac＞bc；②若a=1a；③内错角相等；④90°的圆周角所对的弦是直径．其中原命题与逆命题均为真命题的个数是（）A．1个B．2个C．3个D．4个【答案】A【解析】【分析】先对原命题进行判断，再判断出逆命题的真假即可．【详解】解:①若a＞b，则ac＞bc是假命题，逆命题是假命题；②若a=1，则a=a是真命题，逆命题是假命题；③内错角相等是假命题，逆命题是假命题；④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；其中原命题与逆命题均为真命题的个数是1个；故选A．点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要熟悉课本中的性质定理．6．如图，△ABC的外接圆是⊙O，半径AO=5，sinB=25，则线段AC的长为（）A．1 B．2 C．4 D．5【答案】C【解析】【分析】首先连接CO并延长交⊙O于点D，连接AD，由CD是⊙O的直径，可得∠CAD=90°，又由⊙O的半径是5，sinB=25，即可求得答案．【详解】解：连接CO并延长交⊙O于点D，连接AD，由CD 是⊙O 的直径，可得∠CAD=90°，∵∠B 和∠D 所对的弧都为弧AC ，∴∠B=∠D ，即sinB=sinD=25， ∵半径AO=5，∴CD=10， ∴2sin 105AC AC D CD ===， ∴AC=4，故选：C.【点睛】本题考查了同弧所对的圆周角相等，以及三角函数的内容，注意到直径所对的圆周角是直角是解题的关键.7．如图，AC BC ⊥，8AC BC ==，以BC 为直径作半圆，圆心为点O ；以点C 为圆心，BC 为半径作»AB ，过点O 作AC 的平行线交两弧于点D 、E ，则图中阴影部分的面积是（ ）A ．20833π- B ．20833π+C ．20833π D ．20433π 【答案】A【解析】【分析】 如图，连接CE ．图中S 阴影＝S 扇形BCE −S 扇形BOD −S △OCE ．根据已知条件易求得OB ＝OC ＝OD ＝4，BC ＝CE ＝8，∠ECB ＝60°，OE ＝3，所以由扇形面积公式、三角形面积公式进行解答即可．【详解】解：如图，连接CE ．∵AC⊥BC，AC＝BC＝8，以BC为直径作半圆，圆心为点O；以点C为圆心，BC为半径作弧AB，∴∠ACB＝90°，OB＝OC＝OD＝4，BC＝CE＝8．又∵OE∥AC，∴∠ACB＝∠COE＝90°．∴在Rt△OEC中，OC＝4，CE＝8，∴∠CEO＝30°，∠ECB＝60°，OE＝43，∴S阴影＝S扇形BCE−S扇形BOD−S△OCE＝2260811-4-443 36042ππ⨯⨯⨯⨯=20-83 3π故选：A．【点睛】本题考查了扇形面积的计算．不规则图形的面积一定要注意分割成规则图形的面积进行计算．8．如图，在⊙O，点A、B、C在⊙O上，若∠OAB＝54°，则∠C()A．54°B．27°C．36°D．46°【答案】C【解析】【分析】先利用等腰三角形的性质和三角形内角和计算出∠AOB的度数，然后利用圆周角解答即可.【详解】解：∵OA＝OB，∴∠OBA＝∠OAB＝54°，∴∠AOB＝180°﹣54°﹣54°＝72°，∴∠ACB＝12∠AOB＝36°．故答案为C．【点睛】本题考查了三角形内角和和圆周角定理,其中发现并正确利用圆周角定理是解题的关键.9．木杆AB斜靠在墙壁上，当木杆的上端A沿墙壁NO竖直下滑时，木杆的底端B也随之沿着射线OM方向滑动．下列图中用虚线画出木杆中点P随之下落的路线，其中正确的是（）A．B．C．D．【答案】D【解析】解：如右图，连接OP，由于OP是Rt△AOB斜边上的中线，所以OP=12AB，不管木杆如何滑动，它的长度不变，也就是OP是一个定值，点P就在以O为圆心的圆弧上，那么中点P下落的路线是一段弧线．故选D．10．如图，抛物线y＝ax2﹣6ax+5a（a＞0）与x轴交于A、B两点，顶点为C点．以C点为圆心，半径为2画圆，点P 在⊙C 上，连接OP ，若OP 的最小值为3，则C 点坐标是（ ）A ．522(,22-B ．（4，﹣5）C ．（3，﹣5）D ．（3，﹣4）【答案】D【解析】【分析】首先根据二次函数的解析式求出点A 、B 、C 三点的坐标，再由当点O 、P 、C 三点共线时，OP 取最小值为3，列出关于a 的方程，即可求解．【详解】∵2650y ax ax a a +-=（＞） 与x 轴交于A 、B 两点， ∴A （1，0）、B （5，0），∵226534y ax ax a a x a =+=---（） ， ∴顶点34C a （，-）， 当点O 、P 、C 三点共线时，OP 取最小值为3，∴OC ＝OP+2＝5， 29165(0)a a +=> ，∴1a = ，∴C （3，﹣4），故选：D ．【点睛】本题考查了二次函数的图象和性质，解题的关键是明确圆外一点到圆上的最短距离即该点与圆心的距离减去半径长．11．如图，O e 中，若66OA BC AOB ⊥∠=o 、，则ADC ∠的度数为（ ）A ．33°B ．56°C ．57°D ．66°【答案】A【解析】【分析】 根据垂径定理可得»»ACAB =，根据圆周角定理即可得答案． 【详解】∵OA ⊥BC ，∴»»ACAB =， ∵∠AOB=66°，∠AOB 和∠ADC 分别是»AB和»AC 所对的圆心角和圆周角， ∴∠ADC=12∠AOB=33°， 故选：A ．【点睛】 本题考查垂径定理及圆周角定理，垂直于弦的直径平分弦，并且平分这条弦所对的两条弧；在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；熟练掌握相关定理是解题关键．12．如图，ABC V 是O e 的内接三角形，且AB AC =，56ABC ∠=︒，O e 的直径CD 交AB 于点E ，则AED ∠的度数为（ ）A ．99︒B ．100︒C ．101°D ．102︒【答案】D【解析】【分析】 连接OB ，根据等腰三角形的性质得到∠A ，从而根据圆周角定理得出∠BOC ，再根据OB=OC 得出∠OBC ，即可得到∠OBE ，再结合外角性质和对顶角即可得到∠AED 的度数.【详解】解：连接OB，∵AB=AC，∴∠ABC=∠ACB=56°，∴∠A=180°-56°-56°=68°=12∠BOC，∴∠BOC=68°×2=136°，∵OB=OC，∴∠OBC=∠OCB=（180°-136°）÷2=22°，∴∠OBE=∠EBC-∠OBC=56°-22°=34°，∴∠AED=∠BEC=∠BOC-∠OBE=136°-34°=102°.故选D.【点睛】本题考查了圆周角定理，等腰三角形的性质，外角的性质，解题的关键是作出辅助线OB，得到∠BOC的度数.13．如图，圆O是△ABC的外接圆，∠A＝68°，则∠OBC的大小是( )A．22°B．26°C．32°D．68°【答案】A【解析】试题分析：根据同弧所对的圆心角等于圆周角度数的两倍，则∠BOC=2∠A=136°，则根据三角形内角和定理可得：∠OBC+∠OCB=44°，根据OB=OC可得：∠OBC=∠OCB=22°.考点：圆周角的计算14．如图，在边长为8的菱形ABCD中，∠DAB=60°，以点D为圆心，菱形的高DF为半径画弧，交AD 于点E ，交CD 于点G ，则图中阴影部分的面积是 （ ）A ．183π-B ．183πC ．32316πD ．1839π-【答案】C【解析】【分析】 由菱形的性质得出AD=AB=8，∠ADC=120°，由三角函数求出菱形的高DF ，图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积，根据面积公式计算即可．【详解】解：∵四边形ABCD 是菱形，∠DAB=60°，∴AD=AB=8，∠ADC=180°-60°=120°，∵DF 是菱形的高，∴DF ⊥AB ，∴DF=AD •sin60°=383= ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积 =2120(43)84332316ππ⨯⨯=． 故选：C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算；由三角函数求出菱形的高是解决问题的关键．15．下列命题中正确的个数是（ ）①过三点可以确定一个圆②直角三角形的两条直角边长分别是5和12，那么它的外接圆半径为6.5③如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米④三角形的重心到三角形三边的距离相等．A ．1个B ．2个C ．3个D ．4个【答案】A【解析】【分析】①根据圆的作法即可判断；②先利用勾股定理求出斜边的长度，然后根据外接圆半径等于斜边的一半即可判断；③根据圆与圆的位置关系即可得出答案；④根据重心的概念即可得出答案．【详解】①过不在同一条直线上的三点可以确定一个圆，故错误；②∵直角三角形的两条直角边长分别是5和12， ∴斜边为2251213+= ,∴它的外接圆半径为.113652⨯=，故正确； ③如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米或1厘米，故错误； ④三角形的内心到三角形三边的距离相等，故错误；所以正确的只有1个，故选：A ．【点睛】本题主要考查直角三角形外接圆半径，圆与圆的位置关系，三角形内心，重心的概念，掌握直角三角形外接圆半径的求法，圆与圆的位置关系，三角形内心，重心的概念是解题的关键．16．若正六边形的半径长为4，则它的边长等于（ ）A ．4B ．2C ．23D ．43【答案】A【解析】试题分析：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4．故选A ． 考点：正多边形和圆．17．如图，四边形ABCD 是⊙O 的内接四边形，若∠BOD=86°，则∠BCD 的度数是（ ）A ．86°B ．94°C ．107°D ．137° 【答案】D【解析】【分析】【详解】解：∵∠BOD=86°，∴∠BAD=86°÷2=43°，∵∠BAD+∠BCD=180°，∴∠BCD=180°-43°=137°，即∠BCD的度数是137°．故选D．【点睛】本题考查圆内接四边形的对角互补．②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．18．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”.除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形(如图1)，它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形. 图2是等宽的勒洛三角形和圆形滚木的截面图.图1图2有如下四个结论：①勒洛三角形是中心对称图形②图1中，点A到BC上任意一点的距离都相等③图2中，勒洛三角形的周长与圆的周长相等④使用截面是勒洛三角形的滚木来搬运东西，会发生上下抖动上述结论中，所有正确结论的序号是（）A．①②B．②③C．②④D．③④【答案】B【解析】【分析】逐一对选项进行分析即可.【详解】①勒洛三角形不是中心对称图形，故①错误；②图1中，点A到BC上任意一点的距离都相等，故②正确；③图2中，设圆的半径为r∴勒洛三角形的周长=12032180rrππ⨯=g g圆的周长为2rπ∴勒洛三角形的周长与圆的周长相等，故③正确；④使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动，故④错误故选B【点睛】本题主要考查中心对称图形，弧长公式等，掌握中心对称图形和弧长公式是解题的关键.19．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（ ）A ．13B ．12C ．34D ．1【答案】B【解析】 【分析】根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长． 【详解】圆锥的底面周长是：π；设圆锥的底面半径是r ，则2πr=π．解得：r=12． 故选B ．【点睛】本题考查了圆锥的计算，正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．20．在平面直角坐标系内，以原点O 为圆心，1为半径作圆，点P 在直线323y x =+上运动，过点P 作该圆的一条切线，切点为A ，则PA 的最小值为( )A ．3B ．2C 3D 2 【答案】D【解析】【分析】先根据题意，画出图形，令直线3x+ 23x 轴交于点C ，与y 轴交于点D ，作OH ⊥CD 于H ，作OH ⊥CD 于H ；然后根据坐标轴上点的坐标特点，由一次函数解析式，求得C 、D 两点的坐标值； 再在Rt △POC 中，利用勾股定理可计算出CD 的长，并利用面积法可计算出OH 的值； 最后连接OA ，利用切线的性质得OA ⊥PA ，在Rt △POH 中，利用勾股定理，得到21PA OP =-PA 的最小值即可.【详解】如图，令直线3x+23x轴交于点C，与y轴交于点D，作OH⊥CD于H，当x=0时，y=3D（0，3当y=033，解得x=-2，则C（-2，0），∴222(23)4CD=+=，∵12OH•CD=12OC•OD，∴OH=233 4⨯=连接OA，如图，∵PA为⊙O的切线，∴OA⊥PA，∴2221PA OP OA OP=-=-当OP的值最小时，PA的值最小，而OP的最小值为OH的长，∴PA22(3)12-=故选D.【点睛】本题考查了切线的性质，解题关键是熟记切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．。
人教版初中数学圆的经典测试题含答案
人教版初中数学圆的经典测试题含答案一、选择题1．如图，有一个边长为2cm 的正六边形纸片，若在该纸片上沿虚线剪一个最大圆形纸片，则这个圆形纸片的半径是（ ）A ．3cmB ．2cmC ．23cmD ．4cm【答案】A【解析】【分析】 根据题意画出图形，再根据正多边形圆心角的求法求出∠AOB 的度数，最后根据等腰三角形及直角三角形的性质解答即可．【详解】解：如图所示，正六边形的边长为2cm ，OG ⊥BC ，∵六边形ABCDEF 是正六边形，∴∠BOC=360°÷6=60°，∵OB=OC ，OG ⊥BC ，∴∠BOG=∠COG=12∠BOC =30°， ∵OG ⊥BC ，OB=OC ，BC=2cm ， ∴BG=12BC=12×2=1cm ， ∴OB=sin 30BG =2cm ， ∴OG=2222213OB BG -=-=，∴圆形纸片的半径为3cm ，故选：A ．【点睛】本题考查的是正多边形和圆，根据题意画出图形，利用直角三角形的性质及正六边形的性质解答是解答此题的关键．2．如图，在平行四边形ABCD 中，BD ⊥AD ，以BD 为直径作圆，交于AB 于E ，交CD 于F ，若BD=12，AD ：AB=1：2，则图中阴影部分的面积为（ ）A ．123B ．1536π-πC ．30312π-D ．48336π-π【答案】C【解析】【分析】易得AD 长，利用相应的三角函数可求得∠ABD 的度数，进而求得∠EOD 的度数，那么一个阴影部分的面积=S △ABD -S 扇形DOE -S △BOE ，算出后乘2即可．【详解】连接OE ，OF ．∵BD=12，AD ：AB=1：2，∴AD=43 ，AB=83，∠ABD=30°，∴S △ABD =×43×12=243,S 扇形=603616,633933602OEB S ππ⨯==⨯⨯=∵两个阴影的面积相等，∴阴影面积=()224369330312ππ⨯--=- .故选：C【点睛】本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积．3．如图，已知AB 是⊙O 是直径，弦CD ⊥AB ，AC 2，BD =1，则sin ∠ABD 的值是( )A ．2B ．13C ．23D ．3【答案】C【解析】【分析】 先根据垂径定理，可得BC 的长，再利用直径对应圆周角为90°得到△ABC 是直角三角形，利用勾股定理求得AB 的长，得到sin ∠ABC 的大小，最终得到sin ∠ABD【详解】解：∵弦CD ⊥AB ，AB 过O ，∴AB 平分CD ，∴BC =BD ，∴∠ABC =∠ABD ，∵BD =1，∴BC =1，∵AB 为⊙O 的直径，∴∠ACB =90°，由勾股定理得：AB ()22222213AC BC +=+=， ∴sin ∠ABD =sin ∠ABC =23AC AB = 故选：C ．【点睛】本题考查了垂径定理、直径对应圆周角为90°、勾股定理和三角函数，解题关键是找出图形中的直角三角形，然后按照三角函数的定义求解4．已知下列命题：①若a ＞b ，则ac ＞bc ；②若a=1a ；③内错角相等；④90°的圆周角所对的弦是直径．其中原命题与逆命题均为真命题的个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】A【解析】【分析】先对原命题进行判断，再判断出逆命题的真假即可．【详解】解:①若a＞b，则ac＞bc是假命题，逆命题是假命题；②若a=1，则a=a是真命题，逆命题是假命题；③内错角相等是假命题，逆命题是假命题；④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；其中原命题与逆命题均为真命题的个数是1个；故选A．点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要熟悉课本中的性质定理．5．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（）A．20°B．35°C．40°D．55°【答案】B【解析】【分析】连接FB，由邻补角定义可得∠FOB=140°，由圆周角定理求得∠FEB=70°，根据等腰三角形的性质分别求出∠OFB、∠EFB的度数，继而根据∠EFO＝∠EBF-∠OFB即可求得答案.【详解】连接FB，则∠FOB=180°-∠AOF=180°-40°=140°，∴∠FEB＝12∠FOB=70°，∵FO＝BO，∴∠OFB＝∠OBF=(180°-∠FOB)÷2=20°，∵EF＝EB，∴∠EFB＝∠EBF=(180°-∠FEB)÷2=55°，∴∠EFO＝∠EBF-∠OFB=55°-20°=35°，故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.6．如图，△ABC的外接圆是⊙O，半径AO=5，sinB=25，则线段AC的长为（）A．1 B．2 C．4 D．5【答案】C【解析】【分析】首先连接CO并延长交⊙O于点D，连接AD，由CD是⊙O的直径，可得∠CAD=90°，又由⊙O的半径是5，sinB=25，即可求得答案．【详解】解：连接CO并延长交⊙O于点D，连接AD，由CD是⊙O的直径，可得∠CAD=90°，∵∠B和∠D所对的弧都为弧AC，∴∠B=∠D，即sinB=sinD=25，∵半径AO=5，∴CD=10，∴2sin 105AC AC D CD ===， ∴AC=4，故选：C.【点睛】 本题考查了同弧所对的圆周角相等，以及三角函数的内容，注意到直径所对的圆周角是直角是解题的关键.7．如图，ABC ∆是O 的内接三角形，45A ∠=︒，1BC =，把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，点A 的对应点为点D ，则点A ，D 之间的距离是（）A ．1B ．2C ．3D ．2【答案】A【解析】【分析】 连接AD ，构造△ADB ，由同弧所对应的圆周角相等和旋转的性质，证△ADB 和△DBE 全等，从而得到AD=BE=BC=1.【详解】如图，连接AD ，AO ，DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，∴AB=DE ，90AOD ∠=︒，45CAB BDE ∠=∠=︒∴1452ABD AOD ∠=∠=︒（同弧所对应的圆周角等于圆心角的一半）， 即45ABD EDB ∠=∠=︒，又∵DB=BD ，∴DAB BED ∠=∠（同弧所对应的圆周角相等），在△ADB 和△DBE 中ABD EDB AB EDDAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD （ASA ）,∴AD=EB=BC=1.故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用；顶点在圆上，两边都与圆相交的角角圆周角；掌握三角形全等的判定是解题的关键.8．已知某圆锥的底面半径为3 cm ，母线长5 cm ，则它的侧面展开图的面积为（ ） A ．30 cm 2B ．15 cm 2C ．30π cm 2D ．15π cm 2【答案】D【解析】试题解析：根据圆锥的侧面展开图的面积计算公式得：S ＝RL π＝15π故选D.9．如图，已知AB 是⊙O 的直径，CD 是弦，且CD ⊥AB ，BC=3，AC=4，则sin ∠ABD 的值是（ ）A ．43B ．34C ．35D ．45【答案】D【解析】【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC ，再根据勾股定理求得AB=5，即可求sin ∠ABD 的值．【详解】∵AB 是⊙O 的直径，CD ⊥AB ，∴弧AC=弧AD ，∴∠ABD=∠ABC ．根据勾股定理求得AB=5，∴sin∠ABD=sin∠ABC=45．故选D．【点睛】此题综合考查了垂径定理以及圆周角定理的推论，熟悉锐角三角函数的概念．10．如图，以Rt△ABC的直角边AB为直径作⊙O交BC于点D，连接AD，若∠DAC＝30°，DC＝1，则⊙O的半径为（）A．2 B3C．23D．1【答案】B【解析】【分析】先由圆周角定理知∠BDA=∠ADC=90°，结合∠DAC=30°，DC=1得AC=2DC=2，∠C=60°，再由3【详解】∵AB是⊙O的直径，∴∠BDA＝∠ADC＝90°，∵∠DAC＝30°，DC＝1，∴AC＝2DC＝2，∠C＝60°，则在Rt△ABC中，AB＝ACtanC＝3，∴⊙O3，故选：B．【点睛】本题主要考查圆周角定理，解题的关键是掌握半圆（或直径）所对的圆周角是直角和三角函数的应用．11．如图，在平面直角坐标系中，已知C（3，4），以点C为圆心的圆与y轴相切．点A、B在x轴上，且OA=OB．点P为⊙C上的动点，∠APB=90°，则AB长度的最小值为（）A．4 B．3 C．7 D．8【答案】A【解析】【分析】连接OC，交⊙C上一点P，以O为圆心，以OP为半径作⊙O，交x轴于A、B，此时AB的长度最小，根据勾股定理和题意求得OP=2，则AB的最小长度为4．【详解】解：如图，连接OC，交⊙C上一点P，以O为圆心，以OP为半径作⊙O，交x轴于A、B，此时AB的长度最小，∵C（3，4），∴OC22，34∵以点C为圆心的圆与y轴相切．∴⊙C的半径为3，∴OP=OC﹣3=2，∴OP=OA=OB=2，∵AB是直径，∴∠APB=90°，∴AB长度的最小值为4，故选：A．【点睛】本题考查了圆切线的性质、坐标和图形的性质、圆周角定理、勾股定理，找到OP的最小值是解题的关键.12．如图，在Rt△ABC中，∠ABC=90°，AB=23BC=2，以AB的中点为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为( )A ．5342π-B ．5342π+C ．23π-D ．432π-【答案】A【解析】【分析】连接OD ，过点O 作OH ⊥AC ，垂足为 H ，则有AD=2AH ，∠AHO=90°，在Rt △ABC 中，利用∠A 的正切值求出∠A=30°，继而可求得OH 、AH 长，根据圆周角定理可求得∠BOC =60°，然后根据S 阴影=S △ABC -S △AOD -S 扇形BOD 进行计算即可.【详解】连接OD ，过点O 作OH ⊥AC ，垂足为 H ，则有AD=2AH ，∠AHO=90°，在Rt △ABC 中，∠ABC=90°，AB=23，BC=2，tan ∠A=23323BC AB ==， ∴∠A=30°，∴OH=12OA=32，AH=AO•cos ∠A=33322⨯=，∠BOC=2∠A=60°， ∴AD=2AH=3，∴S 阴影=S △ABC -S △AOD -S 扇形BOD =()26031132323222360π⨯⨯⨯-⨯⨯-=5342π-， 故选A.【点睛】本题考查了垂径定理，圆周角定理，扇形面积，解直角三角形等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.13．如图，已知ABC ∆和ABD ∆都O 是的内接三角形，AC 和BD 相交于点E ，则与ADE ∆的相似的三角形是（ ）A ．BCE ∆B ．ABC ∆ C ．ABD ∆ D ．ABE ∆【答案】A【解析】【分析】 根据同弧和等弧所对的圆周角相等， 则AB 弧所对的圆周角BCE BDA ∠=∠，CEB ∠和DEA ∠是对顶角，所以ADE BCE ∆∆∽．【详解】解：BCE BDA ∠=∠，CEB DEA ∠=∠ADE BCE ∴∆∆∽，故选：A ．【点睛】 考查相似三角形的判定定理： 两角对应相等的两个三角形相似，关键就是牢记同弧所对的圆周角相等．14．如图，点I 是Rt △ABC 的内心，∠C ＝90°，AC ＝3，BC ＝4，将∠ACB 平移使其顶点C 与I 重合，两边分别交AB 于D 、E ，则△IDE 的周长为（ ）A ．3B ．4C ．5D ．7【答案】C【解析】【分析】 连接AI 、BI ，根据三角形的内心的性质可得∠CAI ＝∠BAI ，再根据平移的性质得到∠CAI ＝∠AID ，AD ＝DI ，同理得到BE ＝EI ，即可解答.【详解】连接AI 、BI ，∵∠C＝90°，AC＝3，BC＝4，∴AB＝22+＝5AC BC∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI＝∠BAI，由平移得：AC∥DI，∴∠CAI＝∠AID，∴∠BAI＝∠AID，∴AD＝DI，同理可得：BE＝EI，∴△DIE的周长＝DE+DI+EI＝DE+AD+BE＝AB＝5故选C．【点睛】此题考查了平移的性质和三角形内心的性质，解题关键在于作出辅助线15．如图，圆O是△ABC的外接圆，∠A＝68°，则∠OBC的大小是( )A．22°B．26°C．32°D．68°【答案】A【解析】试题分析：根据同弧所对的圆心角等于圆周角度数的两倍，则∠BOC=2∠A=136°，则根据三角形内角和定理可得：∠OBC+∠OCB=44°，根据OB=OC可得：∠OBC=∠OCB=22°.考点：圆周角的计算16．如图，AB是⊙O的直径，弦CD⊥AB于E点，若AD=CD= 23BC的长为()A ．3πB ．23πC ．33πD ．233π 【答案】B【解析】【分析】根据垂径定理得到3CE DE ==，BC BD = ，∠A=30°，再利用三角函数求出OD=2，即可利用弧长公式计算解答.【详解】如图：连接OD ，∵AB 是⊙O 的直径，弦CD ⊥AB 于E 点，AD =CD = 23，∴3CE DE ==，BC BD = ，∠A=30°， ∴∠DOE=60°，∴OD=2sin 60DE =， ∴BC 的长=BD 的长=60221803ππ⨯=， 故选：B.【点睛】此题考查垂径定理，三角函数，弧长公式，圆周角定理，是一道圆的综合题.17．如图，有一圆锥形粮堆，其侧面展开图是半径为6m 的半圆，粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食，此时，小猫正在B 处，它要沿圆锥侧面到达P 处捕捉老鼠，则小猫所经过的最短路程长为（ ）A ．3mB ．33mC ．35mD ．4m【答案】C【解析】【分析】【详解】 如图，由题意得：AP =3，AB =6，90.BAP ∠=∴在圆锥侧面展开图中223635.BP m =+= 故小猫经过的最短距离是35.m故选C.18．如图，四边形ABCD 是⊙O 的内接正方形，点P 是劣弧弧AB 上任意一点（与点B 不重合），则∠BPC 的度数为（ ）A ．30°B ．45°C ．60°D ．90°【答案】B【解析】 分析：接OB ，OC ，根据四边形ABCD 是正方形可知∠BOC=90°，再由圆周角定理即可得出结论．详解：连接OB ，OC ，∵四边形ABCD 是正方形，∴∠BOC=90°，∴∠BPC=12∠BOC=45°． 故选B ．点睛：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．19．如图，⊙O 过点B 、C ，圆心O 在等腰直角△ABC 的内部，∠BAC ＝90°，OA ＝1，BC ＝6，则⊙O 的半径为（ ）A ．23B ．13C ．4D ．32【答案】B【解析】【分析】如下图，作AD ⊥BC ，设半径为r ，则在Rt △OBD 中，OD=3－1，OB=r ，BD=3，利用勾股定理可求得r.【详解】如图，过A 作AD ⊥BC ，由题意可知AD 必过点O ，连接OB ；∵△BAC 是等腰直角三角形，AD ⊥BC ，∴BD=CD=AD=3；∴OD=AD-OA=2；Rt △OBD 中，根据勾股定理，得：22BD OD 13+故答案为：B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用，解题关键是利用等腰直角三角形ABC 判定点O 在AD 上.20．如图，弧 AB 等于弧CD ，OE AB ⊥于点E ，OF CD ⊥于点F ，下列结论中错误．．的是（ ）A ．OE=OFB ．AB=CDC ．∠AOB =∠COD D ．OE ＞OF【答案】D【解析】【分析】 根据圆心角、弧、弦的关系可得B 、C 正确，根据垂径定理和勾股定理可得A 正确，D 错误．【详解】解：∵AB CD =，∴AB ＝CD ，∠AOB ＝∠COD ，∵OE AB ⊥，OF CD ⊥，∴BE ＝12AB ，DF ＝12CD ， ∴BE ＝DF ，又∵OB ＝OD ， ∴由勾股定理可知OE ＝OF ，即A 、B 、C 正确，D 错误，故选：D ．【点睛】本题考查了圆心角、弧、弦的关系，垂径定理，勾股定理，熟练掌握基本性质定理是解题的关键．。
人教版初中数学圆的真题汇编含答案解析
人教版初中数学圆的真题汇编含答案解析一、选择题1．如图，在ABC ∆中，5AB =，3AC =，4BC =，将ABC ∆绕一逆时针方向旋转40︒得到ADE ∆，点B 经过的路径为弧BD ，则图中阴影部分的面积为( )A ．1463π-B ．33π+C ．3338π-D ．259π 【答案】D【解析】【分析】 由旋转的性质可得△ACB ≌△AED ，∠DAB=40°，可得AD=AB=5，S △ACB =S △AED ，根据图形可得S 阴影=S △AED +S 扇形ADB -S △ACB =S 扇形ADB ，再根据扇形面积公式可求阴影部分面积．【详解】∵将△ABC 绕A 逆时针方向旋转40°得到△ADE ，∴△ACB ≌△AED ，∠DAB=40°，∴AD=AB=5，S △ACB =S △AED ，∵S 阴影=S △AED +S 扇形ADB -S △ACB =S 扇形ADB ，∴S 阴影=4025360π⨯=259π， 故选D.【点睛】本题考查了旋转的性质，扇形面积公式，熟练掌握旋转的性质：①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.2．如图，已知AB 是⊙O 是直径，弦CD ⊥AB ，AC =22，BD =1，则sin ∠ABD 的值是( )A ．2B ．13C 22D ．3【答案】C【解析】【分析】先根据垂径定理，可得BC 的长，再利用直径对应圆周角为90°得到△ABC 是直角三角形，利用勾股定理求得AB 的长，得到sin ∠ABC 的大小，最终得到sin ∠ABD【详解】解：∵弦CD ⊥AB ，AB 过O ，∴AB 平分CD ，∴BC =BD ，∴∠ABC =∠ABD ，∵BD =1，∴BC =1，∵AB 为⊙O 的直径，∴∠ACB =90°，由勾股定理得：AB =()22222213AC BC +=+=， ∴sin ∠ABD =sin ∠ABC =223AC AB = 故选：C ．【点睛】本题考查了垂径定理、直径对应圆周角为90°、勾股定理和三角函数，解题关键是找出图形中的直角三角形，然后按照三角函数的定义求解3．将直尺、有60°角的直角三角板和光盘如图摆放，A 为60°角与直尺的交点，B 为光盘与直尺的交点，AB =4，则光盘表示的圆的直径是( )A ．4B ．3C ．6D ．43【答案】B【解析】【分析】 设三角板与圆的切点为C ，连接OA 、OB ，根据切线长定理可得AB=AC=3，∠OAB=60°，然后根据三角函数，即可得出答案.【详解】设三角板与圆的切点为C ，连接OA 、OB ，由切线长定理知，AB =AC =3，AO 平分∠BAC ，∴∠OAB =60°，在Rt △ABO 中，OB =AB tan ∠OAB =43， ∴光盘的直径为83．故选：B ．【点睛】本题主要考查了切线的性质，解题的关键是熟练应用切线长定理和锐角三角函数.4．如图，AC BC ⊥，8AC BC ==，以BC 为直径作半圆，圆心为点O ；以点C 为圆心，BC 为半径作»AB ，过点O 作AC 的平行线交两弧于点D 、E ，则图中阴影部分的面积是（ ）A ．20833π- B ．20833π+ C ．20833π- D ．20433π+ 【答案】A【解析】【分析】 如图，连接CE ．图中S 阴影＝S 扇形BCE −S 扇形BOD −S △OCE ．根据已知条件易求得OB ＝OC ＝OD ＝4，BC ＝CE ＝8，∠ECB ＝60°，OE ＝43，所以由扇形面积公式、三角形面积公式进行解答即可．【详解】解：如图，连接CE ．∵AC ⊥BC ，AC ＝BC ＝8，以BC 为直径作半圆，圆心为点O ；以点C 为圆心，BC 为半径作弧AB ，∴∠ACB ＝90°，OB ＝OC ＝OD ＝4，BC ＝CE ＝8．又∵OE ∥AC ，∴∠ACB ＝∠COE ＝90°．∴在Rt △OEC 中，OC ＝4，CE ＝8，∴∠CEO ＝30°，∠ECB ＝60°，OE ＝43， ∴S 阴影＝S 扇形BCE −S 扇形BOD −S △OCE ＝2260811-4-44336042ππ⨯⨯⨯⨯ =20-833π 故选：A ．【点睛】 本题考查了扇形面积的计算．不规则图形的面积一定要注意分割成规则图形的面积进行计算．5．如图，ABC ∆是O e 的内接三角形，45A ∠=︒，1BC =，把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，点A 的对应点为点D ，则点A ，D 之间的距离是（）A ．1B 2C 3D ．2【答案】A【解析】【分析】 连接AD ，构造△ADB ，由同弧所对应的圆周角相等和旋转的性质，证△ADB 和△DBE 全等，从而得到AD=BE=BC=1.【详解】如图，连接AD ，AO ，DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，∴AB=DE ，90AOD ∠=︒，45CAB BDE ∠=∠=︒ ∴1452ABD AOD ∠=∠=︒（同弧所对应的圆周角等于圆心角的一半）， 即45ABD EDB ∠=∠=︒，又∵DB=BD ，∴DAB BED ∠=∠（同弧所对应的圆周角相等），在△ADB 和△DBE 中 ABD EDB AB ED DAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD （ASA ）,∴AD=EB=BC=1. 故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用；顶点在圆上，两边都与圆相交的角角圆周角；掌握三角形全等的判定是解题的关键.6．如图，边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1，边B 1C 1与CD 交于点O ，则图中阴影部分的面积是（ ）A ．224π-- B ．224π- C ．142π+ D ．142π- 【答案】B【解析】【分析】先根据正方形的边长，求得CB 1=OB 1=AC-AB 12，进而得到211(21)2OB C S =V ，再根据S △AB1C1=12，以及扇形的面积公式即可得出图中阴影部分的面积． 【详解】 连结DC 1，∵∠CAC 1＝∠DCA ＝∠COB 1＝∠DOC 1＝45°，∴∠AC 1B 1＝45°，∵∠ADC ＝90°，∴A ，D ，C 1在一条直线上，∵四边形ABCD 是正方形，∴AC ＝2，∠OCB 1＝45°，∴CB 1＝OB 1∵AB 1＝1，∴CB 1＝OB 1＝AC ﹣AB 1＝2﹣1，∴211111(21)22OB C S OB CB ∆=⋅⋅=-， ∵1111111111222AB C S AB B C =⋅=⨯⨯=V ， ∴图中阴影部分的面积＝2245(2)11(21)22360224ππ⨯⨯---=-+． 故选B ．【点睛】本题考查了旋转的性质，正方形性质、勾股定理以及扇形面积的计算等知识点的综合应用，主要考查学生运用性质进行计算的能力．解题时注意：旋转前、后的图形全等．7．如图，ABC V 中，90ACB ∠=︒，O 为AB 中点，且4AB =，CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，则OD 的最小值为（ ）．A ．1B ．22C 21D ．222【答案】D【解析】【分析】根据三角形角平分线的交点是三角形的内心，得到DO 最小时，DO 为三角形ABC 内切圆的半径，结合切线长定理得到三角形为等腰直角三角形，从而得到答案．【详解】解：Q CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，D ∴为ABC ∆的内心，OD ∴最小时，OD 为ABC ∆的内切圆的半径，,DO AB ∴⊥过D 作,,DE AC DF BC ⊥⊥ 垂足分别为,,E F,DE DF DO ∴==∴ 四边形DFCE 为正方形，O Q 为AB 的中点，4,AB =2,AO BO ∴==由切线长定理得：2,2,,AO AE BO BF CE CF r ======sin 4522,AC BC AB ∴==•︒=222,CE AC AE ∴=-=-Q 四边形DFCE 为正方形，,CE DE ∴=222,OD CE ∴==-故选D ．【点睛】本题考查的动态问题中的线段的最小值，三角形的内心的性质，等腰直角三角形的性质，锐角三角函数的计算，掌握相关知识点是解题关键．8．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，点D 在BA 的延长线上，CD 与⊙O 交于另一点E ，DE=OB=2，∠D=20°，则弧BC 的长度为（ ）A．23πB．13πC．43πD．49π【答案】A【解析】【分析】连接OE、OC，如图，根据等腰三角形的性质得到∠D=∠EOD=20°，根据外角的性质得到∠CEO=∠D+∠EOD=40°，根据等腰三角形的性质得到∠C=∠CEO=40°，根据外角的性质得到∠BOC=∠C+∠D=60°，根据求弧长的公式得到结论.【详解】解：连接OE、OC，如图，∵DE=OB=OE，∴∠D=∠EOD=20°，∴∠CEO=∠D+∠EOD=40°，∵OE=OC，∴∠C=∠CEO=40°，∴∠BOC=∠C+∠D=60°，∴»BC的长度=260?2360π⨯=23π，故选A.【点睛】本题考查了弧长公式：l=••180n Rπ（弧长为l，圆心角度数为n，圆的半径为R），还考查了圆的认识及等腰三角形的性质及三角形外角的性质，熟练掌握等腰三角形的性质和三角形外角性质是关键．9．在Rt△ABC中，∠ACB=90°.AC=8，BC=3，点D是BC边上动点，连接AD交以CD为直径的圆于点E，则线段BE长度的最小值为( )A．1 B．32C．3D．52【答案】A【解析】【分析】根据直径所对的圆周角为直角可知∠CED=90°，则∠AEC=90°，设以AC为直径的圆的圆心为O，若BE最短，则OB最短，根据直角三角形斜边上的中线等于斜边的一半可得OE=12AC=4，在Rt△OBC中，根据勾股定理可求得OB=5，即可得解.【详解】解：连接CE，∵E点在以CD为直径的圆上，∴∠CED=90°，∴∠AEC=180°-∠CED=90°，∴E点也在以AC为直径的圆上，设以AC为直径的圆的圆心为O，若BE最短，则OB最短，∵AC=8，∴OC=12AC=4，∵BC=3，∠ACB=90°，∴OB=22OC BC=5，∵OE=OC=4，∴BE=OB-OE=5-4=1.故选A.【点睛】本题考查了直径所对的圆周角为直角，直角三角形的性质和勾股定理.10．中国科学技术馆有“圆与非圆”展品，涉及了“等宽曲线”的知识．因为圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了例以外，还有一些几何图形也是“等宽曲线”，如勒洛只角形(图1)，它是分别以等边三角形的征个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧．三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆．下列说法中错误的是( )A ．勒洛三角形是轴对称图形B ．图1中，点A 到¶BC上任意一点的距离都相等 C ．图2中，勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都相等 D ．图2中，勒洛三角形的周长与圆的周长相等【答案】C【解析】【分析】根据轴对称形的定义，可以找到一条直线是的图像左右对着完全重合，则为轴对称图形.鲁列斯曲边三角形有三条对称轴. 鲁列斯曲边三角形可以看成是3个圆心角为60°，半径为DE 的扇形的重叠，根据其特点可以进行判断选项的正误.【详解】鲁列斯曲边三角形有三条对称轴，就是等边三角形的各边中线所在的直线，故正确；点A 到¶BC上任意一点的距离都是DE ，故正确; 勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都不相等，1O 到顶点的距离是到边的中点的距离的2倍，故错误；鲁列斯曲边三角形的周长=3×60180DE DE ππ⨯=⨯ ,圆的周长=22DE DE ππ⨯=⨯ ,故说法正确.故选C.【点睛】主要考察轴对称图形，弧长的求法即对于新概念的理解．11．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（ ）A ．13B ．12C ．34D ．1【答案】B【解析】【分析】根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长．【详解】圆锥的底面周长是：π；设圆锥的底面半径是r ，则2πr=π．解得：r=12． 故选B ．【点睛】本题考查了圆锥的计算，正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．12．如图，在菱形ABCD 中，60ABC ∠=︒，1AB =，点P 是这个菱形内部或边上的一点，若以点P ，B ，C 为顶点的三角形是等腰三角形，则P ，D （P ，D 两点不重合）两点间的最短距离为（ ）A ．12B ．1C 3D 31【答案】D【解析】【分析】分三种情形讨论①若以边BC 为底．②若以边PC 为底．③若以边PB 为底．分别求出PD 的最小值，即可判断．【详解】解：在菱形ABCD 中，∵∠ABC=60°，AB=1，∴△ABC ，△ACD 都是等边三角形，①若以边BC 为底，则BC 垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“，即当点P 与点A 重合时，PD 值最小，最小值为1；②若以边PC 为底，∠PBC 为顶角时，以点B 为圆心，BC 长为半径作圆，与BD 相交于一点，则弧AC （除点C 外）上的所有点都满足△PBC 是等腰三角形，当点P 在BD 上时，PD1③若以边PB 为底，∠PCB 为顶角，以点C 为圆心，BC 为半径作圆，则弧BD 上的点A 与点D 均满足△PBC 为等腰三角形，当点P 与点D 重合时，PD 最小，显然不满足题意，故此种情况不存在；上所述，PD 的最小值为1故选D ．【点睛】本题考查菱形的性质、等边三角形的性质、等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．13．一个圆锥的底面半径是5，高为12，则这个圆锥的全面积是（ ）A ．60πB ．65πC ．85πD ．90π【答案】D【解析】【分析】根据勾股定理求出圆锥侧面母线长，再根据圆锥的全面积=底面积+侧面积求出答案.【详解】∵圆锥的底面半径是5，高为12，13=，∵圆锥的侧面积=51365ππ⨯⨯=，圆锥的底面积=2525ππ⨯=，∴圆锥的全面积=652590πππ+=，故选：D.【点睛】此题考查圆锥的全面积，圆锥侧面母线长与底面圆的半径、圆锥的高的关系，熟记计算公式是解题的关键.14．如图，抛物线y ＝ax 2﹣6ax+5a （a ＞0）与x 轴交于A 、B 两点，顶点为C 点．以C 点为圆心，半径为2画圆，点P 在⊙C 上，连接OP ，若OP 的最小值为3，则C 点坐标是（ ）A ．5252(,)22-B ．（4，﹣5）C ．（3，﹣5）D ．（3，﹣4）【答案】D【解析】【分析】首先根据二次函数的解析式求出点A 、B 、C 三点的坐标，再由当点O 、P 、C 三点共线时，OP 取最小值为3，列出关于a 的方程，即可求解．【详解】∵2650y ax ax a a +-=（＞） 与x 轴交于A 、B 两点， ∴A （1，0）、B （5，0），∵226534y ax ax a a x a =+=---（） ， ∴顶点34C a （，-）， 当点O 、P 、C 三点共线时，OP 取最小值为3，∴OC ＝OP+2＝5，∴29165(0)a a +=> ，∴1a = ，∴C （3，﹣4），故选：D ．【点睛】本题考查了二次函数的图象和性质，解题的关键是明确圆外一点到圆上的最短距离即该点与圆心的距离减去半径长．15．如图，AB 是⊙O 的直径，AC 是⊙O 的切线，OC 交⊙O 于点D ，若∠ABD ＝24°，则∠C 的度数是（ ）A．48°B．42°C．34°D．24°【答案】B【解析】【分析】根据切线的性质求出∠OAC，结合∠C＝42°求出∠AOC，根据等腰三角形性质求出∠B＝∠BDO，根据三角形外角性质求出即可．【详解】解：∵∠ABD＝24°，∴∠AOC＝48°，∵AC是⊙O的切线，∴∠OAC＝90°，∴∠AOC+∠C＝90°，∴∠C＝90°﹣48°＝42°，故选：B．【点睛】考查了切线的性质，圆周角定理，三角形内角和定理，解此题的关键是求出∠AOC的度数，题目比较好，难度适中．16．如图，已知某圆锥轴截面等腰三角形的底边和高线长均为10cm，则这个圆锥的侧面积为（）A．50cm2B．50πcm2C．52D．5cm2【答案】D【解析】【分析】根据勾股定理求出圆锥的母线长，求出底面圆周长，根据扇形面积公式计算即可．【详解】解：如图所示，∵等腰三角形的底边和高线长均为10cm，22＝55，圆锥底面圆半105径为5，∴这个圆锥的底面圆周长=2×π×5=10π，即为侧面展开扇形的弧长，圆锥的侧面积＝155cm2，2故选：D．【点睛】本题考查了圆锥的计算，解题的关键是弄清楚圆锥的侧面积的计算方法，特别是圆锥的轴截面是等腰三角形，勾股定理的应用，以及圆锥的底面周长等于圆锥的侧面扇形的弧长．17．如图，AB是⊙O的直径，弦CD⊥AB于点M，若CD＝8 cm，MB＝2 cm，则直径AB的长为（）A．9 cm B．10 cm C．11 cm D．12 cm【答案】B【解析】【分析】由CD⊥AB，可得DM=4．设半径OD=Rcm，则可求得OM的长，连接OD，在直角三角形DMO中，由勾股定理可求得OD的长，继而求得答案．【详解】解：连接OD，设⊙O半径OD为R,∵AB是⊙O的直径，弦CD⊥AB于点M，∴DM=12CD=4cm，OM=R-2,在RT△OMD中，OD²=DM²+OM²即R²=4²+(R-2)²,解得：R=5,∴直径AB的长为:2×5=10cm．故选B．【点睛】本题考查了垂径定理以及勾股定理．注意掌握辅助线的作法及数形结合思想的应用．18．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为（）A．23B．13C．4 D．32【答案】B【解析】【分析】如下图，作AD⊥BC，设半径为r，则在Rt△OBD中，OD=3－1，OB=r，BD=3，利用勾股定理可求得r.【详解】如图，过A作AD⊥BC，由题意可知AD必过点O，连接OB；∵△BAC是等腰直角三角形，AD⊥BC，∴BD=CD=AD=3；∴OD=AD-OA=2；Rt△OBD中，根据勾股定理，得：OB= 22+=BD OD13故答案为：B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用，解题关键是利用等腰直角三角形ABC判定点O在AD上.19．如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（）A．15°B．30°C．60°D．75°【答案】D【解析】【分析】【详解】连接OD，∵CA，CD是⊙O的切线，∴OA⊥AC，OD⊥CD，∴∠OAC=∠ODC=90°，∵∠ACD=30°，∴∠AOD=360°﹣∠C﹣∠OAC﹣∠ODC=150°，∵OB=OD，∴∠DBA=∠ODB=12∠AOD=75°．故选D．考点：切线的性质；圆周角定理．20．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC 的长为（）A．25cm B．45 cm C．25cm或45cm D．23cm或43cm【答案】C【解析】连接AC，AO，∵O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=12AB=12×8=4cm,OD=OC=5cm,当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴==3cm，∴CM=OC+OM=5+3=8cm，∴==；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5−3=2cm，在Rt△AMC中==cm.故选C.。
新人教版初中数学九年级数学上册第四单元《圆》检测题(有答案解析)
一、选择题1．如图，AB 是半圆O 的直径，20BAC =︒∠，则D ∠的度数是（ ）A ．70°B ．100°C ．110°D ．120°2．为落实好扶贫工作，某村驻村干部帮助村民修建了一个粮仓，该粮仓的屋顶是一个圆锥，为了合理购买、不浪费原材料，需要进行计算1个屋顶的侧面积大小，该圆锥母线长为5m ，底面圆周长为8m π，则1个屋顶的侧面积等于（ ）2m ．（结果保留π）A ．40πB ．20πC ．16πD ．80π 3．如图，在O 中，AB ，AC 为互相垂直且相等的两条弦，⊥OD AB ，OE AC ⊥，垂足分别为D ，E ，若4AB =，则O 的半径是（ ）A ．22B ．2C ．3D ．42 4．中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花，图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到12AC BD cm ==，C ，D 两点之间的距离为3cm ，圆心角为60︒，则图中摆盘的面积是（ ）A ．212cm πB ．224cm πC ．236cm πD ．248cm π5．如图，⊙O 的直径12CD =，AB 是⊙O 的弦，AB CD ⊥，垂足为P ，:1:2CP PO =，则AB 的长为（ ）A ．45B ．215C ．16D ．86．如图，A ，B ，C 三点在O 上，若120ACB ∠=︒，则AOB ∠的度数是（ ）A ．60︒B ．90︒C ．100︒D ．120︒7．点A ，B 的坐标分别为A (4，0)，B (0，4)，点C 为坐标平面内一点，BC ﹦2，点M 为线段AC 的中点，连接OM ，则OM 的最大值为（ ）A ．22＋1B ．22＋2C ．42＋1D ．42-2 8．如图，MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN=30°，点B 为劣弧AN 的中点，P 是直径MN 上一动点，则PA+PB 的最小值为（ ）A 2B ．1C ．2D ．229．已知AB 是经过圆心O 的直线，P 为O 上的任意一点，则点P 关于直线AB 的对称点P '与O 的位置关系是（ ） A ．点P '在⊙○内 B ．点P '在O 外 C ．点P '在O 上 D ．无法确定10．如图，大半圆中有n 个小半圆，若大半圆弧长为1L ，n 个小半圆弧长的和为2L ，大半圆的弦AB ，BC ，CD 的长度和为3L ．则（ ）A ．123L L L =>B ．123L L L =<C ．无法比较1L 、2L 、3L 间的大小关系D ．132L L L >>11．如图，在△ABC 中，（1）作AB 和BC 的垂直平分线交于点O ；（2）以点O 为圆心，OA 长为半径作圆；（3）⊙O 分别与AB 和BC 的垂直平分线交于点M ，N ；（4）连接AM ，AN ，CM ，其中AN 与CM 交于点P ．根据以上作图过程及所作图形，下列四个结论：①BC ＝2NC ；②AB ＝2AM ；③点P 是△ABC 的内心；④∠MON ＋2∠MPN ＝360°． 其中正确结论的个数是（ ）A ．1B ．2C ．3D ．412．如图，C 、D 是以AB 为直径的O 上的两个动点（点C 、D 不与A 、B 重合），在运动过程中弦CD 始终保持长度不变，M 是弦CD 的中点，过点C 作CP AB ⊥于点P ．若3CD =，5AB =，PM x =，则x 的最大值是（ ）A ．4B 5C ．2.5D ．23二、填空题13．如图，扇形AOB 的圆心角是直角，半径为23，C 为OB 边上一点，将△AOC 沿AC 边折叠，圆心O 恰好落在弧AB 上的点D ，则阴影部分面积为___________14．如图，点A ，B ，C 在O 上，顺次连接A ，B ，C ，O ．若四边形ABCO 为平行四边形，则AOC ∠=________︒．15．如图，⊙O 的直径16AB =，半径OC AB ⊥，E 为OC 的中点， DE OC ⊥，交⊙O 于点D ，过点D 作DF AB ⊥于点F ．若 P 为直径AB 上一动点，则PC PD +的最小值为 ________ ．16．将面积为3πcm 2的扇形围成一个圆锥的侧面，若扇形的圆心角是120°，则该圆锥底面圆的半径为_____cm ．17．如图，已知点C 是半圆О上一点，将弧BC 沿弦BC 折叠后恰好经过点,O 若半圆O 的半径是2,则图中阴影部分的面积是________________________．18．如图，四边形ABCD 内接于O ，若76A ∠=︒，则C ∠=_______ °．19．如图，直线AB ，CD 相交于点O ，∠AOC=30°，半径为1cm 的的圆心P 在射线OA 上，且与点O 的距离为6cm ，以1cm/s 的速度沿由A 向B 的方向移动，那么与直线CD 相切时，圆心P 的运动时间为 _____．20．在半径为4cm 的圆中，长为4cm 的弦所对的圆周角的度数为________三、解答题21．如图，已知AB 是O 的一条弦，DE 是O 的直径且DE AB ⊥于点C ． （1）若3,5OC OA ==，求AB 的长；（2）求证：EAO BAD ∠=∠．22．如图，已知,90Rt ABC ACB ∆∠=︒．（1）请在图中用无刻度的直尺和圆规作一个圆，使得圆心О在边AC 上，且与边,AB BC 所在直线相切（不写作法，保留作图痕迹);（2）在（1）的条件下，若9,12AC BC ==，求O 的半径．23．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，ABC ∆的顶点均在格点上，点B 的坐标为()1,0．（1）画出ABC ∆关于x 轴对称的111A B C ∆，写出1C 点的坐标；（2）画出将ABC ∆绕原点O 按逆时针旋转90︒所得的222A B C ∆，写出2B 点的坐标并求出A 运动经过的路径的长度．24．如图，在平面直角坐标系中，Rt △ABC 的斜边AB 在y 轴上，∠C=90°，边AC 与x 轴交于点D ，AE 平分∠BAC 交边BC 于点E ，经过点A 、D 、E 的圆的圆心F 恰好在y 轴上，⊙F 与y 轴相交于另一点G ．(1)求证：BC 是⊙F 的切线；(2)若点A 、D 的坐标分别为A(0,−1)，D(2,0)，求⊙F 的半径；(3)请直接写出线段AG 、AD 、CD 三者之间满足的数量关系：___________________．25．如图，长方形的长为a ，宽为2a ，用整式表示图中阴影部分的面积，并计算当2a =时阴影部分的面积（π取3.14）．26．如图，在△ABC 中，∠C =90°，AB =10，BC +AC =14，且BC >AC ．（1）求BC 的长；（2）在线段BC 上求作一点Q ，使得以点Q 为圆心，QC 为半径的⊙Q 刚好与AB 相切，请运用尺规作图找出符合条件的点Q ，并求出⊙Q 的半径．（不写作法，保留作图痕迹）【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】先根据圆周角定理可得90ACB ∠=︒，再根据直角三角形的性质可得70B ∠=︒，然后根据圆内接四边形的性质即可得．【详解】AB 是半圆O 的直径，90ACB ∴∠=︒，20BAC ∠=︒，9070B BAC ∴∠=︒-∠=︒， 又四边形ABCD 是圆O 内接四边形，180110D B ∴∠=︒-∠=︒，故选：C ．【点睛】本题考查了圆周角定理、直角三角形的性质、圆内接四边形的性质，熟练掌握圆周角定理是解题关键．2．B解析：B【分析】先根据底面周长可求得底面圆的半径，再根据圆锥的侧面积公式计算即可求解．【详解】解：∵2πr=8π，∴r=4，又∵母线l=5，∴圆锥的侧面积＝πrl ＝π×4×5＝20π．故选：B ．【点睛】本题考查了圆锥的侧面积计算方法，牢记有关圆锥和扇形之间的对应关系是解决本题的关键．3．A解析：A【分析】根据垂径定理可知，AE=CE ，AD=BD ，易证四边形ODAE 是正方形，即可求得．【详解】如图，连接OA∵⊥OD AB ，OE AC ⊥，AB ⊥AC∴四边形ODAE 是矩形，AE=CE ，AD=BD又∵4AB AC ==，∴AE=AD=2∴四边形ODAE 是正方形，且边长为2∴O 的半径OA=22故选A【点睛】本题考查垂径定理，掌握垂径定理的条件和结论是解题的关键．4．C解析：C【分析】首先证明△OCD 是等边三角形，求出OC=OD=CO=3cm ，再根据S 阴影=S 扇形OAB -S 扇形OCD ，求解即可．【详解】解：如图，连结CD ．∵OC=OD ，∠O=60°，∴△OCD 是等边三角形，∴OC=OD=CO=3cm ，∴OA=OC+AC=15cm ，∴OB=OA=15cm ，∴S 阴影=S 扇形OAB -S 扇形OCD =226015603360360ππ⋅⋅⋅⋅-=236cm π． 故选C ．【点睛】本题考查了扇形的面积，等边三角形的性质与判定等知识．扇形的面积=2360n r π︒． 5．A解析：A【分析】连接OA ，先根据⊙O 的直径CD ＝12，CP ：PO ＝1：2求出CO 及OP 的长，再根据勾股定理可求出AP 的长，进而得出结论．【详解】连接OA ，∵⊙O 的直径CD ＝12，CP ：PO ＝1：2，∴CO ＝6，PO=4，∵AB ⊥CD ，∴22OA OP -2264-5，∴AB ＝2AP ＝22545⨯=故选：A ．【点睛】本题考查了垂径定理和勾股定理的应用，解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r ，弦长为a ，这条弦的弦心距为d ，则有等式2222a r d ⎛⎫=+ ⎪⎝⎭成立，知道这三个量中的任意两个，就可以求出另外一个． 6．D解析：D【分析】在优弧AB 上取一点D ，连接AD 、BD ，根据圆内接四边形的性质计算可得∠D ，然后根据圆周角定理即可求解．【详解】解：在优弧AB 上取一点D ，连接AD 、BD ，∵四边形ADBC 是⊙O 的内接四边形，∴∠D+∠ACB=180°，∵120ACB ∠=︒∴∠D=60°∴∠AOB=120°，故选：D ．【点睛】本题考查的是圆内接四边形的性质和圆周角定理，掌握圆内接四边形的对角互补是解题的关键．7．A解析：A【分析】根据同圆的半径相等可知：点C 在半径为2的B 上，通过画图可知，C 在BD 与圆B 的交点时，OM 最小，在DB 的延长线上时，OM 最大，根据三角形的中位线定理可得结论．【详解】解：如图，点C 为坐标平面内一点，2BC =，C ∴在B 上，且半径为2，取4OD OA ，连接CD ， AM CM =，OD OA =，OM ∴是ACD ∆的中位线， 12OM CD ， 当OM 最大时，即CD 最大，而D ，B ，C 三点共线时，当C 在DB 的延长线上时，OM 最大， 4OB OD ，90BOD ∠=︒，BD ∴= 422CD ， 1142222122OM CD ，即OM 的最大值为1；故选：A ．【点睛】本题考查了坐标和图形的性质，三角形的中位线定理等知识，确定OM 为最大值时点C 的位置是解题的关键．8．A解析：A【分析】过B 作关于直线MN 的对称点B ′，连接OA 、OB 、OB ′、AB ′，如图，由轴对称的性质可知AB ′即为PA +PB 的最小值，由同弧所对的圆心角和圆周角的性质可知∠AON ＝2∠AMN ＝2×30°＝60°，由对称的性质可知∠B ′ON ＝∠BON ＝30°，即可求出∠AOB ′的度数，再由等腰直角三角形的性质即可求解．【详解】解：作点B 关于MN 的对称点B ′，连接OA 、OB 、OB ′、AB ′，如图，则AB ′与MN 的交点即为PA +PB 的最小时的点P ，且PA +PB 的最小值＝AB ′，∵∠AMN ＝30°，OA=OM ，∴∠AON ＝2∠AMN ＝2×30°＝60°，∵点B 为劣弧AN 的中点，∴∠BON ＝12∠AON ＝12×60°＝30°， 由对称性可得∠B ′ON ＝∠BON ＝30°，∴∠AOB ′＝∠AON +∠B ′ON ＝60°+30°＝90°，∴△AOB ′是等腰直角三角形，∴AB ′，即PA +PB ．故选：A ．【点睛】本题考查了圆周角定理、轴对称的性质以及等腰直角三角形的性质等知识，解答此题的关键是根据题意作出辅助线、构造出直角三角形，利用勾股定理求解．9．C解析：C【分析】圆是轴对称图形，直径所在的直线就是对称轴，从而得到圆上的点关于对称轴对称的点都在圆上求解．【详解】解：∵圆是轴对称图形，直径所在的直线就是对称轴，∴点P 关于AB 的对称点P′与⊙O 的位置为：在⊙O 上，故选：C ．【点睛】本题考查了点与圆的位置关系，利用了圆的对称性求解．10．A解析：A【分析】利用圆周长公式计算1L 和2L 的长．根据圆周长公式分别写出1L 和2L 的表达式进行比较，再根据“两点之间线段最短的性质”得出13L L >，即可选出答案．【详解】解：设n 个小半圆半径依次为1r ，2r ，⋯，n r ．则大圆半径为()12n r r r ++⋯+()112n L r r r π∴=++⋯+，212n L r r r πππ=++⋯+()12n r r r π=++⋯+，12L L ∴=；根据“两点之间线段最短的性质”可得：13L L >，123L L L ∴=>．．故选A ．【点睛】本题考查了半圆弧长的计算，两点之间线段最短的性质，是基础题，难度不大． 11．C解析：C【分析】利用垂径定理可对①②进行判断；利用圆周角定理可得到CM 、AN 为角平分线，则利用三角形内心的定义可对③进行判断；根据P 是△ABC 的内心得出∠APC=90°+12∠B ，进而得出∠MON+∠B=180°，再代入求解即可．【详解】解：作BC 的垂直平分线，则ON 平分BC ，则BC ＝2NC ，所以①正确；作AB 的垂直平分线，则OM 平分AB ，则AB ＝2AM ，2AM ＞AB ，所以②错误； ∵M 点为AB 的中点，∴∠ACM=∠BCM ，∵点N 为BC 的中点，∴∠BAN=∠CAN ，故P 点为△ABC 的内心，所以③正确；∵∠APC=180°-∠PAC-∠PCA=180°-12∠BAC-12∠BCA=180°-12(∠BAC+∠BCA)=180°-12(180°-∠B)=90°+12∠B ， ∴2∠MPN=2∠APC=180°+∠B ，又OM ⊥AB ，ON ⊥BC ，∴∠MON+∠B=180°，∴∠MON+2∠MPN=∠MON+180°+∠B=180°+180°=360°，故④正确，∴正确的结论有3个，故选：C ．【点睛】本题考查了垂径定理、圆周角定理、三角形内心及外心的性质、线段的垂直平分线的尺规作图等，熟练掌握各图形的性质及尺规作图步骤是解决本题的关键．12．C解析：C【分析】如图：延长CP 交O 于N ，连接DN ，易证12PM DN =，所以当DN 为直径时，PM 的值最大．【详解】解：如图：延长CP 交O 于N ，连接DN ．AB CN ⊥，CP PN ∴=，CM DM =， 12PM DN ∴=， ∴当DN 为直径时，PM 的值最大，最大值为52． 故选：C ．【点睛】本题考查是圆的综合题，垂径定理，三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题．二、填空题13．【分析】根据题意和折叠的性质可以得到OA=AD ∠OAC=∠DAC 然后根据OA=OD 即可得到∠OAC 和∠DAC 的度数再根据扇形AOB 的圆心角是直角半径为2可以得到OC 的长结合图形可知阴影部分的面积就是解析：343π-【分析】根据题意和折叠的性质，可以得到OA=AD ，∠OAC=∠DAC ，然后根据OA=OD ，即可得到∠OAC 和∠DAC 的度数，再根据扇形AOB 的圆心角是直角，半径为23，可以得到OC 的长，结合图形，可知阴影部分的面积就是扇形AOB 的面积减△AOC 和△ADC 的面积．【详解】解：连接OD ，∵△AOC 沿AC 边折叠得到△ADC ，∴OA=AD ，∠OAC=∠DAC ，又∵OA=OD ，∴OA=AD=OD，∴△OAD是等边三角形，∴∠OAC=∠DAC=30°，∵扇形AOB的圆心角是直角，半径为23，∴OC=2，∴阴影部分的面积是：2902322360(23)π⨯⨯-⨯=343π-故答案为343π-．【点睛】本题考查扇形面积的计算，解答本题的关键是明确扇形面积的计算公式，利用数形结合的思想解答．14．120【分析】连接OB先证明四边形ABCD是菱形然后再说明△AOB△OBC 为等边三角形最后根据等边三角形的性质即可解答【详解】解：如图：连接OB∵点在上∴OA=OC=OB∵四边形为平行四边形∴四边形解析：120【分析】连接OB，先证明四边形ABCD是菱形，然后再说明△AOB、△OBC为等边三角形，最后根据等边三角形的性质即可解答．【详解】解：如图：连接OB∵点A，B，C在O上∴OA=OC=OB∵四边形ABCO为平行四边形∴四边形ABCO是菱形∴OA=OC=OB=AB=BC∴△AOB、△OBC为等边三角形∴∠AOB=∠BOC=60°∴∠AOC=120°．故答案为120．【点睛】本题主要考查了圆的性质和等边三角形的性质，根据题意证得△AOB、△OBC为等边三角形是解答本题的关键．15．【分析】延长CO交⊙O于G连接GD交AB于P根据两点之间线段最短可知PC+PD的最小值为GD由勾股定理分别求得DEDG即可解答【详解】解：延长CO交⊙O于G连接GD交AB于P则PC+PD的最小值为G解析：83【分析】延长CO交⊙O于G，连接GD交AB于P，根据两点之间线段最短可知PC+PD的最小值为GD，由勾股定理分别求得DE、DG即可解答．【详解】解：延长CO交⊙O于G，连接GD交AB于P，则PC+PD的最小值为GD，连接OD，则OD=OG=OC= 12AB=8，∵E为OC的中点，∴OE=12OC=4，∴EG=4+8=12，∵DE OC⊥，∴在Rt△OED中，22228443OD OE-=-=，在Rt△GED中，2222(43)1283ED EG+=+=故答案为：3【点睛】本题考查勾股定理、最短路径问题、圆的有关概念与性质，熟练掌握勾股定理和圆的性质是解答的关键．16．1【分析】直接利用已知得出圆锥的母线长再利用圆锥侧面展开图与各部分对应情况得出答案【详解】解：设圆锥的母线长为Rcm底面圆的半径为rcm∵面积为3πcm2的扇形围成一个圆锥的侧面扇形的圆心角是120解析：1【分析】直接利用已知得出圆锥的母线长，再利用圆锥侧面展开图与各部分对应情况得出答案．【详解】解：设圆锥的母线长为Rcm ，底面圆的半径为rcm ，∵面积为3πcm 2的扇形围成一个圆锥的侧面，扇形的圆心角是120°， ∴2120360R π⨯＝3π， 解得：R ＝3，由题意可得：2πr ＝1203180π⨯， 解得：r ＝1．故答案为：1．【点睛】此题主要考查了圆锥的计算，正确得出母线长是解题关键． 17．【分析】过点O 作OD ⊥BC 于E 交半圆O 于D 点连接CD 如图根据垂径定理由OD ⊥BC 得BE ＝CE 再根据折叠的性质得到ED ＝EO 则OE ＝OB 则可根据含30度的直角三角形三边的关系得∠OBC ＝30°即∠AB解析：23π 【分析】过点O 作OD ⊥BC 于E ，交半圆O 于D 点，连接CD ，如图，根据垂径定理由OD ⊥BC 得BE ＝CE ，再根据折叠的性质得到ED ＝EO ，则OE ＝12OB ，则可根据含30度的直角三角形三边的关系得∠OBC ＝30°，即∠ABC ＝30°则∠AOC=60°，由于OC ＝OB ，则弓形OC 的面积＝弓形OB 的面积，然后根据扇形的面积公式及S 阴影部分＝S 扇形OAC 即可得到阴影部分的面积．【详解】如图：过点O 作OD ⊥BC 于E ，交半圆O 于D 点，连接CD ，∵OD ⊥BC ，∴BE ＝CE ，∵半圆O 沿BC 所在的直线折叠，圆弧BC 恰好过圆心O ，∴ED ＝EO ，∴OE ＝12OB ， ∴∠OBC ＝30°，即∠ABC ＝30°，∴∠AOC=60°；∵OC ＝OB ，∴弓形OC 的面积＝弓形OB 的面积，∴S 阴影部分＝S 扇形OAC ＝260223603ππ⋅= ． 【点睛】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了垂定定理、圆周角定理和扇形的面积公式．18．104【分析】根据圆内接四边形的对角互补列式计算即可【详解】解：∵四边形ABCD 内接于⊙O ∴∠A+∠C ＝180°∴∠C ＝180°﹣∠A ＝180°﹣76°＝104°故答案为：104【点睛】本题考查的是解析：104【分析】根据圆内接四边形的对角互补列式计算即可．【详解】解：∵四边形ABCD 内接于⊙O ，∴∠A +∠C ＝180°，∴∠C ＝180°﹣∠A＝180°﹣76°＝104°，故答案为：104．【点睛】本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键． 19．4秒或8秒【分析】⊙P 与CD 相切应有两种情况一种是在射线OA 上另一种在射线OB 上设对应的圆的圆心分别在MN 两点当P 在M 点时根据切线的性质在直角△OME 中根据30度的角所对的直角边等于斜边的一半即可求 解析：4秒或8秒【分析】⊙P 与CD 相切应有两种情况，一种是在射线OA 上，另一种在射线OB 上，设对应的圆的圆心分别在M ，N 两点．当P 在M 点时，根据切线的性质，在直角△OME 中，根据30度的角所对的直角边等于斜边的一半，即可求得OM 的长，进而求得PM 的长，从而求得由P 到M 移动的时间；根据ON=OM ，即可求得PN ，也可以求得求得由P 到M 移动的时间．【详解】①当⊙P 在射线OA 上，设⊙P 于CD 相切于点E ，P 移动到M 时，连接ME ．∵⊙P 与直线CD 相切，∴∠OEM=90°，∵在直角△OPM 中，ME=1cm ，∠AOC=30°，∴OM=2ME=2cm ，则PM=OP-OM=6-2=4cm ，∵⊙P 以1cm/s 的速度沿由A 向B 的方向移动，∴⊙P 移动4秒时与直线CD 相切；②当⊙P 的圆移动到直线CD 的右侧，同理可求ON=2则PN=6+2=8cm ．∴⊙P 移动8秒时与直线CD 相切．故答案为：4秒或8秒．【点睛】本题主要考查了切线的性质和直角三角形的性质，注意已知圆的切线时，常用的辅助线是连接圆心与切点，本题中注意到分两种情况讨论是解题的关键．20．或【分析】首先根据题意画出图形然后在优弧上取点C 连接ACBC 在劣弧上取点D 连接ADBD 易得是等边三角形再利用圆周角定理即可得出答案【详解】解：如图在优弧上取点C 连接ACBC 在劣弧上取点D 连接ADBD解析：30或150︒【分析】首先根据题意画出图形，然后在优弧上取点C ，连接AC 、BC ，在劣弧上取点D ，连接AD 、BD ，易得OAB 是等边三角形，再利用圆周角定理，即可得出答案．【详解】解：如图，在优弧上取点C ，连接AC 、BC ，在劣弧上取点D ，连接AD 、BD ，4,4OA OB cm AB cmOA OB AB ===∴==OAB∴是等边三角形，601302180150AOBC AOBD C∴∠=︒∴∠=∠=︒∴∠=︒-∠=︒∴所对的圆周角度数为：30或150︒故答案为：30或150︒．【点睛】本题考查圆周角定理及等边三角形的判定与性质，注意两种情况．三、解答题21．（1）8AB=；（2）见解析【分析】（1）由DE⊥AB，得∠OCA＝90°，OC＝3，OA＝5，通过勾股定理即可求出AC；由DE是⊙O的直径，所以DE平分AB，得到AB＝2AC，即可得到AB；（2）由OA＝OE，得∠EAO＝∠E，而直径DE⊥AB，则AD BD=，所以∠E＝∠BAD，由此得到∠EAO＝∠BAD．【详解】（1）∵DE⊥AB∴∠OCA=90°，则OC2+AC2=OA2又∵OC＝3，OA＝5，∴AC=4，∵DE是⊙O的直径，且DE⊥AB，∴AB＝2AC=8（2）证明∵ EO=AO，∴∠E=∠EAO又∵DE是⊙O的直径，且DE⊥AB，∴AD BD=，∴∠E=∠BAD∴∠EAO ＝∠BAD ．【点睛】本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．同时考查了垂径定理以及勾股定理．22．（1）见解析；（2）O 的半径为4 【分析】（1）先作∠ABC 的角平分线，交AC 于点O ，然后过O 作AB 的垂线，交AB 于E ，以O 为圆心，OE 为半径作圆即可；（2）先利用勾股定理求出AB ，然后由OBC ABO ABC S S S ∆∆∆+=即可求出O 的半径．【详解】解:（1）如图所示：（2）设直线AB 与O 切于点D ，连接OD ，则,OD AB ⊥90,ACB ∴∠=︒22222291215AB AC BC ∴=+=+=．15,AB ∴=设O 的半径为,r由得OBC ABO ABC S S S ∆∆∆+=1215912,r r +=⨯4,r ∴=即O 的半径为4【点睛】本题考查了尺规作图，切线的性质，理解题意熟练掌握角平分线和垂线的作图是解题的关键．23．（1）如图，111A B C ∆为所作，见解析；1C (3,-1)；（2）如图，222A B C ∆为所作，见解析；A 运动经过的路径的长度为2π 【分析】（1）根据网格结构找出点A 、B 、C 关于x 轴的对称点1A 、1B 、1C 的位置，然后顺次连接即可，再根据平面直角坐标系写出点1C 的坐标即可；（2）根据网格结构找出点A 、B 、C 关绕点O 按照逆时针旋转90°后的对应点2A 、2B 、2C 的位置，然后顺次连接即可，再根据平面直角坐标系写出点2B 的坐标再根据弧长公式求解即可；【详解】（1）如图，111A B C ∆为所作∴ 1C (3，-1) ，(2)如图，222A B C ∆为所作∴2B (0，1)，∵点A(2，2)，∴ OA=22，∵∠2AOA =90°∴A 运动经过的路径的长度为：90222ππ⋅⋅=【点睛】本题考查了利用旋转变换与对称轴变换作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键；24．（1）见解析；（2）52；（3）AG=AD+2CD ．【分析】（1）连接EF ，根据角平分线的定义、等腰三角形的性质得到∠FEA=∠EAC ，得到FE ∥AC ，根据平行线的性质得到∠FEB=∠C=90°，证明结论；（2）连接FD ，设⊙F 的半径为r ，根据勾股定理列出方程，解方程即可；（3）作FR ⊥AD 于R ，得到四边形RCEF 是矩形，得到EF=RC=RD+CD ，根据垂径定理解答即可．【详解】（1）证明：连接EF ，∵AE 平分∠BAC ，∴∠FAE=∠CAE ，∵FA=FE ，∴∠FAE=∠FEA ，∴∠FEA=∠EAC ，∴FE ∥AC ，∴∠FEB=∠C=90°，即BC 是⊙F 的切线；（2）解：连接FD ，∵A(0,−1)，D(2,0)，∴OA=1,OD=2.在Rt △FOD 中，∵222OF OD DF += 设⊙F 的半径为r ，∴r 2=（r-1）2+22，解得，r=52，即⊙F 的半径为52； （3）解：AG=AD+2CD ．证明：作FR ⊥AD 于R ，则∠FRC=90°，又∵BC 是⊙F 的切线；∴∠FEC=∠C=∠FRC=90°，∴四边形RCEF 是矩形，∴EF=RC=RD+CD ，∵FR ⊥AD ，AF=FD,∴AR=RD ， ∴EF=RD+CD=12AD+CD ， ∴AG=2FE=AD+2CD ．【点睛】本题考查的是切线的判定、垂径定理的应用、矩形的判定和性质，掌握相关知识是解题的关键．25．2(2)4a π-，1.14 【分析】根据对称性用a 表示出阴影的面积，再将a=2代入求解即可．【详解】解：由题意可知：S 阴=211442222a a a π⎡⎤⎛⎫-⋅⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 2(2)4a π-= 当2a =时，S 阴=(3.142)4 1.144-⨯=． 【点睛】本题考查列代数式、代数式求值、圆的面积公式、三角形的面积公式，解答的关键是找出面积之间的关系，利用基本图形的面积公式解决问题．26．（1）BC =8；（2）图见解析，⊙Q 的半径为3【分析】（1）由勾股定理列出方程求解即可；（2）作∠BAC 的平分线交BC 于点Q ，则点Q 即为所求作的点；再运用面积法即可求出⊙Q 的半径．【详解】解：（1）∵∠C =90°，AB =10，BC +AC =14，∴222AB AC BC =+,设AC=x ，BC=14-x ，则有 222(14)10x x +-=解得，16x =，28x =∵BC >AC∴BC=8；（2）作∠BAC 的平分线交BC 于点Q ，则点Q 即为所求作的点，如图，∵∠ACB=90°∴QC ⊥AC过Q 作QE ⊥AB ，垂足为点E ，∴QC=QE又ABC ACQ ABQ S S S ∆∆∆=+ ∴222AC BC AC QC AB QE =+ ∴68106QE QC ⨯=+ ∵QE=QC∴QE=QC=3，即圆的半径为3【点睛】考查了圆的综合题．涉及了勾股定理，一元二次方程的解法，切线的性质，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∴ AC AB ，
∵∠AOB=66°，∠AOB 和∠ADC 分别是 AB 和 AC 所对的圆心角和圆周角， ∴∠ADC= 1 ∠AOB=33°，
2
故选：A． 【点睛】 本题考查垂径定理及圆周角定理，垂直于弦的直径平分弦，并且平分这条弦所对的两条 弧；在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一 半；熟练掌握相关定理是解题关键．
如图 BC 与 OA 相交于 H
∵OA⊥BC，
∴CH=BH， AC AB ，
∴∠AOB=2∠CDA=60°，
∴BH=OB⋅sin∠AOB= 3 ， ∴BC=2BH=2 3 ，
故选 D． 【点睛】 本题考查的是垂径定理、圆周角定理，熟练掌握垂直于弦的直径平分这条弦，并且平分弦 所对的两条弧是解题的关键．
【详解】 解：连接 CO 并延长交⊙O 于点 D，连接 AD，
由 CD 是⊙O 的直径，可得∠CAD=90°， ∵∠B 和∠D 所对的弧都为弧 AC，
∴∠B=∠D，即 sinB=sinD= 2 ， 5
∵半径 AO=5， ∴CD=10，
∴ sin D AC AC 2 ， CD 10 5
∴AC=4， 故选：C. 【点睛】 本题考查了同弧所对的圆周角相等，以及三角函数的内容，注意到直径所对的圆周角是直 角是解题的关键.
A．1 个
B．2 个
C．3 个
D．4 个
【答案】A
【解析】
【分析】
先对原命题进行判断，再判断出逆命题的真假即可．
【详解】
解:①若 a＞b，则 ac＞bc 是假命题，逆命题是假命题；
②若 a=1，则 a =a 是真命题，逆命题是假命题；
③内错角相等是假命题，逆命题是假命题；
④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；
下列说法中错误的是( ) A．勒洛三角形是轴对称图形
B．图 1 中，点 A 到 BC 上任意一点的距离都相等 C．图 2 中，勒洛三角形上任意一点到等边三角形 DEF 的中心 O1 的距离都相等
D．图 2 中，勒洛三角形的周长与圆的周长相等 【答案】C 【解析】 【分析】 根据轴对称形的定义，可以找到一条直线是的图像左右对着完全重合，则为轴对称图形.鲁 列斯曲边三角形有三条对称轴. 鲁列斯曲边三角形可以看成是 3 个圆心角为 60°，半径为 DE 的扇形的重叠，根据其特点可以进行判断选项的正误. 【详解】 鲁列斯曲边三角形有三条对称轴，就是等边三角形的各边中线所在的直线，故正确；
A．4
B．8 3
C．6
D． 4 3
【答案】B
【解析】
【分析】
设三角板与圆的切点为 C，连接 OA、OB，根据切线长定理可得 AB=AC=3，∠OAB=60°，然
后根据三角函数，即可得出答案.
【详解】
设三角板与圆的切点为 C，连接 OA、OB，
由切线长定理知，AB=AC=3，AO 平分∠BAC， ∴∠OAB=60°，
圆锥的母线 AB 与 O 相切于点 B ，
OB AB ，
在 RtAOB 中， OA 18 5 13， OB 5，
AB 132 52 12 ，
1 OA BH 1 OB AB ，
2
2
BH 512 60 ， 13 13
圆锥形纸帽的底面圆的半径为 BH 60 ，母线长为 12， 13
形纸帽的表面 1 2 60 12 720 (cm2 ) ．
圆的直径正好是大正方形边长，
根据勾股定理，其小正方形对角线为 2 ，即圆的直径为 2 ，
大正方形的边长为 2 ，
则大正方形的面积为
2
2
2
，则小球停在小正方形内部（阴影）区域的概率为
1 2
．
故选： C ．
【点睛】
概率 相应的面积与总面积之比，本题实质是确定圆的内接正方形和外切正方形的边长
比．设较小吧边长为单位 1 是在选择填空题中求比的常见方法.
人教版初中数学圆的经典测试题含答案解析
一、选择题 1．如图，在 ABC 中， AB 5， AC 3， BC 4 ，将 ABC 绕一逆时针方向旋转 40 得到 ADE ，点 B 经过的路径为弧 BD ，则图中阴影部分的面积为( )
A． 14 6 3
B． 33
C． 33 3 8
D． 25 9
离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.
2．如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为 O， 三角尺的直角顶点 C 落在直尺的 10cm 处，铁片与直尺的唯一公共点 A 落在直尺的 14cm 处，铁片与三角尺的唯一公共点为 B，下列说法错误的是（ ）
∴∠BOG=∠COG= 1 ∠BOC =30°， 2
∵OG⊥BC，OB=OC，BC=2cm，
∴BG= 1 BC= 1 ×2=1cm， 22
∴OB= BG =2cm， sin 30
∴OG= OB2 BG2 22 12 3 ，
∴圆形纸片的半径为 3 cm，
故选：A．
【点睛】 本题考查的是正多边形和圆，根据题意画出图形，利用直角三角形的性质及正六边形的性 质解答是解答此题的关键．
5．如图，△ABC 的外接圆是⊙O，半径 AO=5，sinB= 2 ，则线段 AC 的长为（ ） 5
A．1
B．2
C．4
D．5
【答案】C
【解析】
【分析】
首先连接 CO 并延长交⊙O 于点 D，连接 AD，由 CD 是⊙O 的直径，可得∠CAD=90°，又由
⊙O 的半径是 5，sinB= 2 ，即可求得答案． 5
9．用一个直径为10cm 的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具，不倒翁 轴截面如图所示，圆锥的母线 AB 与 O 相切于点 B ，不倒翁的顶点 A 到桌面 L 的最大距 离是18cm .若将圆锥形纸帽表面全涂上颜色，则涂色部分的面积为（ ）
A． 60 cm2
B． 600 cm2 13
7．如图，点 A，B，C，D 都在半径为 2 的⊙O 上，若 OA⊥BC，∠CDA=30°，则弦 BC 的长 为（ ）
A．4 【答案】B 【解析】 【分析】
B．2 2
C． 3
D．2 3
根据垂径定理得到 CH=BH， AC BC ，根据圆周角定理求出∠AOB，根据正弦的定义求出
BH，计算即可． 【详解】
∠A 的正切值求出∠A=30°，继而可求得 OH、AH 长，根据圆周角定理可求得∠BOC =60°，
然后根据 S 阴影=S△ABC-S△AOD-S 扇形 BOD 进行计算即可.
【详解】
连接 OD，过点 O 作 OH⊥AC，垂足为 H，
则有 AD=2AH，∠AHO=90°，
在 Rt△ABC 中，∠ABC=90°，AB= 2 3 ，BC=2，tan∠A= BC 2 3 ， AB 2 3 3
在 Rt△ABO 中，OB=ABtan∠OAB=4 3 ， ∴光盘的直径为 8 3 ．
故选：B． 【点睛】 本题主要考查了切线的性质，解题的关键是熟练应用切线长定理和锐角三角函数.
4．已知下列命题：
①若 a＞b，则 ac＞bc；
②若 a=1，则 a =a；
③内错角相等；
④90°的圆周角所对的弦是直径． 其中原命题与逆命题均为真命题的个数是（ ）
其中原命题与逆命题均为真命题的个数是 1 个；
故选 A．
点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个
命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两
个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要
熟悉课本中的性质定理．
∴△ACB≌△AED，∠DAB=40°，
∴AD=AB=5，S△ACB=S△AED， ∵S 阴影=S△AED+S 扇形 ADB-S△ACB=S 扇形 ADB，
∴S 阴影= 40 25 = 25 ， 360 9
故选 D.
【点睛】
本题考查了旋转的性质，扇形面积公式，熟练掌握旋转的性质：①对应点到旋转中心的距
8．如图，有一个边长为 2cm 的正六边形纸片，若在该纸片上沿虚线剪一个最大圆形纸
片，则这个圆形纸片的半径是（ ）
A． 3cm
B． 2cm
C． 2 3cm
D． 4cm
【答案】A 【解析】 【分析】 根据题意画出图形，再根据正多边形圆心角的求法求出∠AOB 的度数，最后根据等腰三角 形及直角三角形的性质解答即可． 【详解】 解：如图所示，正六边形的边长为 2cm，OG⊥BC， ∵六边形 ABCDEF 是正六边形， ∴∠BOC=360°÷6=60°， ∵OB=OC，OG⊥BC，
6．如图，小明随意向水平放置的大正方形内部区域抛一个小豆子，则小豆子落在小正方形 内部及边界（阴影）区域的概率为（ ）
A． 3 4
B． 1 3
C． 1 2
D． 1 4
【答案】C
方形的面积，这个比值就是所求的概率．
【详解】
解：设小正方形的边长为 1，则其面积为 1．
故选 C.
【点睛】
主要考察轴对称图形，弧长的求法即对于新概念的理解．
11．如图， O 中，若 OA BC、AOB 66 ，则 ADC 的度数为（ ）
A．33° 【答案】A 【解析】 【分析】
B．56°
C．57°
D．66°
根据垂径定理可得 AC AB ，根据圆周角定理即可得答案．
【详解】 ∵OA⊥BC，
C． 720 cm2 13
D． 72 cm2
【答案】C
【解析】
【分析】
连接 OB ，如图，利用切线的性质得 OB AB ，在 RtAOB 中利用勾股定理得
AB
12