高考中数学的多选题
高考数学的立体几何多选题含答案

高考数学的立体几何多选题含答案一、立体几何多选题1.已知球O 为正方体1111ABCD A B C D -的内切球,平面11A C B 截球O 的面积为24π,下列命题中正确的有( )A .异面直线AC 与1BC 所成的角为60°B .1BD ⊥平面11AC B C .球O 的表面积为36πD .三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ,1A B ,通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ;通过反证法证明B ;由已知平面11A C B 截球O 的面积为24π求出正方体棱长,进而求出内切球的表面积可判断C ;利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ,连接11A C ,1A B ,由正方体1111ABCD A B C D -,可知11//A C AC ,11AC B ∴∠为异面直线AC 与1BC 所成的角,设正方体边长为a,则1111AC A B BC ==,由等边三角形知1160A C B ∠=,即异面直线AC 与1BC 所成的角为60,故A 正确; 对于B ,假设1BD ⊥平面11A C B ,又1A B ⊂平面11A C B ,则11BD B A ⊥,设正方体边长为a ,则11A D a =,1A B =,1BD =,由勾股定理知111A D B A ⊥,与假设矛盾,假设不成立,故1BD 不垂直于平面11A C B ,故B 错误; 对于C ,设正方体边长为a,则11AC =,内切球半径为2a,设内切球的球心O 在面11A C B 上的投影为O ',由等边三角形性质可知O '为等边11A C B △的重心,则11123233O A AC a ='=⨯=,又12OA a =,∴球心O 到面11A C B 的距离6a ==,又球心与截面圆心的连线垂直于截面,∴=,又截面圆的面积2246S a ππ⎛⎫= ⎪ ⎪⎝⎭=,解得12a =,则内切球半径为6,内切球表面积214644S ππ==⨯,故C 错误;对于D ,由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=,故D 正确; 故选:AD【点睛】关键点点睛:本题考查了正方体和它的内切球的几何结构特征,关键是想象出截面图的形状,从而求出正方体的棱长,进而求出内切球的表面积及三棱锥的体积,考查了空间想象能力,数形结合的思想,属于较难题.2.如图,矩形ABCD 中,M 为BC 的中点,将ABM 沿直线AM 翻折成1AB M ,连结1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得1CN AB ⊥ B .翻折过程中,CN 的长是定值C .若AB BM =,则1AM BD ⊥D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -外接球的体积是43π 【答案】BD【分析】对于A ,取AD 中点E ,连接EC 交MD 与F ,可得到EN NF ⊥,又EN CN ⊥,且三线,,NE NF NC 共面共点,不可能;对于B ,可得由1NEC MAB ∠=∠(定值),112NE AB =(定值),AM EC =(定值),由余弦定理可得NC 是定值.对于C ,取AM 中点O ,连接1,B O DO ,假设1AM B D ⊥,易得AM ⊥面1ODB ,即可得OD AM ⊥,从而AD MD =,显然不一定成立.对于D ,当平面B 1AM ⊥平面AMD 时,三棱锥B 1﹣AMD 的体积最大,可得球半径为1,体积是43π. 【详解】对于A 选项:如图1,取AD 中点E ,连接EC 交MD 与F , 则11////NE AB NF MB ,,又11AB MB ⊥,所以EN NF ⊥, 如果1CN AB ⊥,可得EN CN ⊥,且三线,,NE NF NC 共面共点, 不可能,故A 选项不正确;对于B 选项:如图1,由A 选项可得1AMB EFN ≈△△,故1NEC MAB ∠=∠(定值),112NE AB =(定值),AM EC =(定值), 故在NEC 中,由余弦定理得222cos CN CE NE NE CE NEC =+-⋅⋅∠,整理得222212422AB AB AB CN AM AM BC AB AM =+-⋅⋅=+ 故CN 为定值,故B 选项正确.对于C 选项:如图,取AM 中点O ,连接1,B O DO , 由AB BM =,得1B O AM ⊥,假设1AM B D ⊥,111B D B O B =,所以AM ⊥面1ODB ,所以OD AM ⊥,从而AD MD =,显然不恒成立,所以假设不成立,可得C 选项不正确.对于D 选项:由题易知当平面1AB M 与平面AMD 垂直时,三棱锥1B AMD -的体积最大,此时1B O ⊥平面AMD ,则1B O OE ⊥,由1AB BM ==,易求得122BO =,2DM =22221122122B E OB OE ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 因此1EB EA ED EM ===,E 为三棱锥1B AMD -的外接球球心,此外接球半径为1,体积是43π.故D 选项正确. 故答案为:BD . 【点睛】本题主要考查了线面、面面平行与垂直的判定和性质定理,考查了空间想象能力和推理论证能力,属于难题.本题C 选项的解题的关键在于采用反证法证明,进而推出矛盾解题,D 选项求解的关键在于把握平面1AB M 与平面AMD 垂直时,三棱锥1B AMD -的体积最大.3.在长方体1111ABCD A B C D -中,4AB BC ==,18AA =,点P 在线段11A C 上,M 为AB 的中点,则( ) A .BD ⊥平面PACB .当P 为11AC 的中点时,四棱锥P ABCD -外接球半径为72C .三棱锥A PCD -体积为定值D .过点M 作长方体1111ABCD A B C D -的外接球截面,所得截面圆的面积的最小值为4π 【答案】ACD【分析】利用线面垂直的判定定理可判断A 选项的正误;判断出四棱锥P ABCD -为正四棱锥,求出该四棱锥的外接球半径,可判断B 选项的正误;利用等体积法可判断C 选项的正误;计算出截面圆半径的最小值,求出截面圆面积的最小值,可判断D 选项的正误. 【详解】对于A 选项,因为AB BC =,所以,矩形ABCD 为正方形,所以,BD AC ⊥, 在长方体1111ABCD A B C D -中,1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1BD AA ∴⊥,1AC AA A ⋂=,AC 、1AA ⊂平面PAC ,所以,BD ⊥平面PAC ,A 选项正确;对于B 选项,当点P 为11A C 的中点时,PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形,所以,四棱锥P ABCD -为正四棱锥, 取AC 的中点N ,则PN 平面ABCD ,且四棱锥P ABCD -的外接球球心在直线PN上,设该四棱锥的外接球半径为R ,由几何关系可得222PN R AN R -+=, 即2288R R -+=,解得92R =,B 选项错误; 对于C 选项,2114822ACDSAD CD =⋅=⨯=, 三棱锥P ACD -的高为18AA =,因此,116433A PCD P ACD ACD V V S AA --==⋅=△,C 选项正确;对于D 选项,设长方体1111ABCD A B C D -的外接球球心为E ,则E 为1BD 的中点, 连接EN 、MN ,则1142EN DD ==,122MN AD ==, E 、N 分别为1BD 、BD 的中点,则1//EN DD , 1DD ⊥平面ABCD ,EN ∴⊥平面ABCD ,MN ⊂平面ABCD ,EN MN ∴⊥,EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α,点E 到平面α的距离为d ,直线EM 与平面α所成的角为θ,则sin d EM θθ==≤ 当且仅当2πθ=时,等号成立,长方体1111ABCD A B C D -的外接球半径为R '==,所以,截面圆的半径()()222226252r R d '=-≥-=,因此,截面圆面积的最小值为4π,D 选项正确.故选:ACD. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.4.在三棱锥M ABC -中,下列命题正确的是( )A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.5.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 为球心,6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ,同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确.因为在直角三角1BA C 中,1A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥, 因为EFEH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒, 故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.6.在边长为2的等边三角形ABC 中,点,D E 分别是边,AC AB 上的点,满足//DE BC 且AD ACλ=,(()01λ∈,),将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中,下列结论不成立的是( )A .在边A E '上存在点F ,使得在翻折过程中,满足//BF 平面A CD 'B .存在102λ∈⎛⎫⎪⎝⎭,,使得在翻折过程中的某个位置,满足平面A BC '⊥平面BCDEC .若12λ=,当二面角A DE B '--为直二面角时,||A B '=D .在翻折过程中,四棱锥A BCDE '-体积的最大值记为()f λ,()f λ【答案】ABC 【分析】对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,即可判断出结论.对于B ,102λ∈⎛⎫⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,即可判断出结论. 对于C ,12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,可得AM ⊥平面BCDE .可得22A B AM BM '=+,结合余弦定理即可得出.对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,利用导数研究函数的单调性即可得出.【详解】对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,如图所示,则可得FN 平行且等于BG ,即四边形BGNF 为平行四边形, ∴//NG BE ,而GN 始终与平面ACD 相交,因此在边A E '上不存在点F ,使得在翻折过程中,满足//BF 平面A CD ',A 不正确.对于B ,102λ∈⎛⎫ ⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,因此不满足平面A BC '⊥平面BCDE ,因此B 不正确. 对于C.12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,如图所示:可得AM ⊥平面BCDE ,则22223111010()1()21cos120222A B AM BM '=+=++-⨯⨯⨯︒=≠,因此C 不正确;对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,()213f λλ'=-,可得3λ=时,函数()f λ取得最大值()312313f λ⎛⎫=-=⎪⎝⎭,因此D 正确. 综上所述,不成立的为ABC. 故选:ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值,考查了推理能力空间想象能力与计算能力,属于难题.7.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确; 故选:ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.8.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.9.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若3PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且3PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()313PD =∈,,则12PD =,即点P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为3=,可判断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】 如图:∵正四棱柱1111ABCD A B C D -的底面边长为2, ∴1122B D =11AA =, ∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确;∵()313PD =,,11DD =,则12PD P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接2221322122++=,面积为94π,故D 正确. 故选:ABD . 【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.10.如图所示,在棱长为1的正方体1111ABCD A B C D -中,过对角线1BD 的一个平面交棱1AA 于点E ,交棱1CC 于点F ,得四边形1BFD E ,在以下结论中,正确的是( )A .四边形1BFD E 有可能是梯形B .四边形1BFD E 在底面ABCD 内的投影一定是正方形C .四边形1BFDE 有可能垂直于平面11BB D D D .四边形1BFD E 面积的最小值为62【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形;1BFD E 在底面ABCD 内的投影是四边形ABCD ;当与两条棱上的交点是中点时,四边形1BFD E 垂直于面11BB D D ;当E ,F 分别是两条棱的中点时,四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E , 如图所示,因为平面11//ABB A 平面11DCC D ,且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =,因此,同理1//D E BF ,故四边形1BFD E 为平行四边形,因此A 错误;对于选项B ,四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ,因此B 正确; 对于选项C ,当点E F 、分别为11,AA CC 的中点时,EF ⊥平面11BB D D ,又EF ⊂平面1BFD E ,则平面1BFD E ⊥平面11BB D D ,因此C 正确;对于选项D ,当F 点到线段1BD 的距离最小时,此时平行四边形1BFD E 的面积最小,此时点E F 、分别为11,AA CC 的中点,此时最小值为162322=,因此D 正确. 故选:BCD【点睛】关键点睛:解题的关键是理解想象出要画的平面是怎么样的平面,有哪些特殊的性质,考虑全面即可正确解题.。
新高考数学多选题模拟测试卷(题目及详细答案)

高中数学多选题荟萃一、《函数、导数》多选题1、设0,1a a >≠且,函数1()log 1ax f x x -=+在(1,)+∞单调递减,则()f x ( ACD ) A .在(,1)-∞-上单调递减,在(1,1)-上单调递增 B .在(,1)-∞-上单调递增,在(1,1)-上单调递减 C .在(,1)-∞-上,)(x f 的值域为)0,(-∞D .在),1(+∞上,)(x f 的值域为)0(∞+,2、已知函数)(x f 在定义域)0(∞+,上的单调函数,若对于任意)0(∞+∈,x ,都有()12f f x x ⎛⎫-= ⎪⎝⎭,则的值是( AB ) A .)(x f 为减函数B .165f ⎛⎫= ⎪⎝⎭C .6)5(=fD .)(x f 值域为)0(∞+,【解】因为函数()f x 在定义域()0+∞,上是单调函数,且()12f f x x ⎛⎫-= ⎪⎝⎭,所以()1f x x -为一个常数,令这个常数为n ,则有()1f x n x -=,且()2f n =,将()2f n =代入上式可得()12f n n n=+=,解得1n =,所以()11f x x=+3、已知函数20()2(1)10a x f x x f x x ⎧+≤⎪=+⎨⎪-+>⎩,,,若对任意的),3(+∞-∈a ,关于x 的方程kx x f =)(都有3个不同的根,则k 的值不可能等于( ABD ) A .1B .2C .3D .44、已知函数1()1f x x=-,若关于x 的方程2()()0f x bf x c ++=恰有6个不同的实数解,则,b c 的取值情况可能的是( ACD )A .10,0b c -<<=B .10,0b c c ++>>C .10,0b c c ++<>D .10,01b c c ++=<< 【方法】画出)(x f 的图像,注意对称性和渐近线;2()()0f x bf x c ++=有两个不等实数根2121,)(,)(t t t x f t x f <==假设或;则直线的图像有六个交点与)(;21x f y t y t y ===;令c bt t t t t ++=<221)(,ϕ, 则(1)10,021<<=t t 时,120;01)1(;0)0(<-<>++===bc b c ϕϕ (2)1,1021≥<<t t 时,01)1(;0)0(≤++=>=c b c ϕϕ5、已知函数f (x )=e x +a ln x 的定义域是D ,关于函数f (x )给出下列命题其中正确命题的序号是( BD )A 、对于任意a ∈(0,+∞),函数f (x )是D 上的减函数;B 、对于任意a ∈(-∞,0),函数f (x )存在最小值;C 、存在a ∈(0,+∞),使得对于任意的x ∈D ,都有f (x )>0成立; D 、存在a ∈(-∞,0),使得函数f (x )有两个零点.6、定义在()+∞∞-,上的偶函数()x f 满足()()x f x f -=+1,且在[]0,1-上是增函数,下面是关于)(x f 的判断,其中正确的判断是( ABD )A 、()x f 的图像关于点对称B 、()x f 的图像关于直线1=x 对称;C 、()x f 在[0,1]上是增函数;D 、()()02f f =.7[]0,1上单调递增,则( BC )A .实数a 的取值范围是()1,1-B 、实数a 的取值范围是[]1,1-C 、当0>a 时,函数)(x f 有最小值a 2D 、函数)(x f 为偶函数,则a = 1【解】当0a >在区间[]0,1上单调递增, 在区间[]0,1上单调递增,则,解得](0,1a ∈, 当0a =在区间[]0,1上单调递增,满足条件. 当0a <在R 上单调递增,令,解得1a -≥,综上所述,实数a 的取值范围[]1,1-8、已知函数212,2()1|log |,2x x f x x x ⎧≤⎪=⎨⎪>⎩,()g x x b =+,若函数()()y f x g x =+有两个不同的零点,则实数b 的取值可以为( AB )A .1-B .32-C .1D .329、定义在R 上的偶函数()f x ,当0x ≥时,有(1)()f x f x +=-,且当[0,1)x ∈时,2()log (1)f x x =+.则下列命题中正确的命题为( AC ) A.0)2022()2021(=-+f f B.函数()f x 在定义域上是周期为2的周期函数 C.直线y x =与函数()f x 的图像有1个交点D.函数()f x 的值域为]1,1[-【解】可在同一平面直角坐标系中画出直线y x =和函数()f x 的图象如图所示,根据图象可知选项A 中0)2022()2021(=-+f f 正确;对于选项B ,函数()f x 在定义域上不是周期函数,所以B 不正确;对于选项C ,根据函数图象可知y x =与()f x 的图象有1个交点,所以C 正确;对于选项D ,根据图象,函数()f x 的值域是(1,1)-,所以D 错误.故选AC .二、《不等式》多选题1、若)lg(lg lg ,0,0b a b a b a +=+>>,则( ABC )A 、b a +的最小值为4B 、ab 的最小值为4C 、211122≥+b aD 21122≥+b a2、已知()()()2f x x m x n =---,且α、β是方程f (x )=0的两根,则下列不等式不可能成立的是 ( BCD ) A m n βα<<< B m n αβ<<< C m n αβ<<< D n m αβ<<<3、设2()f x x bx c =++(R x ∈),且满足()()0f x f x '+>。
高考数学-向量与立体几何试题及详解

1.1~1.3 习题课1.【多选题】下列命题中,是真命题的是( )A .同平面向量一样,任意两个空间向量都不能比较大小B .两个相等的向量,若起点相同,则终点也相同C .只有零向量的模等于0D .共线的单位向量都相等 答案 ABC解析 对于A ,向量是有向线段,不能比较大小,故A 为真命题;对于B ,两向量相等说明它们的方向相同,模长相等,若起点相同,则终点也相同,故B 为真命题;对于C ,零向量为模长为0的向量,故C 为真命题;对于D ,共线的单位向量是相等向量或相反向量,故D 为假命题.2.若a =e 1+e 2+e 3,b =e 1-e 2-e 3,c =e 1+e 2,d =e 1+2e 2+3e 3({e 1,e 2,e 3}为空间的一个基底)且d =x a +y b +z c ,则x ,y ,z 的值分别为( ) A.52,-12,-1 B.52,12,1 C .-52,12,1 D.52,-12,1答案 A解析 d =x a +y b +z c =(x +y +z )e 1+(x -y +z )e 2+(x -y )e 3.又因为d =e 1+2e 2+3e 3,所以⎩⎪⎨⎪⎧x +y +z =1,x -y +z =2,x -y =3,解得⎩⎨⎧x =52,y =-12,z =-1.3.设x ,y ∈R ,向量a =(x ,1,1),b =(1,y ,1),c =(2,-4,2),且a ⊥b ,b ∥c ,则|a +b |=( ) A .2 2 B.10 C .3 D .4 答案 C解析 因为b ∥c ,所以2y =-4×1,所以y =-2,所以b =(1,-2,1).因为a ⊥b ,所以a ·b =x +1×(-2)+1=0,所以x =1,所以a =(1,1,1),a +b =(2,-1,2).所以|a +b |=22+(-1)2+22=3.4.在四面体ABCD 中,AB ,BC ,BD 两两垂直,且AB =BC =1,点E 是AC 的中点,异面直线AD 与BE 所成角为θ,且cos θ=1010,则该四面体的体积为( )A.13B.23C.43D.83 答案 A5.【多选题】已知向量AB →=(1,1,1),AC →=(1,2,-1),AD →=(3,y ,1),下列结论正确的是( )A .若A ,B ,C ,D 四点共面,则∃λ,μ∈R ,使得AD →=λAB →+μAC →,λ=2B .若A ,B ,C ,D 四点共面,则∃λ,μ∈R ,使得AD →=λAB →+μAC →,μ=2 C .若A ,B ,C ,D 四点共面,则y =4 D .当AD ⊥AC 时,y =1 答案 AC解析 由A ,B ,C ,D 四点共面,得∃λ,μ∈R ,使得AD →=λAB →+μAC →,所以λ(1,1,1)+μ(1,2,-1)=(3,y ,1),所以⎩⎪⎨⎪⎧λ+μ=3,λ+2μ=y ,λ-μ=1,解得⎩⎪⎨⎪⎧λ=2,μ=1,y =4,故A 、C 正确,B 不正确.由AD ⊥AC ,得AD →⊥AC →,所以AD →·AC →=0.所以3+2y -1=0,解得y =-1,D 不正确.6.【多选题】如图,已知空间四边形ABCD 的各边和对角线的长都为a ,点M ,N ,E ,F 分别是AB ,CD ,BC ,AD 的中点,则( )A .MN ⊥AB B .MN ⊥CDC .向量AN →与CM →所成角的余弦值为23D .四边形MENF 为正方形 答案 ABD解析 设AB →=p ,AC →=q ,AD →=r .由题意可知,|p |=|q |=|r |=a ,且p ,q ,r 三个向量两两夹角均为60°.MN →=AN →-AM →=12(AC →+AD →)-12AB →=12(q +r -p ),所以MN →·AB →=12(q +r -p )·p =12(q ·p +r ·p -p 2)=12(a 2cos 60°+a 2cos 60°-a 2)=0.所以MN →⊥AB →,即MN ⊥AB .同理可证MN ⊥CD ,A 、B 正确.设向量AN →与MC →的夹角为θ,因为AN →=12(AC →+AD →)=12(q +r ),MC →=AC →-AM →=q -12p ,所以AN →·MC →=12(q +r )·⎝⎛⎭⎫q -12p =12(q 2-12q ·p +r ·q -12r ·p )=12(a 2-12a 2cos 60°+a 2cos 60°-12a 2cos 60°)=12⎝⎛⎭⎫a 2-a 24+a 22-a 24=a 22.又因为|AN →|=|MC →|=32a ,所以AN →·MC →=|AN →||MC →|cos θ=32a ×32a ×cos θ=a 22.所以cos θ=23.从而向量AN →与CM →所成角的余弦值为-23,C 错误.因为ME →=12AC →,FN →=12AC →,所以ME →=FN →.所以四边形MENF 为平行四边形.因为EN →=12BD →=12(AD →-AB →),所以EN →·ME →=12(AD →-AB →)·12AC →=0.所以EN →⊥ME →,|EN →|=|ME →|=12a .所以四边形MENF 为正方形.D 正确.7.从点P (1,2,3)出发,沿着向量v =(-4,-1,8)的方向取点Q ,使|PQ |=18,则Q 点的坐标为( )A .(-1,-2,3)B .(9,4,-13)C .(-7,0,19)D .(1,-2,-3) 答案 C8.【多选题】如图,在三棱锥P -ABC 中,△ABC 为等边三角形,△P AC 为等腰直角三角形,P A =PC =4,平面P AC ⊥平面ABC ,D 为AB 的中点,则( )A .AP ⊥BCB .异面直线AC 与PD 所成角的余弦值为24 C .异面直线PC 与AB 所成角的余弦值为24D .三棱锥P -ABC 的体积为1663答案 BCD解析 取AC 的中点O ,连接OP ,OB .因为P A =PC ,所以AC ⊥OP ,因为平面P AC ⊥平面ABC ,平面P AC ∩平面ABC =AC ,所以OP ⊥平面ABC ,又因为AB =BC ,所以AC ⊥OB .以O 为坐标原点,建立如图所示的空间直角坐标系.因为△P AC 是等腰直角三角形,P A =PC =4,△ABC 为等边三角形,所以A (0,-22,0),B (26,0,0),C (0,22,0),P (0,0,22),D (6,-2,0),所以AP →=(0,22,22),BC →=(-26,22,0),AP →·BC →=8≠0,A 不正确;因为AC →=(0,42,0),PD →=(6,-2,-22),所以cos 〈AC →,PD →〉=AC →·PD →|AC →||PD →|=-842×4=-24,则异面直线AC 与PD 所成角的余弦值为24,B 正确;因为PC →=(0,22,-22),AB →=(26,22,0),所以cos 〈PC →,AB →〉=PC →·AB →|PC →||AB →|=84×42=24,所以异面直线PC 与AB 所成角的余弦值为24,C 正确;三棱锥P -ABC 的体积V P -ABC =13S △ABC ·PO =13×34×(42)2×22=1663,D 正确. 9.在四面体OABC 中,棱OA ,OB ,OC 两两垂直,且OA =1,OB =2,OC =3,G 为△ABC的重心,则OG →·(OA →+OB →+OC →)=________.答案 14310.已知e 1,e 2是空间单位向量,e 1·e 2=12,若空间向量b 满足b ·e 1=2,b ·e 2=52,且对于任意x ,y ∈R ,有|b -(x e 1+y e 2)|≥|b -(x 0e 1+y 0e 2)|=1,x 0,y 0∈R ,则|b |=________. 答案 2 2解析 问题等价于|b -(x e 1+y e 2)|当且仅当x =x 0,y =y 0时取到最小值1,平方即|b |2+x 2+y 2-2b ·e 1x -2b ·e 2y +2e 1·e 2xy =|b |2+x 2+y 2-4x -5y +xy .已知上式在x =x 0,y =y 0时取到最小值1,x 2+y 2+(y -4)x -5y +|b |2=⎝⎛⎭⎪⎫x +y -422+34(y -2)2-7+|b |2,所以⎩⎨⎧x 0+y 0-42=0,y 0-2=0,-7+|b |2=1.解得⎩⎪⎨⎪⎧x 0=1,y 0=2,|b |=2 2.11.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,M ,E ,F 分别为PQ ,AB ,BC 的中点,则异面直线EM 与AF 所成角的余弦值是________.答案303012.如图,已知棱长为a 的正方体ABCD -A 1B 1C 1D 1中,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系,过点B 作BM ⊥AC 1于点M ,则点M 的坐标为________.答案 ⎝⎛⎭⎫2a 3,a 3,a 3解析 由题意,知A (a ,0,0),B (a ,a ,0),C 1(0,a ,a ),设M (x ,y ,z ), 则AC 1→=(-a ,a ,a ),AM →=(x -a ,y ,z ),BM →=(x -a ,y -a ,z ).因为BM →⊥AC 1→,所以BM →·AC 1→=0. 所以-a (x -a )+a (y -a )+az =0,即x -y -z =0.①因为AC 1→∥AM →,所以设AM →=λAC 1→,则x -a =-λa ,y =λa ,z =λa (λ∈R ),即x =a -λa ,y =λa ,z =λa .②由①②,得x =2a 3,y =a 3,z =a3.所以点M 的坐标为⎝⎛⎭⎫2a 3,a 3,a 3. 13.如图,已知ABCD -A 1B 1C 1D 1是四棱柱,底面ABCD 是正方形,AA 1=3,AB =2,且∠C 1CB=∠C 1CD =60°,设CD →=a ,CB →=b ,CC 1→=c .(1)试用a ,b ,c 表示A 1C →;(2)已知O 为对角线A 1C 的中点,求CO 的长.解析 (1)A 1C →=A 1A →+AD →+DC →=-AA 1→+BC →-CD →=-CC 1→-CB →-CD →=-c -b -a =-a -b -c .(2)由题意知|a |=2,|b |=2,|c |=3,a ·b =0,a ·c =2×3×12=3,b ·c =2×3×12=3,∵CO →=12CA 1→=12(a +b +c ),∴|CO →|=14(a +b +c )2=14(a 2+b 2+c 2+2a ·b +2a ·c +2b ·c )=14×(22+22+32+0+2×3+2×3)=294=292.14.已知空间三点A (0,2,3),B (-2,1,6),C (1,-1,5).(1)若点D 在直线AC 上,且BD →⊥AC →,求点D 的坐标; (2)求以BA ,BC 为邻边的平行四边形的面积.解析 (1)由题意知,AC →=(1,-3,2),点D 在直线AC 上, 设AD →=λAC →=λ(1,-3,2)=(λ,-3λ,2λ), ∴D (λ,2-3λ,2λ+3), BD →=(λ,2-3λ,3+2λ)-(-2,1,6) =(λ+2,1-3λ,2λ-3), ∵BD →⊥AC →, ∴AC →·BD →=(1,-3,2)·(λ+2,1-3λ,2λ-3)=λ+2-3+9λ+4λ-6=14λ-7=0,∴λ=12,∴D ⎝⎛⎭⎫12,12,4. (2)∵BA →=(2,1,-3),BC →=(3,-2,-1), ∴|BA →|=22+12+(-3)2=14, |BC →|=32+(-2)2+(-1)2=14, ∴BA →·BC →=2×3+1×(-2)+(-3)×(-1)=7,∴cos B =cos 〈BA →,BC →〉=BA →·BC →|BA →||BC →|=714×14=12,∴sin B =32,∴S =14×14×32=73,∴以BA ,BC 为邻边的平行四边形的面积为7 3.15.正方体ABCD -A 1B 1C 1D 1的棱长为1,以D 为原点,DA →,DC →,DD 1→所在直线为x ,y ,z 轴建立直角坐标系Dxyz ,点M 在线段AB 1上,点N 在线段BC 1上,且MN ⊥AB 1,MN ⊥BC 1.求:(1)〈AB 1→,BC 1→〉; (2)MN →的坐标.解析 (1)由题意可知D (0,0,0),A (1,0,0),B (1,1,0),B 1(1,1,1),C 1(0,1,1),所以AB 1→=(0,1,1),BC 1→=(-1,0,1), AB 1→·BC 1→=0×(-1)+1×0+1×1=1, |AB 1→|=02+12+12=2, |BC 1→|=(-1)2+02+12=2,所以cos 〈AB 1→,BC 1→〉=AB 1→·BC 1→|AB 1→||BC 1→|=12×2=12.所以〈AB 1→,BC 1→〉=π3.(2)设点M (1,x ,x ),N (y ,1,1-y ), 则MN →=(y -1,1-x ,1-x -y ).因为MN →·AB 1→=0,MN →·BC 1→=0,即⎩⎪⎨⎪⎧(y -1,1-x ,1-x -y )·(0,1,1)=0,(y -1,1-x ,1-x -y )·(-1,0,1)=0,化简得⎩⎪⎨⎪⎧2-2x -y =0,2-x -2y =0,解得⎩⎨⎧x =23,y =23,所以MN →的坐标为⎝⎛⎭⎫-13,13,-13.1.【多选题】已知向量a =(1,1,0),则与a 共线的单位向量e 等于( ) A.⎝⎛⎭⎫-22,-22,0B .(0,1,0) C.⎝⎛⎭⎫22,22,0D .(1,1,1)答案 AC 2.在四面体OABC 中,空间的一点M 满足OM →=14OA →+16OB →+λOC →,若M ,A ,B ,C 四点共面,则λ等于( ) A.712 B.13 C.512 D.12 答案 A3.在正四面体ABCD 中,E 是BC 的中点,那么( ) A.AE →·BC →<AE →·CD → B.AE →·BC →=AE →·CD → C.AE →·BC →>AE →·CD → D.AE →·BC →与AE →·CD →不能比较大小 答案 C解析 因为AE →·BC →=12(AB →+AC →)·(AC →-AB →)=12(|AC →|2-|AB →|2)=0,AE →·CD →=(AB →+BE →)·CD →=AB →·(BD →-BC →)+12BC →·CD →=|AB →|·|BD →|·cos 120°-|AB →|·|BC →|·cos 120°+12|BC →|·|CD →|cos 120°<0.所以AE →·BC →>AE →·CD →.4.已知a =(1,-2,3),b =(-1,1,-4),c =(1,-3,m ),则“m =1”是“{a ,b ,c }构成空间的一个基底”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 答案 A解析 当m =1时,c =(1,-3,1),易得a ,b ,c 不共面,即{a ,b ,c }能构成空间的一个基底,即“m =1”是“{a ,b ,c }构成空间的一个基底”的充分条件;当{a ,b ,c }能构成空间的一个基底时,则a ,b ,c 不共面,设a ,b ,c 共面,即c =x a +y b ,解得⎩⎪⎨⎪⎧x -y =1,y -2x =-3,3x -4y =m ,即⎩⎪⎨⎪⎧x =2,y =1,m =2,即当{a ,b ,c }能构成空间的一个基底时,m ≠2,即当{a ,b ,c }能构成空间的一个基底时,不能推出m =1,即“m =1”是“{a ,b ,c }构成空间的一个基底”的不必要条件.综上所述,“m =1”是“{a ,b ,c }构成空间的一个基底”的充分不必要条件.5.已知P (3cos α,3sin α,1)和Q (2cos β,2sin β,1),则|PQ →|的取值范围是( ) A .[0,5] B .[1,25] C .[1,5] D .(1,5) 答案 C6.在四面体O -ABC 中,G 是底面△ABC 的重心,且OG →=xOA →+yOB →+zOC →,则log 3|xyz |等于________. 答案 -37.已知空间三点A (2,1,0),B (2,2,1),C (0,1,2).(1)求AB →·AC →的值;(2)若(AB →+kAC →)⊥(AB →+AC →),求k 的值.解析 (1)因为A (2,1,0),B (2,2,1),所以AB →=(0,1,1).又C (0,1,2),所以AC →=(-2,0,2),所以AB →·AC →=0×(-2)+1×0+1×2=2.(2)由(1)可知AB →=(0,1,1),AC →=(-2,0,2),所以AB →+kAC →=(-2k ,1,2k +1),AB →+AC →=(-2,1,3).因为(AB →+kAC →)⊥(AB →+AC →),所以4k +1+3(2k +1)=0,解得k =-25.8.如图所示,在四棱锥P -ABCD 中,底面ABCD 为矩形,侧棱P A ⊥底面ABCD ,AB =3,BC =1,P A =2,E 为PD 的中点.(1)求AC 与PB 所成角的余弦值;(2)在侧面P AB 内找一点N ,使NE ⊥平面P AC ,求N 点的坐标. 解析 (1)由题意,建立如图所示的空间直角坐标系,则A (0,0,0),B (3,0,0),C (3,1,0),D (0,1,0),P (0,0,2),E ⎝⎛⎭⎫0,12,1, 从而AC →=(3,1,0),PB →=(3,0,-2). 设AC 与PB 的夹角为θ,则cos θ=|AC →·PB →||AC →|·|PB →|=327=3714.∴AC 与PB 所成角的余弦值为3714.(2)由于N 点在侧面P AB 内,故可设N 点坐标为(x ,0,z ),则NE →=⎝⎛⎭⎫-x ,12,1-z , 由NE ⊥平面P AC 可得,⎩⎪⎨⎪⎧NE →·AP →=0,NE →·AC →=0,即⎩⎨⎧⎝⎛⎭⎫-x ,12,1-z ·(0,0,2)=0,⎝⎛⎭⎫-x ,12,1-z ·(3,1,0)=0,化简得⎩⎪⎨⎪⎧z -1=0,-3x +12=0,∴⎩⎪⎨⎪⎧x =36,z =1,即N 点的坐标为⎝⎛⎭⎫36,0,1时,NE ⊥平面P AC .。
高考数学的立体几何多选题及答案
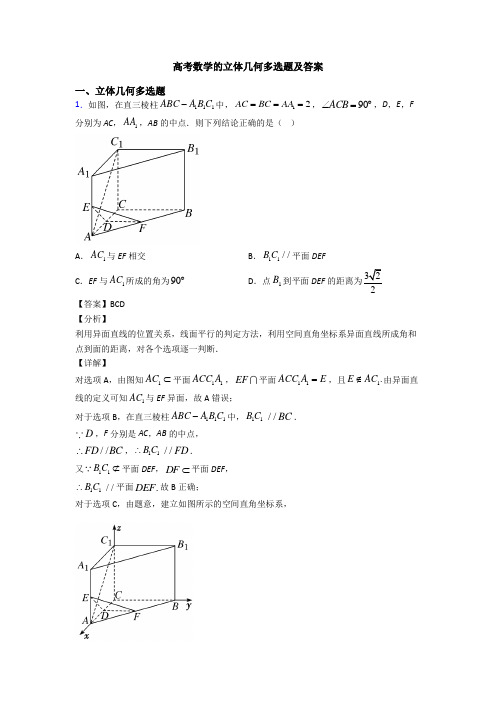
高考数学的立体几何多选题及答案一、立体几何多选题1.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF 平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·102DB n d n-+∴===, ∴点1B 到平面DEF 的距离为2,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.已知正方体1111ABCD A B C D -的棱长为2,点E ,F 在平面1111D C B A 内,若||5AE =,AC DF ⊥,则( )A .点E 的轨迹是一个圆B .点F 的轨迹是一个圆C .EF 21-D .AE 与平面1A BD 21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项,需要对各个选项一一验证. 选项A :由2211||5AE AA A E =+=1||1A E =,分析得E 的轨迹为圆;选项B :由AC DBF ⊥,而点F 在11B D 上,即F 的轨迹为线段11B D ,; 选项C :由E 的轨迹为圆,F 的轨迹为线段11B D ,可分析得min ||EF d r =-; 选项D :建立空间直角坐标系,用向量法求最值. 【详解】 对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =,即点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上;故A 正确;对于B: 正方体1111ABCD A B C D -中,AC ⊥BD ,又AC DF ⊥,且BD ∩DF=D ,所以AC DBF ⊥,所以点F 在11B D 上,即F 的轨迹为线段11B D ,故B 错误;对于C:在平面1111D C B A 内,1A 到直线11B D 的距离为2,d =当点E ,F 落在11A C 上时,min ||21EF =-;故C 正确; 对于D:建立如图示的坐标系,则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上,可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =,则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1,则()1,1,1n =, 设AE 与平面1A BD 所成角为α,则:22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时,sin α有最大值222153015++=, 故D 正确 故选:CD 【点睛】多项选择题是2020年高考新题型,需要要对选项一一验证.4.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P =,则满足条件的P 点有且只有一个 B .若12A P =,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B D C ,则1A P 长的最小值为2D .若12A P =且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 长的最大值为2;结合以上条件点P 与B 或D 重合,利用12sin 60A P r =︒,求出63r =,进而求出面积. 【详解】对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD 【点睛】(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.5.在三棱锥M ABC -中,下列命题正确的是( ) A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++ C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得.【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.6.在长方体1111ABCD A B C D -中,AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a,0a ⎡∈⎣,(2,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,,22)R λλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,2)D R λλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时12282()()05555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则44()33R,142()33D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.7.已知直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==,D 是AC 的中点,O 为1A C 的中点.点P 是1BC 上的动点,则下列说法正确的是( )A .当点P 运动到1BC 中点时,直线1A P 与平面111ABC 5 B .无论点P 在1BC 上怎么运动,都有11A P OB ⊥C .当点P 运动到1BC 中点时,才有1A P 与1OB 相交于一点,记为Q ,且113PQ QA = D .无论点P 在1BC 上怎么运动,直线1A P 与AB 所成角都不可能是30° 【答案】ABD 【分析】构造线面角1PA E ∠,由已知线段的等量关系求1tan EPPA E AE∠=的值即可判断A 的正误;利用线面垂直的性质,可证明11A P OB ⊥即可知B 的正误;由中位线的性质有112PQ QA =可知C 的正误;由直线的平行关系构造线线角为11B A P ∠,结合动点P 分析角度范围即可知D 的正误 【详解】直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==选项A 中,当点P 运动到1BC 中点时,有E 为11B C 的中点,连接1A E 、EP ,如下图示即有EP ⊥面111A B C∴直线1A P 与平面111A B C 所成的角的正切值:1tan EPPA E AE∠= ∵112EP BB =,22111152AE A B B E BB =+= ∴15tan PA E ∠=,故A 正确选项B 中,连接1B C ,与1BC 交于E ,并连接1A B ,如下图示由题意知,11B BCC 为正方形,即有11B C BC ⊥而AB BC ⊥且111ABC A B C -为直三棱柱,有11A B ⊥面11B BCC ,1BC ⊂面11B BCC ∴111A B BC ⊥,又1111A B B C B =∴1BC ⊥面11A B C ,1OB ⊂面11A B C ,故11BC OB ⊥ 同理可证:11A B OB ⊥,又11A B BC B ⋂=∴1OB ⊥面11A BC ,又1A P ⊂面11A BC ,即有11A P OB ⊥,故B 正确选项C 中,点P 运动到1BC 中点时,即在△11A B C 中1A P 、1OB 均为中位线∴Q为中位线的交点∴根据中位线的性质有:112PQQA=,故C错误选项D中,由于11//A B AB,直线1A P与AB所成角即为11A B与1A P所成角:11B A P∠结合下图分析知:点P在1BC上运动时当P在B或1C上时,11B A P∠最大为45°当P在1BC中点上时,11B A P∠最小为23arctan30>=︒∴11B A P∠不可能是30°,故D正确故选:ABD【点睛】本题考查了利用射影定理构造线面角,并计算其正弦值;利用线面垂直证明线线垂直;中位线的性质:中位线交点分中位线为1:2的数量关系;由动点分析线线角的大小8.如图,正方体1111ABCD A B C D-的棱长为1,线段11B D上有两个动点E,F,且2EF=则下列结论正确的是()A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =112213312A BEF BEF V S AO -∆∴=⨯==A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 452FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR =由余弦定理得13cos AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.9.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +170【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos AA AC AAC ''==∠=, 所以217042222()105AC '=+-⨯⨯⨯-=.故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.10.半正多面体(semiregularsolid)亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2,则()A.BF⊥平面EABB.该二十四等边体的体积为20 3C.该二十四等边体外接球的表面积为8πD.PN与平面EBFN所成角的正弦值为2 2【答案】BCD【分析】A用反证法判断;B先补齐八个角成正方体,再计算体积判断;C先找到球心与半径,再计算表面积判断;D先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A,假设A对,即BF⊥平面EAB,于是BF AB⊥,90ABF∠=︒,但六边形ABFPQH为正六边形,120ABF∠=︒,矛盾,所以A错;对于B,补齐八个角构成棱长为2的正方体,则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=,所以B对;对于C,取正方形ACPM对角线交点O,即为该二十四等边体外接球的球心, 其半径为2R =,其表面积为248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS , 所以PN 与平面EBFN 所成角即为PNS ∠, 其正弦值为22PS PN ==,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
高中数学多项选择题100道

高中数学多项选择题100道1. 已知集合A={x|ax ≤2},B={2, 2},若B ⊆A ,则实数a 的值可能是 ( ABC )A.-1B.1C.-2D.22.若函数f(x)=|x-a|在区间 [2,3] 上是单调函数,则实数a 的取值范围可以是 ( AB )A.a ≤2B.a ≥3C. a ≥2D. a ≤33. ()22,x x f x 已知函数则正确的说法是-=- ( BCD )A.f (x )的定义域为{x|x ≠0}B.f (x )的值域为RC.f (x )为奇函数D.f (x )是R 上的增函数4.若函数f (x )在区间(-2,3)上是增函数,则使y =f (x +5)单调递增的区间是( BC ) A.(3,8) B.(-7,-4) C.(-5,-3 ) D.(0,5)5.设M 是函数1()1xf x x -=+的定义域,集合P M ⊆,若对任意12,x x P ∈,当12x x <时,都有12()()f x f x >,集合P 可以是 ( ABCD )A.{x|x<-2}B.{x|<-1}C.{x|x>-1}D.{x|>0}6.设f (x )是定义在R 上的奇函数,且f (x -2)=-f (x ),则一定有 ( ABD )A.f (2)=0B.f (x )是以4为周期的周期函数C.f (x )的图象关于y 轴对称D.f (x+2)=f (-x )7. ,,4=6=9a b c a b c 已知为正数,且,则有( AD ) 2211212ab bc ac ab bc ac c a b c b aA. B. C. D.8. 21(),[]122xx f x x x 已知函数表示不超过的最大整数,=-+{|[()]}M y y f x M 集合,则下列各数中,属于集合的是 ( BC )A.-2B.-1C.0D.19.设指数函数)1,0()(≠>=a a a x f x ,则有( ACD ) A.()()f x y f x f y ()+= B.()()f xy f x f y ()=C.()()f x f x y f y ()-= D.3(3)[()]f x f x =10.01,,a a x y 已知且,为正数,则下列各式中错误的是>≠ ( AC )log log ()log log log log log log log log na a a a a a a a aa xx y x y xnx xx y y y y xA. B.C. D.11.若1<x <10,则正确的不等式有 ( ACD )A.(lgx)2<lgx 2B.lgx 2<lg(lgx)C.lg(lgx)<lgx 2D.lg(lgx)<(lgx)212.下列函数中,为奇函数的是 ( ABCD )32()lg(1)()|sin 1||sin 1|182()2()1221x x x f x f x x x x f x f x A. B.C. D.13.下列函数中既是奇函数,又在区间[-1,1]上单调递增的是 ( ABC )A.f(x)=2xB.f(x)=sinxC.f(x)=tanxD.f(x)=2x14.下列函数中既是偶函数,又在区间(0,+∞)上为增函数的是 ( BD )A.y=cosxB.y=x 2C.y=x 3D.y=log 2|x|15.下列函数中,有2个零点的是 ( ABD )2||lg ||()ln 2()12()21x x y x f x x x f x x f x x A. B.C. D.16. 在R 上定义的函数f(x)是偶函数,且f(x)= f(2-x),若f(x)在区间[1,2]是减函数,则函数f(x) ( ABC )A.在区间[-3,-2]上是减函数B.在区间[-2,-1]上是增函数C.在区间[0,1]上是增函数D.在区间[2,3]上是减函数17.已知函数1()1x f x x+=-,又记*11(),()(())()k k f f x f x f f x k N +==∈,则 下列各式中,正确的有 ( ABD ) 2016201720182020201920211()()1()()1()()1x f x x f x x f x f x f x f x A. B.C. D. 18.设f(x)是R 上的任意函数,则下列叙述正确的是 ( CD )A.f(x)f(-x)是奇函数B.|f(x)|是偶函数C.f(x)-f(-x)是奇函数D.f(x)+f(-x)是偶函数19.对函数b ax x x f ++=23)(作代换()x g t ,则总不改变()f x 的值域的代换是 ( AD )20.5()log ()(0.5)()(1)()tan t g t t g t g t t g t t A. B. C. D.20.设二次函数f(x)=ax 2+2ax+1在[-3,2]上有最大值4,则实数a 的值可能是 ( CD )A.8/3B.1C.3/8D.-321. 已知函数f(x)的定义域为R ,且f(x+1)和f(x+2)都是奇函数,则 ( ABC )A.f(x)为奇函数B.f(x)为周期函数C.f(x+3)为奇函数D.f(x+4)为偶函数22.下列求导运算正确的是 ( AB )2222111()1(log )()2()2ln2x x x x x e xe x x x A. B. C. D.ππ''''-=+=== 23.下列求导结果正确的是 ( BCD )22321[(sin 3)]2(sin 3)(tan )cos 1cos2(sin cos3)3sin cos4()sin 22x x x x x x x x x x A. B.C. D.''-=-=+''==- 24.下列函数中,在(0,+∞)上为增函数的是 ( BCD )A.2x y xe B.x xe y = C.32261y x x D.ln(1)y x x 25.设(),()f xg x 是定义在R 上的恒大于0的可导函数,且()()()()f x g x f x g x ,则当b x a <<时有 ( BC )()()()()()()()()()()()()()()()()f xg x f b g b f a g x f x g a f x g b f b g x f x g x f a g a A. B.C. D.>>>>26.已知函数f(x)=x 3-3x 2,当x ∈[-2,+∞)时,下列结论中正确的是 ( ABCD )A.f(x)的极大值为0B.f(x)的极小值为-4C.f(x)没有最大值D.f(x)的最小值为-2027.已知函数y=f(x)的导函数y=f ′(x)的图像如下,则下列说法中正确的是 ( AC )A.x 1是极小值点B.x 2是极大值点C.x 3是极大值点D.x 4是极小值点28.设函数()f x 的定义域为R,00(0)x x ≠是()f x 的极大值点,则有 ( ABD )A.0x 是()f x -的极小值点B.0x -是()f x -的极大值点C.0x -是()f x -的极小值点D.0x -是()f x --的极小值点29.已知p , q 都是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件,则 ( BD )A .p 是q 的不充分也不必要条件 B. p 是s 的充分条件C.r 是q 的必要不充分条件D.s 是q 的充要条件30.使不等式110x 成立的一个充分不必要条件是 ( AC )A.x>2B.x<0C.x<-1或x>1D.-1<x<031.设数列}{n a 的前n 项和为2n S pn qn r ,那么在下列条件中,能使}{n a为等差数列是 ( AB )0,0,00,,00,0,00,0,0p q r p q R r p q r p q r A. B.C. D. 32.在等差数列{a n }中,若a 2=21,a 6=9,则能使前n 项和S n 取最大值的正整数n 是 ( BC )A.7B.8C.9D.1033.等比数列{a n }中,a 3=7,前3项之和S 3=21, 则公比q 的值可能是 ( AC )A.-1/2B.1/2C.1D.-134.定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{a n },{f(a n )}仍是等比数列,则称f (x )为“保等比数列函数”. 以下都是定义在(-∞,0)∪(0,+∞)上的函数,其中为“保等比数列函数”的是 ( AC )A.f(x)=x ²B.f(x)=2xC.f(x)=||xD.f(x)=ln|x|35. 2{}(,0)n n a n S a n bn a b a 设数列的前项和为常数,且,则下列各式中正确的是 ( ABCD ) 152********+=++=235a a a a a a a S a S a A. B. C. D.36.已知直角三角形三边的长成等差数列,周长为24,则下列结论中正确的是 ( ABCD )A.较小内角的正弦为3/5B.较小内角的正切为3/4C.外接圆的半径为5D.内切圆的半径为237.关于x 的不等式x 2+ax-2a 2<0的解集,正确的结论是 ( ABC )A.若a>0,则解集为(-2a,a)B.若a<0,则解集为(a,-2a)C.若a=0,则解集为ψ C.若a ≠0,则解集为(-2a,a)∪(a,-2a)38.22cos 10x x 不等式的解集可能是θ-+≤ ( BCD )A.RB.{1}C.{-1}D.ψ39.下列不等式中与3<x 同解的不等式为 ( BD )112222|1|3|1|23233lg(1)lg(1)11x x x x x x x x x x x x x x x x A. B.C. D.--+<+<<<++++-+-+ 40.下列函数中,最小值为2的是 ( BC ) 222log log 2(0,1)()13(0)()2x x x y x x x y e e x R x x y x y x R x x A.且 B.C. D.-=+>≠=+∈++=>=∈+ 41.下列命题中正确的是 ( BC ) A.若b a >,则 22b a > B.若b a >,则33a b C.若||b a >,则22b a > D.若b a >||,则33ab 42.已知,x y R ,则以下不等式中恒成立的是 ( ABCD ) 2244332222962221x y xyx y x y xy x y xy x y xy x A. B.C. D.+≥+≥++≥+≥--43.已知x>y>z ,且x+y+z=0,则下列不等式中恒成立的是 ( AC )A.xy>xzB.xz>yzC.x 2>xyD.x|y|>z|y|44.,,1a b c a b c 已知为正数,且,则下列不等式中正确的是++= ( ABD )22211113927abc a b c a b c a b c A. B.3 C. D.45.已知x,y 为实数,则下列结论中正确的有 ( AC )A.若xy>0,则|x+y|=|x|+|y|B.若xy>0,则|x-y|>|x|-|y|C.若xy<0,则|x-y|=|x|+|y|D.若xy<0,则|x+y|<|x|-|y|46.下列函数中,在区间(0,π)上为增函数的是 ( ABC ) sin cos tan sin 242x x y y x y y x A. B. C. D.47.下列函数中是奇函数,且最小正周期是π的函数是 ( ACD )A.tan y x =-B.sin 2x y =C.sin(2)y x π=-D.3πcos(2)2y x =+ 48.已知函数f (x )=sin ⎝⎛⎭⎫ωx +π4(ω>0)的最小正周期为π,则 ( ABCD ) A. f (x )的图象关于点(38,0)对称 B. f (x )的图象关于直线x =8对称 C. f (x )在[,]88上为增函数 D. f (x ) 在3[,]88上为减函数 49.下列x 的值中,能使sin3x ·sin2x =cos3x ·cos2x 成立的是 ( ABD )A.-54°B.18°C.36°D.72°50.下列各式中,正确的是 ( ABC )11sin15sin 75cos20cos40cos80481tan1513tan15231tan15tan15A. B.C. D.51.在△ABC 中,已知sinA+cosA=1/5,则下列各式中,正确的是 ( ABCD )A.sin2A =-24/25B.sinA-osA=7/5C.cos2A=-7/25D.tanA =-4/352.已知ABC 中,内角,,A B C 所对的边分别为,,a b c ,且1c ,3C . 若sin()sin sin2A B C B ,则ABC 的面积可能是 ( AB )53 若向量b 与向量(2,1)a 平行,且52||=b ,则向量b 的坐标可能是 ( AC )A.(4,-2)B.(-4,-2)C.(-4,2)D.(4,2)54.设λ为实数,则下列各式中正确的是 ( AD ) ()())||||||()()()a b a b a b a b a b a b c a b c a b c a c b c A.( B.C. D.λλλ====+=+55.在△ABC 中,下列结论正确的是 ( AC )0,0,0,0,AB BC ABC AB BC ABC AB BC ABC AB BC ABC A.若则为直角三角形B.若则不是直角三角形C.若则为钝角三角形D.若则为锐角三角形=∆≠∆>∆<∆56.在△ABC 中,已知AB =5,BC =3,AC =4,则下列结论正确的有 ( AB )0169()25AC BC AB AC AB BC BC CA AB A. B. C. D.===+=57.使两个非零向量m 、n 互相垂直条件是 ( ABD )2220||||()()0||m n m n m n m n m n m n m n A. B. C. D.=+=-+-=+=+ 58.在直角三角形ABC 中,已知向量AB =(2,3),AC =(1,k ),则k 的值可能是 ( ABCD )211333322A. B. C. D.+-- 59.下列命题中,正确的是 ( AD )A.平行于同一条直线的两条直线平行B.平行于同一个平面的两条直线平行C.垂直同一条直线的两条直线平行D.垂直同一个平面的两条直线平行60.已知两个平面垂直,则下列命题中正确的是 ( BD )A.一个平面内的已知直线必垂直于另一个平面的任意一条直线B.一个平面内的已知直线必垂直于另一个平面的无数条直线C.一个平面内的任一条直线必垂直于另一个平面D.一个平面内平行垂直交线的直线必垂直另一个平面61.在正方体ABCD -A 1B 1C 1D 1中,任意两条面对角线所成的角可能等于 ( ABC )A.0°B.60°C.90°D.120°62.已知a 、b 是两条异面直线,直线c//a ,则直线c 与直线b ( ABC )A.可能平行B.可能相交C.可能异面D.可能重合63.用一个平面去截正方体,截面图形可能是 ( ABCD )A.三角形B.四边形C.五边形D.六边形64.如图,已知正四棱锥P-ABCD的侧棱长与底面边长的比为3,则下列垂直关系正确的是( ABD )A.平面PAC⊥平面ABCDB.平面PAC⊥平面PBDC.平面PBC⊥平面PCDD.平面PAD⊥平面PBC65. 如图,四棱锥P—ABCD的底面为正方形,PA⊥底面ABCD,则下列结论中正确的是 ( ABCD )A.BD⊥PCB.CD//平面PABC.PB与平面PAC所成的角等于PD与平面PAC所成的角D.平面PBC与底面所成的角等于平面PCD与底面所成的角66.如图,在三棱锥A-BCD中,AB=CD,直线AB与CD成60°的角,点M、N分别是BC、AD的中点,则直线AB和MN所成的角可能为 ( AB )A.30°B.60°C.120°D.150°67.如图,在长方体ABCD-A1B1C1D1的棱长为1,E,F,G分别是棱BC,CC1,BB1的中点,则 ( BC )A.直线DD1与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体所得的截面面积为9/8D.点C与点G到平面AEF的距离相等68.在下列四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,那么能得出AB∥平面的是 ( AD )69.已知三条直线mx+y+3=0,x-y-2=0,2x-y+2=0不能构成一个三角形三边所在的直线,则m的值可能是 ( BCD )A.-4/3B.-1C.-2D.-3/470.直线l过点P(4,1),且横截距是纵截距的2倍,则直线l方程可能是 ( AC ) A.x+2y-6=0 B.x-2y-2=0 C.x-4y=0 D.无法确定71.使直线3mx+(m+5)y+1=0与直线(1-m)x+my-3=0相互垂直的m的值可以是 ( AB )A.0B.4C.-4D.不存在72. 设直线1=kxy与圆x2+y2=1相交于P、Q两点,O为原点,且∠POQ=120°,+则k的值可能为 ( AB ) --3322A. B. C. D.73.直线l 过M (3,3/2)--,且被圆2522=+y x 截得的弦长为8,则直线l 的方程可能是 ( AC )A.3-=xB.3/2y =-C.34150x y ++=D.20x y +=74.椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点A 、B 是它的焦点,长轴长为2a,焦距为2c,静放在点A 的小球(小球的半径忽略不计)从点A 沿直线出发,经椭圆壁反射后第一次回到点A 时,小球经过的路程是可能是 ( BCD )A.2aB.4aC.2(a+c)D. 2(a -c)75. 动点P(x, y)与两个定点(-1, 0), (1, 0)的连线的斜率之积为a (a ≠0),则P 点的轨迹可能是( ABC ) A.圆 B.椭圆 C.双曲线 D.抛物线76.已知圆22:2450C x y x y ,则 ( ABC )2222222224502450+245004250C x x y x y C y x y x y C x y x y C x y x y x y A.圆关于轴对称的圆的方程为B.圆关于轴对称的圆的方程为C.圆关于原点对称的圆的方程为D.圆关于直线对称的圆的方程为77.已知定点M(0,-1)、N(0,1), 则满足1t a n ()t a n PM PN 为锐角θθθ+=+的点P 的轨迹可能是(AC ) A.椭圆 B.双曲线 C.线段 D.不存在78. 当θ∈(0,π)时,方程x 2cos θ+y 2sin θ=sin2θ所表示的曲线有可能是 ( ABCD )A.椭圆B.双曲线C.直线D.圆79.设双曲线的左、右焦点分别是F 1、F 2,左、右顶点分别为M 、N ,若△PF 1F 2的顶点P 在双曲线上, 则△PF 1F 2的内切圆与边F 1F 2的切点位置是 ( AB )A.可能与点M 重合B.可能与点N 重合C.可能在线段MN 的内部D.不能确定80.离心率为2/3,长轴长为6的椭圆的标准方程可能是 ( AB )222222221111955936202036x y x y x y x y +=+=+=+=A. B. C. D.81.22224,119494x y x y k k k 已知则曲线和有相同的<+=+=-- ( ACD )A. 焦点B.离心率C.对称轴D.对称中心82.已知双曲线的方程为22(0)169x y k k -=≠,则下列与k 无关的是 ( CD )A.焦点坐标B.顶点坐标C.渐近线方程D.离心率83.设方程x 24-t +y 2t -2=1所表示的曲线为C ,则正确的命题是 ( ACD )A.若t<2,则曲线C 为双曲线B.若2<t<4,则曲线C 为椭圆C.若t>4,则曲线C 为双曲线D.若3<t<4,则曲线C 是焦点在y 轴上的椭圆.84. 221,,912x y a a 已知实数成等比数列,则圆锥曲线的离心率可能是+= ( BC ) 32B. C. D.85.若直线1y kx =+与双曲线2214y x -=有且只有一个交点,则k 的值可能是 ( ABCD )A.2- D.286. 经过直线y=2x 与圆x 2+y 2=5的交点的抛物线的标准方程可能是 ( ABCD ) 2222114444y x y x x y x y A. B. C. D. 87. 把6本不同的书分成三堆或分给三人,则以下分法种数正确的是 ( ABC )A.分给3人,甲得1本,乙得2本,丙得3本的分法有123653C C C 种B.分成3堆,一堆1本,一堆2本,一堆3本的分法有123653C C C 种.C.平均分给甲、乙、丙三人的分法有222426C C C =90种D.平均分成三堆的分法有222426C C C 种88.把甲、乙、丙等7个人排成一排,下列排法的种数正确的是 ( ABC ) A.甲、乙、丙排在一起的排法有5353A A 种B.甲、乙、丙互不相邻的排法有4345A A 种C.甲不排头,乙不排尾的排法有61156555A A A A +种D.甲、乙、丙按自左向右的顺序(不一定相邻) 的排法有 773A 种 89.由数字0、1、2、3、4、5组成的能被5整除且无重复数字的五位数共有 ( AC )4343413454555445(2)(2)(5A A A A A A A A A.个 B.个 C.)个 D.个90.袋中有4个不同的红球,6个不同的白球,每次取出4个球,取出一个红球记2分,取出一个白球记1分,那么,使总分不小于5分的取球方法总数是 ( AC )13223144444344646464461064623C C C C C C C C C C C C C A. B. C. D.++++- 91. 3*1(+)(),n x n N x对于二项式以下判断中正确的有 ( AB ) A.存在正整数n ,展开式中有常数项B.存在正整数n ,展开式中有x 的一次项C.对任意正整数n ,展开式中没有常数项D.对任意正整数n ,展开式中没有x 的一次项92.31022)x 在二项式的展开式中,下列说法正确的是 ( ABC )A.有2个系数为有理数的项B.没有常数项C.没有含x 2的项D.没有含x 4的项93.同时掷两枚骰子,以下结论正确的是 ( ABCD )A.点数之和为2的概率是1/36B.点数之和为5的概率是1/9D.两枚骰子点数相同的概率是1/6 C.至少出现一个6点向上的概率是11/3694.把一枚硬币连续抛掷3次,以下概率正确的是 ( AD )A.三次都出现正面的概率是1/8B.一次出现正面,二次出现背面的概率是3/8C.前两次为正面,第三次为背面的概率为3/8D.至少有一次正面朝上的概率7/895.有编号为1,2,3,4,5,6的六个房间,安排4人入住,每人可以随意进入那一间,每个房间入住人数不限,则下列概率正确的是 ( ACD )A. 1-4号房各住1人的概率为4446AB.恰有4间房各住1人的概率为4646C C.5号房住2人的概率为224456C D.1号房住1人,6号房住3人的概率为1446C 96.设导弹发射的事故率为1100,若发射10次,其出事故的次数为ξ, 则下列结论中正确的是 ( ABD )3737731010199101000199199(3)()()(7)()()100100100100ED P C P C A. B.C. D. 97.盒中有2个白球,3个黑球,从中任取3个,以ξ表示取到的白球个数,η表示取到的黑球个数,则有 ( BC )A.Eξ=EηB.Eξ=3-EηC.D ξ=D ηD.D ξ=3-D η98.设某大学的女生体重y (单位:kg )与身高x (单位:cm )具有线性相关关系,根据一组样本数据(x i ,y i )(i=1,2,…,n ),用最小二乘法建立的回归方程为ˆy=0.85x-85.71,则下列结论中正确的是 ( ABC ) A.y 与x 具有正的线性相关关系B.回归直线过样本点的中心(,)x yC.若该大学某女生身高增加1cm ,则其体重约增加0.85kgD.若该大学某女生身高为170cm ,则可断定其体重必为58.79kg99.为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[40,50),[50,60),[60,70),[70,80),由此得到频率分布直方图如图,据此得到的以下估计值正确的是 ( ABD )A.产品数量在区间[60,80)的人数为12B.这组数据的众数65C.这组数据的中位数为60D.这组数据的平均数62100.设12,z z 为复数,则以下关于复数的模的结论正确的是 ( ABD ) 11121222212121212||||||||||(0)||||||||||||||z z z z z z z z z z z z z z z z z A. B.C. D.。
高考数学试卷全国卷多选

一、选择题(本大题共10小题,每小题6分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列各数中,无理数是()A. √2B. 3.14159C. 0.1010010001...D. 1/32. 已知函数f(x) = x^2 - 4x + 4,则f(x)的图像是()A. 顶点在x轴上的抛物线B. 顶点在y轴上的抛物线C. 顶点在原点上的抛物线D. 顶点在x轴上的圆3. 在等差数列{an}中,若a1 = 2,公差d = 3,则第10项an等于()A. 28B. 29C. 30D. 314. 若复数z满足|z-1| = |z+1|,则复数z对应的点在()A. x轴上B. y轴上C. 第一象限D. 第二象限5. 函数y = 2^x在定义域内的单调性是()A. 单调递增B. 单调递减C. 先增后减D. 先减后增6. 已知等比数列{an}中,a1 = 1,公比q = 2,则第n项an等于()A. 2^nB. 2^(n-1)C. 2^(n+1)D. 2^n/27. 下列各对数式中,等价的是()A. log2(4) = log4(16)B. log3(27) = log9(81)C. log5(25) = log10(100)D. log7(49) = log7(7^2)8. 若向量a = (2, 3),向量b = (-1, 2),则向量a·b等于()A. 7B. -7C. 5D. -59. 在△ABC中,∠A = 60°,∠B = 45°,则sinC等于()A. √3/2B. 1/2C. √2/2D. 110. 下列命题中,正确的是()A. 对于任意实数x,x^2 ≥ 0B. 对于任意实数x,x^3 ≥ 0C. 对于任意实数x,|x| ≥ 0D. 对于任意实数x,|x| ≤ x二、填空题(本大题共5小题,每小题10分,共50分。
请将答案填在答题卡上相应位置。
2023年新高考数学多选题评分标准

2023年新高考数学多选题评分标准全文共四篇示例,供读者参考第一篇示例:2023年新高考数学多选题评分标准一、多选题设置及要求在2023年新高考数学考试中,多选题通常由一道题目和多个选项组成。
学生需根据题目向选项中作出正确选择,选出所有正确答案。
通常,多选题的选项数量会设定在4-6个之间,其中有1-4个为正确选项。
多选题有多个正确答案的特点要求考生在做题时要细心,不能疏忽。
要求考生具备较强的逻辑思维和解决问题的能力,能够正确筛选选项,选择出所有正确答案。
二、多选题评分标准1. 题目本身的评分标准多选题的难易程度和评分质量直接受到题目设置的影响。
评分标准首先需要对题目本身进行评估。
评分标准会根据题目的难易程度、选项的设置合理性和答案之间的区分度等因素进行综合评估。
2. 答案选择的评分标准考生在做多选题时,需要选择所有符合题意的正确答案。
在评分时,评分者会根据考生选出的正确答案的准确性和完整性进行评分。
如果考生漏选了正确答案或者选择了错误答案,都会影响得分。
解题过程是考生得分的关键。
评分者会根据考生在解题过程中的逻辑思维能力、推理能力和解决问题的能力进行综合评定。
如果考生选择了正确答案但无法合理解释选择的过程,可能会导致得分减少。
评分标准将会重点考察考生解题的合理性和逻辑性。
三、评分细则1. 每个正确答案得分均相等,每个错误答案扣除一定分数,未选择的正确答案不得分。
2. 多选题的总分等于正确答案的总分减去错误答案的总分。
如果得分为负数,则得0分。
3. 解题过程符合逻辑、正确清晰的考生将得到额外加分。
4. 如果考生没有选择任何答案,不符合题目要求,将被视为全错得0分。
5. 如果考生选择了所有正确答案并且没有选择错误答案,将获得满分。
四、评分的公正性与透明性在评分过程中,评分者需要严格按照评分标准进行评定,确保评分的公正性和透明性。
评分者需要对每个考生的答卷进行仔细评阅,确保评分的准确性。
评分标准也需要在考前向考生和教师充分公布,以便考生和教师了解评分的标准和流程。
高考数学多选题专项练习附答案

一、函数的概念与基本初等函数多选题1.一般地,若函数()f x 的定义域为[],a b ,值域为[],ka kb ,则称为的“k 倍跟随区间”;若函数的定义域为[],a b ,值域也为[],a b ,则称[],a b 为()f x 的“跟随区间”.下列结论正确的是( )A .若[]1,b 为()222f x x x =-+的跟随区间,则2b =B .函数()11f x x=+存在跟随区间 C .若函数()f x m =1,04m ⎛⎤∈- ⎥⎝⎦D .二次函数()212f x x x =-+存在“3倍跟随区间” 【答案】ABCD 【分析】根据“k 倍跟随区间”的定义,分析函数在区间内的最值与取值范围逐个判断即可. 【详解】对A, 若[]1,b 为()222f x x x =-+的跟随区间,因为()222f x x x =-+在区间[]1,b 为增函数,故其值域为21,22b b ⎡⎤-+⎣⎦,根据题意有222b b b -+=,解得1b =或2b =,因为1b >故2b =.故A 正确; 对B,因为函数()11f x x =+在区间(),0-∞与()0,+∞上均为减函数,故若()11f x x=+存在跟随区间[],a b 则有11+11+a b b a ⎧=⎪⎪⎨⎪=⎪⎩,解得:12a b ⎧=⎪⎪⎨⎪=⎪⎩. 故存在, B 正确.对C, 若函数()f x m =[],a b ,因为()f x m =,故由跟随区间的定义可知b m a b a m ⎧=-⎪⇒-=⎨=⎪⎩a b < 即()()()11a b a b a b -=+-+=-,因为a b <,1=.易得01≤<.所以(1a m m =-=--,令t =20t t m --=,同理t =20t t m --=,即20t t m --=在区间[]0,1上有两根不相等的实数根.故1400m m +>⎧⎨-≥⎩,解得1,04m ⎛⎤∈- ⎥⎝⎦,故C 正确.对D,若()212f x x x =-+存在“3倍跟随区间”,则可设定义域为[],a b ,值域为[]3,3a b .当1a b <≤时,易得()212f x x x =-+在区间上单调递增,此时易得,a b 为方程2132x x x -+=的两根,求解得0x =或4x =-.故存在定义域[]4,0-,使得值域为[]12,0-. 故D 正确. 故选:ABCD. 【点睛】本题主要考查了函数新定义的问题,需要根据题意结合函数的性质分析函数的单调性与取最大值时的自变量值,并根据函数的解析式列式求解.属于难题.2.若定义在R 上的函数()f x 满足()()0f x f x ,当0x <时,23()22f x x ax a =++(a ∈R ),则下列说法正确的是( )A .若方程()2af x ax =+有两个不同的实数根,则0a <或48a << B .若方程()2af x ax =+有两个不同的实数根,则48a << C .若方程()2af x ax =+有4个不同的实数根,则8a > D .若方程()2af x ax =+有4个不同的实数根,则4a > 【答案】AC 【分析】由题知()f x 是R 上的奇函数,则由0x <时的解析式可求出()f x 在R 上的解析式.先讨论特殊情况0x =为方程的根,则可求出0a =,此时方程化为()0f x =,而函数()f x 为R 上的减函数,则方程仅有一个根.当0x ≠时,由分段函数分类讨论得出0x <时,1(1)2(1)a x x =-+++-+,0x >时,4242a x x =-++-.利用数形结合思想,画出图象,则可得知方程()2af x ax =+不同的实数根个数分别为2个和4时,参数a 的取值范围. 【详解】 因为()()0f x f x 所以()()f x f x -=-,所以()f x 是R 上的奇函数,(0)0f =,当0x >时,0x -<,23()22f x x ax a -=-+, 所以23()()22f x f x x ax a =--=-+-, 综上2232,02()0,032,02x ax a x f x x x ax a x ⎧++<⎪⎪==⎨⎪⎪-+->⎩,若0x =是方程()2af x ax =+的一个根, 则0a =,此时()2af x ax =+,即()0f x =, 而22,0()0,0,0x x f x x x x ⎧<⎪==⎨⎪->⎩,在R 上单调递减,当0a =时,原方程有一个实根. 当0x <时,23222a x ax a ax ++=+, 所以20x ax a ++=,当1x =-时不满足,所以21(1)21(1)x a x x x =-=-++++-+, 当0x >时,23222ax ax a ax -+-=+, 所以220x ax a -+=,当2x =时不满足,所以242422x a x x x ==-++--,如图:若方程()2af x ax =+有两个不同的实数根, 则0a <或48a <<;若方程()2af x ax =+有4个不同的实数根,则8a >. 故选:AC 【点睛】关键点点睛:本题的关键是将方程()2af x ax =+进行参数分离,再借助数形结合法,求出对应的参数的取值范围.3.已知函数22,0()(2),0x x x f x f x x ⎧--<=⎨-≥⎩,以下结论正确的是( )A .函数()f x 在区间[2,4]上是减函数B .(2020)(2021)1f f +=C .若方程()10()f x mx m R --=∈恰有5个不相等的实根,则11,46m ⎛⎫∈-- ⎪⎝⎭ D .若函数()y f x k =-在区间(,6)-∞上有8个零点()*8,i x i i N ≤∈,则8116i i x ==∑【答案】BCD 【分析】对于A ,画出函数的图象即可判断;对于B ,由函数的周期性可计算求解;对于C ,方程()10()f x mx m R --=∈恰有5个不相等的实根等价于()y f x =与直线1y mx =+有5个交点,画出图形即可判断求解;对于D ,函数()y f x k =-在区间(,6)-∞上有8个零点,则()y f x =与y k =有8个交点,由对称性可求解. 【详解】由题可知当0x ≥时,()f x 是以2为周期的函数,则可画出()f x 的函数图象,对于A ,根据函数图象可得,()f x 在()2,3单调递增,在()3,4单调递减,故A 错误; 对于B ,()()()2020020f f f ==-=,()()()2021111f f f ==-=,则(2020)(2021)1f f +=,故B 正确;对于C ,方程()10()f x mx m R --=∈恰有5个不相等的实根等价于()y f x =与直线1y mx =+有5个交点,如图,直线1y mx =+过定点()0,1A ,观察图形可知AB AC k m k <<,其中()()4,0,6,0B C ,则11,46AB AC k k =-=-,故11,46m ⎛⎫∈-- ⎪⎝⎭,故C 正确;对于D ,若函数()y f x k =-在区间(,6)-∞上有8个零点,则()y f x =与y k =有8个交点,如图,可知这八个零点关于2x =对称,则814416ii x==⨯=∑,故D 正确.故选:BCD. 【点睛】关键点睛:本题考查函数与方程的综合问题,解题的关键是判断出函数的周期性,画出函数的图象,即可将方程的解的个数问题、函数的零点问题转化为函数图象的交点问题,利用数形结合的思想可快捷解决问题.4.设s,t 0>,若满足关于x s 恰有三个不同的实数解123,x x x s <<=则下列选项中,一定正确的是( )A .1230x x x ++>B .6425s t ⋅=C .45t s = D .14425s t +=【答案】CD 【分析】设()f x ()f x 为偶函数,从而有1230x x x ++=,因此方程()=f x s必有一解为0,代入得s =,分0x t ≤≤和x t >两种情况得出函数()f x 的单调性和最值,从而求得s t ,,可得选项. 【详解】设()f x ()f x 为偶函数,所以1230x x x ++=,所以()=f x s ,其中必有一解为0,则()0 f s s ==∴=,①当0x t ≤≤时,()f x ≤当且仅当0x =时取等号;②当x t >时,()f x =(),t +∞上递增, ()f x s ==,54454x t x t t x t x t =-++=⇒=⇒=,又()f x 在(),t +∞上递增,35 4x t ∴=,即3564516=,42545x s t t s t =====, 6454144, 2516525t s t s ∴=⨯=+=. 故选:CD. 【点睛】本题考查函数与方程的综合知识,关键构造合适的函数,判断函数的奇偶性,单调性,最值,属于较难题.5.设[]x 表示不超过x 的最大整数,如:[]1.21=,[]1.22-=-,[]y x =又称为取整函数,在现实生活中有着广泛的应用,诸如停车收费,出租车收费等均按“取整函数”进行计费,以下关于“取整函数”的描述,正确的是( ) A .x R ∀∈,[][]22x x =B .,x y R ∀∈,若[][]x y =,则1x y ->-C .x R ∀∈,[][]122x x x ⎡⎤++=⎢⎥⎣⎦D .不等式[][]2230x x --≥的解集为{|0x x <或}2x ≥【答案】BCD 【分析】通过反例可得A 错误,根据取整函数的定义可证明BC 成立,求出不等式2230t t --≥的解后可得不等式[][]2230x x --≥的解集,从而可判断D 正确与否. 【详解】对于A , 1.5x =-,则[][][]()233,2224x x =-=⨯--==-,故[][]22x x ≠,故A 不成立.对于B ,[][]x y m ==,则1,1m x m m y m ≤<+≤<+, 故1m y m --<-≤-,所以1x y ->-,故B 成立. 对于C ,设x m r =+,其中[),0,1m Z r ∈∈, 则[]11222x x m r ⎡⎤⎡⎤++=++⎢⎥⎢⎥⎣⎦⎣⎦,[][]222x m r =+, 若102r ≤<,则102r ⎡⎤+=⎢⎥⎣⎦,[]20r =,故[][]122x x x ⎡⎤++=⎢⎥⎣⎦;若112r <<,则112r ⎡⎤+=⎢⎥⎣⎦,[]21r =,故[][]122x x x ⎡⎤++=⎢⎥⎣⎦,故C 成立. 对于D ,由不等式[][]2230x x --≥可得[]1x ≤-或[]32x ≥, 故0x <或2x ≥,故D 正确. 故选:BCD 【点睛】本题考查在新定义背景下恒等式的证明与不等式的解法,注意把等式的证明归结为整数部分和小数部分的关系,本题属于较难题.6.对于具有相同定义域D 的函数()f x 和()g x ,若存在函数()h x kx b =+(k ,b 为常数),对任给的正数m ,存在相应的0x D ∈,使得当x D ∈且0x x >时,总有()()()()00f x h x mh x g x m⎧<-<⎪⎨<-<⎪⎩,则称直线:l y kx b =+为曲线()y f x =与()y g x =的“分渐近线”.给出定义域均为{}|1D x x =>的四组函数,其中曲线()y f x =与()y g x =存在“分渐近线”的是( )A .()2f x x =,()g x =B .()102xf x -=+,()23x g x x-=C .()21x f x x+=,()ln 1ln x x g x x +=D .()221x f x x =+,()()21xg x x e -=--【答案】BD 【分析】根据分渐近线的定义,对四组函数逐一分析,由此确定存在“分渐近线”的函数. 【详解】解:()f x 和()g x 存在分渐近线的充要条件是x →∞时,()()0,()()f x g x f x g x -→>.对于①,()2f x x =,()g x =当1x >时,令()()()2F x f x g x x =-=,由于()20F x x '=->,所以()h x 为增函数,不符合x →∞时,()()0f x g x -→,所以不存在分渐近线; 对于②,()1022xf x -=+>,()232,(1)x g x x x-=<> ()()f x g x ∴>,2313()()10210xx x f x g x x x--⎛⎫-=+-=+ ⎪⎝⎭,因为当1x >且x →∞时,()()0f x g x -→,所以存在分渐近线;对于③,21()x f x x+=,ln 1()ln x x g x x +=,21111111()()ln ln ln x x nx f x g x x x x x x x x x++-=-=+--=-当1x >且x →∞时,1x 与1ln x 均单调递减,但1x的递减速度比1ln x 快,所以当x →∞时,()()f x g x -会越来越小,不会趋近于0,所以不存在分渐近线;对于④,22()1x f x x =+,()()21xg x x e -=--,当x →∞时,22()()220+1222+1x x x f x g x x e x x e--=-+++=→,且()()0f x g x ->,因此存在分渐近线.故存在分渐近线的是BD .故选:BD . 【点睛】本小题主要考查新定义概念的理解和运用,考查函数的单调性,属于难题.7.已知()f x 是定义域为(,)-∞+∞的奇函数,()1f x +是偶函数,且当(]0,1x ∈时,()()2f x x x =--,则( )A .()f x 是周期为2的函数B .()()201920201f f +=-C .()f x 的值域为[-1,1]D .()f x 的图象与曲线cos y x =在()0,2π上有4个交点 【答案】BCD 【分析】对于A ,由()f x 为R 上的奇函数,()1f x +为偶函数,得()()4f x f x =-,则()f x 是周期为4的周期函数,可判断A ;对于B ,由()f x 是周期为4的周期函数,则()()202000f f ==,()()()2019111f f f =-=-=-,可判断B .对于C ,当(]01x ∈,时,()()2f x x x =--,有()01f x ≤<,又由()f x 为R 上的奇函数,则[)10x ∈-,时,()10f x -≤<,可判断C . 对于D ,构造函数()()cos g x f x x =-,利用导数法求出单调区间,结合零点存在性定理,即可判断D . 【详解】 根据题意,对于A ,()f x 为R 上的奇函数,()1f x +为偶函数,所以()f x 图象关于1x =对称,(2)()()f x f x f x +=-=- 即(4)(2)()f x f x f x +=-+= 则()f x 是周期为4的周期函数,A 错误; 对于B ,()f x 定义域为R 的奇函数,则()00f =,()f x 是周期为4的周期函数,则()()202000f f ==;当(]0,1x ∈时,()()2f x x x =--,则()()11121f =-⨯-=,则()()()()201912020111f f f f =-+=-=-=-, 则()()201920201f f +=-;故B 正确.对于C ,当(]01x ∈,时,()()2f x x x =--,此时有()01f x ≤<,又由()f x 为R 上的奇函数,则[)10x ∈-,时,()10f x -≤<, (0)0f =,函数关于1x =对称,所以函数()f x 的值域[11]-,.故C 正确. 对于D ,(0)0f =,且(]0,1x ∈时,()()2f x x x =--,[0,1],()(2)x f x x x ∴∈=--,[1,2],2[0,1],()(2)(2)x x f x f x x x ∴∈-∈=-=--, [0,2],()(2)x f x x x ∴∈=--,()f x 是奇函数,[2,0],()(2)x f x x x ∴∈-=+, ()f x 的周期为4,[2,4],()(2)(4)x f x x x ∴∈=--,[4,6],()(4)(6)x f x x x ∴∈=---, [6,2],()(6)(8)x f x x x π∴∈=--,设()()cos g x f x x =-,当2[0,2],()2cos x g x x x x ∈=-+-,()22sin g x x x '=-++,设()(),()2cos 0h x g x h x x =''=-+<在[0,2]恒成立,()h x 在[0,2]单调递减,即()g x '在[0,2]单调递减,且(1)sin10,(2)2sin20g g '=>'=-+<, 存在00(1,2),()0x g x ∈'=,0(0,),()0,()x x g x g x ∈'>单调递增, 0(,2),()0,()x x g x g x ∈'<单调递减,0(0)1,(1)1cos10,()(1)0,(2)cos20g g g x g g =-=->>>=->,所以()g x 在0(0,)x 有唯一零点,在0(,2)x 没有零点, 即2(]0,x ∈,()f x 的图象与曲线cos y x =有1个交点,当[]24x ∈,时,,()()2cos 6+8cos x x g x f x x x =-=--, 则()26+sin g x x x '=-,()()26+sin x x h x g x ='=-,则()2+cos >0h x x '=,所以()g x '在[]24,上单调递增, 且()()3sin3>0,22+sin20g g '='=-<,所以存在唯一的[][]12324x ∈⊂,,,使得()0g x '=, 所以()12,x x ∈,()0g x '<,()g x 在()12,x 单调递减,()14x x ∈,,()>0g x ',()g x 在()14x ,单调递增,又()31cos30g =--<,所以()1(3)0g x g <<,又()()2cos2>0,4cos4>0g g =-=-,所以()g x 在()12,x 上有一个唯一的零点,在()14x ,上有唯一的零点, 所以当[]24x ∈,时,()f x 的图象与曲线cos y x =有2个交点,, 当[]46x ∈,时,同[0,2]x ∈,()f x 的图象与曲线cos y x =有1个交点, 当[6,2],()(6)(8)0,cos 0x f x x x y x π∈=--<=>,()f x 的图象与曲线cos y x =没有交点,所以()f x 的图象与曲线cos y x =在()0,2π上有4个交点,故D 正确; 故选:BCD . 【点睛】本题考查抽象函数的奇偶性、周期性、两函数图像的交点,属于较难题.8.下列命题正确的是( )A .已知幂函数21()(1)m f x m x --=+在(0,)+∞上单调递减则0m =或2m =-B .函数2()(24)3f x x m x m =-++的有两个零点,一个大于0,一个小于0的一个充分不必要条件是1m <-.C .已知函数31()sin ln 1x f x x x x +⎛⎫=++⎪-⎝⎭,若(21)0f a ->,则a 的取值范围为1,2⎛⎫+∞ ⎪⎝⎭D .已知函数()f x 满足()()2f x f x -+=,1()x g x x+=,且()f x 与()g x 的图像的交点为()()()112288,,,,x y x y x y 则128128x x x y y y ++⋯++++⋯+的值为8【答案】BD 【分析】根据幂函数的性质,可判定A 不正确;根据二次函数的性质和充分条件、必要条件的判定,可得判定B 是正确;根据函数的定义域,可判定C 不正确;根据函数的对称性,可判定D 正确,即可求解. 【详解】对于A 中,幂函数21()(1)m f x m x--=+,可得11m +=±,解得0m =或2m =-,当0m =时,函数1()f x x -=在(0,)+∞上单调递减;当2m =-时,函数()f x x =在(0,)+∞上单调递增,所以A 不正确;对于B 中,若函数2()(24)3f x x m x m =-++的有两个零点,且一个大于0,一个小于0,则满足(0)30f m =<,解得0m <,所以1m <-是函数2()(24)3f x x m x m =-++的有两个零点,且一个大于0,一个小于0的充分不必要条件,所以B 是正确; 对于C 中,由函数31()sin ln()1x f x x x x +=++-,则满足101xx+>-,解得11x -<<, 即函数()f x 的定义域为(1,1)-,所以不等式(21)0f a ->中至少满足1211a -<-<, 即至少满足01a <<,所以C 不正确;对于D 中,函数()f x 满足()()2f x f x -+=,可得函数()y f x =的图象关于(0,1)点对称, 又由11()x x g x x x-+--==-,可得()()2g x g x -+=,所以函数()y g x =的图象关于(0,1)点对称,则1281280428x x x y y y ++⋯++++⋯+⨯+==,所以D 正确.故选:BD. 【点睛】本题主要考查了以函数的基本性质为背景的命题的真假判定,其中解答中熟记函数的基本性质,逐项判定是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.9.设函数cos2cos2()22x x f x -=-,则( ) A .()f x 在0,2π⎛⎫⎪⎝⎭单调递增B .()f x 的值域为33,22⎡⎤-⎢⎥⎣⎦C .()f x 的一个周期为πD .4f x π⎛⎫+ ⎪⎝⎭的图像关于点,04π⎛⎫ ⎪⎝⎭对称【答案】BC 【分析】根据余弦函数及指数函数的单调性,分析复合函数的单调区间及值域,根据周期定义检验所给周期,利用函数的对称性判断对称中心即可求解. 【详解】令cos2t x =,则12222ttt t y -=-=-,显然函数12222t t tty -=-=-为增函数, 当0,2x π⎛⎫∈ ⎪⎝⎭时,cos2t x =为减函数, 根据复合函数单调性可知,()f x 在0,2π⎛⎫⎪⎝⎭单调递减, 因为cos2[1,1]t x =∈-, 所以增函数12222ttt t y -=-=-在cos2[1,1]t x =∈-时,3322y -≤≤, 即()f x 的值域为33,22⎡⎤-⎢⎥⎣⎦;因为cos2()cos2(cos2c )os222)(2()2x x x x x x f f πππ+-+-=-=+-=, 所以()f x 的一个周期为π,因为sin 2sin 2224x x f x π-⎛⎫+=- ⎪⎝⎭,令sin 2sin 22(2)xx h x --=, 设(,)P x y 为sin 2sin 22(2)xx h x --=上任意一点,则(,)2P x y π'--为(,)P x y 关于,04π⎛⎫⎪⎝⎭对称的点, 而sin 2(sin 2())22sin 2sin 2()22222x x x x h y x y πππ-----=-==≠--,知点(,)2P x y π'--不在函数图象上,故()h x 的图象不关于点,04π⎛⎫⎪⎝⎭对称,即4f x π⎛⎫+ ⎪⎝⎭的图像不关于点,04π⎛⎫ ⎪⎝⎭对称.故选:BC 【点睛】本题主要考查了余弦函数的性质,指数函数的性质,复合函数的单调性,考查了函数的周期性,值域,对称中心,属于难题.10.已知函数12()123x x x f x x x x ++=+++++,下列关于函数()f x 的结论正确的为( ) A .()f x 在定义域内有三个零点 B .函数()f x 的值域为R C .()f x 在定义域内为周期函数 D .()f x 图象是中心对称图象【答案】ABD 【分析】将函数变形为111()3123f x x x x ⎛⎫=-++⎪+++⎝⎭,求出定义域,结合导数求函数的单调性即可判断BC ,由零点存在定理结合单调性可判断A ,由()()46f x f x --=+可求出函数的对称点,即可判断D. 【详解】解:由题意知,1111()111312311123f x x x x x x x ⎛⎫=-+-+-=-++ ⎪++++++⎝⎭, 定义域为()()()(),33,22,11,-∞-⋃--⋃--⋃-+∞,()()()22211()01213f x x x x '=++>+++,所以函数在()()()(),3,3,2,2,1,1,-∞------+∞定义域上单调递增,C 不正确;当1x >-时,()3371230,004111523f f ⎛⎫-=-++<=+> ⎪⎝⎭,则()1,-+∞上有一个零点, 当()2,1x ∈--时,750,044f f ⎛⎫⎛⎫-<-> ⎪ ⎪⎝⎭⎝⎭,所以在()2,1x ∈--上有一个零点, 当()3,2x ∈--时,1450,052f f ⎛⎫⎛⎫-<-> ⎪ ⎪⎝⎭⎝⎭,所以在()3,2x ∈--上有一个零点, 当3x <-,()0f x >,所以在定义域内函数有三个零点,A 正确; 当0x <,1x +→-时,()f x →-∞,当x →+∞时,()f x →+∞, 又函数在()1,-+∞递增,且在()1,-+∞上有一个零点,则值域为R ,B 正确;()1111(4)363612311123f x f x x x x x x x ⎡⎤⎛⎫⎛⎫--=+++=--++=- ⎪ ⎪⎢⎥++++++⎝⎭⎝⎭⎣⎦, 所以()()46f x f x --=+,所以函数图象关于()2,3-对称,D 正确; 故选:ABD. 【点睛】 结论点睛:1、()y f x =与()y f x =-图象关于x 轴对称;2、()y f x =与()y f x =-图象关于y 轴对称;3、()y f x =与()2y f a x =-图象关于x a =轴对称;4、()y f x =与()2y a f x =-图象关于y a =轴对称;5、()y f x =与()22y b f a x =--图象关于(),a b 轴对称.二、导数及其应用多选题11.已知(0,1)x ∈,则下列正确的是( )A .cos 2x x π+<B .22xx <C .sin 2x >D .1ln 1x x <- 【答案】ABC 【分析】构造函数()sin f x x x =-证明其在0,2π⎛⎫⎪⎝⎭单调递减,即可得sin 22x x ππ⎛⎫-<-⎪⎝⎭即可判断选项A ;作出2yx 和2x y =的函数图象可判断选项B ;作出()sin2xf x =,()h x =的图象可判断选项C ;构造函数()1ln 1x g x x =+-利用导数判断其在()0,1x ∈上的单调性即可判断选项D ,进而可得正确选项.【详解】对于选项A :因为()0,1x ∈,所以022x ππ<-<,令()sin f x x x =-,()cos 10f x x '=-≤,()sin f x x x =-在0,2π⎛⎫⎪⎝⎭单调递减,所以()()00f x f <=,即sin x x <,所以sin 22x x ππ⎛⎫-<- ⎪⎝⎭即cos 2x x π<-,可得cos 2x x π+<,故A 正确, 对于选项B :由图象可得()0,1x ∈,22x x <恒成立,故选项B 正确;对于选项C :要证22sin 24xx x >+ 令()sin 2x f x =,()224xh x x =+()()f x f x -=-,()sin2xf x =是奇函数, ()()h x h x -=,()224x h x x =+是偶函数, 令2224144x t x x ==-++ ,则y t = 因为24y x =+在()0,∞+单调递增,所以2414t x =-+在()0,∞+单调递增,而y t =调递增,由符合函数的单调性可知()224x h x x =+在()0,∞+单调递增, 其函数图象如图所示:由图知当()0,1x ∈时22sin 24xx x >+C 正确; 对于选项D :令()1ln 1x g x x =+-,()01x <<,()221110x g x x x x-'=-=<, 所以()1ln 1x g x x=+-在()0,1单调递减,所以()()1ln1110g x g >=+-=, 即1ln 10x x+->,可得1ln 1x x >-,故选项D 不正确.故选:ABC 【点睛】思路点睛:证明不等式恒成立(或能成立)一般可对不等式变形,分离参数,根据分离参数后的结果,构造函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构成函数,根据导数的方法,利用分类讨论求函数的最值,即可得出结果.12.已知函数()3sin f x x x ax =+-,则下列结论正确的是( )A .()f x 是奇函数B .当3a =-时,函数()f x 恰有两个零点C .若()f x 为增函数,则1a ≤D .当3a =时,函数()f x 恰有两个极值点【答案】ACD 【分析】利用函数奇偶性的定义可判断A 选项的正误;利用导数分析函数()f x 的单调性,可判断B 选项的正误;利用导数与函数单调性的关系可判断C 选项的正误;利用导数以及零点存在定理可判断D 选项的正误. 【详解】对于A 选项,函数()3sin f x x x ax =+-的定义域为R ,()()()()33sin sin f x x x ax x x ax f x -=-+-+=--+=-,函数()f x 为奇函数,A 选项正确;对于B 选项,当3a =-时,()3sin 3f x x x x =++,则()2cos 330f x x x '=++>,所以,函数()f x 在R 上为增函数,又()00f =,所以,函数()f x 有且只有一个零点,B 选项错误;对于C 选项,()2cos 3f x x x a '=+-,由于函数()f x 为增函数,则()0f x '≥对任意的x ∈R 恒成立,即23cos a x x ≤+. 令()23cos g x x x =+,则()6sin g x x x '=-,则()6cos 0g x x ''=->,所以,函数()g x '在R 上为增函数,当0x <时,()()00g x g ''<=,此时,函数()g x 为减函数; 当0x >时,()()00g x g ''>=,此时,函数()g x 为增函数. 所以,()()min 01g x g ==,1a ∴≤,C 选项正确;对于D 选项,当3a =时,()3sin 3f x x x x =+-,则()2cos 33f x x x '=+-.由B 选项可知,函数()f x '在(),0-∞上单调递减,在()0,∞+上单调递增,()()11cos10f f ''-==>,()020f '=-<,由零点存在定理可知,函数()f x '在()1,0-和()0,1上都存在一个零点, 因此,当3a =时,函数()f x 有两个极值点,D 选项正确. 故选:ACD. 【点睛】结论点睛:利用函数的单调性求参数,可按照以下原则进行:(1)函数()f x 在区间D 上单调递增()0f x '⇔≥在区间D 上恒成立; (2)函数()f x 在区间D 上单调递减()0f x '⇔≤在区间D 上恒成立; (3)函数()f x 在区间D 上不单调()f x '⇔在区间D 上存在极值点;(4)函数()f x 在区间D 上存在单调递增区间x D ⇔∃∈,使得()0f x '>成立; (5)函数()f x 在区间D 上存在单调递减区间x D ⇔∃∈,使得()0f x '<成立.13.对于函数2ln ()xf x x=,下列说法正确的有( )A .()f x 在x =12eB .()f x 有两个不同的零点C .(2)f f f <<D .若21()f x k x>-在(0,)+∞上有解,则2e k <【答案】ACD 【分析】利用导数求出函数的单调区间,进一步求出函数的极值可判断A ;利用函数的单调性和函数值的范围判断B ;利用函数的单调性比较出函数值的大小关系判断C ;利用不等式有解问题的应用判断D . 【详解】函数2ln ()x f x x =,所以2431ln 212ln ()(0)x x xx x f x x x x⨯-⨯-'==>, 令()0f x '=,即2ln 1x =,解得x =当0x <<()0f x '>,故()f x在上为单调递增函数.当x >()0f x '<,故()f x在)+∞上为单调递减函数.所以()f x在x =12f e=,故A 正确;当0x <<()0f x '>,()f x在上为单调递增函数,因为()10f =,所以函数()f x在上有唯一零点,当x ≥2ln ()0xf x x=>恒成立,即函数()f x在)+∞上没有零点, 综上,()f x 有唯一零点,故B 错误.由于当x >()0f x '<,()f x在)+∞上为单调递减函数,因为2>>>(2)f f f <<,故C 正确;由于21()f x k x >-在(0,)+∞上有解,故221ln 1()x k f x x x +<+=有解,所以2ln 1()max x k x +<,设2ln 1()x g x x +=,则32ln 1()x g x x --'=,令()0g x '=,解得x =当x >()0f x '<,故()f x在)+∞上为单调递减函数.当0x <<时,()0f x '>,故()f x在上为单调递增函数.所以()22max e eg x g e ==-=. 故2ek <,故D 正确.故选:ACD . 【点睛】方法点睛:本题通过对多个命题真假的判断,综合考查导数的应用,这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.14.设函数cos 2()2sin cos xf x x x=+,则( )A .()()f x f x π=+B .()f x 的最大值为12C .()f x 在,04π⎛⎫- ⎪⎝⎭单调递增 D .()f x 在0,4π⎛⎫⎪⎝⎭单调递减 【答案】AD 【分析】先证明()f x 为周期函数,周期为π,从而A 正确,再利用辅助角公式可判断B 的正误,结合导数的符号可判断C D 的正误. 【详解】()f x 的定义域为R ,且cos 2()2sin cos xf x x x=+,()()()()cos 22cos 2()2sin cos 2sin cos x xf x f x x x x xππππ++===++++,故A 正确.又2cos 22cos 2()42sin cos 4sin 2x x f x x x x ==++,令2cos 24sin 2xy x=+,则()42cos 2sin 22y x y x x ϕ=-=+,其中cos ϕϕ==1≤即2415y ≤,故y ≤≤当y =时,有1cos 4ϕϕ==,此时()cos 21x ϕ+=即2x k ϕπ=-,故max 15y =,故B 错误. ()()()()()22222sin 24sin 22cos 2414sin 2()4sin 24sin 2x x x x f x x x ⎡⎤-+--+⎣⎦'==++,当0,4x π⎛⎫∈ ⎪⎝⎭时,()0f x '<,故()f x 在0,4π⎛⎫⎪⎝⎭为减函数,故D 正确. 当,04x π⎛⎫∈- ⎪⎝⎭时,1sin20x -<<,故314sin 21x -<+<, 因为2t x =为增函数且2,02x π⎛⎫∈- ⎪⎝⎭,而14sin y t =+在,02π⎛⎫- ⎪⎝⎭为增函数,所以()14sin 2h x x =+在,04π⎛⎫- ⎪⎝⎭上为增函数, 故14sin 20x +=在,04π⎛⎫-⎪⎝⎭有唯一解0x , 故当()0,0x x ∈时,()0h x >即()0f x '<,故()f x 在()0,0x 为减函数,故C 不正确. 故选:AD 【点睛】方法点睛:与三角函数有关的复杂函数的研究,一般先研究其奇偶性和周期性,而单调性的研究需看函数解析式的形式,比如正弦型函数或余弦型函数可利用整体法来研究,而分式形式则可利用导数来研究,注意辅助角公式在求最值中的应用.15.设函数()ln f x x x =,()212g x x =,给定下列命题,其中正确的是( ) A .若方程()f x k =有两个不同的实数根,则1,0k e⎛⎫∈- ⎪⎝⎭; B .若方程()2kf x x =恰好只有一个实数根,则0k <;C .若120x x >>,总有()()()()1212m g x g x f x f x ->-⎡⎤⎣⎦恒成立,则m 1≥;D .若函数()()()2F x f x ag x =-有两个极值点,则实数10,2a ⎛⎫∈ ⎪⎝⎭. 【答案】ACD 【分析】利用导数研究函数的单调性和极值,且将题意转化为()y f x =与y k =有两个不同的交点,即可判断A 选项;易知1x =不是该方程的根,当1x ≠时,将条件等价于y k =和ln xy x=只有一个交点,利用导数研究函数的单调性和极值,从而可推出结果,即可判断B 选项;当120x x >>时,将条件等价于1122()()()()mg x f x mg x f x ->-恒成立,即函数()()y mg x f x =-在(0,)+∞上为增函数,通过构造新函数以及利用导数求出单调区间,即可求出m 的范围,即可判断C 选项;2()ln (0)F x x x ax x =->有两个不同极值点,根据导数的符号列出不等式并求解,即可判断D 选项. 【详解】解:对于A ,()f x 的定义域(0,)+∞,()ln 1f x x '=+, 令()0f x '>,有ln 1x >-,即1x e>, 可知()f x 在1(0,)e 单调递减,在1+e∞(,)单调递增,所以极小值等于最小值, min 11()()f x f e e∴==-,且当0x →时()0f x →,又(1)0f =,从而要使得方程()f x k =有两个不同的实根,即()y f x =与y k =有两个不同的交点,所以1(,0)k e∈-,故A 正确; 对于B ,易知1x =不是该方程的根,当1x ≠时,()0f x ≠,方程2()kf x x =有且只有一个实数根,等价于y k =和ln xy x=只有一个交点, 2ln 1(ln )-'=x y x ,又0x >且1x ≠, 令0y '>,即ln 1x >,有x e >, 知ln xy x=在0,1()和1e (,)单减,在+e ∞(,)上单增, 1x =是一条渐近线,极小值为e ,由ln xy x=大致图像可知0k <或=k e ,故B 错误;对于C ,当120x x >>时,[]1212()()()()m g x g x f x f x ->-恒成立, 等价于1122()()()()mg x f x mg x f x ->-恒成立, 即函数()()y mg x f x =-在(0,)+∞上为增函数, 即()()ln 10y mg x f x mx x =-''--'=≥恒成立,即ln 1+≥x m x在(0,)+∞上恒成立, 令ln 1()x r x x +=,则2ln ()xr x x-'=, 令()0r x '>得ln 0x <,有01x <<,从而()r x 在(0,1)上单调递增,在(1,)+∞上单调递减, 则max ()(1)1r x r ==,于是m 1≥,故C 正确;对于D ,2()ln (0)F x x x ax x =->有两个不同极值点, 等价于()ln 120F x x ax +-'==有两个不同的正根, 即方程ln 12x a x+=有两个不同的正根,由C 可知,021a <<,即102a <<,则D 正确. 故选:ACD.【点睛】关键点点睛:本题考查导数的应用,利用导数研究函数的单调性和极值,以及利用导数解决函数的零点问题和恒成立问题从而求参数范围,解题的关键在于将零点问题转化成两个函数的交点问题,解题时注意利用数形结合,考查转化思想和运算能力.16.已知函数()32f x x ax x c =+-+(x ∈R ),则下列结论正确的是( ).A .函数()f x 一定存在极大值和极小值B .若函数()f x 在1()x -∞,、2()x ,+∞上是增函数,则2123x x -≥ C .函数()f x 的图像是中心对称图形D .函数()f x 的图像在点00())(x f x ,(0x R ∈)处的切线与()f x 的图像必有两个不同的公共点 【答案】ABC 【分析】首先求函数的导数2()3210f x x ax =+-=',再根据极值点与导数的关系,判断AB 选项;证明()()2()333a a af x f x f -++--=-,判断选项C ;令0a c ==,求切线与()f x 的交点个数,判断D 选项.【详解】A 选项,2()3210f x x ax =+-='的24120a ∆=+>恒成立,故()0f x '=必有两个不等实根,不妨设为1x 、2x ,且12x x <,令()0f x '>,得1x x <或2x x >,令()0f x '<,得12x x x <<,∴函数()f x 在12()x x ,上单调递减,在1()x -∞,和2()x ,+∞上单调递增, ∴当1x x =时,函数()f x 取得极大值,当2x x =时,函数()f x 取得极小值,A 对, B 选项,令2()3210f x x ax =+-=',则1223ax x +=-,1213x x ⋅=-,易知12x x <,∴213x x -==≥,B对, C 选项,易知两极值点的中点坐标为(())33a a f --,,又23()(1)()333a a a f x x x f -+=-+++-,∴()()2()333a a af x f x f -++--=-, ∴函数()f x 的图像关于点(())33aa f --,成中心对称,C 对,D 选项,令0a c ==得3()f x x x =-,()f x 在(0)0,处切线方程为y x =-, 且3y xy x x =-⎧⎨=-⎩有唯一实数解, 即()f x 在(0)0,处切线与()f x 图像有唯一公共点,D 错, 故选:ABC . 【点睛】方法点睛:解决函数极值、最值综合问题的策略:1、求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小;2、求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论;3、函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.17.对于定义域为R 的函数()f x ,()'f x 为()f x 的导函数,若同时满足:①()00f =;②当x ∈R 且0x ≠时,都有()0xf x '>;③当120x x <<且12x x =时,都有()()12f x f x <,则称()f x 为“偏对称函数”.下列函数是“偏对称函数”的是( )A .21()xx f x ee x =--B .2()1xf x e x =+- C .31,0(),0x e x f x x x ⎧-≥=⎨-<⎩D .42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩【答案】ACD 【分析】结合“偏对称函数”的性质,利用导数的方法,分别讨论四个函数是否满足三个条件,即可得到所求结论. 【详解】条件①()00f =;由选项可得:001(0)00f e e =--=,02(0)010f e =+-=,03(0)10f e =-=,4()ln(10)0f x =-=,即ABCD 都符合;条件②0()0()0x xf x f x >⎧'>⇔⎨'>⎩,或0()0x f x <⎧⎨'<⎩; 即条件②等价于函数()f x 在区间(,0)-∞上单调递减,在区间(0,)+∞上单调递增;对于21()xx f x ee x =--,则()()21()11212x x x xf x e e e e =-+-=-',由0x >可得,()()120(1)1x xf x e e '-=+>,即函数1()f x 单调递增;由0x <可得,()()120(1)1xxf x ee '-=+<,即函数1()f x 单调递减;满足条件②;对于2()1xf x e x =+-,则2()10x f x e =+>'显然恒成立,所以2()1xf x e x =+-在定义域上单调递增,不满足条件②;对于31,0(),0x e x f x x x ⎧-≥=⎨-<⎩,当0x <时,3()f x x =-显然单调递减;当0x ≥时,3()1x f x e =-显然单调递增;满足条件②;对于42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩,当0x ≤时,4()ln(1)f x x =-显然单调递减;当0x >时,4()2f x x =显然单调递增,满足条件②; 因此ACD 满足条件②;条件③当120x x <<且12x x =时,12x x -=,都有()()12f x f x <,即()()()()21220f x f x f x f x -=-->,对于21()xx f x ee x =--,()()212122211211x x x x f x f x e e e e x x -=-+--+()()()()22222222222222x x x x x x x x x e e e e e e e x e ----=----=-+-,因为222x x e e -+≥=,当且仅当22x x e e -=,即20x =时,等号成立, 又20x >,所以222x x e e -+>, 则()()()()2222122211222xx x x f x f x e ee e xx ----=--->令()xxg x e ex -=--,0x >,所以()1110x x e e g x -'=+->=>在0x >上显然恒成立, 因此()xxg x e ex -=--在0x >上单调递增,所以()()00g x g >=,即()()()222121120xx f x f x e ex -->-->,所以()()1211f x f x >满足条件③;对于31,0(),0x e x f x x x ⎧-≥=⎨-<⎩,()()2232311211x xf x f x e x x e -=--=-+,令()1xh x e x =--,0x >,则()10xh x e '=->在0x >上显然恒成立,所以()()00h x h >=,则()()23231210xf x f x e x --=>-,即()()3231f x f x >满足条件③;对于42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩,()()()()212122442ln 12ln 1f x f x x x x x -=--=-+, 令()()2ln 1u x x x =-+,0x >, 则()1221101u x x'=->-=>+在0x >上显然恒成立,所以()()00u x u >=, 则()()()1422422ln 10f x f x x x -=-+>,即()()1442f x f x >满足条件③; 综上,ACD 选项是“偏对称函数”, 故选:ACD. 【点睛】 思路点睛:求解此类函数新定义问题时,需要结合函数新定义的概念及性质,结合函数基本性质,利用导数的方法,通过研究函数单调性,值域等,逐项判断,即可求解.(有时也需要构造新的函数,进行求解.)18.已知函数()()2214sin 2x xe xf x e -=+,则下列说法正确的是( ) A .函数()y f x =是偶函数,且在(),-∞+∞上不单调 B .函数()y f x '=是奇函数,且在(),-∞+∞上不单调递增 C .函数()y f x =在π,02⎛⎫-⎪⎝⎭上单调递增 D .对任意m ∈R ,都有()()f m f m =,且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解:对A ,()()222114sin =2cos 2x x xx e x e f x x e e-+=+-,定义域为R ,关于原点对称,()2211=2cos()2cos()()x x x xe ef x x x f x e e--++---=-=, ()y f x ∴=是偶函数,其图像关于y 轴对称,()f x ∴在(),-∞+∞上不单调,故A 正确;对B ,1()2sin xxf x e x e '=-+, 11()2sin()=(2sin )()x xx x f x e x e x f x e e--''-=-+---+=-, ()f x '∴是奇函数,令1()2sin xx g x e x e=-+, 则1()+2cos 2+2cos 0x x g x e x x e'=+≥≥, ()f x '∴在(),-∞+∞上单调递增,故B 错误;对C ,1()2sin x x f x e x e'=-+,且()'f x 在(),-∞+∞上单调递增, 又(0)0f '=,π,02x ⎛⎫∴∈- ⎪⎝⎭时,()0f x '<,()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减,故C 错误;对D ,()y f x =是偶函数,且在(0,)+∞上单调递增,()()f m f m ∴=,且()(0)0f m f ≥=,故D 正确.故选:AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面: (1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域; (2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.19.已知()2sin x f x x x π=--.( )A .()f x 的零点个数为4B .()f x 的极值点个数为3C .x 轴为曲线()y f x =的切线D .若()12()f x f x =,则12x x π+=【答案】BC 【分析】首先根据()0f x '=得到21cos xx π-=,分别画出21xy π=-和cos y x =的图像,从而得到函数的单调性和极值,再依次判断选项即可得到答案. 【详解】()21cos xf x x π'=--,令()0f x '=,得到21cos xx π-=.分别画出21xy π=-和cos y x =的图像,如图所示:由图知:21cos xx π-=有三个解,即()0f x '=有三个解,分别为0,2π,π. 所以(),0x ∈-∞,()21cos 0xf x x π'=-->,()f x 为增函数,0,2x π⎛⎫∈ ⎪⎝⎭,()21cos 0x f x x π'=--<,()f x 为减函数,,2x ππ⎛⎫∈ ⎪⎝⎭,()21cos 0x f x x π'=-->,()f x 为增函数,(),x π∈+∞,()21cos 0xf x x π'=--<,()f x 为减函数.所以当0x =时,()f x 取得极大值为0,当2x π=时,()f x 取得极小值为14π-,当x π=时,()f x 取得极大值为0,所以函数()f x 有两个零点,三个极值点,A 错误,B 正确.因为函数()f x 的极大值为0,所以x 轴为曲线()y f x =的切线,故C 正确. 因为()f x 在(),0-∞为增函数,0,2π⎛⎫⎪⎝⎭为减函数, 所以存在1x ,2x 满足1202x x π<<<,且()()12f x f x =,显然122x x π+<,故D 错误.故选:BC 【点睛】本题主要考查导数的综合应用,考查利用导数研究函数的零点,极值点和切线,属于难题.20.已知实数a ,b ,c ,d 满足2111a a e cb d --==-,其中e 是自然对数的底数,则()()22a cb d -+-的值可能是( )A .7B .8C .9D .10【答案】BCD 【分析】由题中所给的等式,分别构造函数()2xf x x e =-和()2g x x =-+,则()()22a cb d -+-的表示()y f x =上一点(),M a b 与()y g x =上一点(),Ncd 的距离的平方,利用导数的几何意义可知当()01f x '=-时,切点到直线的距离最小,再比较选项.【详解】由212a a a e b a e b-=⇒=-,令()2x f x x e =-,()12x f x e '∴=-由1121cd c d -=⇒=-+-,令()2g x x =-+ 则()()22a cb d -+-的表示()y f x =上一点(),M a b 与()y g x =上一点(),Ncd 的距离的平方,设()y f x =上与()y g x =平行的切线的切点为()000,M x y 由()0001210xf x e x '=-=-⇒=,∴切点为()00,2M -所以切点为()00,2M -到()y g x =的距离的平方为28=的距离为(),M a b 与(),N c d 的距离的平方的最小值.故选:BCD. 【点睛】本题考查构造函数,利用导数的几何意义求两点间距离的最小值,重点考查转化思想,构造函数,利用几何意义求最值,属于偏难题型.三、三角函数与解三角形多选题21.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且2a =,sin 2sin B C =,有以下四个命题中正确的是( )A .满足条件的ABC 不可能是直角三角形B .ABC 面积的最大值为43C .当A =2C 时,ABC 的周长为2+D .当A =2C 时,若O 为ABC 的内心,则AOB 的面积为13【答案】BCD 【分析】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考中的多选题(历年真题改编)一、集合与常用逻辑用语1.(2017新课标Ⅰ改编)下面四个命题中,是真命题为( )A.若复数z 满足1z∈R ,则z ∈R ; B.若复数z 满足2z ∈R ,则z ∈R ;C.若复数1z ,2z 满足12z z ∈R ,则12z z =;D.若复数z ∈R ,则z ∈R .答案AD 【解析】设i z a b =+(,a b ∈R ),则2211i (i)a b z a b a b-==∈++R ,得0b =,所以z ∈R ,A 正确;2222(i)2i z a b a b ab =+=-+∈R ,则0ab =,即0a =或0b =,不能确定z ∈R ,B 不正确;若z ∈R ,则0b =,此时i z a b a =-=∈R ,D 正确.2.(2014湖南改编)已知命题p :若x y >,则x y -<-;命题q :若x y >,则22x y >.则下列命题为真命题的是A . B. C. D.答案BC 【解析】由不等式的性质可知,命题p 是真命题,命题q 为假命题,故A:为假命题,B:为真命题,C:q ⌝为真命题,则为真命题,D:p ⌝为假命题,则为假命题,所以选C .3.(2013四川改编)设n P P P ,,,⋯⋯21为平面a 内的n 个点,在平面a 内的所有点中,若点P 到点n P P P ,,,⋯⋯21的距离之和最小,则称点P 为点12n P P P ⋅⋅⋅,,,的一个“中位点”,例如,线段AB 上的任意点都是端点A ,B 的中位点,则下列命题为真命题的是A.若三个点A ,B ,C 共线,C 在线段AB 上,则C 是A ,B ,C 的中位点;B.直角三角形斜边的中点是该直角三角形三个顶点的中位点;C.若四个点A ,B ,C ,D 共线,则它们的中位点存在且唯一;D.梯形对角线的交点是该梯形四个顶点的唯一中位点;答案AD 【解析】由“中位点”可知,若C 在线段AB 上,则线段AB 上任一点都为“中位点”,p q ∧p q ∨()p q ∧⌝()p q ⌝∨p q ∧p q ∨()p q ∧⌝()p q ⌝∨C 也不例外,故A 正确;对于B 假设在等腰Rt △ABC 中,∠ACB =90°,如图所示,点P 为斜边AB 中点,设腰长为2,则|P A |+|PB |+|PC |=32|AB |=C 为“中位点”,则|CB |+|CA |=4<B 错;对于C ,若B ,C 三等分AD ,若设|AB |=|BC |=|CD |=1,则|BA |+|BC |+|BD |=4=|CA |+|CB |+|CD |,故C 错;对于D ,在梯形ABCD 中,对角线AC 与BD 的交点为O ,在梯形ABCD 内任取不同于点O 的一点M ,则在△MAC 中,|MA |+|MC |>|AC |=|OA |+|OC |,同理在△MBD 中,|MB |+|MD |>|BD |=|OB |+|OD |,则得,|MA |+|MB |+|MC |+|MD |>|OA |+|OB |+|OC |+|OD |,故O 为梯形内唯一中位点是正确的.二、函数的概念和性质4.(2019全国Ⅰ理1改编)关于函数,则下列结论正确的是A.f (x )是偶函数B.f (x )在区间(,)单调递增C.f (x )在有4个零点D.f (x )的最大值为2答案AD【解析】,则函数是偶函数,故A 正确.当时,, 则为减函数,故B 错误. ()sin |||sin |f x x x =+2ππ[,]-ππ()sin sin |i |sin s n f x x x x x f x -=-+-=+=()()()f x π,π2x ⎛⎫∈ ⎪⎝⎭sin sin sin sin x x x x ==,sin sin 2sin f x x x x =+=()当,, 由得,得或, 由是偶函数,得在上还有一个零点,即函数在上有3个零点,故C 错误.当时,取得最大值2,故D 正确, 故正确的结论是AD .5.(2017山东改编)若函数e ()x f x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是()A.()2x f x -=B.()3x f x -=C.3()f x x =D.2()2f x x =+答案AD【解析】A:()2()2x x x x e e f x e -=⋅=在R 上单调递增,故()2x f x -=具有M 性质; B:()3()3x x x x e e f x e -=⋅=在R 上单调递减,故()3x f x -=不具有M 性质; C:3()x x e f x e x =⋅,令3()x g x e x =⋅,则322()3(2)x x x g x e x e x x e x '=⋅+⋅=+, ∴当2x >-时,()0g x '>,当2x <-时,()0g x '<,∴3()x x e f x e x =⋅在(),2-∞-上单调递减,在()2,-+∞上单调递增,故()3f x x =不具有M 性质; D:2()(2)x x e f x e x =+,令()()22x g x e x =+,则22()(2)2[(1)1]0x x x g x e x e x e x '=++⋅=++>, ∴2()(2)x x e f x e x =+在R 上单调递增,故2()2f x x =+具有M 性质.6.(2011福建改编)设V 是全体平面向量构成的集合,若映射:f V R →满足:对任意向量11(,)x y a =∈V ,22(,)x y b =∈V ,以及任意λ∈R ,均有((1))()(1)(),f f f λλλλ+-=+-a b a b 则称映射f 具有性质P .下列映射中,具有性质P 的映射的是0πx ≤≤sin sin sin sin 2sin f x x x x x x =+=+=()0f x =()2sin 0x =0x =πx =()f x [π0-,)πx =-()f x []ππ-,sin 1sin 1x x ==,()f xA.12:,(),(,);f V R f m x y m x y V →=-=∈B.222:,(),(,);f V R f m x y m x y V →=+=∈C.33:,()1,(,).f V R f m x y m x y V →=++=∈D.233:,(),(,).f V R f m x y m x y V →=+=∈答案AC【解析】∵11(,)x y a =,22(,)x y b =,R λ∈,所以1212(1)((1),(1))x x y y λλλλλλ+-=+-+-a b对于A,具有性质P 的映射,同理可验证C 符合,BD 不符合7.(2010福建改编)已知定义域为0+∞(,)的函数()f x 满足:①对任意0x ∈+∞(,),恒有(2)=2()f x f x 成立;当(1,2]x ∈时,()=2f x x -.下列结论正确的是()A.对任意Z m ∈,有(2)=0m fB.函数()f x 的值域为[0+∞,)C.存在Z n ∈,使得(2+1)=9n fD.“函数()f x 在区间(,)a b 上单调递减”的充要条件是“存在Z k ∈,使得1(,)(2,2)k k a b +⊆”答案ABD【解析】A:,正确; B:取,则;,从而 ,其中,,从而,正确;C:,假设存在使,∵121[2,2)n n n ++∈,∴1(21)22121n n n n f ++=--=-,∴219,210n n +==,1111212(),((1))((1),(1))f m x y f a b f x x y y λλλλλλ=-+-=+-+-12121122(1)(1)()(1)()x x y y x y x y λλλλλλ=+----=-+--()(1)()f a f b λλ=+-0)2(2)2(2)22()2(111====⋅=---f f f f m m m m ]2,2(1+∈m m x ]2,1(2∈m x m m x x f 22)2(-=x x f x f x f m m m -====+12)2(2)2(2)( ,2,1,0=m ),0[)(+∞∈x f 122)12(1--=++n m n f n 9)12(=+n f这与n Z ∈矛盾,所以该命题错误;D 根据前面的分析容易知道该选项正确.三、函数的综合应用8.(2017山东改编)若函数e ()x f x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是().A.()2x f x -=B.2()f x x =C.()3x f x -=D.()cos f x x =答案AD【解析】A:()2()2x x x x e e f x e -=⋅=在R 上单调递增,故()2x f x -=具有M 性质; B:()3()3x x x x e e f x e -=⋅=在R 上单调递减,故()3x f x -=不具有M 性质; C:3()x x e f x e x =⋅,令3()x g x e x =⋅,则322()3(2)x x x g x e x e x x e x '=⋅+⋅=+, ∴当2x >-时,()0g x '>,当2x <-时,()0g x '<,∴3()x x e f x e x =⋅在(),2-∞-上单调递减,在()2,-+∞上单调递增,故()3f x x =不具有M 性质; D:2()(2)x x e f x e x =+,令()()22x g x e x =+,则22()(2)2[(1)1]0x x x g x e x e x e x '=++⋅=++>, ∴2()(2)x x e f x e x =+在R 上单调递增,故2()2f x x =+具有M 性质.9.(2014四川改编)以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数()x ϕ组成的集合:对于函数()x ϕ,存在一个正数M ,使得函数()x ϕ的值域包含于区间[,]M M -.例如,当31()x x ϕ=,2()sin x x ϕ=时,1()x A ϕ∈,2()x B ϕ∈.下列命题是真命题的是()A.设函数()f x 的定义域为D ,则“()f x A ∈”的充要条件是“b R ∀∈,a D ∃∈,()f a b =”;B.函数()f x B ∈的充要条件是()f x 有最大值和最小值;C.若函数()f x ,()g x 的定义域相同,且()f x A ∈,()g x B ∈,则()()f x g x B +∉;D.若函数2()ln(2)1x f x a x x =+++(2x >-,a R ∈)有最大值,则()f x B ∈.ACD 【解析】对于A ,根据题中定义,()A f x ∈⇔函数()y f x =,x D ∈的值域为R ,由函数值域的概念知,函数()y f x =,x D ∈的值域为,R b R a D ⇔∀∈∃∈()f a b =,所以A 正确;对于B ,例如函数||1()()2x f x =的值域(0,1]包含于区间[1,1]-,所以()f x B ∈,但()f x 有最大值l ,没有最小值,所以B 错误;对于C ,若()()f x g x B +∈,则存在一个正数1M ,使得函数()()f x g x B +∈的值域包含于区间11[,]M M -,所以1M -≤()f x 1()g x M +≤,由()g x B ∈知,存在一个正数2M ,使得函数()g x 的值域包含于区间22[,]M M -,所以22()M g x M -≤≤,亦有 22()M g x M -≤-≤,两式相加得12()M M -+≤()f x ≤12M M +,于是()f x B ∈,与已知“()f x A ∈”矛盾,故()()f x g x B +∉,即C 正确;对于D ,如果0a >, 那么,()x f x →+∞→+∞,如果0a <,那么2,()x f x →-→+∞,所以()f x 有最大值,必须0a =,此时2()1x f x x =+在区间(2,)-+∞上,有11()22f x -≤≤, 所以()f x B ∈,即D 正确.四、导数与微积分10.(2014安徽改编)若直线l 与曲线C 满足下列两个条件: )(i 直线l 在点()00,y x P 处与曲线C 相切;)(ii 曲线C 在P 附近位于直线l 的两侧,则称直线l 在点P 处“切过”曲线C .下列命题正确的是()A.直线0:=y l 在点()0,0P 处“切过”曲线C :3y x =B.直线1:-=x l 在点()0,1-P 处“切过”曲线C :2)1(+=x yC.直线x y l =:在点()0,0P 处“切过”曲线C :x y sin =D.直线x y l =:在点()0,0P 处“切过”曲线C :x y tan =答案ACD【解析】对于A ,203,|0x y x y =''==,所以:0l y =是曲线3:C y x =在点()0,0P 处的切线,画图可知曲线3:C y x =在点()0,0P 附近位于直线l 的两侧,A 正确;对于B ,因为12(1),|0x y x y =-''=+=,所以:1l x =-不是曲线C :2)1(+=x y 在点()0,1-P 处的切线,B 错误;对于C ,0cos ,|1x y x y =''==,在点()0,0P 处的切线为x y l =:,画图可知曲线C :x y sin =在点()0,0P 附近位于直线l 的两侧,C 正确;对于D ,21cos y x '=,021|1cos 0x y ='==,在点()0,0P 处的切线为x y l =:,画图可知曲线C :x y tan =在点()0,0P 附近位于直线l 的两侧,D 正确.11.(2015安徽改编)设30x ax b ++=,其中,a b 均为实数,下列条件中,使得该三次方程仅有一个实根的是()A.3,3a b =-=-B.3,2a b =-=C.3,2a b =->D.0,2a b ==;答案ACD【解析】令,当时,, 则在R 上单调递增函数,此时仅有一个实根,所以D 对;当时,由得,所以是的极小值点. 由,得,即,C 对.是的极大值点,由,得,即,A 对. 12.(2015四川)已知函数x x f 2)(=,ax x x g +=2)((其中R a ∈).对于不相等的实数21,x x ,设2121)()(x x x f x f m --=,2121)()(x x x g x g n --=,下列命题中是真命题的是() A.对于任意不相等的实数21,x x ,都有0>m ;B.对于任意的a 及任意不相等的实数21,x x ,都有0>n ;C.对于任意的a ,存在不相等的实数21,x x ,使得n m =;D.对于任意的a ,存在不相等的实数21,x x ,使得n m -=.答案AD【解析】A.设,函数单调递增,所有,, 32(),()3f x x ax b f x x a '=++=+0a ≥()0f x '≥()f x 30x ax b ++=3a =-2()330f x x '=-<11x -<<1x =()f x (1)0f >31310b -⋅+>2b >1x =-()f x (1)0f -<3(1)3(1)0b --⋅-+<2b <-12x >x 2x 122>2x x120x x则=>0,所以正确; B.设>,则,则 ,可令=1,=2,,则,所以错误;C.因为,由B 得:,分母乘到右边, 右边即为,所以原等式即为=,即为=,令,则原题意转化为对于任意的,函数存在不相等的实数, 使得函数值相等,,则,则,令,且,可得为极小值. 若,则,即,单调递增,不满足题意, 所以错误.D.由C 得=,则, 设,有,使其函数值相等,则不恒为单调.,,恒成立, 单调递增且,.所以先减后增,满足题意,所以正确.五、三角函数与解三角形13.(2014新课标Ⅰ)在下列函数中,最小正周期为π的函数是()A.|2|cos x y =B.|cos |x y =C.)62cos(π+=x y D.)42tan(π-=x y 答案ABC【解析】A:|2|cos x y =,最小正周期为π;B:|cos |x y =,最小正周期为π;C:m =1212()()f x f x x x --121222x x x x 1x 2x 120x x ->1212()()g x g x n x x 22121212()x x a x x x x 12121212()()x x x x a x x a x x 1x 2x 4a =-10n =-<m n 2121)()(x x x f x f --12x x a =++12()()g x g x -12()()f x f x -12()()g x g x -12()()f x g x -12()()f x g x ()()()h x f x g x =-a ()()()h x f x g x =-1x 2x 2()2x h x x ax =--()2ln 22x h x x a '=--()2(ln 2)2xh x ''=-0()0h x ''=012x <<0()h x '10000a =-0()0h x '>0()0h x '>()h x 12()()f x f x -12()()g x g x -1122()()()()f x g x g x f x +=+()()()h x f x g x =+1x 2x ()h x 2()2x h x x ax =++()2ln 22x h x x a '=++()2()2ln 220x h x ''=+>()h x '()0h '-∞<()0h '+∞>()h x)62cos(π+=x y ,最小正周期为π;D:)42tan(π-=x y ,最小正周期为2π.最小正周期为π的函数为ABC .14.(2019全国Ⅲ理改编)设函数=sin ()(>0),已知在有且仅有5个零点,下述结论正确的是()A.在()有且仅有3个极大值点B.在()有且仅有2个极小值点C.在()单调递增D.的取值范围是[) 答案CD【解析】当时,, 因为在有且仅有5个零点,所以, 所以,故AB 错,D 正确, 当时,,若在单调递增,则,即,因为,故C 正确. 15.(2011安徽改编)设()f x =sin 2cos2a x b x +,其中,a b ∈R ,0ab ≠,若()()6f x f π≤对一切则x ∈R 恒成立,则以下结论正确的是().A.11()012f π= B.7()10f π<()5f π C.()f x 既不是奇函数也不是偶函数D.()f x 的单调递增区间是2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦答案AC ()f x 5x ωπ+ω()f x []0,2π()f x 0,2π()f x 0,2π()f x 0,10πω1229510,[0,2]x ∈π,2555x ωωπππ⎡⎤+∈π+⎢⎥⎣⎦()f x [0,2]π5265ωπππ+<π1229510ω<(0,)10x π∈(2),5510x ωωππ+π⎡⎤+∈⎢⎥⎣⎦()f x 0,10π⎛⎫ ⎪⎝⎭(2)102ω+ππ<3ω<1229510ω<【解析】()sin 2cos2)f x a x b x x ϕ=++(其中tan b a ϕ=),因此对一切x R ∈,()|()|6f x f π≤恒成立,所以sin()13πϕ+=±, 可得()6k k Z πϕπ=+∈,故())6f x x π=+.而1111())012126f πππ=⨯+=,所以A 正确;74717|()||||123030f πππ==,17|()||530f ππ=, 所以7|()||()|105f f ππ=,故B 错;C 明显正确;D 错误. 16.(2012安徽改编)设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是.A.若2ab c >;则3C π<B.若2a b c +>;则3C π<C.若333a b c +=;则2C π<D.若()2a b c ab +<;则2C π>答案ABC 【解析】A.222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< B.2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< C.当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾 D.取2,1a b c ===满足()2a b c ab +<得:2C π<六、平面向量 17.(2013广东改编)设a 是已知的平面向量且0≠a ,关于向量a 的分解,若向量b ,c 和a 在同一平面内且两两不共线,下列命题中的则真命题的是()A.给定向量b ,总存在向量c ,使=+a b c ;B.给定向量b 和c ,总存在实数和,使λμ=+a b c ;C.给定单位向量b 和正数,总存在单位向量c 和实数,使λμ=+a b c ;D.给定正数和,总存在单位向量b 和单位向量c ,使λμ=+a b c ;答案AB【解析】利用向量加法的三角形法则,易的A 是对的;利用平面向量的基本定理,易的B λμμλλμ是对的;以的终点作长度为的圆,这个圆必须和向量有交点,这个不一定能满足,C 是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须,所以D 是假命题.七、不等式18.(2014新课标Ⅰ改编)不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .下面四个命题中,是真命题是()A.(,),22x y D x y ∀∈+≥-B.(,),22x y D x y ∃∈+≥,C.(,),23x y D x y ∀∈+≤D.(,),21x y D x y ∃∈+≤-.答案AB【解析】画出可行域如图中阴影部分所示,由图可知,当目标函数2z x y =+经过可行域内的点A (2,-1)时,取得最小值0,故20x y +≥,因此12,p p 是真命题.19.(2010安徽改编)若0,0,2a b a b >>+=,则下列不等式对一切满足条件的,a b 恒成立的是().A.1ab ≤≤C.222a b +≥D.112a b+≥ 答案ACD【解析】令1a b ==,排除B;由21a b ab =+≥⇒≤,命题A 正确;222()2422a b a b ab ab +=+-=-≥, 命题C 正确;1122a b a b ab ab++==≥,命题D 正确. 八、立体几何 a μλb =+λμλμ+≥b c a20.(2016年全国II 改编),αβ是两个平面,m ,n 是两条线,下面四个命题中,是真命题是()A.如果m n ⊥,m α⊥,n β∥,那么αβ⊥.B.如果m α⊥,n α∥,那么m n ⊥.C.如果a β∥,m α⊂,那么m β∥.D.如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等.答案BCD【解析】对于命题A ,可运用长方体举反例证明其错误:如图,不妨设AA '为直线m ,CD 为直线n ,ABCD 所在的平面为α.ABC D ''所在的平面为β,显然这些直线和平面满足题目条件,但αβ⊥不成立.命题B 正确,证明如下:设过直线n 的某平面与平面α相交于直线l ,则l n ∥, 由m α⊥,有m l ⊥,从知m n ⊥结论正确.由平面与平面平行的定义知命题C 正确.由平行的传递性及线面角的定义知命题D 正确.21.(2017新课标Ⅲ改编)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,下列结论正确的是()A.当直线AB 与a 成60°角时,AB 与b 成30°角;B.当直线AB 与a 成60°角时,AB 与b 成60°角;C.直线AB 与a 所成角的最小值为45°;D.直线AB 与a 所成角的最小值为60°;答案BC【解析】如图BDEF 为底面圆的内接正方形,设AC=BC=1, 则2AB AD AE AF FB FE ED BD ========,即侧面均为等边三角形,∵AC ⊥底面BDEF ,假设a FB ∥,由题意b BD ∥,当直线AB 与a 成60°角时,由图可知AB 与b 成60°角,所以A 错,B 正确;假设a EB ∥,可知C 正确,D 错.FED C B A。
