RC电路充电时间计算
RC电路充放电时间计算

RC电路充放电时间计算V0 为电容上的初始电压值;V1 为电容最终可充到或放到的电压值;Vt 为t时刻电容上的电压值。
则,Vt="V0"+(V1-V0)* [1-exp(-t/RC)]或,t = RC*Ln[(V1-V0)/(V1-Vt)]求充电到90%VCC的时间。
(V0=0,V1=VCC,Vt=0.9VCC)代入上式: 0.9VCC=0+VCC*[[1-exp(-t/RC)]既 [[1-exp(-t/RC)]=0.9;exp(-t/RC)=0.1- t/RC=ln(0.1)t/RC=ln(10)??? ln10约等于2.3也就是t=2.3RC。
带入R=10k?? C=10uf得。
t=2.3*10k*10uf=230msRC回路充放电时间的推导过程需要用高等数学,简单的方法只要记住RC回路的时间常数τ=R×C,在充电时,每过一个τ的时间,电容器上电压就上升(1-1/e)约等于0.632倍的电源电压与电容器电压之差;放电时相反。
如C=10μF,R=10k,则τ=10e-6×10e3=0.1s 在初始状态Uc=0时,接通电源,则过0.1s(1τ)时,电容器上电压Uc为0+(1-0)×0.632=0.632倍电源电压U,到0.2s(2τ)时,Uc为0.632+(1-0.632)×0.632=0.865倍U……以此类推,直到t=∞时,Uc=U。
放电时同样运用,只是初始状态不同,初始状态Uc=U。
单片机复位(上电复位和按键复位,复位脉宽10ms,R常取值10k~47k,c 取值10~100uf,电容大些为好):原理:如果复位是高电平复位,加电后电容充电电流逐渐减少,此时经电阻接地的单片机IO是没电压的,因为电容是隔直流的,直到充电完毕开始放电,放电的过程同样是电流逐渐减少的,开始放电时电流很大,加到电阻上后提供给IO高电平,一段时间(电容器的充放电参数:建立时间等)后,电流变弱到0,但是复位引脚已经有了超过3us的高电平,所以复位就完成了;手动复位,如加按键,则是直接将电容短路,给复位引脚送高电平,此部分就只有电容在起作用;当然电源较大(一般3.3v-5v)的话,加电阻是为了分压,防止烧坏引脚。
RC电路充放电时间的计算(含计算公式)
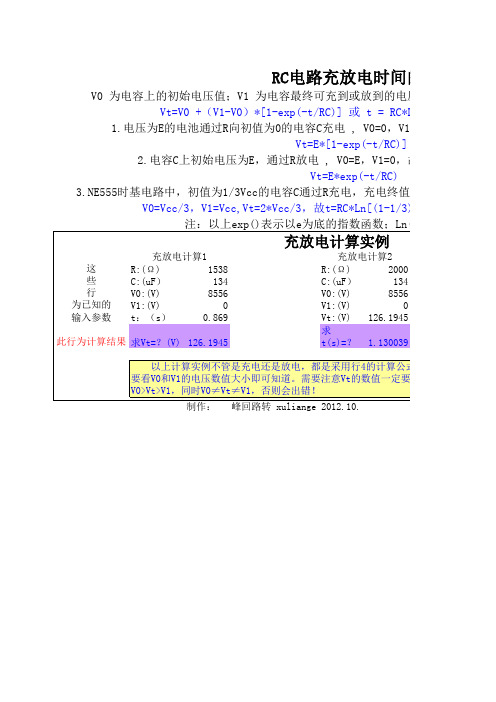
V0 为电容上的初始电压值;V1 为电容最终可充到或放到的电压值;Vt 为t时刻 Vt=V0 +(V1-V0)*[1-exp(-t/RC)] 或 t = RC*Ln[(V1 - V0)/(V1 1.电压为E的电池通过R向初值为0的电容C充电 , V0=0,V1=E,故充到t时刻 Vt=E*[1-exp(-t/RC)] 2.电容C上初始电压为E,通过R放电 , V0=E,V1=0,故放到t时刻电容上 Vt=E*exp(-t/RC) 3.NE555时基电路中,初值为1/3Vcc的电容C通过R充电,充电终值为Vcc,问充到2/ V0=Vcc/3,V1=Vcc,Vt=2*Vcc/3,故t=RC*Ln[(1-1/3)/(1-2/3)]=RC*Ln 注:以上exp()表示以e为底的指数函数;Ln()是e为底的对数函
充放电计算实例
这 些 行 为已知的 输入参数 此行为计算结果 充放电计算1 R:(Ω ) 1538 C:(uF) 134 V0:(V) 8556 V1:(V) 0 t:(s) 0.869 求Vt=?(V) 126.1945 充放电计算2 R:(Ω ) 2000 C:(uF) 134 V0:(V) 8556 V1:(V) 0 Vt:(V) 126.1945 求t(s)=? 1.130039
以上计算实例不管是充电还是放电,都是采用行4的计算公式,至于是计算的是 要看V0和V1的电压数值大小即可知道。需要注意Vt的数值一定要介于V0和V1之间方可 V0>Vt>V1,同时V0≠Vt≠V1,否则会出错! 制作: 峰回路转 xuliange 2012.10.
电时间的计算
放到的电压值;Vt 为t时刻电容上的电压值。则: t = RC*Ln[(V1 - V0)/(V1 - Vt)] V0=0,V1=E,故充到t时刻电容上的电压为: (-t/RC)] ,V1=0,故放到t时刻电容上的电压为: -t/RC) 充电终值为Vcc,问充到2/3Vcc需要的时间是多少? n[(1-1/3)/(1-2/3)]=RC*Ln2 =0.693RC 函数;Ln()是e为底的对数函数
电容rc充电时间计算方法

电容rc充电时间计算方法
宝子,今天咱们来唠唠电容RC充电时间的计算方法哈。
电容充电这个事儿呢,就像是给一个小瓶子注水一样,只不过这里面有电阻在捣乱,让充电速度变慢啦。
那这个充电时间是咋算的呢?这里面有个公式哦。
这个公式就是T = RC,这里的T就是充电时间常数啦,R是电阻的大小,单位是欧姆,C呢就是电容的大小,单位是法拉。
不过要注意哦,这个公式算出来的时间常数T,可不是说电容完全充满电的时间哈。
电容充电是一个逐渐的过程,它的电压是按照指数规律上升的。
如果想要知道电容充电到某个电压值大概需要多久,那就得用到更复杂一点的公式啦。
但是呢,在工程应用或者简单估算的时候,这个T = RC就很有用啦。
比如说,你有一个100欧姆的电阻和0.1法拉的电容,那这个充电时间常数T就等于100乘以0.1,也就是10秒啦。
这意味着啥呢?这就表示电容充电的速度大概是这么个情况,每过10秒,它的充电状态就有一个比较明显的变化哦。
宝子,你可能会想,为啥是这么个公式呢?其实啊,电阻就像一个小关卡,它限制着电流的大小,电流小了,电容充电就慢啦。
电容就像一个小仓库,越大的电容能装的“电”就越多,所以电阻和电容一起就决定了充电的快慢啦。
你要是在做一些小电路实验,或者自己捣鼓一些电子小玩意儿,这个电容充电时间的计算可就很重要喽。
要是算错了,可能你的小电路就不能按照你想要的方式工作啦。
比如说你做个小闪光灯电路,电容充电时间没算对,那闪光灯闪的频率可能就乱套了呢。
所以啊,这个小知识虽然看起来有点小复杂,但掌握了还是很有用滴。
。
rc电路电容充放电时间的计算(含计算公式)

rc电路电容充放电时间的计算(含计算公式)英文版RC Circuit Capacitor Charging and Discharging Time Calculation (Including Calculation Formulas)In an RC circuit, the capacitor's charging and discharging process is governed by the interaction between the resistance (R) and capacitance (C) elements. Understanding how to calculate the charging and discharging times of a capacitor in an RC circuit is crucial for analyzing and designing electronic circuits.Charging Time Calculation:When a capacitor is being charged in an RC circuit, the time taken for it to reach a particular voltage level is known as the charging time. This time can be calculated using the formula: (t_{charge} = RC \ln\left(\frac{V_{final}}{V_{initial}}\right))where:(t_{charge}) is the charging time.(R) is the resistance in the circuit.(C) is the capacitance in the circuit.(V_{final}) is the final voltage across the capacitor.(V_{initial}) is the initial voltage across the capacitor (usually 0 for a completely discharged capacitor).The natural logarithm ((\ln)) is used in this formula to account for the exponential nature of capacitor charging.Discharging Time Calculation:Similarly, when a capacitor is being discharged in an RC circuit, the time taken for it to reach a particular voltage level is known as the discharging time. This time can be calculated using the formula:(t_{discharge} = RC \ln\left(\frac{V_{initial}}{V_{final}}\right)) where:(t_{discharge}) is the discharging time.(R) and (C) have the same meanings as in the charging formula.(V_{initial}) is the initial voltage across the capacitor.(V_{final}) is the final voltage across the capacitor (usually 0 for a completely discharged capacitor).Again, the natural logarithm is used in the discharging time calculation.Conclusion:Understanding the charging and discharging time calculation formulas for capacitors in RC circuits is essential for effective circuit analysis and design. These formulas provide a quantitative understanding of how the resistance and capacitance values in an RC circuit affect the rate at which a capacitor charges or discharges. By manipulating these values, engineers can fine-tune the behavior of electronic circuits to meet specific design requirements.中文版RC电路电容充放电时间的计算(含计算公式)在RC电路中,电容器的充放电过程是由电阻(R)和电容(C)元件之间的相互作用所决定的。
RC电容充放电时间计算

当t= 4RC时,电容电压=0.98E;
当t= 5RC时,电容电压=0.99E;
可见,经过3~5个RC后,充电过程基本结束ቤተ መጻሕፍቲ ባይዱ
放电时间计算:
初始电压为E的电容C通过R放电
V0=E,Vu=0,故电容器放电,任意时刻t,电容上的电压为:
Vt=E*exp(-t/RC)
t=RCLn[E/Vt]
以上exp()表示以e为底的指数;Ln()是e为底的对数。
电容充电放电时间计算公式:
设,V0 为电容上的初始电压值;
Vu 为电容充满终止电压值;
Vt 为任意时刻t,电容上的电压值。
则,
Vt=V0+(Vu-V0)* [1-exp(-t/RC)]
如果,电压为E的电池通过电阻R向初值为0的电容C充电
V0=0,充电极限Vu=E,
故,任意时刻t,电容上的电压为:
Vt=E*[1-exp(-t/RC)]
t=RCLn[E/(E-Vt)]
如果已知某时刻电容上的电压Vt,根据常数可以计算出时间t。
公式涵义:
完全充满,Vt接近E,时间无穷大;
当t= RC时,电容电压=0.63E;
当t= 2RC时,电容电压=0.86E;
电容恒流充电时间计算

电容恒流充电时间计算电容恒流充电时间是指在恒定电流条件下,将一个电容器充电至特定电压所需要的时间。
电容恒流充电时间的计算公式为t=RC,其中t表示充电时间,R表示电阻值,C表示电容值。
在实际应用中,电容恒流充电时间的计算是非常重要的,尤其在电子工程和电气工程领域。
下面将详细介绍电容恒流充电时间的计算方法以及相关的应用。
一、电容恒流充电时间的计算方法为了计算电容恒流充电时间,首先需要知道电容器的电容值和电阻值。
电容器的电容值可以通过产品标识或测量得到,电阻值可以通过测量或电路设计得到。
1. 根据电容值和电阻值计算RC的值,即RC=电容值×电阻值。
2. 将RC的值代入公式t=RC,即可得到电容恒流充电时间t的值。
需要注意的是,电容恒流充电时间的单位通常为秒(s),所以在计算时需要将电容值和电阻值转换为国际单位制。
二、电容恒流充电时间的应用电容恒流充电时间的应用非常广泛,特别是在电子电路设计和电气设备中。
以下是一些常见的应用场景:1. 电子电路设计中的电容充电时间计算:在设计电子电路时,需要考虑电容充电时间,以确保电路正常工作。
通过计算电容恒流充电时间,可以确定电路中电容器的充电速度和充电时间,从而保证电路的稳定性和可靠性。
2. 电池充电时间计算:在充电设备中,需要根据电池容量和充电电流来计算电池的充电时间。
通过计算电容恒流充电时间,可以确定电池的充电时间,从而确保电池能够充满并正常工作。
3. 电容器充电时间的优化:在一些应用中,需要尽可能缩短电容器的充电时间,以提高系统的响应速度和效率。
通过计算电容恒流充电时间,可以选择合适的电容值和电阻值,以达到最短的充电时间。
4. 电容器放电时间的计算:除了充电时间,电容器的放电时间也是重要的参数。
通过计算电容恒流充电时间,可以得到电容器放电的时间常数,从而确定电容器的放电速度和放电时间。
总结:电容恒流充电时间的计算是电子电路设计和电气工程中的重要内容。
RC电路充放电时间计算

RC电路充放电时间计算RC电路是由电容器C和电阻器R组成的电路,在充电和放电过程中,会出现一些特定的时间计算问题。
本文将详细介绍RC电路充放电时间的计算方法。
首先,我们来看充电过程。
在充电开始时,电容器C还未充满电,电源的电压会通过电阻R逐渐充满电容器C。
充电的时间可以用充电时间常数τ来表示,充电时间常数τ等于电容器C与电阻器R的乘积,即τ=RC。
充电时间常数τ可以表示充电过程的特性,它表示了充电过程充满63.2%电量所需的时间。
通常我们使用电容器充电至充满电量所需的时间作为充电的时间计算参考。
充电过程中,电容器充电到电源电压的约99.3%需要多长时间呢?我们可以使用逃逸指数法来计算。
假设充电电压达到电源电压的99.3%所需的时间为t1,而充电时间常数τ为RC。
那么根据逃逸指数法的定义,99.3%的电源电压是电容器充电到63.2%电量所需要的时间,即t1 = τ * ln(1/(1-0.993))。
通过这个公式,我们可以计算出电容器充电到电源电压的约99.3%所需的时间。
接下来,我们来看放电过程。
放电过程与充电过程类似,只是电容器中的电荷会逐渐流出,电容器的电压也会逐渐降低。
放电的时间也可以用放电时间常数τ来表示,放电时间常数τ仍然等于电容器C与电阻器R的乘积,即τ=RC。
放电时间常数τ可以表示放电过程的特性,它表示了电容器放电到37.0%电量所需的时间。
通常我们使用电容器放电至其初始电压的一半所需的时间作为放电的时间计算参考。
放电过程中,电容器放电到初始电压的一半需要多长时间呢?使用逃逸指数法计算,假设放电时间常数τ为RC,放电电压降到初始电压一半所需的时间为t2、根据逃逸指数法的定义,37.0%的电源电压是电容器放电到初始电压一半所需的时间,即t2 = τ * ln(1/(1-0.5))。
通过这个公式,我们可以计算出电容器放电到初始电压一半所需的时间。
在实际应用中,我们可以根据需要计算充电和放电时间,以确定电容器电压的变化情况。
rc电路计算

计算RC电路的参数涉及电阻(R)和电容(C)。
以下是一些常见的RC电路计算问题和相应的计算公式:
1. RC电路的时间常数(τ)计算:
τ = R * C
2. RC电路的充电时间(t)计算:
t = 5 * τ (充电时间为RC电路达到63.2%的稳定电压所需的时间) 3. RC电路的放电时间(t)计算:
t = 5 * τ (放电时间为RC电路达到36.8%的稳定电压所需的时间) 4. RC电路的充电过程的电压(V)计算:
V = V0 * (1 - e^(-t/τ)) (V0为初始电压,t为充电时间,τ为时间常数) 5. RC电路的放电过程的电压(V)计算:
V = V0 * e^(-t/τ) (V0为初始电压,t为放电时间,τ为时间常数)
这些公式适用于理想的RC电路,其中没有考虑额外的电阻、电感或其他复杂的影响因素。
在实际应用中,可能需要考虑更多的因素来精确计算RC电路的行为。
请注意,以上公式仅提供了一些基本的计算方法,具体应用中可能会有不同的情况和计算要求。
在实际使用中,建议参考相关的电路理论和手册,并结合具体的电路参数和条件进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RC电路充电时间计算
简单RC电路充电时间的计算方法。
时间常数为tao=RC,一般三个tao就能完全充满电
V0 为电容上的初始电压值;
V1 为电容最终可充到或放到的电压值;
Vt 为t时刻电容上的电压值。
则,
Vt="V0"+(V1-V0)* [1-exp(-t/RC)]
或,
t = RC*Ln[(V1-V0)/(V1-Vt)]
求充电到90%VCC的时间。
(V0=0,V1=VCC,Vt=0.9VCC)
代入上式:0.9VCC=0+VCC*[[1-exp(-t/RC)]
既[[1-exp(-t/RC)]=0.9;
exp(-t/RC)=0.1
- t/RC=ln(0.1)
t/RC=ln(10) ln10约等于2.3
也就是t=2.3RC。
带入R=10k C=10uf得。
t=2.3*10k*10uf=230ms
RC回路充放电时间的推导过程需要用高等数学,简单的方法只要记住RC回路的时间常数τ=R×C,在充电时,每过一个τ的时间,
电容器上电压就上升(1-1/e)约等于0.632倍的电源电压与电容器电压之差;放电时相反。
如C=10μF,R=10k,则τ=10e-6×10e3=0.1s 在初始状态Uc=0时,接通电源,则过0.1s(1τ)时,电容器上电压Uc为0+(1-0)×0.63 2=0.632倍电源电压U,到0.2s(2τ)时,Uc为0.632+(1-0.632)×0.632=0.865倍U……以此类推,直到t=∞时,Uc=U。
放电时同样运用,只是初始状态不同,初始状态Uc=U。
单片机复位(上电复位和按键复位,复位脉宽10ms,R常取值10k~47k,c取值10~100uf,电容大些为好):
原理:如果复位是高电平复位,加电后电容充电电流逐渐减少,此时经电阻接地的单片机IO是没电压的,因为电容是隔直流的,直到充电完毕开始放电,放电的过程同样是电流逐渐减少的,开始放电时电流很大,加到电阻上后提供给IO高电平,一段时间(电容器的充放电参数:建立时间等)后,电流变弱到0,但是复位引脚已经有了超过3us的高电平,所以复位就完成了;
手动复位,如加按键,则是直接将电容短路,给复位引脚送高电平,此部分就只有电容在起作用;当然电源较大(一般3.3v-5v)的话,加电阻是为了分压,防止烧坏引脚。
1.放电是一个一阶电路的零输入响应,
SPICE Model
R 1 0 R
C 1 0 C IC=UC
我们有公式:UR-Uc=0,而UR=i*R, i=dUc/dt;
所以,有RC*dUc/dt+Uc=0;从而有初始条件有:Uc=UC*EXP(-t/RC),令τ=1/RC为时间常数,我们得到放电方程为Uc=UC*EXP(-t/τ),
其放电时间一般为3~5τ,理由是5τ时Uc=0.0067UC,已很小。
2. 充电方程类似,可以自己分析吧!。
