公务员考试数字推理基础知识各种特殊数字集(最全)
行测数字推理题各种规律汇总
□等差数列及其变式「例题1」2，5，8，（）A 10B 11C 12D 13「解答」从上题的前3个数字可以看出这是⼀个典型的等差数列，即后⾯的数字与前⾯数字之间的差等于⼀个常数。
题中第⼆个数字为5，第⼀个数字为2，两者的差为3，由观察得知第三个、第⼆个数字也满⾜此规律，那么在此基础上对未知的⼀项进⾏推理，即8+3=11，第四项应该是11，即答案为B.「例题2」3，4，6，9，（），18A 11B 12C 13D 14「解答」答案为C.这道题表⾯看起来没有什么规律，但稍加改变处理，就成为⼀道⾮常容易的题⽬。
顺次将数列的后项与前项相减，得到的差构成等差数列1，2，3，4，5，……。
显然，括号内的数字应填13.在这种题中，虽然相邻两项之差不是⼀个常数，但这些数字之间有着很明显的规律性，可以把它们称为等差数列的变式。
□等⽐数列及其变式「例题3」3，9，27，81（）A 243B 342C 433D 135「解答」答案为A.这也是⼀种最基本的排列⽅式，等⽐数列。
其特点为相邻两个数字之间的商是⼀个常数。
该题中后项与前项相除得数均为3，故括号内的数字应填243.「例题4」8，8，12，24，60，（）A 90B 120C 180D 240「解答」答案为C.该题难度较⼤，可以视为等⽐数列的⼀个变形。
题⽬中相邻两个数字之间后⼀项除以前⼀项得到的商并不是⼀个常数，但它们是按照⼀定规律排列的；1，1.5，2，2.5，3，因此括号内的数字应为60×3=180.这种规律对于没有类似实践经验的应试者往往很难想到。
我们在这⾥作为例题专门加以强调。
该题是1997年中央国家机关录⽤⼤学毕业⽣考试的原题。
「例题5」8，14，26，50，（）A 76B 98C 100D 104「解答」答案为B.这也是⼀道等⽐数列的变式，前后两项不是直接的⽐例关系，⽽是中间绕了⼀个弯，前⼀项的2倍减2之后得到后⼀项。
故括号内的数字应为50×2-2=98.□等差与等⽐混合式「例题6」5，4，10，8，15，16，（），（）A 20，18B 18，32C 20，32D 18，32「解答」此题是⼀道典型的等差、等⽐数列的混合题。
数字推理精华
目录1.数字推理基础知识 (1)2.0,4,16,40,80 ,( )此题引出的新解题思路 (8)3.6道数字推理提供给大家练习 ...................................................... 错误!未定义书签。
4.数字推理50道（系列之一） (9)5.5道图形数字推理题目做做！（解析已经奉上） (21)6.由3，4，5，11，14浅谈如何认识数字推理！ (23)7.典型习题详解 (25)8. 数字推理90道试题大礼包【难度篇】 (26)1.【分享】数字推理基础知识第一部分：数字推理的认识数字推理是公务员考试当中最值得花时间学习的部分，言其理主要是通过认真的学习可以保证不丢分。
在国家公务员考试或者地方公务员考试当中，数字推理一般是5题或10题，其分值大概每题在0.8分左右。
其类型更是千奇百怪，无奇不有。
但通过从2002年～2008年这7年的考试题目分析。
我们最终还是找到一些规律和确定了一些认识。
借此写下这篇文章供大家参考。
数字推理就是给出一组数字，但其中缺少一项，要求考生仔细观察这个数列各数字之间的关系，找出其中的排列规律，然后从4个选项中选出自己认为最合适、合理的一个来填补空缺项，使之符合原数列的排列规律。
在寻找规律的时候，我们必须遵循规律的固有的性质：规律的普遍性和延续性。
在这几年公务员考试的过程当中，数字推理的题型发生了很大的变化，从最初简单的等比，等差，差值的数字特性规律渐渐发展到了复合运算，隔项运算，移动运算，甚至是数字本身拆项运算这样复杂的规律。
但其规律的基本性质还是必须遵循的，一组数列一般需要满足三项已知的规律状态，从而推导出第四项数字规律。
如：8，10，14，20，（） A 24 B 28 C 32 D 36此题是数字之间差值构成等差数列关系。
10－8＝2；14－10＝4；20－14＝6；－20＝8 ？＝28如果我们把题目改变一下：10，14，20，（）A 24 B 28 C 32 D 36是否能够根据14－10＝4；20－14＝6；这2项推导出28－20＝8呢？我想大家都能感觉到这是一种非常牵强的做法。
公务员考试数字推理基础知识各种特殊数字集(最全)
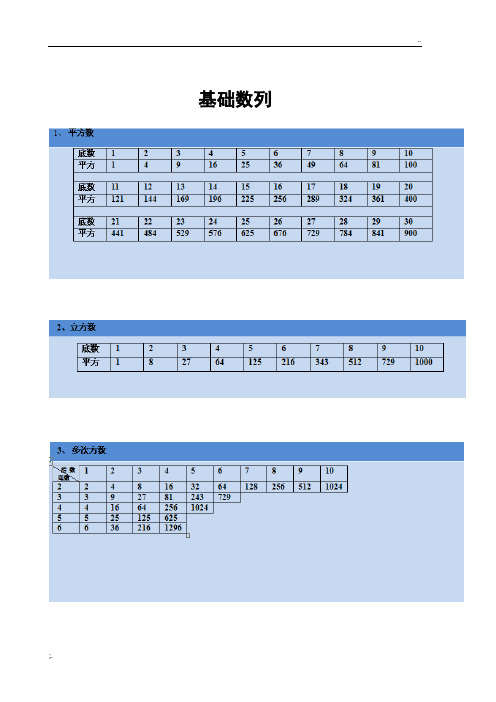
基础数列【例1】质数：2，3，5，7，1l，1 3，17，1 9，23．…【例2】合数：4，6，8，9，10，12，14，15，…【例】1，3，7，1，3，7，…1，7，1，7，l，7，…1，3，7，一1，一3，7，…【例】(1)6，12，19，27，35，( )，48答案：42，首尾相加为54。
(2)3，- l，5，5，11，( )答案：7，首尾相加为10。
等差数列及其变式一、基本等差数列【例】1，4，7，10，l 3，l 6，19，22，25，…【例1】(2007黑龙江，第8题)11，12，15，20，27，( ) A．32 B．34 C．36 D．38【答案】C【解题关键点】【例2】(2002国家，B类，第3题)32，27，23，20，18，( ) A．14 B．15 C．16 D．1 7【答案】D【解题关键点】【例3】(2002国家，B类，第5题)－2，1，7，16，( )，43 A．25 B．28 C．31 D．35【答案】B【解题关键点】【例】3，6，11，( )，27A．15 B．18 C．19 D．24【答案】B【解题关键点】二级等差数列。
（1）相邻两项之差是等比数列【例】0，3，9，21，( )，93A．40 B．45 C. 36 D．38【答案】B【解题关键点】二级等差数列变式（2）相邻两项之差是连续质数【例】11，13，16，21，28，( )A．37 B．39 C.41 D.47【答案】B【解题关键点】二级等差数列变式（3）相邻两项之差是平方数列、立方数列【例】1，2，6，15，（）A．19B．24C．31D．27【答案】C【解题关键点】数列特征明显单调且倍数关系不明显，优先做差。
得到平方数列。
如图所示，因此，选C（4）相邻两项之差是和数列【例】2, 1, 5, 8, 15, 25, ( )A.41B.42C.43D.44【答案】Ｂ【解题关键点】相邻两项之差是和数列（5）相邻两项之差是循环数列【例】1,4,8,13,16,20,( )A. 20B. 25C. 27D. 28【答案】B【解题关键点】该数列相邻两数的差成3，4，5一组循环的规律，所以空缺项应为20+5=25，故选B。
公务员考试数字推理基础知识点和解题方法
第一节数字推理一、基础知识数列A，B，C，D，E，F，（）。
该数列可能存在的规律有：1. B-A=C-B=D-C=E-D=F-E,，则该数列是等差数列。
例：3，5，7，9，112. B/A=C/B=D/C=E/D=F/E，则该数列是等比数列。
例：2，4，8，16，32，643. A，C，E存在某种规律，B，D，F存在某种规律，则该数列称为双重数列。
例：2，3，6，6，10，124. A+B=C，B+C=D，C+D=E，D+E=F，则该数列称为和数列。
例：1，2，3，5，8，135. A+B=C，A+B+C=D，A+B+C+D=E，A+B+C+D+E=F，则该数列称为和数列变式。
例：1，4，5，10，20，406. A×B=C，B×C=D，C×D=E，D×E=F，则该数列称为积数列。
例：1，2，2，4，8，327. A/B=C，B/C=D，C/D=E，D/E=F，则该数列成为商数列。
例：1944，108，18，6，3，28. A，B，C，D，E，F分数变式后，分子分母呈规律变化，则该数列为分数数列。
例：-1，1/2，3/4，5/8，7/169. A，B，C，D，E，F中百位，十位，个位的数字呈规律存在，则该数列称为分段组合数列。
例：124，348，5816，7163210.则该数列为根号数列。
11. A2，B2，C2，D2，E2，F2的结果分别加上或者减去特定的数后呈规律存在，则该数列为平方数列。
例：1，4，9，16，2512. A3，B3，C3，D3，E3，F3的结果分别加上或者减去特定的数后呈规律存在，则该数列为立方数列。
例：1，8，27，64，125，21613. A0，B1，C2，D3，E4，F5的结果分别加上或者减去特定的数后呈规律存在，则该数列为幂次数列。
例：1，2，9，64，62514. A，B，C，D，E，F都是质数，则该数列为质数数列。
15. 数列按照A，B，C，A，B，C这样的周期顺序排列，则该数列为周期数列。
公务员行测指导30种数字推理解题技巧
公务员行测指导：30种数字推理解题技巧一、当一列数中出现几个整数，而只有一两个分数而且是几分之一的时候，这列数往往是负幂次数列。
【例】1、4、3、1、1/5、1/36、（）A.1/92B.1/124C.1/262D.1/343二、当一列数几乎都是分数时，它基本就是分式数列，我们要注意观察分式数列的分子、分母是一直递增、递减或者不变，并以此为依据找到突破口，通过“约分”、“反约分”实现分子、分母的各自成规律。
【例】1/16 2/13 2/5 8/7 4 ( )A 19/3B 8C 39D 32三、当一列数比较长、数字大小比较接近、有时有两个括号时，往往是间隔数列或分组数列。
【例】33、32、34、31、35、30、36、29、（）A. 33B. 37C. 39D. 41四、在数字推理中，当题干和选项都是个位数，且大小变动不稳定时，往往是取尾数列。
取尾数列一般具有相加取尾、相乘取尾两种形式。
【例】6、7、3、0、3、3、6、9、5、（）A.4B.3C.2D.1五、当一列数都是几十、几百或者几千的“清一色”整数，且大小变动不稳定时，往往是与数位有关的数列。
【例】448、516、639、347、178、( )A.163B.134C.785D.896六、幂次数列的本质特征是：底数和指数各自成规律，然后再加减修正系数。
对于幂次数列，考生要建立起足够的幂数敏感性，当数列中出现6？、12？、14？、21？、25？、34？、51？、312？，就优先考虑43、112（53）、122、63、44、73、83、55。
【例】0、9、26、65、124、( )A. 165B. 193C. 217D. 239七、在递推数列中，当数列选项没有明显特征时，考生要注意观察题干数字间的倍数关系，往往是一项推一项的倍数递推。
【例】118、60、32、20、( )A.10B.16C.18D.20八、如果数列的题干和选项都是整数且数字波动不大时，不存在其它明显特征时，优先考虑做差多级数列，其次是倍数递推数列，往往是两项推一项的倍数递推。
国家公务员面试数字推理题725道详解
国家公务员面试-数字推理题725道详解(6) 【501】8，8，12，24，60，( )；；；；分析：选c。
分3组=>(8,8),(12,24),(60,180)，每组后项/前项=>1，2，3等差【502】1，3，7，17，41，（）；；；分析：选B。
第一项+第二项*2=第三项【503】0，1，2，9，( )；；；；分析：选D。
第一项的3次方+1=第二项【504】3，7, 47, 2207，( )分析:答案4870847。
前一个数的平方-2=后一个数【505】2, 7, 16, 39, 94, ( )分析:答案257。
7×2+2=16，16×2+7=39，39×2+16=94，94×2+39=257【506】1944, 108, 18, 6, ( )分析:答案3。
1944/108=18，108/18=6，18/6=3【507】3, 3, 6, ( ), 21, 33, 48分析:答案12。
思路一：差是：0，3，？，？，12，15，差的差是3，所以是6+6=12思路二：3×1=3,3×1=3, 3×2=6, 3×7=21,3×11=33,3×16=48。
1，1，2，4，7，11，16依次相减为0，1，2，3，4，5。
【508】, 3, 7又1/2, 22又1/2，( )分析:答案。
3/2，6/2，15/2，45/2，？/2，倍数是2，，3，。
45×=。
所以是2=【509】1，128, 243, 64, ( )分析:答案5 。
19=1，27=128，35=243，43=64，51=5【510】5，41，149，329，( )分析:答案581。
02+5=5，62+5=41，122+5=149，182+5=329，242+5=581【511】0，1，3，8，21，( )分析:答案55。
数字推理(公务员考试必备
本文由ａｓｋｍｊｎｂｖ贡献 经典数字推理题库 １）平方关系： １１－１２１，１２－１４４ １３－１６９，１４－１９６，１５－２２５，１６－２５６，１７－２８９，１８－３２４，１９－３６１，２０－４００ ２）立方关系： ２－８，３－２７，４－６４，５－１２５，６－２１６，７－３４３，８－５１２，９－７２９，１０－１０００ （１）． ５，６，８，１０，１４，（） Ａ． １２ Ｂ． １４ Ｃ １６ Ｄ １８ ５＝２＋３ ６＝３＋３ ８＝５＋３ １０＝７＋３ １４＝１１＋３ １６＝１３＋３ 连续质数＋３的数列 （２）． －１１，－４，－３，－２，（ ） Ａ．－１， Ｂ．０ Ｃ．３ Ｄ．５ （－２）＾３－３＝－１１ （－１）＾３－３＝－４ ０＾３－３＝－３ １＾３－３＝－２ ２＾３－３＝５ （３）． ７７，６３，２３，１８，４１，３１，（ ） Ａ． －５， Ｂ．６ Ｃ．１２ Ｄ．１８ ７７＋２３＝１００＝１０＾２ ６３＋１８＝８１＝９＾２ ２３＋４１＝６４＝８＾２ １８＋３１＝４９＝７＾２ ４１＋（－５）＝３６＝６＾２ 间隔相加是平方数 （４） １，７，１９，３７，（ ） Ａ． ５７ Ｂ．６１ Ｃ．６６ Ｄ．８０ ７－１＝６ １９－７＝１２ ３７－１９＝１８ ６１－３７＝２４ 等差数列。
或者是 １＾２－０＝１ ３＾２－２＝７ ５＾２－６＝１９ ７＾２－１２＝３７ ９＾２－２０＝６１ ０，２，６，１２，２０ 差为２，４，６，８ （５） ２，６，１０，１８，３２，（ ） Ａ ５７， Ｂ． ５８ Ｃ．６１ Ｄ．６３ ６＋（２＋６）／２＝１０ １０＋（６＋１０）／２＝１８ １８＋（１０＋１８）／２＝３２ ３２＋（１８＋３２）／２＝５７ （６） ２，２，３，５，１４，（ ） Ａ． ５０ Ｂ． ５５ Ｃ．６３ Ｄ．６９ ２×２－１＝３ ２×３－１＝５ ３×５－１＝１４ ５×１４－１＝６９ 两两一组 （７＋３）／（７－３）＝１０／４＝５／２ （６＋５）／（６－５）＝１１／１ （９＋２）／（９－２）＝１１／７ ８＝８／１＝（８＋１）／（８－１）＝９／７ （８） ０，１０，２４，６８，１２０，（ ） Ａ １９６ Ｂ．２１０ Ｃ ２１６ Ｄ ２２２ １＾３－１＝０ ２＾３＋２＝１０ ３＾３－３＝２４ ４＾３＋４＝６８ ５＾３－５＝１２０ ６＾３＋６＝２２２ （９） （９，２，７），（４，３，８），（４９，１２，３１），（０，１７，？） Ａ．３４ Ｂ．５１ Ｃ．４９ Ｄ． ４７ ９开２次方＋２×２＝７ ４开２次方＋３×２＝８ ４９开２次方＋１２×２＝３１ ０开２次方＋１７×２＝３４ （１０） ２１，１７，２２，２１，３１，３７，（ ） Ａ．４８ Ｂ．５３ Ｃ．５６ Ｄ ６１ ２２－２１＝１ ２１－１７＝４ ３１－２２＝９ ３７－２１＝１６ ５６－３１＝２５ （１１） ２，１２，２３，５２，（） Ａ ６１ Ｂ ７４ Ｃ ７６ Ｄ ８２ ２＝０＋２ １＋２＝３ ２＋３＝５ ５＋２＝７ ７＋４＝１１ （１２） １，１，２，６，８，１１，（） Ａ １３ Ｂ １７ Ｃ １８ Ｄ ２０ １＋１＋２＝４ １＋２＋６＝９ ２＋６＋８＝１６ ６＋８＋１１＝２５ ８＋１１＋１７＝３６ （１３） ３，３，９，３３，９３，（） Ａ ２１０ Ｂ ２１３ Ｃ ２１６ Ｄ ２２２ ３－３＝０＝１＾３－１ ９－３＝６＝２＾３－２ ３３－９＝２４＝３＾３－３ ９３－３３＝６０＝４＾３－４ ２１３－９３＝１２０＝５＾３－５ （１４） （７，２８，４），（３，１６，１６），（１０，２０，１０），（２１，？，９） Ａ １０８ Ｂ ６３ Ｃ ４１ Ｄ ２７ （７×４）／１＝２８ （３×１６）／３＝１６ （１０×１０）／５＝２０ （２１×９）／７＝２７ （１５） ４，１１，１７，２０，１５，１，（） Ａ －２４， Ｂ －１６ Ｃ １６ Ｄ ２４ （１１＋１７）－２＊４＝２０ （１７＋２０）－２＊１１＝１５ （２０＋１５）－１７＊２＝１ （１６） ６，９，１５，２１，３３，（ ） Ａ． ５１ Ｂ．４８ Ｃ．４２ Ｄ．３９ ６＝２×３ ９＝３×３ １５＝５×３ ２１＝７×３ ３３＝１１×３ ３９＝１３×３ （１７） ２，３，９，３６，３６０，（ ） Ａ．１３３２０ Ｂ．１３３２２ Ｃ．１２３２０ Ｄ１２３２２ （２＋１）＊３＝９ （３＋１）＊９＝３６ （９＋１）＊３６＝３６０ （３６＋１）＊３６０＝１３３２０ （１８） （１４，１３，３）， （２２，２５，７）， （３６，？，２３） Ａ．５６ Ｂ．６４ Ｃ．６７ Ｄ．７２ １４／２＋３＊２＝１３ ２２／２＋７＊２＝２５ ３６／２＋２３＊２＝６４ （１９） ５，３２，８１，１２８，１２５，（ ） Ａ． ０ Ｂ．２１６ Ｃ．１４４ Ｄ．１８９ ５＝５×１＾３ ３２＝４×２＾３ ８１＝３×３＾３ １２８＝２×４＾３ １２５＝１×５＾３ ０＝０×６＾３ （２０） ０，７，８，６３，２４，（ ） Ａ． ０ Ｂ．２５５ Ｃ．２１５ Ｄ．３２３ １＾２－１＝０ ２＾３－１＝７ ３＊２－１＝８ ４＊３－１＝６３ ５＾２－１＝２４ ６＾３－１＝２１５ （２１）． ２，６，１２，２２，３６，（ ） Ａ．４８ Ｂ．５８ Ｃ．６４ Ｄ．６８ ６－２＝２＊２ １２－６＝２＊３ ２２－１２＝２＊５ ３６－２２＝２＊７ ５８－３６＝２＊１１ （２２）． ４，８，３２，１２８，（ ） Ａ． ２５６ Ｂ．５１２ Ｃ １０２４ Ｄ．２０４８ ２＾２＝４ ２＾３＝８ ２＾５＝３２ ２＾７＝１２８ ２＾１１＝２０４８ （２３）． ７，９，２０，６２，（ ） Ａ． １９４ Ｂ．１９８ Ｃ．１０２ Ｄ．２５０ ７＊１＋２＝９ ９＊２＋２＝２０ ２０＊３＋２＝６２ ６２＊４＋２＝２５０ （２４）． （１２，１３，７），（２３，３１，９），（４３，１２，１０），（３７，１６，？） Ａ．４５ Ｂ．３２ Ｃ．１９ Ｄ．１３ １＊１＋２＊３＝７ ２＊３＋３＊１＝９ ４＊１＋３＊２＝１０ （２５）． ３，１，１２，１６，３０，１００，３９，（ ） Ａ． １７７ Ｂ．１８９ Ｃ．９８ Ｄ．１６９ （３／３）＾２＝１ （１２／３）＾２＝１６ （３０／３）＾２＝１００ （３９／３）＾２＝１６９ （２６） １１，２４，３５，４２，４７，（ ） Ａ．５０ Ｂ．５１ Ｃ．５２ Ｄ．５３ ２４－１１＝１３ ３５－２４＝１１ ４２－３５＝７ ４７－４２＝５ ５０－４７＝３ （２７） １３，７，８，１７，４３，（ ） Ａ． ６７ Ｂ．１１２ Ｃ．８４ Ｄ．１２６ ７×３－１３＝８ ８×３－７＝１７ １７×３－８＝４３ ４３×３－１７＝１１２ （２８） ３，１１／５，１５／７，２，２１／１１，（ ） Ａ．２３／１１ Ｂ．２３／１３ Ｃ．２１／１３ Ｄ．２５／１４ ６／２， １１／５， １５／７， １８／９， ２１／１１， ６－２＝４ １１－５＝６ １５－７＝８ １８－９＝９ ２１－１１＝１０ 选项符合分子－分母是合数序列的 １２ ２３－１１＝１２ 选Ａ （２９） （１２，７，９），（４６，５５，１），（１２，８６，８），（２３，１３，？） Ａ．４ Ｂ．６ Ｃ．８ Ｄ．１０ 看个位数计算 ２＋７＝９ ６＋５＝１１ ２＋６＝８ ３＋３＝６ （３０） ２，６，３０，６０，１３０， （ ） Ａ．１８０ Ｂ．２００ Ｃ．２１０ Ｄ．２４０ １＾３＋１＝２ ２＾３－２＝６ ３＾３＋３＝３０ ４＾３－４＝６０ ５＾３＋５＝１３０ ６＾３－６＝２１０ （３１） ３， ４， ２１， ７５， ２８８，（） Ａ ９００ Ｂ １０８９ Ｃ １０９８ Ｄ １２００ （３＋４）×３＝２１ （４＋２１）×３＝７５ （２１＋７５）×３＝２８８ （７５＋２８８）×３＝１０８９ （３２） ７，５，２，３，－１，（） Ａ．０ Ｂ．２ Ｃ ４ Ｄ －４ Ａ－Ｃ＝Ｂ ７－２＝５ ５－３＝２ ２－（－１）＝３ ３－４＝－１ （３３） （２，３，１３），（３，２，１５），（４，５，？） Ａ．１９ Ｂ．３１ Ｃ ４０ Ｄ ２４ ３＾２＋２＊３＝１５ ４＾２＋５＊３＝３１ （３４） ０，１，２，９，４４，（） Ａ．１２１ Ｂ．１９６ Ｃ．２６５ Ｄ ３００ １＝０×２＋１ ２＝１×３－１ ９＝２×４＋１ ４４＝９×５－１ ２６５＝４４×６＋１ （３５） ５，２，１，２，５，（） Ａ．２ Ｂ．５ Ｃ．８ Ｄ．１０ ２－５＝－３ １－２＝－１ ２－１＝１ ５－２＝３ １０－５＝５ 或者隔项减 １－５＝－４ ２－２＝０ ５－１＝４ １０－２＝８ （３６）、１，３，３，５，４，６，（ ） Ａ．６ Ｂ．７ Ｃ．８ Ｄ．９ １＋３＝４ ３＋３＝６ ３＋５＝８ ５＋４＝９ ４＋６＝１０ ６＋６＝１２ 合数序列 （３７）、－２，－３，０，２７，（ ） Ａ．６４ Ｂ．１２８ Ｃ．１６２ Ｄ．１９２ －２×３＾０＝－２ －１×３＾１＝－３ ０×３＾２＝０ １×３＾３＝２７ ２×３＾４＝１６２ （３８）、０，０，１，５，２３，（ ） Ａ．４６ Ｂ．９７ Ｃ．１０８ Ｄ．１１９ ０！－１＝０ １！－１＝０ ２！－１＝１ ３！－１＝５ ４！－１＝２３ ５！－１＝１１９ ！表示阶乘 （３９） ５９，３３，１８，８，５，（） Ａ．０ Ｂ．１ Ｃ．２ Ｄ．３ ５９－３３＝２６＝５＾２＋１ ３３－１８＝１５＝４＾２－１ １８－８＝１０＝３＾２＋１ ８－５＝３＝２＾２－１ ５－３＝２＝１＾２＋１ （４０）、２，５，１１，４１，９１１，（ ） Ａ．７５６９４１ Ｂ．６４００１１ Ｃ．６３００１１ Ｄ．６７００３１ （５－２）＾２＋２＝１１ （１１－５）＾２＋５＝４１ （９１１－４１）＾２＋４１＝７５６９４１ （看尾数是否是４１） （４１） ２，２，０，４，１６，（ ） Ａ．４８ Ｂ．６４ Ｃ．１２８ Ｄ．１４４ （２－２）＾２＝０ （２－０）＾２＝４ （０－４）＾２＝１６ （４－１６）＾２＝１４４ （４２） ５，１４，３４，７６，（ ） Ａ．１４２ Ｂ．１６３ Ｃ．１６９ Ｄ．１７６ ５＝２×３－１ １４＝３×５－１ ３４＝５×７－１ ７６＝７×１１－１ ？＝１１×１３－１＝１４２ （４３） ３，３，６，１８，７２，（ ） Ａ．２５６ Ｂ．２８８ Ｃ．３６０ Ｄ．３８４ ３／３＝１ ６／３＝２ １８／６＝３ ７２／１８＝４ ３６０／７２＝５ （４４） １５，９，３，３，０，（ ） Ａ．１．５ Ｂ．－１．５ Ｃ． －２ Ｄ．－３ （１５－９）／２＝３ （９－３）／２＝３ （３－３）／２＝０ （３－０）／２＝１．５ （４５） ０，１，０，７，２０，（ ） Ａ．３２ Ｂ．３４ Ｃ．３７ Ｄ．４２ ０＋１＋０＝１＝１＾３ １＋０＋７＝８＝２＾３ ０＋７＋２０＝２７＝３＾３ ７＋２０＋３７＝６４＝４＾２ （４６） －１／２， １／３， ４／５， ９／７， １６／９， （ ） Ａ． ２５／１３ Ｂ．２３／１３ Ｃ．２４／１１ Ｄ．１９／１１ －１＋２＝１ １＋３＝４ ４＋５＝９ ９＋７＝１６ １６＋９＝２５ ２３＋１３＝３６ 选Ｂ （４７） １， ２， ２， ５， ９， １６， （ ） Ａ．２２ Ｂ．２６ Ｃ．３０ Ｄ．３４ １＋２＋２＝５ ２＋２＋５＝９ ２＋５＋９＝１６ ５＋９＋１６＝３０ （４８） ２， ０， ０， ４， ６， （ ） Ａ．３ Ｂ．６ Ｃ．１２ Ｄ．２４ －２×（－１）＾５＝２ －１×０＾４＝０ ０×１＾３＝０ １×２＾２＝４ ２×３＾１＝６ ３×４＾０＝３ Ａ．１０， Ｂ． １５ Ｃ．１８ Ｄ． １２ ６＊４－９＝１５ ７＊２＋７＝２１ ３＊２－５＝１ ５＊３＋３＝１８ ／＊此题质量不高，可不用做＊／ （５０） ２， １， ５， ６， ３１， （ ） Ａ． ４５ Ｂ．６７ Ｃ．７２ Ｄ．７８ ２＾２＋１＝５ １＾２＋５＝６ ５＾２＋６＝３１ ６＾２＋３１＝６７ （５１） ７， ２８， １２４， ３４４， （ ） Ａ．９９０ Ｂ．１３３０ Ｃ．１４３２ Ｄ．１６９１ ２＾３－１＝７ ３＾３＋１＝２８ ５＾３－１＝１２４ ７＾３＋１＝３４４ １１＾３－１＝１３３０ （５２） ３７， ５５， ８２， １２７， （ ） Ａ．１９３ Ｂ．１８８ Ｃ．１７２ Ｄ．１６５ ３＋７＝１０ ５＋５＝１０ ８＋２＝１０ １＋２＋７＝１０ １＋７＋２＝１０ 选Ｃ （５３） １４６， ２５５， ３６６， ４７９， （ ） Ａ． ５８１ Ｂ．５８３ Ｃ．８９１ Ｄ．１０００ 看中间数字 １４６， ２５５， ３６６， ４７９ ４＾２＝１６ 合成１４６ ５＾２＝２５ 合成２５５ ６＾２＝３６ 合成３６６ ７＾２＝４９ 合成４７９ 选项中只有Ｃ满足 （５４） １， ２， ５， １４， ５３， （ ） Ａ． １０２ Ｂ．２０２ Ｃ．３０２ Ｄ．４０２ １＾２＋２×２＝５ ２＾２＋５×２＝１４ ５＾２＋１４×２＝５３ １４＾２＋５３×２＝３０２ （５５） ２，６，１５，２８，（ ） Ａ．５５ Ｂ．５６ Ｃ．５８ Ｄ．６０ ２＝２×１ ６＝３×２ １５＝５×３ ２８＝７×４ ？＝１１×５＝５５ （５６） １／３， １／３， ５／６， ３／２， ９／４， （ ） Ａ．３１／５ Ｂ．３１／１０ Ｃ．６１／２０ Ｄ．６１／３０ １／３－１／３＝０／１ ５／６－１／３＝１／２ ＝６１／２０ （５７） ３， １１， ３２， ７１， １３６， （ ） Ａ．１９９ Ｂ．２２９ Ｃ．２３４ Ｄ．２４３ １＾３＋２＝３ ２＾３＋３＝１１ ３＾３＋５＝３２ ４＾３＋７＝７１ ５＾３＋１１＝１３６ ６＾３＋１３＝２２９ （５８） ２， ３， ５， １１， ２８， １２６， （ ） Ａ．４８６ Ｂ．５８０ Ｃ．７２０ Ｄ．７９５ ２＋３＾２＝１１ ３＋５＾２＝２８ ５＋１１＾２＝１２６ １１＋２８＾２＝７９５ （５９） １， ２， ３， ８， ２７ （ ） Ａ．１６４ Ｂ．２００ Ｃ．２１６ Ｄ．２２４ １＊（２＋１）＝３ ２＊（３＋１）＝８ ３＊（８＋１）＝２７ ８＊（２７＋１）＝２２４ 公式：Ａ＊（Ｂ＋１）＝Ｃ （６０） ４， １２， ２４， ３６， ５０， （ ） Ａ． ６４ Ｂ．６８ Ｃ．７２ Ｄ．８０ １＊４＝４ ２＊６＝１２ ３＊８＝２４ ４＊９＝３６ ５＊１０＝５０ ６＊１２＝７２ ４，６，８，９，１０，１２是合数列 （６１） ７， １３， ２０， ２９， ３８， （ ） Ａ． ５０ Ｂ．５１ Ｃ．５２ Ｄ．５４ ３＾２－２＝７ ４＾２－３＝１３ ５＾２－５＝２０ ６＾２－７＝２９ ７＾２－１１＝３８ ８＾２－１３＝５１ （６２） ２１， ３６， ９６， ４１， ８１， （ ） Ａ． １ Ｂ．３４ Ｃ． ８９ Ｄ．７２ 除以５的余数都是１ 选Ａ （６３） ３， １， ８，１８， ５２，（ ） Ａ． ９６ Ｂ．１２０ Ｃ．１３６ Ｄ．１４０ （３＋１）×２＝８ （１＋８）×２＝１８ （８＋１８）×２＝５２ （１８＋５２）×２＝１４０ （６４） ２，０，２，７，７，１１， （ ） ７＋７＋１１＝２５ ７＋１１＋１８＝３６ （６５） １４， １８， ２４， ３２， ４１， ５１， （ ） Ａ． ６３ Ｂ．６５ Ｃ．６６ Ｄ．６７ １８－１４＝４ ２４－１８＝６ ３２－２４＝８ ４１－３２＝９ ５１－４１＝１０ ６３－５１＝１２ 合数序列 （６６） ８， ４， ４， ６， １２， ３０， （ ） Ａ．４０ Ｂ．４８ Ｃ．７２ Ｄ．９０ ４／８＝０．５ ４／４＝１ ６／４＝１．５ １２／６＝２ ３０／１２＝２．５ ／３０＝３ ？＝９０ （６７） １３４， ２５７， ４１５， ６０６， （ ） Ａ．９１１ Ｂ．８０２ Ｃ．６９１ Ｄ．４５９ １＋３＝４ ２＋５＝７ ４＋１＝５ ６＋０＝６ ４＋５＝９ （６８） ２， －２， ６， －２， ３８， （ ） Ａ．－３４ Ｂ． ４０ Ｃ． ４８ Ｄ．５６ ２＾２－（－２）＝６ （－２）＾２－６＝－２ ６＾２－（－２）＝３８ （－２）＾２－３８＝－３４ （６９） ２，６，２０，４２， （ ） Ａ．８０ Ｂ．９６ Ｃ．１１０ Ｄ．１２０ 【天字１号解析】 ２＾２－２＝２ ３＾２－３＝６ ５＾２－５＝２０ ７＾２－７＝４２ １１＾２－１１＝１１０ （７０） ３，３，６，３，３３，（ ） Ａ．－２４， Ｂ．２７ Ｃ．３６ Ｄ．５４ ３＾２－３＝６ ３＾２－６＝３ ６＾２－３＝３３ ３＾２－３３＝－２４ （７１） ７， ３， １６， ５， ２１， ５ ， ６６， （ ） Ａ．１２ Ｂ． １３ Ｃ．１４ Ｄ．１５ （７２） ３，１，４，９，２５， （ ） Ａ． ９０ Ｂ．１６０ Ｃ．２５６ Ｄ．３４３ （３－１）＾２＝４ （１－４）＾２＝９ （４－９）＾２＝２５ （９－２５）＾２＝２５６ （７３） ７８， ５７， ３６， １９， １０， （ ） Ａ． ２ Ｂ． １ Ｃ．０ Ｄ．－１ ７＊８＋１＝５７ ５＊７＋１＝３６ ３＊６＋１＝１９ １＊９＋１＝１０ １＊０＋１＝１ （７４） １３，１６，２１，３０，４５，（ ） Ａ． ５７ Ｂ．６８ Ｃ．７２ Ｄ．７５ １６－１３＝３ ２１－１６＝５ ３０－２１＝９ ４５－３０＝１５ ６８－４５＝２３ （７５） ３／４，１／２，１／３，２／９，（ ） Ａ．５／１２ Ｂ．１／５ Ｃ．５／２１ Ｄ．４／２７ ３／４ ＊ ２／３＝１／２ １／２ ＊ ２／３＝１／３ １／３ ＊ ２／３＝２／９ ２／９ ＊ ２／３＝４／２７ （７６） １３１，６７，３１，１５，（） Ａ．１１ Ｂ． ９ Ｃ．７ Ｄ．５ １３１－６７＝６４＝８＾２ ６７－３１＝３６＝６＾２ ３１－１５＝１６＝４＾２ １５－１１＝４＝２＾２ （７７） ６，３，８，４，２，８， （ ） Ａ．２ Ｂ．４ Ｃ．６ Ｄ．８ 移动求积看个位数 ６×３＝１８ ３×８＝２４ ８×４＝３２ ４×２＝８ ２×８＝１６ 个位数是６ 选Ｃ （７８） ３，２，１３，３２，１０３，（） Ａ．２２２ Ｂ．３０２ Ｃ．３１６ Ｄ．２５６ ３＋２＝５ ２＋１３＝１５ １３＋３２＝４５ ３２＋１０３＝１３５ １０３＋３０２＝４０５ （７９） ６，１２，１２，１８，２１，（） １２＋１８／２＝２１ １８＋２１／２＝２８．５ （８０） ０，１，６，２３，（ ） Ａ．８６ Ｂ．８１ Ｃ．７６ Ｄ．６１ ３＾０－１＝０ ３＾１－２＝１ ３＾２－３＝６ ３＾３－４＝２３ ３＾４－５＝７６ （８１） ４，１２，２４，３６，５０，（ ） Ａ． ６４ Ｂ．６０ Ｃ．７２ Ｄ．７６ ４＝１×４ １２＝２×６ ２４＝３×８ ３６＝４×９ ５０＝５×１０ ７２＝６×１２ ４，６，８，９，１０，１２ 是合数序列 （８２） ２１，１４，１７，３５，３１，５２，（ ） Ａ．５８ Ｂ．６６ Ｃ．７２ Ｄ．７８ ２１＋１４＝３５ １４＋１７＝３１ １７＋３５＝５２ ３５＋３１＝６６ Ａ＋Ｂ＝Ｄ （８３） ７ ，１０，１８，４２，９０，（ ） Ａ． １８０ Ｂ．２１０ Ｃ．２４０ Ｄ．２７０ １０－７＝３＝２＾２－１ １８－１０＝８＝３＾２－１ ４２－１８＝２４＝５＾２－１ ９０－４２＝４８＝７＾２－１ （８４） ２５， ３５， ５４， ７３， ９２， （ ） Ａ．６６ Ｂ．９７ Ｃ．９８ Ｄ．１０９ ２５： ２＋５＝７ ３５： ３＋５＝８ ５４： ５＋４＝９ ７３： ７＋３＝１０ ９２： ９＋２＝１１ ６６： ６＋６＝１２ （８５） ４， ２， ３， ７， １４， （ ） Ａ．２０ Ｂ．２４ Ｃ．２６ Ｄ．２８ ２－４＝－２ ３－２＝１ ７－３＝４ １４－７＝７ ２４－１４＝１０ －２，１，４，７，１０ 是等差数列 差值是３ （８６） －１， ３， ３， ５， ３７， （ ） Ａ．８７ Ｂ．３２７ Ｃ．７２９ Ｄ．７３５ （－２）＾１＋１＝－１ （－１）＾２＋２＝３ ０＾３＋３＝３ １＾４＋４＝５ （８７） ３／４， ７／１１， １８／２９， ４７／７６， （ ） Ａ．９４／１０１ Ｂ．１２３／１９９ Ｃ．１１３／１７１ Ｄ．７／８ 将所有分子分母都联系起来看 ３，４，７，１１，１８，２９，４７，７６，？，？ ３＋４＝７ ４＋７＝１１ ７＋１１＝１８ …… ４７＋７６＝１２３ ７６＋１２３＝１９９ 这属于裴波纳契数列的分数表达形式！ （８８） －１，０，２７，５１２，（ ） Ａ．１６４ Ｂ．１２９１ Ｃ．３２５５ Ｄ．９３７５ －１＝（－１）＊１＾１ ０＝０＊２＾２ ２７＝１＊３＾３ ５１２＝２＊４＾４ ９３７５＝３＊５＾５ （８９） ７，１０，１６，２２，（ ） Ａ．３１ Ｂ．３２ Ｃ．３３ Ｄ．３４ 【天字１号解析】 ３＊２＋１＝７ ３＊３＋１＝１０ ３＊５＋１＝１６ ３＊７＋１＝２２ ３＊１１＋１＝３４ （９０） ３０，３１，５４，５９，（ ） Ａ．６８ Ｂ．７０ Ｃ．７８ Ｄ．８６ ５＾２＋５＝３０ ６＾２－５＝３１ ７＾２＋５＝５４ ８＾２－５＝５９ ９＾２＋５＝８６ １． ０，２，６，１４，（ ａ ），６２ Ａ．４０ Ｂ．３６ Ｃ．３０ Ｄ．３８ ２． ２，７，２８，６３，（ ｂ ），２１５ Ａ．１１６ Ｂ．１２６ Ｃ．１３８ Ｄ．１４２ ３． －１，９，８，（ ａ ），２５，４２ Ａ．１７ Ｂ．１１ Ｃ．１６ Ｄ．１９ ４． ３，４，７，１６，（ ｄ ），１２４ Ａ．３３ Ｂ．３５ Ｃ．４１ Ｄ．４３ ５． ４０，２３，（ ｃ ），６，１ｌ Ａ．７ Ｂ．１３ Ｃ．１７Ｄ．１９ ６． ０，－ｌ，（ ａ ），７，２８ Ａ．２ Ｂ．３ Ｃ．４ Ｄ．５ ７． ８，１１，１６，（ ｄ ），３２ Ａ．２５ Ｂ．２２ Ｃ．２４ Ｄ．２３ ８． ３，４，（ ），３９，１０３ Ａ．７ Ｂ．９ Ｃ．１１ Ｄ．１２ ９． １，２，２，（ ａ ），８，３２ Ａ．４ Ｂ．３ Ｃ．５ Ｄ．６ １０．１７，２４，３３，４６，（ ａ ），９２ Ａ．６５ Ｂ．６７ Ｃ．６９ Ｄ．７１ １１．１６，１７，１９，２２，２７，（ ），４５ Ａ．３５ Ｂ．３４ Ｃ．３６ Ｄ．３７ １２．８，９６，１４０，１６２，１７３，（ ａ ） Ａ．１７８．５ Ｂ．１７９．５ Ｃ．１８０．５ Ｄ．１８１．５ １３．１１，１０１，１００１，（ ｄ ） Ａ． １１１ Ｂ．１２１ Ｃ．１０１１ Ｄ．１０００１ １４．９，１３，１８，２４，３１，（ ａ ） Ａ．３９ Ｂ．３８ Ｃ．３７ Ｄ．４０ １５．１７，１０， （ ａ ），３，４，－１ Ａ．７ Ｂ．６ Ｃ．８ Ｄ．５ １６．０，１，４，１３，４０，（ ｄ ） Ａ．７６ Ｂ．８５ Ｃ．９４ Ｄ．１２１ １７．６，８，１１，１６，２３，（ ａ ） Ａ．３２ Ｂ．３４ Ｃ．３６ Ｄ．３８ １８．６，１２，１９，２７，３３，（ ｂ ），４８ Ａ．３９ Ｂ．４０ Ｃ．４１ Ｄ．４２ １９．０，５，８，１７，（ ｃ ），３７ Ａ．３１ Ｂ．２７ Ｃ．２４ Ｄ．２２ ２０．４，９，６，１２，８，１５，１０，（ ａ ） Ａ．１８ Ｂ．１３ Ｃ．１６ Ｄ．１５ 答案及详解： ［ｙｃ］１． Ｃ 这是一道等差数列。
公务员考试数字推理题库及详尽解答
私人珍藏、奉献出来——数字推理题典4,18,56,130,( ) A.26 B.24 C.32 D.16 答案是B，各项除3的余数分别是1.0.2.1 0. 对于1、0、2、1、0，每三项相加=>3、3、3 等差 1,3,4,8,16,() A.26 B.24 C.32 D.16 我选B 3-1=2 8-4=4 24-16=8 可以看出2，4，8为等比数列 1，1，3，7，17，41， ( ) A．89 B．99 C．109 D．119 我选B 1*2+1=3 2*3+1=7 2*7+3=17 … 2*41+17=99 1,3,4,8,16,() A.26 B.24 C.32 D.16 我选C 1+3=4 1+3+4=8 … 1+3+4+8=32 1,5,19,49,109,( ) 。
A.170B.180 C 190 D.200 1*1+4=5 5*3+4=19 9*5+4=49 13*7+4=9517*9+4=157 4,18,56,130,( ) A216 B217 C218 D219 我搜了一下，以前有人问过，说答案是A 如果选A的话，我又一个解释每项都除以4=>取余数0、2、0、2、0 仅供参考~：） 1. 256 ，269 ，286 ，302 ，（） A.254 B.307 C.294 D.316 解析： 2+5+6=13 256+13=269 2+6+9=17 269+17=2862+8+6=16 286+16=302 ?=302+3+2=307 2. 72 , 36 , 24 , 18 , ( ) A.12 B.16 C.14.4 D.16.4 解析：（方法一）相邻两项相除, 72 36 24 18 \ / \ / \ / 2/1 3/2 4/3(分子与分母相差1且前一项的分子是后一项的分母) 接下来貌似该轮到5/4,而18/14.4=5/4. 选C （方法二）6×12=72，6×6=36，6×4=24，6×3 =18，6×X 现在转化为求X 12，6，4，3，X 12/6 ，6/4 ， 4/3 ，3/X化简得2/1，3/2，4/3，3/X，注意前三项有规律，即分子比分母大一，则3/X=5/4 可解得：X=12/5 再用6×12/5=14.4 3. 8 , 10 , 14 , 18 ,（） A. 24 B. 32 C. 26 D. 20 分析：8，10，14，18分别相差2，4，4，？可考虑满足2/4=4/?则？＝8 所以，此题选18＋8＝26 4. 3 , 11 , 13 , 29 , 31 ,（） A.52 B.53 C.54 D.55 分析：奇偶项分别相差11－3＝8，29－13＝16＝8×2，？－31＝24＝8×3则可得？＝（）。
公务员考试行测数字推理必知的30个规律
公务员考试行测数字推理必知的30个规律公务员考试中，数字推理是一个非常重要的考试科目。
数字推理是指通过对数字、图形、文字等信息的分析和推理，得出正确的结论。
在数字推理中，有很多规律需要掌握。
本文将介绍公务员考试行测数字推理必知的30个规律。
一、数字规律1. 数字序列规律数字序列规律是指在一组数字中，数字之间的关系所遵循的规律。
常见的数字序列规律有等差数列、等比数列、斐波那契数列等。
2. 数字排列规律数字排列规律是指在一组数字中，数字的排列顺序所遵循的规律。
常见的数字排列规律有逆序、顺序、交替等。
3. 数字替换规律数字替换规律是指在一组数字中，数字被替换成其他数字的规律。
常见的数字替换规律有加减乘除、平方、开方等。
4. 数字组合规律数字组合规律是指在一组数字中，数字之间的组合所遵循的规律。
常见的数字组合规律有排列组合、加减乘除等。
二、图形规律图形旋转规律是指在一组图形中，图形的旋转方向和角度所遵循的规律。
常见的图形旋转规律有顺时针旋转、逆时针旋转等。
6. 图形翻转规律图形翻转规律是指在一组图形中，图形的翻转方向和方式所遵循的规律。
常见的图形翻转规律有水平翻转、垂直翻转等。
7. 图形平移规律图形平移规律是指在一组图形中，图形的平移方向和距离所遵循的规律。
常见的图形平移规律有水平平移、垂直平移等。
8. 图形缩放规律图形缩放规律是指在一组图形中，图形的缩放比例所遵循的规律。
常见的图形缩放规律有放大、缩小等。
9. 图形填充规律图形填充规律是指在一组图形中，图形的填充方式和颜色所遵循的规律。
常见的图形填充规律有交替填充、渐变填充等。
三、文字规律10. 文字替换规律文字替换规律是指在一组文字中，文字被替换成其他文字的规律。
常见的文字替换规律有字母替换、数字替换等。
文字排列规律是指在一组文字中，文字的排列顺序所遵循的规律。
常见的文字排列规律有逆序、顺序、交替等。
12. 文字组合规律文字组合规律是指在一组文字中，文字之间的组合所遵循的规律。
公务员行政能力测试数字推理答题技巧（非常有用）
公务员行政能力测试数字推理答题技巧（非常有用）数字推理一、基本要求熟记熟悉常见数列，保持数字的敏感性，同时要注意倒序。
自然数平方数列：4，1，0，1，4，9，16，25，36，49，64，81，100，121，169，196，225，256，289，324，361，400……自然数立方数列：－8，－1，0，1，8，27，64，125，216，343，512，729，1000质数数列：2，3，5，7，11，13，17……（注意倒序，如17,13,11,7,5,3,2）合数数列：4，6，8，9，10，12，14…….（注意倒序）二、解题思路：1 基本思路：第一反应是两项间相减，相除，平方，立方。
所谓万变不离其综，数字推理考察最基本的形式是等差，等比，平方，立方，质数列，合数列。
相减，是否二级等差。
8，15，24，35，（48）相除，如商约有规律，则为隐藏等比。
4，7，15，29，59，（59*2－1）初看相领项的商约为2，再看4*2-1=7,7*2+1＝15……2 特殊观察：项很多，分组。
三个一组，两个一组4，3，1，12，9，3，17，5，（12）三个一组19，4，18，3，16，1，17，（2）2，－1，4，0，5，4，7，9，11，（14）两项和为平方数列。
400，200，380，190，350，170，300，（130）两项差为等差数列隔项，是否有规律0，12，24，14，120，16（7^3－7）数字从小到大到小，与指数有关1，32，81，64，25，6，1，1/8每个数都两个数以上，考虑拆分相加（相乘）法。
87，57，36，19，（1*9+1）256，269，286，302，（302+3+0+2）数跳得大，与次方（不是特别大），乘法（跳得很大）有关1，2，6，42，（42^2+42）3，7，16，107，（16*107-5）每三项/二项相加，是否有规律。
1，2，5，20，39，（125－20－39）21，15，34，30，51，（10^2-51）C=A^2－B及变形（看到前面都是正数，突然一个负数，可以试试）3，5，4，21，（4^2-21）,4465，6，19，17，344,(-55)-1，0，1，2，9，（9^3+1）C=A^2+B及变形（数字变化较大）1，6，7，43，（49+43）1，2，5，27，（5+27^2）2/3，1/3，2/9，1/6，（2/15）3/1，5/2，7/2，12/5，（18/7）分子分母相减为质数列1/2，5/4，11/7，19/12，28/19，（38/30）分母差为合数列，分子差为质数列。
(完整版)公务员考试1000道数字推理题详解
【1】7，9，-1，5，( )A、4；B、2；C、-1；D、-3分析:选D，7+9=16；9+（-1）=8；（-1）+5=4；5+（-3）=2 , 16，8，4，2等比【2】3，2，5/3，3/2，( )A、1/4；B、7/5；C、3/4；D、2/5分析:选B，可化为3/1，4/2，5/3，6/4，7/5,分子3，4，5，6，7,分母1，2，3，4，5【3】1，2，5，29，（）A、34；B、841；C、866；D、37分析:选C，5=12+22；29=52+22；( )=292+52=866【4】2，12，30，（）A、50；B、65；C、75；D、56；分析:选D，1×2=2；3×4=12；5×6=30；7×8=（）=56【5】2，1，2/3，1/2，（）A、3/4；B、1/4；C、2/5；D、5/6；分析:选C，数列可化为4/2，4/4，4/6，4/8，分母都是4，分子2，4，6，8等差，所以后项为4/10=2/5，【6】4，2，2，3，6，（）A、6；B、8；C、10；D、15；分析:选D，2/4=0.5；2/2=1；3/2=1.5；6/3=2；0.5，1，1.5, 2等比，所以后项为2.5×6=15【7】1，7，8，57，（）A、123；B、122；C、121；D、120；分析:选C，12+7=8；72+8=57；82+57=121；【8】4，12，8，10，（）A、6；B、8；C、9；D、24；分析:选C，(4+12)/2=8；(12+8)/2=10；(8+10)/2=9【9】1/2，1，1，（），9/11，11/13A、2；B、3；C、1；D、7/9；分析:选C，化成1/2,3/3,5/5 ( ),9/11,11/13这下就看出来了只能是(7/7)注意分母是质数列，分子是奇数列。
【10】95，88，71，61，50，（）A、40；B、39；C、38；D、37；分析：选A，思路一：它们的十位是一个递减数字9、8、7、6、5 只是少开始的4 所以选择A。
行测答题技巧简单学系列——数字推理全集
行测答题技巧简单学系列——数字推理全集行测答题技巧系列：行测知识简单学——数字推理全集行政职业能力测试，简称“行测”，是事业单位考试当中重要的组成部分。
其中，数字推理作为其组成部分之一，需要考生具备较强的数字敏感性和一定的数字运算能力。
当然，解答相关题目的前提是了解数字推理中各种数列的形式和特点。
本文就将对相关内容进行介绍。
一、等差数列1.概念：如果一个数列从第二项起，每一项与前一项的差等于同一个常数，那么这个数列就叫做等差数列。
常考题型：二级等差数列，三级等差数列。
例：35,29,24,20,17，( )(逐项作差后得公差为1的等差数列，为二级等差数列。
三级等差数列为二级数列再作差所得。
)2.等差数列的变式作差或持续作差后，得到其他数列或其变式，这是最常考查的等差数列规律。
例：39,62,91,126,149,178，( )(作差后得到“23,29,35”的循环数列)3.等差数列及其变式特征归纳(1)数列中出现个别质数的，一般都是等差数列或其变式，因为指数不具备进行拆分寻求规律的可能性。
(2)含有0的数列很有可能是等差数列，因为0不易做递推变化，多在等差数列或多次方数列中出现，宜首先从作差方向寻求规律。
(3)单调递增或增减交替有可能是等差数列变式。
二、等比数列1.概念：如果一个数列从第二项起，每一项与它前面一项的比等于同一个非零常数，那么该数列就叫做等比数列。
与等差数列类似，二级等比数列，三级等比数列(较少)也是常考点。
2.等比数列变式(1)二级等比数列;(2)作商后得到等差/质数/常数列。
例：4,4,16,144，( )相邻各项的商依次为12,22,32，(42)。
144*16=(2304)。
3.等比数列及其变式特征归纳(1)数项具有良好的整除性;(2)递增/递减趋势明显，会出现先增后减的情况;(3)具有递推关系的等比数列变式可通过估算相邻项间大致倍数反推规律。
三、和数列1.基本形式(1)两项和数列：数列从第三项开始，没意向等于它前两项之和。
(整理)公务员考试十大数字推理规律详解
公务员考试十大数字推理规律详解(2009-6-11 上午 07:55:46)备考规律一：等差数列及其变式【例题】7，11，15，( )A 19B 20C 22D 25【答案】A选项【广州新东方戴斌解析】这是一个典型的等差数列，即后面的数字与前面数字之间的差等于一个常数。
题中第二个数字为11，第一个数字为7，两者的差为4，由观察得知第三个与第二个数字之间也满足此规律，那么在此基础上对未知的一项进行推理，即15+4=19，第四项应该是19，即答案为A。
（一）等差数列的变形一：【例题】7，11，16，22，( )A．28 B．29 C．32 D．33【答案】B选项【广州新东方戴斌解析】这是一个典型的等差数列的变形，即后面的数字与前面数字之间的差是存在一定的规律的，这个规律是一种等差的规律。
题中第二个数字为11，第一个数字为7，两者的差为4，由观察得知第三个与第二个数字之间的差值是5；第四个与第三个数字之间的差值是6。
假设第五个与第四个数字之间的差值是X，我们发现数值之间的差值分别为4，5，6，X。
很明显数值之间的差值形成了一个新的等差数列，由此可以推出X=7,则第五个数为22+7=29。
即答案为B选项。
（二）等差数列的变形二：【例题】7，11，13，14，( )A．15 B．14.5 C．16 D．17【答案】B选项【广州新东方戴斌解析】这也是一个典型的等差数列的变形，即后面的数字与前面数字之间的差是存在一定的规律的，但这个规律是一种等比的规律。
题中第二个数字为11，第一个数字为7，两者的差为4，由观察得知第三个与第二个数字之间的差值是2；第四个与第三个数字之间的差值是1。
假设第五个与第四个数字之间的差值是X。
我们发现数值之间的差值分别为4，2，1，X。
很明显数值之间的差值形成了一个新的等差数列，由此可以推出X=0.5,则第五个数为14+0.5=14.5。
即答案为B选项。
（三）等差数列的变形三：【例题】7，11，6，12，( )A．5 B．4 C．16 D．15【答案】A选项【广州新东方戴斌解析】这也是一个典型的等差数列的变形，即后面的数字与前面数字之间的差是存在一定的规律的，但这个规律是一种正负号进行交叉变换的规律。
行测数量关系技巧：数字推理常考考点总结
行测数量关系技巧：数字推理常考考点总结1500字数量关系是行测考试中的一大常考考点，主要内容包括数字推理和数量关系推理。
在数字推理部分，常考的题型包括数字组合、数字运算、数字排列等。
下面是关于数字推理的一些常考考点总结：一、数字组合：1. 数字组合：给定一组数字，按照一定规律组合后求出结果。
常见的规律有数字之和、数字之差、数字之积等。
2. 数字替换：给定一组数字，将其中某几个数字替换为其他数字，求替换后的结果。
常见的规律有数字之和、数字之差、数字之积等。
二、数字运算：1. 加减乘除：根据给定的加减乘除法则，求解表达式的结果。
2. 数字计算：根据给定的数字以及计算规则，计算最终结果。
常见的规则有数字之和、数字之差、数字之积等。
三、数字排列：1. 数字排序：根据给定的排列规则，求出待排序数字的顺序。
常见的规则有从小到大排列、从大到小排列等。
2. 数字替换：将给定数字按照一定规则进行排列后，将某几个数字替换为其他数字，求替换后的结果。
在数量关系推理部分，常考的题型包括数量比较、数量关系、数量推理等。
下面是关于数量关系推理的一些常考考点总结：一、数量比较：1. 大小比较：根据给定的数值大小进行比较，求出最大值或最小值。
常见的比较方法有大小排列、数值相加、数值相减等。
2. 数量关系：根据给定的数值关系进行推理，求出符合要求的数值。
常见的关系有倍数关系、百分比关系、比例关系等。
二、数量关系：1. 数量变化：根据给定的数量变化规律，推断出下一个数值。
常见的变化规律有线性关系、指数关系、循环关系等。
2. 数量比例：根据给定的数量比例，求出未知的数量。
常见的比例关系有百分比、比例尺、三角函数等。
三、数量推理：1. 数列推理：根据给定的数列规律，推断出下一个数列。
常见的规律有等差数列、等比数列、斐波那契数列等。
2. 数字推理：根据给定的数字规则，推断出满足规则的数字。
常见的规则有数字之和、数字之差、数字之积等。
以上是关于数量关系推理的一些常考考点总结，希望对大家的行测备考有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基础数列【例1】质数：2，3，5，7，1l，1 3，17，1 9，23．…【例2】合数：4，6，8，9，10，12，14，15，…【例】1，3，7，1，3，7，…1，7，1，7，l，7，…1，3，7，一1，一3，7，…【例】(1)6，12，19，27，35，( )，48答案：42，首尾相加为54。
(2)3，- l，5，5，11，( )答案：7，首尾相加为10。
等差数列及其变式一、基本等差数列【例】1，4，7，10，l 3，l 6，19，22，25，…【例1】(2007黑龙江，第8题)11，12，15，20，27，( ) A．32 B．34 C．36 D．38【答案】C【解题关键点】【例2】(2002国家，B类，第3题)32，27，23，20，18，( ) A．14 B．15 C．16 D．1 7【答案】D【解题关键点】【例3】(2002国家，B类，第5题)－2，1，7，16，( )，43 A．25 B．28 C．31 D．35【答案】B【解题关键点】【例】3，6，11，( )，27A．15 B．18 C．19 D．24【答案】B【解题关键点】二级等差数列。
（1）相邻两项之差是等比数列【例】0，3，9，21，( )，93A．40 B．45 C. 36 D．38【答案】B【解题关键点】二级等差数列变式（2）相邻两项之差是连续质数【例】11，13，16，21，28，( )A．37 B．39 C.41 D.47【答案】B【解题关键点】二级等差数列变式（3）相邻两项之差是平方数列、立方数列【例】1，2，6，15，（）A．19B．24C．31D．27【答案】C【解题关键点】数列特征明显单调且倍数关系不明显，优先做差。
得到平方数列。
如图所示，因此，选C（4）相邻两项之差是和数列【例】2, 1, 5, 8, 15, 25, ( )A.41B.42C.43D.44【答案】Ｂ【解题关键点】相邻两项之差是和数列（5）相邻两项之差是循环数列【例】1,4,8,13,16,20,( )A. 20B. 25C. 27D. 28【答案】B【解题关键点】该数列相邻两数的差成3，4，5一组循环的规律，所以空缺项应为20+5=25，故选B。
【结束】【例】（2009年中央机关及其直属机构公务员录用考试行测真题）1，9，35，91，189，( ) A．361 B．341 C．321 D．301【答案】B【解题关键点】原数列后项减前项构成数列8，26，56，98，( )，新数列后项减前项构成数列18，30，42，(54)，该数列是公差为12的等差数列，接下来一项为54，反推回去，可得原数列的空缺项为54+98+189=341，故选B。
如图所示：解法二：立方和数列。
，，，，，，答案为B。
解法三：因式分解数列，原数列经分解因式后变成：1×1，3×3，5×7，7×13，9×21，(11×31)，将乘式的第一个因数和第二个因数分别排列，前一个因数是公差为2的等差数列，后一个因数是二级等差数列，答案也为B。
图示法能把等差(比)数列的结构清晰地表示出来，一般应用于多级等差(比)数列中。
【例2】5，12，21，34，53，80，( )A .121 B．115 C．119 D．117【答案】D【解题关键点】三级等差数列（1）两次作差之后得到等比数列【例】(2005国家，－类，第35题)0，1，3，8，22，63，( )。
A．163 B．174 C．185 D．196【答案】C【解题关键点】前－个数的两倍，分别减去－1，0，1，2，3，4等于后－项。
【结束】（2）两次作差之后得到连续质数【例】1,8,18,33,55,( )A．86 B．87 C．88 D．89【答案】C【解题关键点】1 8 18 33 55 (88)求差7 10 15 22 (33)求差3 5 7 (11) 质数列（3）两次作差之后得到平方数列、立方数列【例】5,12,20,36,79,( )A．185 B．186 C．187 D．188【答案】B【解题关键点】5 12 20 36 79 (186)求差7 8 16 43 (107)求差1 8 27 (64) 立方数列（4）两次作差之后得到和数列【例4】-2, 0, 1, 6, 14, 29, 54, ( )A.95B.96C.97D.98【答案】Ｂ【解题关键点】三级等差数列变式等比数列及其变式【例】l，2，4，8，16，32，64，128，…【解题关键点】首项为1，公比q=2的等比数列（1）相邻两项之比是等比数列【例】2，2，1，14，（）A.1B.3C.4D. 1 4【答案】 D【解题关键点】相邻两项之比是等比数列【例】100，20，2，215，1150，（）A.13750B.1225C. 3D.1500【答案】 A【解题关键点】二级等比数列变式。
【例】4，4，16，144，（）A.162B.2304C. 242D. 512【答案】B【解题关键点】二级等比数列变式。
【例】2，6，30，210，2310，（）A.30160B.30030C. 40300D.32160【答案】B【解题关键点】二级等比数列变式。
【例】1，4，13，40，121，（）A.1093B.364C. 927D.264【答案】B【解题关键点】第二类等比数列变式【例】2，5，13，35，97，（）A.214B.275C. 312D.336【答案】B【解题关键点】第二类等比数列变式【例】3，4，10，33，（）A.56B.69C. 115D.136【答案】D【解题关键点】第二类等比数列变式等比数列及其变式【例】l，2，4，8，16，32，64，128，…【解题关键点】首项为1，公比q=2的等比数列（1）相邻两项之比是等比数列【例】2，2，1，14，（）A.1B.3C.4D. 1 4【答案】 D【解题关键点】相邻两项之比是等比数列【例】100，20，2，215，1150，（）A.13750B.1225C. 3D.1500【答案】 A【解题关键点】二级等比数列变式。
【例】4，4，16，144，（）A.162B.2304C. 242D. 512【答案】B【解题关键点】二级等比数列变式。
【例】2，6，30，210，2310，（）A.30160 B.30030 C. 40300 D.32160【答案】B【解题关键点】二级等比数列变式。
【例】1，4，13，40，121，（）A.1093B.364C. 927D.264【答案】B【解题关键点】第二类等比数列变式【例】2，5，13，35，97，（）A.214B.275C. 312D.336【答案】B【解题关键点】第二类等比数列变式【例】3，4，10，33，（）A.56B.69C. 115D.136【答案】D【解题关键点】第二类等比数列变式积数列及其变式解题模式：观察数列的前三项之间的特征如果前三项之间的关系为积关系，则猜测该数列为积数列，对原数列各相邻项作乘法，并与原数列（从第三项开始）进行比较。
如果前三项之间存在大致的积关系，或者前两项的乘积与第三项之间呈现倍数关系，则猜测该数列为积数列的变式，可以尝试作积后进行和、差、倍数修正。
【例】2，5，10，50，（）A.100B.200C.250D.500【答案】D【解题关键点】二项求积数列【例】1，6，6，36，（）,7776A.96B.216C.866D.1776【答案】B【解题关键点】三项求积数列从第三项开始，每一项等于它前面两项之积。
1×6=6,6×6=36,6×36=（216），36×216=7776（1）相邻两项之积是等差数列（2）相邻两项之积是等比数列（3）相邻两项之积是平方数列、立方数列【例】13，3，112，43，364（）A. 1384B.6475C.352D.332【答案】B【解题关键点】相邻两项之积是平方数列、立方数列（1）前两项之积加固定常数等于第三项【例】2，3，9，30，273,（）A. 8913B. 8193C. 7893D. 12793【答案】B【解题关键点】前两项之积加固定常数等于第三项（2）前两项之积加基本数列等于第三项【例】2，3，5，16，79,（）A. 159B. 349C.1263D. 1265【答案】D【解题关键点】前两项之积加基本数列等于第三项【例】15，5，3,53,（） A.95B. 275 C. 159D. 915【答案】 A【解题关键点】商数列及其变式第一项除以第二项等于第三项，3÷53=95幂次数列【例】-1，2，5，26，（）A.134B.137C.386D.677【答案】D【解题关键点】等差数列的平方加固定常数【例】3，8，17，32，57,（）A.96B.100C.108D.115【答案】B【解题关键点】等差数列的平方加基本数列平方数列变式。
各项依次为21+2，22+4，23+8，24+16，25+32，（26+64），其中每个数字的前项是平方数列，后项是公比为2的等比数列。
【例】343，216，125，64，27,（） A.8 B.9 C.10 D.12 【答案】A【解题关键点】等差数列的立方立方数列，分别为7,6,5,4,3，（2）的立方。
【例】4，9，25，49，121,（） A.144 B.169 C.196 D.225 【答案】B【解题关键点】质数列的立方各项依次写为22，23，25，27，211，底数为连续质数，下一项应是213=（169）。
【例】3，10，29，66，127,（） A.218 B.227 C.189 D.321 【答案】A【解题关键点】等比数列的立方加固定常数各项依分别为21+2，22+2，23+2，24+2，25+2，（26+2），也可以看作三级等差数列。
【例】2，10，30，68,（），222 A.130 B.150 C.180 D.200 【答案】A【解题关键点】等比数列的立方加固定常数各项依分别为31+1，32+2，33+3，34+4，35+5，36+6。
【例】4，13，36，（），268A.97B.81C.126D.179【答案】A【解题关键点】底数按基本数列变化多次方数列变式。
各项依次为4=13+21，13=23+22，36=33+23，（97）=（43+24），268=53+25【例】136，15，1，3,4，（）A.8B.6C.5D.1【答案】A【解题关键点】指数按基本数列变化1 36=26-，15=15-，1=04，3=3，4=22，（1）=31【例】16，27，16，（），1A.5B.6C.7D.8【答案】A【解题关键点】底数和指数交错变化对次方数列。