21.2 1.二次函数y=ax2的图象和性质
九年级数学上册21.2二次函数的图象和性质21.2.1二次函数y=ax2的图象和性质同步练习

21.2.1 二次函数y =ax 2的图象和性质知识点 1 二次函数y =ax 2的图象画法1.请你帮小明完成用描点法画函数y =4x 2图象的有关步骤: 列表:图21-2-1知识点 2 二次函数y =ax 2的图象特征与有关概念 2.关于二次函数y =-23x 2的描述错误的是( )A .它的图象关于y 轴对称B .该抛物线开口向下C .原点是该抛物线上的最高点D .当x 为任意实数时,函数值y 总是负数3.若抛物线y =(6-a )x 2的开口向上,则a 的取值范围是( ) A .a >6 B .a <6 C .a >0 D .a <0 4.已知二次函数y =53x 2与y =-53x 2,下列说法错误的是( )A .它们的图象都关于y 轴对称B .它们的图象的顶点相同C .二次函数y =53x 2的图象都在二次函数y =-53x 2的图象上方D .二次函数y =53x 2与y =-53x 2的图象关于x 轴对称5.若二次函数y =ax 2的图象过点P (-2,4),则该图象必经过点( )A .(2,4)B .(-2,-4)C .(-4,2)D .(4,-2)6.(1)在同一平面直角坐标系中,画出函数y =2x 2,y =12x 2,y =-2x 2与y =-12x 2的图象.(2)观察(1)中所画的图象,回答下列问题:①由图象可知抛物线y =2x 2与抛物线________的形状相同,且关于________轴对称;同样,抛物线y =12x 2与抛物线________的形状相同,也关于________轴对称;②当|a |相同时,抛物线开口大小________;当|a |变大时,抛物线的开口变________(填“大”或“小”);当|a |变小时,抛物线的开口变________(填“大”或“小”).知识点 3 二次函数y =ax 2的性质7.二次函数y =14x 2不具有的性质是( )A .函数图象的开口向上B .图象关于y 轴对称C .y 随x 的增大而增大D .函数的最小值是08.抛物线y =-3x 2的顶点坐标是________,该抛物线上有A (2,y 1),B (12,y 2)两点,则y 1________y 2(填“>”“<”或“=”).9.已知二次函数y =ax 2的图象经过点A (-1,-12),则这个二次函数的表达式为________,当x ________时,函数y 随x 的增大而增大.10.如图21-2-2,在同一平面直角坐标系中画出函数y =12x 2和函数y =-12x 2的图象,已知坐标原点O 为正方形ABCD 对角线的交点,且正方形的边分别与x 轴、y 轴平行,如果点D 的坐标为(2,2),那么阴影部分的面积为( )A .4B .8C .12D .16图21-2-211.若A (-14,y 1),B (-1,y 2),C (12,y 3)为二次函数y =-x 2的图象上的三点,则y 1,y 2,y 3的大小关系是( )A .y 1<y 2<y 3B .y 3<y 2<y 1C.y2<y3<y1 D.y2<y1<y312.当ab>0时,二次函数y=ax2与y=ax+b的图象大致是( )图21-2-313.若对任意实数x,二次函数y=(a+1)x2的值总是非负数,则a的取值范围是________.14.已知二次函数y=ax2的图象经过点(2,-8).(1)求这个二次函数的表达式;(2)说出函数在x取什么值时,有最大值还是最小值,最大值或最小值是多少;(3)当x为何值时,函数y随x的增大而减小?15.如图21-2-4所示,直线l经过点A(4,0),B(0,4),它与抛物线y=ax2在第一象限内相交于点P,且△AOP的面积为4.(1)求直线AB的函数表达式和点P的坐标;(2)求a的值.图21-2-416.如图21-2-5①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B 两点,点A,B的横坐标分别为m,n(m<0,n>0).(1)当m=-1,n=4时,k=______,b=______;当m=-2,n=3时,k=______,b=______;(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;(3)利用(2)中的结论,解答下列问题:如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.①当四边形AOED为菱形时,m与n满足的关系式为____________;②当四边形AOED为正方形时,m=________,n=____________.图21-2-51.解:列表:描点并连线如图:2.D3.B [解析] 因为抛物线的开口向上,所以6-a>0,解得a<6.故选B .4.C [解析] 函数y =53x 2与y =-53x 2都是关于y 轴对称的抛物线,顶点都是原点,故A ,B 选项正确.由于它们的图象大小和形状都相同,开口方向相反,所以它们的图象关于x轴对称,故D 选项正确.5.A [解析] 二次函数y =ax 2的图象是轴对称图形,且对称轴是y 轴,观察各选项可知,点(2,4)和点(-2,4)关于y 轴对称,故点(2,4)也在该函数的图象上.故选A .6.解:(1)略.(2)①y=-2x 2x y =-12x 2 x②相同 小 大7.C [解析] 二次函数y =14x 2,当x >0时,y 随x 的增大而增大;当x <0时,y 随x的增大而减小.8.(0,0) < [解析] 抛物线y =ax 2的顶点坐标是(0,0),比较函数值可以代入计算,也可以利用函数的性质:抛物线开口向下,在对称轴的右边,y 随x 的增大而减小,所以y 1<y 2.9.y =-12x 2<010. B[解析] 由二次函数图象的对称性可知阴影部分的面积为正方形面积的一半,即12×4×4=8.11. C[解析] 由二次项系数的正负性就可以知道抛物线的增减性,如果所给的点没有在对称轴的同一侧,那么可以利用抛物线的对称性,找到这个点的对称点,然后根据增减性再进行判断.因为-1<0,所以当x <0时,y 随x 的增大而增大,又由抛物线的对称性知,y 3的值等于x =-12时的函数值.因为0>-14>-12>-1,所以y 2<y 3<y 1.故选C .12.D [解析] ∵ab>0,∴a ,b 同号.当a >0,b >0时,抛物线开口向上,直线过第一、二、三象限,没有符合题意的选项;当a <0,b <0时,抛物线开口向下,直线过第二、三、四象限.故D 选项符合题意.13. a>-114.解:(1)把x =2,y =-8代入y =ax 2,得-8=22·a ,解得a =-2,∴二次函数的表达式为y =-2x 2.(2)由于a =-2,故抛物线的顶点为最高点, ∴当x =0时,函数有最大值,最大值为0.(3)由于抛物线开口向下,在对称轴的右边,即x >0时,函数y 随x 的增大而减小.15.解:(1)设直线AB 的函数表达式为y =kx +b(k≠0).根据题意,得⎩⎪⎨⎪⎧b =4,4k +b =0,解得⎩⎪⎨⎪⎧k =-1,b =4,∴直线AB 的函数表达式为y =-x +4. 过点P 作PC⊥OA 于点C. 由题意,得12×4·PC=4,∴PC =2.把y =2代入y =-x +4,得2=-x +4, ∴x =2,∴点P 的坐标为(2,2).(2)将点P(2,2)代入y =ax 2,得4a =2, ∴a =12.16.解:(1)当m =-1时,可求得纵坐标y =1;当n =4时,可求得纵坐标y =16,即点A 的坐标为(-1,1),点B 的坐标为(4,16).把点A 、点B 的坐标代入y =kx +b 中,得⎩⎪⎨⎪⎧-k +b =1,4k +b =16,解得⎩⎪⎨⎪⎧k =3,b =4. 当m =-2时,可求得纵坐标y =4;当n =3时,可得纵坐标y =9,即点A 的坐标为(-2,4),点B 的坐标为(3,9).把点A 、点B 的坐标代入y =kx +b 中,得⎩⎪⎨⎪⎧-2k +b =4,3k +b =9,解得⎩⎪⎨⎪⎧k =1,b =6.故答案为3,4,1,6.(2)k =m +n ,b =-mn.证明如下:设点A 的坐标为(m ,m 2),点B 的坐标为(n ,n 2).把点A 、点B 的坐标代入y =kx +b 中,得⎩⎪⎨⎪⎧mk +b =m 2,nk +b =n 2, 解得⎩⎪⎨⎪⎧k =m +n ,b =-mn.(3)由题意,得点D(0,-mn),点A(m ,m 2).①当四边形AOED 为菱形时,有-mn =2m 2,则n =-2m.故答案为n =-2m.②当四边形AOED 为正方形时,有⎩⎪⎨⎪⎧n =-2m ,-mn =-2m ,解得⎩⎪⎨⎪⎧m =-1,n =2.故答案为-1,2.。
沪科版九年级数学上册21.2二次函数y=ax2的图象与性质说课稿

本节课的教学内容为沪科版九年级数学上册21.2二次函数y=ax^2的图象与性质。该章节位于初中数学课程中函数学习的重要部分,是在学习了二次函数的概念及其表达式的基础上,进一步研究二次函数的图象与性质。主要知识点包括:
(3)了解二次函数y=ax^2的图象与系数a的关系,能够根据系数a判断图象的开口方向、对称轴等。
2.过程与方法:
(1)通过观察和分析二次函数y=ax^2的图象,培养学生观察、归纳、总结的能力。
(2)运用数学方法,如数形结合、函数变换等,引导学生探究二次函数的性质。
(3)通过实例分析,使学生能够灵活运用二次函数的图象与性质解决实际问题。
1.数形结合法:通过将二次函数的代数表达式与图象相结合,帮助学生直观地理解函数的性质和变化规律。这种方法符合学生的认知特点,有助于抽象概念的形象化,提高学习效果。
2.探究式教学法:引导学生通过观察、猜想、验证、总结的过程来发现二次函数的性质。这种教学方法能够激发学生的好奇心和探究欲,培养他们的创新精神和实践能力。
(2)二次函数y=ax^2的性质,如单调性、最值等。
(3)二次函数y=ax^2的图象与系数a的关系。
2.教学难点:
(1)如何引导学生理解二次函数y=ax^2的图象特征与系数a的关系。
(2)如何让学生掌握二次函数y=ax^2的性质,并能运用这些性质解决实际问题。
(3)如何培养学生运用数形结合、函数变换等数学方法探究二次函数的性质。
3.展示一个有趣的数学问题,如“如何确定一个抛物线拱门的最高点?”通过问题引导学生思考,自然过渡到二次函数的性质。
(二)新知讲授
在新知讲授阶段,我将采取以下步骤引导学生深入理解二次函数的图象与性质:
22.1.2二次函数y=ax2的图象和性质 参考解析
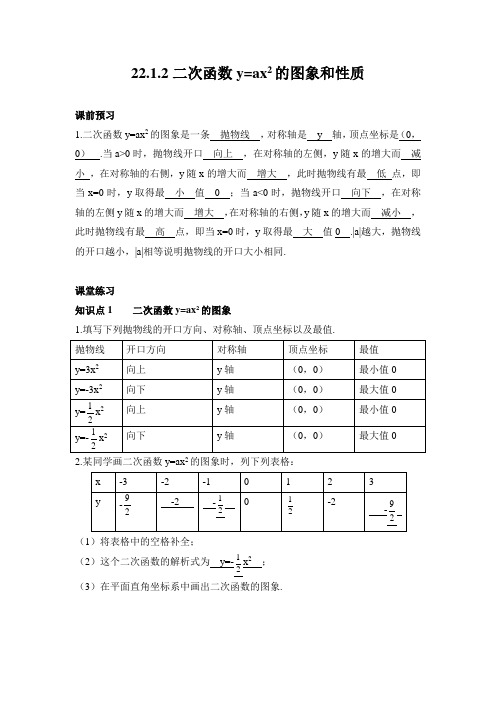
22.1.2二次函数y=ax2的图象和性质课前预习1.二次函数y=ax2的图象是一条抛物线,对称轴是y 轴,顶点坐标是(0,0).当a>0时,抛物线开口向上,在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大,此时抛物线有最低点,即当x=0时,y取得最小值0 ;当a<0时,抛物线开口向下,在对称轴的左侧y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,此时抛物线有最高点,即当x=0时,y取得最大值0 .|a|越大,抛物线的开口越小,|a|相等说明抛物线的开口大小相同.课堂练习知识点1 二次函数y=ax2的图象1.填写下列抛物线的开口方向、对称轴、顶点坐标以及最值.2.某同学画二次函数y=ax2的图象时,列下列表格:(1)将表格中的空格补全;(2)这个二次函数的解析式为y=-1x2;2(3)在平面直角坐标系中画出二次函数的图象.解:(3)函数图象如图所示.知识点2 二次函数y=ax2的性质3.已知二次函数y=(m-2)x2的图象开口向上,则m的取值范围是m>2 .4.下列各点在二次函数y=-2x2图象上的是( B )A.(-1,2)B.(-1,-2)C.(-2,-4)D.(-2,4)5.关于函数y=x2的图象,下列说法错误的是( C )A.它的图象是一条抛物线B.它的开口向上,且关于y轴对称C.它的顶点是抛物线的最高点D.它的顶点在原点处,坐标为(0,0)课时作业1.与二次函数y=x2开口大小相同,方向相反的二次函数是y=-x2.2.二次函数y=-0.2x2的图象是一条开口向下的抛物线,对称轴是y轴,顶点坐标为(0,0).当x= 0 时,函数有最大值0 ;当x >0时,y随x的增大而减小.3.关于函数y=3x2的性质,下列说法正确的是( C )A.无论x为任何实数,y的值总为正B.当x值增大时,y的值也增大C.它的图象关于y轴对称D.它的图象在第一、第三象限内4.已知A (-1,y ₁),B (-2,y ₂)都在二次函数y=x 2上,则y ₁,y ₂之间的大小关系是( C )A.y ₁>y ₂B.y ₁=y ₂C.y ₁<y ₂D.不能确定 5.二次函数y=ax 2(a >0)的图象经过点(3,4),则其图象一定经过点( C ) A.(3,-4) B.(-3,-4) C.(-3,4) D.(4,3)6.如图,当ab >0时,函数y=ax 2与函数y=bx+a 的大致图象是( C )7.二次函数y=2x 2,y=-2x 2,y=12x 2的共同性质是( B ) A.开口向上 B.对称轴是y 轴 C.都有最高点 D.y 随x 的增大而增大 8.已知函数y=(m+2)226m m x +-是关于x 的二次函数. (1)求m 的值;(2)当m 为何值时,函数图象的顶点为最低点? (3)当m 为何值时,函数图象的顶点为最高点? 解:(1)根据二次函数的定义得22026 2.m m m +≠+-=⎧⎨⎩,解得⎩⎨⎧-==.4,221m m ∴m 的值为2或-4;(2)当m=2时,抛物线的开口向上,函数有最小值,函数图象的顶点为最低点; (3)当m=-4时,抛物线的开口向下,函数有最大值,函数图象的顶点为最高点.9.在同一个平面直角坐标系中,画出下列函数的图象:①y=x 2;②y=12x 2;③y=-x 2;④y=-12x 2.从图象上对比,说出解析式中二次项系数a对抛物线的形状有什么影响?解:列表如下描点、连线,函数图象如图所示a的绝对值相同,抛物线的形状相同;a的绝对值越大,开口越小.10.如图,A,B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若2.解:∵AB=22∴BC=122∴点B的横坐标为2代入抛物线的解析式得y=2.∵AB∥x轴,∴点B与点C的纵坐标相同.∴OC=2,即圆的半径为2.由二次函数的对称性得,图中阴影部分的面积等于圆面积的14, 即S 阴影=14π×22=π.11.函数y=ax 2(a ≠0)的图象与直线y=2x-3交于点(1,b ). (1)求a 和b 的值;(2)x 在什么范围时,二次函数y=ax 2中的y 随x 的增大而增大? (3)求抛物线y=ax 2与直线y=-2的两个交点及顶点所围成的三角形的面积. 解:(1)把点(1,b )代入y=2x-3,得b=-1. ∴交点坐标为(1,-1). 把(1,-1)代入y=ax 2,得a=-1. ∴a=-1,b=-1;(2)由(1)得y=-x 2,当x ≤0时,y 随x 的增大而增大; (3)根据题意,得2,2.y x y ⎧=-⎨=-⎩解得2x y ⎧=⎪⎨=-⎪⎩或 2.x y ⎧=⎪⎨=-⎪⎩ ∴两交点坐标分别为(-2),(-2).故S △=12×。
沪科版九年级上21.2.1二次函数的图象和性质(共21张PPT)

(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象 与x轴有交点吗?如果有,交点坐标是什么?
(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(4)当x取什么值时,y的值最小?最小值是什么?你是如何 知道的?
y=-x2
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请 你找出几对对称点,并与同伴交流.
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
你能根据表格中的数据作出猜想
吗?
描点,连线
y 2
驶向胜利 的彼岸
0
-4 -3 -2 -1 -1 1 2 3 4 x -2
-4
-6
?
-8
-10 y=-x2
观察图象,回答问题
描点,连线
驶向胜利 的彼岸
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/8/272021/8/272021/8/272021/8/278/27/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年8月27日星期五2021/8/272021/8/272021/8/27 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年8月2021/8/272021/8/272021/8/278/27/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/8/272021/8/27August 27, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/8/272021/8/272021/8/272021/8/27
二次函数y=ax2的图象和性质ppt课件

例4 如图, 四个二次函数的图象分别对应 ① y=ax2 ;② y=bx2;
③ y=cx2;④ y=dx2,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小; (2)说明a 与c,b 与d 的数量关系.
解:(1)由抛物线的开口方向,知 a > 0,b > 0,c < 0,d < 0,
由抛物线的开口大小,知 |a| > |b|,|c| > |d|, 因此a > b,c < d. ∴ a > b > d > c. (2)∵①与③,②与④分别关于x 轴对称,
∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
课堂练习
1、下列函数中,y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大,开口越小
对称性 顶点最值
关于y轴对称,对称轴方程是直线x=0 顶点坐标是原点(0,0)
当x=0时,y最小值=0 当x=0时,y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图,观察函数y=( k-1)x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的? y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象? 列表、描点、连线
那么,二次函数的图象会是什么样的图形呢?这节课我们 来学习最简单的二次函数y=ax2的图像
不同点: a的值越大,开口越小.
22.1.2 二次函数y=ax2的图象和性质

x
… -2 -1
0
1
y=2x2 …
y=2x2
…
(2)描点并连线:
2
…
…
…
【思路点拨】 首先列表求出函数图象上点的坐标,进而描点连线画出图象即可.注 意连线时一定要用平滑的实线连接.
解:(1)8 2 0 2 8 -8 -2 0 -2 -8 (2)
类型二:二次函数y=ax2图象的性质的应用
例2 已知函数y=ax2的图象过点(1, 1 ).
2
增大而减小.
(2)在其图象上有两点(x1,y1),(x2,y2),且x1>x2>0,比较y1,y2的大小.
【思路点拨】 (2)二次函数y=ax2的对称轴为y轴,由(1)知a<0,所以在其对称轴 的右侧y随x的增大而减小,又x1>x2>0,故y1<y2. 解:(2)因为x1>x2>0, 所以y1<y2.
(1)简述函数y=ax2的性质;
2
【思路点拨】 (1)把点(1, 1 )代入函数y=ax2的解析式求得a的值,即可判定函
数的性质.
2
解:由题意得 a=- 1 ,所以 y=- 1 x2.
2
2
(1)函数 y=- 1 x2,开口向下,在 y 轴左侧 y 随 x 的增大而增大,在 y 轴右侧 y 随 x 的
22.1.2 二次函数y=ax2的图象和性质
1.二次函数y=ax2的图象
二次函数y=ax2的图象是 抛物线 ,对称轴与抛物线的交点叫做 顶点 ,顶点是
(0,0) ,当a>0时,抛物线的开口 向上 ,顶点是抛物线的最 低 点;当a<0时, 抛物线的开口 向下 ,顶点是抛物线的最 高 点.对于y=ax2,|a|越 大 ,抛物 线的开口越小.
21.2 二次函数的图象和性质(2)
1 2 y 2x 图像的开口比y x 图像的开口小 2
y=ax2 (a≠0) 图 象
O
a>0
y
O
a<0 y x
x
开口方向 向上 向下 顶点坐标 (0 ,0) (0 ,0) 对称轴 y轴 y轴 当x<0时, 增 当x<0时, y随着x的增大而增大。 y 随着 x 的增大而减小。 减 当x>0时, 当x>0时, y随着x的增大而减小。 性 y随着x的增大而增大。 x=0时,y最小=0 x=0时,y最大=0 极值 抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小.
的图象,分别指出它们的开口方向,对称轴和顶点 坐标。抛物线有最高点还是最低点?图象何时上升, 下降?
2 -10 -5 5 10 -2
-4
-6
-8
1 y=- x2 2
-10
y=-2x2
-12
y=-x 2
y 2x
抛物线y=ax2(a≠0) 1 2 y x 的图象是顶点在原 2 点、对称轴是y轴所 在直线的抛物线.
m2 m
练习: 已知点A(3,a)在二次函数y=x2的图像上。 (1)求a的值; (2)点B(3,-a)在二次函数y=x2的图像上吗? 思考: 1、已知二次函数y=-x2. (1)当-2<x<3时,求y的取值范围; (2)当-4<y<-1时,求x的取值范围. 2、已知抛物线y=ax2过M(-2,-2) (1)求出这个函数关系式并画出函数图象。 (2)写出抛物线上与点M关于y轴对称的点N的坐标, 并求出△MON的面积。
例题:已知抛物线y=ax2经过点A(-2,-8). (1)求此抛物线的函数解析式; (2)判断点B(-1,- 4)是否在此抛物线上. (3)求出此抛物线上纵坐标为-6的点的坐标.
21.2.1_y=ax2的图象和性质--已修订
y随着x的增大而增大;在 对称轴的左 侧, y随着x的增大而减小,当x= 0 时,
函数y的值最小,最小值是 0 ,抛物 线y=2x2在x轴的
3
上 方(除顶点外)。 增大而增大 ;当x〉0时,y随着x
(2)抛物线 y 2 x 2 在x轴的 下 方(除顶点外),当x
〈0时,y随着x的
的 0是
增大而减小,当x=0时,函数y的值最大,最大值
轴 顶点y 是
向上 ,对称轴是
,
;
(0,0) y轴 ,顶点是 ;
3、函数y=3 x2的图象的开口 向上 ,对称轴是 高 顶点是抛物线的最 点 (0,0)
2、函数y=-3x2的图象的开口 向下 ,对称轴 y轴 (0,0) 是 ,顶点是___ 顶点是抛物线的最 点 低 4、函数y= -0.2x2的图象的开口 向下 ,对称轴是___,y轴 顶点是 (0,0) ;
y ax
2
二次函数: 一般地,形如 y=ax2+bx+c (a、b、c为常数,a≠0) 的函数,叫做二次函数.其中,是x自变量,a,b,c分 别是函数表达式的二次项系数、一次项系数 和常数项.
一次函数的图像是一条直线, 二次函数的图像是 什么形状呢?通常怎样画一个函数的图像?
还记得如何用 描点法画一个 函数的图象呢?
观察函数y=x2的图象,则下列判断中正确的 是( A ) (A) 若a,b互为相反数,则x=a与x=b 的函数值相等; (B) 对于同一个自变量x,有两个函数 值与它对应. (C) 对任一个实数y,有两个x和它对应. y (D) 对任意实数x,都有y>0.
o x
(1)抛物线y=2x2的顶点坐标是 (0,0) , 对称轴是 y轴 ,在 对称轴的右 侧,
《二次函数y=ax^2的图象与性质》知识点解读
《二次函数y=ax²的图象与性质》知识点解读知识点1 二次函数y=ax²的图象及有关概念二次函数的图象函数y=ax2(a≠0)的图象是一条关于y轴对称的曲线,这条曲线叫做抛物线。
实际上,二次函数的图象都是抛物线,y轴是抛物线y=ax2(a≠0)的对称轴,对称轴与抛物线的交点是抛物线的顶点。
用描点法画二次函数y=ax2(a≠0)的图象(1)按步骤列表、描点、连线。
(2)用描点法画二次函数y=ax2(a≠0)的图象时,应在O(0,0)点左右两侧(或在对称轴左右两侧)对称的选取自变量x的值,在计算y的值,这样的对应值选择月密集,描出的图象越精准。
通常情况下,画图一般选取9个点,草图通常取5或7个点,但必须画出抛物线的顶点,然后对称的取其他各点。
实际问题应在自变量取值范围内选取适当的几个点,一般选7个点,再进行描点。
连线时要注意图象的平滑,特别是顶点处更要注意,不能画得太平或者太尖,要顺势用平滑曲线连接。
知识点2 二次函数y=ax²的性质(1)二次函数y=ax2(a≠0)的图象是一条抛物线。
我们把二次函数y=ax2(a≠0)的图象叫做抛物线y=ax2。
(2)抛物线y=ax2(a≠0)的对称轴是y轴(即直线x=0),顶点是原点。
(3)当a>0时,抛物线y=ax2的开口向上,顶点是它的最低点,抛物线在x轴上方(顶点在x轴上),并且向上无限延伸;当a<0时,抛物线y=ax2的开口向下,顶点是它的最高点,抛物线在x 轴下方(顶点在x轴上),并且向下无限延伸。
(4)当a>0时,在y 轴左侧,y随x的增大而减小,在y 在右侧,y随x 的增大而减大,函数y的值,当x=0时最小,最小值是0;当a<0时,在y 在左侧,y随x的增大而增大,在y 在右侧,y随x 的增大而减小,函数y的值,当x=0时最大,最大值是0。
(5)当a 的绝对值越大,图象越靠近y 轴,抛物线开口越窄;当a 的绝对值越小,图象越远离y 轴,抛物线开口越宽。
新沪科版九年级数学上册同步教案:21.2 第1课时 二次函数y=ax^2的图像和性质
21.2 二次函数的图象和性质第1课时 二次函数y=ax 2的图象和性质◇教学目标◇【知识与技能】会用描点法画出函数y=ax 2的图象,理解并掌握抛物线的有关概念及其性质.【过程与方法】经历探索二次函数y=ax 2的图象及性质的过程,获得利用图象研究函数性质的经验,培养学生分析、解决问题的能力.【情感、态度与价值观】培养学生观察、思考、归纳的良好思维品质.◇教学重难点◇【教学重点】理解抛物线的有关概念及性质,会用描点法画出二次函数y=ax 2的图象.【教学难点】用描点法画出二次函数y=ax 2的图象以及探索二次函数的性质.◇教学过程◇一、情境导入从桌面弹射粉笔,从空中平抛粉笔和乒乓球,观察物体在空中的运动路线,思考运动路线有何规律?怎样用数学规律来描述呢?二、合作探究探究点1 二次函数y=ax 2的图象典例1 (1)用描点法在同一坐标系中画出y=12x 2,y=x 2,y=2x 2的图象. (2)比较上述图象,抛物线的开口大小与二次函数的二次项系数有何关系?(3)根据你的研究结果,请你在上述平面直角坐标系中近似画出函数y=32x 2的图象.[解析] (1)y=12x 2,y=x 2,y=2x 2的图象如图所示.(2)抛物线的开口大小与二次函数的二次项系数的关系:系数越大,开口越小.(3)平面直角坐标系中近似画出函数y=32x 2的图象如图虚线所示.已知y=(k+2)x k2+k是二次函数.(1)求k的值;(2)画出函数的图象.[解析](1)∵y=(k+2)x k2+k为二次函数,∴{k 2+k=2,k+2≠0,解得k=1.(2)当k=1时,函数的表达式为y=3x2,用描点法画出函数的图象.列表:描点:(-1,3),(-12,34),(0,0),(12,34),(1,3).连线:用光滑的曲线按x从小到大的顺序连接各点,图象如图所示.探究点2二次函数y=ax2的性质典例2已知点(-3,y1),(1,y2),(√2,y3)都在函数y=x2的图象上,则y1,y2,y3的大小关系是.[解析]方法一:把x=-3,1,√2分别代入y=x2中,得y1=9,y2=1,y3=2,则y1>y3>y2.方法二:如图,作出函数y=x2的图象,把各点依次在函数图象上标出.由图象可知y1>y3>y2.方法三:∵该图象的对称轴为y轴,a>0,∴在对称轴的右边,y随x的增大而增大,而点(-3,y1)关于y轴的对称点为(3,y1).又∵3>√2>1,∴y1>y3>y2.(1)求m的值.(2)当m为何值时,该函数图象的开口向下?(3)当m为何值时,该函数有最小值?(4)试说明函数图象的增减性.[解析] (1)∵函数y=(m+3)x m 2+3m -2是关于x 的二次函数,∴m 2+3m-2=2,m+3≠0,解得m 1=-4,m 2=1.(2)∵函数图象的开口向下,∴m+3<0,∴m<-3,∴当m=-4时,该函数图象的开口向下.(3)∵当m+3>0时,抛物线有最低点,函数有最小值,∴m>-3,∴当m=1时,该函数有最小值.(4)当m=1时,x>0时,y 随x 的增大而增大,x<0时,y 随x 的增大而减小;当m=-4时,x>0时,y 随x 的增大而减小,x<0时,y 随x 的增大而增大.二次函数y=ax 2的最值是图象顶点的纵坐标,当a>0时,函数图象的开口向上,顶点是最低点,三、板书设计二次函数y=ax 2的图象和性质二次函数y=ax 2的图象和性质{ 开口方向顶点坐标:(0,0)对称轴:y 轴最值增减性◇教学反思◇本节课的内容主要是研究二次函数y=ax 2在a 取不同值时的图象,并引出抛物线的有关概念,再根据图象总结抛物线的有关性质.教学过程中,强调学生自主探索和合作交流,在操作中探究二次函数y=ax 2(a>0)的图象与性质,培养学生动手、动脑、探究归纳问题的能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不在 ____
(填“在”或“不在”)该函数图象上.
1.二次函数y=ax2的图象和性质
[归纳] 二次函数 y=ax2 的图象是一条抛物线,当 a>0
下 , 时,抛物线开口向 上 ____,当 a<0 时,抛物线开口向____ 0) . 抛物线的对称轴是 y轴 ____,顶点坐标是 (0,____
1.二次函数y=ax2的图象和性质
②描点、连线,如图21-2-3所示.
1.二次函数y=ax2的图象和性质
[归纳总结] 画函数图象时,要注意自变量的选取具有对 称性.所画图象的两个端点要向两侧适当延伸.
1.二次函数y=ax2的图象和性质
探究问题二 利用函数图象上点的坐标与函数对应值的关系, 判断点是否在函数图象上
例2 已知点 A(-2,1)在抛物线 y=ax2 上,则下列各
课 堂 小 结
二次函数 y=ax2 的图象和性质 顶点 原点 对称轴 y轴 a 的值 a> 0 a< 0 开口方向 向上 向下 增 y随x的 y随x的 当 x>0 时 增大 减小 减 增大而_______ 增大而_______ 情 y随x的 y随x的 当 x<0 时 增大 减小 况 增大而_______ 增大而_______ 最值 当 x=0 时 y 最小=0 y 最大=0
2
1 2 ∴抛物线的关系式是 y= x . 4 1 当 x=2 时,y=1;当 x=1 时,y= ; 4 1 1 当 x=0 时,y=0;当 x=- 时,y= , 2 16 故(1,-2)不在抛物线上.
1.二次函数y=ax2的图象和性质
[归纳总结] 已知点在函数图象上,点的坐标就能使函数
关系式成立,将点的坐标对应的变量的值代入到函数关
=ax2 的开口方向、对称轴和顶点坐标 1 4.二次函数 y= x2 的图象是开口向 上 ____的抛物线, 3
0) . 对称轴是 y轴 ____,顶点坐标是 (0, ____
1 2 5. 二次函数 y=- x 的图象是开口向 下 ____的抛物线, 3 对称轴是 y轴 ____,顶点坐标是 (0,0) ____.点(-1,3)
系式中,即可求出函数关系式或点的另一个坐标.
1.二次函数y=ax2的图象和性质
探究问题三 利用二次函数y=ax2的性质,根据图象判断其增 减性 例 3 [2014· 安徽凤阳三中月考] 已知点 A(-3,y1),B(-1,
2 2 y2),C(2,y3)在抛物线 y= x 上,则 y1,y2,y3 的大小关系是( D ) 3 A.y1<y2<y3 C.y1<y3<y2 B.y1>y2>y3 D.y2<y3<y1
1.二次函数y=ax2的图象和性质
解:(1)设二次函数的表达式为 y=ax2(a≠0),则-3=a×12, 解得 a=-3,所以 y=-3x2. (2)∵a<0,∴二次函数的图象在对称轴右侧部分 y 随 x 的增大 而减小. (3)∵a=-3<0,∴函数有最大值,当 x=0 时,函数的最大 值为 0.
点或更多的点;
描点 (2)________ :先将 y 轴一侧的点描出来,再根据对称性描出 y
轴另一侧的点; 连线 (3)________ :按自变量从小到大或从大到小的顺序将描出的点 平滑的曲线 用__________________ 连接起来.
1.二次函数y=ax2的图象和性质
学习目标 2
阅读教材例 2 与探究内容,知道二次函数 y
[归纳总结] 当所给的点不在抛物线对称轴的一侧时,要根据它
的对称性,将其转化为在对称轴一侧的点,然后再根据增减性
比较函数值的大小.
1.二次函数y=ax2的图象和性质
探究问题四 利用|a|对函数y=ax2的影响,根据|a|比较抛物 线的开口大小
例 4 [2013· 安徽淮北“五校”联考]下列抛物线开口最大的是( A ) 1 2 1 2 A.y=- x B.y=- x 3 2 5 2 C.y= x D.y=(2+ 2)x2 3 1 1 5 [解析] 四个选项中 ,二次项系数的绝对值依次为 , , , 3 2 3 1 1 5 1 2 2+ 2,且 < < <2+ 2,所以 y=- x 的开口最大 ,故选 A. 3 2 3 3
1 2 9.观察探究二次函数 y=- x 的图象,在对称轴的左 2 侧,当 x<0 时,y 随 x 的增大而 增大 ____;在对称轴的右侧, 当 x>0 时,y 随 x 的增大而 减小 ____.
1.二次函数y=ax2的图象和性质
[归纳] 对二次函数y=ax2,当a>0时,在对称轴的左侧,即 x<0时,y随x的增大而减小;在对称轴的右侧,即x>0时,y
y=3x2 „
1.二次函数y=ax2的图象和性质
2.在所给的方格纸中,用描点法作出题1中的函数图象.
[答案] 略
1.二次函数y=ax2的图象和性质
3.观察上题所作的图象可知,y=3x2 的图象是一条 ____, 图象关于 抛物线 ____ 图象上除了点(____ 0 , y轴 对称,
0 ,其余都在 x 轴的上方,故这一点是它的顶点. ____) [ 归 纳 ] 由 函 数 表 达 式画 二 次 函数 y = ax2 的 图 象 , 一 般用 描点法 ,其一般步骤是: ________ 列表 (1)________ :先取原点(0,0),然后在 y 轴两侧对称地取 3 对
1.二次函数y=ax2的图象和性质Байду номын сангаас
[归纳总结] 抛物线 y=ax2 中 a 的绝对值越大,开口越小.
1.二次函数y=ax2的图象和性质
探究问题五 根据二次函数y=ax2的图象和性质,综合运用 相关知识解答问题
例 5 [2014· 安徽宁国黄冈实验学校阶段测试] 已知一个二 次函数图象的对称轴是 y 轴,顶点是原点,且经过点(1,-3). (1)写出这个二次函数的表达式; (2)该图象在对称轴右侧部分,y 随 x 的增大怎样变化? (3)指出这个函数有最大值还是最小值,并求出这个值.
出下列函数的图象, 并比较两个图象之间的关系: (1)y=4x2; (2)y=-4x2.
解:①列表:
x y=4x2 y=-4x2 3 1 1 3 1 „ - -1 - 0 „ 2 2 2 2 4 1 0 1 4 9 „ „ 9 „ -9 -4 - 1 0 -1 -4 -9 „
1.二次函数y=ax2的图象和性质
2 2 [解析] 抛物线 y= x 的开口向上,顶点为(0,0),对称轴是 y 轴, 3 当 x<0 时,y 随 x 的增大而减小,设 C(2,y3)关于 x=1 的对称点 为(-2,y4),则 y4=y3.又∵-3<-2<-1,∴y1>y4>y2,即 y2 <y3<y1.故选 D.
1.二次函数y=ax2的图象和性质
1 2 小 值, 7. 已知二次函数 y= x , 当 x=____ y 有最____ 0 时, 5 是____ 0 .
1.二次函数y=ax2的图象和性质
[归纳] 二次函数 y=ax2,当 a>0,x=____ 0 时,函数值
0 ;当 a<0,x=____ y 有最小值,最小值是___ 0 时,函数值 y 0 . 有最大值,最大值是____
随x的增大而增大.当a<0时,在对称轴的左侧,即x<0时,y
随x的增大而增大;在对称轴的右侧,即x>0时,y随x的增大 而减小.
1.二次函数y=ax2的图象和性质 重难互动探究 探究问题一 利用画二次函数图象的方法,画二次函数y=
ax2的图象 例 1 [教材例题变式题] 在同一平面直角坐标系中,画
1.二次函数y=ax2的图象和性质
学习目标 4 知道二次函数 y=ax2 的图象,会根据图象分析 它的增减性 1 2 8.观察例 2 中二次函数 y= x 的图象,在对称轴的左 2
侧,当 x<0 时,y 随 x 的增大而 减小 ____;在对称轴的右侧, 当 x>0 时,y 随 x 的增大而
增大 ____.
1.二次函数y=ax2的图象和性质
[反思] 二次函数 y=ax2 的图象是抛物线, 其形状是由 a 的绝对值决定的,当 a 相等时,抛物线的形状相同,那么二 次函数 y=ax2+k 与 y=ax2 的图象有什么关系? [答案] 作出二次函数 y=ax2+k 与 y=ax2 的图象,找 出它们之间的关系,即二次函数 y=ax2+k 的图象与 y=ax2 的图象形状相同,只是沿 y 轴向上或向下平移了.
数 学
新课标(HK) 九年级上册
21.2 二次函数的图象和性质
1. 二次函数 y=ax2 的图象和性质
1.二次函数y=ax2的图象和性质
基础自主学习 学习目标1 知道画函数图象的步骤,会画二次函数y=ax2 的图象
1.填表,根据所给的自变量 x 的值,计算出对应的函 数值.
x „ - 3 1 -1 - 0 2 2 27 3 3 0 4 4 1 1 2 3 3 4 3 „ 2 27 „ 4
点不在此抛物线上的是( B ) A.(2,1) C.(0,0) B.(1,-2)
1 1 D.-2,16
[解析] 根据点在抛物线上,先求出抛物线的关系式,然
后判断选项中各点的坐标是否适合抛物线的关系式.
1.二次函数y=ax2的图象和性质
∵点 A(-2,1)在抛物线 y=ax2 上, ∴把 x=-2,y=1 代入到 y=ax2 中, 1 得 1=a×(-2) ,即 a= , 4
学习目标 3 知道二次函数 y=ax2 的最值,会根据图象 求它的最值
6.二次函数 y=-2x2 的图象是一条抛物线,且关于 y
0 ,____) 0 ,图象 轴对称,对称轴与抛物线的交点坐标是(____
上除该点外,所有的点都在 x 轴的 下方 ____,故函数有最大
0 时,y 最大=____ 0 . 值,即当 x=____
1.二次函数y=ax2的图象和性质
[归纳总结] 1.根据二次函数的图象设出函数表达式 y=ax2, 然后利用图象上点的坐标代入求解. 2.二次函数 y=ax2 的增减性取决于二次项系数 a 的符号及 图象相对于对称轴的位置,在判断其增减性时,应先识别 a 的符 号和点的位置.
