(完整word版)七年级实数讲义
《实数》 讲义

《实数》讲义一、实数的概念实数,这个在数学世界中极为基础且重要的概念,是我们理解数量关系和解决数学问题的关键。
简单来说,实数就是包括有理数和无理数的数集。
有理数,我们都很熟悉,像整数(正整数、零、负整数)和分数(正分数、负分数)都属于有理数。
而无理数呢,则是那些无限不循环小数,比如大家熟知的圆周率π,还有根号 2 等等。
实数可以直观地理解为在数轴上能找到对应点的数。
也就是说,数轴上的每一个点都代表着一个实数,反之,每一个实数也都能在数轴上找到对应的点。
二、有理数有理数是实数的重要组成部分。
整数,像-3、0、5 这样的数,它们没有小数部分,清晰明了。
分数呢,比如 1/2、3/4 ,可以表示为两个整数的比值。
有理数具有一些很重要的性质。
比如,两个有理数相加、相减、相乘或相除(除数不为 0),结果仍然是有理数。
而且,有理数是可以用有限小数或无限循环小数来表示的。
我们在日常生活中,很多常见的数量关系都可以用有理数来描述。
比如购物时的价格、物品的数量等等。
三、无理数无理数虽然不像有理数那样“规矩”,但在数学中同样不可或缺。
像根号 2 ,它的值约为 141421356……,这个小数无限且不循环。
圆周率π,约为31415926……,也是一个无限不循环小数。
无理数的发现,让人们对数学的认识更加深入和丰富。
虽然它们的数值看起来没有规律,但通过数学方法和计算,我们可以对它们进行近似和研究。
四、实数的运算实数的运算包括加法、减法、乘法、除法和乘方等。
加法和减法:实数的加法和减法遵循相同的规则,即将对应位上的数字相加或相减,并考虑进位和借位。
乘法:两个实数相乘,先将它们按照整数乘法的规则相乘,然后确定积的符号(同号得正,异号得负),最后根据小数位数确定积的小数点位置。
除法:将除数变为倒数,然后与被除数相乘。
乘方:一个实数的 n 次幂,就是将这个实数乘以自身 n 次。
在进行实数运算时,要特别注意运算顺序,先算乘方、开方,再算乘除,最后算加减。
精品 七年级数学寒假讲义 实数

实数 第01课 平方根1.乘方:“n a ”.乘方的结果叫做幂,a 叫做底数,n 叫做指数,读作a 的n 次方或a 的n 次幂.2.平方:“2a ”,读作a 的平方或a 的二次方.3.平方的性质:任何数的平方都是非负数;算术平方根概念:一般地,如果一个正数的平方等于a ,那么这个数叫做a 的算术平方根,也就是说,如果x 2=a ,(x>0)那么x 叫做a 的算术平方根.则a x = 算术平方根性质:(1)当a ≥0时a ≥0(由定义得出)即非负数的算术平方根是非负数⎭⎬⎫⎩⎨⎧<-≥==)0()0(2a a a a a a (由定义得出)(2)个数性质:正数和0的算术平方根据都只有一个(3)还原性质:当0≥a 时,a a =2)(,即非负数算术平方根的平方等于该非负数 完全平方数:能够完全开方开的尽的数。
如1,4,9,16,...平方根概念:一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根或二次方根,也就是说,如果x 2=a ,那么x 叫做a 的平方根.则a x ±=开平方:求一个数a 的平方根的运算叫做开平方.即求a ±的运算叫开平方. 表示方法:一个正数a 的平方根表示为a ±;若x 2=a (a >0)则x=a ±。
平方根的性质:(1)个数性质:正数有两个平方根,它们互为相反数,0只有一个平方根就是0本身.负数没有平方根 (2)还原性质:(由定义得出)当a ≥0时(a ±)2=a 即:非负数的平方根的平方等于该数 (三)a a a ±-,,的含义:a :当a ≥0时,表示a 的算术平方根a -:当a ≥0时,表示a 的算术平方根的相反数a ±:当a ≥0时,表示a 的平方根平方根的求法: 逆运算法,查表法,计算器,式子计算查表法的理论根据: 如果正数的小数点向右或向左移动2位,那么它的算术平方根的小数点就相应地向右、向左移动一位. 查表外数小数点移动法则:(1)被开方数的小数点要两位两位地移动,移动到使被查数成为有一位或两位整数的数 (2)被开方数的小数点每移动两位,查得的算术平方根的小数点要向相反方向移动一位。
七年级下册实数以及实数的运算讲义

环 球 雅 思 教 育 学 科 教 师 讲 义年 级 : 上 课 次 数 :学 员 姓 名 : 辅 导 科 目 : 学 科 教 师 : 课 题课 型 □ 预习课 □ 同步课 □ 复习课 □ 习题课 授课日期及时段教 学 内 容【基础知识网络总结与新课讲解】6.2 实 数知识点一 无理数的概念定义:无限不循环小数叫做无理数,如π=3.1415926…,2 1.414213=,-1.010010001…,都是无理数。
注意:①既是无限小数,又是不循环小数,这两点必须同时满足;②无限不循环小数与有限小数、无限循环小数的本质区别是:前者不能化成分数,而后两者都可以化成分数;③凡是整数的开不尽的方根都是无理数,如2、3等。
例1 332278,3, 3.141,,,,2,0.1010010001,1.414,0.020202,7378π-----有理数{ } 无理数{ }想一想:有理数与无理数的区别?注意:判断一个数是否为无理数,不能只从形式上看,带根号的不一定是无理数,只有开方开不尽的数是无理数。
练习:下列说法正确的是( )A.分数是无理数B.无限小数是无理数C.不能写成分数形式的数是无理数D.不能再数轴上表示的数是无理数知识点二 实数1. 实数:有理数和无理数统称为实数 实数的分类:① 按定义分类: ② 按大小分类例2.判断下面的语句对不对?并说明判断的理由。
①无限小数都是无理数;②无理数都是无限小数;③带根号的数都是无理数;④有理数都是实数,实数不都是有理数;⑤实数都是无理数,无理数都是实数;⑥实数的绝对值都是非负实数;⑦有理数都可以表示成分数的形式。
2. 实数的几个有关概念:①相反数:a与-a互为相反数,0的相反数是0。
a+b=0⇔a、b互为相反数。
②倒数:若0a≠,则1a称为a的倒数,0没有倒数。
1ab a=⇔、b互为倒数。
③绝对值:一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数,0的绝对值是0。
《实数》 讲义

《实数》讲义一、实数的概念在数学的世界里,实数是我们经常接触和运用的一个重要概念。
那什么是实数呢?简单来说,实数就是有理数和无理数的统称。
有理数包括整数和分数。
整数像-3、-2、-1、0、1、2、3 等等,分数则是可以表示为两个整数之比的数,比如 1/2、3/4 等。
而无理数则是那些不能表示为两个整数之比的数,最常见的就是圆周率π和开方开不尽的数,如√2 等。
二、实数的分类为了更好地理解和研究实数,我们对其进行分类。
1、按定义分类有理数:整数(正整数、0、负整数)和分数(正分数、负分数)。
无理数:无限不循环小数。
2、按正负分类正实数:包括正有理数(正整数和正分数)和正无理数。
零:既不是正数也不是负数。
负实数:包括负有理数(负整数和负分数)和负无理数。
实数具有许多重要的性质,这些性质是我们进行数学运算和解决问题的基础。
1、有序性任意两个实数 a 和 b,要么 a < b,要么 a = b,要么 a > b,这三种关系必有一种成立。
2、稠密性在任意两个不同的实数之间,都存在着无穷多个实数。
3、四则运算封闭性两个实数进行加、减、乘、除(除数不为 0)运算,其结果仍然是实数。
四、实数的数轴表示实数与数轴上的点是一一对应的关系。
也就是说,数轴上的每一个点都对应着一个唯一的实数,反过来,每一个实数也都可以在数轴上找到对应的点。
我们以 0 为原点,向右为正方向,单位长度为 1。
比如,数字 2 就在原点右边 2 个单位长度的位置,-3 就在原点左边 3 个单位长度的位置。
通过数轴,我们可以直观地比较实数的大小。
数轴上右边的点所表示的实数总是大于左边的点所表示的实数。
1、加法同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
一个数与 0 相加,仍得这个数。
例如:3 + 5 = 8,-3 +(-5) =-8,3 +(-5) =-2。
2、减法减去一个数,等于加上这个数的相反数。
(完整版)实数讲义
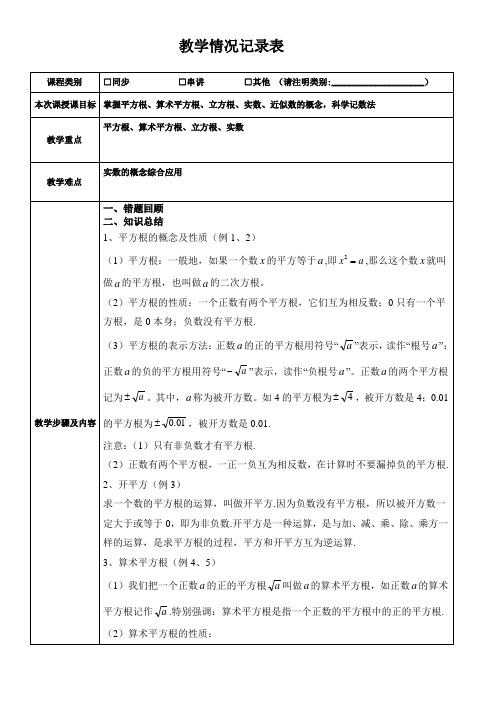
当 时, ,例如
5、立方根的概念及性质(例8)
(1)立方根的定义:一般地,如果一个数 的立方等于 ,即 ,那么这个数 就叫做 的立方根,也叫做 的三次方根.如 ,2叫做8的三次方根.
(2)立方根的性质:一个正数有一个正的立方根,一个负数有一个负的立方根,0的立方根是0.
(3)立方根的表示:数 的立方根用符号“ ”来表示,读作“三次根号 ”。其中, 称为被开方数,3称为根指数。
12、近似数(例15)
接近实际的数或在计算中按要求所取的与某个准确数接近的数,我们把它叫做近似数.
注意:近似数产生的原因主要有两种:(1)有些需要度量的数,由于受到测量工具精度的限制,得到完全准确的数值几乎是不可能的,这就需要用和准确数尽可能接近的数来表示;(2)有时没有必要完全准确,用近似数表示就可以了.
6、开立方(例9)
求一个数的立方根的运算,叫做开立方.
(1)开立方是一种运算,是与加、减、乘、除、乘方一样的运算,是求立方根的过程,立方和开立方互为逆运算.
(2)由立方根的性质可知开立方的结果是唯一的.
7、无理数(例10)
(1)无理数:无限不循环小数叫做无理数.
(2)无理数的常见类型主要有以下3种:
(3)对于带有“文字单位”的近似数,在确定其精确到哪一位时,分为两种情况:文字单位前面是整数,如18亿,则它精确到文字单位这一位(亿位);文字单位前面是小数,如2.61万,则先将它还原为普通数26100,此时1所在的数位(百位)就是它精确到的数位.
三、例题讲解
1、下列各数中,没有平方根的是()
A.1 B.0 C. D.
所有带根号且被开方数是开方开不尽的数;
圆周率 及一些含有 的数;
无理数与有理数的和、差,无理数乘或除以一个不为0的有理数所得的结果.
初中数学七年级下册第六章:实数知识讲解

举一反三:
【变式】已知 x、y 是实数,且 3x 4 +(y2-6y+9)=0,若 axy-3x=y,则实数 a 的值是( )
1
A.
4
1
B.-
4
7
C.
4
7
D.-
4
【答案】A. ∵ 3x 4 +(y-3)2=0,
3, 4
a3
1 1 3
.
4,
a4
1 . 1 4
1, 3
3
4
a5
1. 1 ( 1)
3, 4
a6
1 1 3
.
4, ……..三个一循环,因此 a2009
a2
1 1 ( 1)
3 .
4
3
4
3
类型三、实数大小的比较
3.若 a 2007 , b 2008 ,试不用将分数化小数的方法比较 a、b 的大小.
2008
要点诠释:
若 a a, 则 a 0、 a -a, 则 a 0、 a-b 表示的几何意义就是在数轴上表示数 a 与数 b 的点之间
的距离.
考点三、实数与数轴 规定了原点、正方向和单位长度的直线叫做数轴,数轴的三要素缺一不可. 每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数.
C.3 个
D.4 个
【答案】C;
【解析】在上面所给的实数中,只有 3 , ,-0.1010010001…这三个数是无理数,其它五个数都是
2
有理数,故选 C. 【点评】对实数分类,不能只为表面形式迷惑,而应从最后结果去判断.首先明确无理数的概念,即
“无限不循环小数叫做无理数”.一般来说,用根号表示的数不一定就是无理数,如 4 =2 是
初中数学七年级数学第六章实数(全章节图文详解)

七年级数学第六章实数
实数
七年级数学第六章实数
目录:
1.算术平方根 2.平方根 3.立方根 4.有理数 5.无理数 6.实数定义 7.实数的运算 8.实数的大小比较
七年级数学第六章实数
1.算术平方根的定义: 一般地,如果一个正数x的平方等于 2 a,即 x =a,那么这个正数x叫做a的 算术平方根。a的算术平方根记为 a , 读作“根号a”,a叫做被开方数。
特殊:0的算术平方根是 0 。
记作:0 0
七年级数学第六章实数
2. 平方根的定义:
一般地,如果一个数的平方等于a ,那 么这个数就叫做a 的平方根(或二次方 根).
注意:计算过程中要多保留一位!
七年级数学第六章实数
3.实数运算
当数从有理数扩充到实数以后,实数之
间不仅可以进行加 减 乘 除 乘方运算,
又增加了非负数的开平方运算,任意实数
可以进行开立方运算。进行实数运算时, 有理数的运算法则及性质等同样适用。
七年级数学第六章实数
练习:
2 3 3 2 5 3 3 2
不 要 遗 漏
解: (3 y ) 4 9 4 3 y 9
2
解:
2 3 27 ( x ) 125 3
2 3 125 (x ) 3 27 2 5 x 3 3
2 3 125 x 3 27
1 2 y 2 或y 3 3 3
2 y 3 3
x 1
七年级实数讲义

1月17日复华七年级数学实数12、1 实数得概念一、引入 数得范围至此扩大到了有理数,复习有理数得定义与分类:定义:整数与分数统称为有理数。
分类: 有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数如果把整数瞧作分母为1得分数,那么有理数就就是用两个整数之比表示得分数:)0,(≠q q p qp都是整数,且 质疑:数得扩充就是不就是到此为止了呢?有理数就是不就是够用了?还有没有不就是有理数得数呢? 问题2:正方形ABCD 得边长怎样表示?分析:设正方形ABCD 得边长为x,那么x 2=2,即x 就是这样一个数,它得平方等于2。
这个数表示面积为2得正方形得边长,就是现实世界中真实存在得线段长度。
由于这个数与2有关,我们现在用2(读作“根号2”)来表示。
追问:面积为3得正方形,它得边长又如何表示?若面积为5呢? 问题3:2就是有理数吗? 因为:有理数=分数)0,(≠q q p qp都是整数,且= 而2肯定不能表示为分数(详见P36),,所以2只能就是“无限不循环小数”。
问题4:无限不循环小数还有吗?就是分数吗? Π就是有理数码? 二、归纳1.无理数(1)无限不循环小数叫做无理数。
(2)无理数包括正无理数与负无理数。
(3)只有符号不同得两个无理数,它们互为相反数。
2.实数(1)有理数与无理数统称为实数。
(2)实数可以这样分类:正有理数有理数 零 ——有限小数或无限循环小数实数 负有理数{{正无理数无理数 ——无限不循环小数负无理数三、练习1.将下列各数填入适当得括号内: 0、-3、2、6、3、14159、722、32.0 、5、π、0、3737737773…、 有理数:﹛ ﹜;无理数:﹛ ﹜; 正实数:﹛ ﹜;负实数:﹛ ﹜; 非负数:﹛ ﹜;整 数:﹛ ﹜、 提问:常见得无理数得形式有哪几种?(三种形式) 2.请构造几个大小在3与4之间得无理数。
3.就是非题(1) 无限小数都就是无理数; 无理数都就是无限小数; (2)正实数包括正有理数与正无理数; (3)实数可以分为正实数与负实数两类; (4)带根号得数都就是无理数; (5)不含根号得数不一定就是有理数; (6)实数不就是有理数就就是无理数;(7)无限小数不能化为分数;4.用“就是”、“不就是”、“统称”、“包括”、“叫做”填空,并体会这些词得含义: (1)2 分数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1月17日复华七年级数学实数
12.1 实数的概念
一、引入 数的范围至此扩大到了有理数,复习有理数的定义和分类:定义:整数和分数统称为有理数。
分类: 有理数⎪⎪⎪
⎩
⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩
⎪⎨⎧负分数正分数
分数负整数零正整数整数
如果把整数看作分母为1的分数,那么有理数就是用两个整数之比表示的分数:
)0,(≠q q p q
p
都是整数,且 质疑:数的扩充是不是到此为止了呢?有理数是不是够用了?还有没有不是有理数的数呢? 问题2:正方形ABCD 的边长怎样表示?
分析:设正方形ABCD 的边长为x ,那么x 2=2,即x 是这样一个数,它的平方等于2。
这个数表示面积为2的正方形的边长,是现实世界中真实存在的线段长度。
由于这个数和2有关,我们现在用2(读作“根号2”)来表示。
追问:面积为3的正方形,它的边长又如何表示?若面积为5呢? 问题3:2是有理数吗? 因为:有理数=分数
)0,(≠q q p q
p
都是整数,且= 而2肯定不能表示为分数(详见P36),那就不能是有限小数,也不能是无限循环小数,所以2只能是“无限不循环小数”。
问题4:无限不循环小数还有吗?
Π是有理数码? 二、
归纳
1.无理数
(1)无限不循环小数叫做无理数。
(2)无理数包括正无理数和负无理数。
(3)只有符号不同的两个无理数,它们互为相反数。
2.实数
(1)有理数和无理数统称为实数。
(2)实数可以这样分类:
正有理数
有理数 零 ——有限小数或无限循环小数
实数 负有理数
正无理数
无理数 ——无限不循环小数
负无理数
三、
练习
1.将下列各数填入适当的括号内: 0、-3、2、6、3.14159、
7
22、32.0&&&、5、π、0.3737737773…. 有理数:﹛ ﹜;无理数:﹛ ﹜; 正实数:﹛ ﹜;负实数:﹛ ﹜; 非负数:﹛ ﹜;整 数:﹛ ﹜. 提问:常见的无理数的形式有哪几种?(三种形式)
2.请构造几个大小在3和4之间的无理数。
3.是非题
(1) 无限小数都是无理数; 无理数都是无限小数; (2)正实数包括正有理数和正无理数; (3)实数可以分为正实数和负实数两类; (4)带根号的数都是无理数; (5)不含根号的数不一定是有理数; (6)实数不是有理数就是无理数;
(7)无限小数不能化为分数;
4.用“是”、“不是”、“统称”、“包括”、“叫做”填空,并体会这些词的含义: (1)2 分数。
(2) 0 有理数。
(3) 无限不循环小数 无理数。
(4) 实数 有理数和无理数。
(5) 正整数、0和负整数 整数。
(6) 有理数 有限小数和无限循环小数。
一 知识回顾:
1、一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根或二次方根,也就是说,如果x 2=a ,那么, ( ) 叫做( ) 的平方根.
2、正数有 个平方根,它们 。
用a 表示其中正的平方根,读作“根号a ”另一个
负的平方根记为a -
,其中a 叫做 。
3、0有( )个平方根,是( )。
负数没有平方根求一个数的平方根的运算叫做( )。
{
{ {
四、知识链接: 预习导学
1、正数a 的正的平方根a 叫做a 的算术平方根。
0的算术平方根是0.
a ”表示正数a 的平方根,读作“正负根号a ”a ”表示正数a 的算术平方根
例如 9的平方根是:9=±3. 9的算术平方根是3 .11的平方根是:11. 1111 二、填空题
1、______数有两个平方根,它们的和为______;零的平方根是______;_____数没有平方根
2、0.16的平方根是_______
3、
81
25
的算术平方根是_______ 4、81的正的平方根的平方根是_______ 5、81的平方根是_______
6、25-的平方根是________
7、2
57⎪⎭
⎫
⎝⎛-的平方根是_________
8、6-是_______的一个平方根 9、_______的平方是0.04
9、如果2
x =1.96,那么x=________ 10、1664-的平方根是_______
11、一个正方形的面积是5cm 2,这个正方形的边长是________cm 12、如果x =9,那么x=_______13、()2
3π-的算术平方根是______
14、
()56x 2
=-,则x=_________15、正数k 的两个平方根的和是_________,积是________
二、求下列各数的平方根,注意书写规范
1、16
2、0.01
3、121
4、412
5、1169
27
二、求下列各数的正的平方根,注意书写规范
1、4900
2、2.25
3、36 1
4、1691
5、25
142
6、2516±
7、1613- 9、225 10、2
72⎪⎭
⎫
⎝⎛-- 11、
()28-
12、()2
9-± 13、
()2
5 14、()
2
10-
15、()
2
37±
四、简答题
1、4m 2- 与 1m 3-是同一个数的平方根,求这个数。
2、一个数的平方根m 、n 满足2n 3m 4=-,求这个数。
3、当m 为何值时,6m 2-有意义?当m 为何值时,m 266m 2-+
-有意义?。
