人教下第四讲 数阵图共40页
数阵图一.教师版

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图87654321【答案】87654321【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1)c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行. 若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
五年级下册数学奥数有趣的数阵图人教版

例4:把5~10这六个数,分别填入图中三角形三条边的六 个○内,使每边上的三个○内数的和都是24。
假设重叠数是a、b、c 5+6+7+8+9+10+a+b+c=24×3
45+a+b+c=72 a+b+c=27
8+9+10=27
8 76 9 5 10
2 9 561 3 8 45~10这六个数,分别填入图中三角形三条边的六 个○内,使每边上的三个○内数的和都是24。
中间的三个数只加一次, 三个角上的数都加了两次, 有三个数要设字母吗?
例4:把5~10这六个数,分别填入图中三角形三条边的六 个○内,使每边上的三个○内数的和都是24。
1
3
2
1+2+…+7+8+a+b=21×2 6
5
36+a+b=42 a+b=6
4
8
7
1+5=6或2+4=6
将1、3、5、7、9、11、13、15这八个数,分别填入图中的 八个○内,使得每个大圆上五个○内数的和都是39。
1+3+5+……+15=64
3
5
1
39×2-64=14
7
9
中间的两个圆圈数重叠一次, 15 13 11
例5:将1~8这八个数分别填入下图的○中,使两个大圆 上的五个数之和都等于21。
假设重叠数是a、b
2
3
1
1+2+…+7+8+a+b=21×2 6
第4讲 数阵图
第4讲数阵图认识几种常考的数阵图模型,理解并熟练掌握解题方法。
数阵图定义:将一些数字按照一定的要求排列而成的某些图形一、辐射型数阵图:从一个中点出发,向外作若干条射线,在每条射线上安放同样多个数使其和是一个不变的数。
方法一:试算法(大小配)掐头、去尾、取中间方法二:计算法各数之和+重叠数×重叠次数=线和×线数二、封闭的数阵图:计算法各数之和+重叠数×重叠次数=线和×线数三、复合型数阵图即是辐射型数阵图,又是封闭型数阵图。
将1-7这7个数字分别填入图中各个○内,使每条线段上的三个○内的数之和等于14将1-11填入下图的各个圆圈内,使每条线段上的三个圆圈内的数之和相等。
1、将1-5分别填入圆圈内,使每条线上3个圆圈的数字之和都等于92.将1-9分别填入圆圈内,是每条线上的三个数之和相等将1-6六个数字分别填入下图6个圆圈内,使每条边上的和都等于11.把1-12这十二个数,分别填在如右图中正方形四条边上的十二个圆圈内,使每条边上四个圆圈内数的和都等于22,试求出一个基本解。
1.把1-9个数分别填入○中,使每条边上四个数的和相等于17.2.把1-8个数分别填入○中,使每条边上三个数的和相等12.(1)将1-7七个数字填入下图的七个圆圈内,使每个大圆圈和每条直线上的三个数字之和相等。
(2)将1-6这6个数字分别填入下图的6个圆圈内,使得三条线段上的数字之和都相等。
下图中,是有三个正三角形,将1-9分别填入9个圆圈内,使得三个正三角形三个顶点之和都相等,通过四个圆的每条线段之和也相等1.将1-5这五个数分别填入如果中的圆圈内,使每条线段上三个圆圈内的和相等。
2.将1-10这十个数分别填入下图中的十个○内,使每条线段上四个○内数的和相等,3.将1-9这九个数分别填入图中○内,使每条线段三个数相等.。
第四讲和差问题

第四讲和差问题第一部分:课前检测1.3579+1431―268―7322. 2357+7743―4678―52223. 1680+9753―680―7534. 5180+8120―4160―61405. 6480+4680―680―4806. 8642+2468―6642―24547. 3000―198―297―396―4958. 2468+(1014―234)―(766+468)第二部分:和差问题题型一:明确告知1.小华和小明共收集了180张邮票,小华收集的邮票比小明多20张。
问:小华和小明各收集了多少张邮票?2.两筐水果共重176千克,第一框比第二框多12千克。
问:两筐水果各重多少千克?3.今年弟弟7岁,哥哥12岁,当两人年龄和是33岁时。
问:两人各多少岁?题型二:差不明确1.三年级120名学生去春游,从第一辆车调5名第二辆车上去,这时两车的人数就同样多了。
问:原来两辆车各坐了多少名学生?2.两个水桶共盛水98千克,如果把第一桶里的水倒8千克给第二桶,两个水桶的水就一样多。
问:第一桶原来盛水多少千克?3.甲、乙两班共有学生102人,如果从甲班调3人到乙班,两学生同样多。
问:甲、乙两班各有学生多少?题型三:需要转化1.师徒两人合作零件2小时,共生产零件120个,如果分别做5小时,师傅比徒弟多生产50个。
问:师傅和徒弟每小时各做多少个零件?2.甲、乙两个打字员合打2小时,共打800字,如果分别打3小时,甲比乙多打300字。
问:甲、乙两人每小时各打多少字?3.甲、乙两个打字员合打一份稿件,平均每人每小时打17页,6小时可以完成,当两人打完稿件时,乙比甲多打了12页。
问:甲、乙各打了多少页?第三部分:数阵图1. 把1到8八个数分别填入○中,使每条边上三个数的和相等.2. 把1~9个数分别填入○中,使每条边上四个数的和相等.3. 把1~10填入图中,使五条边上三个○内的数的和相等.第四部分:课后作业一、递等式计算(能巧算的要巧算)1.650+350÷7+13142. 9×8÷9×83. 3690―690÷10―19314. 72÷8×63÷95. 56÷7×48÷66. 765+488―1127. 5888+992―688 8. 2014―997 9. 3696―582―428―686二、应用题1.每袋大米25千克,价钱是56元。
小学数学-数阵图讲解学习PPT文档25页

6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不 盲目。 ——马 克思
ቤተ መጻሕፍቲ ባይዱ
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
完整word版,高思导引四年级第四讲数阵图初步教师版
第4讲数阵图初步内容概述各种较为基本的数阵图问题,了解重数的概念,并以此进行分析;学会分析特殊位置上的数值;某些情况下还需要考虑对称性。
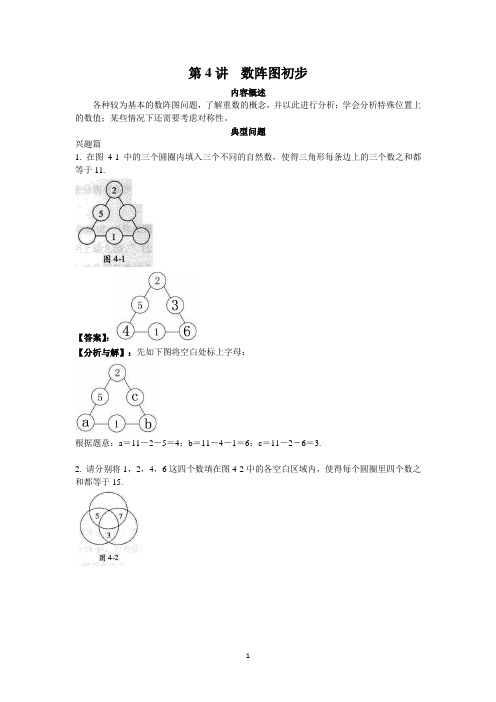
典型问题兴趣篇1. 在图4-1中的三个圆圈内填入三个不同的自然数,使得三角形每条边上的三个数之和都等于11.【答案】:【分析与解】:先如下图将空白处标上字母:根据题意:a=11-2-5=4;b=11-4-1=6;c=11-2-6=3.2. 请分别将1,2,4,6这四个数填在图4-2中的各空白区域内,使得每个圆圈里四个数之和都等于15.【答案】:【分析与解】:如下图,先将空白区域标上字母根据题意:上面圆内四个数之和等于15,可得a+d=15-5-7=3=1+2;同理,b+d=15-5-3=7=1+6;c+d=15-7-3=5=1+4。
由于d属于三个圆的公共部分,经对比发现可得:d=1;a=2;b=6;c=4.3. 如图4-3所示,请在三个空白圆圈内填入三个数,使得每条直线上三个数之和都相等。
【答案】:【分析与解】:如下图:因为8+9+a=b+a+7可得b=10;那么每条线的和=8+3+10=21;那么a=21-8-9=4;c=21-8-7=6.4. 把1至8分别填入图4-4的八个方格内,使得各列上两个数之和都相等,各行四个数之【答案】:1 7 6 48 2 3 5【分析与解】:因为1+2+3+……+8=36;所以每行的和等于36÷2=18;每列的和=36÷4=9;从列入手,可将1~8这八个数分为和等于9的四组:1+8=2+7=3+6=4+5。
再调整使行和等于18:我们发现1+4=2+3;8+5=6+7.经过调整可得答案。
5. 把1至12分别填入图4-5的圆圈内,使图中三个小三角形三条边上的六个数之和相等。
【答案】:【分析与解】:经过观察发现,此图是个具有对称性的图案;若使三个小三角形的三边之和相等;只需要使得图中每条边上的两个数之和相等即可。
因此可将1~12对称性地分为六组如下:1+12=2+11=3+10=4+9=5+8=6+7.6. 在如图4-6所示的3×3方格表内填入1、2、3这三个数字各三次,使得每行每列以及两条对角线上的三个数字之和都相等。
人教下第四讲 数阵图

4
3 2
对于像该题一样较复杂的问题我们 我们可以将复杂条件转化为求重叠的问 题下图的六个○中使得三 角形每条边上的三个数之和都等于9。
(1+2+3+4+5+6)+重叠数之和=9×3 重叠数之和=6 6=1+2+3 2 4 3 6 1 5
【例5】 将1-7这七个数填入下图中,使每条线段上的三个数 之和等于10。 分析:
⑴封闭型数阵图有几个重叠数,重叠次数都是1次。 对于封闭数阵图,有: 已知各数之和+重叠数之和=每边各数之和×边数
我思考,我练习, 闯关没问题!
【例1】 把1、3、5、7、9这五个数分别填右下图中的方格中, 使得横行三数之和与竖列三数之和都等于15。
分析:
中间方格中的数很特殊,横行的三 个数有它,竖列的三个数也有它,我们 把它叫做“重叠数”。 1
Page 5
在情境中学数学, 在数学中感受生活!YE!
1、数阵图:按照一定的规则将一些数填在特定形状的图 形中,我们把这种图形称为数阵图。 2、解数阵图问题的一般步骤: ①求出条件中若干已知数字的和。 ②根据“和相等”,列出关系式,找出重叠数。 ③确定重复用数后,对照“和相等”的条件,用尝试的方 法,求出其他各数。 3、数阵图一般按数字的组合形式分为三类: ①辐射型数阵图 ②封闭型数阵图
对于像该题一样较复杂的问题我们 我们可以将复杂条件转化为求重叠的问 题,再求解。
2、将1、2、3、4、5五个数填入下图,使直线上和 圆上的数字和相等。
(1+2+3+4+5)×2 =一条直线上的数字和×3 一条直线上的数字和=10 2 1
5 4
3
(1+2+3+4+5)+重叠数=10×2
重叠数=5
【例3】 将1-6这六个自然数分别填入下图中,使每个大圆上的 4个数的和都是16。 分析:
人教版四年级数学数阵图(一)例题解析

四年级数学数阵图(一)例题解析我们在三年级已经学习过辐射型和封闭型数阵,其解题的关键在于“重叠数”。
本讲和下一讲,我们学习三阶方阵,就是将九个数按照某种要求排列成三行三列的数阵图,解题的关键仍然是“重叠数”。
我们先从一道典型的例题开始。
例1把1~9这九个数字填写在右图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
分析与解:我们首先要弄清每行、每列以及每条对角线上三个数字之和是几。
我们可以这样去想:因为1~9这九个数字之和是45,正好是三个横行数字之和,所以每一横行的数字之和等于45÷3=15。
也就是说,每一横行、每一竖列以及每条对角线上三个数字之和都等于15。
在1~9这九个数字中,三个不同的数相加等于15的有:9+5+1,9+4+2,8+6+1,8+5+2,8+4+3,7+6+2,7+5+3,6+5+4。
因此每行、每列以及每条对角线上的三个数字可以是其中任一个算式中的三个数字。
例1中的数阵图,我国古代称为“纵横图”、“九宫算”。
一般地,将九个不同的数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图称为三阶幻方。
在例1中如果只要求任一横行及任一竖列的三数之和相等,而不要求两条对角线上的三数之和也相等,则解不唯一,这是因为在例1的解中,任意交换两行或两列的位置,不影响每行或每列的三数之和,故仍然是解。
例2用11,13,15,17,19,21,23,25,27编制成一个三阶幻方。
分析与解:给出的九个数形成一个等差数列,对照例1,1~9也是一个等差数列。
不难发现:中间方格里的数字应填等差数列的第五个数,即应填19;填在四个角上方格中的数是位于偶数项的数,即13,17,21,25,而且对角两数的和相等,即13+25=17+21;余下各数就不难填写了(见右图)。
与幻方相反的问题是反幻方。
将九个数填入3×3(三行三列)的九个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,这样填好后的图称为三阶反幻方。
